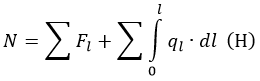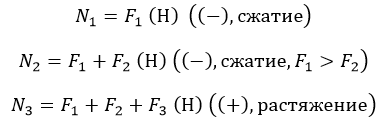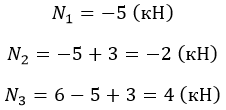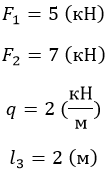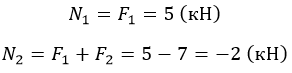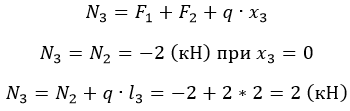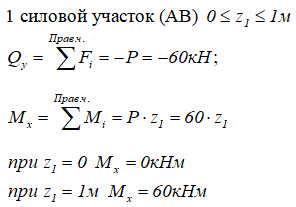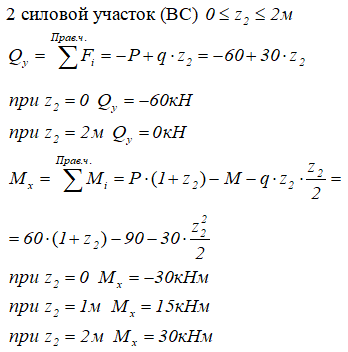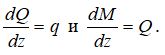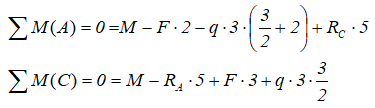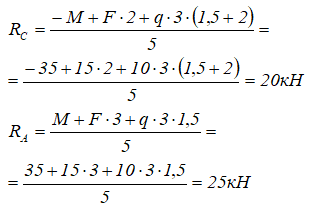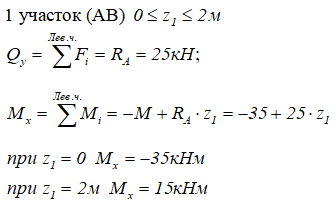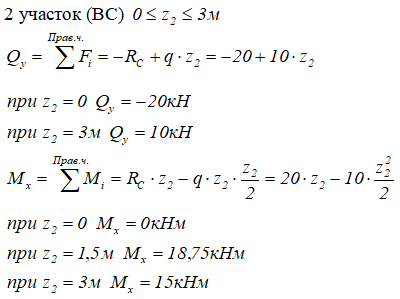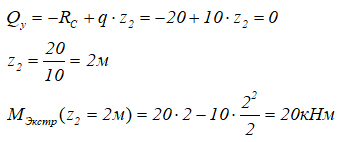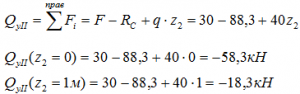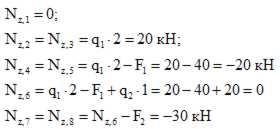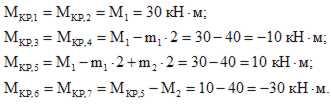Привет! В этом уроке начнём знакомиться с таким видом деформации, как растяжение (сжатие). Обычно, с этой темы и начинают изучать сопротивление материалов — объясняются основные понятия, которые дальше используются на протяжении всего обучения.
Задание, которое будем рассматривать в этой статье, как правило, дается студентам в первую очередь в качестве домашней работы. После изучения материалов этого урока ты научишься строить следующие эпюры: продольных сил, нормальных напряжений, а также осевых перемещений поперечных сечений. Не пугайся мудрёных названий, на самом деле, все эти эпюры строятся очень просто!
Что же давай приступим к изучению!
Построение эпюры продольных сил
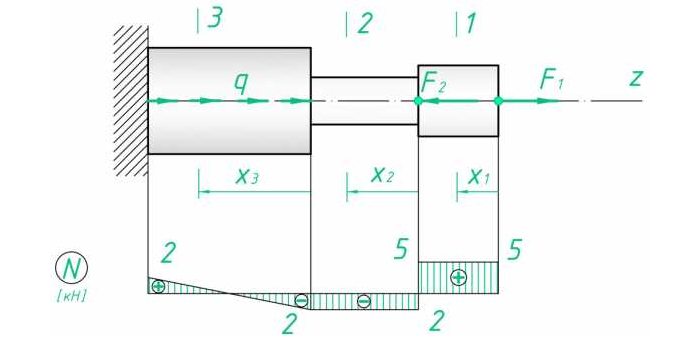
В качестве примера возьмём простенькую расчётную схему стержня (также часто ступенчатый стержень, который работает на растяжение или сжатие, называют брусом). Загрузим наш стержень сосредоточенными силами, вот так:

Теперь наша первостепенная задача – построить эпюру продольных сил. И давай сразу будем разбираться в терминологии.
Что такое эпюра?
Эпюра – это график, который принято строить для визуализации распределения какой-либо величины. В нашем случае, продольной силы.
Построив такой график, мы можем увидеть, где определённая величина достигает максимальных или минимальных значений, что может быть полезно при проведении прочностных расчётов и других. Кроме того, эпюры могут служить вспомогательными инструментами для построения других эпюр, о чём мы будем говорить далее.
Что такое продольная сила?
Продольная сила – это внутренняя сила, которая возникает в сечениях стержня, работающего на растяжение или сжатие под действием внешней нагрузки.
Расчёт эпюры продольных сил
Чтобы построить эпюру продольных сил, нужно разбить брус на несколько участков, где эпюра будет иметь постоянное значение. Конкретно, для этого стержня, границами участков служат те точки, где прикладываются сосредоточенные силы.
То есть для нашего примера, нужно рассмотреть всего 2 участка:

Важно! Эпюра продольных сил, никак не зависит от формы бруса, в отличие от других эпюр, которые будем дальше рассчитывать.
Правило знаков для продольных сил
Правило знаков для продольных сил следующее:
- если внешняя сила (F) растягивает брус, то продольная сила (N) в сечениях будет положительная;
- если внешняя сила (F) сжимает брус, то продольная сила (N) в сечениях будет отрицательная.

Расчёт продольных сил на участках
На первом участке сила F1 растягивает брус на величину 5 кН, поэтому на этом участке, продольная сила будет положительной и равной:
Откладываем это значение на графике — эпюре. Эпюры, принято заштриховывать перпендикулярно к нулевой линии, а также указывать знак продольной силы:

На втором же участке, помимо силы F1, также действует сила F2, которая сжимает брус, поэтому в уравнении ее нужно учесть со знаком «минус»:
Откладываем полученное значение на эпюре:

Расчёт реакции в жёсткой заделке
Прежде всего, следует разобраться с тем, что вообще такое реакция. Всё дело в том, что помимо внутренних усилий, возникающих внутри нагруженного элемента конструкции, в том месте, где закреплён этот элемент, также возникают некоторые силы (сила), которые являются реакцией на внешнюю нагрузку и удерживающие эту конструкцию в состоянии статического равновесия.
Например, стул на котором ты сейчас сидишь и давишь на него своим весом, сопротивляется, чтобы удерживать тебя в состоянии равновесия. Если переводить на язык сопромата, твой вес в этом случае это внешняя сила, а сила с которой стул реагирует на твой вес – это реакция опоры, равная по модулю этой силе, но противоположно направленная.
Так и в нашей конструкции, в жёсткой заделке, также возникает реакция! Осталось только научиться — определять эту силу. Так как она должна компенсировать всю нагрузку, которая приложена к стержню, условие равновесия для нашей схемы можно записать так:
То есть, так как система находится в состоянии равновесия, то сумма всех сил, действующих на конструкцию, будет равна нулю.
Из этого условия равновесия и найдём искомую реакцию. Приложим некоторую силу R в месте, где закреплён наш стержень, при этом направить её можно в любую сторону, хоть влево, хоть вправо, главное, чтобы она была направлена горизонтально, так как у нас вся нагрузка, направлена так, то и реакция в заделке будет возникать исключительно — горизонтальная:

Чтобы составить уравнение равновесия, введём продольную ось – x, относительно неё будем составлять это уравнение, при этом силы, которые будут совпадать с положительным направлением оси x, в уравнении будем учитывать с «плюсом», а противоположно направленные с «минусом»:

Находим из этого уравнения реакцию в заделке:
А теперь, давай обсудим, что можем делать с этим теперь. В нашей конкретной задаче реакция может помочь проверить эпюру продольных сил. Если в первом уроке, считали стержень, строго справа налево, то теперь, зная численное значение реакции, можно рассчитать стержень и слева направо. Или как минимум увидеть, что левый участок эпюры, был построен верно.
Да, можно было вполне обойтись, без расчёта этой реакции конкретно в этом случае. Но, чаще всего, решение задач по сопромату начинается как раз с определения реакций, потому что без этого в большинстве случаев, невозможно определить внутренние усилия, а тем самым произвести какие-либо дальнейшие расчёты. Но с этим мы ещё многократно будем сталкиваться в следующих уроках, особенно в задачах на изгиб.
Построение эпюры нормальных напряжений
В отличие от продольных сил, нормальные напряжения уже зависят от формы бруса, а если точнее, то от площади его поперечных сечений.
Формула для определения нормальных напряжений выглядит так:

Таким образом, чтобы найти нормальное напряжение в любом сечении бруса, нужно: продольную силу в этом сечении разделить на площадь сечения.
Нормальные напряжения, как и продольные силы, изменяются по одному закону в пределах участков. Однако, так как форма бруса сказывается на распределении нормальных напряжений, здесь границами участков также служат места изменения геометрии бруса. Таким образом, для нашей расчетной схемы, нужно рассмотреть три участка и вычислить напряжения, соответственно, 3 раза:

Будем считать, что по условию задачи нам известны все параметры бруса, включая площади поперечных сечений: на первом участке площадь поперечного сечения A1=2 см2, а на втором и третьем A2 = A3 = 4 см2.

Вычисляем напряжения на каждом участке:

По полученным значениям строим эпюру нормальных напряжений:

По полученной эпюре нормальных напряжений, можно определить те поперечные сечения, в которых напряжения будут максимальными (все сечения на участке 1), что полезно при проведении прочностного расчёта.
Построение эпюры осевых перемещений поперечных сечений
Под действием внешней нагрузки поперечные сечения бруса перемещаются вдоль продольной оси. Под нагрузкой брус может как удлиниться, так и укоротиться. И в этом разделе будем учиться определять эти перемещения.
Для начала подготовимся к расчету и расставим точки в характерных сечениях. Чтобы потом к ним привязываться по ходу решения:

Если для первых двух эпюр, расчет начинался справа налево, от свободного конца. То здесь нам нужно начать считать с закрепленного конца, с жесткой заделки и так как сечение A, закреплено жестко, то никакие перемещения этого сечения невозможны, поэтому сразу можем записать:
Эпюра перемещений так же, как и остальные эпюры, меняется по одному закону, в пределах участков. Поэтому, чтобы построить эпюру, достаточно определить эти перемещения в характерных точках.
Перемещение точки B будет складываться из перемещения предыдущего расчетного сечения:
А также удлинения (или укорочения) участка между расчетными сечениями:
В свою очередь, удлинение (или укорочение) любого участка, можно определить по следующей формуле:

Поэтому формулу, для нахождения перемещения сечения B, можно записать и в другом виде:

Подставив все численные значения, найдем искомое перемещение:

Откладываем полученное значение на эпюре:

Также важно отметить, что при вычислении удлинения или укорочения участка (Δl), фактически площадь эпюры продольных сил (ω) делится на жесткость при растяжении или сжатии (EA).


Это свойство нам еще пригодится, когда будем рассматривать более сложную задачу.
Для точек C и D перемещения находятся аналогичным способом, так же как и для точки B, поэтому подробно комментировать не буду, приведу решение.
Точка C

Точка D

Откладываем полученные значения на эпюре:

По полученной эпюре, можно увидеть — в какую сторону и насколько переместится любое поперечное сечение стержня. Наиболее интересной характеристикой здесь является перемещение сечения D, то есть перемещение свободного конца бруса или фактическое удлинение. Как видим, сечение D переместится вправо на величину WD (т. к. значение WD — положительное). То есть, под действием всей нагрузки брус удлинится на 0.575 мм.
Учёт распределённой нагрузки
А теперь предлагаю рассмотреть немного измененную задачу. Приложим к нашему брусу дополнительно распределенную нагрузку q с интенсивностью равной 2 кН/м. После чего рассчитаем и построим все те же эпюры: продольных сил, нормальных напряжений и перемещений.

Чтобы учесть распределенную нагрузку, необходимо интенсивность нагрузки (q) умножить на длину участка, на котором действует нагрузка. В чистом виде, только от распределенной нагрузки, эпюра продольных сил будет треугольная.

Расчет продольных сил
На первом участке, сила по-прежнему растягивает стержень, записываем ее в уравнение с «плюсом», а распределенная нагрузка сжимает, соответственно, ее учитываем с «минусом»:
Найдем значения продольной силы на границах первого участка:

Откладываем рассчитанные значения:

На втором участке, распределенная нагрузка будет действовать точно так же, как и сосредоточенная сила:
Рассчитываем продольную силу на третьем участке:
Строим окончательную эпюру продольных сил:

Расчет нормальных напряжений
Нормальные напряжения рассчитываются точно так же, как и для первой задачи, единственное отличие только в том, что на первом участке необходимо рассчитать напряжения два раза — на границах участка:

По полученным значениям строим эпюру нормальных напряжений:

Расчет перемещений
Для точек A, B и С перемещения рассчитываются аналогично, как в первой задаче:


Строим эпюру перемещений на втором и третьем участке:

Чтобы рассчитать удлинение на первом участке, нужно вычислить площадь эпюры продольных сил на этом участке и разделить на жесткость (EA):


Так как на этом участке, эпюра состоит из двух одинаковых прямоугольных треугольников, но по разные стороны от нулевой линии, с учетом знаков, ожидаемо, получим, что перемещение точки D, будет равно перемещению точки C.



Однако, необходимо учесть еще одну особенность. На участках, где действуют распределенные нагрузки, эпюры перемещений изменяются не по линейному закону, а по квадратичному.
То есть на участке с распределенной нагрузкой, эпюра перемещений всегда будет иметь либо выпуклость, либо вогнутость:

Чтобы понять, как же будет выглядеть эпюра перемещений, на участке с распределённой нагрузкой, нужно проанализировать эпюру продольных сил.
Как видим, начиная от точки C и до пересечения нулевой линии, эпюра продольных сил – отрицательна, а это значит, что эпюра перемещений, на этом отрезке, также должна убывать, как показано зелёной пунктирной линией. Поэтому изображаем эпюру перемещений следующим образом:

Но чтобы окончательно убедиться в верности наших рассуждений, можно также определить экстремум на эпюре перемещений (там, где эпюра достигает своего максимального значения). Или в той точке, где эпюра продольных сил пересекает нулевую линию:


Отмечаем найденное значение на эпюре перемещений:

Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.
Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
где:
-
Fl – действующие на участке l силы (Н);
-
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
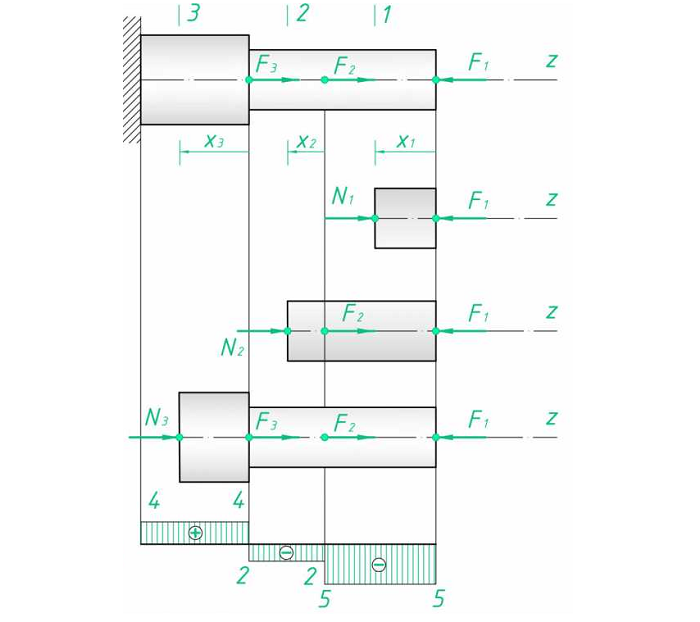
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
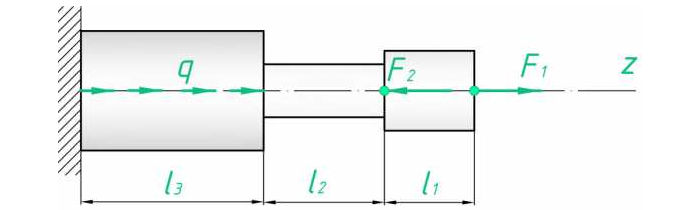
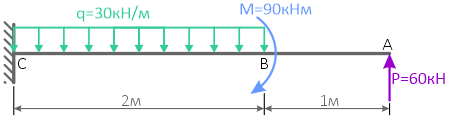
Построить эпюру сил для следующего случая (рис. 2):
Рис. 2
Дано:
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
По полученным данным строим эпюру (рис. 3).
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Примеры построения эпюр для решения задач сопротивления материалов, строительной и технической механики со всеми расчетами, подробными пояснениями и видеоуроками.
Примечание: студентам строительных специальностей эпюры изгибающих моментов надо строить на растянутых слоях балки, поэтому положительные значения Mx необходимо откладывать вниз, а отрицательные — вверх от базовой линии.
Сохранить или поделиться с друзьями
Рассмотрим пару упрощенных и несколько максимально подробных примеров построения эпюр внутренних силовых факторов, напряжений и перемещений для всех способов закрепления и нагружения балок, стержней и валов.
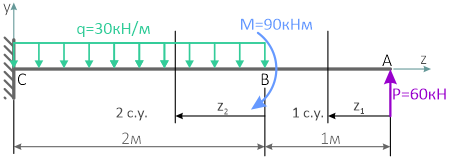
Построение эпюр Qy и Mx для консольной балки
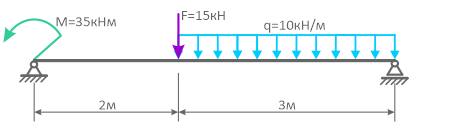
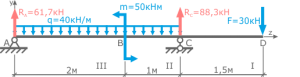
Для заданной консольной балки требуется построить эпюры внутренних силовых факторов Qy и Mx.
Решение
Вычерчиваем расчетную схему нагружения балки в масштабе, с указанием числовых значений приложенных нагрузок.
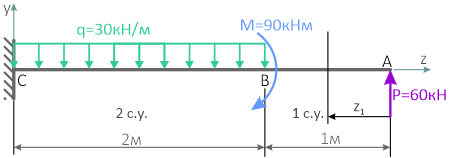
Показываем оси системы координат y-z и обозначаем характерные сечения балки.
Для построения эпюр внутренних силовых факторов консольных балок, опорные реакции можно не определять.
Тогда для расчета значений Qy и Mx необходимо рассматривать противоположную от заделки часть балки, где все внешние усилия известны.
Балка имеет 2 силовых участка.
Рассчитаем, с учетом правил знаков при изгибе, значения внутренних поперечных сил и изгибающих моментов в сечениях балки на каждом силовом участке методом сечений.
На первом участке оба силовых фактора рассчитаны.
Переходим ко второму
Так как эпюра Qy на втором силовом участке не пересекает базовую линию, экстремума на эпюре Mx не будет.
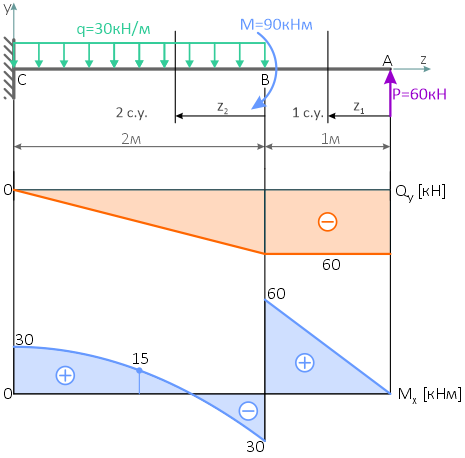
По полученным данным строим эпюры внутренних поперечных сил Qy и изгибающих моментов Mx.
При ручном оформлении решения, эпюры заштриховываются тонкими линиями перпендикулярно базовой (нулевой) линии.
Оформление в электронном виде допускает сплошную однородную заливку площади эпюры.
Проверка построенных эпюр:
- по дифференциальным зависимостям
- в сечениях балки, где приложены сосредоточенные силы, на эпюре Qy имеются скачки значений на величину соответствующей силы;
- в сечениях балки, где приложены изгибающие моменты, на эпюре Mx скачки значений на величину соответствующего момента.
Все условия выполнены, следовательно, эпюры построены верно.
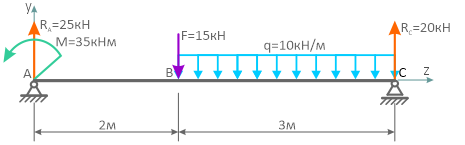
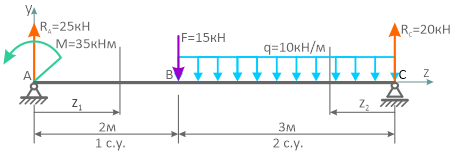
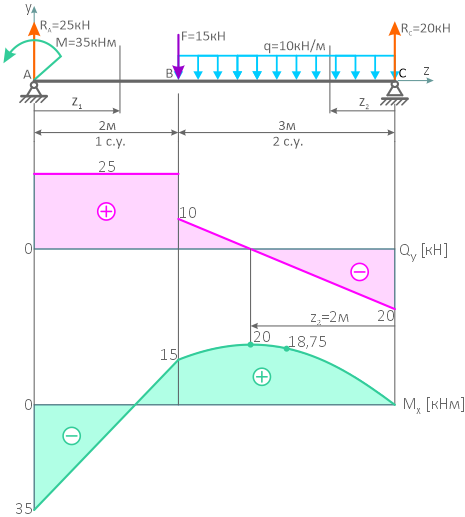
Как строить эпюры для балки на двух опорах
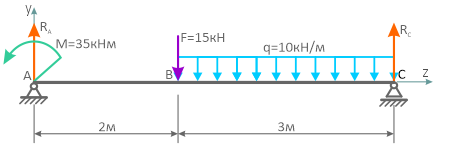
Для заданной расчетной схемы балки на двух шарнирных опорах требуется определить значения и построить эпюры внутренних поперечных сил и изгибающих моментов.
Решение
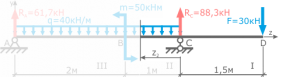
При построении эпюр для участков балки расположенных между опорами необходимо знать величину хотя бы одной из реакций.
Определение реакций в шарнирных опорах балки
Направим реакции опор, например, вверх
и запишем, с учетом правила знаков, суммы моментов нагрузок приложенных к балке относительно точек на опорах
Из составленных уравнений выражаем и находим реакции
Положительные значения указывают на то, что произвольно заданное направление реакций оказалось верным.
Расчет и построение эпюр
Используя метод сечений и соответствующие правила знаков, рассчитаем по каждому участку значения для построения эпюр.
Балка имеет 2 силовых участка.
На первом участке расчет произведем, рассматривая левую отсеченную часть балки
На втором — правую
Значения поперечной силы Qy на границах участка имеют разные знаки, следовательно, на этом участке, на эпюре Mx будет экстремум.
Определим его:
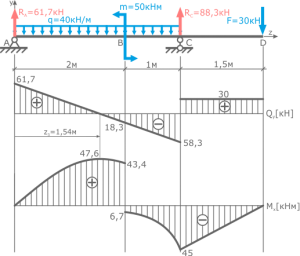
По полученным данным строим эпюры внутренних поперечных сил и изгибающих моментов.
Алгоритм проверки эпюр показан в решении предыдущей задачи.
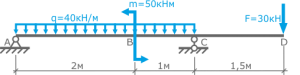
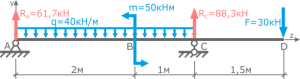
Более подробно ход расчетов и построения эпюр для балки с тремя силовыми участками рассмотрен в следующих задачах.
Подробные примеры построения эпюр
При растяжении-сжатии
Примеры построения эпюр внутренних продольных сил, нормальных напряжений и линейных перемещений для стержней при их растяжении и сжатии.
- эпюра внутренних продольных сил
- эпюра нормальных напряжений в стержне
- построение эпюр внутренних сил, напряжений и перемещений для стального бруса
- построение эпюры внутренних продольных сил для стержня с продольно распределенной нагрузкой
- расчет напряжений с построением эпюры в стержне заданной формы
- построение эпюры перемещений сечений стержня
При кручении
Примеры построения эпюр внутренних крутящих моментов и угловых перемещений сечений вала при кручении.
- Построение эпюры крутящих моментов для вала
- Построение эпюр крутящих моментов и углов закручивания сечений вала
Построение эпюр при изгибе
Примеры построения эпюр внутренних поперечных сил и изгибающих моментов, нормальных и касательных напряжений для балок и рам при изгибе.
Эпюры внутренних силовых факторов
- Построение эпюр поперечных сил Qy и изгибающих моментов Mx для балки (3 участка)
- Эпюра внутренних поперечных сил
- Эпюра внутренних изгибающих моментов балки
- Построение эпюр для рамы
- Проверка эпюр внутренних силовых факторов в рамах
Эпюры напряжений
- эпюра нормальных напряжений двутавра
- эпюра касательных напряжений для двутавра
- эпюра нормальных напряжений прямоугольного сечения
Видеоурок расчетов для построения эпюр внутренних силовых факторов для балки:
Другие видео
Другие примеры решения задач >
Порядок построения эпюр
В рассмотренных выше примерах для построения эпюр выполняется следующая последовательность действий:
- Вычерчивается (в масштабе) расчетная схема элемента с указанием всех размеров и приложенных внешних нагрузок;
Расчетная схема балки - Обозначаются характерные сечения бруса;
- Определяются опорные реакции;
Опорные реакции балки - Рассматриваемый элемент разбивается на силовые участки;
Обозначение силовых участков - Для каждого силового участка выбирается рассматриваемая часть бруса (балки)
Выбранная часть балки и записываются выражения для рассчитываемых внутренних силовых факторов, напряжений или перемещений;Выражения для расчета поперечной силы в сечении балки - Рассчитываются значения на границах участков. В случаях, когда переменная в выражении имеет вторую или более степень можно дополнительно определить значение в середине участка;
- В некоторых случаях необходимо определять экстремумы эпюр;
- После расчета всех значений выполняется построение эпюр.
Эпюры поперечных сил и изгибающих моментов для балки
После построения эпюр желательно выполнять их проверку.
Продольная
сила в сечении численно равна алгебраической
сумме проекций всех сил, приложенных
по одну сторону от рассматриваемого
сечения, на продольную ось стержня.
Правило
знаков для
Nz: условимся считать продольную силу в
сечении положительной, если внешняя
нагрузка, приложенная к рассматриваемой
отсеченной части стержня, вызывает
растяжение и отрицательной – в противном
случае.
Пример
1. Построить
эпюру продольных сил для жестко
защемленной балки (рис.2).
Порядок
расчета:
1.
Намечаем характерные сечения, нумеруя
их от свободного конца стержня к
заделке.
2. Определяем продольную силу
Nz в каждом характерном сечении. При
этом рассматриваем всегда ту отсеченную
часть, в которую не попадает жесткая
заделка.
По
найденным значениям строим эпюру Nz.
Положительные значения откладываются
(в выбранном масштабе) над осью эпюры,
отрицательные – под осью.
рис.
2
3. Построение эпюр крутящих моментов Мкр.
Крутящий
момент в
сечении численно равен алгебраической
сумме внешних моментов, приложенных по
одну сторону от рассматриваемого
сечения, относительно продольной оси
Z.
Правило
знаков для Мкр:
условимся считать крутящий момент в
сечении положительным, если при взгляде
на сечение со стороны рассматриваемой
отсеченной части внешний момент виден
направленным против движения часовой
стрелки и отрицательным – в противном
случае.
Пример
2. Построить
эпюру крутящих моментов для жестко
защемленного стержня (рис.3,а).
Порядок
расчета.
Следует
отметить, что алгоритм и принципы
построения эпюры крутящих моментов
полностью совпадают с алгоритмом и
принципами построения эпюры продольных
сил.
1.Намечаем характерные
сечения.
2.Определяем крутящий момент
в каждом характерном сечении.
По
найденным значениям строим эпюру Мкр
(рис.3,б).
17…..
Метод расчета, при котором расчет
рам на один вид нагрузки производится
методом сил, а на другой — методом
перемещений, называется комбинированным.
Этот метод применяется главным образом
для расчета симметричных многоэтажных
статически неопределимых рам, хотя в
отдельных случаях он может быть применим
и для несимметричных рам.
При
расчете рам комбинированным методом
приложенная к раме произвольная нагрузка
разлагается на симметричную и обратно
симметричную. Расчет на эти виды нагрузки
производится раздельно: на симметричную
нагрузку — методом перемещений, а на
обратно симметричную — методом сил.
Трудоемкость
расчета данной рамы методом сил или
методом перемещений приблизительно
одинаковая, так как степени статической
и кинематической неопределимости рамы
равны и в обоих случаях для решения
требуется составить и решить систему
из девяти канонических уравнений с
девятью неизвестными.
Расчета симметричных рам
Вырезав
узел С в различных состояниях системы
из уравнений равновесия 2Z = О, 2ЛХ = 0 и
ЕМу = 0 определим коэффициенты и Rip; далее
при составлении системы канонических
уравнений следует учесть, что согласно
выражению.
Особенности расчета крыши
деревянных домов,
симметричных рам. Основная система
любой симметричной системы должна быть
симметричной. При этом так же, как и в
методе сил, нагрузку следует разложить
на симметричную и кососимметричную
составляющие, а неизвестные —
сгруппировать. Особенно удобен метод
перемещений при расчете симметричных
систем на действие симметричной нагрузки.
В этом случае в силу симметрии будут
заведомо равны нулю основные неизвестные,
определяющие линейные перемещения
частей рамы (ригелей), расположенных
поперек оси симметрии, а также углы
поворота узлов рамы, лежащих на ее оси
симметрии. Естественно, будут также
равны нулю все кососимметричные
неизвестные.
Изображенная на рис.
1.48, а рама 7 раз кинематически неопределима.
Здесь пу = 5 и пп = 2 (см. рис. 1.48, б). Однако
в силу сказанного выше Z3 = Z4 = Z5 = Z6 =**Z7 = 0
(рис. 1.48, в) и, таким образом, при расчете
рамы надо решать только два уравнения
с двумя неизвестными. На рис. 1.48, г – е
построены единичные и грузовая эпюры
моментов. Следует отметить особенность
характера эпюры моментов на верхнем
ригеле в первом единичном состоянии —
она имеет прямоугольное очертание, так
как построена от одновременного
воздействия
парных углов поворота
18…
Метод перемещений является
вторым основным методом расчета
статически неопределимых систем.
Использование его для расчета сложных
статически неопределимых рам во многих
случаях значительно снижает трудоемкость
расчета по сравнению с методом сил.
Рассмотрим
основные положения метода перемещений.
По существу этот метод является обратным
относительно метода сил.
В
методе сил за основные неизвестные
величины принимают внешние или внутренние
силы, приложенные вместо отброшенных
лишних связей, тогда как взаимные
перемещения сечений, где приложены эти
силы, известны. Для определения неизвестных
составляются уравнения перемещений. В
методе перемещений основными неизвестными
являются перемещения (линейные и угловые)
узлов статически неопределимой системы,
для определения которых составляют
уравнения- равновесия. Определив эти
перемещения, находят внутренние силовые
факторы в произвольных сечениях заданной
системы.
Общее
число неизвестных при расчете статически
неопределимых систем определяется не
статической, а кинематической
неопределимостью. При этом род степенью
кинематической неопределимости
понимается число угловых и линейных
перемещений системы, знание которых
дает возможность определить характер
деформации системы, а следовательно, и
усилия в ее элементах. Деформированный
вид системы будет полностью определен,
если будут известны угловые и линейные
перемещения узлов системы. Степень
кинематической неопределимости системы
будет равна числу углов поворота жестких
узлов плюс число неизвестных линейных
перемещений узлов. Для многих статически
неопределимых систем степень кинематической
неопределимости ниже их степени
статической неопределимости.
В
основу метода перемещений положен ряд
допущений: не учитывается влияние
поперечных и продольных сил на перемещения
точек системы; не учитывается сближение
узлов системы при деформации ее элементов;
концы стержней, сходящихся в одном
жестком узле, поворачиваются при
деформации на один и тот же угол; углы
поворота вследствие их небольшой
величины принимаются равными тангенсам
этих углов.
При
определении степени кинематической
неопределимости число неизвестных
углов поворота узлов всегда равно числу
жестких узлов системы, исключая опорные.
19…
«Расчет статически неопределимых рам
методом перемещений» 1.Определяем
число неизвестных метода перемещений.
n=1+1=2 V=2*6-5-6=2.Выбираем
основную систему метода
перемещений. 3.Записываем
канонические уравнения метода
перемещений. 4.Строим
эпюры изгибающих моментов в основной
системе от и от нагрузки. 5.Определяем
реакции во вновь введённых
связях. 6.Подставляем
найденные значения реакций в уравнения.
7.Определяем
концевые моменты и поперечные силы в
стержнях заданной системы. 8.Строим
эпюры изгибающих моментов и поперечных
сил в заданной системе от нагрузки. 9.Определяем
продольные силы в стержнях рамы, используя
способ вырезания узлов. 10.Строим
эпюру продольных сил в заданной системе
от нагрузки. 11.Выполняем
статическую проверку.
Расчет
статически неопределимых рам методом
перемещений
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #