Мастер
– класс «Создание и решение эвристических ситуационных задач на уроках»
Как я уже говорила, одним из главных
критериев современного урока является создание на нем образовательной ситуации,
интеллектуальной напряженности. Хорошим и проверенным мною способом является
конструирование ситуационных эвристических задач. Такие задачи составляю я сама
для учеников, ученики могут составлять их друг для друга или группа для
группы. В общем виде, ситуационную задачу можно определить как один из видов
учебных материалов, в котором пред учеником ставится познавательная проблема и
предлагается ее решить различными способами. «Ситуационная задача представляет
собой описание конкретной ситуации, более или менее типичной для определенного
вида деятельности. Это описание включает изложение условий деятельности и
желаемого результата. Решение задачи заключается в определении способа
деятельности» (О.Е. Лебедев).
Модель ситуационной задачи может быть
представлена следующим образом:
название задания;
личностно-значимый познавательный вопрос; информация по данному вопросу,
представленная в разнообразном виде; задания на работу с данной информацией.
Конструировать и использовать эвристические
ситуационные задачи в обучении можно в любой возрастной категории ,учитывая
возрастные особенности учащихся, и при изучении различных предметов.
Условиями конструирования и эффективного
использования эвристических образовательных ситуаций будут:
знание учителем детского коллектива, его психологического климата, т.к.
данная ситуация предполагает работу с конкретным ребёнком, на конкретную
личность;
умение учителя настраивать ребят на эмоциональное восприятие предлагаемого
образовательного материала;
готовность учителя к использованию данных ситуаций (т.к. результат,
продукт, до конца неизвестен);
способность учителя самому научиться научить детей создавать своё,
образовывая себя на основе своего внутреннего предназначения и избегая
соблазнов повторять пути, пройденные другими.
Для разработки заданий в ситуативных задачах мне
помогает конструктор задач, разработанный Л.С. Илюшиным. Данный конструктор
представляет собой набор ключевых фраз, своеобразных клише заданий, которые
могут быть предложены учащимся на разных этапах освоения определенной
информации: ознакомления, понимания, применения, анализа, синтеза, оценки. Мы
с вами сейчас попробуем составлять такие задачи , и вы увидите, насколько они
универсальны, они могут применяться в каждом предмете школьного курса, но
особенно результативно я их использую на литературе
|
|
|
|
|
|
|
|
|
|
|
|
|
обоснуйте… |
|
|
|
|
|
|
|
|
список понятий, касающихся… |
ваш взгляд, существуют между… |
|
|
необычный способ, позволяющий… |
для… |
|
порядке… |
|
|
|
|
|
|
текста… |
положение о том, что… |
|
то, что… |
классификацию… |
суждения о… |
|
|
|
|
|
вероятный) сценарий развития… |
для… |
|
|
|
|
|
|
|
Пример
конструирования задачи по работе с текстом
Вместе с фокус – группой составляем задачу по
эпизоду из сказки «Буратино», сюжет которой известен каждому.
Задания
(произвольный выбор ячеек «Конструктора задач» –
7 – 14 – 15 – 23 – 34 – 39)
Предлагаю свой вариант задачи по этой
сказке.
Выясняю, учителя каких дисциплин составили
фокус – группу.
Далее раздаю листы с текстом и
конструктором участникам фокус – группы и прошу создать ситуационную задачу по
своему предмету. Такие же заготовки раздаются в зале и в жюри. Готовые задачи
зачитываются фокус – группой и желающими из зала.
ВЫВОДЫ: Эвристическая задача может применяться в любом
общеобразовательном предмете, она эффективна как модель проведения урока
усвоения новых знаний, и не менее хороша для оценивания знаний.
Эффективность конструирования и использования
эвристических образовательных ситуаций на уроке неоспорима:
они содействуют не только накоплению знаний по предмету для учащихся и
повышению качества обучения, но и развитию их творческого потенциала и
познавательной активности;
основанное на совместной деятельности учителя и ученика, решение
эвристических задач способствует формированию у ребёнка заинтересованности
в собственном приращении знаний к его уже имеющемуся опыту;
систематическая работа в эвристических ситуациях позволяет каждому
учащемуся адаптироваться в учебной обстановке и создать условия для реализации
своих способностей. Даже слабые учащиеся в состоянии решить ситуационную
задачу и тем самым оказаться в ситуации успеха.
Эвристические ситуации создают основу для
исследовательской работы учащегося, предполагающей поиск различных,
неоднозначных, решений. Такая деятельность, безусловно, учит ребёнка умению
существовать в обществе.
К тому же, работая в эвристических ситуациях,
ученик учится слушать мнение другого человека, вести конструктивный диалог,
полилог, что, безусловно, формирует принцип толерантного отношения учащегося
как гражданина.
Как составить
эвристическое задание
Жукова Наталья
Николаевна, учитель математики и информатики высшей квалификационной категории,
МАОУ «Култаевская средняя школа»
Последовательность этапов
может быть иной, но само их наличие создаёт условие для конструирования
качественного эвристического задания.
1. Из образовательных
стандартов по учебному курсу отбираются такие образовательные объекты,
которые становятся основой эвристического задания. Это могут быть фундаментальные
понятия (точка, число, таблица, молекула, знак, время и др.), частнопредметные
понятия (модальные глаголы, тетраэдр, историческое событие, революция, сила
тяжести или сила легкости и др.), конкретные реальные объекты (береза,
карандаш, гвоздь, словарь, полиэтиленовый пакет, зеркало и др.), правила или
закономерности (сложение дробей, закон притяжения, закон единства
противоположностей и др.). Образовательные объекты, выбираемые для составления
задания, отыскиваются в программах, учебниках, задачниках или других пособиях.
Важно, чтобы это были действительно базовые объекты курса, а не просто
дополнительные или развлекательные.
2. Выделяются основные виды
деятельности учащихся в учебном курсе, по которому проводится урок, конкурс
или олимпиада. Например, в английском языке такими видами деятельности являются
чтение, письмо, говорение, аудирование. Каждый вид деятельности включает в себя
отдельные действия-элементы, которые могут стать основой задания. Выбираются те
из них, которые имеют наибольшее отношение к обозначенным образовательным
объектам.
3. Фиксируется форма
возможного образовательного продукта, который будет создан учениками при
выполнении эвристического задания. Например, от учеников требуется выдвинуть
гипотезу, предложить свой способ, найти закономерность, составить таблицу,
предложить алгоритм, разработать программу, определить понятие, разработать
игру, нарисовать образ. Разумеется, ученик будет создавать свой продукт по
отношению к одному из образовательных объектов, которые определены в п.1, и с
использованием одного из тех видов деятельности, которые обозначены в п.2.
4. Определяются эвристические
методы, с помощью которых предлагается выполнение учеником задания. Иногда
эти методы прописываются в задании явным образом («Для решения этой задачи
примените метод гиперболизации»), но могут формулироваться и в неявном виде.
Эвристическое задание может предложить ученикам найти наибольшее количество тех
или иных методов решения задания («Предложите как можно больше способов
сложения однозначных чисел с переходом через десяток», «Придумайте несколько
способов определения скорости полета воробья»).
5. Эвристическое задание записывается
в общем структурном виде. В формулировке явно указываются объект задания
(явление тяготения, инфляция и др.), предполагаемые виды деятельности ученика
(исследование брошенного листа бумаги или рост курса доллара), ожидаемый
продукт (закономерность падения листа бумаги или курса доллара) и его форма
(предложите формулу взаимозависимости введенных вами величин или экономических
факторов).
6. текст задания формулируется
и шлифуется с учетом его занимательности, увлекательности,
«зажигательности», доступности для учащихся. Способов формулирования
эвристических заданий может быть сколь угодно много, например, «найти причину
происхождения, разреши противоречие», «почему так, а не иначе», «если бы»,
«пусть невозможное станет возможным», «какова закономерность», «составь
модель», «исследуй реальность» и и.п. Сухую формулировку содержательного
задания можно предварительно оживить сказочным, фантастическим или бытовым
сюжетом («На Землю прилетел инопланетянин», «Колобок встретился с пиццей» и
т.д.). Важно, чтобы занимательность или простота задания предполагали
возможность проявления способностей ученика с любым уровнем подготовки.
7. Определяется название
задания или олимпиадной номинации. Здесь два пути: а) название номинации
определяется первоначально, и само задание потом подстраивается под него; б)
сначала составляется задание, затем для него отыскивается наиболее подходящее
название номинации. В названии номинации может быть отражен как объект, так и
вид деятельности. При составлении заданий полезен прием, когда одна номинация
получает несколько форм выражения задания для разных возрастных категорий
детей.
Формы выражения могут
отличаться:
а) разными видами
деятельности (например, младшим ученикам предлагается составить загадку про
выдранный объект, более страшим – разработать кроссворд или дидактическую игру,
выпускникам – провести исследование по данной теме);
б) разным уровнем или
объемом создаваемого учениками продукта (младшие рисуют образ числа 3, старшие
– его символ, выпускники проводят комплексное исследование – арифметическое,
геометрическое, лингвистическое).
При разработке задания продумываются
критерии оценки его выполнения, т.е. определяется, какие параметры
созданного учеником продукта будут оцениваться. Например, если задание
предполагает отыскание закономерности, то критериями оценки могут стать
количество выявленных учеником взаимосвязанных элементов, оригинальность
обнаруженных связей между ними, отражение этих связей в формуле или описании.
Кроме того, всегда есть универсальные критерии оценки творческой работы:
мировоззренческая глубина, самобытность, многовариантность подходов,
соответствие условию задания, оригинальность формы представления результата и
т.п.
Чтобы организовать
творческую деятельность учеников, одной формулировки открытого задания может
быть недостаточно. При отсутствии навыков самоорганизации продуктивной
деятельности у школьников могут возникнуть затруднения в получении
качественного образовательного продукта. В этом случае помогают алгоритмические
описания, задающие учащимся этапы или направления их деятельности (но не ее
содержание!).
Приведем пример
алгоритмического предписания для учеников по исследованию образовательного
объекта – феномена. Под феноменом здесь понимается необычное явление в природе,
культуре, науке, в любой образовательной области.
1.
Обозначьте
обнаруженный вами феномен понятием, рисунком или символом.
2.
Опишите свои
чувства и мысли, возникшие при наблюдении феномена.
3.
Выразите
необычность феномена, его суть, которая отличает его от других похожих явлений.
4.
Сформулируйте
возникший у вас вопрос или проблему.
5.
Составьте план
своего дальнейшего исследования феномена.
6.
Предложите
версию, гипотезу, объясняющую феномен.
7.
Сделайте вывод из
исследования. Проведите рефлексию деятельности и выполните ее самооценку.
Основные технологические
рекомендации – важнейшее средство организации творческой работы учащихся,
ориентировочная основа их деятельности. Алгоритмизация действий в данном случае
не мешает, а способствует индивидуальной самореализации учеников. Репродуктивно
передаваемые ученикам способы действий позволяют им творить на технологической
основе с гарантированным результатом.
Одним из важных умений
учителя творческой ориентации является умение переводить традиционные закрытые
задания в открытые. Если учитель освоил такую процедуру, то его ученики будут в
состоянии творчества всегда – на уроках, во время контрольных работ или
зачетов, при выполнении домашней работы, на протяжении всей образовательной
деятельности.
(А.В.Хуторской
«Дидактика», гл. 7, § 2)
Как составить эвристическое задание
Последовательность этапов может быть иной, но само их наличие создаёт условие для конструирования качественного эвристического задания.
1. Из образовательных стандартов по учебному курсу отбираются такие образовательные объекты, которые становятся основой эвристического задания. Это могут быть фундаментальные понятия (точка, число, таблица, молекула, знак, время и др.), частнопредметные понятия (модальные глаголы, тетраэдр, историческое событие, революция, сила тяжести или сила легкости и др.), конкретные реальные объекты (береза, карандаш, гвоздь, словарь, полиэтиленовый пакет, зеркало и др.), правила или закономерности (сложение дробей, закон притяжения, закон единства противоположностей и др.). Образовательные объекты, выбираемые для составления задания, отыскиваются в программах, учебниках, задачниках или других пособиях. Важно, чтобы это были действительно базовые объекты курса, а не просто дополнительные или развлекательные.
2. Выделяются основные виды деятельности учащихся в учебном курсе, по которому проводится урок, конкурс или олимпиада. Например, в английском языке такими видами деятельности являются чтение, письмо, говорение, аудирование. Каждый вид деятельности включает в себя отдельные действия-элементы, которые могут стать основой задания. Выбираются те из них, которые имеют наибольшее отношение к обозначенным образовательным объектам.
3. Фиксируется форма возможного образовательного продукта, который будет создан учениками при выполнении эвристического задания. Например, от учеников требуется выдвинуть гипотезу, предложить свой способ, найти закономерность, составить таблицу, предложить алгоритм, разработать программу, определить понятие, разработать игру, нарисовать образ. Разумеется, ученик будет создавать свой продукт по отношению к одному из образовательных объектов, которые определены в п.1, и с использованием одного из тех видов деятельности, которые обозначены в п.2.
4. Определяются эвристические методы, с помощью которых предлагается выполнение учеником задания. Иногда эти методы прописываются в задании явным образом («Для решения этой задачи примените метод гиперболизации»), но могут формулироваться и в неявном виде. Эвристическое задание может предложить ученикам найти наибольшее количество тех или иных методов решения задания («Предложите как можно больше способов сложения однозначных чисел с переходом через десяток», «Придумайте несколько способов определения скорости полета воробья»).
5. Эвристическое задание записывается в общем структурном виде. В формулировке явно указываются объект задания (явление тяготения, инфляция и др.), предполагаемые виды деятельности ученика (исследование брошенного листа бумаги или рост курса доллара), ожидаемый продукт (закономерность падения листа бумаги или курса доллара) и его форма (предложите формулу взаимозависимости введенных вами величин или экономических факторов).
6.Текст задания формулируется и шлифуется с учетом его занимательности, увлекательности, «зажигательности», доступности для учащихся. Способов формулирования эвристических заданий может быть сколь угодно много, например, «найти причину происхождения, разреши противоречие», «почему так, а не иначе», «если бы», «пусть невозможное станет возможным», «какова закономерность», «составь модель», «исследуй реальность» и и.п. Сухую формулировку содержательного задания можно предварительно оживить сказочным, фантастическим или бытовым сюжетом («На Землю прилетел инопланетянин», «Колобок встретился с пиццей» и т.д.). Важно, чтобы занимательность или простота задания предполагали возможность проявления способностей ученика с любым уровнем подготовки.
7. Определяется название задания или олимпиадной номинации. Здесь два пути: а) название номинации определяется первоначально, и само задание потом подстраивается под него; б) сначала составляется задание, затем для него отыскивается наиболее подходящее название номинации. В названии номинации может быть отражен как объект, так и вид деятельности. При составлении заданий полезен прием, когда одна номинация получает несколько форм выражения задания для разных возрастных категорий детей.
Формы выражения могут отличаться:
а) разными видами деятельности (например, младшим ученикам предлагается составить загадку про выдранный объект, более страшим – разработать кроссворд или дидактическую игру, выпускникам – провести исследование по данной теме);
б) разным уровнем или объемом создаваемого учениками продукта (младшие рисуют образ числа 3, старшие – его символ, выпускники проводят комплексное исследование – арифметическое, геометрическое, лингвистическое).
При разработке задания продумываются критерии оценки его выполнения, т.е. определяется, какие параметры созданного учеником продукта будут оцениваться. Например, если задание предполагает отыскание закономерности, то критериями оценки могут стать количество выявленных учеником взаимосвязанных элементов, оригинальность обнаруженных связей между ними, отражение этих связей в формуле или описании. Кроме того, всегда есть универсальные критерии оценки творческой работы: мировоззренческая глубина, самобытность, многовариантность подходов, соответствие условию задания, оригинальность формы представления результата и т.п.
Чтобы организовать творческую деятельность учеников, одной формулировки открытого задания может быть недостаточно. При отсутствии навыков самоорганизации продуктивной деятельности у школьников могут возникнуть затруднения в получении качественного образовательного продукта. В этом случае помогают алгоритмические описания, задающие учащимся этапы или направления их деятельности (но не ее содержание!).
Приведем пример алгоритмического предписания для учеников по исследованию образовательного объекта – феномена. Под феноменом здесь понимается необычное явление в природе, культуре, науке, в любой образовательной области.
-
Обозначьте обнаруженный вами феномен понятием, рисунком или символом.
-
Опишите свои чувства и мысли, возникшие при наблюдении феномена.
-
Выразите необычность феномена, его суть, которая отличает его от других похожих явлений.
-
Сформулируйте возникший у вас вопрос или проблему.
-
Составьте план своего дальнейшего исследования феномена.
-
Предложите версию, гипотезу, объясняющую феномен.
-
Сделайте вывод из исследования. Проведите рефлексию деятельности и выполните ее самооценку.
Основные технологические рекомендации – важнейшее средство организации творческой работы учащихся, ориентировочная основа их деятельности. Алгоритмизация действий в данном случае не мешает, а способствует индивидуальной самореализации учеников. Репродуктивно передаваемые ученикам способы действий позволяют им творить на технологической основе с гарантированным результатом.
Одним из важных умений учителя творческой ориентации является умение переводить традиционные закрытые задания в открытые. Если учитель освоил такую процедуру, то его ученики будут в состоянии творчества всегда – на уроках, во время контрольных работ или зачетов, при выполнении домашней работы, на протяжении всей образовательной деятельности.

Эвристические задания, задачи и беседы
Преподаватель ВКК:
Малахова М. И.

Эпиграф:
«В учениках живут «спящие» открытия». Не верите? Тогда предложите детям выполнить эвристическое задание. И Вы обязательно сумеете открыть Ваших учеников с новой стороны»
А. В.Хуторской

Эвристическое задание –
учебное задание, имеющее целью создание учеником личного образовательного продукта с использованием эвристических способов и форм деятельности (А.В.Хуторской).

Главный признак эвристического задания –
его открытость, т.е. отсутствие заранее известного результата его выполнения. Поэтому другое название эвристических заданий – открытые задания .
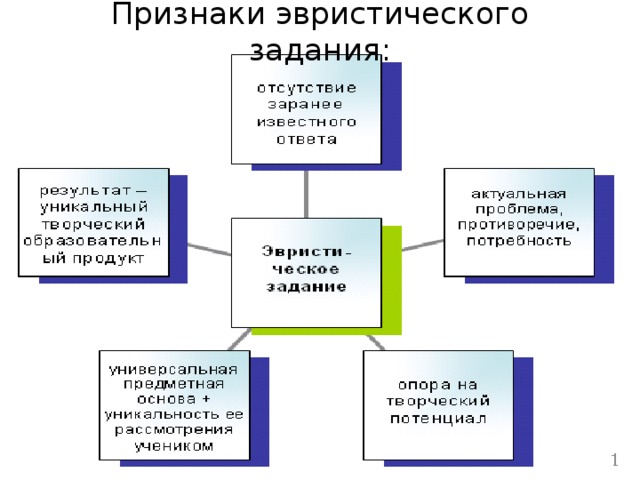
Признаки эвристического задания:
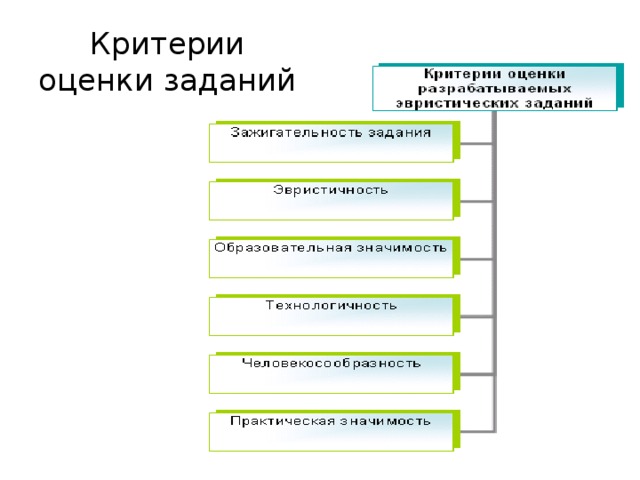
Критерии оценки заданий

Особенность эвристического задания в том, что ответ на него заранее не знает даже преподаватель

Качества личности, мобилизуемые у обучающихся при выполнении эвристических заданий:
умение чувствовать окружающий мир, задавать вопросы, отыскивать причины явлений, обозначать свое понимание или непонимание вопроса и др.)
Когнитивные
вдохновленность, фантазия, гибкость ума, чуткость к противоречиям; раскованность мыслей и чувств, движений; прогностичность; наличие своего мнения и др.)
Креативные
способность осознания целей учебной деятельности и умение их пояснить; умение поставить цель и организовать её достижение; способность к нормотворчеству; рефлексивное мышление; коммуникативные качества
Оргдеятель-
ностные
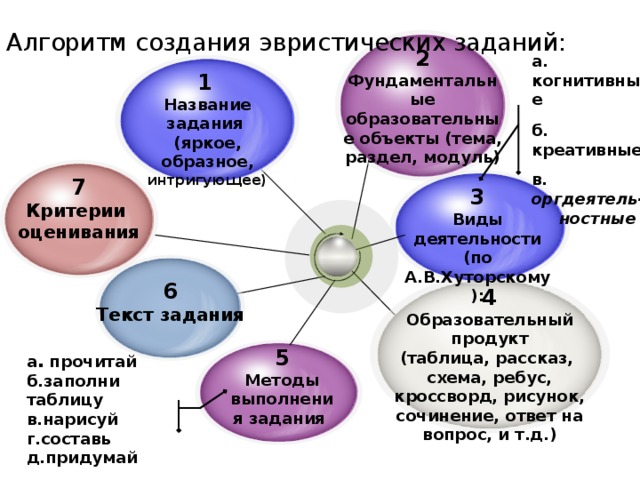
Алгоритм создания эвристических заданий:
2
Фундаментальные образовательные объекты (тема,
раздел, модуль)
1
Название задания (яркое, образное, интригующее)
а. когнитивные
б. креативные
в. оргдеятель-
ностные
7
Критерии
оценивания
3
Виды деятельности (по А.В.Хуторскому):
6
Текст задания
4
Образовательный продукт
(таблица, рассказ,
схема, ребус, кроссворд, рисунок, сочинение, ответ на вопрос, и т.д.)
5
Методы выполнения задания
а . прочитай
б.заполни таблицу
в.нарисуй
г.составь
д.придумай

Примеры эвристических заданий:
Тема урока: «Вода. Растворы» 1.Название задания: «Эта удивительная вода»
Текст задания: Вода… Её можно назвать как угодно – от романтического «источник жизни» до сухого и научного «H 2 O»…Многим вода кажется самой простой субстанцией, которую только можно себе представить. Однако, в действительности вода является крайне таинственным веществом. Ведь она скрывает много загадочного, и многие её свойства не изучены до сих пор. Придумайте и проведите исследование свойств водопроводной воды доступными вам методами. Результаты исследования оформите в виде небольшого отчета по плану: – Цель исследования; – Гипотеза; – Оборудование, реактивы; – Какие опыты проводил; – Результаты исследования; – Выводы.
Тема: «Основные классы неорганических соединений»
Тост Клеопатры
Римский историк Кай Плиний Старший (23 – 79 гг.н.э.) пересказал легенду о жемчужинах Клеопатры. Египетская царица устроила пир в честь римского полководца Марка Антония. А надо сказать, что среди сокровищ сказочно богатой Клеопатры больше всего славились серьги с огромными грушевидными жемчужинами, массу которых историки оценивали в 40,2г. Желая поразить римского гостя, Клеопатра растворила одну из жемчужин в кубке с вином и выпила это вино за здоровье Антония. В течение 5минут обсудите в группе достоверность предлагаемой легенды с точки зрения химического процесса растворения. Выскажите мнение от группы. Предложите название жидкости, которая, могла бы содержаться в кубке, чтобы растворить жемчужину. Составьте молекулярную формулу основного вещества, составляющего жемчуг и перламутр на основе данных о массовых долях элементов в веществе: 40% кальция, 12% углерода, 48% кислорода. Дополнительные сведения: Жемчуг – это округлые, с перламутровым отливом образования из минерала арагонита. Основное вещество в его составе – карбонат кальция. Жемчуг может образовываться в раковинах моллюсков, которые выделяют перламутр. По составу жемчуг и перламутр одинаковы. Растворимость жемчуга в вине такая же, как в воде.
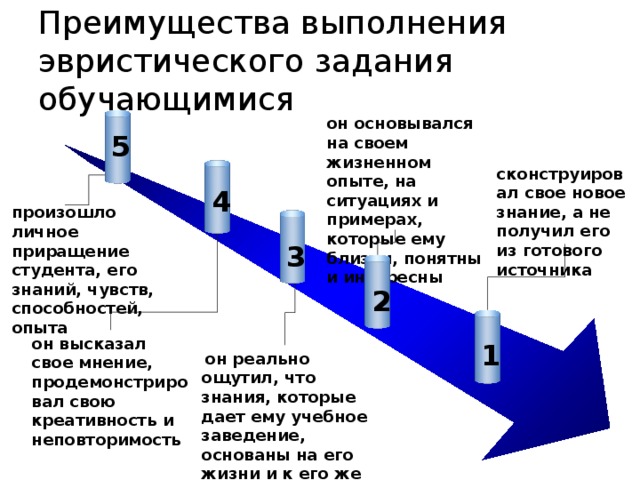
Преимущества выполнения эвристического задания обучающимися
он основывался на своем жизненном опыте, на ситуациях и примерах, которые ему близки, понятны и интересны
5
сконструировал свое новое знание, а не получил его из готового источника
4
произошло личное приращение студента, его знаний, чувств, способностей, опыта
3
2
он высказал свое мнение, продемонстрировал свою креативность и неповторимость
1
он реально ощутил, что знания, которые дает ему учебное заведение, основаны на его жизни и к его же жизни имеют применение

Классификация методов решения эвристических задач:
Метод «вживания»
Посредством чувственно-образных и мысленных представлений студент пытается «переселиться» в изучаемый объект, почувствовать и познать его изнутри.
«Представьте себе, что вы то растение, которое стоит перед вами, ваша голова — это цветок, туловище — стебель, руки — листья, ноги — корни…»

Метод смыслового видения
Метод видения заключается в нахождении или построении студентом связей между объектом и его символом. После выяснения характера отношений символа и его объекта (например, свет— символ добра, спираль—символ бесконечности, голубь — символ мира, блин — символ Масленицы)

Метод придумывания
Сущность метода: создание нового, неизвестного ранее продукта, в результате определённых умственных действий. Используются такие приёмы, как замещение качеств одного объекта качествами другого; поиск свойств объекта в иной среде; изменение элемента изучаемого объекта и описание свойств нового, изменённого

Метод «Если бы»
Сущность метода: составляется описание или рисуется картина о том, что произойдёт, если в мире что-то изменится, если с объектом произойдут изменения. Подобный метод не только развивает способность воображения, но и позволяет лучше понять устройство реального мира, его фундаментальные физические основы.

Метод гиперболизации
Сущность метода: мысленно увеличивается или уменьшается объект познания, его отдельные части или качества. Новые свойства объекта приводят иногда к необычным идеям и решениям задачи

Метод «Мозговой штурм»
Сущность метода «мозговой штурм»: коллективный сбор как можно большего числа идей, в результате освобождения участников от инерции мышления и стереотипов в непринуждённой обстановке. Работа происходит в нескольких группах по схеме: выдвижение гипотез, проверка гипотез и их критическое оценивание, представление группой наиболее оптимального способа решения. Окончательно отбираются только те идеи, которые не были отвергнуты.
Алекс Осборн

Пример использования метода «Мозговой штурм»
В городе Россошь в 1978 году был построен химический завод по производству минеральных азотных удобрений. Разработайте предложения по охране природы города и здоровья его жителей

Примером использования метода «Если бы…» является эвристическое задание «Ох уж эта Репка» при изучении тем по биологии: «Пластический обмен. Фотосинтез», «Изменчивость»


Эвристическая беседа
состоящая из серии взаимосвязанных вопросов, каждый из которых служит шагом на пути к решению проблемы и большинство которых требует от учащихся не только воспроизведения своих знаний, но и осуществления небольшого поиска.

Фрагмент эвристической беседы по дисциплине «Биология» при изучении темы: «Борьба за существование»
Постановка проблемы
В природе рождается гораздо больше особей, чем может выжить. Например, одуванчик дает 100 семян. Из них на следующий год могло бы вырасти 100 растений, каждое из которых дало бы по 100 семян, следовательно, при беспрепятственном размножении число потомков одного одуванчика заняло бы площадь в 15 раз больше всей суши Земли через 30 лет. Но такого числа потомков никогда не бывает. Как вы это объясните?

Решение проблемы
- Обучающийся: Вероятно, велика гибель организмов.
- Преподаватель: Верно. С чем это связано?
- Обучающийся: Растениям не хватает территории, воды и минеральных веществ.
- Преподаватель: Это одна из причин – недостаток ресурсов. Какие еще причины можете назвать?
- Обучающийся: Растения поедают животные. Их вытесняют другие, более «сильные» растения.
- Преподаватель: Верно. Вторая причина – отношения с другими видами. Еще есть причины?
- Обучающийся: Может, из-за резкого изменения климата?
- Преподаватель: Таким образом, третья причина – влияние неблагоприятных условий среды. Подведите итог вышесказанному и дайте название процессу, постоянно происходящему в природе, в результате которого большая часть потомства может погибнуть?
- Обучающийся: Борьба за существование.

- Преподаватель: Что же приводит к ее возникновению?
- Обучающийся: К возникновению борьбы за существование приводят отношения особей внутри вида, между разными видами и неблагоприятными условиями среды.
- Преподаватель: Ч. Дарвин пришел к тем же выводам, на их основе выделил три формы борьбы за существование. Можете ли вы предположить, как он их назвал?
- Обучающийся: Внутривидовая, межвидовая и с неблагоприятными условиями среды.
- Преподаватель: Верно. Какую из этих форм борьбы за существование Дарвин называл самой острой и почему?
- Обучающиеся высказывают предположения, а затем приходят к выводу, что самая острая внутривидовая борьба, так как особи одного вида используют одинаковые ресурсы и приспособлены к одинаковым условиям среды.

Эвристическая беседа
- облегчает процесс творческой деятельности,
- способствует непроизвольному формированию памяти, то есть обучающиеся способны не только воспроизводить формулировки понятий, но и анализировать и преобразовывать их.

Овладев педагогическим инструментарием эвристического обучения, Вы сможете на качественно новом уровне решать задачи развития у обучающихся познавательных интересов к изучению учебного предмета, раскрытия их творческой индивидуальности. Вполне вероятно, что среди Ваших учеников будущие Менделеевы, Эйнштейны и Ньютоны!
Помогите им раскрыться и реализовать свой творческий потенциал на Ваших уроках!

«Знания – это дети удивления и любопытства». Луи де Бройль
Ира ЦЕЛИЩЕВА,
г. Шуя,
Ивановская обл.
Эвристические задачи
Одной из наиболее сложных проблем школьного
обучения остается проблема развития
самостоятельности мышления учащихся.
Существующие программы и учебники по математике
предоставляют учителю большие возможности для
развития мышления учащихся. Однако если
логические действия учащихся при современном
обучении развиваются достаточно активно, то
развитие их умственной инициативы,
эвристических элементов мышления значительно
отстает. Как показывают психологические
исследования и наши наблюдения, учащиеся
начальной школы, уверенно оперируя довольно
сложными приемами и абстрактными понятиями,
усвоенными с помощью учителя, нередко
обнаруживают полную беспомощность в простейших
ситуациях, где требуется проявить минимум
умственной инициативы, сообразительности. Не
случайно поэтому за последние годы в
методической печати уделяется большое внимание
решению так называемых нестандартных задач,
развивающих эвристическое мышление. При этом
большая часть предлагаемых материалов
рекомендуется для использования не на уроке, а во
внеклассной работе. И это вполне оправдано.
Поисковая деятельность учащихся, направленная
на решение эвристических задач и его графическое
оформление, а также обсуждение различных
вариантов решения и анализ типичных ошибок
требуют значительного времени, выделять которое
на уроке при его современной насыщенности
учебным материалом не всегда возможно.
В то же время развитие умственной инициативы,
эвристических элементов мышления учащихся
требует определенной системы.
На наш взгляд, наиболее благоприятные условия
для построения такой системы предоставляет на
сегодня именно внеклассная работа, где имеется
возможность посвящать решению нестандартных
задач полностью каждое занятие и проводить эту
работу в определенной последовательности.
В своей статье мы хотим поделиться опытом
применения системы решения эвристических задач
во внеклассной работе с учащимися 1–2-х классов,
которую регулярно проводят студенты факультета
педагогики и психологии в период непрерывной
педагогической практики в течение всего
учебного года.
Планирование работы потребовало от нас прежде
всего отбора наиболее подходящих для работы с
младшими школьниками видов эвристических задач
в целях их всестороннего использования.
Задачи на оперирование понятиями
“все”, “некоторые”, “отдельные”
Это задачи-вопросы вида:
1. Все ученики вашего класса пойдут
завтра в кино. Пойдешь ли в кино ты?
2. В парке растут деревья и кустарники. Сирень
– кустарник. Растет ли в парке сирень?
3. На дереве сидели 4 синицы и 6 воробьев. 5 птиц
улетело. Был ли среди них хотя бы 1 воробей?
Объясни.
Задачи на установление временных,
пространственных и функциональных отношений
Примеры задач данного вида:
1. Сережа считал, что пришел на
футбольный матч за 15 мин до начала, но его часы
отстали на 10 мин, а проведение матча
задержалось на 20 мин. Сколько времени ждал
Сережа начала матча?
2. Деревянный окрашенный кубик распилили
пополам. Сколько стало окрашенных и неокрашенных
граней у каждой половины?
3. Бревно длиной 6 м распилили на 6 равных
частей. Сколько раз пришлось распиливать бревно?
4. Как отмерить 3 л воды, если есть кружки
7 л и 2 л?
5. Коля живет на 6 этаже, а Петя на 3 этаже этого
же подъезда. Сколько ступенек до Петиной
квартиры, если до Колиной 60?
Задачи на придумывание способов
обозначения схематизации и символизации
различных отношений
1. Вырази схематически отношения, в
которых находятся:
а) город, поселок, деревня;
б) море, озеро, лужа;
в) солдат, сержант, офицер;
г) лето, зима, весна, осень;
д) город, улица в нем и дом на этой улице.
2. Даны три отрезка. Обозначь их и
запиши несколько равенств, связывающих длины
этих отрезков:
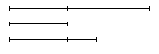
Задачи на комбинаторные действия
1. Петя (П), Коля (К) и Вася (В)
хотят сесть на скамейку. Как можно их рассадить?
Сколько всевозможных вариантов посадки ты
можешь указать? Запиши их.
2. Составь как можно больше примеров, используя
цифры 2, 4, 8.
3. Во дворе гуляли куры и собаки. Мальчик
посчитал их лапы, получилось 10 лап. Сколько могло
быть кур и сколько собак?
4. Во дворе стояли мотоциклы, легковые машины и
мотоциклы с колясками. Мальчик насчитал всего 13
колес. Сколько могло стоять во дворе машин,
мотоциклов и мотоциклов с колясками?
5. Составь всевозможные фигуры из четырех
одинаковых элементов:
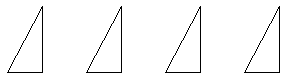
6. Покажи, как из данной фигуры можно
получить прямоугольник.

Задачи на установление сходства и
соответствия
Это задачи на придумывание слова,
соответствующего по значению данному; на
определение предметов, содержащих данную
геометрическую фигуру; на придумывание пар
предметов, находящихся в таких же отношениях, как
предметы данной пары; на выделение из группы
предметов тех, которым присущ общий признак, и
т.п. Вот примеры таких задач:
1. Придумай свои пары предметов,
которые находятся в таких же отношениях, как
предметы в следующих парах:
а) колесо – машина,
машина – шофер;б) топор – дерево,
дерево – кровать;
2. Найди лишнее слово в ряду: сливки,
сало, сметана, творог. Объясни, почему оно лишнее.
3. Допиши еще несколько слов в ряду:
а) лужа, пруд, озеро…
б) солдат, сержант, офицер…
4. Определи, какая фигура лишняя и
почему.
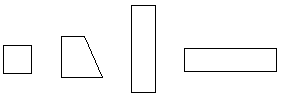
Задачи на активный перебор вариантов
отношений
1. Как разделить 6 яблок на 6 человек,
чтобы каждый получил по одному яблоку и одно
осталось в корзинке?
2. Из каких знакомых тебе фигур
состоит эта фигура:
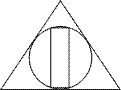
3. Заполни цифрами квадрат так, чтобы
сумма чисел по всем направлениям была равна 15.

4. Нарисуй такую же фигуру без отрыва
карандаша от бумаги и не проводя два раза одну и
ту же линию.
При подборе задач каждого вида мы
придерживались следующих принципов:
Задачи должны:
-
соответствовать возможностям
учащихся как по объему элементов, так и по
сложности их отношений; -
быть близкими жизненному (но не
обязательно учебному) опыту ребенка и в то же
время содержать элемент новизны, необычности
формулировки, нестандартности решения; -
стимулировать прежде всего
самостоятельные умственные усилия каждого
ученика, способствовать раскрытию его
творческой индивидуальности.
Внеклассные занятия проводились
один раз в неделю по 45 мин. На каждом занятии
дети получали для решения по 6–7 задач разных
видов. Степень трудности задач каждого вида как
по объему, так и по сложности отношений
возрастала по мере приобретения детьми умения
анализировать и решать их. Решение каждой задачи,
особенно на первых занятиях, мы подробно
анализировали, давая возможность высказаться
всем желающим, чтобы каждому было интересно и
понятно, где и что он решил правильно, а где
ошибался и почему.
Работа началась с решения задачи, не
содержащей числовых данных: “Все ученики
вашего класса идут завтра в кино. Пойдешь ли в
кино ты?” Дети по распространенной в быту
привычке восприняли слово “все” в условии
задачи как “большинство” или “все”,
“кроме меня”, и в ответе учитывали только
свое желание или нежелание пойти в кино, то есть
исключали себя из множества учащихся своего
класса. Потребовалось дополнительное
разъяснение значения слова “все” по
сравнению со словами “часть”,
“некоторые”, “отдельные”.
Немалые затруднения вызвала у детей
и другая задача, не требовавшая выполнения
арифметических действий: “На дереве сидели 4
синицы и 6 воробьев. 5 птиц улетело. Улетел ли
среди них хотя бы один воробей?” Большинство
учащихся по опыту решения обычных задач решили и
эту задачу двумя арифметическими действиями
(4 + 6 = 10; 10 – 5 = 5) и записали в
ответе: “Один воробей улетел”.
Только трое учеников сразу дали
правильное решение и записали, что 5 птиц больше,
чем 4 синицы, значит, хотя бы один воробей улетел.
Анализируя решение, мы предлагали
рассказать, как дети рассуждали, как
представляли себе то, что описано в задаче. Кроме
того, детям предложили перечислить все возможные
варианты состава улетевших птиц. При этом было
выяснено, что наименьшее число улетевших
воробьев может быть только 1 и что для этого
достаточно сравнить числа 4 и 5 в условии задачи.
Самыми трудными на первых занятиях
оказались задачи на установление
пространственных отношений, как, например:
“Деревянный окрашенный кубик распилили
пополам. Сколько окрашенных и неокрашенных
сторон (граней) оказалось у каждой половины?”
Мы считали, что, опираясь на образное
представление хорошо знакомого предмета, дети
быстро решат эту задачу. Поэтому, не показывая
кубика, предложили представить окрашенный кубик,
мысленно распилить его пополам и посчитать,
сколько будет окрашенных и неокрашенных сторон у
каждой половины. Однако только один ученик
ответил, что у каждой половины будет 5 окрашенных
и одна неокрашенная сторона, то есть имел одно из
двух возможных решений. Остальные не смогли дать
и этого решения. Активное манипулирование
образом только во внутреннем плане оказалось
непосильным для учащихся. Только наглядный показ
распиливания кубика на объемной модели и
практический подсчет окрашенных и неокрашенных
граней после распиливания по диагональному
сечению, и по сечению, параллельному одной из
граней, помогли детям убедиться в возможности
двух решений этой задачи.
Вызвала затруднения и одна из первых
задач на комбинаторные действия: “Во дворе
стояли легковые машины, мотоциклы и мотоциклы с
колясками. Мальчик насчитал всего 13 колес.
Сколько могло быть машин, мотоциклов и
мотоциклов с колясками?”
Затруднение вызвало то, что в данной
задаче три неизвестных, а явно обозначенных
числовых данных только одно (13 колес). В
результате беседы было выяснено, что в условии
задачи не одно, а четыре числовых данных, так как
кроме общего числа колес известно, что у
мотоцикла 2 колеса, у мотоцикла с коляской – 3, а у
машины – 4. Но и после этого оказалось, что решить
задачу обычным путем с помощью арифметических
действий трудно. Мы предложили детям
использовать для обозначения условия задачи
круги. Учащиеся легко догадались сделать такие
обозначения:
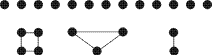
Опираясь на условные обозначения,
многие пришли к правильному решению. Однако при
его анализе выяснилось, что учащиеся решали
задачу не рассуждая, путем простого перебора
разных сочетаний машин с последующим подсчетом
общего числа колес. В дальнейшей беседе мы
показали два возможных пути рассуждения при
решении данной задачи.
1. Сколько могло быть легковых
машин? Выяснили, что число колес машины (4 колеса)
укладывается в общем числе колес 3 раза, но тогда
на все мотоциклы остается только 1 колесо, что
невозможно. Значит, машин могло быть 2 или 1. Если
машин было 2 (8 колес), то оставшиеся 5 колес могут
приходиться только на 1 мотоцикл и 1 мотоцикл с
коляской. Если машина была 1, то освободившиеся 4
колеса могут приходиться только на 2 мотоцикла.
2. Сколько будет колес, если
предположить, что во дворе было по одной машине
каждого вида? Выяснили, что 1 машина, 1 мотоцикл и 1
мотоцикл с коляской будут иметь вместе 9 колес,
что при этом до 13 колес не хватило бы 4 колеса. А
отсюда легко установить, что эти 4 колеса могут
приходиться или на 1 машину, или на 2 мотоцикла.
Так дети познакомились с решением
задачи с помощью схем и опорой на свой жизненный
опыт, а также с помощью рассуждений и некоторых
предположений.
Учитывая важность схематизации и
символизации для выражения различных отношений,
на одном из первых занятий мы предложили для
решения только с помощью схем такую задачу.
“Изобрази условными знаками свой город, свою
улицу и дом, в котором ты живешь”.
Учащиеся предложили изобразить
данные отношения в виде отрезков разной длины:
большой отрезок – город, поменьше – улица, еще
меньше – дом. Это свидетельствовало о том, что
дети имеют правильное представление о
соразмерности элементов данного отношения. Но
было необходимо, чтобы дети установили и
выразили и другую особенность данного отношения
– включение элементов одного множества в другое.
Для этого в беседе было выяснено, что улица
находится в городе и является его частью, а дом –
частью улицы. После этого учащиеся сами
предложили изобразить город и улицу в нем в виде
включенных друг в друга геометрических фигур,
например, в виде круга и расположенного внутри
него квадрата, а дом – в виде треугольника внутри
квадрата. В результате решение было выражено
схемой.
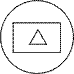
Решение этой задачи потребовало от
учащихся анализа жизненной ситуации, сравнения
элементов множеств, установление факта
включения элементов одного множества в другое,
придумывания своих средств схематизации, что
развивает творческое воображение детей.
Необычность формулировки условий
задач, нестандартность решения, возможность
творческого поиска вызвали у детей большой
интерес. Они с нетерпением ждали каждого занятия
и активно участвовали в работе.
На первых занятиях для
самостоятельного решения всем детям
предлагалась одна и та же задача. После того как
дети познакомились с особенностями условия и
решения задач каждого вида, методика работы была
изменена. На последующих занятиях раздавались
индивидуальные карточки-задания, состоящие из
6–7 задач различных видов.
Карточки-задания составлялись с
таким расчетом, чтобы в каждой из них было хотя бы
два-три задания, посильных для всех учащихся.
Поэтому каждый ученик обязательно находил в
полученной карточке задания, с которыми он
справлялся самостоятельно, испытывая радость
успеха.
Ответы решенных задач учащиеся
записывали на отдельных листках и сдавали на
проверку. После проверки подробно
анализировались допущенные ошибки и различные
способы решения задач по вариантам
карточек-заданий. Через несколько занятий дети
освоились с новыми условиями работы и начали
увереннее представлять свои действия.
Наиболее успешно дети справлялись с
решением задач логического типа, особенно тех, в
которых им был хорошо знаком или материал (числа,
геометрические фигуры, конкретные предметы), или
операции (анализ признаков геометрических фигур,
продолжение последовательности чисел с
определенной закономерностью чередования и др.).
Задачи, требующие исключительно внутреннего
плана действий, установления сложных отношений,
перестановки и комбинирования простых
элементов, перебора вариантов, решались на
первых порах с большим трудом. Однако следует
отметить, что именно эти действия особенно
заметно прогрессировали у детей в процессе
внеклассной работы.
За время занятий произошли заметные
изменения в отношении детей к эвристическим
задачам, а также к выполнению других заданий по
математике. Об этом свидетельствуют не только
наши наблюдения и анализ детских работ, но и
сравнительная оценка деятельности учащихся
учителями этих классов. Значительно повысился
интерес детей к обучению. Они стали более
самостоятельными в способах оформления работ,
нахождения и использования вспомогательных
приемов и средств. В целом подход к решению любых
задач стал более гибким. Возросла
самостоятельность и изобретательность учащихся
в способах обозначения элементов задачи и их
отношений. Рассуждения их стали более
последовательными и доказательными. Особенно
заметно развился навык учащихся по решению
задач, имеющих несколько вариантов правильных
ответов, и задач, решаемых методом перебора
вариантов отношений.
Проведенная работа и ее результаты
позволяют сделать вывод о том, что
систематическое решение эвристических задач на
внеклассных занятиях является эффективным
средством повышения интереса детей к обучению
математике, развития их умственной инициативы и
творческой активности.
Карточка-задание 1
1. В доме живут Коля и Наташа. Около
дома гуляет только Наташа. Где Коля?
2. Сережа считал, что пришел на
футбольный матч за 15 мин до начала, но его часы
отставали на 10 мин, а начало матча на 20 мин
задержалось. Сколько времени ждал Сережа начала
матча?
3. У Толи на 8 яблок больше, чем у Оли.
Сколько яблок должен Толя отдать Оле, чтобы яблок
у них стало поровну?
4. Как отмерить 1 л воды, если есть
кружки 5 л и 2 л?
5. Какое слово “лишнее” и почему?
а) лошадь, корова, волк, кошка,
собака;
б) молоко, масло, сало, сливки, простокваша.
6. Нарисуй отдельно простые фигуры,
из которых состоит эта фигура:
7. Найди закономерность и более
легкий способ вычисления:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9.
Карточка-задание 2
1. Пианино – музыкальный инструмент.
У Ивановых есть музыкальный инструмент. Какой?
2. Лена подарила несколько открыток
подруге, и у нее осталось столько же. Потом она
подарила брату половину оставшихся. Брат получил
5. Сколько открыток было у Лены?
3. На двух полках одинаковое число
книг. С первой полки переложили на вторую 3 книги.
На какой полке стало книг больше и на сколько?
4. Какое слово “лишнее” и почему?
а) лошадь, корова, волк, кошка,
собака;
б) сон, нос, сом, кот, мак.
5. Одна часть ребят вашего класса
пошла в лес, а другая – на реку. Оля не пошла ни в
лес, ни на реку. Учится ли Оля в вашем классе?
6. На чертеже изображены 9 кружочков.
Перечеркни все кружочки четырьмя прямыми
линиями, не отрывая карандаша от бумаги.

7. Напиши хотя бы одно следующее
число в каждой последовательности чисел:
а) 15, 20, 25, 30, …
б) 3, 6, 12, 24, 48, …
в) 1, 2, 1, 1, 3, 1, …
