Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.
Уравнение прямой в отрезках – описание и примеры
Пусть на плоскости расположена прямоугольная система координат Oxy.
Прямая линия на плоскости в декартовой системе координат Oxy задается уравнением вида xa+yb=1, где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях Ox и Oy. Длины отрезков считаются от начала координат.
Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a, 0 и 0, b принадлежат данной прямой линии, так как aa+0b=1⇔1≡1 и 0a+bb=1⇔1≡1. Точки a, 0 и b, 0 расположены на осях координат Ox и Oy и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b. Знак «-» обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.
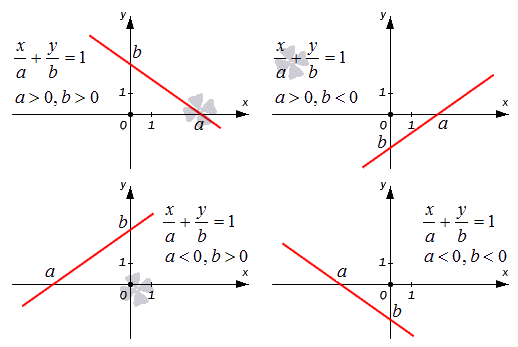
Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат Oxy на схематическом чертеже. Уравнение прямой в отрезках xa+yb=1 применяется для построения прямой линии в декартовой системе координат Oxy. Для этого нам необходимо отметить на осях точки a, 0 и b, 0, а затем соединить эти точки линией при помощи линейки.
На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.
Рассмотрим пример.
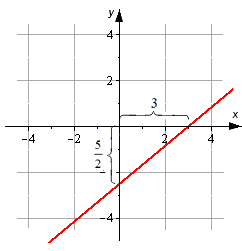
Прямая линия задана уравнением прямой в отрезках вида x3+y-52=1. Необходимо построить эту прямую на плоскости в декартовой системе координат Oxy.
Решение
Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3, 0, 0, -52. Отметим их и проведем линию.
Приведение общего уравнения прямой к уравнению прямой в отрезках
Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.
Полное общее уравнение прямой линии на плоскости имеет вид Ax+By+C=0, где А, В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на –С. При этом, коэффициенты при x и y мы отправляем в знаменатели:
Ax+By+C=0⇔Ax+By=-C⇔⇔A-Cx+B-Cy=1⇔x-CA+y-CB=1
Для осуществления последнего перехода мы воспользовались равенством pq=1qp, p≠0, q≠0.
В результате, мы осуществили переход от общего уравнения прямой Ax+By+C=0 к уравнению прямой в отрезках xa+yb=1, где a=-CA, b=-CB.
Разберем следующий пример.
Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x-7y+12=0.
Решение
Переносим одну вторую в правую часть равенства x-7y+12=0⇔x-7y=-12.
Делим обе части равенства на -12: x-7y=-12⇔1-12x-7-12y=1.
Преобразуем полученное равенство к нужному виду: 1-12x-7-12y=1⇔x-12+y114=1.
Мы получили уравнение прямой в отрезках.
Ответ: x-12+y114=1
В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.
Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида xa+yb=1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y.
xa+yb=1⇔xa+yb-1=0⇔1a·x+1b·y-1=0
Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».
Уравнение прямой в отрезках имеет вид x23+y-12=1. Необходимо написать общее уравнение прямой на плоскости.
Решение
Действует по заранее описанному алгоритму:
x23+y-12=1⇔123·x+1-12·y-1=0⇔⇔32·x-112·y-1=0
Ответ: 32·x-112·y-1=0
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Уравнение прямой в отрезках
В данной статье мы рассмотрим уравнение прямой в отрезках. Представим методы преобразования уравнения прямой в отрезках в уравнение прямой в общем виде и обратно. Рассмотрим численные примеры.
Уравнение прямой в отрезках представляется следующей формулой:
где a и b числа, отличные от нуля.
Отметим, что числа a и b в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает прямая на осях Ox и Oy (Рис.1).
Действительно. Подставляя в (1) y=0, получим x=a, если же подставить в (1) x=0, то получим y=b. Таким образом прямая L проходит через точки M1(a, 0) и M2(0, b).
Пример 1. Составить уравнение прямой, которая пересекает оси Ox и Oy в точках −1 и 3, соответственно.
Решение. Подставляя значения a=−1 и b=3 в (1), получим:
Ответ:
Приведение уравнения прямой в отрезках к общему виду
Левая часть уравнения (1) приведем к общему знаменателю:
Далее, умножив обе части уравнения на ab, получим:
или
Пример 2. Уравнение прямой в отрезках представлено следующим уравнением:
Перевести уравнение к общему виду.
Решение. Приведем левую часть уравнения к общему знаменателю:
Умножив обе части уравнения на −20, получим:
или
Ответ:
Приведение общего уравнения прямой на плоскости к уравнению прямой в отрезках
Пусть задано общее уравнение прямой на плоскости:
где A, B, C − отличные от нуля числа.
Сделаем следующие преобразования. Переведем свободный член C на правую часть уравнения и разделим обе части уравнения на −C:
Уравнение (2) можно переписать в следующем виде:
Сделаем следующие обозначения:
Тогда получим уравнение прямой в отрезках (1).
Пример 3. Привести общее уравнение прямой
к уравнению прямой в отрезках.
Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение прямой в отрезках. Воспользуемся формулой (3). Имеем: A=5, B=8, C=−3. Подставив эти значения в формулу (3), получим:
или
Ответ:
Уравнение прямой в отрезках: описание, примеры, решение задач
Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.
Уравнение прямой в отрезках – описание и примеры
Пусть на плоскости расположена прямоугольная система координат O x y .
Прямая линия на плоскости в декартовой системе координат O x y задается уравнением вида x a + y b = 1 , где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях O x и O y . Длины отрезков считаются от начала координат.
Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a , 0 и 0 , b принадлежат данной прямой линии, так как a a + 0 b = 1 ⇔ 1 ≡ 1 и 0 a + b b = 1 ⇔ 1 ≡ 1 . Точки a , 0 и b , 0 расположены на осях координат O x и O y и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b . Знак « – » обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.
Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат O x y на схематическом чертеже. Уравнение прямой в отрезках x a + y b = 1 применяется для построения прямой линии в декартовой системе координат O x y . Для этого нам необходимо отметить на осях точки a , 0 и b , 0 , а затем соединить эти точки линией при помощи линейки.
На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.
Прямая линия задана уравнением прямой в отрезках вида x 3 + y – 5 2 = 1 . Необходимо построить эту прямую на плоскости в декартовой системе координат O x y .
Решение
Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3 , 0 , 0 , – 5 2 . Отметим их и проведем линию.
Приведение общего уравнения прямой к уравнению прямой в отрезках
Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.
Полное общее уравнение прямой линии на плоскости имеет вид A x + B y + C = 0 , где А , В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на – С . При этом, коэффициенты при x и y мы отправляем в знаменатели:
A x + B y + C = 0 ⇔ A x + B y = – C ⇔ ⇔ A – C x + B – C y = 1 ⇔ x – C A + y – C B = 1
Для осуществления последнего перехода мы воспользовались равенством p q = 1 q p , p ≠ 0 , q ≠ 0 .
В результате, мы осуществили переход от общего уравнения прямой A x + B y + C = 0 к уравнению прямой в отрезках x a + y b = 1 , где a = – C A , b = – C B .
Разберем следующий пример.
Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x – 7 y + 1 2 = 0 .
Решение
Переносим одну вторую в правую часть равенства x – 7 y + 1 2 = 0 ⇔ x – 7 y = – 1 2 .
Делим обе части равенства на – 1 2 : x – 7 y = – 1 2 ⇔ 1 – 1 2 x – 7 – 1 2 y = 1 .
Преобразуем полученное равенство к нужному виду: 1 – 1 2 x – 7 – 1 2 y = 1 ⇔ x – 1 2 + y 1 14 = 1 .
Мы получили уравнение прямой в отрезках.
Ответ: x – 1 2 + y 1 14 = 1
В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.
Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида x a + y b = 1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y .
x a + y b = 1 ⇔ x a + y b – 1 = 0 ⇔ 1 a · x + 1 b · y – 1 = 0
Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».
Уравнение прямой в отрезках имеет вид x 2 3 + y – 12 = 1 . Необходимо написать общее уравнение прямой на плоскости.
Решение
Действует по заранее описанному алгоритму:
x 2 3 + y – 12 = 1 ⇔ 1 2 3 · x + 1 – 12 · y – 1 = 0 ⇔ ⇔ 3 2 · x – 1 12 · y – 1 = 0
Ответ: 3 2 · x – 1 12 · y – 1 = 0
Отрезок. Формула длины отрезка.
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 – y1, а на ось х длина проекции равна х2 – х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.
Уравнение прямой
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k – угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x – x 1 | = | y – y 1 |
| x 2 – x 1 | y 2 – y 1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) – координаты точки лежащей на прямой, a = < l , m >- координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x – 1 2 – 1 = y – 7 3 – 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y – N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x – x 1 | = | y – y 1 | = | z – z 1 |
| x 2 – x 1 | y 2 – y 1 | z 2 – z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 |
x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) – координаты точки лежащей на прямой, – координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x – x 0 | = | y – y 0 | = | z – z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
[spoiler title=”источники:”]
http://www.calc.ru/Formula-Dliny-Otrezka.html
http://ru.onlinemschool.com/math/library/analytic_geometry/line/
[/spoiler]
Длина, как уже отмечалось, обозначается знаком модуля.
Если даны две точки плоскости и
, то длину отрезка
можно вычислить по формуле:
Если даны две точки пространства и
, то длину отрезка
можно вычислить по формуле:
Примечание: соответствующие координаты можно переставить местами: и
,
но это нестандартный вариант.
Задача 3
Даны точки и
. Найти длину отрезка
.
Решение: по соответствующей формуле:
Ответ: (единицы)
Обратите внимание на вынесение множителя из-под корня: (см. Приложение Школьные материалы). Это крайне
желательное действие, если оно возможно. Ибо будет придирка со стороны преподавателя. С высокой вероятностью.
И для наглядности снова выполню чертёж, тут есть что сказать:
Отрезок – это не вектор, а обычный ненаправленный
отрезок. И перемещать его куда-либо, конечно, нельзя.
Кроме того, если вы выполните чертеж в масштабе: 1 ед. = 1 см (две тетрадные клетки), то полученный ответ можно проверить обычной линейкой, непосредственно измерив длину
отрезка . Но проще, конечно, использовать Калькулятор (приложен к книге).
Кстати, в ответе не забываем указать размерность: «единицы». В условии не сказано, ЧТО это – миллиметры, сантиметры, метры
или километры. Поэтому математически грамотным решением будет общая формулировка: «единицы» – сокращенно «ед.».
Задание для самостоятельного решения с отрезком в пространстве:
Задача 4
Даны точки и
. Найти длину отрезка
.
Решение и ответ в конце книги.


| Оглавление |
Автор: Aлeксaндр Eмeлин
Уравнением
прямой в отрезках называется
уравнение
вида
(4)
где
а
и b
– абсцисса и ордината точек пересечения
прямой с осями Ох
и Оу,
т.е. длины
отрезков,
отсекаемых прямой на координатных осях,
взятые с соответствующими знаками.
Пример
4. Общее
уравнение прямой 2х
– 3у
– 6 = 0 привести к уравнению в отрезках.
Решение:
запишем данное уравнение в виде 2х
– 3у=6
и разделим обе его части на свободный
член:
.
Это и есть уравнение данной прямой в
отрезках.
Пример
5. Через
точку А (1;2)
провести прямую, отсекающую на
положительных полуосях координат равные
отрезки.
Решение:
Пусть уравнение искомой прямой имеет
вид
По условию а=b.
Следова-тельно, уравнение принимает
вид х +
у =
а.
Так как точка А (1; 2) принадлежит этой
прямой, значит ее координаты удовлетворяют
уравнению х
+ у =
а;
т.е. 1 + 2 = а,
откуда а
= 3. Итак, искомое уравнение записывается
следующим образом: х
+ у = 3, или
х + у – 3
= 0.
Пример
6. Для прямой
написать
уравнение в отрезках. Вычислить площадь
треугольника, образованного этой прямой
и осями координат.
Решение:
Преобразуем данное уравнение следующим
образом:
,
или
.
В
результате получим уравнение
,
которое и
является уравнением данной прямой в
отрезках. Треугольник, образованный
данной прямой и осями координат, является
прямоугольным треугольником с катетами,
равными 4 и 3, поэтому его площадь равна
S
=
(кв.
ед.)

26
2.1.4 Уравнение прямой, проходящей через точку в данном направлении
Уравнение
прямой, проходящей через т.у А(ха;
уа)
и имеющей
угловой коэффициент k,
записывается в виде
у
– уа=k
(x
– xa).
(5)
Пример 7.
Составить уравнение прямой, проходящий
через точку (–2; 5) и образующей с осью
Ох
угол 45º.
Решение:
Угловой коэффициент искомой прямой k=
tg
45º = 1. Поэтому, воспользовавшись уравнением
(5), получаем у
– 5 = x
– (–2), или
х – у + 7
= 0.
2.1.5 Уравнение прямой, проходящей через две точки
Уравнение
прямой, проходящей через две точки т.
А (х1;
у1)
и т.В (х2;
у2),
имеет вид
(6)
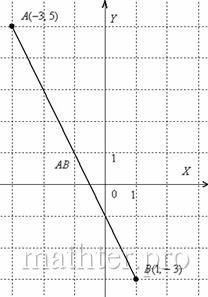
Пример
8. Составить
уравнение прямой, проходящей через
точки А(–3;
5) и
В(7;
–2).
Решение:
Воспользуемся уравнением (6):
,
или
,
откуда 7х
+ 10у
– 29 = 0.
2.1.6 Нормальное уравнение прямой
Пусть
дана прямая С, проходящая через данную
точку Мо(Хо; Уо) и перпендикулярная
вектору
(А;В). Любой вектор
,
перпендикулярный данной прямой
,
называется ее нормальным
вектором.
Выберем
на прямой произвольную т. М(х;у).
Тогда
,
а значит их скалярное произведение
.
Это равенство можно записать в координатах
А(
х-хо
)+В( у-уо
)=0
(7)
Уравнение
(7) называется нормальным
уравнением прямой.
Пример
9.
Даны точки М1
(2;-1) и М2(4;
5). Написать уравнение прямой, проходящей
через
точку
М1
перпендикулярно
вектору
Решение:
Нормальный вектор искомой прямой
имеет
координаты (2;6), следовательно по формуле
(7) получим уравнение 2(х-2)+6(у+1)=0
или х+3у
+1=0.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #