В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат Oxyz в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x, y, и z, которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Любую плоскость, заданную в прямоугольной системе координат Oxyz трехмерного пространства, можно определить уравнением Ax + By + Cz + D = 0. В свою очередь, любое уравнение Ax + By + Cz + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A, B, C, D – некоторые действительные числа, и числа A, B, C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
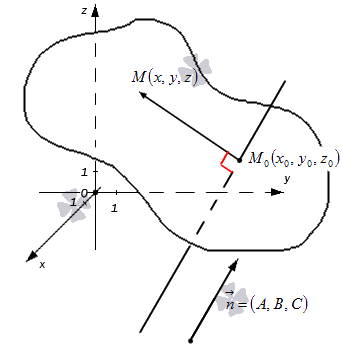
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида Ax + By + Cz + D = 0. Допустим, задана некоторая плоскость и точка M0(x0, y0, z0), через которую эта плоскость проходит. Нормальным вектором этой плоскости является n→= (A, B, C). Приведем доказательство, что указанную плоскость в прямоугольной системе координат Oxyz задает уравнение Ax + By + Cz + D = 0.
Возьмем произвольную точку заданной плоскости M(x, y, z).В таком случае векторы n→= (A, B, C) и M0M→=(x-x0, y-y0, z-z0) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n→, M0M→=Ax-x0+B(y-y0)+C(z-z0)=Ax+By+Cz-(Ax0+By0+Cz0)
Примем D=-(Ax0+By0+Cz0) , тогда уравнение преобразуется в следующий вид: Ax + By + Cz + D = 0. Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида Ax + By + Cz + D = 0 задает некоторую плоскость в прямоугольной системе координат Oxyz трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А, B, C одновременно не являются равными нулю. Тогда существует некоторая точка M0(x0, y0, z0), координаты которой отвечают уравнению Ax + By + Cz + D = 0, т.е. верным будет равенство Ax0 + By0 + Cz0 + D = 0. Отнимем левую и правую части этого равенства от левой и правой частей уравнения Ax + By + Cz + D = 0. Получим уравнение вида
A(x-x0) + B(y-y0) + C(z-z0) + D = 0, и оно эквивалентно уравнению Ax + By + Cz + D = 0. Докажем, что уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает некоторую плоскость.
Уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n→=(A, B, C) и M0M→=x-x0, y-y0, z-z0. Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A(x-x0) + B(y-y0) + C(z-z0) + D = 0 множество точек M(x, y, z) задает плоскость, у которой нормальный вектор n→=(A, B, C). При этом плоскость проходит через точку M(x0, y0, z0). Иначе говоря, уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает в прямоугольной системе координат Oxyz трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение Ax + By + Cz + D = 0 также определяет эту плоскость. Теорема доказана полностью.
Уравнение вида Ax + By + Cz + D = 0 называют общим уравнением плоскости в прямоугольной системе координат Oxyz трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ·Ax+λ·By+λ·Cz+λ·D=0, где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением Ax+By+Cz+D=0, поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x-2·y+3·z-7=0 и -2·x+4·y-23·z+14=0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида Ax+By+Cz+D=0( при конкретных значениях чисел A, B, C, D). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
Укажем пример как иллюстрацию этих утверждений.
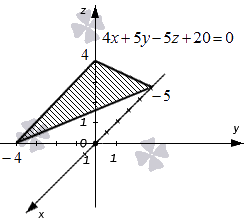
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4x + 5y – 5z + 20 = 0, и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4x + 5y – 5z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
Общее уравнение плоскости, проходящей через точку
Повторимся: точка M0(x0, y0, z0) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением Ax+By+Cz+D=0 в том случае, когда подставив координаты точки M0(x0, y0, z0) в уравнение Ax+By+Cz+D=0, мы получим тождество.
Заданы точки M0(1, -1, -3) и N0(0, 2, -8) и плоскость, определяемая уравнением 2x+3y-z-2=0. Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М0 в исходной уравнение плоскости:
2·1+3·(-1)-(-3)-2=0⇔0=0
Мы видим, что получено верное равенство, значит точка M0(1, -1, -3) принадлежит заданной плоскости.
Аналогично проверим точку N0. Подставим ее координаты в исходное уравнение:
2·0+3·2-(-8)-2=0⇔12=0
Равенство неверно. Таким, образом, точка N0(0, 2, -8) не принадлежит заданной плоскости.
Ответ: точка М0 принадлежит заданной плоскости; точка N0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n→=(A, B, C) – нормальный вектор для плоскости, определяемой уравнением Ax+By+Cz+D=0. Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2x+3y-z+5=0. Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x, y, z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n→ исходной плоскости имеет координаты 2, 3, -1 . В свою очередь, множество нормальных векторов запишем так:
λ·n→=λ·2, λ·3, -λ, λ∈R, λ≠0
Ответ: λ·2, λ·3, -λ, λ∈R, λ≠0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n→=(A, B, C)является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M0(x0, y0, z0), принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n→=(A, B, C) будет выглядеть так: Ax+By+Cz+D=0. По условию задачи точка M0(x0, y0, z0) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство:Ax0+By0+Cz0+D=0
Вычитая соответственно правые и левые части исходного уравнения и уравнения Ax0+By0+Cz0+D=0, получим уравнение вида A(x-x0)+B(y-y0)+C(z-z0)=0. Оно и будет уравнением плоскости, проходящей через точку M0(x0, y0, z0) и имеющей нормальный вектор n→=(A, B, C).
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М (x, y, z) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n→=(A, B, C) и M0M→=(x-x0, y-y0, z-z0) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n→, M0M→=A(x-x0)+B(y-y0)+C(z-z0)=0
Задана точка М0(-1, 2, -3), через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n→=(3, 7, -5). Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x0=-1, y0=2, z0=-3, A=3, B=7, C=-5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A(x-x0)+B(y-y0)+C(z-z0)=0
И получим:
3(x-(-1))+7(y-2)-5(z-(-3))=0⇔3x+7y-5z-26=0
- Допустим, М (x, y, z) – некоторая точки заданной плоскости. Определим координаты вектора M0M→ по координатам точек начала и конца:
M0M→=(x-x0, y-y0, z-z0)=(x+1, y-2, z+3)
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n→, M0M→=0⇔3(x+1)+7(y-2)-5(z+3)=0⇔⇔3x+7y-5z-26=0
Ответ: 3x+7y-5z-26=0
Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А, B, C, D отличны от нуля, общее уравнение плоскости Ax+By+Cz+D=0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
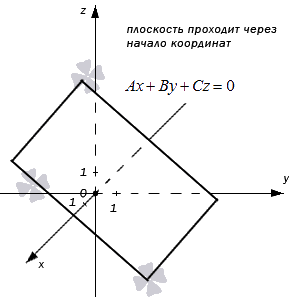
- В случае, когда D = 0, мы получаем общее неполное уравнение плоскости: Ax+By+Cz+D=0⇔Ax+By+Cz=0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О (0, 0, 0), то придем к тождеству:
A·0+B·0+C·0=0⇔0≡0
- Если А = 0, В ≠ 0, С ≠ 0, или А ≠ 0, В = 0, С ≠0, или А ≠ 0, В ≠ 0, С = 0, то общие уравнения плоскостей имеют вид соответственно: By+Cz+D=0, или Ax+Cz+D=0, или Ax+By+D=0. Такие плоскости параллельны координатным осям Оx, Oy, Oz соответственно. Когда D=0, плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей By+Cz+D=0, Ax+Cz+D=0 и Ax+By+D=0 задают плоскости, которые перпендикулярны плоскостям Oyz, Oxz, Ozy соответственно.

- При А=0, В=0, С≠0, или А=0, В≠0, С=0, или А≠0, В=0, С=0 получим общие неполные уравнения плоскостей: Cz+D=0 ⇔z+DC=0⇔z=-DC⇔z=λ, λ∈R или By+D=0⇔y+DB=0⇔y=-DB⇔y=λ, λ∈R или Ax+D=0⇔x+DA=0⇔x=-DA⇔x=λ, λ∈R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям Oxy, Oxz, Oyz соответственно и проходят через точки 0, 0, -DC, 0, -DB, 0 и -DA, 0, 0 соответственно. При D=0 уравнения самих координатных плоскостей Oxy, Oxz, Oyz выглядят так: z=0, y=0, x=0
соответственно.

Задана плоскость, параллельная координатной плоскости Oyz и проходящая через точку М0(7, -2, 3). Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости Oyz, а, следовательно, может быть задана общим неполным уравнением плоскости Ax+D=0, A≠0⇔x+DA=0. Поскольку точка M0(7, -2, 3) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x+DA=0, иначе говоря, должно быть верным равенство 7+DA=0 . Преобразуем: DA=-7, тогда требуемое уравнение имеет вид: x-7=0.
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости Oyz. Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости Oyz: i→=(1, 0, 0). Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A(x-x0)+B(y-y0)+C(z-z0)=0⇔⇔1·(x-7)+0·(y+2)+0·(z-3)=0⇔⇔x-7=0
Ответ: x-7=0
Задана плоскость, перпендикулярная плоскости Oxy и проходящая через начало координат и точку М0(-3, 1, 2).
Решение
Плоскость, которая перпендикулярна координатной плоскости Oxy определяется общим неполным уравнением плоскости Ax+By+D=0 (А≠0, В≠0). Условием задачи дано, что плоскость проходит через начало координат, тогда D=0 и уравнение плоскости принимает вид Ax+By=0⇔x+BAy=0.
Найдем значение BA. В исходных данных фигурирует точка М0(-3, 1, 2), координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: -3+BA·1=0, откуда определяем BA=3.
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x+3y=0.
Ответ: x+3y=0.
23 ноября 2012
В этом уроке мы рассмотрим, как с помощью определителя составить уравнение плоскости. Если вы не знаете, что такое определитель, зайдите в первую часть урока — «Матрицы и определители». Иначе вы рискуете ничего не понять в сегодняшнем материале.
Уравнение плоскости по трем точкам
Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:
Задача. В пространстве даны три точки, не лежащие на одной прямой. Их координаты:
M = (x1, y1, z1);
N = (x2, y2, z2);
K = (x3, y3, z3);Требуется составить уравнение плоскости, проходящей через эти три точки. Причем уравнение должно иметь вид:
Ax + By + Cz + D = 0
где числа A, B, C и D — коэффициенты, которые, собственно, и требуется найти.
Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ — подставить координаты в уравнение Ax + By + Cz + D = 0. Получится система из трех уравнений, которая легко решается.
Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.
Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием без каких-либо обоснований и доказательств.
Уравнение плоскости через определитель
Хватит лирики, приступаем к делу. Для начала — теорема о том, как связаны определитель матрицы и уравнение плоскости.
Теорема. Пусть даны координаты трех точек, через которые надо провести плоскость: M = (x1, y1, z1); N = (x2, y2, z2); K = (x3, y3, z3). Тогда уравнение этой плоскости можно записать через определитель:
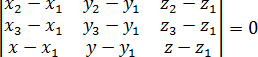
Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:
Задача. Составьте уравнение плоскости, проходящей через точки:
A1 = (0, 0, 1);
B = (1, 0, 0);
C1 = (1, 1, 1);
Составляем определитель и приравниваем его к нулю:
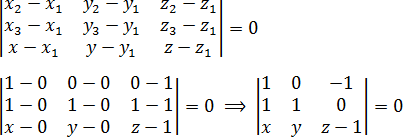
Раскрываем определитель:
a = 1 · 1 · (z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · (z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;
Как видите, при расчете числа d я немного «причесал» уравнение, чтобы переменные x, y и z шли в правильной последовательности. Вот и все! Уравнение плоскости готово!
Задача. Составьте уравнение плоскости, проходящей через точки:
A = (0, 0, 0);
B1 = (1, 0, 1);
D1 = (0, 1, 1);
Сразу подставляем координаты точек в определитель:
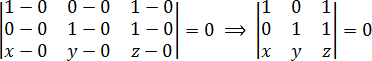
Снова раскрываем определитель:
a = 1 · 1 · z + 0 · 1 · x + 1 · 0 · y = z;
b = 1 · 1 · x + 0 · 0 · z + 1 · 1 · y = x + y;
d = a − b = z − (x + y) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;
Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно, но все-таки рекомендуется — чтобы упростить дальнейшее решение задачи.
Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель — и все, уравнение готово.
На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит x2 или x3, а в какой — просто x. Чтобы окончательно разобраться с этим, давайте проследим, откуда берется каждое число.
Откуда берется формула с определителем?
Итак, разбираемся, откуда возникает такое суровое уравнение с определителем. Это поможет вам запомнить его и успешно применять.
Все плоскости, которые встречаются в задаче C2, задаются тремя точками. Эти точки всегда отмечены на чертеже, либо даже указаны прямо в тексте задачи. В любом случае, для составления уравнения нам потребуется выписать их координаты:
M = (x1, y1, z1);
N = (x2, y2, z2);
K = (x3, y3, z3).
Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:
T = (x, y, z)
Берем любую точку из первой тройки (например, точку M) и проведем из нее векторы в каждую из трех оставшихся точек. Получим три вектора:
MN = (x2 − x1, y2 − y1, z2 − z1);
MK = (x3 − x1, y3 − y1, z3 − z1);
MT = (x − x1, y − y1, z − z1).
Теперь составим из этих векторов квадратную матрицу и приравняем ее определитель к нулю. Координаты векторов станут строчками матрицы — и мы получим тот самый определитель, который указан в теореме:
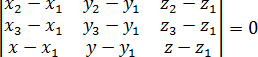
Эта формула означает, что объем параллелепипеда, построенного на векторах MN, MK и MT, равен нулю. Следовательно, все три вектора лежат в одной плоскости. В частности, и произвольная точка T = (x, y, z) — как раз то, что мы искали.
Замена точек и строк определителя
У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2. Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:
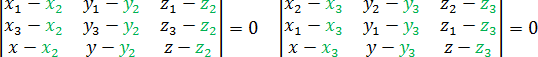
Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки T = (x; y; z) в самом верху. Пожалуйста, если вам так удобно:
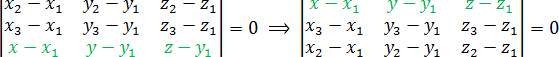
Некоторых смущает, что в одной из строчек присутствуют переменные x, y и z, которые не исчезают при подстановке точек. Но они и не должны исчезать! Подставив числа в определитель, вы должны получить вот такую конструкцию:
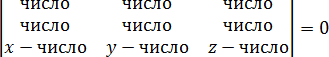
Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:
Ax + By + Cz + D = 0
Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.
Задача. Составьте уравнение плоскости, проходящей через точки:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1).
Итак, рассматриваем 4 точки:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1);
T = (x, y, z).
Для начала составим стандартный определитель и приравниваем его к нулю:
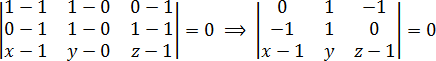
Раскрываем определитель:
a = 0 · 1 · (z − 1) + 1 · 0 · (x − 1) + (−1) · (−1) · y = 0 + 0 + y;
b = (−1) · 1 · (x − 1) + 1 · (−1) · (z − 1) + 0 · 0 · y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;
Все, мы получили ответ: x + y + z − 2 = 0.
Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными x, y, z не внизу, а вверху:
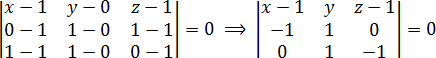
Вновь раскрываем полученный определитель:
a = (x − 1) · 1 · (−1) + (z − 1) · (−1) · 1 + y · 0 · 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) · 1 · 0 + y · (−1) · (−1) + (x − 1) · 1 · 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;
Мы получили точно такое же уравнение плоскости: x + y + z − 2 = 0. Значит, оно действительно не зависит от порядка строк. Осталось записать ответ.
Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.
В рассмотренной выше задаче мы использовали точку B1 = (1, 0, 1), но вполне можно было взять C = (1, 1, 0) или D1 = (0, 1, 1). В общем, любую точку с известными координатами, лежащую на искомой плоскости.
Смотрите также:
- Видеоурок по задачам C2: уравнение плоскости через определитель

- Уравнение плоскости в задаче C2. Часть 1: матрицы и определители

- Тест к уроку «Что такое числовая дробь» (легкий)

- Сводный тест по задачам B15 (1 вариант)

- Однородные тригонометрические уравнения: общая схема решения

- Задача B4: тарифы на сотовую связь

В декартовых координатах каждая плоскость
определяется уравнением первой степени
относительно неизвестных х, у и zи каждое уравнение первой степени с
тремя неизвестными определяет плоскость.
Возьмем произвольный вектор
![]() с началом в точке
с началом в точке![]() .
.
Выведем уравнение геометрического
места точек М(x,y,z),
для каждой из которых вектор![]() перпендикулярен
перпендикулярен
вектору![]() .
.
Запишем условие перпендикулярности
векторов:
![]() (13.1)
(13.1)
Полученное уравнение линейное относительно
x,y,z,
следовательно, оно определяет плоскость,
проходящую через точку![]() перпендикулярно вектору
перпендикулярно вектору![]() .
.
Вектор![]() называют нормальным вектором плоскости.
называют нормальным вектором плоскости.
Раскрывая скобки в полученном уравнении
плоскости и обозначая число![]() буквойD, представим его
буквойD, представим его
в виде:
Ax+By+Cz+D= 0.
(13.2)
Это уравнение называют общим уравнением
плоскости. А, В, С иD–
коэффициенты уравнения, А2+ В2+ С2![]() 0.
0.
1. Неполные уравнения плоскости.
Если в общем уравнении плоскости один,
два или три коэффициента равны нулю, то
уравнение плоскости называют неполным.
Могут представиться следующие случаи:
1) D= 0 – плоскость проходит
через начало координат;
2) А = 0 – плоскость параллельна оси Ох;
3) В = 0 – плоскость параллельна оси Оу;
4) С = 0 – плоскость параллельна оси Оz;
5) А = В = 0 – плоскость параллельна
плоскости ХОY;
6) А = С = 0 – плоскость параллельна
плоскости ХОZ;
7) В = С = 0 – плоскость параллельна
плоскости YOZ;
8) А = D= 0 – плоскость
проходит через ось Ох;
9) В = D= 0 – плоскость
проходит через ось Оу;
10) С = D= 0 – плоскость
проходит через ось Оz;
11) А = В = D= 0 – плоскость
совпадает с плоскостьюXOY;
12) А = С = D= 0 – плоскость
совпадает с плоскостьюXOZ;
13) С = В = D= 0 – плоскость
совпадает с плоскостьюYOZ.
2. Уравнение плоскости в отрезках.
Если в общем уравнении плоскости D![]() 0,
0,
то его можно преобразовать к виду
![]() ,
,
(13.3)
которое называют уравнением плоскости
в отрезках.
![]() – определяют длины отрезков, отсекаемых
– определяют длины отрезков, отсекаемых
плоскостью на координатных осях.
3. Нормальное уравнение плоскости.
Уравнение
![]() ,
,
(13.4)
где
![]() – направляющие косинусы нормального
– направляющие косинусы нормального
вектора плоскости![]() ,
,
называют нормальным уравнением плоскости.
Для приведения общего уравнение плоскости
к нормальному виду его надо умножить
на нормирующий множитель![]() :
:![]() ,
,
при этом знак перед корнем выбирают из
условия
![]() .
.
Расстояние dот точки![]() до плоскости определяют по формуле:
до плоскости определяют по формуле:![]() .
.
4. Уравнение плоскости, проходящей
через три точки
![]() .
.
Возьмем произвольную точку плоскости
М(x,y,z)
и соединим точку М1с каждой из
трех оставшихся. Получим три вектора![]() .
.
Для того, чтобы три вектора принадлежали
одной плоскости, необходимо и достаточно,
чтобы они были компланарны. Условием
компланарности трех векторов служит
равенство нулю их смешанного произведения,
то есть![]() .
.
Записывая это равенство через координаты
точек, получим искомое уравнение:
 .
.
(13.5)
5. Угол между плоскостями.
Плоскости могут быть параллельны,
совпадать или пересекаться, образуя
двугранный угол![]() .
.
Пусть две плоскости заданы общими
уравнениями![]() и
и![]() .
.
Чтобы плоскости совпадали, нужно, чтобы
координаты любой точки, удовлетворяющей
первому уравнению, удовлетворяли бы и
второму уравнению.
Это будет иметь место, если
![]() .
.
Если
![]() ,
,
то плоскости параллельны.
Угол
![]() ,
,
образованный двумя пересекающимися
плоскостями, равен углу, образованному
их нормальными векторами. Косинус угла
между векторами определяется по формуле:![]()
Если
![]() ,
,
то плоскости перпендикулярны.
Пример 21. Составить уравнение
плоскости, которая проходит через две
точки![]() и
и![]() перпендикулярно к плоскости
перпендикулярно к плоскости![]() .
.
Решение:
Запишем искомое уравнение в общем
виде:![]() .
.
Так как плоскость должна проходить
через точки![]() и
и![]() ,
,
то координаты точек должны удовлетворять
уравнению плоскости. Подставляя
координаты точек![]() и
и![]() ,
,
получаем:![]() и
и![]() .
.
Из условия перпендикулярности плоскостей
имеем:
![]() .
.
Вектор![]() расположен в искомой плоскости и,
расположен в искомой плоскости и,
следовательно, перпендикулярен
нормальному вектору:![]() .
.
Объединяя полученные уравнения, имеем:

Решив систему, получим:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
Искомое уравнение имеет вид:
![]() .
.
Второй способ. Нормальный вектор
![]() заданной плоскости имеет координаты
заданной плоскости имеет координаты![]() .
.
Вектор![]() .
.
Нормальный вектор![]() искомой плоскости перпендикулярен
искомой плоскости перпендикулярен
вектору![]() и вектору
и вектору![]() ,
,
т.е. коллинеарен векторному произведению![]() .
.
Вычислим векторное произведение: .
.
Вектор
![]() .
.
Запишем уравнение плоскости, проходящей
через точку![]() перпендикулярно вектору
перпендикулярно вектору![]() :
:
![]() ,
,
или![]() искомое
искомое
уравнение.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение. Направляющими векторами плоскости называются два неколлинеарных вектора, лежащих в этой плоскости.
Уравнения плоскости в координатной форме
Общее уравнение плоскости в декартовой системе координат:
![[Ax + By + Cz + D = 0, qquad (A^2 + B^2 + C^2)
e 0,]](https://umath.ru/wp-content/ql-cache/quicklatex.com-dab9d65a4b00106fffb322cf99c6b219_l3.png)
при этом вектор с координатами является нормальным вектором к плоскости.
Уравнение плоскости, проходящей через три точки, не лежащие на одной прямой, можно получить, если решить систему уравнений

Здесь и — координаты трёх точек плоскости. Заметим, что уравнений в системе три, а переменных — четыре. То есть решение этой системы мы получаем с точностью до коэффициента. Этот коэффициент роли не играет — после подстановки решения в уравнение плоскости на него можно сократить. Рассмотрим это на примере.
- Параметрические уравнения плоскости:
-

- Здесь — некоторая точка плоскости, и — координаты направляющих веторов плоскости, — параметры.
Уравнения плоскости в векторном виде
- Нормальное векторное уравнение плоскости:
-
![[( extbf{r} - extbf{r}_0, extbf{n}) = 0, qquad ( extbf{n}
e 0),]](https://umath.ru/wp-content/ql-cache/quicklatex.com-7cb581ae3680a9e3cc2dc584abecdc0b_l3.png)
- где — нормальный вектор плоскости.
- Это уравнение также можно записать в виде
-
![[( extbf{r}, extbf{n}) = D, qquad ( extbf{n}
e 0).]](https://umath.ru/wp-content/ql-cache/quicklatex.com-a279e3c74272105dd57089c5aa46a317_l3.png)
Если вектор — единичный (его длина равна ), то величина есть расстояние от точки до плоскости. Смысл этого уравнения в том, что проекция радиус-вектора любой точки плоскости на нормаль к ней есть постоянная величина, равная расстоянию до этой плоскости.
- Уравнение плоскости, проходящей через три точки с радиус-векторами и можно записать в векторном виде:
- Если радиус векторы имеют соответственно координаты то в координатной форме это уравнение запишется так:
Источник: https://umath.ru/theory/uravnenie-ploskosti/
Уравнения плоскости: общее, через три точки, нормальное
Чтобы получить общее уравнение плоскости, разберём плоскость, проходящую через заданную точку.
Пусть в пространстве есть три уже известные нам оси координат — Ox, Oy и Oz. Подержим лист бумаги так, чтобы он оставался плоским. Плоскостью будет сам лист и его продолжение во всех направлениях.
Пусть P произвольная плоскость в пространстве. Всякий перпендикулярный ей вектор называется вектором нормали к этой плоскости. Естественно, речь идёт о ненулевом векторе.

Если известна какая-нибудь точка плоскости P и какой-нибудь вектор нормали к ней, то этими двумя условиями плоскость в пространстве вполне определена (через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору). Общее уравнение плоскости будет иметь вид:
![]()
Итак, условия, которыми задаётся уравнение плоскости, есть. Чтобы получить само уравнение плоскости, имеющее приведённый выше вид, возьмём на плоскости P произвольную точку M с переменными координатами x, y, z.
Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис. 1).
Для этого, согласно условию перпендикулярности векторов, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, то есть
.
![]()
![]()
![]()
![]()
Так как точка M(x; y; z) выбрана на плоскости произвольно, то последнему уравнению удовлетворяют координаты любой точки, лежащей на плоскости P. Для точки N, не лежащей на заданной плоскости, , т.е. равенство (1) нарушается.
Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .
Решение. Используем формулу (1), еще раз посмотрим на неё:
![]()
В этой формуле числа A, B и C координаты вектора , а числа x0, y0 и z0 — координаты точки .
Вычисления очень простые: подставляем эти числа в формулу и получаем
![]()
Умножаем всё, что нужно умножить и складываем просто числа (которые без букв). Результат:
![]()
Требуемое уравнение плоскости в этом примере оказалось выражено общим уравнением первой степени относительно переменных координат x, y, z произвольной точки плоскости.
Итак, уравнение вида
![]()
называется общим уравнением плоскости.
Пример 2. Построить в прямоугольной декартовой системе координат плоскость, заданную уравнением .
Решение. Для построения плоскости необходимо и достаточно знать какие-либо три её точки, не лежащие на одной прямой, например, точки пересечения плоскости с осями координат.
Как найти эти точки? Чтобы найти точку пересечения с осью Oz, нужно в уравнение, данное в условии задачи, вместо икс и игрека подставить нули: x = y = 0. Поэтому получаем z = 6. Таким образом, заданная плоскость пересекает ось Oz в точке A(0; 0; 6).
Точно так же находим точку пересечения плоскости с осью Oy. При x = z = 0 получаем y = −3, то есть точку B(0; −3; 0).
И, наконец, находим точку пересечения нашей плоскости с осью Ox. При y = z = 0 получим x = 2, то есть точку C(2; 0; 0). По трём полученным в нашем решении точкам A(0; 0; 6), B(0; −3; 0) и C(2; 0; 0) строим заданную плоскость.
Решения типичных задач, которые бывают на контрольных работах — в пособии «Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке».
Рассмотрим теперь частные случаи общего уравнения плоскости. Это случаи, когда те или иные коэффициенты уравнения (2) обращаются в нуль.
1. При D = 0 уравнение определяет плоскость, проходящую через начало координат, так как координаты точки 0(0; 0; 0) удовлетворяют этому уравнению.
2. При A = 0 уравнение определяет плоскость, параллельную оси Ox, поскольку вектор нормали этой плоскости перпендикулярен оси Ox (его проекция на ось Ox равна нулю). Аналогично, при B = 0 плоскость параллельная оси Oy, а при C = 0 плоскость параллельна оси Oz.
3. При A = D = 0 уравнение определяет плоскость, проходящую через ось Ox, поскольку она параллельна оси Ox (A = 0) и проходит через начало координат (D = 0). Аналогично, плоскость проходит через ось Oy, а плоскость через ось Oz.
4. При A = B = 0 уравнение определяет плоскость, параллельную координатной плоскости xOy, поскольку она параллельна осям Ox (A = 0) и Oy (B = 0). Аналогично, плоскость параллельна плоскости yOz, а плоскость — плоскости xOz.
5. При A = B = D = 0 уравнение (или z = 0) определяет координатную плоскость xOy, так как она параллельна плоскости xOy (A = B = 0) и проходит через начало координат (D = 0). Аналогично, уравнение y = 0 в пространстве определяет координатную плоскость xOz, а уравнение x = 0 — координатную плоскость yOz.
Пример 3. Составить уравнение плоскости P, проходящей через ось Oy и точку .
Решение. Итак, плоскость проходит через ось Oy. Поэтому в её уравнении y = 0 и это уравнение имеет вид . Для определения коэффициентов A и C воспользуемся тем, что точка принадлежит плоскости P.
- Поэтому среди её координат есть такие, которые можно подставить в уравнению плоскости, которое мы уже вывели (). Смотрим ещё раз на координаты точки:
- M0(2; −4; 3).
- Среди них x = 2, z = 3. Подставляем их в уравнение общего вида и получаем уравнение для нашего частного случая:
- 2A + 3C = 0.
- Оставляем 2A в левой части уравнения, переносим 3C в правую часть и получаем
- A = −1,5C.
- Подставив найденное значение A в уравнение , получим
- или .
- Это и есть уравнение, требуемое в условии примера.
Решить задачу на уравнения плоскости самостоятельно, а затем посмотреть решение
Пример 4. Определить плоскость (или плоскости, если больше одной) относительно координатных осей или координатных плоскостей, если плоскость (плоскости) задана уравнением .
Посмотреть правильное решение и ответ.
Решения типичных задач, которые бывают на контрольных работах — в пособии «Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке».
Нет времени вникать в решение? Можно заказать работу! Пройти тест по теме Прямая и плоскость
Уравнение плоскости, проходящей через три точки
Как уже упоминалось, необходимым и достаточным условием для построения плоскости, кроме одной точки и вектора нормали, являются также три точки, не лежащие на одной прямой.
Пусть даны три различные точки , и , не лежащие на одной прямой. Так как указанные три точки не лежат на одной прямой, векторы и не коллинеарны, а поэтому любая точка плоскости лежит в одной плоскости с точками , и тогда и только тогда, когда векторы , и компланарны, т.е. тогда и только тогда, когда смешанное произведение этих векторов равно нулю.
Используя выражение смешанного произведения в координатах, получим уравнение плоскости
(3)
После раскрытия определителя это уравнение становится уравнением вида (2), т.е. общим уравнением плоскости.
- Пример 5. Составить уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой:
- , ,
- и определить частный случай общего уравнения прямой, если такой имеет место.
- Решение. По формуле (3) имеем:
- Раскрываем определитель по первой строке:
- Получили общее уравнение плоскости
- или после деления на -2:
- .
Это уравнение, в котором A = 0, т.е. оно определяет плоскость, параллельную оси Ox.
Решения типичных задач, которые бывают на контрольных работах — в пособии «Задачи на плоскость: параллельность, перпендикулярность, пересечение трёх плоскостей в одной точке».
Нормальное уравнение плоскости. Расстояние от точки до плоскости
- Нормальным уравнением плоскости называется её уравнение, записанное в виде
- ,
- где — направляющие косинусы нормали плоскости, — расстояние от начала координат до плоскости.
Нормалью к плоскости называется вектор, направление которого совпадает с направлением прямой, проведённой через начало координат перпендикулярно данной плоскости.
(Есть полная аналогия с нормалью к прямой на плоскости, с той лишь разницей, что нормальное уравнение прямой существует в двух измерениях, а нормальное уравнение плоскости — в трёх).
Пусть M — какая угодно точка пространства. Для нахождения отклонения точки M от плоскости следует в левую часть нормального уравнения плоскости подставить на место x, y и z подставить координаты этой точки.
Это правило позволяет найти и расстояние от точки M до плоскости: расстояние равно модулю отклонения, т.е.
,
так как расстояние не может быть отрицательным числом.
- Общее уравнение плоскости
- приводится к нормальному виду почленным умножением на нормирующий множитель, определяемый формулой
- .
Знак нормирующего множителя берётся противоположным знаку свободного члена в общем уравнении плоскости.
Пример 6. Привести уравнение плоскости к нормальному виду.
- Решение. Вычислим нормирующий множитель:
- .
- Знак нормирующего множителя положительный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим требуемое в условии примера нормальное уравнение плоскости:
- .
Пример 7. Вычислить величину отклонения и расстояния от точки до прямой, если точка задана координатами (-2; -4; 3), а плоскость задана общим уравнением .
Решение. Сначала приведём уравнение плоскости к нормальному виду. Вычислим нормирующий множитель:
- .
- Знак нормирующего множителя отрицательный, то есть, противоположен знаку свободного члена в общем уравнении плоскости. Умножим общее уравнение почленно на нормирующий множитель и получим нормальное уравнение плоскости:
- .
- Вычислим отклонение точки от плоскости:
- Найдём теперь расстояние от точки до плоскости как модуль отклонения:
Нет времени вникать в решение? Можно заказать работу! Пройти тест по теме Прямая и плоскость
Всё по теме «Прямая и плоскость»
Источник: https://function-x.ru/equations_of_plane.html
Презентация по математике на тему “Уравнение плоскости”
Инфоурок › Математика ›Презентации›Презентация по математике на тему «Уравнение плоскости»








Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
ЕЩЁ ПОДУМАЙте…
2 слайд Описание слайда:
Уравнение плоскости Преподаватель математики Семяшкина Ирина Васильевна ГПОУ «Ижемкий политехнический техникум»
3 слайд Описание слайда:
Цель: познакомить учащихся с понятием уравнения плоскости и её особыми случаями задания; Выработать практические навыки по изучаемой теме при решении задач.
4 слайд Описание слайда:
Проверка готовности. Греческий, латинский 3 (аксиома А1) , (ABC) Параллельно, пересекаться, совпадать Какой алфавит используют для обозначения плоскости? Сколькоточек достаточно, чтобыобозначить плоскость? Какобозначают плоскость? Как могут располагаться плоскости по отношению друг к другу?
5 слайд Описание слайда:
Общее уравнение плоскости Ax+By+Cz+D=0 где А, В, С, D – числовые коэффициенты
6 слайд Описание слайда:
Уравнения координатных плоскостей x = 0, плоскость Оyz y = 0, плоскость Оxz z = 0, плоскость Оxy
7 слайд Описание слайда:
Особые случаи уравнения: D = 0 Ax+By+Cz = 0 плоскость проходит через начало координат. А = 0 Ву + Cz +D = 0 плоскость параллельна оси Ох. В = 0 Ах + Cz +D = 0 плоскость параллельна оси Оу. C = 0 Ax+By+D = 0 плоскость параллельна оси Oz.
8 слайд Описание слайда:
Особые случаи уравнения: А = В = 0 Сz + D = 0 плоскость параллельна плоскости Оху. А = С = 0 Ву + D = 0 плоскость параллельна плоскости Охz. В = C= 0 Ах+D = 0 плоскость параллельна плоскости Оуz.
9 слайд Описание слайда:
Особые случаи уравнения: A = D = 0 By+Cz = 0 плоскость проходит через ось Ox. B = D = 0 Ax + Cz = 0 плоскость параллельна оси Оy. C = D = 0 Ах + By = 0 плоскость параллельна оси Оz.
10 слайд Описание слайда:
совпадают, если существует такое число k, что Две плоскости в пространстве: параллельны, если существует такое число k, что В остальных случаях плоскости пересекаются.
11 слайд Описание слайда:
Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору Итак, пусть произвольная плоскость в пространстве. Всякий перпендикулярный ей ненулевой вектор называется вектором нормали к этой плоскости. n1 n2
12 слайд Описание слайда:
Если известна какая-нибудь точка плоскости M0 и какой-нибудь вектор нормали к ней, то через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору. Общее уравнение плоскости будет иметь вид: Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору M0 A(x-x0)+B(y-y0)+C(z-z0)=0 n (A;B;C)
13 слайд Описание слайда:
Чтобы получить уравнение плоскости, имеющее приведённый вид, возьмём на плоскости произвольную точку M(x;y;z).
Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис), а для этого, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е. Вектор задан по условию.
Координаты вектора найдём по формуле : Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме: A(x-x0)+B(y-y0)+C(z-z0)=0
14 слайд Описание слайда:
Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору . Используем формулу A(x-x0)+B(y-y0)+C(z-z0)=0 Решение: Ответ: 5x + y — 4z — 3=0
15 слайд Описание слайда:
Уравнение плоскости, проходящей через три точки После раскрытия определителя это уравнение становится уравнением общего вида. Пусть даны три различные точки, не лежащие на одной прямой. Используя выражение смешанного произведения в координатах, получим уравнение плоскости:
16 слайд Описание слайда:
Пример 2. Составить уравнение плоскости, проходящей через три данные точки, не лежащие на одной прямой: ; и . Решение: Ответ: -4y + 2z — 2=0
17 слайд Описание слайда:
При равенстве нулю свободного коэффициента D уравнения общего уравнения плоскости уравнение определяет Плоскость, параллельную координатной плоскости Oxy Плоскость, проходящую через начало координат Полуплоскость Линию пересечения плоскостей ПРОВЕРИМ, ЧТО МЫ ЗАПОМНИЛИ….
18 слайд Описание слайда:
Вектор нормали это… Всякий ненулевой вектор Всякий перпендикулярный ненулевой вектор Всякий перпендикулярный плоскости ненулевой вектор Всякий перпендикулярный плоскости вектор
19 слайд Описание слайда:
Общее уравнение плоскости это… Ax+By+Cz=0 Ax+By+Cz=D Ax+By+Cz+D=0 A(x-x0)+B(y-y0)+C(z-z0)=0
20 слайд Описание слайда:
Домашнее задание рассмотреть другие способы нахождения уравнения плоскости; Решить задачу: В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания равна 4, и диагональ боковой грани равна 5. Написать уравнение плоскостей А1В1E и плоскости основания призмы.
21 слайд Описание слайда:
Используемые ресурсы: ПЛОСКОСТИ http://kramshifer.Ub.Ua/ru/board/view/38313/ ГЛАДЬ РЕКИ http://www.Raschetrasstoyanie.Com/%D0%A2%D0%BE%D0%BB%D1%81%D1%82%D0%BE%D0%B2%D1%81%D0%BA%D0%B8%D0%B9_%D0%9B%D0%B8%D1%81%D0%BA%D0%B8/%D1%84%D0%BE%D1%82%D0%BE ПЛОСКИЕ КАМНИ http://aqueouspic.Ru/smotret-komedii-romanticheskie-onlajn.Html ШАХМАТНАЯ ДОСКА http://www.1chess.Ru/index.Php?Show_aux_page=45 СМАЙЛИКИ http://www.baby.ru/blogs/post/314439509-43854232/
22 слайд Описание слайда:
Плоскость Oхy Z Y X O
23 слайд Описание слайда:
Плоскость Oхz Z Y X O
24 слайд Описание слайда:
Плоскость Oyz Z Y X O
25 слайд Описание слайда:
Плоскость параллельная плоскости Охy Z Y X O
26 слайд Описание слайда:
Плоскость параллельная плоскости Охz Z Y X O
27 слайд Описание слайда:
Плоскость параллельная плоскости Оyz Z Y X O
28 слайд Описание слайда:
Плоскость параллельная Оси ох Z Y X O
29 слайд Описание слайда:
СПАСИБО ЗА ВНИМАНИЕ
30 слайд
31 слайд
Скрыть
Важно! Узнайте, чем закончилась проверка учебного центра «Инфоурок»?
Общая информация
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Источник: https://infourok.ru/prezentaciya-po-matematike-na-temu-uravnenie-ploskosti-1753323.html
Уравнение плоскости по трем точкам
 Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим.
Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим. 

 2012-03-18
2012-03-18
Главная » СТАТЬИ » 14 Задание (2016) (C2) » Уравнение плоскости по трем точкам
Во многих стереометрических задачах, связанных с нахождением расстояния от точки до плоскости или расстояния между скрещивающимися прямыми, или угла между плоскостями, требуется найти уравнение плоскости. В этой статье я расскажу, как найти уравнение плоскости, если известны координаты трех точек, через которые она проходит.
Уравнение плоскости имеет вид: ![]() , где , , и — числовые коэффициенты.
, где , , и — числовые коэффициенты.
![]()
Так как точки принадлежат плоскости, то при подстановке их координат в уравнение плоскости, мы получим верные равенства.
Так как у нас три точки, мы должны получить систему из трех уравнений с четырьмя неизвестными. Примем коэффициент равным 1. Для этого разделим уравнение плоскости на . Получим:
Мы можем переписать это уравнение в виде:
Внимание! Если плоскость проходит через начало координат, то принимаем d=0.
- Чтобы найти коэффициенты А, В и С, подставим координаты точек , и в уравнение плоскости .
- Получим систему уравнений:
- Решив ее, мы найдем значения коэффициентов А, В и С.
- Решим задачу.
В правильной четырехугольной призме со стороной основания 12 и высотой 21 на ребре взята точка так, что равно 8. на ребре взята точка так, что равно 8. Написать уравнение плоскости :
- Поскольку для нахождения уравнения плоскости нам понадобятся координаты точек, я сразу помещаю призму в систему координат:
- Запишем координаты точек:
- Подставим их в систему уравнений:
- Отсюда:
- Подставим найденные коэффициенты в уравнение плоскости:
- Чтобы избавиться от дробных коэффициентов, умножим обе части уравнения плоскости на . Получим:
- Ответ: уравнение плоскости
И.В. Фельдман, репетитор по математике.
Источник: https://ege-ok.ru/2012/03/18/uravnenie-ploskosti
Общее уравнение плоскости : описание, примеры, решение задач, найти множество точек координатной
В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве.
Пусть нам дана прямоугольная система координат Oxyz в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x, y, и z, которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек.
Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Теорема 1
Любую плоскость, заданную в прямоугольной системе координат Oxyz трехмерного пространства, можно определить уравнением Ax + By + Cz + D = 0. В свою очередь, любое уравнение Ax + By + Cz + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A, B, C, D – некоторые действительные числа, и числа A, B, C не равны одновременно нулю.
Доказательство
Теорема состоит из двух частей. Разберем доказательство каждой из них.
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида Ax + By + Cz + D = 0. Допустим, задана некоторая плоскость и точка M0(x0, y0, z0), через которую эта плоскость проходит. Нормальным вектором этой плоскости является n→= (A, B, C). Приведем доказательство, что указанную плоскость в прямоугольной системе координат Oxyz задает уравнение Ax + By + Cz + D = 0.
Возьмем произвольную точку заданной плоскости M(x, y, z).В таком случае векторы n→= (A, B, C) и M0M→=(x-x0, y-y0, z-z0) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n→, M0M→=Ax-x0+B(y-y0)+C(z-z0)=Ax+By+Cz-(Ax0+By0+Cz0)
Примем D=-(Ax0+By0+Cz0) , тогда уравнение преобразуется в следующий вид: Ax + By + Cz + D = 0. Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида Ax + By + Cz + D = 0 задает некоторую плоскость в прямоугольной системе координат Oxyz трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А, B, C одновременно не являются равными нулю. Тогда существует некоторая точка M0(x0, y0, z0), координаты которой отвечают уравнению Ax + By + Cz + D = 0, т.е. верным будет равенство Ax0 + By0 + Cz0 + D = 0. Отнимем левую и правую части этого равенства от левой и правой частей уравнения Ax + By + Cz + D = 0. Получим уравнение вида
A(x-x0) + B(y-y0) + C(z-z0) + D = 0, и оно эквивалентно уравнению Ax + By + Cz + D = 0. Докажем, что уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает некоторую плоскость.
Уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n→=(A, B, C) и M0M→=x-x0, y-y0, z-z0.
Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A(x-x0) + B(y-y0) + C(z-z0) + D = 0 множество точек M(x, y, z) задает плоскость, у которой нормальный вектор n→=(A, B, C). При этом плоскость проходит через точку M(x0, y0, z0).
Иначе говоря, уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает в прямоугольной системе координат Oxyz трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение Ax + By + Cz + D = 0 также определяет эту плоскость. Теорема доказана полностью.

Уравнение вида Ax + By + Cz + D = 0 называют общим уравнением плоскости в прямоугольной системе координат Oxyz трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ·Ax+λ·By+λ·Cz+λ·D=0, где λ – некое действительное число, не равное нулю.
Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением Ax+By+Cz+D=0, поскольку описывает то же самое множество точек трехмерного пространства.
Например, уравнения x-2·y+3·z-7=0 и -2·x+4·y-23·z+14=0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида Ax+By+Cz+D=0( при конкретных значениях чисел A, B, C, D). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
Укажем пример как иллюстрацию этих утверждений.
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства.
Заданной плоскости отвечает общее уравнение вида 4x + 5y – 5z + 20 = 0, и ему соответствуют координаты любой точки этой плоскости.
В свою очередь, уравнение 4x + 5y – 5z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.

Общее уравнение плоскости, проходящей через точку
Повторимся: точка M0(x0, y0, z0) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением Ax+By+Cz+D=0 в том случае, когда подставив координаты точки M0(x0, y0, z0) в уравнение Ax+By+Cz+D=0, мы получим тождество.
Пример 1
Заданы точки M0(1, -1, -3) и N0(0, 2, -8) и плоскость, определяемая уравнением 2x+3y-z-2=0. Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
- Решение
- Подставим координаты точки М0 в исходной уравнение плоскости:
- 2·1+3·(-1)-(-3)-2=0⇔0=0
- Мы видим, что получено верное равенство, значит точка M0(1, -1, -3) принадлежит заданной плоскости.
- Аналогично проверим точку N0. Подставим ее координаты в исходное уравнение:
- 2·0+3·2-(-8)-2=0⇔12=0
Равенство неверно. Таким, образом, точка N0(0, 2, -8) не принадлежит заданной плоскости.
Ответ: точка М0 принадлежит заданной плоскости; точка N0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n→=(A, B, C) — нормальный вектор для плоскости, определяемой уравнением Ax+By+Cz+D=0. Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
Пример 2
В прямоугольной системе координат задана плоскость 2x+3y-z+5=0. Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x, y, z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n→ исходной плоскости имеет координаты 2, 3, -1 . В свою очередь, множество нормальных векторов запишем так:
λ·n→=λ·2, λ·3, -λ, λ∈R, λ≠0
Ответ: λ·2, λ·3, -λ, λ∈R, λ≠0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n→=(A, B, C)является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M0(x0, y0, z0), принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n→=(A, B, C) будет выглядеть так: Ax+By+Cz+D=0. По условию задачи точка M0(x0, y0, z0) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство:Ax0+By0+Cz0+D=0
Вычитая соответственно правые и левые части исходного уравнения и уравнения Ax0+By0+Cz0+D=0, получим уравнение вида A(x-x0)+B(y-y0)+C(z-z0)=0. Оно и будет уравнением плоскости, проходящей через точку M0(x0, y0, z0) и имеющей нормальный вектор n→=(A, B, C).
- Возможно получить это уравнение другим способом.
- Очевидным фактом является то, что все точки М (x, y, z) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n→=(A, B, C) и M0M→=(x-x0, y-y0, z-z0) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
- n→, M0M→=A(x-x0)+B(y-y0)+C(z-z0)=0
Пример 3
Задана точка М0(-1, 2, -3), через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n→=(3, 7, -5). Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x0=-1, y0=2, z0=-3, A=3, B=7, C=-5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A(x-x0)+B(y-y0)+C(z-z0)=0
И получим:
3(x-(-1))+7(y-2)-5(z-(-3))=0⇔3x+7y-5z-26=0
- Допустим, М (x, y, z) – некоторая точки заданной плоскости. Определим координаты вектора M0M→ по координатам точек начала и конца:
- M0M→=(x-x0, y-y0, z-z0)=(x+1, y-2, z+3)
- Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
- n→, M0M→=0⇔3(x+1)+7(y-2)-5(z+3)=0⇔⇔3x+7y-5z-26=0
- Ответ: 3x+7y-5z-26=0
Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А, B, C, D отличны от нуля, общее уравнение плоскости Ax+By+Cz+D=0 называютполным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
- В случае, когда D = 0, мы получаем общее неполное уравнение плоскости: Ax+By+Cz+D=0⇔Ax+By+Cz=0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О (0, 0, 0), то придем к тождеству:
A·0+B·0+C·0=0⇔0≡0

- Если А = 0, В ≠ 0, С ≠ 0, или А ≠ 0, В = 0, С ≠0, или А ≠ 0, В ≠ 0, С = 0, то общие уравнения плоскостей имеют вид соответственно: By+Cz+D=0, или Ax+Cz+D=0, или Ax+By+D=0. Такие плоскости параллельны координатным осям Оx, Oy, Oz соответственно. Когда D=0, плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей By+Cz+D=0, Ax+Cz+D=0 и Ax+By+D=0 задают плоскости, которые перпендикулярны плоскостям Oyz, Oxz, Ozy соответственно.

- При А=0, В=0, С≠0, или А=0, В≠0, С=0, или А≠0, В=0, С=0 получим общие неполные уравнения плоскостей: Cz+D=0 ⇔z+DC=0⇔z=-DC⇔z=λ, λ∈R или By+D=0⇔y+DB=0⇔y=-DB⇔y=λ, λ∈R или Ax+D=0⇔x+DA=0⇔x=-DA⇔x=λ, λ∈R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям Oxy, Oxz, Oyz соответственно и проходят через точки 0, 0, -DC, 0, -DB, 0 и -DA, 0, 0 соответственно. При D=0 уравнения самих координатных плоскостей Oxy, Oxz, Oyz выглядят так: z=0, y=0, x=0
соответственно.

Пример 4
Задана плоскость, параллельная координатной плоскости Oyz и проходящая через точку М0(7, -2, 3). Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости Oyz, а, следовательно, может быть задана общим неполным уравнением плоскости Ax+D=0, A≠0⇔x+DA=0.
Поскольку точка M0(7, -2, 3) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x+DA=0, иначе говоря, должно быть верным равенство 7+DA=0 .
Преобразуем: DA=-7, тогда требуемое уравнение имеет вид: x-7=0.
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости Oyz.
Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости Oyz: i→=(1, 0, 0).
Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A(x-x0)+B(y-y0)+C(z-z0)=0⇔⇔1·(x-7)+0·(y+2)+0·(z-3)=0⇔⇔x-7=0
Ответ: x-7=0
Пример 5
Задана плоскость, перпендикулярная плоскости Oxy и проходящая через начало координат и точку М0(-3, 1, 2).
Решение
Плоскость, которая перпендикулярна координатной плоскости Oxy определяется общим неполным уравнением плоскости Ax+By+D=0 (А≠0, В≠0). Условием задачи дано, что плоскость проходит через начало координат, тогда D=0 и уравнение плоскости принимает вид Ax+By=0⇔x+BAy=0.
Найдем значение BA. В исходных данных фигурирует точка М0(-3, 1, 2), координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: -3+BA·1=0, откуда определяем BA=3.
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x+3y=0.
Ответ: x+3y=0.
Источник: https://Zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-ploskosti/
Решение типовых задач по теме “Плоскость”. Уравнение плоскости. Часть 1

Решение типовых задач по теме «Плоскость». Составить уравнение плоскости
Задача №1. Даны точки и . Написать уравнение плоскости, проходящей через точку и перпендикулярно к вектору .
Решение. Уравнение связки плоскостей, проходящей через точку , будет
![]()
Нормальный вектор
![]()
Подставляем проекции 2, 6 и 5 вектора на место A, В и С в уравнение связки, будем иметь:
или
Это и есть уравнение искомой плоскости (рис.1).
Ответ:
Задача №2. Написать уравнение плоскости, проходящей через точки , и .
Решения задач №1 и №2 подробно изложены в следующем видео
Задача №3. Написать уравнение плоскости, проходящей через точки и и перпендикулярной к плоскости 2x+4y+6z-7=0. Решение. Пусть М(х,у,z) произвольная точка искомой плоскости. Тогда векторы и принадлежат этой плоскости. Векторы и компланарны с нормальным вектором данной плоскости 2х+4y+бz-7=0.
Поэтому смешанное произведение этих трех векторов равно нулю:
или
Источник: https://math-helper.ru/vyisshaya-matematika/reshenie-tipovyih-zadach-po-teme-ploskost-uravnenie-ploskosti
Как составить уравнение плоскости
Плоскость является одним из основных понятий, связывающих планиметрию и стереометрию (разделы геометрии). Эта фигура также часто встречается в задачах по аналитической геометрии. Чтобы составить уравнение плоскости, достаточно иметь координаты трех ее точек.
Для второго основного способа составления уравнения плоскости необходимо указать координаты одной точки и направление нормального вектора.  Если известны координаты трех точек, через которые проходит плоскость, то запишите уравнение плоскости в виде определителя третьего порядка. Пусть (х1, х2, х3), (у1, у2, у3) и (z1, z2, z3) – координаты первой, второй и третьей точки соответственно. Тогда уравнение плоскости, проходящей через эти три точки, выглядит следующим образом:│ x-x1 y-y1 z-z1 ││x2-x1 y2-y1 z2-z1│ = 0
Если известны координаты трех точек, через которые проходит плоскость, то запишите уравнение плоскости в виде определителя третьего порядка. Пусть (х1, х2, х3), (у1, у2, у3) и (z1, z2, z3) – координаты первой, второй и третьей точки соответственно. Тогда уравнение плоскости, проходящей через эти три точки, выглядит следующим образом:│ x-x1 y-y1 z-z1 ││x2-x1 y2-y1 z2-z1│ = 0
│x3-x1 y3-y1 z3-z1│
Пример: составить уравнение плоскости, проходящей через три точки с координатами: (-1; 4; -1), (-13; 2; -10), (6; 0; 12). Решение: подставляя координаты точек в вышеприведенную формулу, получим:│x+1 y-4 z+1 ││-12 -2 -9 │ =0│ 7 -4 13 │В принципе, это и есть уравнение искомой плоскости. Однако если разложить определитель по первой строке, то получится более простое выражение:-62*(х+1) + 93*(у-4) + 62*(z+1) = 0.
Разделив обе части уравнения на 31 и приведя подобные, получим:
-2х+3у+2z-12=0.Ответ: уравнение плоскости, проходящей через точки с координатами(-1; 4; -1), (-13; 2; -10) и (6; 0; 12)
-2х+3у+2z-12=0.
Если уравнение плоскости, проходящей через три точки, требуется составить без использования понятия «определитель» (младшие классы, тема – системы линейных уравнений), то воспользуйтесь следующим рассуждением.
Уравнение плоскости в общем виде имеет вид Ах+ВуСz+D=0, причем одной плоскости соответствует множество уравнений с пропорциональными коэффициентами. Для простоты вычислений параметр D обычно принимают равным 1, если плоскость не проходит через начало координат (для плоскости, проходящей через начало координат, D=0).
Так как координаты точек, принадлежащих плоскости, должны удовлетворять вышеприведенному уравнению, то в итоге получается система из трех линейных уравнений:-A+4B-C+1=0-13A+2B-10C+1=06A+12C+1=0,решив которую и избавившись от дробей, получим вышеприведенное уравнение
(-2х+3у+2z-12=0).
Если заданы координаты одной точки (х0, у0, z0) и координаты вектора нормали (А, В, С), то чтобы составить уравнение плоскости, просто запишите уравнение:А(х-х0)+В(у-у0)+С(z-z0)=0.
После приведения подобных это и будет уравнением плоскости.
Если требуется решить задачу составления уравнения плоскости, проходящей через три точки, в общем виде, то разложите уравнение плоскости, записанной через определитель, по первой строке:(x-x1)*(у2-y1)*(z3-z1) – (x-x1)*(z2-z1)*(y3-y1) – (y-y1)*(x2-x1)*(z3-z1) + (y-y1)*(z2-z1)*(x3-x1) + (z-z1)*(x2-x1)*(y3-y1) – (z-z1)*(y2-y1)*(x3-x1) = 0.
Хотя это выражение и более громоздкое, зато в нем не используется понятие определителя и оно более удобно для составления программ.
- составить уравнение плоскости проходящей
- Войти на сайт
- или
Источник: https://www.kakprosto.ru/kak-92763-kak-sostavit-uravnenie-ploskosti
9.7. Уравнение плоскости
Рассмотрим произвольную точку в пространстве и некоторый вектор Очевидно, что геометрическим местом точек таких, что вектор перпендикулярен вектору будет плоскость, проходящая через точку M перпендикулярно прямой, для которой вектор является направляющим. Нашей задачей будет установить уравнение плоскости, то есть найти соотношение, которому удовлетворяют координаты точки A.
- Запишем условие перпендикулярности векторов с использованием скалярного произведения:
- Запишем последнее равенство в координатах:
- Поскольку все наши выкладки были равносильными, то это и есть уравнение плоскости, проходящей через заданную точку. Преобразуем его к виду
- Обозначая получим
- Это и есть так называемое общее уравнение плоскости.
Определение 9.19.
Вектор называется нормальным вектором (или просто нормалью) для плоскости, заданной общим уравнением (1).
Нормальный вектор к плоскости перпендикулярен ей, что следует из самого вывода уравнения плоскости.
Рассмотрим плоскость 3x + 2y + z – 6 = 0. Пусть A – точка пересечения этой плоскости с осью Ox, то есть A(2; 0; 0). Точка B(0; 3; 0) – это точка пересечения данной плоскости с осью Oy, точка C(0; 0; 6) – с осью Oz (чертеж 9.7.1). Уравнение называется уравнением плоскости в отрезках на осях.
Эта плоскость пересекает оси Ox, Oy, Oz соответственно в точках A(a; 0; 0), B(0; b; 0), C(0; 0; c).
Плоскость, изображенная на чертеже 9.7.1, имеет такое уравнение в отрезках на осях:
| High end escorts Paris |
| High end escorts Paris |
| cipriani-models.com |
Источник: https://mathematics.ru/courses/stereometry/content/chapter9/section/paragraph7/theory.html
Уравнение плоскости.
Навигация по странице:
- Плоскость – определение
- Общее уравнение плоскости
- Уравнение плоскости в отрезках
- Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали
- Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой
Определение. Плоскость – есть поверхность, полностью содержащая, каждую прямую, соединяющую любые её точки.
Общее уравнение плоскости
Любую плоскость можно задать уравнением плоскости первой степени вида
A x + B y + C z + D = 0
где A, B и C не могут быть одновременно равны нулю.
Уравнение плоскости в отрезках
Если плоскость пересекает оси OX, OY и OZ в точках с координатами (a, 0, 0), (0, b, 0) и (0, 0, с), то она может быть найдена, используя формулу уравнения плоскости в отрезках
| x | + | y | + | z | = 1 |
| a | b | c |
Уравнение плоскости, проходящей через точку, перпендикулярно вектору нормали
Чтобы составить уравнение плоскости, зная координаты точки плоскости M(x0, y0, z0) и вектора нормали плоскости n = {A; B; C} можно использовать следующую формулу.
A(x – x0) + B(y – y0) + C(z – z0) = 0
Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой
Если заданы координаты трех точек A(x1, y1, z1), B(x2, y2, z2) и C(x3, y3, z3), лежащих на плоскости, то уравнение плоскости можно найти по следующей формуле
| x – x1 | y – y1 | z – z1 | = 0 |
| x2 – x1 | y2 – y1 | z2 – z1 | |
| x3 – x1 | y3 – y1 | z3 – z1 |
