Как составить формулу суммы ряда

Общий член ряда представляе собой рациональную дробь. Выполним разложение дроби на простейшие с помощью метода неопределенных коэффициентов:

$$ frac{1}{(2n+1)(2n+3)} = frac{A}{2n+1} + frac{B}{2n+3} = frac{A(2n+3)+B(2n+1)}{(2n+1)(2n+3)} $$

Приравниваем числитель последней дроби к числителю первой дроби:

$$ A(2n+3)+B(2n+1) = 1 $$

Раскрываем скобки:

$$ 2An + 3A + 2Bn + B = 1 $$

Теперь определяем находим неизвестные коэффициенты:

$$ begin{cases} n^0: &2A+2B=0 \ n^1: &3A+B=1 end{cases}Rightarrow begin{cases} A=frac{1}{2} \ B=-frac{1}{2} end{cases} $$

После разложения общий член ряда записывается следующим образом:

$$ a_n =frac{1}{(2n+1)(2n+3)}=frac{1}{2} frac{1}{2n+1} – frac{1}{2} frac{1}{2n+3} $$

Далее составим частичную сумму ряда: $$ S_n = a_1 + a_2 + a_3 + a_4 + … + a_n $$

$$ a_1 = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) $$

$$ a_2 = frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) $$

$$ a_3 = frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) $$

$$ …………………………………. $$

$$ a_{n-1}=frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) $$

$$ a_n = frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) $$

Замечание

Достаточно часто читатели нам присылают просьбы найти суммы своих рядов по причине того, что они не понимают, откуда получается $ a_{n-1} $. Обратите внимание, чтобы составить $ a_{n-1} $ необходимо подставить в $ a_n $ вместо буковки $ n $ выражение $ n-1 $. После выполнить раскрытие скобок.

Итого, получаем:

$$ S_n = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}bigg ) + frac{1}{2} bigg (frac{1}{5}-frac{1}{7}bigg ) + frac{1}{2} bigg (frac{1}{7}-frac{1}{9}bigg ) + … $$

$$ … + frac{1}{2} bigg (frac{1}{2n-1}-frac{1}{2n+1} bigg ) + frac{1}{2} bigg (frac{1}{2n+1}-frac{1}{2n+3} bigg ) = $$

Выносим дробь одну вторую $ frac{1}{2} $ за скобки:

$$ = frac{1}{2} bigg (frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9} … + $$

$$ + … frac{1}{2n-1} – frac{1}{2n+1} + frac{1}{2n+1} – frac{1}{2n+3} bigg) = $$

Замечаем, что в скобках есть подобные слагаемые, которые взаимно уничтожаются. Остаются только лишь два из них:

$$ S_n = frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) $$

Теперь осталось вычислить предел частичной суммы $ S_n $. Если он существует и конечен, то он является суммой ряда, а сам ряд сходится:

$$ S=lim_{ntoinfty} S_n = lim_{ntoinfty} frac{1}{2}bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = $$

$$ = frac{1}{2} lim_{ntoinfty} bigg (frac{1}{3}-frac{1}{2n+3} bigg ) = frac{1}{2} cdot frac{1}{3} = frac{1}{6} $$

Нахождение суммы числового ряда. Первая часть.

В теме про основные понятия числовых рядов было указано определение суммы ряда. Вот оно:

Если существует конечный предел $S=lim_{ntoinfty}S_n$, то его называют суммой ряда $sumlimits_{n=1}^{infty}u_n$ и сам ряд именуют сходящимся. Если же $lim_{ntoinfty}S_n=infty$ или $lim_{ntoinfty}S_n$ не существует, то ряд называют расходящимся.

Если понятие “частичная сумма” вызывает вопросы, то советую посмотреть раздел про частичную сумму ряда, обратив внимание на пример №4. В этом примере подробно раскрывается суть частичной суммы и остатка.

В данной теме нас будет интересовать вопрос нахождения сумм числовых рядов по определению. Определение суммы ряда опирается на значение $lim_{ntoinfty}S_n$, поэтому для нахождения суммы нам нужно выполнить два шага:

1. Составить n-ю частичную сумму $S_n$;
2. Найти $lim_{ntoinfty}S_n$ (если он существует).

Если конечный $lim_{ntoinfty}S_n$ существует, то его значение и будет суммой рассматриваемого ряда, а сам ряд будет именоваться сходящимся. Если же $lim_{ntoinfty}S_n=infty$ или $lim_{ntoinfty}S_n$ не существует, то ряд будет расходиться. Есть несколько стандартных приёмов, которые применяются для нахождения суммы числовых рядов. Например, для нахождения суммы ряда, общий член которого имеет вид рациональной дроби $u_n=frac{P(n)}{Q(n)}$, вполне подходит такой алгоритм:

1. Разложить дробь $frac{P(n)}{Q(n)}$ на элементарные дроби (процедура разложения описана тут).
2. Записать выражение для частичной суммы $S_n$, используя результаты предыдущего пункта.
3. Перегруппировать слагаемые в выражении для $S_n$, приведя их к удобному для сокращения виду.
4. Используя результат предыдущего пункта, найти $lim_{ntoinfty}S_n$.

Для нахождения суммы ряда нередко удобно использовать и такое свойство:

Пусть общий член ряда $sumlimits_{n=1}^{infty}u_n$ можно представить в виде $u_n=b_{n+1}-b_n$. Если существует конечный предел $lim_{ntoinfty}b_n=b$, то ряд $sumlimits_{n=1}^{infty}u_n$ сходится. При этом частичная сумма ряда равна $S_{n}=b_{n+1}-b_1$, а сумма ряда $S=b-b_1$.

Доказательство этого свойства может быть интересно не всем читателям, поэтому я скрою его под примечание.

Доказательство свойства: показатьскрыть

Во всех изложенных ниже примерах члены рядов будем обозначать буквами $u_1$ (первый член ряда), $u_2$ (второй член ряда) и так далее. Запись $u_n$ будет обозначать общий член ряда.

Пример №1

Найти сумму ряда $sumlimits_{n=1}^{infty}(-1)^{n+1}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=(-1)^{n+1}$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов числового ряда:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=\=(-1)^2+(-1)^3+(-1)^4+(-1)^5+ldots+(-1)^{n+1}=1-1+1-1+ldots+(-1)^n.
$$

Вопрос в следующем: чему равна эта сумма? Если в частичных суммах мы станем брать чётное количество слагаемых, они попарно сократятся:

begin{aligned}
& S_2=1-1=0;\
& S_4=1-1+1-1=0;\
& S_6=1-1+1-1+1-1=0;\
& S_8=1-1+1-1+1-1+1-1=0.
end{aligned}

Итак, частичная сумма, содержащая чётное количество слагаемых, равна 0. Т.е. если $n$ – чётное число, то $S_n=0$. Фразу “n – чётное число” можно записать так: $n=2k$, $kin N$. В самом деле, подставляя вместо $k$ значения 1, 2, 3, 4 будем получать $n=2cdot 1=2$, $n=2cdot 2=4$, $n=2cdot 3=6$, $n=2cdot 4=8$ и так далее. Итак, $S_{2k}=0$.

Если мы станем брать нечётное количество слагаемых (1, 3, 5 и т.д.), то сумма станет равна 1:

begin{aligned}
& S_1=1;\
& S_3=1-1+1=1;\
& S_5=1-1+1-1+1=1;\
& S_7=1-1+1-1+1-1+1=1.
end{aligned}

Таким образом, если $n$ – нечётное число, то $S_n=1$. Фразу “n – нечётное число” можно записать так: $n=2k-1$, $kin N$. В самом деле, подставляя вместо $k$ значения 1, 2, 3, 4 будем получать $n=2cdot 1-1=1$, $n=2cdot 2-1=3$, $n=2cdot 3-1=5$, $n=2cdot 4-1=7$ и так далее. Итак, $S_{2k-1}=1$.

Формально равенство $S_{2k-1}=1$ можно доказать с помощью формулы $S_{2k}=S_{2k-1}+u_{2k}$. Так как $S_{2k}=0$, то $S_{2k-1}+u_{2k}=0$, т.е. $S_{2k-1}=-u_{2k}$. Так как $u_{2k}=(-1)^{2k+1}=left((-1)^2right)^kcdot (-1)^1=-1$, то $S_{2k-1}=-(-1)=1$.

Возникает вопрос: как быть с пределом $lim_{ntoinfty}S_n$? Ведь если $n$ – чётное число, т.е. $n=2k$, то:

$$
lim_{ntoinfty}S_n=lim_{ktoinfty}S_{2k}=lim_{ktoinfty}0=0.
$$

С другой стороны, если $n$ – нечётное число, то:

$$
lim_{ntoinfty}S_n=lim_{ktoinfty}S_{2k-1}=lim_{ktoinfty}1=1.
$$

Что мы получили? А получили мы следующее: последовательность частичных сумм ${S_n}$ имеет две подпоследовательности: ${S_{2k-1}}$ и ${S_{2k}}$, пределы которых различны. Следовательно, последовательность ${S_n}$ не имеет предела. Вывод: ряд не имеет суммы, т.е. расходится.

Здесь стоит обратить внимание вот на что: следует различать случаи, когда предел равен бесконечности (см. следующий пример №2), и когда предела попросту не существует. Хотя и в том и в другом случаях ряд будет расходиться.

Ответ: ряд расходится.

Пример №2

Найти сумму ряда $sumlimits_{n=1}^{infty}(3n+1)$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=3n+1$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов заданного числового ряда:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=4+7+10+13+ldots+3n+1.
$$

Эту сумму можно записать в более коротком виде. Дело в том, что последовательность 4, 7, 10, 13 и т.д. есть арифметическая прогрессия, первый член которой равен 4, а разность равна 3. Сумма первых n членов этой прогрессии такова:

$$
4+7+10+13+ldots+3n+1=frac{4+3n+1}{2}cdot n=frac{3n+5}{2}cdot{n}.
$$

Итак, $S_n=frac{3n+5}{2}cdot n$. Найдем $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{3n+5}{2}cdot nright)=+infty.
$$

Так как $lim_{ntoinfty}S_n=+infty$, то ряд расходится.

Если немного выйти за рамки данной темы, то стоит отметить, что расходимость этого ряда легко доказывается с помощью необходимого признака сходимости.

Ответ: ряд расходится.

Пример №3

Найти сумму ряда $sumlimits_{n=1}^{infty}frac{2}{(2n+1)(2n+3)}$.

Решение

Так как нижний предел суммирования равен 1, то общий член ряда записан под знаком суммы: $u_n=frac{2}{(2n+1)(2n+3)}$. Составим n-ю частичную сумму ряда, т.е. просуммируем первые $n$ членов заданного числового ряда:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=frac{2}{3cdot 5}+frac{2}{5cdot 7}+frac{2}{7cdot 9}+frac{2}{9cdot 11}+ldots+frac{2}{(2n+1)(2n+3)}.
$$

Почему я пишу именно $frac{2}{3cdot 5}$, а не $frac{2}{15}$, будет ясно из дальнейшего повествования. Однако запись частичной суммы ни на йоту не приблизила нас к цели. Нам ведь нужно найти $lim_{ntoinfty}S_n$, но если мы просто запишем:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{2}{3cdot 5}+frac{2}{5cdot 7}+frac{2}{7cdot 9}+frac{2}{9cdot 11}+ldots+frac{2}{(2n+1)(2n+3)}right),
$$

то эта запись, совершенно верная по форме, ничего нам не даст по сути. Чтобы найти предел, выражение частичной суммы предварительно нужно упростить.

Для этого есть стандартное преобразование, состоящее в разложении дроби $frac{2}{(2n+1)(2n+3)}$, которая представляет общий член ряда, на элементарные дроби. Вопросу разложения рациональных дробей на элементарные посвящена отдельная тема (см., например, пример №3 на этой странице). Раскладывая дробь $frac{2}{(2n+1)(2n+3)}$ на элементарные дроби, будем иметь:

$$
frac{2}{(2n+1)(2n+3)}=frac{A}{2n+1}+frac{B}{2n+3}=frac{Acdot(2n+3)+Bcdot(2n+1)}{(2n+1)(2n+3)}.
$$

Приравниваем числители дробей в левой и правой частях полученного равенства:

$$
2=Acdot(2n+3)+Bcdot(2n+1).
$$

Чтобы найти значения $A$ и $B$ есть два пути. Можно раскрыть скобки и перегруппировать слагаемые, а можно просто подставить вместо $n$ некие подходящие значения. Сугубо для разнообразия в этом примере пойдём первым путём, а следующем – будем подставлять частные значения $n$. Раскрывая скобки и перегруппировывая слагаемые, получим:

$$
2=2An+3A+2Bn+B;\
2=(2A+2B)n+3A+B.
$$

В левой части равенства перед $n$ стоит ноль. Если угодно, левую часть равенства для наглядности можно представить как $0cdot n+ 2$. Так как в левой части равенства перед $n$ стоит ноль, а в правой части равества перед $n$ стоит $2A+2B$, то имеем первое уравнение: $2A+2B=0$. Сразу разделим обе части этого уравнения на 2, получив после этого $A+B=0$.

Так как в левой части равенства свободный член равен 2, а в правой части равенства свободный член равен $3A+B$, то $3A+B=2$. Итак, имеем систему:

$$
left{begin{aligned}
& A+B=0;\
& 3A+B=2.
end{aligned}right.
$$

Можно решать эту систему методом Крамера, методом Гаусса или с помощью обратной матрицы. Однако проще всего банально выразить из первого уравнения $A=-B$ и подставить во второе:

$$
3cdot (-B)+B=2;; -2B=2; ; B=-1.
$$

Так как $B=-1$, то $A=-B=1$. Подставляя найденные значения $A=1$ и $B=-1$ в формулу $frac{2}{(2n+1)(2n+3)}=frac{A}{2n+1}+frac{B}{2n+3}$, будем иметь:

$$
frac{2}{(2n+1)(2n+3)}=frac{1}{2n+1}+frac{-1}{2n+3}=frac{1}{2n+1}-frac{1}{2n+3}.
$$

Итак, $u_n=frac{1}{2n+1}-frac{1}{2n+3}$. Используем полученное разложение для того, чтобы упростить формулу частичной суммы ряда. Покажу сначала решение стандартным путём, принятым в большинстве решебников и методичек.

Первый способ упрощения формулы для частичной суммы.

Мы получили разложение общего члена ряда на две дроби: $u_n=frac{1}{2n+1}-frac{1}{2n+3}$. Чтобы этот результат был более наглядным, я распишу несколько первых членов ряда по этой формуле:

begin{aligned}
& u_1=frac{2}{3cdot 5}=frac{1}{3}-frac{1}{5};\
& u_2=frac{2}{5cdot 7}=frac{1}{5}-frac{1}{7};\
& u_3=frac{2}{7cdot 9}=frac{1}{7}-frac{1}{9};\
& u_4=frac{2}{9cdot 11}=frac{1}{9}-frac{1}{11}.
end{aligned}

Давайте распишем частичную сумму, учитывая полученное разложение каждого элемента:

$$
S_n=u_1+u_2+u_3+u_4+ldots+u_n=frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9}+frac{1}{9}-frac{1}{11}+ldots+frac{1}{2n+1}-frac{1}{2n+3}.
$$

Как видите, все слагаемые этой суммы сокращаются, – кроме первого и последнего:

Итак, $S_n=frac{1}{3}-frac{1}{2n+3}$. Этот способ упрощения формулы для частичной суммы имеет простую суть: разложить общий член ряда на элементарные дроби, а потом сократить слагаемые.

Однако можно ли считать вышеуказанные рассуждения строгим доказательством? Полагаю, что в общем случае нет, и поясню почему. Дело в том, что мы должны “увидеть” (как любят писать некоторые авторы – “легко увидеть”), что слагаемые сокращаются. А если мы “увидим” не все слагаемые, которые останутся после сокращения? Где гарантии, что мы сократим именно то, что нужно? Нет гарантий. Понятно, что в случае рассматриваемой конкретной задачи всё тривиально и очевидно, но далеко не все частичные суммы рядов имеют такую простую структуру.

Формулу $S_n=frac{1}{3}-frac{1}{2n+3}$ можно принять в качестве гипотезы, которую ещё нужно доказать. Доказательство удобнее всего проводить методом математической индукции. Так как доказательством заинтересуются не все читатели, то я его скрыл под примечание.

Доказательство формулы $S_n=frac{1}{3}-frac{1}{2n+3}$: показатьскрыть

В стандартном курсе высшей математики обычно довольствуются “вычёркиванием” сокращающихся слагаемых, не требуя никаких доказательств. Итак, мы получили выражение для n-й частичной суммы: $S_n=frac{1}{3}-frac{1}{2n+3}$. Найдём значение $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{1}{3}-frac{1}{2n+3}right)=frac{1}{3}-0=frac{1}{3}.
$$

Вывод: заданный ряд сходится и сумма его $S=frac{1}{3}$.

Второй способ упрощения формулы для частичной суммы.

Этот способ основан на свойстве, записанном в начале страницы. По сути, он схож с предыдущим, – разница лишь в применении уже готовой теоремы, доказанной нами ранее. Вернёмся к записи общего члена ряда:

$$
u_n=frac{1}{2n+1}-frac{1}{2n+3}
=frac{-1}{2n+3}-frac{-1}{2n+1}
$$

Обозначим $b_n=frac{-1}{2n+1}$, тогда $b_{n+1}=frac{-1}{2(n+1)+1}=frac{-1}{2n+3}$. Таким образом, $u_{n}=b_{n+1}-b_{n}$. При этом $lim_{ntoinfty}b_n=0$. Согласно упомянутому свойству, ряд $sumlimits_{n=1}^{infty}u_n$ сходится. При этом его сумма равна $S=0-b_1=frac{1}{3}$. Если есть необходимость, можно записать и частичную сумму ряда:

$$
S_n
=b_{n+1}-b_1
=frac{-1}{2n+3}-left(-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$

Третий способ упрощения формулы для частичной суммы.

Честно говоря, я сам предпочитаю большей частью именно этот способ 🙂 Давайте запишем частичную сумму в сокращённом варианте:

$$
S_n=sumlimits_{k=1}^{n}u_k=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}.
$$

Мы получили ранее, что $u_k=frac{1}{2k+1}-frac{1}{2k+3}$, поэтому:

$$
S_n=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right).
$$

Сумма $S_n$ содержит конечное количество слагаемых, поэтому мы можем переставлять их так, как нам заблагорассудится. Я хочу сначала сложить все слагаемые вида $frac{1}{2k+1}$, а уж затем переходить к слагаемым вида $frac{1}{2k+3}$. Это означает, что частичную сумму мы представим в таком виде:

$$
S_n
=frac{1}{3}-frac{1}{5}+frac{1}{5}-frac{1}{7}+frac{1}{7}-frac{1}{9}+frac{1}{9}-frac{1}{11}+ldots+frac{1}{2n+1}-frac{1}{2n+3}=\
=frac{1}{3}+frac{1}{5}+frac{1}{7}+frac{1}{9}+ldots+frac{1}{2n+1}-left(frac{1}{5}+frac{1}{7}+frac{1}{9}+ldots+frac{1}{2n+3}right).
$$

Конечно, развёрнутая запись крайне неудобна, поэтому представленное выше равенство оформим более компактно:

$$
S_n=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right)=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}.
$$

Теперь преобразуем выражения $frac{1}{2k+1}$ и $frac{1}{2k+3}$ к одному виду. Приведём, например, дробь $frac{1}{2k+3}$ к виду $frac{1}{2k+1}$. Выражение в знаменателе дроби $frac{1}{2k+3}$ я представлю в таком виде:

$$
frac{1}{2k+3}=frac{1}{2k+2+1}=frac{1}{2(k+1)+1}.
$$

И сумму $sumlimits_{k=1}^{n}frac{1}{2k+3}$ теперь можно записать так:

$$
sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2(k+1)+1}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}.
$$

Если равенство $sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ не вызывает вопросов, то пойдём далее. Если же вопросы есть, то прошу развернуть примечание.

Как мы получили преобразованную сумму? показатьскрыть

Таким образом, частичную сумму можно представить в следующем виде:

$$
S_n=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=2}^{n+1}frac{1}{2k+1}.
$$

Заметьте, что суммы $sumlimits_{k=1}^{n}frac{1}{2k+1}$ и $sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ отличаются лишь пределами суммирования. Сделаем эти пределы одинаковыми. Начнём с первой суммы.

Сделаем так, чтобы верхний предел суммирования стал равен $n+1$. Если $k=n+1$, то $frac{1}{2k+1}=frac{1}{2n+3}$. Прибавляя и вычитая из первой суммы $frac{1}{2n+3}$, получим:

$$
sumlimits_{k=1}^{n}frac{1}{2k+1}
=sumlimits_{k=1}^{n}frac{1}{2k+1}+frac{1}{2n+3}-frac{1}{2n+3}
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}
$$

Для второй суммы $sumlimits_{k=2}^{n+1}frac{1}{2k+1}$ сделаем так, чтобы нижний предел суммирования был равен 1. Если $k=1$, то $frac{1}{2k+1}=frac{1}{3}$. Прибавляя и вычитая $frac{1}{3}$, получим:

$$
sumlimits_{k=2}^{n+1}frac{1}{2k+1}
=sumlimits_{k=2}^{n+1}frac{1}{2k+1}+frac{1}{3}-frac{1}{3}
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{3}
$$

С учётом полученных результатов, выражение для $S_n$ примет такой вид:

$$
S_n
=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}-left(sumlimits_{k=1}^{n}frac{1}{2k+1}-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$

Если пропустить все пояснения, то процесс нахождения сокращённой формулы для n-й частичной суммы примет такой вид:

$$
S_n=sumlimits_{k=1}^{n}u_k
=sumlimits_{k=1}^{n}frac{2}{(2k+1)(2k+3)}
=sumlimits_{k=1}^{n}left(frac{1}{2k+1}-frac{1}{2k+3}right)=\

=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=1}^{n}frac{1}{2k+3}
=sumlimits_{k=1}^{n}frac{1}{2k+1}-sumlimits_{k=2}^{n+1}frac{1}{2k+1}=\

=sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{2n+3}-left(sumlimits_{k=1}^{n+1}frac{1}{2k+1}-frac{1}{3}right)
=frac{1}{3}-frac{1}{2n+3}
$$

Напомню, что мы приводили дробь $frac{1}{2k+3}$ к виду $frac{1}{2k+1}$. Разумеется, можно поступить и наоборот, т.е. представить дробь $frac{1}{2k+1}$ в виде $frac{1}{2k+3}$. Конечное выражение для частичной суммы не изменится. Процесс нахождения частичной суммы в этом случае я скрою под примечание.

Как найти $S_n$, если приводить к виду иной дроби? показатьскрыть

Итак, $S_n=frac{1}{3}-frac{1}{2n+3}$. Находим предел $lim_{ntoinfty}S_n$:

$$
lim_{ntoinfty}S_n=lim_{ntoinfty}left(frac{1}{3}-frac{1}{2n+3}right)=frac{1}{3}-0=frac{1}{3}.
$$

Заданный ряд сходится и сумма его $S=frac{1}{3}$.

Ответ: $S=frac{1}{3}$.

Продолжение темы нахождения суммы ряда будет рассмотрено во второй и третьей частях.

Формулы и уравнения рядов
• Числовые ряды
• Функциональные ряды
• Тригонометрические ряды. Ряд Фурье

Примеры решения рядов здесь.

Числовые ряды

Факториал и двойные факториалы:

— формула Стирлинга.

Геометрическая прогрессия:

|q|<1.

Основные определения и теоремы о рядах:

{u_n} — заданная бесконечная числовая последовательность,

— числовой ряд,
u_n — члены ряда,
– частичные суммы ряда.

Сумма ряда:

сходится, S — сумма ряда.

или ряд сходится и суммы нет.

Отбрасывание конечного числа членов ряда не влияет на его сходимость (но влияет на сумму).

Свойства сходящихся рядов:

Теоремы сравнения рядов с положительными членами:
≥ 0, ≥ 0.
1. ≤
   Если сходится, то сходится;
   если расходится, то расходится.
2. v_n ≠ 0, 0 < k < ∞.
   Либо и , и сходятся,
   либо и , и расходятся.

Достаточные признаки сходимости числовых рядов с положительными членами (u_n > 0)
• Признак Даламбера
  Если существует , то : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0.
• Признак Коши
  Если существует , то : сходится, если l < 1; расходится, если l > 1; признак не дает ответа, если l = 0.
• Интегральный признак сходимости
  1) u_n > 0; 2) u_n ≥ u_n+1; 3) f(x) — непрерывная невозрастающая функция, f(n) = u_n.
  Либо и , и сходятся,
  либо и , и расходятся.

Примеры числовых рядов
1. : сходится, если a > 1; расходится, если a ≤ 1.
2. : сходится, если a < 1; расходится, если a ≥ 1.
3. : сходится.
4. : сходятся, |q| < 1; расходятся, |q| ≥ 1.
5. : сходится;
6. : сходится, если a > 1; расходится, если a ≤ 1.
7. 
8. : сходится условно.
9. : сходится абсолютно.
10. : сходится абсолютно.

Функциональные ряды

Функциональный ряд – сумма вида

При из функционального ряда получается числовой ряд

Если для числовой ряд сходится, то точка называется точкой сходимости функционального ряда. Если в каждой точке числовые ряды сходятся, то функциональный ряд называется сходящимся в области . Совокупность всех точек сходимости образует область сходимости функционального ряда.

– частичные суммы ряда. Функциональный ряд сходится к функции f(x), если

Равномерная сходимость

Функциональный ряд, сходящийся для всех из области сходимости, называется равномерно сходящимся в этой области, если ∀ε > 0 существует не зависящий от x номер N(ε), такой, что при n > N(ε) выполняется неравенство R_n(x) < ε для всех x из области сходимости, где — остаток ряда.

Геометрический смысл равномерной сходимости:

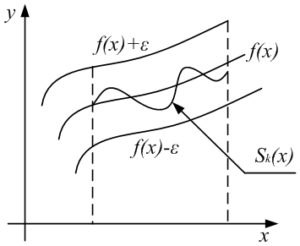
если окружить график функции y = f(x) «ε-полоской», определяемой соотношением f(x)−ε > y > f(x)+ε, то графики всех частичных сумм S_k(x), начиная с достаточно большого k, ∀x ∈ [a, b] целиком лежат в этой «ε-полоске», окружающей график предельной функции y = f(x).

— называется мажорируемым в области , если существует такой сходящийся числовой ряд u_n > 0, что для ∀x ∈ D f_n(x) ≤ u_n, n = 1, 2, …. Ряд называется мажорантой ряда

Признак Вейерштрасса (признак равномерной сходимости функционального ряда): функциональный ряд сходится равномерно в области сходимости, если он является мажорируемым в этой области.

Степенные ряды:
— степенной ряд по степеням
При – степенной ряд по степеням x.

Область сходимости степенного ряда:
Радиус сходимости, интервал сходимости R, x ∈ (-R, R):
или
При |x| < R ряд сходится, при |x| > R – расходится;
в точках x = ±R – дополнительное исследование.

На интервале сходимости ряд сходится абсолютно;
на любом отрезке из интервала сходимости он сходится равномерно.

Свойства степенных рядов
1. Степенной ряд сходится равномерно на [−R′, R′]
   ∀R′ < R, его можно почленно дифференцировать и интегрировать в интервале сходимости.
2. 
3. Ряды, полученные почленным дифференцированием и интегрированием, имеют тот же интервал сходимости.

Разложение элементарных функций в степенные ряды

1. , x ∈ (−∞; ∞).
2. ,
   x ∈ (−∞; ∞).
3. , x ∈ (−∞; ∞).
4. , x ∈ (−∞; ∞).
5. , x ∈ (−∞; ∞).
6. 
   , x ∈ (−1; 1].
7. 
   , x ∈ [−1; 1).
8. ,
   x ∈ (−1; 1).
9. , x ∈ [−1; 1].
10. , x ∈ [−1; 1].
11. , x ∈ (−1; 1).
12. , x ∈ (−1; 1).
13. , x ∈ (−1; 1).
14. , x ∈ (−1; 1).
15. , x ∈ (−1; 1].

Тригонометрические ряды

Ряд Фурье для функции с произвольным периодом Т=2l, f(x+2l) = f(x):

где

Разложение в ряд Фурье непериодических функций, заданных на отрезке x ∈ [0; l] или на отрезке x ∈ [-l; l]
Произвольная функция f(x) задана на отрезке [0; l]; на отрезок [-l; 0] она может быть продолжена произвольным образом:
– некоторая кусочно-монотонная функция.
Наиболее часто встречающиеся продолжения:
• f₁(x)=f(-x), x ∈ [-l; 0] (четное продолжение)
  
  где x ∈ [0; l] n = 0, 1, 2,…
• f₁(x) = —f(−x), x ∈ [-l; 0]
  (нечетное продолжение)
  
  где x ∈ [0; l] n = 1, 2,…
• На всю действительную ось ϕ(x) продолжается периодически с периодом 2l, ϕ(x) = ϕ(x + 2l). Функция ϕ(x) разлагается в ряд Фурье, причем в точках x = ±l выполняется условие: где то есть,
  – левый предел f(x) в точке x = l,
  – правый предел f(x) в точке x = l.

Содержание:

1. Понятие суммы ряда
2. Вычисление суммы ряда почленным интегрированием
3. Вычисление суммы ряда почленным дифференцированием

Понятие суммы ряда

Постановка задачи. Найти сумму ряда

где — целые числа.

План решения. Суммой ряда называется предел последовательности его частичных сумм , т.е.

где

1. По условию задачи

Если корни знаменателя различаются на целое число, т.е. где — натуральное число, то члены последовательности частичных сумм ряда легко найти, так как в выражении многие слагаемые взаимно уничтожаются.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

2. Разлагаем общий член ряда на элементарные дроби:

и выписываем несколько членов ряда так, чтобы было видно, какие слагаемые сокращаются при вычислении частичных сумм ряда.

3. Находим -ю частичную сумму ряда:

,

сократив соответствующие слагаемые.

4. Вычисляем сумму ряда по формуле (1)

и записываем ответ.

Пример:

Найти сумму ряда

Решение:

1. Корни знаменателя и различаются на целое число, т.е. Следовательно, члены последовательности частичных сумм ряда легко найти, так как в выражении многие слагаемые взаимно уничтожаются.

2. Разлагаем общий член ряда на элементарные дроби

и выписываем несколько членов ряда:

3. Сокращая все слагаемые, какие возможно, находим -ю частичную сумму ряда:

4. Вычисляем сумму ряда по формуле (1):

Ответ:

Возможно вам будут полезны данные страницы:

Вычисление суммы ряда почленным интегрированием

Постановка задачи. Найти сумму функционального ряда вида

и указать область сходимости ряда к этой сумме.

План решения.

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

Если , ряд расходится. Если , ряд сходится условно (по признаку Лейбница). Следовательно, область сходимости определяется неравенствами

2. Делаем в исходном ряде замену , получим степенной ряд

с областью сходимости .

3. Известна формула для вычисления суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке , целиком принадлежащем интервалу сходимости, и используя формулу (2), получаем

Заметим, что так как ряд (1) сходится в граничной точке , то сумма ряда непрерывна в этой точке (справа). Следовательно,

6. Вычисляем интеграл, делаем замену на и записываем ответ: сумму ряда и область его сходимости.

Замечание. Если ряд имеет вид

то применяем теорему о почленном интегрировании степенного ряда дважды или разлагаем дробь на элементарные:

и вычисляем сумму каждого ряда почленным интегрированием.

Пример:

Найти сумму ряда

и указать область сходимости ряда к этой сумме.

Решение:

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

В граничных точках при ряд расходится, при ряд сходится условно.

Следовательно, данный ряд сходится при всех .

2. Сделаем замену Получим геометрический ряд (1) с областью сходимости

3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно интегрировать на любом отрезке , целиком принадлежащем интервалу сходимости, и используя формулу (4), получаем

Заметим, что так как ряд (1) сходится в граничной точке , то его сумма непрерывна в этой точке (справа). Следовательно, формула (5) справедлива при всех .

6. Заменяя на , получаем при

Ответ.

Вычисление суммы ряда почленным дифференцированием

Постановка задачи. Найти сумму функционального ряда вида

и указать область сходимости ряда к этой сумме.

План решения.

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством

Если , ряд расходится (не выполнено необходимое условие сходимости). Следовательно, область сходимости определяется неравенствами .

2. Делаем в исходном ряде замену и записываем его в виде суммы двух рядов

Следовательно, достаточно найти суммы рядов

и

3. Известна формула для суммы членов бесконечно убывающей геометрической прогрессии

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (1), получаем

6. Вычисляем производную и делаем замену на . Записываем ответ: сумму ряда и область его сходимости.

Замечание. Если ряд имеет вид

то вычисляем сумму трех рядов, причем при вычислении суммы ряда

применяем теорему о почленном дифференцировании степенного ряда дважды.

Пример:

Найти сумму ряда

и указать область сходимости ряда к этой сумме.

Решение:

1. Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенством . Отсюда . В граничных точках ряд расходится, так как не выполнено необходимое условие сходимости. Следовательно, ряд сходится в интервале .

2. Делаем в исходном ряде замену и записываем его в виде суммы двух рядов

Следовательно, достаточно найти суммы рядов

3. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии:

Следовательно, при всех .

4. Кроме того, имеем очевидное равенство

5. Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя формулу (2), получаем

Таким образом,

Заменяя на , получим

Ответ.

Данная статья представляет собой структурированную и подробную информацию, которая может пригодиться во время разбора упражнений и задач. Мы рассмотрим тему числовых рядов.

Данная статья начинается с основных определений и понятий. Далее мы стандартные варианты и изучим основные формулы. Для того, чтобы закрепить материал, в статье приведены основные примеры и задачи.

Базовые тезисы

Для начала представим систему: a1, a2…, an,… , где ak∈R, k=1,2….

Для примера, возьмем такие числа, как: 6,3,-32,34,38,-316,… .

Числовой ряд – это сумма членов ∑akk=1∞=a1+a2+…+an+… .

Чтобы лучше понять определение, рассмотрим данный случай, в котором q = -0.5: 8-4+2-1+12-14+…=∑k=1∞(-16)·-12k .

ak является общим или k–ым членом ряда.

Он выглядит примерно таким образом -16·-12k .

Частичная сумма ряда выглядит примерно таким образом Sn=a1+a2+…+an , в которой n –любое число. Sn является n-ой суммой ряда.

Например, ∑k=1∞(-16)·-12k есть S4=8-4+2-1=5 .

S1,S2,…,Sn,… образуют бесконечную последовательность числового ряда.

Для ряда n –ая сумму находится по формуле Sn=a1·(1-qn)1-q=8·1–12n1–12=163·1–12n . Используем следующую последовательность частичных сумм: 8,4,6,5,…,163·1–12n,… .

Ряд ∑k=1∞ak является сходящимся тогда, когда последовательность обладает конечным пределом S=lim Snn→+∞ . Если предела нет или последовательность бесконечна, то ряд ∑k=1∞ak называется расходящимся.

Суммой сходящегося ряда ∑k=1∞ak является предел последовательности ∑k=1∞ak=lim Snn→+∞=S .

В данном примере lim Snn→+∞=lim 163т→+∞·1-12n=163·lim n→+∞1–12n=163 , ряд ∑k=1∞(-16)·-12k сходится. Сумма равна 163: ∑k=1∞(-16)·-12k=163 .

Сумма подобного вида как ∑k=1∞=1+12+13+…+1n+… – это гармонический числовой ряд.

Сумма ∑k=1∞1ks=1+12s+13s+…+1ns+… , где s –действительное число, является обобщенно гармоническим числовым рядом.

Определения, рассмотренные выше, помогут вам для решения большинства примеров и задач.

Для того, чтобы дополнить определения, необходимо доказать определенные уравнения.

1. ∑k=1∞1k – расходящийся.

Действуем методом от обратного. Если он сходится, то предел конечен. Можно записать уравнение как limn→+∞Sn=S и limn→+∞S2n=S . После определенных действий мы получаем равенство limn→+∞(S2n-Sn)=0 .

Напротив,

S2n-Sn=1+12+13+…+1n+1n+1+1n+2+…+12n–1+12+13+…+1n=1n+1+1n+2+…+12n

Справедливы следующие неравенства 1n+1>12n, 1n+1>12n,…, 12n-1>12n . Получаем, что S2n-Sn=1n+1+1n+2+…+12n>12n+12n+…+12n=n2n=12 . Выражение S2n-Sn>12 указывает на то, что limn→+∞(S2n-Sn)=0 не достигается. Ряд расходящийся.

1. b1+b1q+b1q2+…+b1qn+…=∑k=1∞b1qk-1

Необходимо подтвердить, что сумма последовательности чисел сходится при q<1 , и расходится при q≥1 .

Согласно приведенным выше определениям, сумма n членов определяется согласно формуле Sn=b1·(qn-1)q-1 .

Если q<1 верно 

 limn→+∞Sn=limn→+∞b1·qn-1q-1=b1·limn→+∞qnq-1-limn→+∞1q-1==b1·0-1q-1=b1q-1

Мы доказали, что числовой ряд сходится.

При q = 1 b1+b1+b1+…∑k=1∞b1 . Суммы можно отыскать с использованием формулы Sn=b1·n , предел бесконечен limn→+∞Sn=limn→+∞b1·n=∞. В представленном варианте ряд расходится.

Если q = -1, то ряд выглядит как b1-b1+b1-…=∑k=1∞b1(-1)k+1 . Частичные суммы выглядят как Sn=b1 для нечетных n, и Sn=0 для четных n. Рассмотрев данный случай, мы удостоверимся, что предела нет и ряд является расходящимся.

При q>1 справедливо limn→+∞Sn=limn→+∞b1·(qn-1)q-1=b1·limn→+∞qnq-1-limn→+∞1q-1==b1·∞-1q-1=∞

Мы доказали, что числовой ряд расходится.

1. Ряд ∑k=1∞1ks сходится, если s > 1 и расходится, если s≤ 1 .

Для s = 1 получаем ∑k=1∞1k , ряд расходится.

При s < 1 получаем 1ks≥1k для k, натурального числа. Так как ряд является расходящимся ∑k=1∞1k , то предела нет. Следуя этому, последовательность ∑k=1∞1ks неограниченна. Делаем вывод, что выбранный ряд расходится при s < 1.

Необходимо предоставить доказательства, что ряд ∑k=1∞1ks сходится при s > 1.

Представим S2n-1-Sn-1 :

S2n-1-Sn-1=1+12s+13s+…+1(n-1)s+1ns+1(n+1)s+…+1(2n-1)s–1+12s+13s+…+1(n-1)s=1ns+1(n+1)s+…+1(2n-1)s

Допустим, что 1(n+1)s<1ns, 1(n+2)s<1ns, …, 1(2n-1)s<1ns , тогда S2n-1-Sn-1=1ns+1(n+1)s+…+1(2n-1)s<<1ns+1ns+…+1ns=nns=1ns-1

Представим уравнение для чисел, которые являются натуральными и четными n=2:   S2n-1-Sn-1=S3-S1=12s+13s<12s-1n=4:   S2n-1-Sn-1=S7-S3=14s+15s+16s+17s<14s-1=12s-12n=8:  S2n-1-Sn-1=S15-S7=18s+19s+…+115s<18s-1=12s-13…

Получаем:

∑k=1∞1ks=1+12s+13s+14s+…+17s+18s+…+115s+…==1+S3-S1+S7-S3+S15+S7+…<<1+12s-1+12s-12+12s-13+…

Выражение 1+12s-1+12s-12+12s-13+… – это сумма геометрической прогрессии q=12s-1 . Согласно исходным данным при s>1, то0<q<1 . Получаем, ∑k=1∞<1+12s-1+12s-12+12s-13+…=11-q=11-12s-1 . Последовательность ряда при s > 1 увеличивается и ограничивается сверху 11-12s-1 . Представим, что есть предел и ряд является сходящимся ∑k=1∞1ks .

Второй вариант ряд – это частный случай третьего варианта.

Приведем примеры для каждого случая соответственно:

 6+3+32+34+38+316+…6-3+32-34+38-316+…6+3-32+34+38-316+…

Для третьего варианта также можно определить абсолютную и условную сходимость.

Знакочередующийся ряд ∑k=1∞bk абсолютно сходится в том случае, когда ∑k=1∞bk также считается сходящимся.

Подробно разберем несколько характерных вариантов

Если ряды 6-3+32-34+38-316+… и 6+3-32+34+38-316+… определяются как сходящиеся, то верно считать, что 6+3+32+34+38+316+…

Знакопеременный ряд ∑k=1∞bk считается условно сходящимся в том случае, если ∑k=1∞bk – расходящийся, а ряд ∑k=1∞bk считается сходящимся.

Подробно разберем вариант ∑k=1∞(-1)k+1k=1-12+13-14+… . Ряд ∑k=1∞(-1)k+1k=∑k=1∞1k , который состоит из абсолютных величин, определяется как расходящийся. Этот вариант считается сходящимся, так как это легко определить. Из данного примера мы узнаем, что ряд ∑k=1∞(-1)k+1k=1-12+13-14+… будет считаться условно сходящимся.

Особенности сходящихся рядов

Проанализируем свойства для определенных случаев

1. Если ∑k=1∞ak будет сходится, то и ряд ∑k=m+1∞ak также признается сходящимся. Можно отметить, что ряд без m членов также считается сходящимся. В случае, если мы добавляем к ∑k=m+1∞ak несколько чисел, то получившийся результат также будет сходящимся.
2. Если ∑k=1∞ak сходится и сумма = S, то сходится и ряд ∑k=1∞A·ak , ∑k=1∞A·ak=A·S , где A –постоянная.
3. Если ∑k=1∞ak и ∑k=1∞bk являются сходящимися , суммы A и B тоже, то и ряды ∑k=1∞ak+bk и ∑k=1∞ak-bk также сходятся . Суммы будут равняться A + B и A – B соответственно.

Необходимое условие для определения, является ли ряд сходящимся

Если ряд ∑k=1∞ak является сходящимся, то предел его k-ого члена =0: limk→+∞ak=0 .

Если мы проверим любой вариант, то нужно не забывать о непременном условии. Если оно не выполняется, то ряд расходится. Если limk→+∞ak≠0 , то ряд расходящийся.

Следует уточнить, что условие важно, но не достаточно. Если равенство limk→+∞ak=0 выполняется , то это не гарантирует, что ∑k=1∞ak является сходящимся.

Приведем пример. Для гармонического ряда ∑k=1∞1k условие выполняется limk→+∞1k=0 , но ряд все равно расходится.

Как определить сходимость знакоположительного ряда.

Если постоянно пользоваться указанными признаками, придется постоянно вычислять пределы. Данный раздел поможет избежать сложностей во время решения примеров и задач. Для того, чтобы определить сходимость знакоположительного ряда, существует определенное условие.

Для сходимости знакоположительного ∑k=1∞ak, ak>0 ∀k=1,2,3,… нужно определять ограниченную последовательность сумм.

Как сравнивать ряды

Существует несколько признаков сравнения рядов. Мы сравниваем ряд, сходимость которого предлагается определить, с тем рядом, сходимость которого известна.

Первый признак

∑k=1∞ak и∑k=1∞bk – знакоположительные ряды. Неравенство ak≤bk справедливо для k = 1, 2, 3, … Из этого следует, что из ряда ∑k=1∞bk мы можем получить∑k=1∞ak . Так как ∑k=1∞ak расходится, то ряд∑k=1∞bk можно определить как расходящийся.

Данное правило постоянно используется для решения уравнений и является серьезным аргументом, которое поможет определить сходимость. Сложности могут состоять в том, что подобрать подходящий пример для сравнения можно найти далеко не в каждом случае. Довольно часто ряд выбирается по принципу, согласно которому показатель k-ого члена будет равняться результату вычитания показателей степеней числителя и знаменателя k-ого члена ряда. Допустим, что ak=k2+34k2+5 , разность будет равна 2 – 3 = -1. В данном случае можно определить, что для сравнения необходим ряд с k-ым членом bk=k-1=1k , который является гармоническим.

Для того, чтобы закрепить полученный материал, детально рассмотрим пару типичных вариантов.

Второй признак

Допустим, что ∑k=1∞ak и ∑k=1∞bk – знакоположительные числовые ряды.

Если limk→+∞akbk≠∞ , то ряд ∑k=1∞bk сходится, и ∑k=1∞ak сходится также.

Если limk→+∞akbk≠0 , то так как ряд ∑k=1∞bk расходится, то ∑k=1∞ak также расходится.

Если limk→+∞akbk≠∞ и limk→+∞akbk≠0 , то сходимость или расходимость ряда означает сходимость или расходимость другого.

Рассмотрим ∑k=1∞1k3+3k-1 с помощью второго признака. Для сравнения ∑k=1∞bk возьмем сходящийся ряд∑k=1∞1k3 . Определим предел: limk→+∞akbk=limk→+∞1k3+3k-11k3=limk→+∞k3k3+3k-1=1

Согласно второму признаку можно определить, что сходящийся ряд∑k=1∞1k3 означается, что первоначальный вариант также сходится.

Согласно приведенным выше тезисам, расходящийся ряд влечет собой расходимость исходного ряда.

Третий признак

Рассмотрим третий признак сравнения.

Допустим, что ∑k=1∞ak и _∑k=1∞bk – знакоположительные числовые ряды. Если условие выполняется для некого номера ak+1ak≤bk+1bk , то сходимость данного ряда∑k=1∞bk означает, что ряд ∑k=1∞ak также является сходящимся. Расходящийся ряд ∑k=1∞ak влечет за собой расходимость ∑k=1∞bk .

Признак Даламбера

Представим, что ∑k=1∞ak – знакоположительный числовой ряд. Если limk→+∞ak+1ak<1, то ряд является сходящимся, если limk→+∞ak+1ak>1 , то расходящимся.

Замечание 1

Признак Даламбера справедлив в том случае, если предел бесконечен.

Если limk→+∞ak+1ak=-∞ , то ряд является сходящимся, если limk→∞ak+1ak=+∞ , то расходящимся.

Если limk→+∞ak+1ak=1 , то признак Даламбера не поможет и потребуется провести еще несколько исследований.

Радикальный признак Коши

Допустим, что ∑k=1∞ak – это знакоположительный ряд. Еслиlimk→+∞akk<1 , то ряд является сходящимся, если limk→+∞akk>1 , то расходящимся.

Замечание 2

Данный признак будет считаться справедливым только в том случае, если предел бесконечен. Другими словами, если limk→+∞akk=-∞, то ряд сходится, если limk→+∞akk=+∞ , то ряд расходится.

Еслиlimk→+∞akk=1 , то данный признак не дает никакой информации – требуется проведение дополнительного анализа.

Данный признак может быть использован в примерах, которые легко определить. Случай будет характерным тогда, когда член числового ряда – это показательно степенное выражение.

Для того, чтобы закрепить полученную информацию, рассмотрим несколько характерных примеров.

Интегральный признак Коши

Допустим, что ∑k=1∞ak является знакоположительным рядом. Необходимо обозначить функцию непрерывного аргумента y = f(x), которая совпадаетan= f(n) . Если y = f(x) больше нуля, не прерывается и убывает на [a; +∞) , где a≥1

, то в случае, если несобственный интеграл ∫a+∞f(x)dx является сходящимся, то рассматриваемый ряд также сходится. Если же он расходится, то в рассматриваемом примере ряд тоже расходится.

При проверке убывания функции можно использовать материал, рассмотренный на предыдущих уроках.

Признак Раабе

Допустим, что ∑k=1∞ak – знакоположительный числовой ряд.

Если limk→+∞k·akak+1<1 , то ряд расходится, еслиlimk→+∞k·akak+1-1>1 , то сходится.

Данный способ определения можно использовать в том случае, если описанные выше техники не дают видимых результатов.

Исследование на абсолютную сходимость

Для исследования берем ∑k=1∞bk . Используем знакоположительный ∑k=1∞bk . Мы можем использовать любой из подходящих признаков, которые мы описывали выше. Если ряд ∑k=1∞bk сходится, то исходный ряд является абсолютно сходящимся.

Расходимость знакопеременных рядов

Если ряд ∑k=1∞bk – расходящийся, то соответствующий знакопеременный ряд ∑k=1∞bk либо расходящийся, либо условно сходящийся.

Лишь признак Даламбера и радикальный признак Коши помогут сделать выводы о ∑k=1∞bk по расходимости из модулей ∑k=1∞bk . Ряд ∑k=1∞bk также расходится, если не выполняется необходимое условие сходимости, то есть, если limk→∞+bk≠0 .

Признаки для условной сходимости

Признак Лейбница

Если величины членов знакочередующегося ряда убывают b1>b2>b3>…>… и предел модуля =0 при k→+∞ , то ряд ∑k=1∞bk сходится.

Признак Абеля-Дирихле

∑k=1+∞uk·vk сходится в том случае, если {uk} не возрастает, а последовательность ∑k=1+∞vk ограничена.