Как составить формулу зависимости величин

Я не понимаю, как учителя умудряются объяснять нынешнюю математику нынешним современным ученикам, влюблённых в гаджеты. Лично я объясняю через алгоритмы программирования.

До карантина я сутки думала, как объяснить сыну принцип решения составных уравнений. Придумала лайфхак “Взлом уравнения”, показала своему школьнику и сын стал щелкать уравнения, как орешки.

В карантине я два дня пыталась сама понять материал математики 3 класса на тему “формула зависимостей между величинами”. Но когда начала программировать задачи, сразу выработался алгоритм. По нему и осваиваем эту непонятную тему. Делюсь своим алгоритмом, вдруг кому-то пригодится.

1. Надо сначала записать условия задачи, чтобы выявить что нам известно и что неизвесто.

2. Вспомнить общую формулу для решения подобных задач. У моего школьника сейчас задачи на скорость и расстояние. Поэтому для нас общая формула s=t*v или v=s:t.

3. Прорешать задачу с каждой известной величиной по общей формуле.

4. В прорешанных примерах увидеть постоянную и переменную величину.

5. Записать общую формулу, изменив в ней цифрой ту символьную часть, которая постоянно повторяется в каждом примере. Так мы получили формулу зависимостей между величинами.

6. Теперь можно сделать табличку расчета, у которой в первой строке записываются заранее известные величины, а во второй строке то, что надо было найти.

Про лайфхак “Взлом уравнения” напишу попозже. Есть у меня на него одна задумка, но она пока в секрете.

…

p.s. Сейчас вы прочитали статью из блога в яндекс.дзене “Лайфхаки неЛОГОПЕДА“, в котором собраны лайфхаки запуска речи у малыша, фишки коммуникаций со школьником и другие мамские жизненные хитрости программиста с умением писать тексты. Я не логопед и не педагог. Просто я много читаю книг про детей. Ещё я сочиняю детские квест-сказки про Непослушкина и пишу сториз-книги.

Если вам нравятся мои рассуждения и мысли в текстах этого блога, то вам точно понравится моя книга «52 фишки адаптации ребёнка к детскому саду» и другие в книжном интернет-магазине электронных книг на ЛитРес.ру.

Есть вопросы? Задавайте в комментариях. Отвечу, когда в следующий раз загляну в дзен. Или пишите мне в соц.сети вконтакте или инстаграм. Мой аккаунт там @krasna_devica. Отвечаю лично всем сама. Без чат-ботов.

© Яна Терентьева

Что такое прямая зависимость

Содержание статьи

Прямая зависимость

Как и многие другие виды зависимостей, прямая зависимость в математике может быть выражена формулой, отражающей характер взаимосвязи между ее компонентами. Так, формула, соответствующая прямой зависимости, обыкновенно имеет вид y = kx. В указанном соотношении y представляет собой функцию, то есть зависимую переменную, определяемую значениями других компонентов, входящих в состав формулы. x в данном случае выполняет роль аргумента, то есть независимой переменной, значение которой определяет значение зависимой переменной, то есть функции.

При этом обе этих переменных, как зависимая, так и независимая, имеют свойство изменять свое значение. При этом третий компонент формулы, коэффициент k, представляет собой определенное число, которое в данной формуле является постоянным и не изменяется. Таким образом, формула прямой зависимости может, например, иметь вид y = 5x. При этом стандартный вид формулы, отражающей прямую зависимость, предполагает, что в качестве коэффициента используются положительные числа, а ноль и отрицательные числа не могут выступать в качестве таких коэффициентов.

Примеры прямой зависимости

Таким образом, содержательно наличие прямой зависимости между двумя переменными означает, что увеличение независимой переменной обязательно вызовет увеличение зависимой переменной, причем размер этого увеличения будет определяться коэффициентом k. Так, в приведенном выше примере увеличение x на единицу приведет к увеличению y на 5, поскольку коэффициент k = 5.

Примеров прямой зависимости в повседневной жизни можно найти достаточно много. Так, например, при условии сохранения неизменной скорости движения объекта длина пройденного им пути будет находиться в прямой зависимости от времени, которое он потратил на дорогу. Например, если скорость пешехода составляет 6 километров в час, за два часа он пройдет 12 километров, а за 4 часа — 24 километра. Таким образом, зависимость между рассматриваемыми величинами в этом случае будет выражена формулой y = 6x, где y — пройденный путь, а x — количество часов в пути.

Таким же прямо пропорциональным образом будет возрастать общая стоимость покупки в магазине при увеличении количества единиц приобретаемого товара при условии, что речь идет об одинаковых товарах. Например, если речь идет о приобретении одинаковых тетрадей, каждая из которых стоит 4 рубля за штуку, покупая 8 тетрадей, человек должен будет уплатить 32 рубля, а за 18 тетрадей — уже 72 рубля. В этом случае зависимость будет выражена формулой y = 4x, где y — общая сумма покупки, а x — стоимость одной тетради.

Источник

Прямая и обратная пропорциональность

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

• Прямая зависимость. Чем больше одна величина, тем больше вторая. Чем меньше одна величина, тем меньше вторая величина.
• Обратная зависимость. Чем больше одна величина, тем меньше вторая. Чем меньше одна величина, тем больше вторая.

Зависимости также можно классифицировать по формам: функциональная и статистическая.

Функциональная зависимость между двумя переменными величинами характеризуется тем, что каждому значению одной из них соответствует вполне определенное и единственное значение другой.

В математике функциональной зависимостью переменной Y от переменной Х называют зависимость вида y = f(x), где каждому допустимому значению X ставится в соответствие по определенному правилу единственно возможное значение Y.

Статистическая зависимость — это зависимость случайных величин, когда изменение одной переменной приводит к изменению другой.

Если изменение одной из случайных величин влечет изменение среднего другой случайной величины, то статистическую зависимость называют корреляционной. Сами случайные величины, связанные корреляционной зависимостью, оказываются коррелированными.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

• Прямая пропорциональность. Это зависимость, при которой увеличение одного числа ведет к увеличению другого во столько же раз. А уменьшение одно числа ведет к уменьшению другого во столько же раз.
• Обратная пропорциональность. Это зависимость, при которой уменьшение одного числа ведет к увеличению другого во столько же раз. А увеличение числа наоборот ведет к уменьшению другого во столько же раз.

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

Свойство прямо пропорциональной зависимости:

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

• при постоянной скорости пройденный маршрут прямо-пропорционально зависит от времени;
• периметр квадрата и его сторона — прямо-пропорциональные величины;
• стоимость конфет, купленных по одной цене, прямо-пропорционально зависит от их количества.

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности

y = kx,

где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Графиком прямо пропорциональной зависимости величин является прямая линия.

Например, при k = 2 график выглядит так:

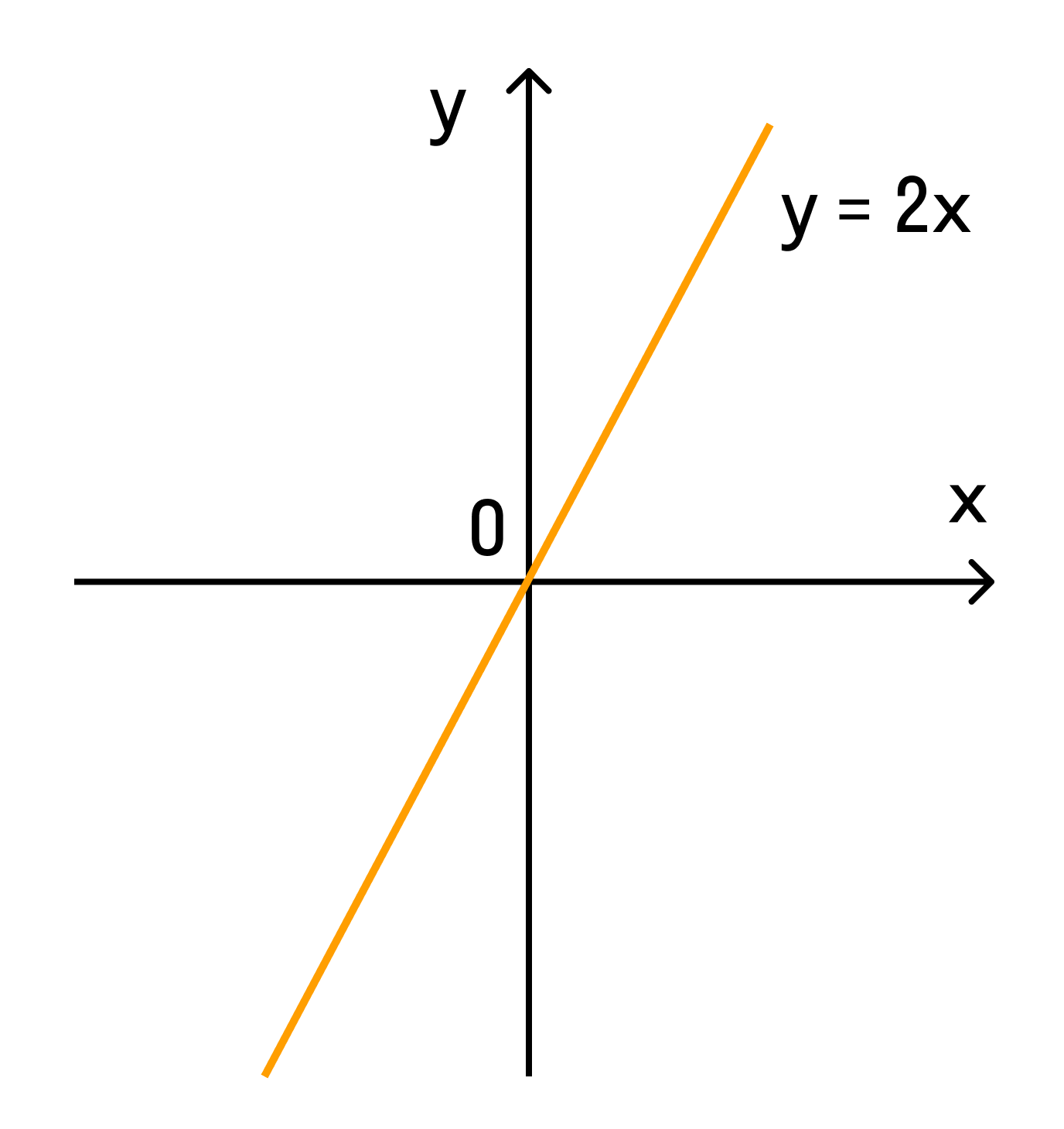
Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

1. Вспомним формулу для определения пути через скорость и время: S = V * t.
2. Так как оба автомобиля проделали одинаковый путь, можно составить пропорцию из двух выражений: 70 * 2 = V * 7
3. Найдем скорость второго автомобиля: V = 70 * 2/7 = 20

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

• х = 1 (блогер) * 30 (раз) : 12/8 (дней).
• х = 1 * 30 : 12/8
• х = 20

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

• время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины;
• при одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи;
• количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене.

Формула обратной пропорциональности

где y и x — это переменные величины,

k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

Графиком обратно пропорциональной зависимости величин является гипербола.

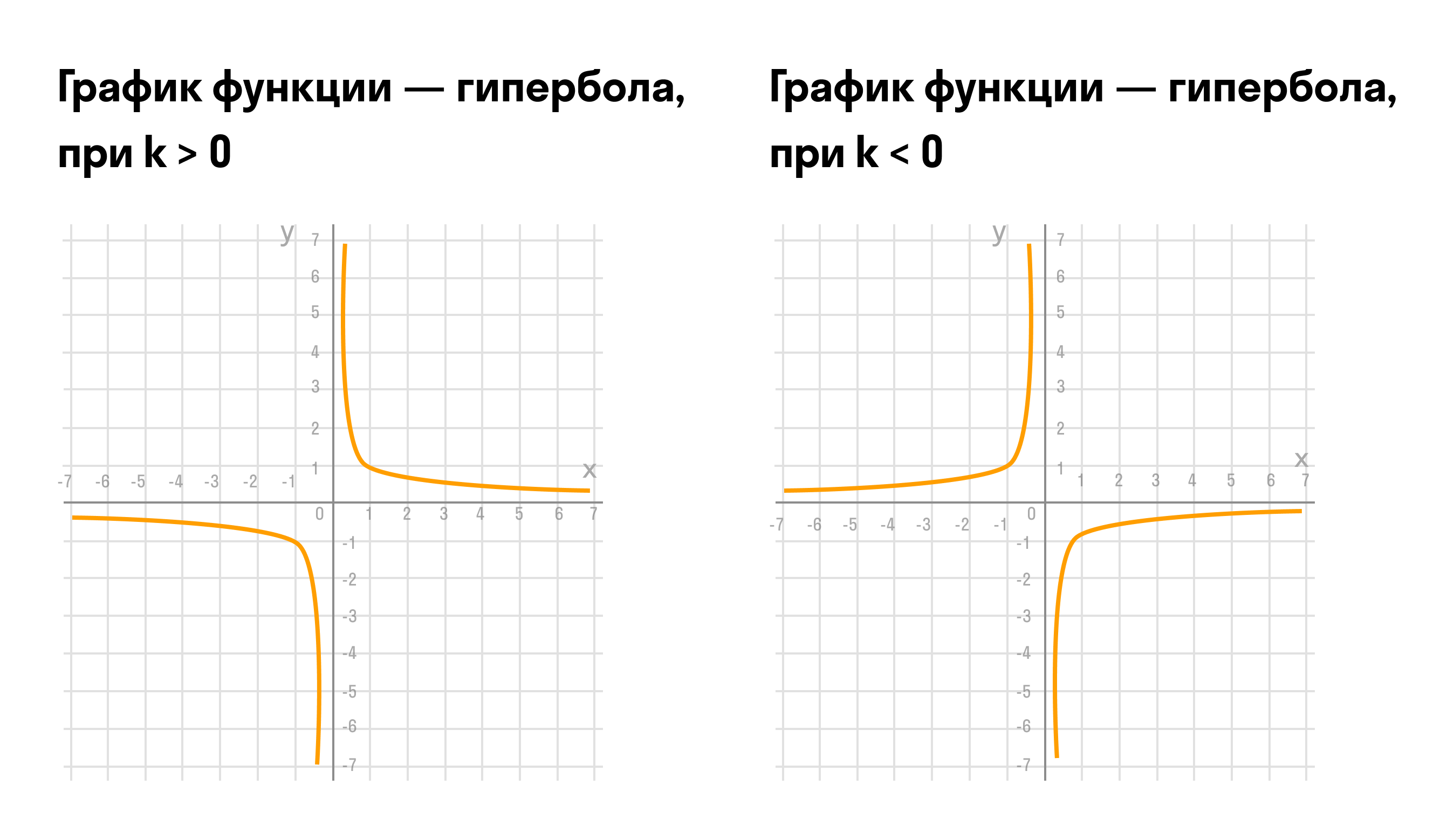
Свойства функции обратной пропорциональности:

1. Область определения — множество всех действительных чисел, кроме x = 0.

Область значений — все действительные числа, кроме y = 0.

Не имеет наибольших и наименьших значений.

Является нечетной, и ее график симметричен относительно начала координат.

Непериодическая.

Ее график не пересекает оси координат.

Не имеет нулей.

Если k > 0 (аргумент возрастает), функция пропорционально убывает на каждом из своих промежутков. Если k 0) отрицательные значения функции находятся в промежутке (-∞; 0), а положительные — (0; +∞). При убывании аргумента (k

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

1. В заполненном столбце стрелку ставим в направлении от большего числа к меньшему.
2. Чем больше людей, тем меньше времени нужно для выполнения определенной работы (раскрутки канала). Значит, это обратно пропорциональная зависимость.
3. Поэтому направим вторую стрелку в противоположную сторону. Обратная пропорция выглядит так:

1. Пусть за х дней могут раскрутить канал 30 человек. Составляем пропорцию: 30 : 24 = 5 : х
2. Чтобы найти неизвестный член пропорции, нужно произведение средних членов разделить на известный крайний член: х = 24 * 5 : 30; х = 4
3. Значит, 30 человек раскрутят канал за 4 дня.

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Составим пропорцию: v1/v2 = t2/t1.

Соотношения равны, но перевернуты относительно друг друга.

Подставим известные значения: 75/52 = t2/13

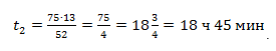
Источник

Урок 23 Бесплатно Прямая и обратная пропорциональные зависимости

На этом уроке мы рассмотрим, что такое прямая и обратная пропорциональные зависимости, научимся оформлять и решать задачи с помощью пропорции, устанавливая пропорциональную зависимость между величинами в ней, рассмотрим примеры задач на прямую и обратную пропорциональную зависимость.

Прямая и обратная пропорциональность

Давайте сначала разберемся, что такое пропорциональность.

Пропорциональность — это зависимость двух величин друг от друга таким образом, что значение отношения этих величин остается постоянным.

Зависимость величин друг от друга может быть прямой и обратной.

Отношение между величинами описываются прямой или обратной пропорциональностью.

Прямая пропорциональность выражается так: (mathbf)

Обратная пропорциональность выражается так: (mathbf>)

где k — это число, которое называют коэффициентом пропорциональности.

x и y величины, зависящие друг от друга.

Пример

Площадь прямоугольника равна (mathbf), где S— это площадь прямоугольника, а — длина прямоугольника, b — ширина прямоугольника.

Если один из множителей произведения — постоянная величина, то произведение прямо пропорционально второму множителю.

Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.

По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.

Какова эта зависимость, сейчас и рассмотрим.

Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.

Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.

Пусть одна клетка равна 1 см. Рассмотрим рисунок:

Ширина прямоугольника b постоянная величина

b = 4 см

a₁ = 6 см

Увеличим ширину прямоугольника — сторону a₁ на 1 см, получим

a₂ = 7 см

Найдем площади прямоугольников S₁ и S₂

(mathbf = a_ <1>cdot b = 6 cdot 4 = 24>) см 2

(mathbf = a_ <2>cdot b = 7 cdot 4 = 28>) см 2

Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.

Рассмотрим другой вариант зависимости

Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см

Площадь прямоугольника S постоянная величина

S = 24 см 2

b₁ = 4 см

Увеличим высоту прямоугольника- сторону прямоугольника b₁ на 2 см_, получим

b₂ = 6 см

Найдем ширину прямоугольника- сторону a₂

Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.

Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:

1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.

2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.

Примеров прямой и обратной пропорциональности множество.

Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.

Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.

Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается

Пройти тест и получить оценку можно после входа или регистрации

Алгоритм решение задач с прямой и обратной пропорциональной зависимостью

Алгоритм решения задач на пропорциональную зависимость состоит из нескольких основных пунктов:

1. Обозначить буквой значение неизвестной величины (чаще всего для этого выбирают латинскую букву Х)
2. Проанализировать задачу и кратко записать ее условия (краткую запись можно делать в виде таблицы или изображать в виде логической схемы)
3. Установить зависимость между величинами
4. В краткой записи задачи обозначить стрелками пропорциональную зависимость

— Стрелки, которые направлены в одну сторону, обозначают прямую пропорциональную зависимость величин

— Стрелки, которые направлены в разные стороны, обозначают обратную пропорциональную зависимость величин.

5. Записать пропорцию, учитывая характер пропорциональности величин

6. Составить уравнение

7. Найти неизвестный член уравнения (искомую величину)

8. Записать ответ задачи

Важно помнить, что при составлении краткой записи задачи величины с одинаковыми единицами измерения записывают друг под другом.

Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи.

Если между величинами обратная пропорциональная зависимость, то при составлении пропорции одноименные величины меняются местами в одном любом из столбцов таблицы (логической схемы) краткой записи задачи.

Другими словами, при прямо пропорциональной зависимости отношение значений одной величины равно отношению соответствующих значений другой величины.

При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.

Пройти тест и получить оценку можно после входа или регистрации

Источник

Adblock
detector

Прямая и обратная пропорциональность

• Прямая пропорциональность
• Формула прямой пропорциональности
• Обратная пропорциональность
• Формула обратной пропорциональности

Пропорциональность — это зависимость одной величины от другой, при которой изменение одной величины приводит к изменению другой во столько же раз.

Пропорциональность величин может быть прямой и обратной.

Прямая пропорциональность

Прямая пропорциональность — это зависимость двух величин, при которой одна величина зависит от второй величины так, что их отношение остаётся неизменным. Такие величины называются прямо пропорциональными или просто пропорциональными.

Рассмотрим пример прямой пропорциональности на формуле пути:

s = vt,

где  s  — это путь,  v  — скорость, а  t  — время.

При равномерном движении путь пропорционален времени движения. Если взять скорость  v  равной  5 км/ч,  то пройденный путь  s  будет зависеть только от времени движения  t:

Скорость v = 5 км/ч
Время t (ч)	1	2	4	8	16
Путь s (км)	5	10	20	40	80

Из примера видно, что во сколько раз увеличивается время движения  t,  во столько же раз увеличивается пройденное расстояние  s.  В примере мы увеличивали время каждый раз в 2 раза, так как скорость не менялась, то и расстояние увеличивалось тоже в два раза.

В данном случае скорость  (v = 5 км/ч)  является коэффициентом прямой пропорциональности, то есть отношением пути ко времени, которое остаётся неизменным:

следовательно,

5	=	10	=	20	=	40	=	80	= 5.
1	2	4	8	16

Если время движения остаётся неизменным, то при равномерном движении расстояние будет пропорционально скорости:

Время  t = 2 ч
Скорость  v (км/ч)	5	15	45	90
Расстояние  s (км)	10	30	90	180

В этом примере коэффициентом прямой пропорциональности, то есть, отношением пути к скорости, которое остаётся неизменным, является время  (t = 2 ч):

следовательно,

10	=	30	=	90	=	180	= 2.
5	15	45	90

Из данных примеров следует, что две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз другая увеличивается (или уменьшается) во столько же раз.

Формула прямой пропорциональности

Формула прямой пропорциональности:

y = kx,

где  y  и  x  — это переменные величины, а  k  — это постоянная величина, называемая коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных  y  и  x  равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Обратная пропорциональность

Обратная пропорциональность — это зависимость двух величин, при которой увеличение одной величины приводит к пропорциональному уменьшению другой. Такие величины называются обратно пропорциональными.

Рассмотрим пример обратной пропорциональности на формуле пути:

s = vt,

где  s  — это путь,  v  — скорость, а  t  — время.

При прохождении одного и того же пути с разной скоростью движения время будет обратно пропорционально скорости. Если взять путь  s  равным  120 км,  то потраченное на преодоление этого пути время  t  будет зависеть только от скорости движения  v:

Путь  s = 120 км
Скорость  v (км/ч)	10	20	40	80
Время  t (ч)	12	6	3	1,5

Из примера видно, что во сколько раз увеличивается скорость движения  v,  во столько же раз уменьшается время  t.  В примере мы увеличивали скорость движения каждый раз в 2 раза, а так как расстояние, которое нужно преодолеть, не менялось, то количество времени на преодоление данного расстояния сокращалось тоже в два раза.

В данном случае путь (s = 120 км) является коэффициентом обратной пропорциональности, то есть произведением скорости на время:

s = vt,

следовательно,

10 · 12 = 20 · 6 = 40 · 3 = 80 · 1,5 = 120.

Из данного примера следует, что две величины называются обратно пропорциональными, если при увеличении одной из них в несколько раз другая уменьшается во столько же раз.

Формула обратной пропорциональности

Формула обратной пропорциональности:

где  y  и  x  — это переменные величины, а  k  — это постоянная величина, называемая коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных  y  и  x,  равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

xy = k.