Пример. Найти общее решение уравнения
y′′′−6 y′′+11y′−6 y = 0 ,
|
если известно, |
что функции |
y |
= ex , y |
2 |
= e2x , y = e3x |
являются его |
||||||||||||
|
решениями. |
1 |
3 |
||||||||||||||||
|
Решение: |
Это |
ЛОДУ |
третьего |
порядка. |
Покажем, что |
|||||||||||||
|
y |
= ex , y |
2 |
= e2x , y = e3x образуют фундаментальную систему функций: |
|||||||||||||||
|
1 |
3 |
|||||||||||||||||
|
e x |
e2 x |
e3x |
1 |
1 |
1 |
|||||||||||||
|
W (x) = |
e x |
2e2x |
3e3x |
= e x e2x e3x |
1 2 |
3 |
= |
|||||||||||
|
e x |
4e2x |
9e3x |
1 |
4 |
9 |
|||||||||||||
= e6x (18 +3 + 4 − 2 −9 −12)= 2e6 x ≠ 0.
Тогда общее решение будет
y =С1y1+С2y2+С3y3 = С1ex+С2e2x+С3e3x. Ответ: y = С1ex+С2e2x+С3e3x. ■
Линейное однородное дифференциальное уравнение (ЛОДУ) n-ого порядка с постоянными коэффициентами имеет вид:
|
y(n) + a1 y(n−1) + a2 y(n−2) +…… + an−1 y′+ an y = 0 , |
(6.8) |
где все коэффициенты a1, a2, a3, …, an-1, an – числа (в частности, некоторые могут быть и нулями).
|
Рассмотрим уравнение второго порядка |
|
|
y′′+ a1 y′+ a2 y = 0. |
(6.9) |
Заметим, что в силу свойств однородных линейных уравнений нам достаточно найти два частных решений, составляющих фундаментальную систему решений уравнения (6.9), чтобы затем найти общее.
Будем искать частное решение уравнения (6.9) в виде
где k – число, которое подберем так, чтобы функция (6.10) удовлетворяла уравнению (6.9).
|
Дифференцируя |
дважды |
у, |
найдем y′ = kekx , y′′ = k 2 ekx ; |
||
|
подставляя в (6.9), |
получим |
||||
|
k 2ekx + a k ekx + a |
2 |
ekx = 0, |
|||
|
1 |
сокращая на ekx ≠ 0 , имеем
27

|
k 2 + a k + a |
2 |
= 0. |
(6.11) |
|
1 |
Это алгебраическое квадратное уравнение относительно k , оно будет называться характеристическим уравнением уравнения (6.9).
Итак, чтобы функция y = ekx была частным решением уравнения (6.9), нужно, чтобы k удовлетворяло уравнению (6.11).
Пусть k1 и k2 – корни характеристического уравнения (6.11), т.е.
|
k |
= |
−a ± |
a |
2 |
−4a |
2 . |
|||||||||||||
|
1 |
1 |
||||||||||||||||||
|
1,2 |
2 |
||||||||||||||||||
|
Возможны случаи: |
|||||||||||||||||||
|
1. Корни k1 и k2 уравнения (6.2.4) действительные и различные, |
|||||||||||||||||||
|
т.е. k1 ≠ k2 |
(в этом случае дискриминант D = a 2 − 4a |
2 |
> 0 ). |
||||||||||||||||
|
Тогда формула (6.10) даст два частных решения: |
1 |
||||||||||||||||||
|
y = ek1x , y |
2 |
= ek2 x . |
|||||||||||||||||
|
1 |
|||||||||||||||||||
|
Эти частные решения образуют фундаментальную систему решений |
|||||||||||||||||||
|
уравнения (6.9), так как |
|||||||||||||||||||
|
y2 |
= e(k2 −k1 ) x ≠ C |
(т.к. k ≠ k |
2 |
) . |
|||||||||||||||
|
y1 |
1 |
||||||||||||||||||
|
Следовательно, общее решение уравнения (6.9) будет иметь вид |
|||||||||||||||||||
|
y = C ek1x |
+ C |
ek2 x . |
(6.12) |
||||||||||||||||
|
1 |
2 |
||||||||||||||||||
|
Пример. |
Решить уравнение |
y′′+3y′+ 2 y = 0 . |
|||||||||||||||||
|
Решение. |
Это ЛОДУ второго порядка. |
Составим характеристическое |
|||||||||||||||||
|
уравнение: |
k 2 +3k + 2 = 0. |
||||||||||||||||||
|
Находим его корни: |
k1=-2, k2=-1. |
||||||||||||||||||
|
Частные решения имеют вид |
y = e−2x , y |
2 |
= e−x . |
||||||||||||||||
|
y = С1e-2x+С2e-x |
1 |
||||||||||||||||||
|
Тогда |
будет общим решением. |
||||||||||||||||||
|
Ответ: y = С1e-2x+С2e-x. |
■ |
||||||||||||||||||
|
2.Корни характеристического уравнения (6.11) действительные и |
|||||||||||||||||||
|
равные, т. е. |
k1 = k2 = k. |
a1 |
|||||||||||||||||
|
В этом случае |
D = a 2 − 4a |
= 0 и |
k1 = k2 = k = − |
. |
|||||||||||||||
|
1 |
2 |
2 |
|||||||||||||||||
|
В данном случае формула |
(6.10) дает |
нам одно частное решение |
y1 = ek x . Остается найти другое частное решение y2, образующее вместе с решением y1 фундаментальную систему решений уравнения (6.9).
Покажем, что таким решением будет функция вида y2 = xek x .
28
|
′ |
k x |
k x |
||||||||||||||||||||||||||||||||||||||||||
|
Найдем |
+ x k e |
, |
||||||||||||||||||||||||||||||||||||||||||
|
y2 = e |
||||||||||||||||||||||||||||||||||||||||||||
|
′′ |
k x |
k x |
2 |
k x |
k x |
2 |
k x |
|||||||||||||||||||||||||||||||||||||
|
+ k e |
+ xk e |
= 2k e + k xe . |
||||||||||||||||||||||||||||||||||||||||||
|
y2 = k e |
||||||||||||||||||||||||||||||||||||||||||||
|
Подставим y2, y’2, |
y”2 |
в уравнение (6.9) и воспользуемся формулой |
||||||||||||||||||||||||||||||||||||||||||
|
(6.12): |
2k ek x + k 2 xek x + a1ek x + a1k xek x + a2 xek x ≡ 0 , |
|||||||||||||||||||||||||||||||||||||||||||
|
−a |
−a |
−a |
−a |
−a |
||||||||||||||||||||||||||||||||||||||||
|
−a e |
1 |
x + a12 xe |
1 |
x + a e |
1 |
x − a12 xe |
1 |
x + a |
xe |
1 |
x ≡ 0, |
|||||||||||||||||||||||||||||||||
|
2 |
2 |
2 |
2 |
2 |
2 |
|||||||||||||||||||||||||||||||||||||||
|
1 |
4 |
1 |
2 |
|||||||||||||||||||||||||||||||||||||||||
|
−a1 |
||||||||||||||||||||||||||||||||||||||||||||
|
4a |
2 |
− a |
2 |
x |
||||||||||||||||||||||||||||||||||||||||
|
x |
1 |
e 2 |
≡ 0 . |
|||||||||||||||||||||||||||||||||||||||||
|
4 |
||||||||||||||||||||||||||||||||||||||||||||
|
y2 |
||||||||||||||||||||||||||||||||||||||||||||
|
Так как |
= x ≠ C , |
то |
y |
и |
y |
2 |
образуют фундаментальную |
|||||||||||||||||||||||||||||||||||||
|
y1 |
1 |
|||||||||||||||||||||||||||||||||||||||||||
|
k1 = k2 = k |
функция |
|||||||||||||||||||||||||||||||||||||||||||
|
систему решений. Таким образом, при |
||||||||||||||||||||||||||||||||||||||||||||
|
y = C1ek |
x |
+ C2 xek |
x |
(6.13) |
||||||||||||||||||||||||||||||||||||||||
|
есть общее решение уравнения (6.9). |
||||||||||||||||||||||||||||||||||||||||||||
|
Пример. |
Решить уравнение |
y′′+ 2 y′+ y = 0 . |
||||||||||||||||||||||||||||||||||||||||||
|
Решение. Это ЛОДУ второго порядка. Составим характеристическое |
||||||||||||||||||||||||||||||||||||||||||||
|
уравнение: |
k 2 + 2k +1 = 0. |
|||||||||||||||||||||||||||||||||||||||||||
|
Находим его корни: k1 = k2 = −1. |
= e−x |
= xe−x . |
||||||||||||||||||||||||||||||||||||||||||
|
Частные решения имеют вид: |
y |
, y |
2 |
|||||||||||||||||||||||||||||||||||||||||
|
y = C e−x |
xe−x |
1 |
||||||||||||||||||||||||||||||||||||||||||
|
Тогда |
+C |
2 |
будет |
общим |
решением |
данного |
||||||||||||||||||||||||||||||||||||||
|
уравнения. |
1 |
|||||||||||||||||||||||||||||||||||||||||||
|
y = C e−x +C |
xe−x . |
|||||||||||||||||||||||||||||||||||||||||||
|
Ответ: |
2 |
■ |
||||||||||||||||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
3. Корни характеристического уравнения (6.11) комплексно- |
||||||||||||||||||||||||||||||||||||||||||||
|
сопряженные, т. е. |
k1 =α +iβ , |
k2 =α −iβ , β ≠ 0 |
(в этом случае |
|||||||||||||||||||||||||||||||||||||||||
|
D= a 2 – 4a < 0). |
||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
|||||||||||||||||||||||||||||||||||||||||||
|
Можно показать (подставляя в уравнение (6.9)) , что |
||||||||||||||||||||||||||||||||||||||||||||
|
y |
= eαx cos βx |
и |
y |
2 |
= eαx sin βx |
|||||||||||||||||||||||||||||||||||||||
|
1 |
||||||||||||||||||||||||||||||||||||||||||||
|
являются частными решениями уравнения (6.11). |
||||||||||||||||||||||||||||||||||||||||||||
|
Так как |
y2 |
= tgβx ≠ C |
(β ≠ 0) |
, |
то |
y и |
y |
2 |
образуют |
|||||||||||||||||||||||||||||||||||
|
y1 |
1 |
|||||||||||||||||||||||||||||||||||||||||||
|
фундаментальную систему решений, |
следовательно, |
29
|
y = eαx (C cos βx + C |
2 |
sin βx ) |
(6.14) |
|
|
1 |
||||
|
есть общее решение уравнения (6.9). |
||||
|
Пример. Решить уравнение |
y′′+ 2 y′+ 2 y = 0 . |
|||
|
Решение. Это ЛОДУ второго порядка. Составим характеристическое |
||||
|
уравнение: |
||||
|
k 2 + 2k + 2 = 0. |
||||
|
Его корни: k1 = −1 +i , k2 = −1 −i . |
||||
|
В данном примере α = −1, |
β =1. |
Пользуясь формулой (6.14), получим общее решение:
y = e−x (C1 cos x + C2 sin x). Ответ: y = e−x (C1 cos x + C2 sin x). ■
4. Рассмотрим уравнение (6.8):
|
y(n) + a1 y(n−1) + a2 y(n−2) +… + an−1 y′+ an y = 0 . |
||||||||||||||||||||||||
|
Составим для него характеристическое уравнение: |
||||||||||||||||||||||||
|
k n + a k n−1 + a |
2 |
k n−2 +…. + a |
n |
k + a |
n |
= 0 . |
(6.15) |
|||||||||||||||||
|
1 |
−1 |
k1, k2, k3…,kn. |
||||||||||||||||||||||
|
Пусть уравнение (6.2.8) имеет n |
различных корней |
|||||||||||||||||||||||
|
Если, кроме того, все |
n |
корней – действительные, то |
||||||||||||||||||||||
|
y =C ek1x + C |
2 |
ek2 x + C ek3 x +… + C |
n |
ekn x |
(6.16) |
|||||||||||||||||||
|
1 |
3 |
|||||||||||||||||||||||
|
есть общее решение уравнения (6.8). |
||||||||||||||||||||||||
|
Если же среди корней есть комплексный корень |
k1 =α +iβ , |
β ≠ 0 , |
||||||||||||||||||||||
|
то уравнение |
(6.15) |
имеет |
также сопряженный |
комплексный |
корень |
|||||||||||||||||||
|
k2 =α −iβ . |
Этой паре комплексных корней соответствуют два частных |
|||||||||||||||||||||||
|
решения: |
= eαx cos βx |
= eαx |
||||||||||||||||||||||
|
y |
и y |
2 |
sin βx . |
|||||||||||||||||||||
|
1 |
k3, k4, k5…,kn |
– |
||||||||||||||||||||||
|
и в этом случае (в предположении, что корни |
||||||||||||||||||||||||
|
действительные и различные) общее решение уравнения (6.8) имеет вид |
||||||||||||||||||||||||
|
y = eαx (C cos βx + C |
2 |
sin βx )+С ek3 x + C |
4 |
ek4 x +… + C |
n |
xkn x . |
||||||||||||||||||
|
1 |
3 |
|||||||||||||||||||||||
|
Пусть теперь корни |
k1, k2, k3…,kn – |
действительные, но k1=k2=k3, |
||||||||||||||||||||||
|
а числа k4, k5, k6…,kn |
различны между собой и не совпадают с |
k1. |
В |
|||||||||||||||||||||
|
этом случае, говорят, что |
k1 – корень кратности 3. |
|||||||||||||||||||||||
|
Общее решение имеет вид |
ek4 x + C ek5 x |
ekn x . |
||||||||||||||||||||||
|
y = ek1x (C + C |
2 |
x + C x2 ) + C |
4 |
+… + C |
n |
|||||||||||||||||||
|
1 |
3 |
5 |
30
Рассмотрим ещё случай, когда есть кратные комплексносопряженные
|
корни k1 = k2 =α +iβ , |
k3 = k4 =α −iβ , β ≠ 0 , а остальные корни |
||||||||||||||||||
|
k5, k6…,kn |
действительные и различные. Общее решение в этом случае |
||||||||||||||||||
|
имеет вид |
y = eαx [(C +C |
x)cos βx + (C +C |
x) sin βx] |
||||||||||||||||
|
2 |
4 |
+ |
|||||||||||||||||
|
1 |
3 |
||||||||||||||||||
|
+ C ek5 x + C |
ek6 x |
+… + C |
ekn x . |
||||||||||||||||
|
5 |
6 |
n |
|||||||||||||||||
|
Пример 1. |
Решить уравнение |
yIV −13y′′+36 y = 0 . |
|||||||||||||||||
|
Решение. |
Это |
ЛОДУ четвертого порядка. Составим |
|||||||||||||||||
|
характеристическое уравнение: |
|||||||||||||||||||
|
k 4 −13k 2 +36 = 0 . |
|||||||||||||||||||
|
Находим корни этого уравнения: k1 = 2 , k2 = −2 , |
k3 = 3, k4 = −3. |
||||||||||||||||||
|
Частные решения будут иметь вид |
|||||||||||||||||||
|
y = e2 x , y |
2 |
= e−2 x , |
y = e3x |
, y |
4 |
= e−3x . |
|||||||||||||
|
1 |
3 |
||||||||||||||||||
|
Тогда |
y = C e2 x + C |
e−2x + C e3x + C |
e−3x |
будет общим |
|||||||||||||||
|
1 |
2 |
3 |
4 |
||||||||||||||||
|
решением |
уравнения. |
||||||||||||||||||
|
Ответ: |
y = C e2 x |
+ C |
e−2x + C e3x |
+ C |
e−3x . |
■ |
|||||||||||||
|
1 |
2 |
3 |
4 |
||||||||||||||||
|
Пример 2. Решить уравнение |
y′′′+ y′′−5y′+3y = 0. |
||||||||||||||||||
|
Решение. |
Это ЛОДУ третьего порядка. Составим характеристическое |
||||||||||||||||||
|
уравнение: |
k3 + k 2 −5k +3 = 0 . |
Его корни: k1 = k2 =1, k3 = −3.
Следовательно, частные решения будут иметь вид:
|
y = ex , y |
2 |
= xex , y = e−3x . |
||||||
|
1 |
3 |
|||||||
|
Тогда y = C ex + C |
2 |
xex + C e−3x |
будет общим решением уравнения. |
|||||
|
1 |
3 |
|||||||
|
Ответ: y = C ex +C |
2 |
xex +C e−3x . |
■ |
|||||
|
1 |
3 |
|||||||
|
Пример 3. Решить уравнение |
yIV +8y′′+16 y = 0. |
|||||||
|
Решение. Это ЛОДУ четвертого порядка. |
||||||||
|
Составим характеристическое уравнение: k 4 +8k 2 +16 = 0 или |
||||||||
|
(k 2 + 4)2 = 0 . |
||||||||
|
Найдем его корни: |
k1 = k2 = 2i , |
k3 = k4 = −2i . |
То есть в нашем |
|||||
|
примере α = 0, β = 2, а кратность корня равна двум. |
||||||||
|
Тогда общее решение: |
+C2 x)cos 2x + (C3 +C4 x)sin 2x . |
|||||||
|
y = (C1 |
||||||||
|
Ответ: y = (C1 +C2 x)cos 2x + (C3 +C4 x)sin 2x . |
■ |
31
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Макеты страниц
Если задана система  линейно независимых функций
линейно независимых функций  имеющих непрерывные производные до
имеющих непрерывные производные до  порядка включительно на промежутке X, то существует одно и только одно приведенное однородное линейное дифференциальное уравнение
порядка включительно на промежутке X, то существует одно и только одно приведенное однородное линейное дифференциальное уравнение  порядка, для которого эти функции образуют фундаментальную систему решений (т. е. базис в пространстве решений). Чтобы доказать это утверждение, надо сначала написать приведенное уравнение
порядка, для которого эти функции образуют фундаментальную систему решений (т. е. базис в пространстве решений). Чтобы доказать это утверждение, надо сначала написать приведенное уравнение  порядка с данной системой решений, а потом доказать, что иных приведенных уравнений с той же фундаментальной системой решений не существует.
порядка с данной системой решений, а потом доказать, что иных приведенных уравнений с той же фундаментальной системой решений не существует.
Требуемое уравнение составляется так: приравниваем к нулю определитель  порядка
порядка

Разложив его по элементам первой строки, получим уравнение вида

где  алгебраическое дополнение элементов
алгебраическое дополнение элементов  первой строки определителя (1). В частности, коэффициент при
первой строки определителя (1). В частности, коэффициент при  может отличаться лишь знаком от минора
может отличаться лишь знаком от минора

т. е. от вронскиана  Поскольку по условию решения
Поскольку по условию решения  линейно независимы, этот вронскиан отличен от нуля на промежутке X. И потому можно разделить на него обе части уравнения, получив искомое приведенное уравнение с данной фундаментальной системой решений
линейно независимы, этот вронскиан отличен от нуля на промежутке X. И потому можно разделить на него обе части уравнения, получив искомое приведенное уравнение с данной фундаментальной системой решений 
Пример. Напишем приведенное однородное линейное дифференциальное уравнение второго порядка, имеющее фундаментальную систему решений:  .
.
Решение. Составляем определитель третьего порядка

и приравниваем его к нулю. Раскрывая определитель, получаем:

Значит, приведенное уравнение имеет вид:

Его особыми точками являются точки, где  или
или  т. е. точки
т. е. точки  .
.
Нам осталось показать, что другого приведенного уравнения  порядка с той же фундаментальной системой решений
порядка с той же фундаментальной системой решений  не существует. Проведем доказательство от противного. Предположим, что функции
не существует. Проведем доказательство от противного. Предположим, что функции  образуют фундаментальную систему решений как для уравнения
образуют фундаментальную систему решений как для уравнения  так и для уравнения
так и для уравнения  где L и М — различные приведенные дифференциальные операторы
где L и М — различные приведенные дифференциальные операторы  порядка. Тогда для любого k имеем:
порядка. Тогда для любого k имеем:  а потому и
а потому и 
Однородные системы линейных алгебраических уравнений. Фундаментальная система решений. Первая часть.
Однородные системы линейных алгебраических уравнений. Нулевое (тривиальное) решение.
Для начала стоит вспомнить, что такое однородные системы линейных алгебраических уравнений. В теме “Система линейных алгебраических уравнений. Основные термины. Матричная форма записи” вопрос классификации систем осуществлялся подробно, здесь же лишь вкратце напомню основные термины. Итак, система линейных алгебраических уравнений (СЛАУ) называется однородной, если все свободные члены этой системы равны нулю. Например, система $left < begin& 2x_1-3x_2-x_3-x_4=0;\ & -4x_1+5x_2+3x_4=0. end right.$ является однородной, так как все свободные члены этой системы (т.е. числа, стоящие в правых частях равенств) – нули.
Любая однородная СЛАУ имеет хотя бы одно решение – нулевое (его ещё называют тривиальное), в котором все переменные равны нулю. Подставим, например, $x_1=0$, $x_2=0$, $x_3=0$ и $x_4=0$ в записанную выше систему. Получим два верных равенства:
Однако следствие из теоремы Кронекера-Капелли однозначно указывает на то, что если СЛАУ имеет решение, то есть только два варианта. Либо это решение единственно (и тогда СЛАУ называют определённой), либо этих решений бесконечно много (такую СЛАУ именуют неопределённой). Возникает первый вопрос: как выяснить, сколько решений имеет заданная нам однородная СЛАУ? Одно (нулевое) или бесконечность?
Та однородная СЛАУ, которая рассмотрена выше, имеет не только нулевое решение. Подставим, например, $x_1=1$, $x_2=-1$, $x_3=2$ и $x_4=3$:
Мы получили два верных равенства, поэтому $x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$ – тоже является решением данной СЛАУ. Отсюда, кстати, следует вывод: так как наша СЛАУ имеет более чем одно решение, то эта СЛАУ является неопределенной, т.е. она имеет бесконечное количество решений.
Кстати сказать, чтобы не писать каждый раз выражения вроде “$x_1=1$, $x_2=-1$, $x_3=2$, $x_4=3$”, пишут все значения переменных в матрицу-столбец: $left(begin 1 \ -1 \ 2 \ 3 end right)$. Эту матрицу тоже называют решением СЛАУ.
Теперь можно вернуться к вопросу о количестве решений однородной СЛАУ. Согласно следствию из теоремы Кронекера-Капелли, если $r=n$ ($n$ – количество переменных), то СЛАУ имеет единственное решение. Если же $r < n$, то СЛАУ имеет бесконечное количество решений.
Случай $r=n$ не интересен. Для однородных СЛАУ он означает, что система имеет только нулевое решение. А вот случай $r < n$ представляет особый интерес.
Этот случай уже был рассмотрен в теме “Базисные и свободные переменные. Общее и базисное решения СЛАУ”. По сути, однородные СЛАУ – это всего лишь частный случай системы линейных уравнений, поэтому вся терминология (базисные, свободные переменные и т.д.) остаётся в силе.
Что такое базисные и свободные переменные? показатьскрыть
Прежде чем дать определение этим терминам, стоит вспомнить, что означает фраза “ранг матрицы равен $r$”. Она означает, что есть хотя бы один минор $r$-го порядка, который не равен нулю. Напомню, что такой минор называется базисным. Базисных миноров может быть несколько. При этом все миноры, порядок которых выше $r$, равны нулю или не существуют. Теперь можно дать следующее определение:
Выбрать $r$ базисных переменных в общем случае можно различными способами. В примерах я покажу наиболее часто используемый способ выбора.
Фундаментальная система решений однородной СЛАУ.
С однородными СЛАУ связано дополнительное понятие – фундаментальная система решений. Дело в том, что если ранг матрицы системы однородной СЛАУ равен $r$, то такая СЛАУ имеет $n-r$ линейно независимых решений: $varphi_1$, $varphi_2$. $varphi_$.
Часто вместо словосочетания “фундаментальная система решений” используют аббревиатуру “ФСР”. Если решения $varphi_1$, $varphi_2$. $varphi_$ образуют ФСР, и $X$ – матрица переменных данной СЛАУ, то общее решение СЛАУ можно представить в таком виде:
$$ X=C_1cdot varphi_1+C_2cdot varphi_2+ldots+C_cdot varphi_, $$
где $C_1$, $C_2$. $C_$ – произвольные постоянные.
Что значит “линейно независимые решения”? показатьскрыть
В данной ситуации под решением понимается матрица-столбец, в которой перечислены значения неизвестных.
Решения $varphi_1$, $varphi_2$, $ldots$, $varphi_n$ называются линейно зависимыми, если существуют такие константы $alpha_1,;alpha_2,;alpha_3,ldots,alpha_n$, что выполняется следующее равенство:
$$ alpha_1cdot varphi_1+alpha_2cdot varphi_2+ldots+alpha_ncdot varphi_n=O $$
при условии, что среди коэффициентов $alpha_i$ есть хотя бы один, не равный нулю.
Если же указанное выше равенство возможно лишь при условии $alpha_1=alpha_2=ldots=alpha_n=0$, то система решений называется линейно независимой.
Буква “$O$” в данном определении обозначает нулевую матрицу. Проще всего пояснить это определение на конкретном примере. Давайте рассмотрим ту СЛАУ, о которой шла речь в начале темы. Мы уже проверили, что $varphi_1=left(begin 1 \-1 \2 \3 endright)$ – решение данной СЛАУ. Точно так же можно показать, что $varphi_2=left(begin 16 \ 11 \ -4 \ 3 endright)$, $varphi_3=left(begin -5 \ -4 \ 2 \ 0 endright)$, $varphi_4=left(begin 7 \ 5 \ -2 \ 1endright)$ – решения данной системы.
Примем $alpha_1=-1$, $alpha_2=0$, $alpha_3=4$, $alpha_4=3$. Выясним, чему же равно выражение $alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4$:
$$ alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4= -1cdot left(begin 1 \-1 \2 \3 endright)+ 0cdot left(begin 16 \ 11 \ -4 \ 3 endright)+ 4cdot left(begin -5 \ -4 \ 2 \ 0 endright)+ 3cdot left(begin 7 \ 5 \ -2 \ 1endright)=\ =left(begin -1+0-20+21\ 1+0-16+15 \ -2+0+8-6 \ -3+0+0+3endright)= left(begin 0\ 0\ 0\0endright). $$
Итак, существуют такие значения констант $alpha_1$, $alpha_2$, $alpha_3$, $alpha_4$, не все одновременно равные нулю, что выполняется равенство $alpha_1cdot varphi_1+alpha_2cdot varphi_2+alpha_3cdot varphi_3+alpha_4cdot varphi_4=O$. Вывод: совокупность решений $varphi_1$, $varphi_2$, $varphi_3$, $varphi_4$ – линейно зависима.
Для сравнения: равенство $alpha_1cdot varphi_1+alpha_2cdot varphi_2=O$ возможно лишь при условии $alpha_1=alpha_2=0$ (я не буду это доказывать, поверьте на слово 🙂 ). Следовательно, система $varphi_1$, $varphi_2$ является линейно независимой.
Если система является неопределённой, указать фундаментальную систему решений.
Итак, мы имеем однородную СЛАУ, у которой 3 уравнения и 4 переменных: $x_1$, $x_2$, $x_3$, $x_4$. Так как количество переменных больше количества уравнений, то такая однородная система не может иметь единственное решение (чуть позже мы строго докажем это предложение на основе теоремы Кронекера-Капелли). Найдём решения СЛАУ, используя метод Гаусса:
$$ left( begin 3 & -6 & 9 & 13 & 0 \ -1 & 2 & 1 & 1 & 0 \ 1 & -2 & 2 & 3 & 0 end right) rightarrow left|begin & text<поменяем местами первую и третью>\ & text<строки, чтобы первым элементом>\ & text <первой строки стала единица.>endright| rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 0\ -1 & 2 & 1 & 1 & 0 \ 3 & -6 & 9 & 13 & 0 end right) begin phantom <0>\ II+I\ III-3cdot Iend rightarrow left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 3 & 4 & 0 endright) begin phantom <0>\ phantom<0>\ III-IIend rightarrow \ rightarrowleft( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 0 & 0 & 0 endright). $$
Мы завершили прямой ход метода Гаусса, приведя расширенную матрицу системы к ступенчатому виду. Слева от черты расположены элементы преобразованной матрицы системы, которую мы также привели к ступенчатому виду. Напомню, что если некая матрица приведена к ступенчатому виду, то её ранг равен количеству ненулевых строк.
И матрица системы, и расширенная матрица системы после эквивалентных преобразований приведены к ступенчатому виду; они содержат по две ненулевых строки. Вывод: $rang A=rangwidetilde = 2$.
Итак, заданная СЛАУ содержит 4 переменных (обозначим их количество как $n$, т.е. $n=4$). Кроме того, ранги матрицы системы и расширенной матрицы системы равны между собой и равны числу $r=2$. Так как $r < n$, то согласно следствию из теоремы Кронекера-Капелли СЛАУ является неопределённой (имеет бесконечное количество решений).
Найдём эти решения. Для начала выберем базисные переменные. Их количество должно равняться $r$, т.е. в нашем случае имеем две базисные переменные. Какие именно переменные (ведь у нас их 4 штуки) принять в качестве базисных? Обычно в качестве базисных переменных берут те переменные, которые расположены на первых местах в ненулевых строках преобразованной матрицы системы, т.е. на “ступеньках”. Что это за “ступеньки” показано на рисунке:
На “ступеньках” стоят числа из столбцов №1 и №3. Первый столбец соответствует переменной $x_1$, а третий столбец соответствует переменной $x_3$. Именно переменные $x_1$ и $x_3$ примем в качестве базисных.
В принципе, если вас интересует именно методика решения таких систем, то можно пропускать нижеследующее примечание и читать далее. Если вы хотите выяснить, почему можно в качестве базисных взять именно эти переменные, и нельзя ли выбрать иные – прошу раскрыть примечание.
Почему можно принять переменные $x_1$ и $x_3$ в качестве базисных? Для ответа на этот вопрос давайте вспомним, что ранг матрицы системы равен числу $r=2$. Это говорит о том, что все миноры данной матрицы, порядок которых выше 2, либо равны нулю, либо не существуют. Ненулевые миноры есть только среди миноров второго порядка. Выберем какой-либо ненулевой минор второго порядка. Мы можем выбирать его как в исходной матрице системы $A$, т.е. в матрице $left( begin 3 & -6 & 9 & 13 \ -1 & 2 & 1 & 1 \ 1 & -2 & 2 & 3 end right)$, так и в преобразованной матрице системы, т.е. в $left( begin 1 & -2 & 2 & 3 \ 0 & 0 & 3 & 4 \ 0 & 0 & 0 & 0 endright)$. Так как в преобразованной матрице системы побольше нулей, то будем работать именно с нею.
Итак, давайте выберем минор второго порядка, элементы которого находятся на пересечении строк №1 и №2, и столбцов №1 и №2:
$$ M_<2>^<(1)>=left| begin 1 & -2 \ 0 & 0 endright|=1cdot 0-(-2)cdot 0=0. $$
Вывод: выбранный нами минор второго порядка не является базисным, ибо он равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №2 (он соответствует переменной $x_2$), то пара переменных $x_1$ и $x_2$ не могут быть базисными переменными.
Осуществим вторую попытку, взяв минор второго порядка, элементы которого лежат на пересечении строк №1, №2 и столбцов №2 и №4:
$$ M_<2>^<(2)>=left| begin 2 & 3\ 3 & 4 endright|=2cdot 4-3cdot 3=-1. $$
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №2 (он соответствует переменной $x_2$) и столбца №4 (он соответствует переменной $x_4$), то пару переменных $x_2$ и $x_4$ можно принять в качестве базисных.
Сделаем и третью попытку, найдя значение минора, элементы которого расположены на пересечении строк №1, №2 и столбцов №1 и №3:
Вывод: выбранный нами минор второго порядка является базисным, ибо он не равен нулю. Так как элементы этого минора взяты из столбца №1 (он соответствует переменной $x_1$) и столбца №3 (он соответствует переменной $x_3$), то пару переменных $x_1$ и $x_3$ можно принять в качестве базисных.
Как видите, выбор базисных переменных не является однозначным. На самом деле количество вариантов выбора не превышает количество размещений из $n$ элементов по $r$, т.е. не больше чем $C_^$.
В рассматриваемом примере в качестве баисных были приняты переменные $x_1$ и $x_3$ – сугубо из соображений удобства дальнейшего решения. В чём это удобство состоит, будет видно чуток позже.
Базисные переменные выбраны: это $x_1$ и $x_3$. Количество свободных переменных, как и количество решений в ФСР, равно $n-r=2$. Свободными переменными будут $x_2$ и $x_4$. Нам нужно выразить базисные переменные через свободные.
Я предпочитаю работать с системой в матричной форме записи. Для начала очистим полученную матрицу $left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 \ 0 & 0 & 0 & 0 & 0 endright)$ от нулевой строки:
$$ left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 endright) $$
Свободным переменным, т.е. $x_2$ и $x_4$, соответствуют столбцы №2 и №4. Перенесём эти столбцы за черту. Знак всех элементов переносимых столбцов изменится на противоположный:
Почему меняются знаки? Что вообще значит это перенесение столбцов? показатьскрыть
Давайте обратимся к расширенной матрице системы, которая после преобразований имеет вид $left( begin 1 & -2 & 2 & 3 & 0\ 0 & 0 & 3 & 4 & 0 endright)$. Перейдём от матрицы к уравнениям. Первая строка соответствует уравнению $x_1-2x_2+2x_3+3x_4=0$, а вторая строка соответствует уравнению $3x_3+4x_4=0$. Теперь перенесём свободные переменные $x_2$ и $x_4$ в правые части уравнений. Естественно, что когда мы переносим выражение $4x_4$ в правую часть уравнения, то знак его изменится на противоположный, и в правой части появится $-4x_4$.
Если опять записать полученную систему в виде матрицы, то мы и получим матрицу с перенесёнными за черту столбцами.
А теперь продолжим решение обычным методом Гаусса. Наша цель: сделать матрицу до черты единичной. Для начала разделим вторую строку на 3, а потом продолжим преобразования обратного хода метода Гаусса:
$$ left( begin 1 & 2 & 2 & -3\ 0 & 3 & 0 & -4 endright) begin phantom <0>\ II:3 end rightarrow left( begin 1 & 2 & 2 & -3\ 0 & 1 & 0 & -4/3 endright) begin I-2cdot II \ phantom <0>end rightarrow \ rightarrow left(begin 1 & 0 & 2 & -1/3\ 0 & 1 & 0 & -4/3 endright). $$
Матрица до черты стала единичной, метод Гаусса завершён. Общее решение найдено, осталось лишь записать его. Вспоминая, что четвёртый столбец соответствует переменной $x_2$, а пятый столбец – переменной $x_4$, получим:
Нами найдено общее решение заданной однородной СЛАУ. Если есть желание, то полученное решение можно проверить. Например, подставляя $x_1=2x_2-frac<1><3>x_4$ и $x_3=-frac<4><3>x_4$ в левую часть первого уравнения, получим:
$$ 3x_1-6x_2+9x_3+13x_4=3cdot left(2x_2-frac<1><3>x_4right)-6x_2+9cdot left(-frac<4><3>x_4right)+13x_4=0. $$
Проверка первого уравнения увенчалась успехом; точно так же можно проверить второе и третье уравнения.
Теперь найдем фундаментальную систему решений. ФСР будет содержать $n-r=2$ решения. Для нахождения ФСР составим таблицу. В первой строке таблицы будут перечислены переменные: сначала базисные $x_1$, $x_3$, а затем свободные $x_2$ и $x_4$. Всего в таблице будут три строки. Так как у нас 2 свободные переменные, то под свободными переменными запишем единичную матрицу второго порядка, т.е. $left(begin 1 & 0 \0 & 1endright)$. Таблица будет выглядеть так:
Теперь будем заполнять свободные ячейки. Начнём со второй строки. Мы знаем, что $x_1=2x_2-frac<1><3>x_4$ и $x_3=-frac<4><3>x_4$. Если $x_2=1$, $x_4=0$, то:
Найденные значения $x_1=2$ и $x_3=0$ запишем в соответствующие пустые ячейки второй строки:
Заполним и третью строку. Если $x_2=0$, $x_4=1$, то:
Найденные значения $x_1=-frac<1><3>$ и $x_3=-frac<4><3>$ запишем в соответствующие пустые ячейки третьей строки. Таким образом таблица будет заполнена полностью:
Из второй и третьей строки таблицы мы и запишем ФСР. Матрица неизвестных для нашей системы такова: $X=left(begin x_1 \x_2 \x_3 \x_4 endright)$. В том же порядке, в котором в матрице $X$ перечислены переменные, записываем значения переменных из таблицы в две матрицы:
$$ varphi_1=left(begin 2 \1 \0 \0 endright);; varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright). $$
Совокупность $varphi_1=left(begin 2 \1 \0 \0 endright)$, $varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:
$$ X=C_1cdotleft(begin 2 \1 \0 \0 endright)+C_2cdotleft(begin -1/3 \0 \ -4/3 \1 endright), $$
где $C_1$ и $C_2$ – произвольные постоянные.
Ответ: Общее решение: $left <begin& x_1=2x_2-frac<1><3>x_4;\ & x_2in R;\ & x_3=-frac<4><3>x_4;\ & x_4 in R. endright.$. Или так: $X=C_1cdotleft(begin 2 \1 \0 \0 endright)+C_2cdotleft(begin -1/3 \0 \ -4/3 \1 endright)$, где $C_1$ и $C_2$ – произвольные константы. Фундаментальная система решений: $varphi_1=left(begin 2 \1 \0 \0 endright)$, $varphi_2=left(begin -1/3 \0 \ -4/3 \1 endright)$.
Записать ФСР однородной СЛАУ
зная общее решение. Записать общее решение с помощью ФСР.
Общее решение уже было получено в теме “метод Крамера” (пример №4). Это решение таково:
Опираясь на предыдущий пример №1, попробуйте составить ФСР самостоятельно, а потом сверить с ответом.
Ранг матрицы системы $r=3$ (поэтому у нас три базисных переменных), количество переменных $n=5$. Количество свободных переменных и количество решений ФСР равно $n-r=2$.
Так же, как и в предыдущем примере, составим ФСР. При составлении учтём, что $x_1$, $x_2$, $x_3$ – базисные переменные, а $x_4$, $x_5$ – свободные переменные.
Совокупность $varphi_1=left(begin -17/19 \-15/19 \20/19 \1\0 endright)$, $varphi_2=left(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$ и есть ФСР данной системы. Общее решение можно записать теперь так: $X=C_1cdot varphi_1+C_2cdot varphi_2$. Или в развёрнутом виде:
$$ X=C_1cdotleft(begin -17/19 \-15/19 \20/19 \1\0 endright)+C_2cdotleft(begin 144/19 \ 41/19 \ -4/19\0\1 endright), $$
где $C_1$ и $C_2$ – произвольные постоянные.
Ответ: Фундаментальная система решений: $varphi_1=left(begin -17/19 \-15/19 \20/19 \1\0 endright)$, $varphi_2=left(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$. Общее решение: $X=C_1cdotleft(begin -17/19 \-15/19 \20/19 \1\0 endright)+C_2cdotleft(begin 144/19 \ 41/19 \ -4/19\0\1 endright)$, где $C_1$ и $C_2$ – произвольные константы.
Продолжение этой темы рассмотрим во второй части, где разберём ещё один пример с нахождением общего решения и ФСР.
Системы дифференциальных уравнений с примерами решения и образцами выполнения
Также как и обыкновенные дифференциальные уравнения, системы дифференциальных уравнений применяются для описания многих процессов реальной действительности. В частности, к ним относятся различного рода физические и химические процессы, процессы нефте- и газодобычи, геологии, экономики и т.д. Действительно, если некоторые физические величины (перемещение тела, пластовое давление жидкости в фиксированной точке с тремя координатами, концентрация веществ, объемы продаж продуктов) оказываются меняющимися со временем под воздействием тех или иных факторов, то, как правило, закон их изменения по времени описывается именно системой дифференциальных уравнений, т.е. системой, связывающей исходные переменные как функции времени и производные этих функций. Независимой переменной в системе дифференциальных уравнений может выступать не только время, но и другие физические величины: координата, цена продукта и т.д.

Решение систем дифференциальных уравнений
К системе дифференциальных уравнений приводит уже простейшая задача динамики точки: даны силы, действующие на материальную точку; найти закон движения, т. е. найти функции 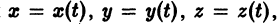 выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид
выражающие зависимость координат движущейся точки от времени. Система, которая при этом получается, в общем случае имеет вид
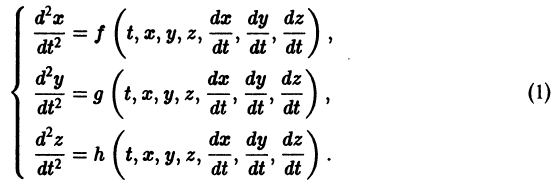
Здесь x, у, z — координаты движущейся точки, t — время, f, g, h — известные функции своих аргументов.
Система вида (1) называется канонической. Обращаясь к общему случаю системы т дифференциальных уравнений с т неизвестными функциями 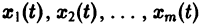 аргумента t, назовем канонической систему вида
аргумента t, назовем канонической систему вида
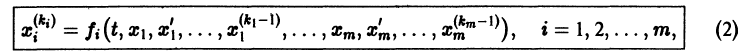
разрешенную относительно старших производных. Система уравнений первого порядка, разрешенных относительно производных от искомых функций,
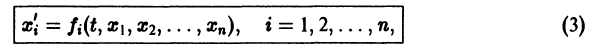
Если 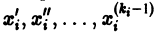 в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из
в (2) принять за новые вспомогательные функции, то общую каноническую систему (2) можно заменить эквивалентной ей нормальной системой, состоящей из 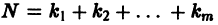 уравнений. Поэтому достаточно рассматривать лишь нормальные системы.
уравнений. Поэтому достаточно рассматривать лишь нормальные системы.
Например, одно уравнение
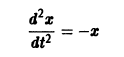
является мастным случаем канонической системы. Положив 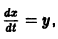 в силу исходного уравнения будем иметь
в силу исходного уравнения будем иметь
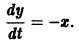
В результате получаем нормальную систему уравнений
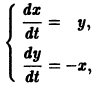
эквивалентную исходному уравнению.
Определение:
Решением нормальной системы (3) на интервале (а, Ь) изменения аргумента t называется всякая система n функций
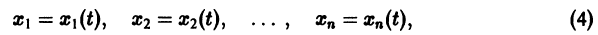
дифференцируемых на интервале а 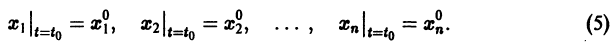
Теорема:
Существования и единственности решения задачи Коши. Пусть имеем нормальную систему дифференциальных уравнений
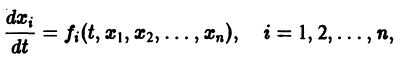
и пусть функции 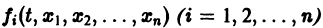 определены в некоторой (n + 1) — мерной области D изменения переменных
определены в некоторой (n + 1) — мерной области D изменения переменных 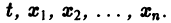 Если существует окрестность
Если существует окрестность 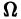 точки
точки 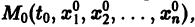 в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным
в которой функции fi непрерывны по совокупности аргументов и имеют ограниченные частные производные по переменным  то найдется интервал
то найдется интервал 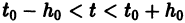 изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям
изменения t, на котором существует единственное решение нормальной системы (3), удовлетворяющее начальным условиям
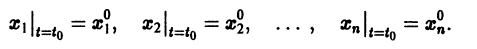
Определение:
Система n функций
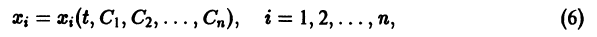
зависящих от t и n произвольных постоянных 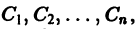 называется общим решением нормальной системы (3) в некоторой области
называется общим решением нормальной системы (3) в некоторой области 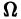 существования и единственности решения задачи Коши, если
существования и единственности решения задачи Коши, если
1) при любых допустимых значениях 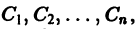 система функций (6) обращает уравнения (3) в тождества,
система функций (6) обращает уравнения (3) в тождества,
2) в области 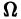 функции (6) решают любую задачу Коши.
функции (6) решают любую задачу Коши.
Решения, получающиеся из общего при конкретных значениях постоянных 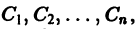 называются частными решениями.
называются частными решениями.
Обратимся для наглядности к нормальной системе двух уравнений,

Будем рассматривать систему значений t, x1, х2 как прямоугольные декартовы координаты точки трехмерного пространства, отнесенного к системе координат 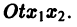 Решение
Решение
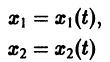
системы (7), принимающее при 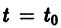 значения
значения 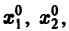 определяет в пространстве некоторую линию, проходящую через точку
определяет в пространстве некоторую линию, проходящую через точку 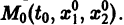 Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку
Эта линия называется интегральной кривой нормальной системы (7). Задача Коши для системы (7) получает следующую геометрическую формулировку: в пространстве переменных t, x1, х2 найти интегральную кривую, проходящую через данную точку 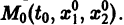 (рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.
(рис. 1). Теорема 1 устанавливает существование и единственность такой кривой.
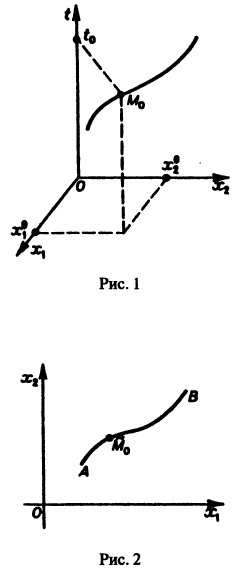
Нормальной системе (7) и ее решению можно придать еще такое истолкование: будем независимую переменную t рассматривать как параметр, а решение
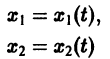
системы — как параметрические уравнения кривой на плоскости 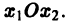 Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение
Эту плоскость переменных х1х2 называют фазовой плоскостью. В фазовой плоскости решение 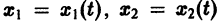 системы (7), принимающее при t = to начальные значения
системы (7), принимающее при t = to начальные значения 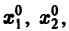 изображается кривой АВ, проходящей через точку
изображается кривой АВ, проходящей через точку 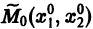 (рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.
(рис. 2). Эту кривую называют траекторией системы (фазовой траекторией). Траектория системы (7) есть проекция интегральной кривой на фазовую плоскость. По интегральной кривой фазовая траектория определяется однозначно, но не наоборот.
Методы интегрирования систем дифференциальных уравнений
Метод исключения
Один из методов интегрирования — метод исключения. Частным случаем канонической системы является одно уравнение n-го порядка, разрешенное относительно старшей производной
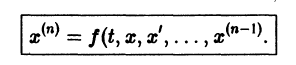
Введя новые функции 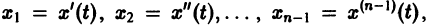 заменим это уравнение следующей нормальной системой n уравнений:
заменим это уравнение следующей нормальной системой n уравнений:
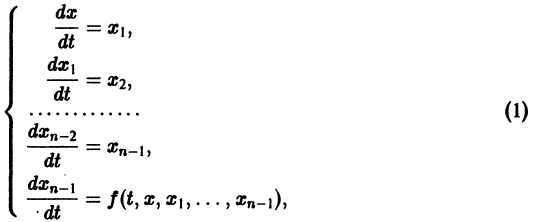
т. е. одно уравнение n-го порядка эквивалентно нормальной системе (1)
Можно утверждать и обратное, что, вообще говоря, нормальная система п уравнений первого порядка эквивалентна одному уравнению порядка n. На этом и основан метод исключения для интегрирования систем дифференциальных уравнений.
Делается это так. Пусть имеем нормальную систему
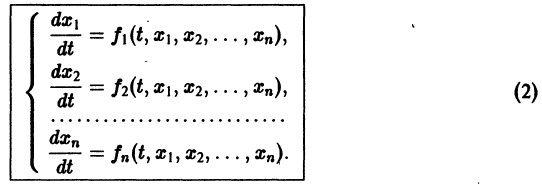
Продифференцируем первое из уравнений (2) по t. Имеем
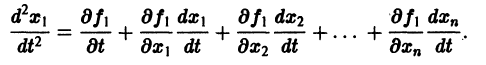
Заменяя в правой части производные 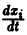 их выражениями
их выражениями 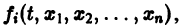 получим
получим
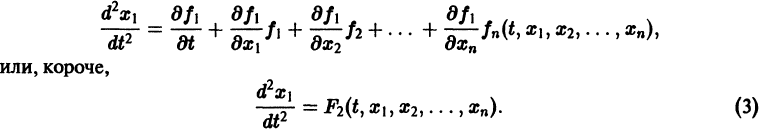
Уравнение (3) снова дифференцируем по t. Принимая во внимание систему (2), получим
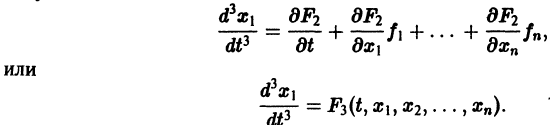
Продолжая этот процесс, найдем
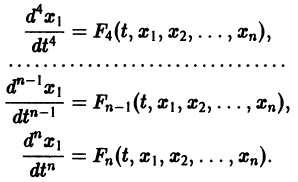
Предположим, что определитель
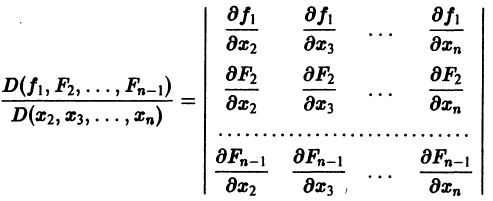
(якобиан системы функций  отличен от нуля при рассматриваемых значениях
отличен от нуля при рассматриваемых значениях 
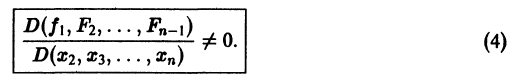
Тогда система уравнений, составленная из первого уравнения системы (2) и уравнений
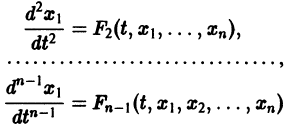
будет разрешима относительно неизвестных 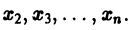 При этом
При этом 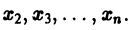 выразятся через
выразятся через 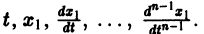
Внося найденные выражения в уравнение
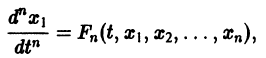
получим одно уравнение n-го порядка
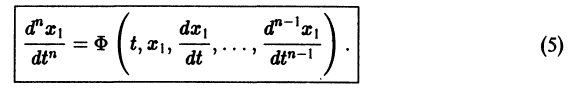
Из самого способа его построения следует, что если 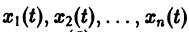 есть решения системы (2), то функция х1(t) будет решением уравнения (5).
есть решения системы (2), то функция х1(t) будет решением уравнения (5).
Обратно, пусть Х1(t) — решение уравнения (5). Дифференцируя это решение по t, вычислим 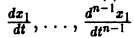 и подставим найденные значения как известные функции
и подставим найденные значения как известные функции
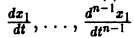
от t в систему уравнений
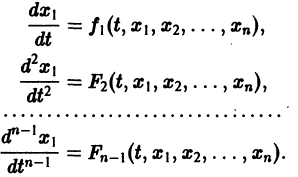
По предположению эту систему можно разрешить относительно 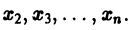 т. е найти
т. е найти  как функции от t.
как функции от t.
Можно показать, что так построенная система функций
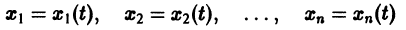
составляет решение системы дифференциальных уравнений (2). Пример:
Требуется проинтегрировать систему

Дифференцируя первое уравнение системы, имеем
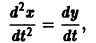
откуда, используя второе уравнение, получаем
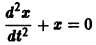
— линейное дифференциальное уравнение второго порядка с постоянными коэффициентами с одной неизвестной функцией. Его общее решение имеет вид
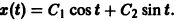
В силу первого уравнения системы находим функцию

Найденные функции x(t), y(t), как легко проверить, при любых значениях С1 и С2 удовлетворяют заданной системе.
Функции x(t), y(t) можно представить в виде
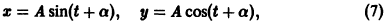
откуда видно, что интегральные кривые системы (6) — винтовые линии с шагом 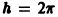 и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).
и с общей осью х = у = 0, которая также является интегральной кривой (рис. 3).
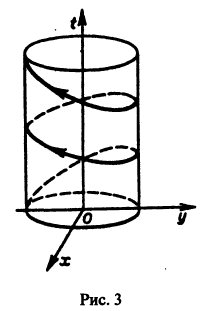
Исключая в формулах (7) параметр t, получаем уравнение
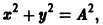
так что фазовые траектории данной системы суть окружности с центром в начале координат — проекции винтовых линий на плоскость хОу.
При А = 0 фазовая траектория состоит из одной точки х = 0, у = 0, называемой точкой покоя системы.
Замечание:
Может оказаться, что функции 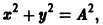 нельзя выразить через
нельзя выразить через 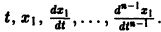 Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений
Тогда уравнения n-го порядка, эквивалентного исходной системе, мы не получим. Вот простой пример. Систему уравнений
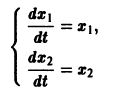
нельзя заменить эквивалентным уравнением второго порядка относительно х1 или x2. Эта система составлена из пары уравнений 1-го порядка, каждое из которых интегрируется независимо, что дает
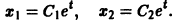
Метод интегрируемых комбинаций
Интегрирование нормальных систем дифференциальных уравнений
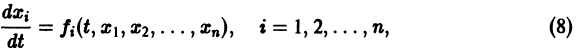
иногда осуществляется методом интегрируемых комбинаций.
Интегрируемой комбинацией называется дифференциальное уравнение, являющееся следствием уравнений (8), но уже легко интегрирующееся.
Пример:
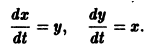
Складывая почленно данные уравнения, находим одну интегрируемую комбинацию:

Вычитая почленно из первого уравнения системы второе, получаем вторую интегрируемую комбинацию:

Мы нашли два конечных уравнения
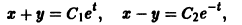
из которых легко определяется общее решение системы:
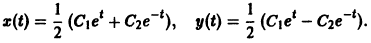
Одна интегрируемая комбинация дает возможность получить одно уравнение
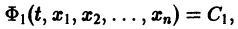
связывающее независимую переменную t и неизвестные функции  Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция
Такое конечное уравнение называется первым интегралом системы (8). Иначе: первым интегралом системы дифференциальных уравнений (8) называется дифференцируемая функция 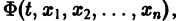 не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.
не равная тождественно постоянной, но сохраняющая постоянное значение на любой интегральной кривой этой системы.
Если найдено п первых интегралов системы (8) и все они независимы, т. е. якобиан системы функций  отличен от нуля:
отличен от нуля:
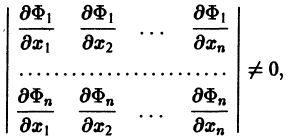
то задача интефирования системы (8) решена (так как из системы
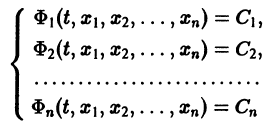
определяются все неизвестные функции 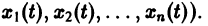
Системы линейных дифференциальных уравнений
Система дифференциальных уравнений называется линейной, если она линейна относительно неизвестных функций и их производных, входящих в уравнение. Система n линейных уравнений первого порядка, записанная в нормальной форме, имеет вид
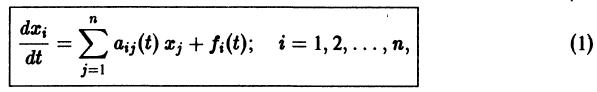
или, в матричной форме,
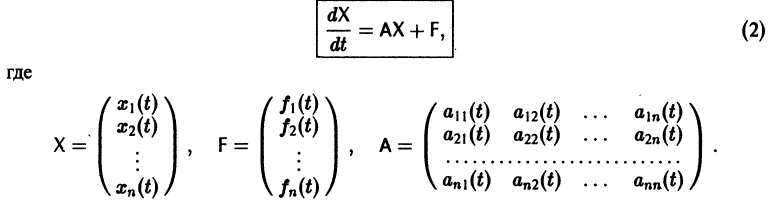
Теорема:
Если все функции 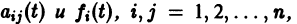 непрерывны на отрезке
непрерывны на отрезке 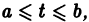 то в достаточно малой окрестности каждой точки
то в достаточно малой окрестности каждой точки 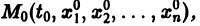 где
где 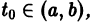 выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).
выполнены условия теоремы существования и единственности решения задачи Коши, следовательно, через каждую такую точку проходит единственная интегральная кривая системы (1).
Действительно, в таком случае правые части системы (1) непрерывны по совокупности аргументов t,  и их частные производные по
и их частные производные по 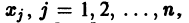 ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам
ограничены, так как эти производные равны непрерывным на отрезке [а,b] коэффициентам 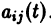
Введем линейный оператор
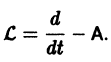
Тогда система (2) запишется в виде
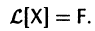
Если матрица F — нулевая, т. е. 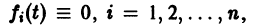 на интервале (а,b), то система (2) называется линейной однородной и имеет вид
на интервале (а,b), то система (2) называется линейной однородной и имеет вид

Приведем некоторые теоремы, устанавливающие свойства решений линейных систем.
Теорема:
Если X(t) является решением линейной однородной системы
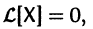
то cX(t), где с — произвольная постоянная, является решением той же системы.
Теорема:
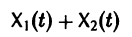
двух решений 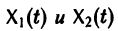 однородной линейной системы уравнений является решением той же системы.
однородной линейной системы уравнений является решением той же системы.
Следствие:
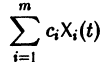
с произвольными постоянными коэффициентами сi решений 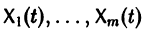 линейной однородной системы дифференциальных уравнений
линейной однородной системы дифференциальных уравнений
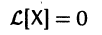
является решением той же системы.
Теорема:
Если 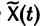 есть решение линейной неоднородной системы
есть решение линейной неоднородной системы
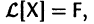
a Xo(t) — решение соответствующей однородной системы

будет решением неоднородной системы 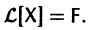
Действительно, по условию,
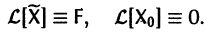
Пользуясь свойством аддитивности оператора 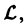 получаем
получаем
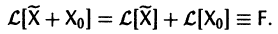
Это означает, что сумма 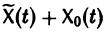 есть решение неоднородной системы уравнений
есть решение неоднородной системы уравнений 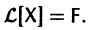
Определение:
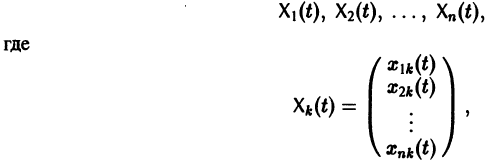
называются линейно зависимыми на интервале a 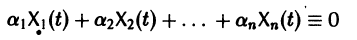
при 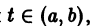 причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при
причем по крайней мере одно из чисел аi, не равно нулю. Если тождество (5) справедливо только при  то векторы
то векторы 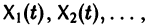
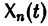 называются линейно независимыми на (а, b).
называются линейно независимыми на (а, b).
Заметим, что одно векторное тождество (5) эквивалентно n тождествам:
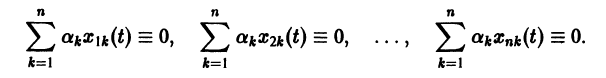
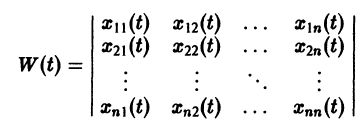
называется определителем Вронского системы векторов 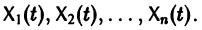
Определение:
Пусть имеем линейную однородную систему

где 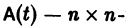 матрица с элементами
матрица с элементами 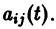 Система n решений
Система n решений
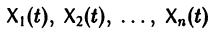
линейной однородной системы (6), линейно независимых на интервале а 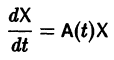
с непрерывными на отрезке 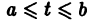 коэффициентами
коэффициентами 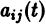 является линейная комбинация п линейно независимых на интервале а
является линейная комбинация п линейно независимых на интервале а 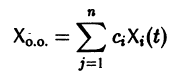
(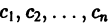 ) — произвольные постоянные числа).
) — произвольные постоянные числа).
Пример:
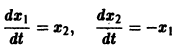
имеет, как нетрудно проверить, решения
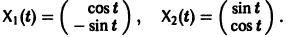
Эти решения линейно независимы, так как определитель Вронского отличен от нуля:
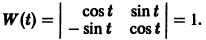
Общее решение системы имеет вид
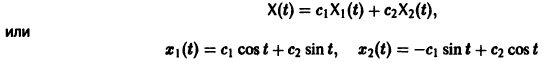
(с1, с2 — произвольные постоянные).
Фундаментальная матрица
Квадратная матрица
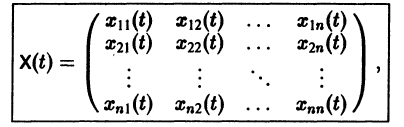
столбцами которой являются линейно независимые решения 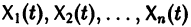 системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению
системы (6), называется фундаментальной матрицей этой системы. Нетрудно проверить, что фундаментальная матрица удовлетворяет матричному уравнению
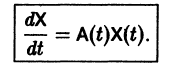
Если Х(t) — фундаментальная матрица системы (6), то общее решение системы можно представить в виде
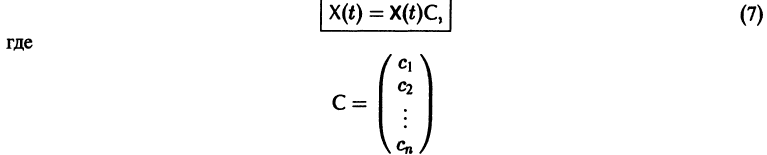
— постоянная матрица-столбец с произвольными элементами. Полагая в (7) t = t0, имеем
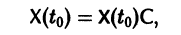
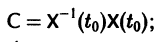
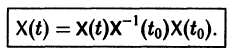
Матрица 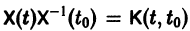 называется матрицей Коши. С ее помощью решение системы (6) можно представить так:
называется матрицей Коши. С ее помощью решение системы (6) можно представить так:
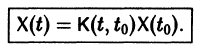
Теорема:
О структуре общего решения линейной неоднородной системы дифференциальных уравнений. Общее решение в области 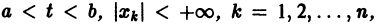 линейной неоднородной системы дифференциальных уравнений
линейной неоднородной системы дифференциальных уравнений

с непрерывными на отрезке 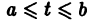 коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения
коэффициентами aij(t) и правыми частями fi(t) равно сумме общего решения
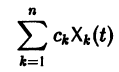
соответствующей однородной системы и какого-нибудь частного решения 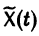 неоднородной системы (2):
неоднородной системы (2):
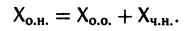
Метод вариации постоянных
Если известно общее решение линейной однородной системы (6), то частное решение неоднородной системы можно находить методом вариации постоянных (метод Лагранжа).
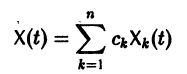
есть общее решение однородной системы (6), тогда
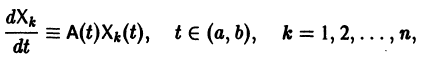
причем решения Xk(t) линейно независимы.
Будем искать частное решение неоднородной системы
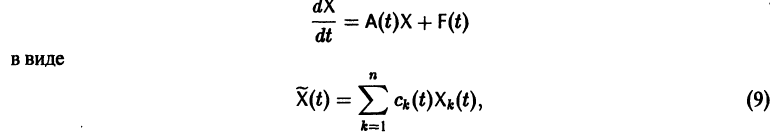
где 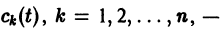 неизвестные функции от t. Дифференцируя
неизвестные функции от t. Дифференцируя 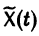 по t, имеем
по t, имеем
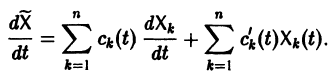
Подставляя 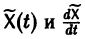 в (2), получаем
в (2), получаем
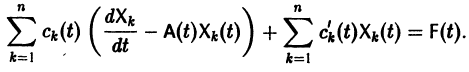
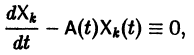
то для определения 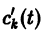 получаем систему
получаем систему
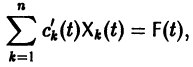
или, в развернутом виде,
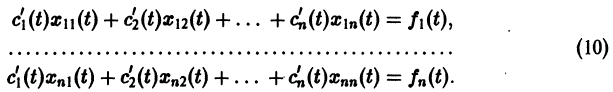
Система (10) есть линейная алгебраическая система относительно 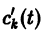 определителем которой является определитель Вронского W(t) фундаментальной системы решений
определителем которой является определитель Вронского W(t) фундаментальной системы решений 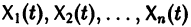 . Этот определитель отличен от нуля всюду на интервале a
. Этот определитель отличен от нуля всюду на интервале a 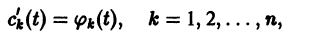
где 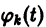 — известные непрерывные функции. Интегрируя последние соотношения, находим
— известные непрерывные функции. Интегрируя последние соотношения, находим
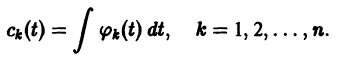
Подставляя эти значения 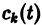 в (9), находим частное решение системы (2)
в (9), находим частное решение системы (2)
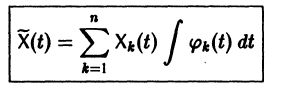
(здесь под символом 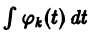 понимается одна из первообразных для функции
понимается одна из первообразных для функции 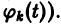
Системы линейных дифференциальных уравнений с постоянными коэффициентами
Рассмотрим линейную систему дифференциальных уравнений
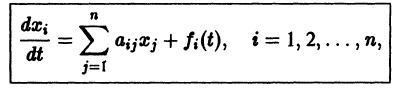
в которой все коэффициенты 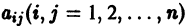 — постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.
— постоянные. Чаще всего такая система интегрируется сведением ее к одному уравнению более высокого порядка, причем это уравнение будет также линейным с постоянными коэффициентами. Другой эффективный метод интегрирования систем с постоянными коэффициентами — метод преобразования Лапласа.
Мы рассмотрим еще метод Эйлера интегрирования линейных однородных систем дифференциальных уравнений с постоянными коэффициентами. Он состоит в следующем.
Метод Эйлера
Будем искать решение системы
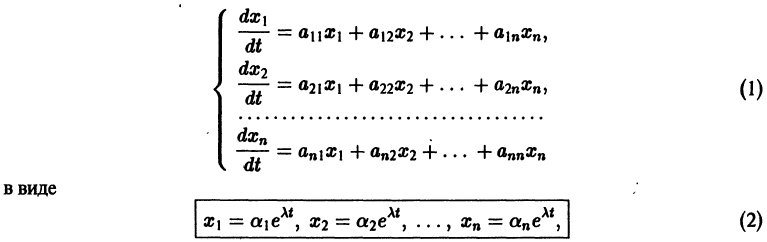
где 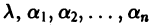 — постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на
— постоянные. Подставляя Xk в форме (2) в систему (1), сокращая на 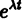 и перенося все члены в одну часть равенства, получаем систему
и перенося все члены в одну часть равенства, получаем систему
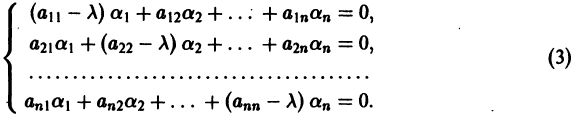
Для того, чтобы эта система (3) линейных однородных алгебраических уравнений с n неизвестными 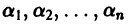 имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:
имела нетривиальное решение, необходимо и достаточно, чтобы ее определитель был равен нулю:
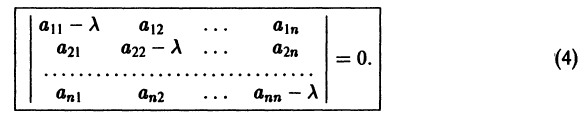
Уравнение (4) называется характеристическим. В его левой части стоит многочлен относительно  степени n. Из этого уравнения определяются те значения
степени n. Из этого уравнения определяются те значения  , при которых система (3) имеет нетривиальные решения
, при которых система (3) имеет нетривиальные решения 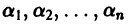 . Если все корни
. Если все корни 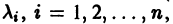 характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения
характеристического уравнения (4) различны, то, подставляя их по очереди в систему (3), находим соответствующие им нетривиальные решения 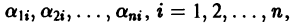 этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде
этой системы n, следовательно, находим п решений исходной системы дифференциальных уравнений (1) в виде

где второй индекс указывает номер решения, а первый — номер неизвестной функции. Построенные таким образом п частных решений линейной однородной системы (1)
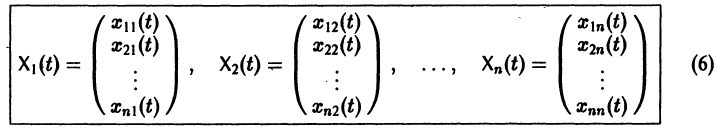
образуют, как можно проверить, фундаментальную систему решений этой системы.
Следовательно, общее решение однородной системы дифференциальных уравнений (1) имеет вид
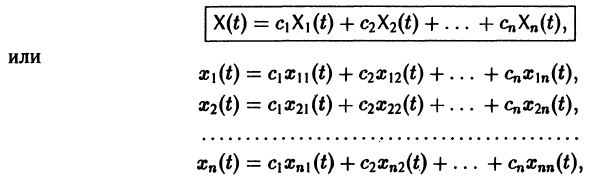
где  произвольные постоянные.
произвольные постоянные.
Случай, когда характеристическое уравнение имеет кратные корни, мы рассматривать не будем.
Пример:
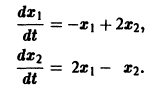
Ищем решение в виде
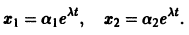

имеет корни 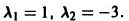
Система (3) для определения a1, а2 выглядит так:

Подставляя в (*) 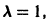 получаем
получаем
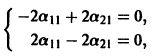
откуда а21 = а11. Следовательно,
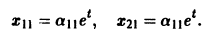
Полагая в 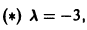 находим a22 = — a12, поэтому
находим a22 = — a12, поэтому
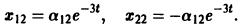
Общее решение данной системы:
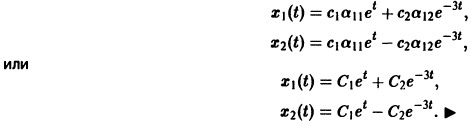
Матричный метод
Изложим еще матричный метод интегрирования однородной системы (1). Запишем систему (1) в виде


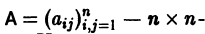 матрица с постоянными действительными элементами
матрица с постоянными действительными элементами 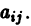
Напомним некоторые понятия из линейной алгебры. Вектор 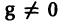 называется собственным вектором матрицы А, если
называется собственным вектором матрицы А, если
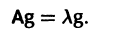
Число  называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения
называется собственным значением матрицы А, отвечающим собственному вектору g, и является корнем характеристического уравнения
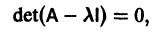
где I — единичная матрица.
Будем предполагать, что все собственные значения 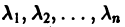 матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует
матрицы А различны. В этом случае собственные векторы g1, g2, …gn линейно независимы и существует 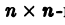 матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что
матрица Т, приводящая матрицу А к диагональному виду, т. е. такая, что
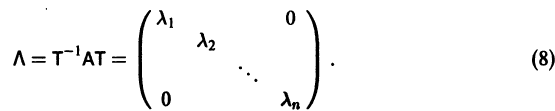
Столбцами матрицы Т являются координаты собственных векторов g1, g2 …, gn матрицы А.
Введем еще следующие понятия. Пусть В(t) — 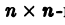 матрица, элементы
матрица, элементы 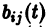 которой суть функции аргумента t, определенные на множестве
которой суть функции аргумента t, определенные на множестве 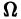 . Матрица В(t) называется непрерывной на
. Матрица В(t) называется непрерывной на 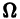 , если непрерывны на
, если непрерывны на 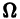 все ее элементы
все ее элементы 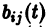 . Матрица В(t) называется дифференцируемой на
. Матрица В(t) называется дифференцируемой на  , если дифференцируемы на
, если дифференцируемы на  все элементы
все элементы 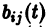 этой матрицы. При этом производной матрицы
этой матрицы. При этом производной матрицы 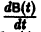 называется матрица, элементами которой являются производные
называется матрица, элементами которой являются производные 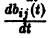 у соответствующих элементов матрицы В(t).
у соответствующих элементов матрицы В(t).
Пусть B(t) — n х n-матрица,
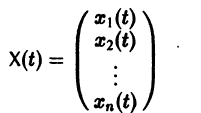
— вектор-столбец. Учитывая правила алгебры матриц, непосредственной проверкой убеждаемся в справедливости формулы
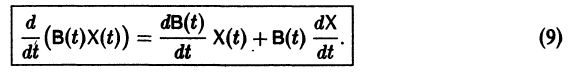
В частности, если В — постоянная матрица, то
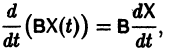
так как 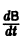 есть нуль-матрица.
есть нуль-матрица.
Теорема:
Если собственные значения 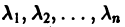 матрицы А различны, то общее решение системы (7) имеет вид
матрицы А различны, то общее решение системы (7) имеет вид
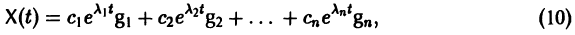
где g1, g2,…, gn — собственные векторы-столбцы матрицы А,  произвольные постоянные числа.
произвольные постоянные числа.
Введем новый неизвестный вектор-столбец Y(t) по формуле

где Т — матрица, приводящая матрицу А к диагональному виду. Подставляя X(t) из (11) в (7), получим систему
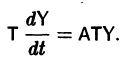
Умножая обе части последнего соотношения слева на 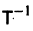 и учитывая, что
и учитывая, что 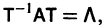 придем к системе
придем к системе
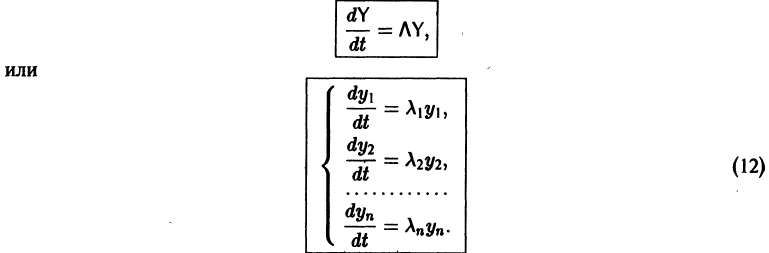
Мы получили систему из n независимых уравнений, которая без труда интегрируется:
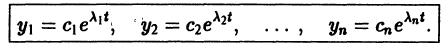
Здесь 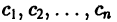 — произвольные постоянные числа.
— произвольные постоянные числа.
Вводя единичные n-мерные векторы-столбцы
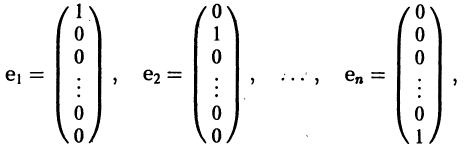
решение Y(t) можно представить в виде
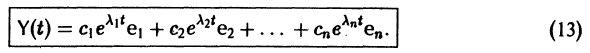
В силу (11) Х(t) = TY(t). Так как столбцы матрицы Т есть собственные векторы матрицы 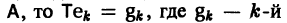 собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):
собственный вектор матрицы А. Поэтому, подставляя (13) в (11), получим формулу (10):
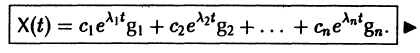
Таким образом, если матрица А системы дифференциальных уравнений (7) имеет различные собственные значения, для получения общего решения этой системы:
1) находим собственные значения 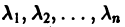 матрицы как корни алгебраического уравнения
матрицы как корни алгебраического уравнения
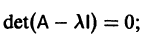
2) находим все собственные векторы g1, g2,…, gn;
3) выписываем общее решение системы дифференциальных уравнений (7) по формуле (10).
Пример:
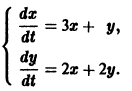
Матрица А системы имеет вид
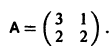
1) Составляем характеристическое уравнение

Корни характеристического уравнения 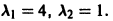
2) Находим собственные векторы
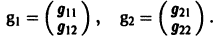
Для  = 4 получаем систему
= 4 получаем систему
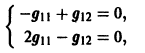
откуда g11 = g12, так что
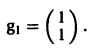
Аналогично для  = 1 находим
= 1 находим
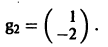
3) Пользуясь формулой (10), получаем общее решение системы дифференциальных уравнений
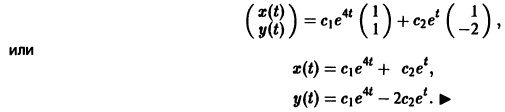
Корни характеристического уравнения могут быть действительными и комплексными. Так как по предположению коэффициенты 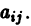 системы (7) действительные, то характеристическое уравнение
системы (7) действительные, то характеристическое уравнение
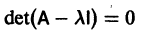
будет иметь действительные коэффициенты. Поэтому наряду с комплексным корнем  оно будет иметь и корень
оно будет иметь и корень  *, комплексно сопряженный с
*, комплексно сопряженный с  . Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению
. Нетрудно показать, что если g — собственный вектор, отвечающий собственному значению  , то
, то  * — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.
* — тоже собственное значение, которому отвечает собственный вектор g*, комплексно сопряженный с g.
При комплексном  решение
решение
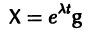
системы (7) также будет комплексным. Действительная часть
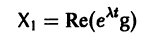
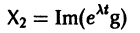
этого решения являются решениями системы (7). Собственному значению  * будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения
* будет отвечать пара действительных решений X1 и -Х2, т. е. та же пара, что и для собственного значения  . Таким образом, паре
. Таким образом, паре  ,
,  * комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.
* комплексно сопряженных собственных значений отвечает пара действительных решений системы (7) дифференциальных уравнений.
Пусть 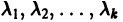 — действительные собственные значения,
— действительные собственные значения, 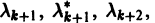
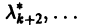 — комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид
— комплексные собственные значения. Тогда всякое действительное решение системы (7) имеет вид
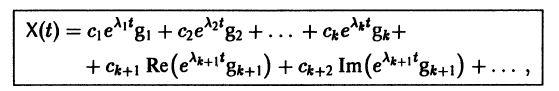
где сi — произвольные постоянные.
Пример:
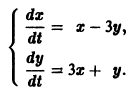
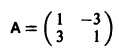
1) Характеристическое уравнение системы

Его корни 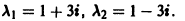
2) Собственные векторы матриц
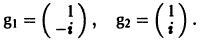
3) Решение системы
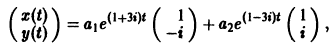
где а1, а2 — произвольные комплексные постоянные.
Найдем действительные решения системы. Пользуясь формулой Эйлера
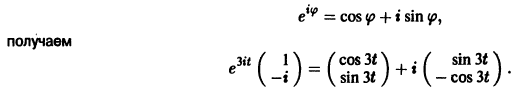
Следовательно, всякое действительное решение системы имеет
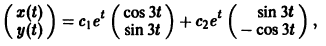
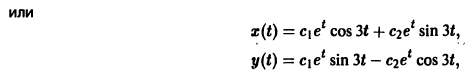
где с1, с2 — произвольные действительные числа.
Понятие о системах дифференциальных уравнений







Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:






















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
ЛДУ с переменными коэффициентами. Метод Лагранжа
Линейные дифференциальные уравнения с переменные коэффициентами
Если известно частное решение уравнения
то его порядок можно понизить на единицу (не нарушая линейности уравнения), полагая , где — новая неизвестная функция, а затем делая замену (можно непосредственно делать замену ).
Если известно частных линейно независимых решений уравнения (32), то порядок уравнения может быть понижен на единиц.
Общее решение уравнения
есть сумма какого-нибудь его частного решения и общего решения соответствующего однородного уравнения (32).
Если известна фундаментальная система соответствующего однородного уравнения (32), то общее решение неоднородного уравнения (33) может быть найдено методом вариации постоянных ( метод Лагранжа ).
Общее решение уравнения (32) имеет вид
где — произвольные постоянные.
Будем искать решение уравнения (33) в виде
где — некоторые пока неизвестные функции от . Для их определения получаем систему
Разрешая эту систему относительно , получаем
где — произвольные постоянные. Внося найденные значения в (34), получаем общее решения уравнения (33).
В частности, для уравнения второго порядка
Решая (36) относительно и , получаем
где и — постоянные интегрирования.
Замечание. Для уравнения , где , система (36) будет выглядеть так:
Пример 1. Найти общее решение уравнения , если есть его частное решение.
Решение. Положим , где — новая неизвестная функция от , тогда
Подставляя в данное уравнение, получаем
Но так как есть частное решение данного уравнения, то , поэтому имеем
Но , а значит , и уравнение (37) примет вид
Перепишем его в виде . Отсюда имеем , откуда
Интегрируя это уравнение, найдем и, следовательно, общее решение данного уравнения будет
Пример 2. Найти общее решение уравнения .
Решение. Общее решение соответствующего однородного уравнения имеет вид (см. пример 1)
и следовательно, его фундаментальная система решений будет
Будем искать общее решение данного уравнения методом вариации произвольных постоянных:
где — постоянные неизвестные функции от , подлежащие определению. Для их нахождения составим следующую систему:
Отсюда находим: . Интегрируя, получаем
Подставляя эти значения и в выражение для , найдем общее решение данного уравнения
Пример 3. Решить уравнение .
Решение. Соответствующее однородное уравнение будет . Его характеристическое уравнение имеет мнимые корни , и общее решение однородного уравнения имеет вид
Общее решение исходного уравнения ищем в виде
где и — неизвестные функции от . Для их нахождения составим систему
Разрешаем эту систему относительно и :
Подставляя выражения и в (38), получаем общее решение данного уравнения
Здесь есть частное решение исходного неоднородного уравнения.
Пример 4. Зная фундаментальную систему решений соответствующего однородного уравнения, найти частное решение уравнения
Решение. Применяя метод вариации постоянных, находим общее решение уравнения (39):
При первые два слагаемых правой части (40) стремятся к бесконечности, причем при любых , неравных нулю одновременно, функция есть бесконечно большая функция при . Третье слагаемое правой части (40) имеет пределом ноль при , что легко установить с помощью правила Лопиталя. Таким образом, функция , которая получается из (40) при и , будет решением уравнения (39), удовлетворяющим условию .
Составление дифференциального уравнения по заданной фундаментальной системе решений
Рассмотрим линейно независимую на отрезке систему функций
имеющих все производные до n-го порядка включительно. Тогда уравнение
где — неизвестная функция, будет линейным дифференциальным уравнением, для которого, как нетрудно видеть, функции составляют фундаментальную систему решений. Коэффициент при в (42) есть определитель Вронского системы (41). Те точки, в которых этот определитель обращается в ноль, будут особыми точками построенного уравнения — в этих точках обращается в ноль коэффициент при старшей производной .
Пример 1. Составить дифференциальное уравнение, для которого образуют фундаментальную систему решений.
Решение. Применяя формулу (42), получаем
Раскрывая определитель в левой части (43) по элементам третьего столбца, будем иметь . Это и есть искомое дифференциальное уравнение.
Пример 2. Составить дифференциальное уравнение, для которого функции фундаментальную систему решений образуют функции .
Решение. Составим уравнение вида (42):
Раскрывая последний определитель по элементам 3-го столбца, будем иметь
В этом примере определитель Вронского обращается в ноль при . Это не противоречит общей теории, в силу которой определитель Вронского фундаментальной системы решений линейного однородного дифференциального уравнения
с непрерывными на отрезке коэффициентами не обращается в ноль ни в одной точке отрезка . Записав уравнение (44) в виде
видим, что коэффициент при терпит разрыв при , так что в точке непрерывность коэффициентов уравнения (45) нарушается.
Разные задачи
Пусть — фундаментальная система линейного однородного уравнения
Тогда имеет место формула Остроградского–Лиувилля
где — определитель Вронского, а — любое значение из отрезка , на котором непрерывны коэффициенты уравнения.
Пример 1. Показать, что линейное дифференциальное уравнение имеет решение вида , где — некоторый многочлен. Показать, что второе решение этого уравнения имеет вид , где — также многочлен.
Решение. Будем искать решение в виде многочлена, например, первой степени: . Подставляя в уравнение, найдем, что . Пусть , тогда ;. таким образом, многочлен будет решением данного уравнения. Перепишем данное уравнение в виде
Пусть — второе частное решение данного уравнения, линейно независимое с первым. Находим определитель Вронского системы решений
здесь . Применяя формулу Остроградского–Лиувилля, будем иметь
где — любое значение , причем , или ; здесь . Для нахождения получили линейное дифференциальное уравнение первого порядка. Деля обе части этого уравнения на , приведем его к виду
[spoiler title=”источники:”]
http://lfirmal.com/ponyatie-o-sistemah-differencialnyh-uravnenij/
http://mathhelpplanet.com/static.php?p=ldu-s-peremennymi-koeffitsientami
[/spoiler]
фундаментальная система решений дифференциального уравнения
Ученик
(69),
закрыт
6 лет назад
Дополнен 6 лет назад
ведь это как-то связано с характеристическим уравнением и его корнями ?
Tetiana van Veen
Мыслитель
(8471)
6 лет назад
Если вы в принципе умеете решать подобные уравнения, но не знаете, что такое фундаментальная система решений, то можно объяснить так:
y”-3y’+2y=0
Характеристическое уравнение k^2-3k+2=0
k1=1, k2=2 – корни характеристического уравнения
Т. к. корни характеристического уравнения действительные и разные, то общее решение заданного уравнения имеет вид
y=C1*e^x+C2*e^(2x)
Функции y1(x)=e^x, y2(x)=e^(2x) – образуют фундаментальную систему решений заданного дифференциального уравнения
S SУченик (69)
6 лет назад
А в случае Неоднород. ДУ это всё то же самое, т. е. – набор функций, которые образуют ФСР заданного но ОДНОРОДНОГО ДУ ?
Рассмотрим однородное линейное дифференциальное уравнение ![]() -го порядка
-го порядка
![]() . (4.2)
. (4.2)
Система ![]() линейно независимых решений уравнения (4.2)
линейно независимых решений уравнения (4.2) ![]() ,
, ![]() , …,
, …, ![]() называется Фундаментальной системой решений.
называется Фундаментальной системой решений.
Теорема 1. Любое однородное линейное Дифференциальное уравнение имеет фундаментальную систему решений.
Доказательство. Возьмем ![]() и рассмотрим
и рассмотрим ![]() различных наборов начальных условий:
различных наборов начальных условий:

Эти наборы начальных условий соответствует некоторым решениям уравнения (4.2) ![]() . Покажем, что эти решения линейно независимы. В силу начальных условий вронскиан решений имеет вид
. Покажем, что эти решения линейно независимы. В силу начальных условий вронскиан решений имеет вид
 .
.
Поскольку ![]() , то рассмотренные функции линейно независимы, поэтому образуют фундаментальную систему решений.
, то рассмотренные функции линейно независимы, поэтому образуют фундаментальную систему решений.
Примечание. Из доказательства теоремы очевидно, что для уравнения (4.2) существует бесчисленное множество фундаментальных систем решений.
Теорема 2. Любое неособенное линейное преобразование фундаментальной системы решений однородного линейного Дифференциального уравнения образует фундаментальную систему решений.
Доказательство. Пусть ![]() – фундаментальная система решений уравнения (4.2). С помощью линейного преобразования получим новую систему функций:
– фундаментальная система решений уравнения (4.2). С помощью линейного преобразования получим новую систему функций:

Здесь ![]() – некоторые числа. Пусть матрица такого преобразования
– некоторые числа. Пусть матрица такого преобразования
 .
.
Поскольку по условию теоремы преобразование неособенное, то ![]() .
.
Докажем, что функции ![]() ,
, ![]() , …,
, …, ![]() образуют фундаментальную систему решений. То, что эти функции являются решениями уравнения (4.2), вытекает из следствия основных теорем 1 и 2 для однородных линейных дифференциальных уравнений из предыдущего подраздела. Докажем, что эти решения линейно независимы. Составим вронскиан для новой системы функций
образуют фундаментальную систему решений. То, что эти функции являются решениями уравнения (4.2), вытекает из следствия основных теорем 1 и 2 для однородных линейных дифференциальных уравнений из предыдущего подраздела. Докажем, что эти решения линейно независимы. Составим вронскиан для новой системы функций
![]()
 .
.
Пусть ![]() – матрица, определителем которой является данный вронскиан. Тогда
– матрица, определителем которой является данный вронскиан. Тогда
 .
.
Из этого равенства следует, что
![]() ,
,
То есть
![]() .
.
Определители в правой части этого равенства отличны от нуля, поэтому
![]()
Ни при одном значении ![]() . А это и значит, что функции
. А это и значит, что функции ![]() линейно независимы. Следовательно, эти функции образуют фундаментальную систему решений.
линейно независимы. Следовательно, эти функции образуют фундаментальную систему решений.
| < Предыдущая | Следующая > |
|---|
