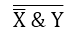Как составить функциональную схему по структурной формуле

Основные направления прикладного использования логики в информатике

1. написание компьютерных программ и их верификация.
2. при проектировании вычислительных устройств используется как теоретический инструмент.
3. Использование логических операций в электронных микросхемах в качестве базовых.
4. логический подход к представлению и решению различных практических задач с использованием вычислительной техники.

Работу большинства вычислительных устройств, которые существуют в настоящее время, прекрасно описывает алгебра логики, разработанная Джорджем Булем. К таким устройствам относятся триггеры, сумматоры, группы переключателей, Кроме того булева алгебра и компьютеры связаны между собой при помощи используемой в ЭВМ двоичной системы счисления. Поэтому в устройствах компьютера можно хранить и преобразовывать и значения логических переменных, и числа.

Логические элементы имеют один (инвертор) или несколько входов, на которые подаются электрические сигналы, обозначаемые условно $0$, если сигнал отсутствует, и $1$, если электрический сигнал имеется. Выход у логических элементов один, откуда снимается новый, преобразованный электрический сигнал.

«Логика и компьютер» 👇

Все электронные схемы компьютера могут быть реализованы с помощью трёх базовых логических элементов И, ИЛИ, НЕ.

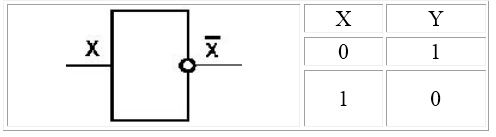
Логический элемент НЕ (инвертор). Простейший логический элемент, реализующий функцию отрицания (инверсию). Унарный элемент – элемент, у которого один вход и один выход.

На функциональных схемах обозначается

Если на вход инвертора подаётся $1$, то на выходе реализуется $0$ и наоборот.

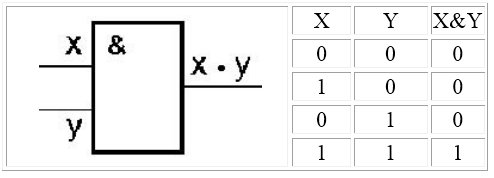
Логический элемент И (конъюнктор) реализует умножение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:

Если на входе конъюнктора все входные сигналы имеют значение $1$, то на выходе тоже будет сигнал $1$, в противном случае на выходе будет сигнал $0$.

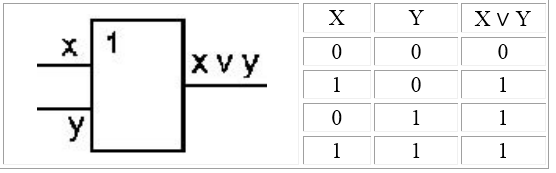
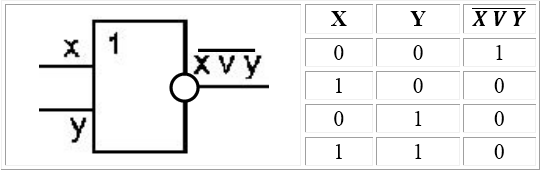
Логический элемент ИЛИ (дизъюнктор) реализует сложение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:

Если на вход дизъюнктора поступает хотя бы один сигнал равный $1$, то выходе тоже будет сигнал $1$.

Роль базовых логических элементов в создании схем играют ещё два логических элемента: И-НЕ и ИЛИ-НЕ.

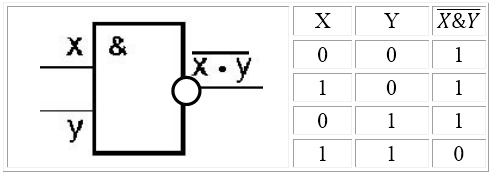
Логический элемент И-НЕ (отрицание конъюнкции) выполняет логическую функцию штрих Шеффера. Операция бинарная, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается следующим образом:

Логический элемент ИЛИ-НЕ (отрицание дизъюнкции) выполняет логическую функцию стрелка Пирса. Тоже бинарная операция, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается так:

Функциональные схемы

Сигнал, который вырабатывает один логический элемент, можно подать на вход другого элемента. Это даст возможность образовать цепочку из отдельных логических элементов – функциональную схему.

Как по заданной функциональной схеме записать структурную формулу?

Элемент И осуществляет конъюнкцию $bar{X}$ и $Y$, над результатом в элементе НЕ выполняется операция отрицания, то есть вычисляется значение выражения

Записали, что структурной формулой данной функциональной схемы является формула

Для функциональной схемы нужно составить таблицу значений сигналов на входах и выходах схемы, по которой можно понять, какую функцию выполняет данная схема, – таблицу истинности.

Составим таблицу истинности для вышеприведённой схемы. Количество столбцов таблицы равно суммарному количеству входов и выходов нужной схемы. Итого $5$ столбцов. Количество строк таблицы равно $2^n$, где $n$ – количество входов (здесь два), строк $4$.

Обработка любой информации на компьютере − выполнение процессором различных арифметических и логических операций. Для этого в составе процессора есть арифметико-логическое устройство (АЛУ), которое состоит из ряда устройств, построенных на логических элементах, рассмотренных выше. Главными устройствами являются триггеры, полусумматоры, сумматоры, шифраторы, дешифраторы, счетчики, регистры.

Конструируется логическое устройство по следующему алгоритму:

1. по заданным условиям работы проектируемого узла (т.е. по соответствию его входных и выходных сигналов) строится таблица истинности;
2. конструируется логическая функция данного узла по таблице истинности, выполняется при необходимости её преобразование (упрощение), если cоставляется функциональная схема проектируемого узла по формуле логической функции;
3. реализуется полученная схема.

Перед нами задача: создать логическое устройство, которое имеет несколько входов и один выход. На входы подаются сигналы 0 или 1. Такие сигналы могут обозначать, к примеру, значения поданного голоса при голосовании. 0 обозначает «я против», 1 обозначает «я – за». Сигнал на выходе должен показать итоговый результат голосования – да / нет, в зависимости от поданных голосов. Интересно было бы рассмотреть полный процесс создания такого логического устройства. Но прямо сейчас, на этом уроке, мы можем изучить теоретические расчёты, которые предваряют техническое изготовление логического устройства.

Цель урока: познакомить учащихся с задачами инженерного характера: как построить оптимальное логическое устройство по словесному описанию его работы.

Задачи

Обучающие:

• научить формализовать условия содержательной текстовой задачи и представлять их в виде таблицы истинности;
• получить СДНФ и СКНФ по полученной таблице истинности (совершенная дизъюнктивная нормальная форма – СДНФ и совершенная конъюнктивная нормальная форма – СКНФ);
• упростить СДНФ (или СКНФ) с целью обеспечения оптимальности функциональных схем, их реализующих;
• построить функциональную схему в соответствии с реализуемой структурной формулой;
• проверить соответствие логической схемы реализуемой структурной формуле.

Развивающая

• Учить видеть структуру там, где она есть, и быть готовым работать со структурой адекватными методами.

Воспитательная

• Поднять ценность теории алгебры логики ибо она применима на практике.

Тип урока: урок получения новых знаний, приближенных к инженерной теории.

Вид урока: урок закрепления изучаемого материала.

Планируемые результаты

• Мы узнаем: алгоритм построения функциональной схемы по таблице истинности.
• Мы научимся: формализовать текстовое содержание задачи ради построения таблицы истинности.
• Мы сможем: построить оптимальную функциональную схему на основе упрощенной структурной формулы.

Оборудование и средства обучения: доска, мел, конспекты лекций, у каждого ученика и учителя есть методическое пособие Лыскова В.Ю. Логика в информатике / В.Ю.Лыскова, Е.А.Ракитина. – 2-е изд. – М.: Лаборатория Базовых Знаний, 2006, распечатки бланков централизованного тестирования по информатике 2006 года для каждого ученика и учителя.

План урока

1 этап. Организационный этап.

2 этап. Объявление темы и актуализация знаний.

3 этап. Формирование новых знаний: образцы решения задач и обсуждение.

4 этап. Домашнее задание.

Ход урока

1 этап. Организационный этап

Здравствуйте. Присаживайтесь. Отметим отсутствующих и приступим к уроку.

2 этап. Объявление темы и актуализация знаний

Сегодняшнее число. Тема урока «Оптимальное логическое устройство: его функциональная схема и структурная формула».

Что такое функциональная схема и что такое структурная формула – эти понятия не вызывают затруднений, надеюсь. Давайте их проговорим. Кто желает?

(Ответ должен быть проговорен вслух.

Ответ:

Схема соединения логических элементов называется функциональной схемой.

Структурная формула – это форма описания функции, реализуемой логическим устройством.

Логическое устройство – цепочка из логических элементов, в которой выходы одних элементов являются входами других.)

Теперь, что такое оптимальность? Давайте подумаем. Ваш вариант ответа?

(Ответ:

«Оптимальность – это достижение наилучшего результата в данных условиях при минимальных затратах времени и усилий участников», – гласит Словарь терминов по общей и социальной педагогике.)

Сегодня нам понадобятся знания логических элементов, алгоритм составления СДНФ и СКНФ, а также ваши хорошие навыки упрощения логических выражений.

Проведем короткую проверочную работу в качестве «разминки».

(Учитель раздает карточки проверочной работы – учащиеся письменно отвечают на вопросы. Двоих вызывает к доске – выполнять проверочную работу. Остальные пишут на местах.)

Вопросы проверочной работы:

1. Нарисуйте логические элементы и подпишите их названия.
2. Дана таблица истинности для двух переменных.

X	Y	F(X, Y)
0	0	0
0	1	1*
1	0	1*
1	1	0

По этой таблице составить СДНФ и СКНФ.

Результаты на доске учитель проверяет сразу. И сообщает оценки сразу.

(Правильные ответы:

1. Логические значения 0 и 1 – это цифровые сигналы. Они поступают, преобразовываются и выходят из так называемых логических элементов. Логические элементы выполняют дизъюнкцию, конъюнкцию, инверсию; логические устройства выполняют: сложение по модулю 2, эквивалентность, импликацию, коимпликацию, элемент Вебба (или-не), элемент Шеффера (и-не). Смотри Рисунок 1.

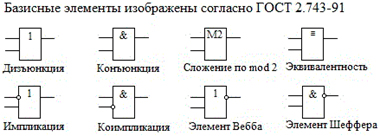
Рисунок 1

2. Обратимся к Методическому пособию Лысковой В.Ю., где описаны алгоритмы получения СДНФ и СКНФ. Привожу фрагмент пособия, чтобы материал урока был целостным. «Существует алгоритм, позволяющий по известной таблице истинности построить схему устройства. В основе алгоритма лежит теорема алгебры логики: любую функцию, кроме констант 0 и 1, можно представить в виде СДНФ, так и СКНФ. Совершенная дизъюнктивная нормальная форма – СДНФ и совершенная конъюнктивная нормальная форма – СКНФ.

Алгоритм получения СДНФ по таблице истинности.

1. Отметить те строки таблицы истинности, в последнем столбце которых стоят 1:

X	Y	F(X, Y)
0	0	0
0	1	1*
1	0	1*
1	1	0

2. Выписать для каждой отмеченной строки конъюнкцию всех переменных следующим образом: если значение некоторой переменной в данной строке равно 1, то в конъюнкцию включать саму эту переменную, если равно 0, о ее отрицание:

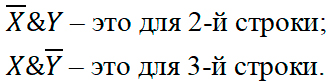
3. Все полученные конъюнкции связать в дизъюнкцию:

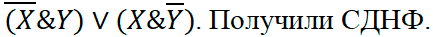
3 этап. Формирование новых знаний: образцы решения задач и обсуждение результатов

Задача 1 «Устройство для голосования». (Из Методического пособия Лысковой В.Ю., стр. 97. Задачу перепечатываю.)

«Пусть в некотором конкурсе решается вопрос о допуске того или иного участника к следующему туру тремя членами жюри: P, Q, R. Решение положительно тогда и только тогда, когда хотя бы двое членов жюри высказываются за допуск, причем среди них обязательно должен быть председатель жюри Q. Необходимо разработать устройство для голосования, в котором каждый член жюри нажимает на одну из кнопок – «За» или «Против», а результат голосования всех трех членов жюри определяется по тому, загорится (решение принято) или нет (решение не принято) сигнальная лампочка.

Формально это можно выразить так: требуется составить функциональную схему устройства, которое на выходе выдавало бы 1, если участник допускается к следующему туру, и 0, если не допускается.»

Решение

1. Нужно рассмотреть всевозможные комбинации голосов жюри. Если голос «против», то будем обозначать его нулем. Если голос «за», то обозначим его единицей. Жюри состоит из трех человек. Значит, надо составить все трехбитные двоичные коды. Их будет 8.

Затем напротив каждого кода записать вывод – допускается или нет участник к следующему туру. Работу жюри представим в виде таблицы истинности:

P	Q	R	F(P, Q, R)	Решение
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1	допускается
1	0	0	0
1	0	1	0
1	1	0	1	допускается
1	1	1	1	допускается

2. Если мы хотим построить формулу некоторой функции по таблице истинности, то необходимо получить СДНФ или СКНФ по таблице истинности. Для этого берем таблицу истинности нашей задачи

P	Q	R	F(P, Q, R)	Решение
0	0	0	0
0	0	1	0
0	1	0	0
0	1	1	1	*
1	0	0	0
1	0	1	0
1	1	0	1	*
1	1	1	1	*

и отмечаем звездочкой в столбце Решение три строки, в которых F(P, Q, R) = 1. Записываем для этих строк конъюнкции всех переменных и объединяем конъюнкции в СДНФ. Смотри Рисунок 2.

Рисунок 2

Мы провели упрощение СДНФ. Вместо первоначальных десяти логических операций осталось две.

3. Для самоконтроля проведем работу по формированию и преобразованию СКНФ. Запишем для строк таблицы, которые оканчиваются нулями, дизъюнкции переменных и свяжем полученные дизъюнкции в конъюнкцию. Получим СКНФ. Смотри Рисунок 3.

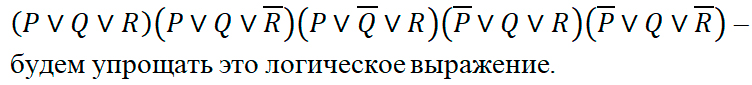
Рисунок 3

Мы провели упрощение СКНФ. Видим, что полученные СДНФ и СКНФ эквивалентны.

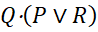
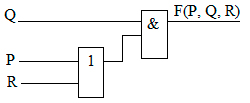
4. Теперь нарисуем функциональную схему устройства по структурной формуле: . Смотри Рисунок 4.

Рисунок 4

В полученной схеме задействовано всего 2 логических элемента: дизъюнктор и конъюнктор.

5. Докажем, что функциональная схема соответствует СДНФ. Для этого построим таблицы истинности и для функциональной схемы и для структурной формулы и сравним их. Смотри Рисунок 5.

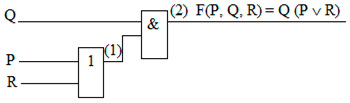
Рисунок 5

P	Q	R	Выход (1)	Выход (2)
0	0	0	0	0
0	0	1	1	0
0	1	0	0	0
0	1	1	1	1
1	0	0	1	0
1	0	1	1	0
1	1	0	1	1
1	1	1	1	1

P	Q	R	P v R	Q&(P v R)
0	0	0	0	0
0	0	1	1	0
0	1	0	0	0
0	1	1	1	1
1	0	0	1	0
1	0	1	1	0
1	1	0	1	1
1	1	1	1	1

Последние столбцы обеих таблиц совпадают. Это значит, что построенная функциональная схема соответствует структурной формуле, то есть соответствует СДНФ.

Решение завершено.

Давайте выработаем полезный алгоритм построения оптимальной функциональной схемы по таблице истинности. Так и назовем его – Полезный алгоритм.

Полезный алгоритм

1. Строим саму таблицу истинности по условиям задачи.

2. По таблице истинности строим СДНФ или СКНФ в зависимости от того, каких строк меньше в последнем столбце таблицы. Если меньше 1, значит, строим СДНФ. Если меньше 0, то строим СКНФ.

3. Этап необязательный. Можно построить обе совершенные формы и убедиться, что они эквивалентны.

4. Провести упрощение СДНФ и/или СКНФ.

5. Нарисовать функциональную схему, соответствующую полученной логической формуле.

Задача 2 «Будь эффективным!» (Задача А5 из бланков централизованного тестирования 2006 года по информатике.) Давайте закрепим свои знания и умения в вопросе «прочтения» функциональных логических схем.

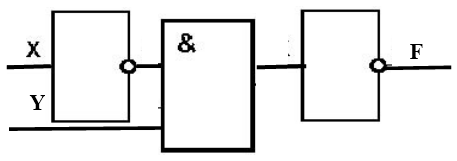
Есть схема устройства. Смотри Рисунок 6.

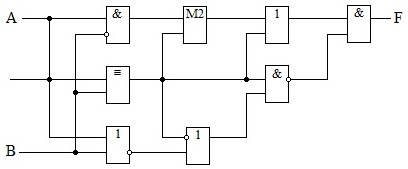
Рисунок 6

Какую логическую функцию реализует функция F?

1) 1

2) А

3) В

4) 0

Решение

Будем определять структурную формулу по заданной функциональной схеме. Посмотрим на финальный логический элемент схемы – это конъюнктор. У него два входа. Распишем по отдельности формулы для первого и второго входа, затем логически перемножим их.

На первом входе конъюнктора. Смотри Рисунок 7.

Рисунок 7

На втором входе конъюнктора. Смотри Рисунок 8.

Рисунок 8

Теперь выполним финальную конъюнкцию. Смотри Рисунок 9.

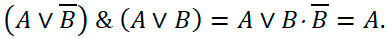
Рисунок 9

Мы получили, что в предложенной схеме сигнал на выходе будет совпадать с сигналом А на входе.

Ответ: 2.

Прошу обратить особое внимание на изображение функциональной схемы.

Во-первых, увидьте особую эстетику изображения функциональной схемы: линии – параллельные и перпендикулярные, образуют строгий рисунок схемы.

Во-вторых, удобство восприятия схемы обеспечивается симметричным расположением логических элементов.

В-третьих, логические элементы подписаны.

И четвертое, схема «растет» и «читается» слева направо: в крайней левой позиции есть входы, в крайней правой позиции – выход F функциональной схемы.

Эти четыре замечания назовем Правилами изображения функциональных схем, и к следующему уроку выучим эти Правила назубок.

Перейдем к домашнему заданию.

4 этап. Домашнее задание

1. Выучить наизусть Полезный алгоритм и Правила изображения функциональных схем.

2. Из методического пособия Лысковой задача 2 на стр. 112 – аналог классной задачи «Устройство для голосования».

3. Из распечаток ЦТ 2006 задача А5 – аналог классной задачи «Будь эффективным!»

Если ко мне вопросов нет, то всем спасибо и до следующей встречи.

Известно,
что дискретные устройства могут строиться
на различных наборах логических
элементов. Важно, чтобы эти наборы были
полными, т.е. реализовывали бы функционально
полную систему логических функций.

Напомним,
что к наиболее распространенным
функционально полным наборам логических
элементов относятся следующие наборы:

1) из трех
элементов И, ИЛИ, НЕ (основной набор);

2) из двух
элементов И, НЕ;

3) из двух
элементов ИЛИ, НЕ;

4) из одного
элемента ИЛИ-НЕ (НИ-НИ, элемент Пирса);

5) из одного
элемента И-НЕ (элемент Шеффера).

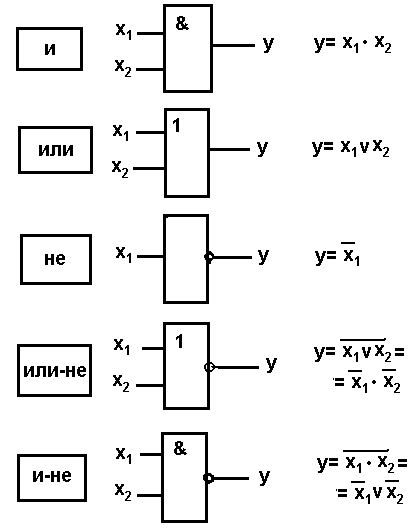
Логические
элементы И, ИЛИ, НЕ реализуют соответственно
функции конъюнкции, дизъюнкции и
отрицания (инверсии) и обозначаются по
ГОСТу как показано на рис. 1.15.

Универсальный
элемент ИЛИ-НЕ реализует функцию
отрицания дизъюнкции (стрелка Пирса).
Выходной сигнал равен произведению
инверсий входных сигналов. Универсальный
элемент И-НЕ реализует функцию отрицания
конъюнкции (штрих Шеффера). Выходной
сигнал равен сумме инверсий входных
сигналов.

Любая
логическая функция представляет собой
набор символов, связанных знаками
дизъюнкции, конъюнкции и инверсии.
Других операций нет. Поэтому возможность
реализации любой логической функции с
помощью основного набора логических
элементов (И, ИЛИ, НЕ) очевидна, а с помощью
остальных наборов – не очевидна.

С помощью
универсального приема двойного
инверсирования можно показать, как
реализуются основные операции алгебры
логики (конъюнкция, дизъюнкция и инверсия)
на функционально полных наборах,
состоящих из одного и двух логических
элементов.

Рис 1.5.

Рассмотрим, например, реализацию основных
операций алгебры логики на наборе
ИЛИ-НЕ.

Необходимо
рассмотреть реализацию трех основных
функций.

Операция
НЕ. В элементе ИЛИ-НЕ задействуется
только один вход, тогда элемент работает
как инвертор (рис. 1.16). Используется один
элемент ИЛИ-НЕ.

Операция
И.Воспользуемся приемом двойной
инверсии:

Видим, что
следует реализовать функцию отрицания
дизъюнкции для двух инверсных сигналов
(рис. 1.7). Необходимы три элемента ИЛИ-НЕ.

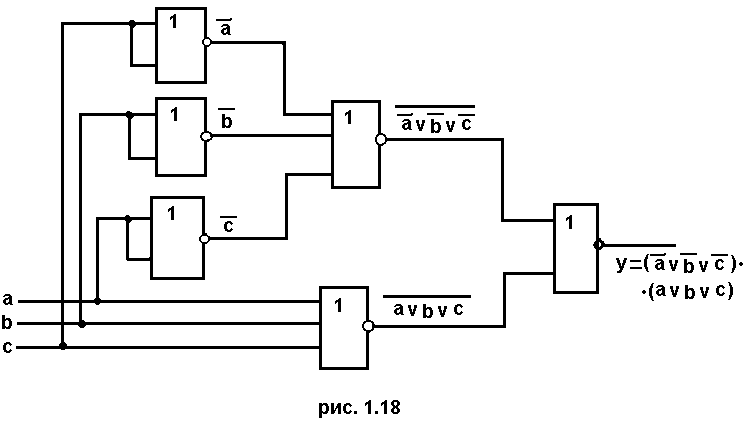
Операция
ИЛИ.

Имеем инверсию
от инверсии дизъюнкции, т.е. сначала
ИЛИ-НЕ, потом НЕ. Для реализации необходимы
два элемента ИЛИ-НЕ (рис. 1.18).

Рассмотрим
реализацию основных операций алгебры
логики на наборе И-НЕ.

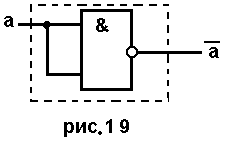
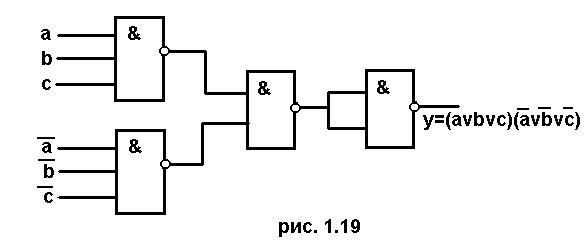
Операция
НЕ.В элементе И-НЕ задействуется
только один вход, тогда элемент работает
как инвертор (рис. 1.19). Используется один
элемент И-НЕ.

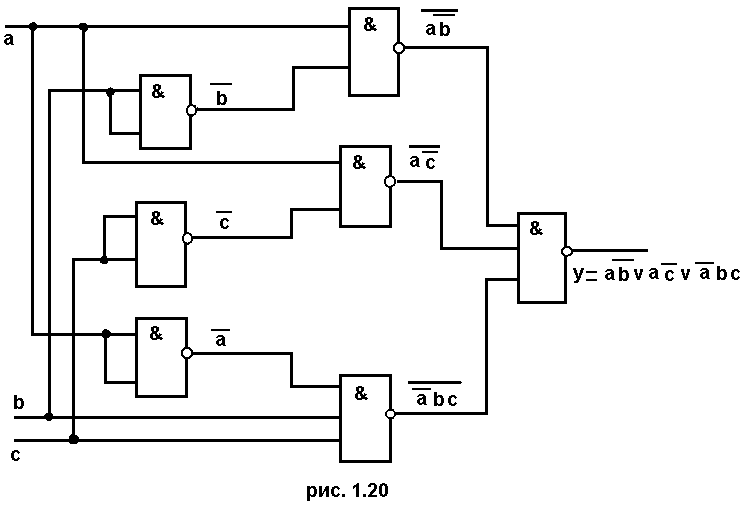
Операция
И.Воспользуемся приемом двойной
инверсии.Имеем инверсию от инверсии конъюнкции,
т.е. сначала И-НЕ, потом НЕ. Для реализации
требуется 2 элемента И-НЕ (рис. 1.20).

Операция ИЛИ.Имеем инверсию от конъюнкции инверсий,
т.е. сначала два раза НЕ, а затем И-НЕ
(рис. 1.11).

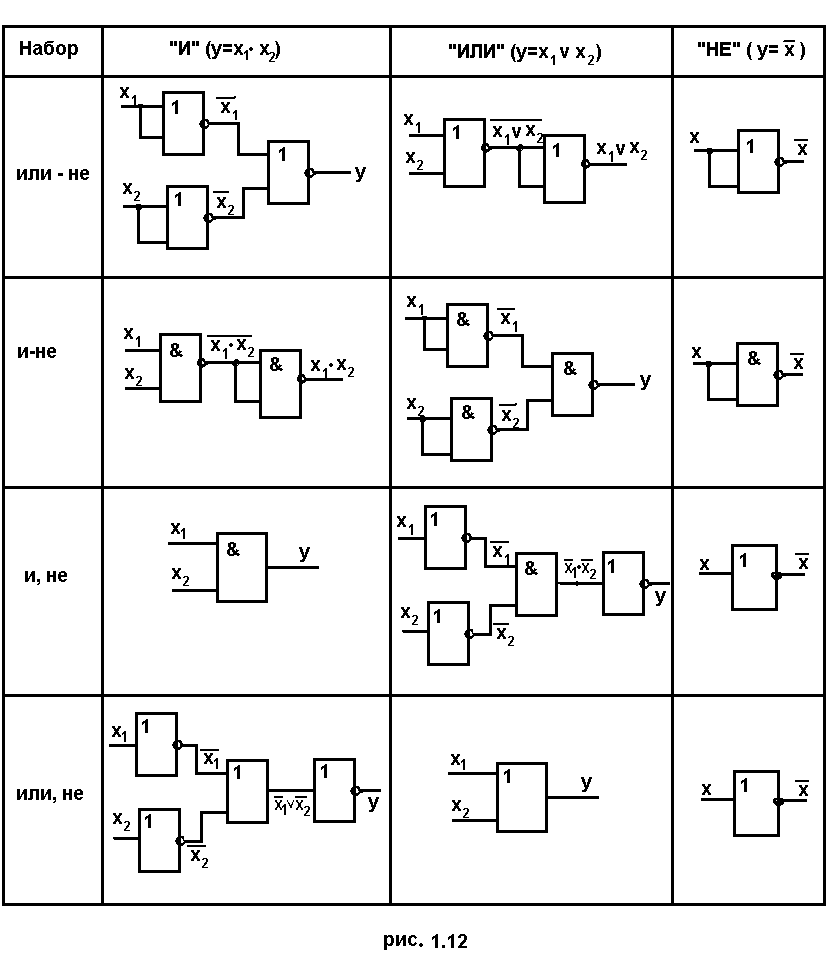
Аналогичным образом
получаем реализацию основных операций
алгебры логики для остальных функционально
полных наборов (рис. 1.12).

В случае
большого числа переменных соответственно
увеличивается количество входов или
входных инверторов.

Классическая
методика построения функциональной
схемы ДУ по логической функции, которую
оно реализует, заключается в следующем:

– по известной
логической функции построить структурную
схему ДУ в основных операциях алгебры
логики (И, ИЛИ, НЕ);

– выбрать
функционально полный набор БЛЭ для
реализации ДУ;

– перейти от
структурной схемы к функциональной с
учетом правил реализации основных
операций на выбранном наборе элементов;

– произвести
упрощения схемы.

Упрощения
производятся, как правило, за счет
исключения из схемы двух последовательно
стоящих инверторов.

Рассмотрим
примеры построения функциональной
схемы БДУ на наборах И-НЕ, ИЛИ-НЕ.

Пример 5.
Даны условия работы ДУ в виде логической
функции:

.

Построить
функциональную схему.

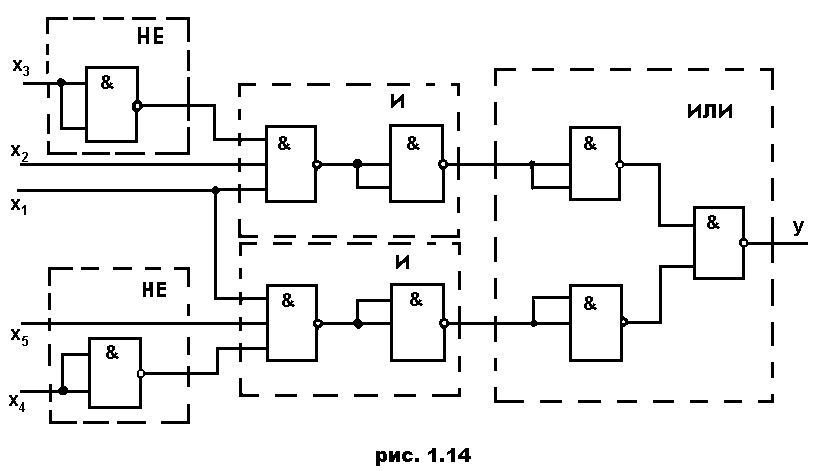
Строим структурную
схему ДУ (рис. 1.13), затем по правилам
реализации операций (см. рис. 1.20) –
функциональную схему ДУ на элементах
И-НЕ (рис. 1.14).

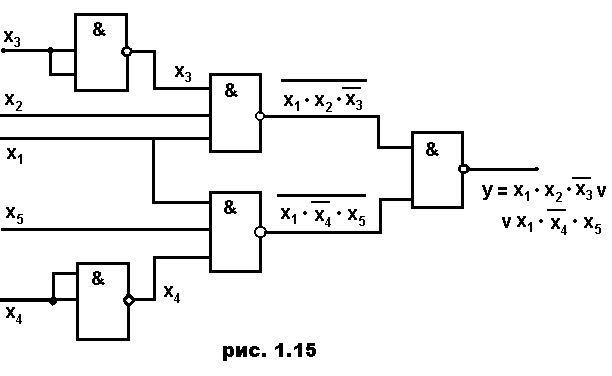
Последовательно
соединенные два инвертора компенсируют
друг друга и могут быть из схемы исключены.
После упрощения получаем окончательную
функциональную схему (рис. 1.15), состоящую
из 5 элементов И-НЕ.

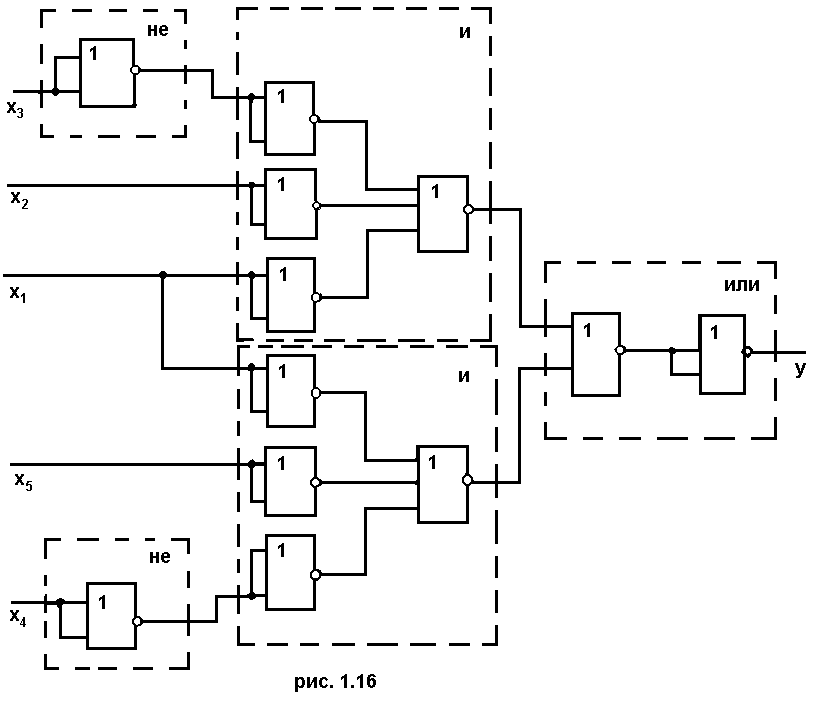
Теперь
построим для этого же примера функциональную
схему на элементах ИЛИ-НЕ. Используем
ту же структурную схему (см. рис.1.13).
Получаем схему (рис. 1.16), содержащую 12
элементов ИЛИ-НЕ.

Путем
исключения последовательных инверторов
и объединения сигнала,
схема сокращается на 5 элементов и
остается 7 элементов ИЛИ-НЕ (рис. 1.17).

Изложенная методика
построения функциональной схемы ДУ
является универсальной, т.е. всегда лает
правильное решение – работоспособную
схему, но, как правило, слишком громоздкую.

В инженерной
практике обычно, обладая известным
навыком преобразования логических
функций, выполняют этап преобразования
исходного аналитического выражения
(условия работы ДУ, полученные в результате
абстрактного синтеза) к виду, удобному
для реализации на выбранном наборе БЛЭ.

В результате
этого этапа исходная функция записывается
сразу в операторах И-НЕ для реализации
на сериях интегральных элементов с
базовым элементом И-НЕ, либо в операторах
ИЛИ-НЕ для реализации на сериях БЛЭ
“Логика”, “Логика-Т” и т.д. с базовым
элементом ИЛИ-НЕ.

Для
преобразования функции, как правило,
пользуются универсальным приемом
двойного инверсирования.

Двойное
инверсирование функции, записанной в
ДНФ, дает форму операторов И-НЕ, а двойное
инверсирование функции, записанной в
КНФ, дает форму операторов ИЛИ-НЕ.

Таким образом,
если для построения ДА принят набор
И-НЕ, то исходную функцию (условия работы
ДА), полученную в результате абстрактного
синтеза, следует преобразовать в ДНФ,
а если принят набор ИЛИ-НЕ, то исходную
функцию следует преобразовать в КНФ.

Пример 12. Построить
функциональную схему БДУ на наборе
ИЛИ-НЕ в соответствии с условиями работыУсловия работы (исходная функция) уже
написаны в КНФ. Применяем прием двойного
инверсирования:

Получили
выражение, записанное в операторах
ИЛИ-НЕ. Функциональная схема ДУ,
построенная по данному выражению,
изображена на рис. 1.18.

Если нужно построить
эту функцию на наборе И-НЕ, то исходную
функцию следует привести к ДНФ, а затем
исследовать прием двойной инверсии.
Однако эту функцию можно упростить по
правилу: если ЛФ записанным в ДНФ (КНФ),
а нужно ее реализовать на наборе ИЛИ-НЕ
(И-НЕ), то прием двойного инверсирования
применяют дважды – сначала над каждым
членом исходной функции, затем над самой
функцией. Построим ЛФ
на наборе И-НЕ:

Схема
приведена на рис. 1.19 (считаем, что
известные сигналы уже получены).

Пример 13.
Построить функциональную схему БДУ на
наборе И-НЕ в соответствии с условиями
работы.
Условия работы (исходная функция) уже
записаны в ДНФ. Применяем прием двойного
инверсирования:

.

Получили
выражение, записанное сразу в операторах
И-НЕ. Очевидно, что функциональная схема
ДУ имеет вид, изображенный на рис. 1.20.

Попробуем еще
преобразовать исходное выражение в
направлении уменьшения числа операций
ИЛИ (так как базовый элемент принят
И-НЕ):

.

Полученное выражение
также записано в операторах И-НЕ.
Функциональная схема его представлена
на рис. 1.21.

Заметим, что
в подобных случаях функциональные схемы
удобно строить “с конца” аналитического
выражения.

Сравнивая
рис. 1.30 и 1.31, видим, что достигнута
экономия в два элемента И-НЕ.

В случае
синтеза многовыходных ДА без памяти
следует после получения минимизированных
выражений для нахождения сигналов на
каждом выходе провести преобразования
системы уравнений с целью объединения
одинаковых групп членов, членов или их
частей в разных уравнениях, а после
этого строить функциональную схему ДА.

Следующий
этап – физический синтез. Он имеет своей
целью переход от функциональной схемы
структуры проектируемого ДУ к
принципиальной электрической схеме.
На этом этапе выбираются типы бесконтактных
элементов, обеспечиваются дополнительные
требования: надежность, технологичность,
удобство контроля и т.д.

Раздел 5. Функциональные схемы

Раздел 5. Функциональные схемы Основные логические элементы функциональных схем Логические элементы — устройства, предназначенные для обработки информации в цифровой форме. Элемент “И” (AND) или “конъюнктор” Элемент “ИЛИ” (OR) или “дизъюнктор” Элемент “НЕ” (NOT) или “инвертор” Элемент “И-НЕ” (NAND) Элемент “ИЛИ-НЕ” (NOR) Для того, чтобы понять как работают данные логические элементы, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется «таблица истинности». Таблицы истинности широко применяются в цифровой технике для описания работы логических схем. Сумматор и триггер     Арифметико-логическое устройство процессора (АЛУ) обязательно содержит в своем составе такие элементы как сумматоры. Эти схемы позволяют складывать двоичные числа. Как происходит сложение? Допустим, требуется сложить двоичные числа 1001 и 0011. Сначала складываем младшие разряды (последние цифры): 1+1=10. Т.е. в младшем разряде будет 0, а единица – это перенос в старший разряд. Далее: 0 + 1 + 1(от переноса) = 10, т.е. в данном разряде снова запишется 0, а единица уйдет в старший разряд. На третьем шаге: 0 + 0 + 1(от переноса) = 1. В итоге сумма равна 1100. Полусумматор     Теперь не будем обращать внимание на перенос из предыдущего разряда и рассмотрим только, как формируется сумма текущего разряда. Если были даны две единицы или два нуля, то сумма текущего разряда равна 0. Если одно из двух слагаемых равно единице, то сумма равна единице. Получить такие результаты можно при использовании вентиля ИСКЛЮЧАЮЩЕГО ИЛИ. Перенос единицы в следующий разряд происходит, если два слагаемых равны единице. И это реализуемо вентилем И. Тогда сложение в пределах одного разряда (без учета возможной пришедшей единицы из младшего разряда) можно реализовать изображенной ниже схемой, которая называется полусумматором. У полусумматора два входа (для слагаемых) и два выхода (для суммы и переноса). На схеме изображен полусумматор, состоящий из вентилей ИСКЛЮЧАЮЩЕЕ ИЛИ и И. Сумматор В отличие от полусумматора сумматор учитывает перенос из предыдущего разряда, поэтому имеет не два, а три входа. Чтобы учесть перенос приходится схему усложнять. По-сути она получается, состоящей из двух полусумматоров. Рассмотрим один из случаев. Требуется сложить 0 и 1, а также 1 из переноса. Сначала определяем сумму текущего разряда. Судя по левой схеме ИСКЛЮЧАЮЩЕЕ ИЛИ, куда входят a и b, на выходе получаем единицу. В следующее ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы. Следовательно, сумма будет равна 0. Теперь смотрим, что происходит с переносом. В один вентиль И входят 0 и 1 (a и b). Получаем 0. Во второй вентиль (правее) заходят две единицы, что дает 1. Проход через вентиль ИЛИ нуля от первого И и единицы от второго И дает нам 1. Проверим работу схемы простым сложением 0 + 1 + 1 = 10. Т.е. 0 остается в текущем разряде, и единица переходит в старший. Следовательно, логическая схема работает верно. Работу данной схемы при всех возможных входных значениях можно описать следующей таблицей истинности. Примеры заданий на анализ и синтез функциональных схем     Для построения функциональных схем необходимо знать как обозначаются логические операции.     Анализом называется построение формулы алгебры логики (если необходимо – ее таблицы истинности) по заданной функциональной схеме.     Пример.     Записать формулу по данной функциональной схеме.     Внимательно смотрим на схему и смотрим сколько всего входных параметров, в данном случае их 2 – это X и Y, идем далее по схеме, X получает обратное значение НЕ(X), далее НЕ(Х) и Y образуют дизъюнкцию, формулу записываем следующим образом:      Синтезом функциональной схемы по заданной формуле называют построение структуры функциональной схемы, соответствующей заданной формуле алгебры логики.     Пример.     Построить функциональную схему по данной формуле.     Смотрим на формулу и выясняем сколько элементов содержится в формуле, в данном случае их также 2 – это X и Y, рисуем две точки на небольшом расстоянии друг от друга, одну подписываем X, другую – Y. Далее смотрим и замечаем, что нам нужно получить отрицание Y, соответственно от точки Y ведем небольшой отрезок и рисуем отрицание, т.е. прямоугольник с кружочком на выходе, X у нас без отрицания, поэтому просто строим после отрицания Y конъюкцию, т.е. прямоугольник с амперсандом внутри, и подводим к конъюкции отрезок из точки X. Список источников

Построение функциональных схем

Преподаватель информатики Кузнецкого филиала ГАПОУ ПО ПМПК

Коткова Наталья Геннадьевна

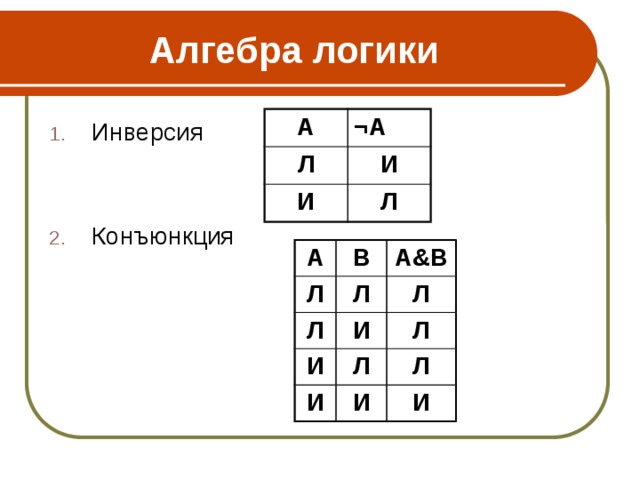
Алгебра логики

А

¬А

Л

И

И

Л

• Инверсия

• Конъюнкция

А

Л

В

А &В

Л

Л

Л

И

И

И

Л

Л

Л

И

И

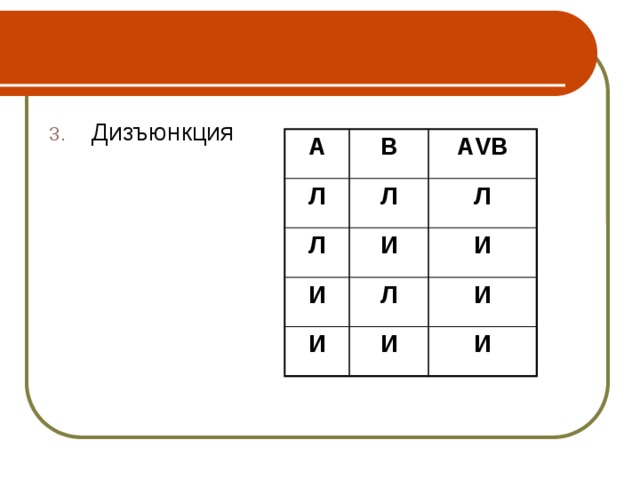
• Дизъюнкция

А

В

Л

Л

Л

А VВ

И

Л

И

И

Л

И

И

И

И

Комбинационная логическая схема

Комбинационной логической схемой называется цифровая схема, в которой выходные сигналы определяются только теми сигналами, которые поступают на вход схемы в тот же момент времени.

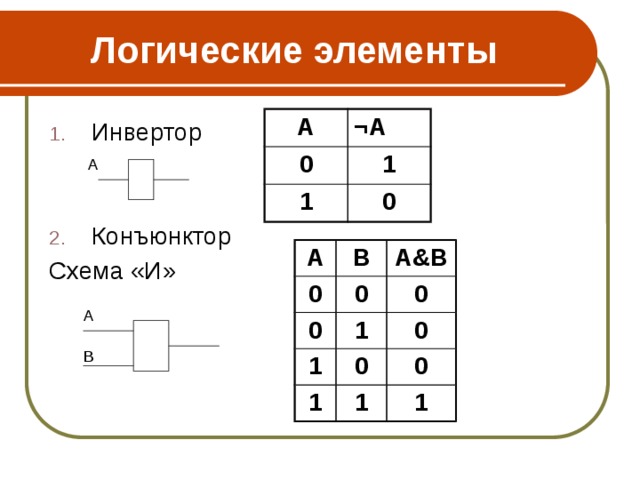
Логические элементы

А

0

¬А

1

1

0

• Инвертор

• Конъюнктор

Схема «И»

A

А

0

В

0

0

А &В

0

1

1

1

0

0

1

0

1

A

B

Логические элементы

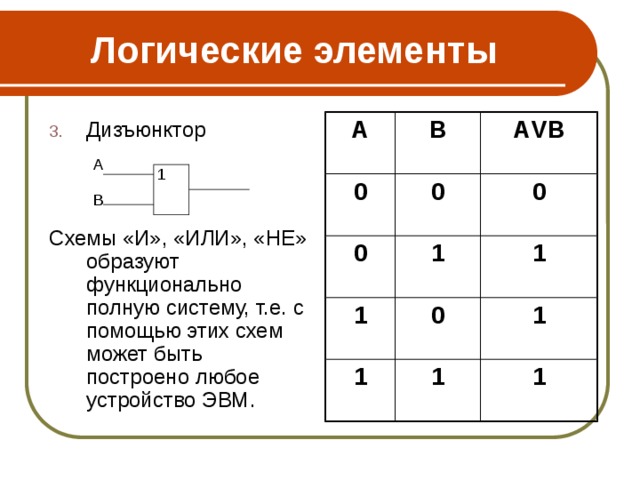
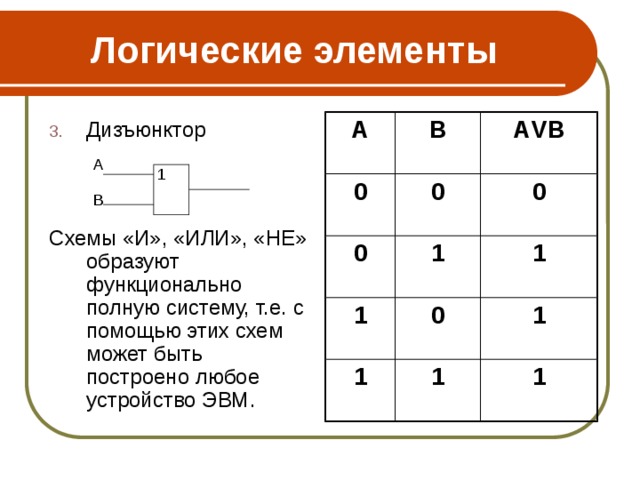
• Дизъюнктор

Схемы «И», «ИЛИ», «НЕ» образуют функционально полную систему, т.е. с помощью этих схем может быть построено любое устройство ЭВМ.

А

В

0

АV В

0

0

1

0

1

1

1

0

1

1

1

A

1

B

Построение функциональных логических схем логических устройств

• Цепочка из логических элементов, в которой выходы одних элементов являются входами других, называется логическим устройством
• Схема соединения логических элементов, реализующая логическую функцию, называется функциональной схемой .
• Формой описания функции, реализуемой логическим устройством, является структурная формула .

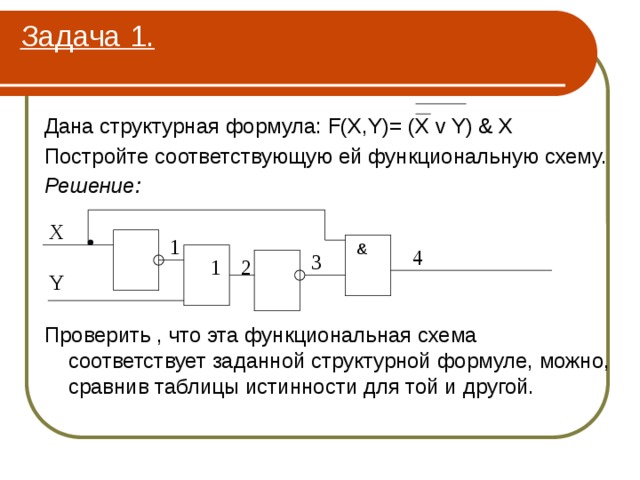
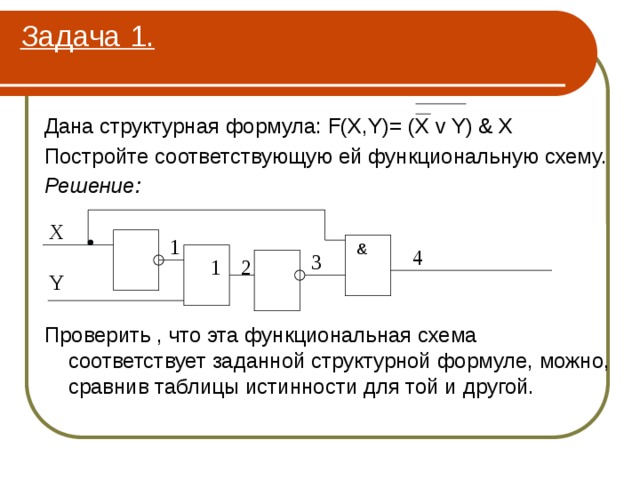
Задача 1.

Дана структурная формула: F(X,Y)= (X v Y) & X

Постройте соответствующую ей функциональную схему.

Решение:

Проверить , что эта функциональная схема соответствует заданной структурной формуле, можно, сравнив таблицы истинности для той и другой.

X

1

&

4

3

2

1

Y

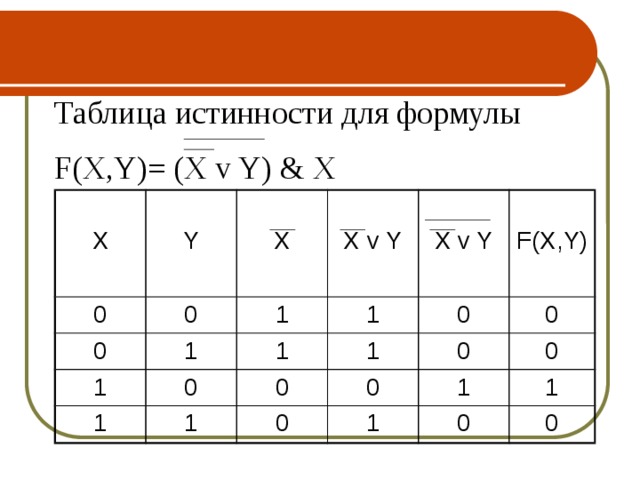
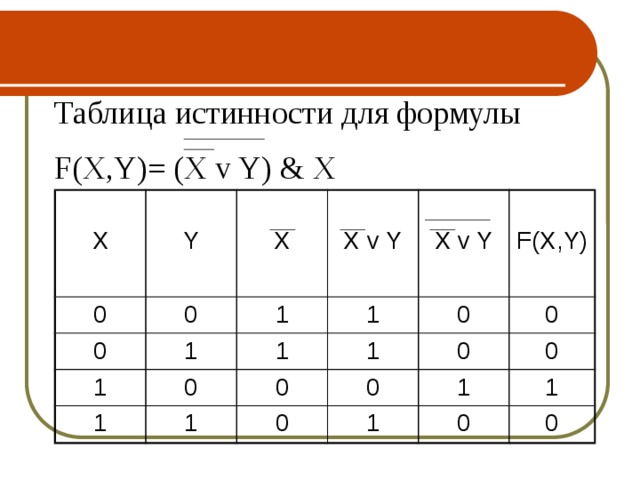
Таблица истинности для формулы

F(X,Y)= (X v Y) & X

0

X

0

Y

0

X

1

1

1

1

0

X v Y

1

1

X v Y

1

0

1

0

0

0

F(X,Y)

0

0

1

1

0

1

0

0

Логические элементы

• Дизъюнктор

Схемы «И», «ИЛИ», «НЕ» образуют функционально полную систему, т.е. с помощью этих схем может быть построено любое устройство ЭВМ.

А

В

0

АV В

0

0

1

0

1

1

1

0

1

1

1

A

1

B

Построение функциональных логических схем логических устройств

• Цепочка из логических элементов, в которой выходы одних элементов являются входами других, называется логическим устройством
• Схема соединения логических элементов, реализующая логическую функцию, называется функциональной схемой .
• Формой описания функции, реализуемой логическим устройством, является структурная формула .

Задача 1.

Дана структурная формула: F(X,Y)= (X v Y) & X

Постройте соответствующую ей функциональную схему.

Решение:

Проверить , что эта функциональная схема соответствует заданной структурной формуле, можно, сравнив таблицы истинности для той и другой.

X

1

&

4

3

2

1

Y

Таблица истинности для формулы

F(X,Y)= (X v Y) & X

0

X

0

Y

0

X

1

1

1

1

0

X v Y

1

1

X v Y

1

0

1

0

0

0

F(X,Y)

0

0

1

1

0

1

0

0

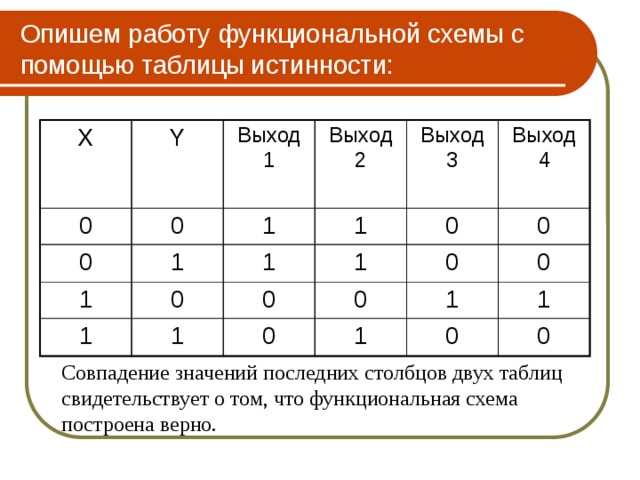
Опишем работу функциональной схемы с помощью таблицы истинности:

X

0

Y

0

Выход 1

0

1

1

1

Выход 2

1

0

Выход 3

1

1

0

0

1

1

Выход 4

0

0

0

0

0

1

1

1

0

0

Совпадение значений последних столбцов двух таблиц свидетельствует о том, что функциональная схема построена верно.

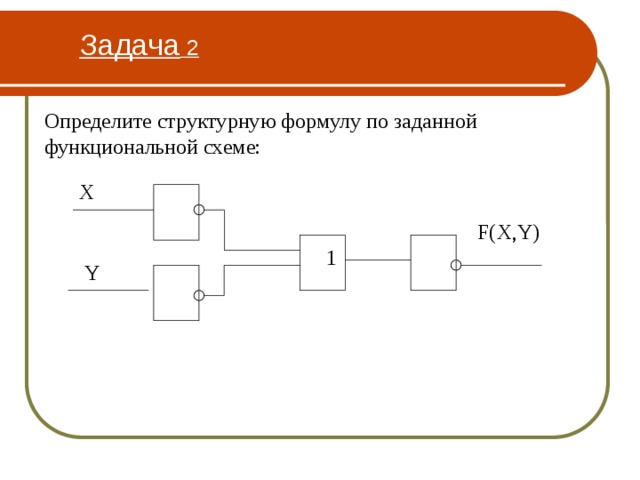
Задача 2

Определите структурную формулу по заданной функциональной схеме:

X

F(X,Y)

1

Y

Спасибо

за

внимание