Известно,
что дискретные устройства могут строиться
на различных наборах логических
элементов. Важно, чтобы эти наборы были
полными, т.е. реализовывали бы функционально
полную систему логических функций.
Напомним,
что к наиболее распространенным
функционально полным наборам логических
элементов относятся следующие наборы:
1) из трех
элементов И, ИЛИ, НЕ (основной набор);
2) из двух
элементов И, НЕ;
3) из двух
элементов ИЛИ, НЕ;
4) из одного
элемента ИЛИ-НЕ (НИ-НИ, элемент Пирса);
5) из одного
элемента И-НЕ (элемент Шеффера).
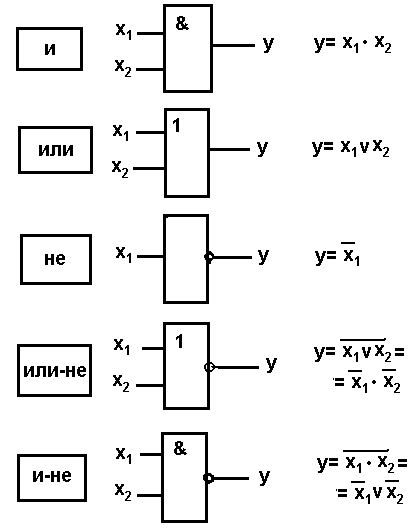
Логические
элементы И, ИЛИ, НЕ реализуют соответственно
функции конъюнкции, дизъюнкции и
отрицания (инверсии) и обозначаются по
ГОСТу как показано на рис. 1.15.
Универсальный
элемент ИЛИ-НЕ реализует функцию
отрицания дизъюнкции (стрелка Пирса).
Выходной сигнал равен произведению
инверсий входных сигналов. Универсальный
элемент И-НЕ реализует функцию отрицания
конъюнкции (штрих Шеффера). Выходной
сигнал равен сумме инверсий входных
сигналов.
логическая функция представляет собой
набор символов, связанных знаками
дизъюнкции, конъюнкции и инверсии.
Других операций нет. Поэтому возможность
реализации любой логической функции с
помощью основного набора логических
элементов (И, ИЛИ, НЕ) очевидна, а с помощью
остальных наборов – не очевидна.
С помощью
универсального приема двойного
инверсирования можно показать, как
реализуются основные операции алгебры
логики (конъюнкция, дизъюнкция и инверсия)
на функционально полных наборах,
состоящих из одного и двух логических
элементов.
Рис 1.5.
Рассмотрим, например, реализацию основных
операций алгебры логики на наборе
ИЛИ-НЕ.
Необходимо
рассмотреть реализацию трех основных
функций.
Операция
НЕ. В элементе ИЛИ-НЕ задействуется
только один вход, тогда элемент работает
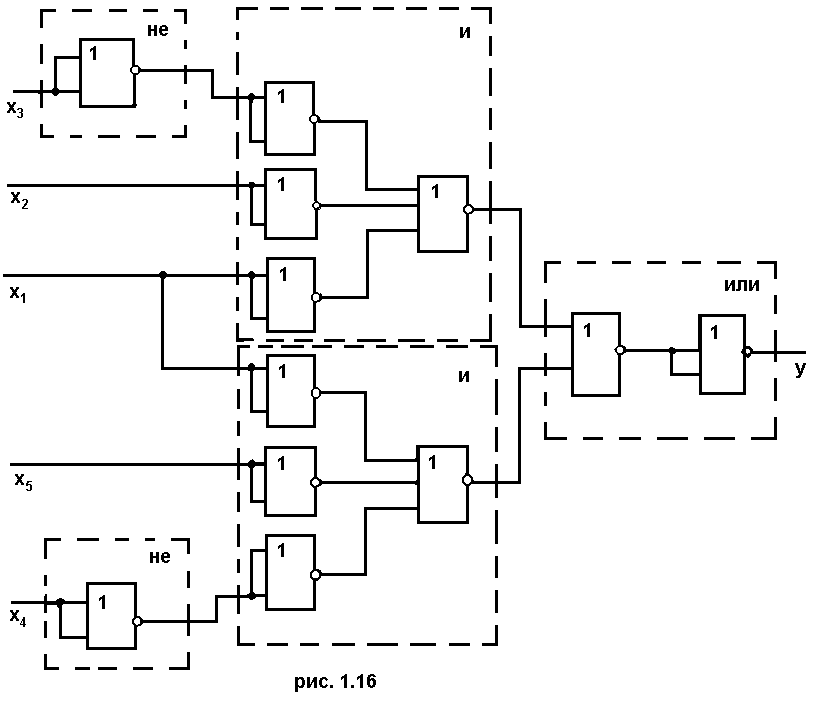
как инвертор (рис. 1.16). Используется один
элемент ИЛИ-НЕ.
Операция
И.Воспользуемся приемом двойной
инверсии:
Видим, что
следует реализовать функцию отрицания
дизъюнкции для двух инверсных сигналов
(рис. 1.7). Необходимы три элемента ИЛИ-НЕ.
Операция
ИЛИ.
Имеем инверсию
от инверсии дизъюнкции, т.е. сначала
ИЛИ-НЕ, потом НЕ. Для реализации необходимы
два элемента ИЛИ-НЕ (рис. 1.18).
Рассмотрим
реализацию основных операций алгебры
логики на наборе И-НЕ.
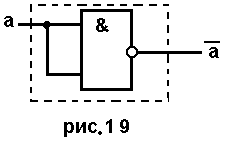
Операция
НЕ.В элементе И-НЕ задействуется
только один вход, тогда элемент работает
как инвертор (рис. 1.19). Используется один
элемент И-НЕ.
Операция
И.Воспользуемся приемом двойной
инверсии.Имеем инверсию от инверсии конъюнкции,
т.е. сначала И-НЕ, потом НЕ. Для реализации
требуется 2 элемента И-НЕ (рис. 1.20).
Операция ИЛИ.Имеем инверсию от конъюнкции инверсий,
т.е. сначала два раза НЕ, а затем И-НЕ
(рис. 1.11).
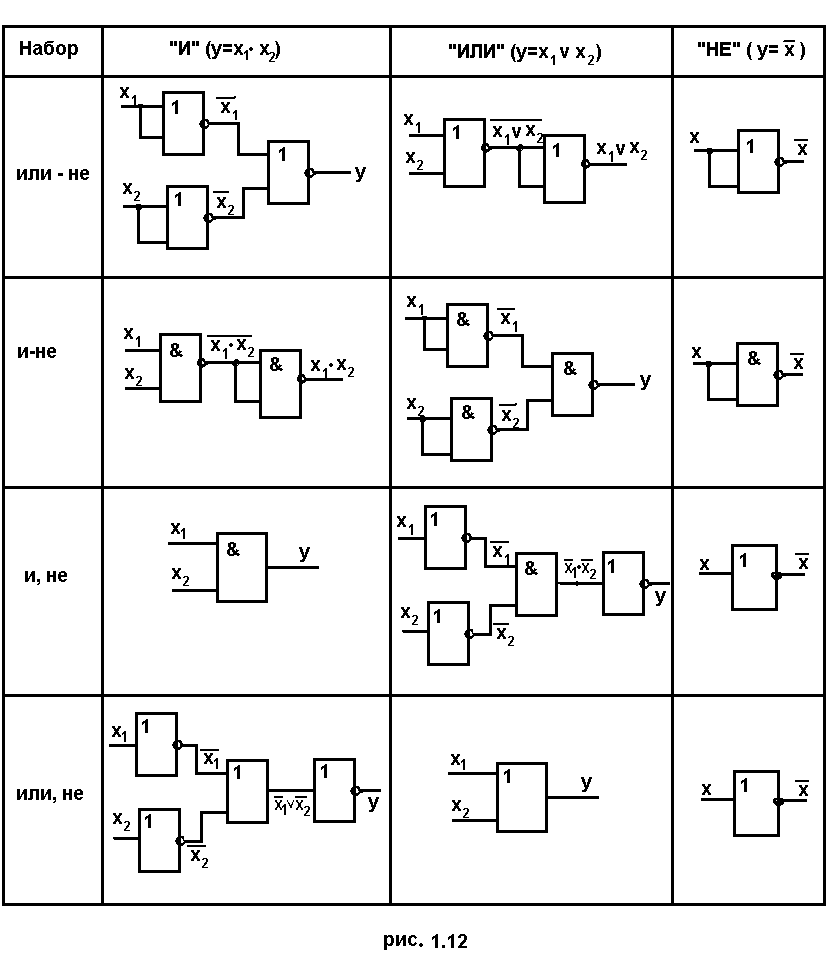
Аналогичным образом
получаем реализацию основных операций
алгебры логики для остальных функционально
полных наборов (рис. 1.12).
В случае
большого числа переменных соответственно
увеличивается количество входов или
входных инверторов.
Классическая
методика построения функциональной
схемы ДУ по логической функции, которую
оно реализует, заключается в следующем:
– по известной
логической функции построить структурную
схему ДУ в основных операциях алгебры
логики (И, ИЛИ, НЕ);
– выбрать
функционально полный набор БЛЭ для
реализации ДУ;
– перейти от
структурной схемы к функциональной с
учетом правил реализации основных
операций на выбранном наборе элементов;
– произвести
упрощения схемы.
Упрощения
производятся, как правило, за счет
исключения из схемы двух последовательно
стоящих инверторов.
Рассмотрим
примеры построения функциональной
схемы БДУ на наборах И-НЕ, ИЛИ-НЕ.
Пример 5.
Даны условия работы ДУ в виде логической
функции:
.
Построить
функциональную схему.
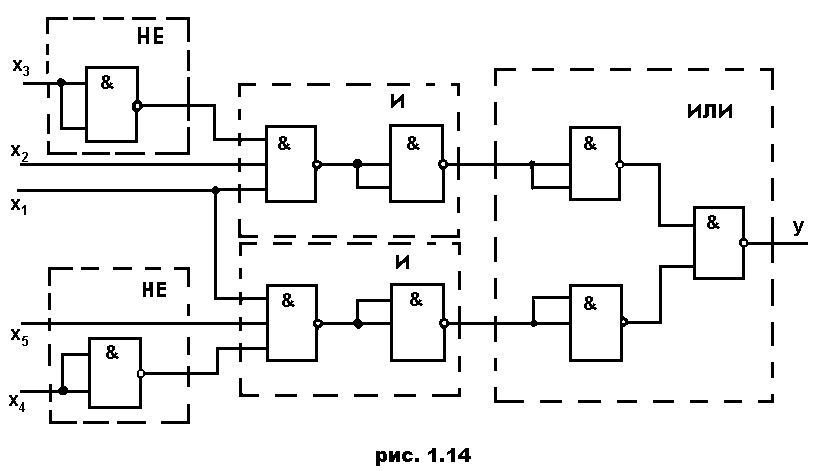
Строим структурную
схему ДУ (рис. 1.13), затем по правилам
реализации операций (см. рис. 1.20) –
функциональную схему ДУ на элементах
И-НЕ (рис. 1.14).
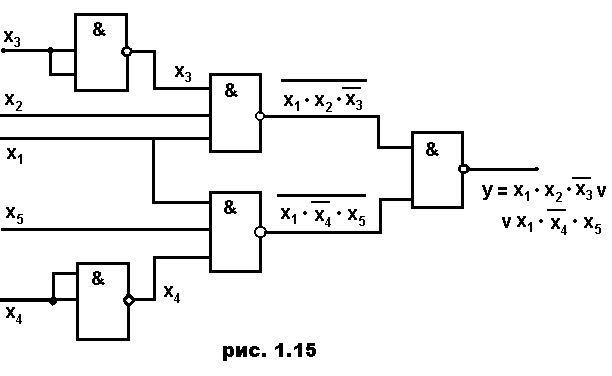
Последовательно
соединенные два инвертора компенсируют
друг друга и могут быть из схемы исключены.
После упрощения получаем окончательную
функциональную схему (рис. 1.15), состоящую
из 5 элементов И-НЕ.
Теперь
построим для этого же примера функциональную
схему на элементах ИЛИ-НЕ. Используем
ту же структурную схему (см. рис.1.13).
Получаем схему (рис. 1.16), содержащую 12
элементов ИЛИ-НЕ.
Путем
исключения последовательных инверторов
и объединения сигнала,
схема сокращается на 5 элементов и
остается 7 элементов ИЛИ-НЕ (рис. 1.17).
Изложенная методика
построения функциональной схемы ДУ
является универсальной, т.е. всегда лает
правильное решение – работоспособную
схему, но, как правило, слишком громоздкую.
В инженерной
практике обычно, обладая известным
навыком преобразования логических
функций, выполняют этап преобразования
исходного аналитического выражения
(условия работы ДУ, полученные в результате
абстрактного синтеза) к виду, удобному
для реализации на выбранном наборе БЛЭ.
В результате
этого этапа исходная функция записывается
сразу в операторах И-НЕ для реализации
на сериях интегральных элементов с
базовым элементом И-НЕ, либо в операторах
ИЛИ-НЕ для реализации на сериях БЛЭ
“Логика”, “Логика-Т” и т.д. с базовым
элементом ИЛИ-НЕ.
Для
преобразования функции, как правило,
пользуются универсальным приемом
двойного инверсирования.
Двойное
инверсирование функции, записанной в
ДНФ, дает форму операторов И-НЕ, а двойное
инверсирование функции, записанной в
КНФ, дает форму операторов ИЛИ-НЕ.
Таким образом,
если для построения ДА принят набор
И-НЕ, то исходную функцию (условия работы
ДА), полученную в результате абстрактного
синтеза, следует преобразовать в ДНФ,
а если принят набор ИЛИ-НЕ, то исходную
функцию следует преобразовать в КНФ.
Пример 12. Построить
функциональную схему БДУ на наборе
ИЛИ-НЕ в соответствии с условиями работыУсловия работы (исходная функция) уже
написаны в КНФ. Применяем прием двойного
инверсирования:
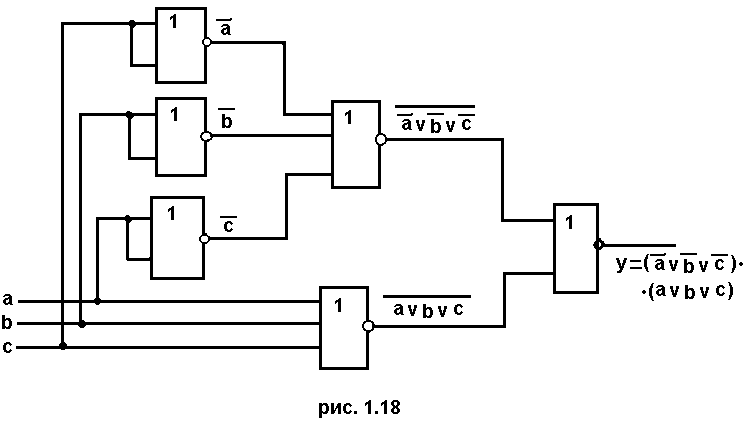
Получили
выражение, записанное в операторах
ИЛИ-НЕ. Функциональная схема ДУ,
построенная по данному выражению,
изображена на рис. 1.18.
Если нужно построить
эту функцию на наборе И-НЕ, то исходную
функцию следует привести к ДНФ, а затем
исследовать прием двойной инверсии.
Однако эту функцию можно упростить по
правилу: если ЛФ записанным в ДНФ (КНФ),
а нужно ее реализовать на наборе ИЛИ-НЕ
(И-НЕ), то прием двойного инверсирования
применяют дважды – сначала над каждым
членом исходной функции, затем над самой
функцией. Построим ЛФ
на наборе И-НЕ:
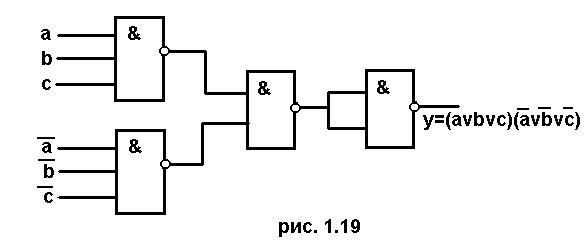
Схема
приведена на рис. 1.19 (считаем, что
известные сигналы уже получены).
Пример 13.
Построить функциональную схему БДУ на
наборе И-НЕ в соответствии с условиями
работы.
Условия работы (исходная функция) уже
записаны в ДНФ. Применяем прием двойного
инверсирования:
.
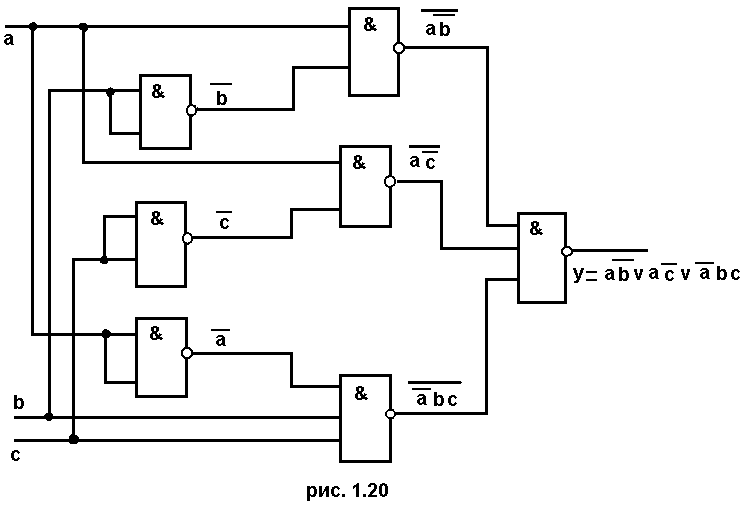
Получили
выражение, записанное сразу в операторах
И-НЕ. Очевидно, что функциональная схема
ДУ имеет вид, изображенный на рис. 1.20.
Попробуем еще
преобразовать исходное выражение в
направлении уменьшения числа операций
ИЛИ (так как базовый элемент принят
И-НЕ):
.
Полученное выражение
также записано в операторах И-НЕ.
Функциональная схема его представлена
на рис. 1.21.
Заметим, что
в подобных случаях функциональные схемы
удобно строить “с конца” аналитического
выражения.
Сравнивая
рис. 1.30 и 1.31, видим, что достигнута
экономия в два элемента И-НЕ.
В случае
синтеза многовыходных ДА без памяти
следует после получения минимизированных
выражений для нахождения сигналов на
каждом выходе провести преобразования
системы уравнений с целью объединения
одинаковых групп членов, членов или их
частей в разных уравнениях, а после
этого строить функциональную схему ДА.
Следующий
этап – физический синтез. Он имеет своей
целью переход от функциональной схемы
структуры проектируемого ДУ к
принципиальной электрической схеме.
На этом этапе выбираются типы бесконтактных
элементов, обеспечиваются дополнительные
требования: надежность, технологичность,
удобство контроля и т.д.
Методическая
разработка урока по теме: «Построение функциональных схем по заданной
логической функции»
Номинация
конкурса: методическая разработка в общеобразовательном учреждении по
информатике
ФИО учителя: Юрченко
Надежда Михайловна, учитель информатики муниципального автономного
общеобразовательного учреждения лицей № 1 г.Апшеронска Краснодарского края
Класс: 10
Предмет:
информатика и ИКТ
Тема урока: Построение
функциональных схем по заданной логической функции
Требуемое время: 1
учебный час.
Учебник: Угринович
Н.Д. Информатика и информационные технологии. Профильный курс, 10 класс,-М.:БИНОМ.
Лаборатория знаний,2009-2011
Описание
урока
Учебно-методическая
разработка к уроку информатики на тему «Построение функциональных схем по
заданной логической функции».
Урок: повторение,
ознакомление с новым материалом, закрепление.
Цели:
–
Образовательная –
повторить изученный материал, познакомить учащихся с возможностями построения
функциональных схем по заданной логической функции и их упрощения с применением
законов булевой алгебры;
–
Развивающая –
развивать умение учащихся оперировать понятиями, законами и схемами булевой
алгебры, развивать информационную культуры обучающихся через неявную
демонстрацию новых возможностей известных приложений (Excel);
–
Воспитательная –
продолжить формирование логического мышления; способствовать развитию
познавательного интереса к предмету.
Задачи:
– закрепление
знаний о логических выражениях, законах булевой алгебры; основных логических
элементов (И, ИЛИ, НЕ);
– отработка
навыков построения логических схем по заданным логическим функциям, упрощение
логических функций, построение новых упрощенных схем.
Оборудование:
Компьютерный
класс с рабочими местами для учеников и учителя. Для показа демонстрационного
материала в ходе объяснения, проведении актуализации и проверки изученного
материала необходимы интерактивная доска или мультимедиа проектор.
Дидактический
материал, программное обеспечение: рабочие печатные задания для
учащихся, электронные приложения к уроку (Power point, Excel).
План
урока:
–
Организационный
момент.
–
Повторение,
выполнение печатных заданий.
–
Объяснение
нового материала.
–
Работа
с печатными заданиями.
–
Тестирование
на компьютере.
–
Подведение
итогов.
Содержание
урока
I.
Организационная
часть.
Сообщение темы и
постановка целей урока
Здравствуйте ребята!
Сегодня мы с вами повторим материал, изученный
на предыдущих занятиях и изучим новый. Цель нашего урока – познакомиться с
возможностями построения функциональных схем, а в конце урока выполнить ряд
печатных заданий и небольшое тестовое задание, которые помогут оценить, как вы
усвоили тему.
II.
Повторение
пройденного материала .
Для
актуализации знаний учащимся дается задание «Расшифровать фразу». Для этого
необходимо в печатном задании решить примеры на определение значения логических
выражений и выбрать нужную букву(возможен вариант отсутствия ответа – значит
это пробел). На доске выбирается правильный ответ, в результате чего
записывается нужная буква. После решения всех примеров, из открытых букв
складывается фраза. Учащиеся работают у доски и одновременно выполняют задание
в рабочем печатном задании. Затем на экране(и в задании) предлагается
восстановить законы логики:
III. Объяснение
нового материала.
В
ходе объяснения актуализируются знания учащихся о таблицах истинности
логических операций, ведется беседа о работе простейших схем(вентилей),
реализующих логические элементы. Учащиеся знакомятся с алгоритмом построения функциональных
схем по заданной логической функции, учатся упрощать функции с использованием
законов булевой алгебры, определяя, целесообразно это или нет.
IV.
Закрепление нового материала
Для
закрепления изученного материала учащиеся на доске и в рабочих заданиях
выполняют комплекс упражнений различного типа:
V.
Текущий контроль.
Для
проверки степени усвоения нового материала учащимся предлагается выполнить на компьютерах(нечетный
номер – 1вариант, четный – 2вариант) тестовую работу с выбором правильного
ответа по вариантам (программа Excel).
VI.Подведение
итогов.
Учитель
подводит итоги урока, выставляет оценки. Определяет домашнее задание.
Литература:
1. Н. Угринович
“Информатика и информационные технологии ” Профильный курс,
10 класс,-М.:БИНОМ. Лаборатория знаний,2009-2011
2. Л.Л.Босова
и др. “Математические основы информатики”, М.: БИНОМ. Лаборатория
знаний,
2010 год
3. Журнал
“Информатика в школе” № 6 за 2005 год
4. http://www.klyaksa.net
5. http://festival.1september.ru/articles/510936/
6. http://doma10.ucoz.ru/logika/pril2.swf
7. http://videouroki.net
Примеры решения задач «Логические основы работы компьютера»
Теория по этой теме по этой теме Пройти тестирование по этой теме Контрольная по этой теме
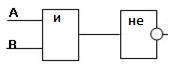
№1.
Дана логическая функция: F(А,В) = ¬ (А / В). Постройте соответствующую ей функциональную схему.
Решение:
Функциональная схема будет содержать 2 входа А и В. Рассмотрим логическое выражение и определим порядок действий в нем:
1) первым выполняется логическое умножение А / В, следовательно, сигналы с входов А и В подаются на конъюнктор;
2) далее выполняется логическое отрицание ¬(А / В), следовательно, сигнал, полученный на выходе из конъюнктора должен быть инвертирован, т.е. подан на инвертор.
Выход инвертора является выходом функциональной схемы.
Изобразим схему, следуя данным действиям:
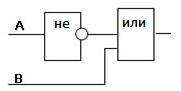
№2.
Определите логическую функцию, соответствующую заданной функциональной схеме:
Решение:
Функциональная схема содержит 2 входа А и В. Вход А инвертирован и его выход является входом дизъюнктора. Вход В подает сигнал на дизъюнктор. Выход дизъюнктора является выходом функциональной схемы.
Итак, последовательность действий:
1) ¬A — сигнал входа А инвертирован;
2) ¬A / B — на дизъюнктор подают инвертированный сигнал входа А и нормальный входа В.
Выход дизъюнктора является выходом функциональной схемы. Следовательно, логическая функция F –это функция двух переменных А и В и имеет вид:
F(A, B) = ¬A / B
Ответ: F(A, B) = ¬A / B
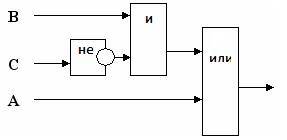
№3.
Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F=A/B/ ¬C, если А=1, В=1, С=1.
Решение:
Значение логического выражения — 1
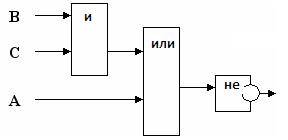
№4.
Постройте логическую схему, соответствующую логическому выражению и найдите значение логического выражения: F= ¬(A/B/C),если А=0, В=1, С=1.
Решение:
Значение логического выражения — 1
Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация на тему Построение функциональных схем по заданной логической функции
Содержание
-
1.
Построение функциональных схем по заданной логической функции -
2.
Пусть задана функция y=x1*x2 v ¬x3(x1 v -
3.
ˆПостроить функциональную схему по заданной функцииy=x1*x2 v ¬x3(x1 v x2*x3)ˆ vˆNot vх1х2х3×2*x3x1x1*x2( )¬x3y -
4.
Теперь преобразуем функцию, согласно законам булевой алгебры -
5.
Построим функциональную схему по преобразованной функции:y= x1*x2 -
6.
Скачать презентанцию
Пусть задана функция y=x1*x2 v ¬x3(x1 v x2*x3)Составим алгоритм построения функциональной схемы:1.Провести три токопроводящих линии х1, х2, х3.2.На третьей линии проинвертировать х3.3.Затем строим скобку, согласно порядка действий.4.Скобку умножаем на ¬x3.5.Соединяем конъюнкцией
Слайды и текст этой презентации
Слайд 1Построение функциональных схем по заданной логической функции

Слайд 2
Пусть задана функция y=x1*x2 v ¬x3(x1 v x2*x3)
Составим алгоритм построения
функциональной схемы:
1.Провести три токопроводящих линии х1, х2, х3.
2.На третьей линии
проинвертировать х3.
3.Затем строим скобку, согласно порядка действий.
4.Скобку умножаем на ¬x3.
5.Соединяем конъюнкцией х1 и х2
6.Соединяем дизъюнкцией первую и вторую части функции.
Алгоритм построения функциональной схемы:

Слайд 3ˆ
Построить функциональную схему по заданной функции
y=x1*x2 v ¬x3(x1 v x2*x3)
ˆ
v
ˆ
Not
v
х1
х2
х3
x2*x3
x1
x1*x2
( )
¬x3
y
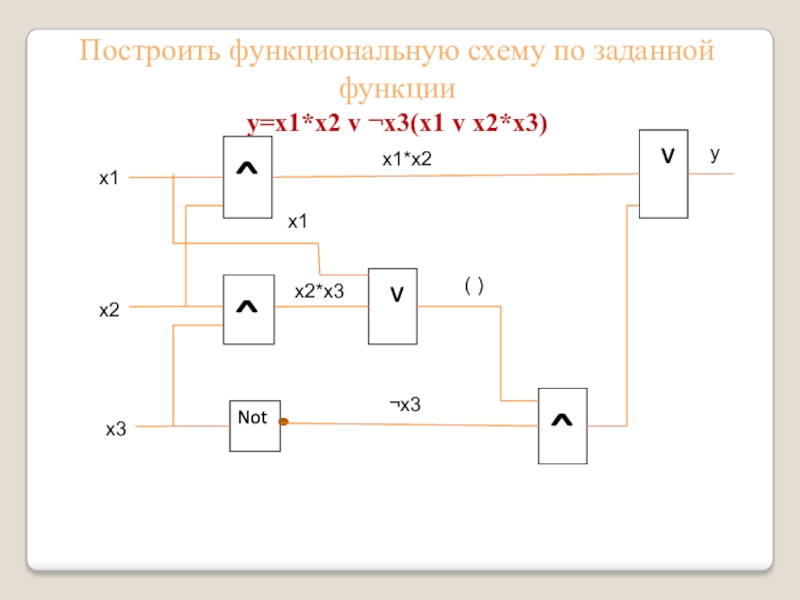
Слайд 4Теперь преобразуем функцию, согласно законам булевой алгебры раскрывая скобки:
y=x1*x2 v
¬x3(x1 v x2*x3)= x1*x2 v ¬x3*x1 v ¬x3* x2*x3,
по
закону дополнительности подчеркнутая часть равна нулю, следовательно преобразованная функция будет выглядеть следующим образом:
y= x1*x2 v ¬x3*x1

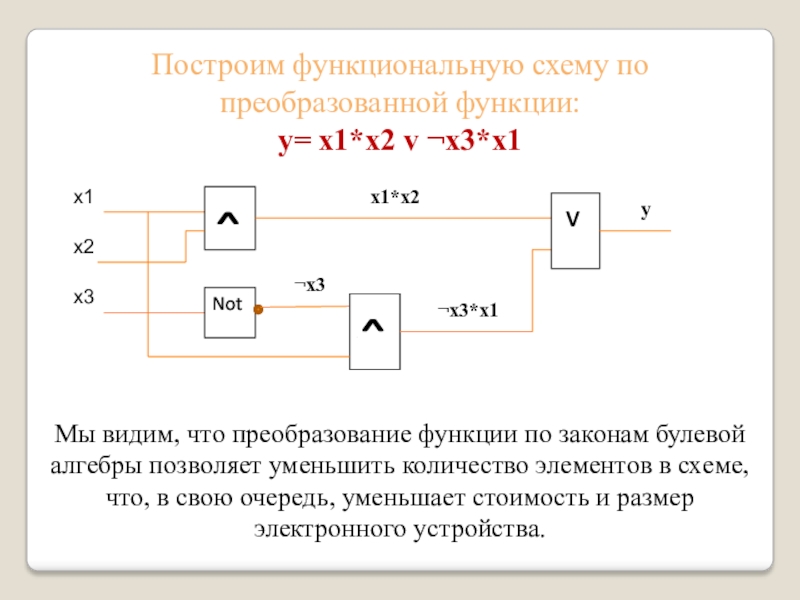
Слайд 5Построим функциональную схему по преобразованной функции:
y= x1*x2 v ¬x3*x1
x1
x2
x3
Not
ˆ
¬x3
ˆ
¬x3*x1
x1*x2
v
y
Мы видим, что преобразование функции по
законам булевой алгебры позволяет уменьшить количество элементов в схеме, что, в свою очередь, уменьшает стоимость и размер электронного устройства.
Редактор схемы логических элементов
Сервис представляет собой ряд калькуляторов: создание схемы из логических элементов, построение таблицы истинности по булевой функции (с помощью него можно будет также упростить эту функцию) и редактор карт Карно.
С помощью первой программы можно онлайн создать схему логических элементов. По построенной схеме находятся СКНФ, СДНФ, полином Жегалкина. Имеется возможность минимизировать булеву функцию.
Если схему необходимо построить по заданной таблице истинности, то используйте этот калькулятор (иногда задается просто строка, например, f=10001011).
- Ввод данных
- Параметры схемы
- Решение
- Видеоинструкция
- Оформление Word
Количество переменных
Стандарт изображений элементов
Инверсные входы
|
INV |
AND |
NAND |
OR |
NOR |
XOR |
MOD |
IF |
Размеры графического полотна
Ширина
Высота
Созданную логическую схему можно сохранить в форматах docx и png (меню Действия).
По логической схеме можно построить СКНФ, СДНФ, полином Жегалкина, карты Вейча-Карно, а также минимизировать булеву функцию.
Здесь будет показано решение
Инструкция к сервису
Для добавления логического элемента необходимо выделить его левой кнопкой мыши, а затем щелкнуть мышкой на рабочем поле.
Чтобы соединить элементы, их необходимо предварительно выбрать (один клик мыши по объекту), а затем нажать на кнопку Соединить. Для соединения с переменной xi нажмите на соответствующее ей название.
Построенную схему можно сохранить в формате docx или png.
Булевы функции
С помощью этого калькулятора по булевой функции строится таблица истинности, определяются свойства функции и другие параметры (см. вкладку Параметры решения
). При этом вводится только само логическое выражение без префикса. Например, при f(x,y,z) = x → y!z, ввести необходимо только x → y!z.
Введеное выражение также можно упростить, используя законы логики высказываний (на следующем шаге выбрать параметр Упростить выражение
).
(...) – ввод скобок, x -отрицание (NOT, !, ¬), & – логическое И, AND, ∧, *, v – логическое ИЛИ, OR, ∨, = – эквивалентность, ˜, ≡, ↔, ⊕ – сумма по модулю 2, | – штрих Шеффера, И-НЕ, AND-NOT, ↓ – стрелка Пирса, ИЛИ-НЕ, OR-NOT, ← – обратная импликация.
Для вложенного отрицания необходимо использовать знак !. Например, x v y = !(x v y) или x v y = x v !y
По найденной таблице истинности можно определить логические значения высказываний, например, при x=0, y=0, z=1
Чтобы проверить высказывание на истинность или ложность, функцию необходимо вводить без знака равно
(=). Например, A+B→A&B=1, необходимо ввести A+B→A&B. Если в результате преобразований получится, что f=1, то высказывание истинно, если f=0 – ложно.
Логические (функциональные) элементы {v,&, ¬} являются наиболее распространенными: в силу полноты системы любую булеву функцию (БФ) можно представить в виде суперпозиции дизъюнкции, конъюнкции и отрицания. В качестве функциональных элементов (ФЭ) можно рассматривать любые булевы функции, при этом их можно соединять друг с другом, подавая выходы одних элементов на входы других (суперпозиция БФ).
Область определения БФ E – конечное множество, поэтому БФ можно задать с помощью таблицы истинности, содержащей |E|=2n строк. Столбец значений БФ при этом представляет собой двоичное слово длиной 2n. Поэтому количество различных БФ n переменных равно 22n.
-
Отрицание, ¬
x f
0 1
1 0 -
Конъюнкция, &
x y f
0 0 0
0 1 0
1 0 0
1 1 1 -
Дизъюнкция, v
x y f
0 0 0
0 1 1
1 0 1
1 1 1 -
Сумма по модулю 2, x⊕y
x y f
0 0 0
0 1 1
1 0 1
1 1 0 -
Стрелка Пирса, x↓y
x y f
0 0 1
0 1 0
1 0 0
1 1 0 -
Эквивалентность, x↔y
x y f
0 0 1
0 1 0
1 0 0
1 1 1 -
Импликация, x→y
x y f
0 0 1
0 1 1
1 0 0
1 1 1 -
Штрих Шеффера, x|y
x y f
0 0 1
0 1 1
1 0 1
1 1 0
Другие БФ строятся из элементарных с помощью суперпозиций функций.
Основные равносильности логики высказываний
| Название | Формула |
| Закон исключенного третьего | X v !X ≡ И |
| Закон противоречия | X & !X ≡ Л |
| Закон коммутативности | X & Y ≡ Y & X X v Y ≡ Y v X |
| Закон ассоциативности | (X & Y)&Z ≡ X&(Y&Z) (X v Y) v Z ≡ X v (Y v Z) |
| Закон дистрибутивности | X&(Y v Z) ≡ X&Y v X&Z X v Y&Z ≡ (X v Y)&(X v Z) |
| Закон двойного отрицания | !!X ≡ X |
| Закон идемпотентности | X&X ≡ X, X v X ≡ X |
| Законы де Моргана | !(X v Y) ≡ !X & !Y !(X & Y) ≡ !X v !Y |
| Закон поглощения | X v X&Y ≡ X X&(X v Y) ≡ X |
| Законы склеивания | (X & Y)v(X & !Y) ≡ X (X v Y)&(X v !Y) ≡ X |
| Замена импликации | X → Y ≡ !X v Y |
| Замена эквиваленции | X = Y ≡ X&Y v !X&!Y |
Пример. Упростите выражение: (x˅y˅z)→(x˅y)*(x˅z)
Упростим функцию, используя основные законы логики высказываний.
Замена импликации: A → B = !A v B
Для нашей функции:
(x v y v z)→((x v y) (x v z)) = x v y v z v (x v y) (x v z)
Упростим функцию, используя законы де Моргана: !(A v B) = !A & !B
Для нашей функции:
x v y v z = x y z
По закону дистрибутивности:
(x v y) (x v z) = x v x z v y x v y z
получаем:
f = x y z v x v x z v y x v y z
После элементарных преобразований получаем:
f = x y z v x v x z v y x v y z = x y z v x v y z
f = y z v y z v x
Минимизация булевых функций
В данном сервисе для минимизации булевых функций используются метод Квайна и карт Карно-Вейча. После получения минимальной формы имеется возможность заново построить логическую схему. Если исходная схема понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).
Сократить БФ можно, применяя некоторые равносильности логики высказываний:
- Kx v K ≡ K – тождество поглощения;
- Kx v Kx ≡ K – тождество склеивания;
- Kx v Ky ≡ K(xvy) – дистрибутивный закон,
где K– элементарная конъюнкция. Большинство методов минимизации БФ основываются на первых двух тождествах. А третье – дистрибутивный закон – уменьшает количество букв в формуле, но выводит формулу из класса ДНФ.
При минимизации БФ используют различные термины (и обозначения) для полных элементарных конъюнкций (ПЭК). Наиболее часто используются термины «минтерм» и «конституента единицы». (Для полных элементарных дизъюнкций (ПЭД) используются термины «макстерм» и «конституента нуля»). Слово «конституента» означает «составляющая», а название «минтерм» исходит из определения конъюнкции, как минимального значения ее операндов. При этом используются обозначения mi – для минтерма и Mi – для макстерма. Номер i соответствует двоичной записи той оценки переменных, для которой mi=1.
Метод карт Карно
Склеить можно как целиком всю карту, либо только выделенные единицы (меню Операции).
Количество переменных
Сетка
После минимизации можно получить логическую схему функции и построить таблицу истинности (кнопка Далее)
Этот метод используется для БФ не более, чем с шестью аргументами и основан на тождестве склеивания: Kx v Kx ≡ K – две элементарные конъюнкции (ЭК) склеиваются, если они отличаются только знаком инверсии одного аргумента. Чтобы облегчить нахождение таких пар (четверок, восьмерок,…) склеивающихся ЭК, используют специальное представление БФ в виде таблицы – карты Карно (другое название – диаграмма Вейча). Чтобы заполнить карту Карно необходимо щелкнуть левой кнопкой мышки на соответствующую ячейку.
Карта Карно обладает той особенностью, что две ПЭК, соответствующие соседним клеткам карты, отличаются знаком инверсии только одного аргумента, т.е. их можно склеивать. Причем соседними являются не только клетки, например, с номерами 1 и 3, но и клетки с номерами 12 и 8, 12 и 4, т.е. карту можно «сворачивать» в цилиндр, соединяя горизонтальные (вертикальные) ее границы.
Две единицы «склеиваются» каждый раз, когда они стоят рядом в строке или столбце (карту можно свернуть в цилиндр). В результате склеивания число букв, входящих в ПЭК, уменьшается на единицу.
Минимизая функции через равносильные преобразования
см. таблицу равносильных преобразований
Алгоритм минимизии логической функции
- Замена импликации и эквиваленции.
- Упрощение функции через законы де Моргана.
- Раскрытие скобок, используя законы поглощения, исключенного третьего, противоречия.
- Минимизация через закон дистрибутивности.
Алгоритм Куайна построения сокращенной ДНФ
- Получить СДНФ функции.
- Провести все операции неполного склеивания.
- Провести все операции поглощения.
Построение логической схемы по таблице истинности
По заданной СДНФ (по таблице истинности) определяются существенные и фиктивные переменные, полином Жегалкина и принадлежность классам T0,T1, S, M, L. Также можно создать новую логическую схему (если не выбран пункт Строить новую схему при минимизации булевой функции). Если вычисления происходят по исходной схеме и она понадобится в дальнейшем, то ее можно предварительно сохранить (меню Действия/Сохранить).
Название переменных можно изменить. Для этого их необходимо выбрать (первая строка таблицы).
Количество переменных
Ввести как вектор значений (в виде строки)
| a | b | c | f |
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 |
Для установки параметров решения, необходимо нажать Далее.
Пример. Найдите СДНФ(А) и СКНФ(А) с помощью равносильных преобразований и таблицы истинности, если A = xvyv(x→y)&x
Таблица истинности
| x | y | x | y | xvy | xvy | x→y | (x→y)&x | xvyv(x→y)&x |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
Упростим функцию, используя основные законы логики высказываний.
Замена импликации
A → B = !A v B
Для нашей функции:
x→y = x v y
f = x v y v (x v y) x
Упростим функцию, используя законы де Моргана онлайн.
!(A v B) = !A & !B
!(A & B) = !A v !B
Для нашей функции:
x v y = x y
f = x y v (x v y) x
По закону дистрибутивности:
x x = 0
(x v y) x = y x
x y v (x v y) x = x y v y x
f = x y
Используя равносильные преобразования, найдем СДНФ(А).
СДНФ(А) = x y
Используя равносильные преобразования, найдем СДНФ(А).
1. Для получения элементарных дизъюнкций используем закон дистрибутивности XvYZ=(XvY)(XvZ).
2. Закон исключенного третьего Xv!X=1. При этом элементарную дизъюнкцию можно отбросить (в силу равносильности C & 1 = C).
3. По закону поглощения XvXYZ = X
A = x y
Из КНФ А путем равносильных преобразований получаем СКНФ А, последовательно добиваясь выполнения четырех свойств СКНФ А.
1. Если элементарная дизъюнкция В, входящая в КНФ А, не содержит переменную xi, тогда заменяем В на Bv(xi & !xi) = (B v xi)(B v !xi)
2. Если в некоторую элементарную дизъюнкцию В переменная xi входит дважды, то лишнюю переменную нужно отбросить, так как xi v xi = xi.
3. Если КНФ А содержит две одинаковых элементарных дизъюнкций, то одну можно отбросить, так как B & B = B
4. Если в элементарную дизъюнкцию входит пара xi v !xi, то ее можно отбросить так как xi v !xi=1, а истинное высказывание из конъюнкции можно выбросить (в силу равносильности C & 1 = C).
A = (x v y y) (y v x x) = (x v y) (x v y) (y v x) (y v x)
A = (x v y) (x v y) (y v x) (y v x)
СКНФ(А) = (x v y) (x v y) (x v y)
Совершенная дизъюнктивная нормальная форма формулы (СДНФ) это равносильная ей формула, представляющая собой дизъюнкцию элементарных конъюнкций, обладающая свойствами:
1. Каждое логическое слагаемое формулы содержит все переменные, входящие в функцию F(x1,x2,…xn).
2. Все логические слагаемые формулы различны.
3. Ни одно логическое слагаемое не содержит переменную и её отрицание.
4. Ни одно логическое слагаемое формулы не содержит одну и ту же переменную дважды.
F = x y
Совершенная конъюнктивная нормальная форма формулы (СКНФ) это равносильная ей формула, представляющая собой конъюнкцию элементарных дизъюнкций, удовлетворяющая свойствам:
1. Все элементарные дизъюнкции содержат все переменные, входящие в функцию F(x1,x2,…xn).
2. Все элементарные дизъюнкции различны.
3. Каждая элементарная дизъюнкция содержит переменную один раз.
4. Ни одна элементарная дизъюнкция не содержит переменную и её отрицание
F = (x v y) (x v y) (x v y)
Список литературы
- Нефедов В.Н., Осипова В.А. Курс дискретной математики. М.,1992.
- Бауэр Ф.Л., Гооз Г. Информатика. Вводный курс: Часть 2, М.: Мир, 1990.
- Горбатов В.А. Основы дискретной математики. – М.: Высш. школа, 1986. – 312 с.
Количество входов
Текст
РазмерЦвет
Линия
ТолщинаЦвет
пунктирная – – – –
Размеры в px и фон
wh
Номер входа
Текст
РазмерЦвет
Линия
ТолщинаЦвет
пунктирная – – –
Введите название переменных
Введите название переменных
Количество входов у элемента