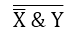Как составить функциональную схему в информатике

Функциональные схемы и структурные формулы логических устройств — Построение алгебры высказываний — Краткий теоретический справочник

Всякое устройство ЭВМ, выполняющее некоторое действие над цифровыми сигналами, можно рассматривать как функциональный преобразователь, на входы которого с помощью цифровых сигналов подаются значения аргументов функции (исходные двоичные числа), а на выходах получают значения функций, реализующих указанное действие для этих аргументов (выходные двоичные числа).

Преобразователь, который, получая сигналы об истинности отдельных высказываний, обрабатывает их и в результате выдаёт значение логических операций (отрицания, суммы, произведения), называется логическим элементом.

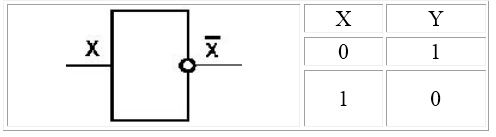
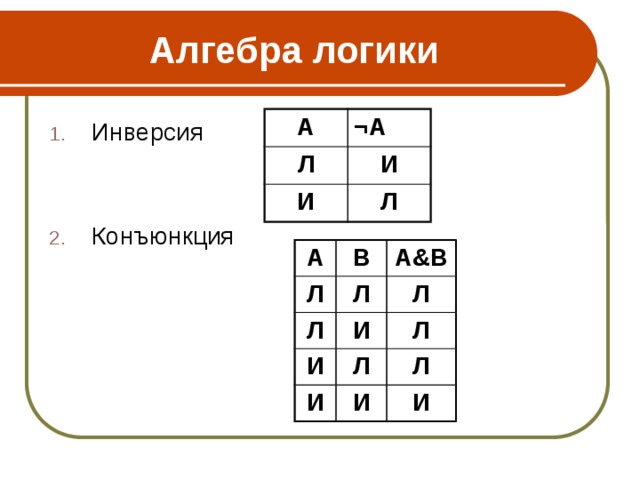
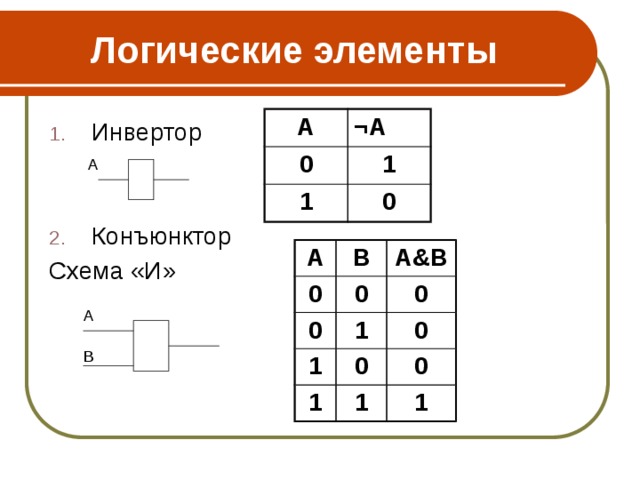
1. Логический элемент «НЕ» (инвертор) выдаёт на выходе сигнал, противоположный сигналу на входе. То есть если на входе в инвертор поступает 1, то на выходе будет 0, и наоборот. Физически инвертор можно реализовать при помощи реле с нормально замкнутыми (подпружиненными) контактами. Когда на обмотку реле подаётся ток (входной сигнал равен 1), реле срабатывает и размыкает соединение. Когда тока в цепи нет, цепь становится замкнутой. Условное обозначение инвертора представлено на рисунке 6.

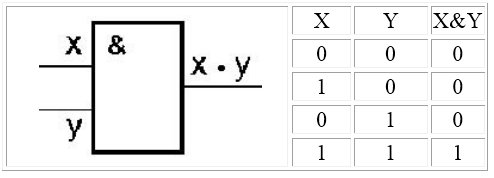
2. Логический элемент «И» (конъюнктор) выдаёт на выходе значение логического произведения входных сигналов. Физически конъюнктор можно реализовать последовательным соединением переключателей. Условное обозначение конъюнктора представлено на рисунке 7.

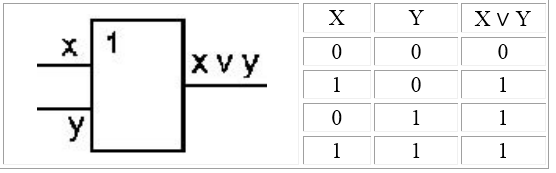
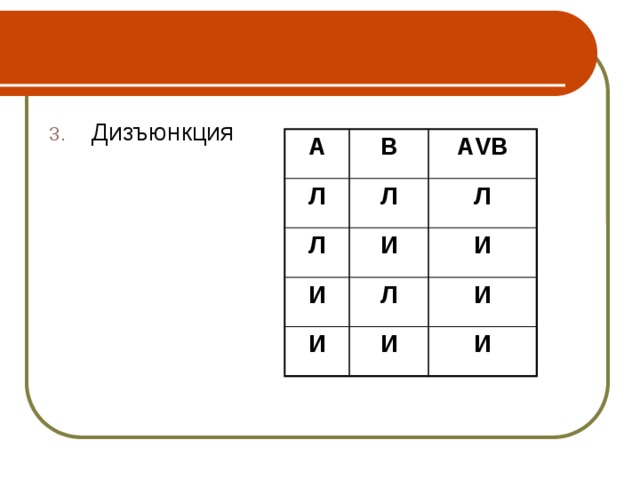
3. Логический элемент «ИЛИ» (дизъюнктор) выдаёт на выходе значение логического сложения входных сигналов. Физически дизъюнктор можно реализовать параллельным соединением переключателей. Условное обозначение конъюнктора представлено на рисунке 8.

4. Цепочку логических элементов, в которой выходы одних элементов являются входами других, называют логическим устройством.

Схема соединения логических элементов, реализующая логическую функцию, называется функциональной (логической) схемой.

Формой описания функции, реализуемой логическим устройством, является (структурная) формула.

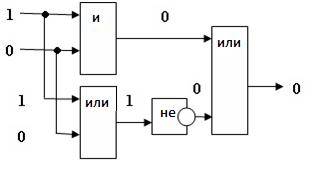
Пример. Определим формулу по заданной функциональной схеме (см. рис. 9).

Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.

Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.

Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.

Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.

© 2014-2022 Все права на дизайн сайта принадлежат С.Є.А.

Источник

Логика и компьютер

Вы будете перенаправлены на Автор24

Логика в информатике – это те отрасли знания и направления исследований, в которых логика применяется в информатике и искусственном интеллекте. В информатике логика оказалась гораздо более эффективной, чем это было в математике.

Основные направления прикладного использования логики в информатике

1. написание компьютерных программ и их верификация.
2. при проектировании вычислительных устройств используется как теоретический инструмент.
3. Использование логических операций в электронных микросхемах в качестве базовых.
4. логический подход к представлению и решению различных практических задач с использованием вычислительной техники.

Стандартное математическое представление любого вычисления − это отображение переменных (их внутреннего состояния) вычислительного устройства на входе в новое состояние на выходе. В алгебре логики решается стандартная задача, а именно: определяется функциональная полнота логических связок, то есть проверяется, является ли фиксированный набор логических операций достаточным для того, чтобы представить новое результирующее значение путём комбинации любых других (базовых) функций. А это значит, что базовые логические устройства должны быть универсальными и позволять решать большое число задач.

Работу большинства вычислительных устройств, которые существуют в настоящее время, прекрасно описывает алгебра логики, разработанная Джорджем Булем. К таким устройствам относятся триггеры, сумматоры, группы переключателей, Кроме того булева алгебра и компьютеры связаны между собой при помощи используемой в ЭВМ двоичной системы счисления. Поэтому в устройствах компьютера можно хранить и преобразовывать и значения логических переменных, и числа.

Логические элементы — это электронные устройства, которые по определенному закону преобразуют проходящие через них двоичные электрические сигналы.

Логические элементы имеют один (инвертор) или несколько входов, на которые подаются электрические сигналы, обозначаемые условно $0$, если сигнал отсутствует, и $1$, если электрический сигнал имеется. Выход у логических элементов один, откуда снимается новый, преобразованный электрический сигнал.

Готовые работы на аналогичную тему

Все электронные схемы компьютера могут быть реализованы с помощью трёх базовых логических элементов И, ИЛИ, НЕ.

Логический элемент НЕ (инвертор). Простейший логический элемент, реализующий функцию отрицания (инверсию). Унарный элемент – элемент, у которого один вход и один выход.

На функциональных схемах обозначается

Если на вход инвертора подаётся $1$, то на выходе реализуется $0$ и наоборот.

Логический элемент И (конъюнктор) реализует умножение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:

Если на входе конъюнктора все входные сигналы имеют значение $1$, то на выходе тоже будет сигнал $1$, в противном случае на выходе будет сигнал $0$.

Логический элемент ИЛИ (дизъюнктор) реализует сложение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:

Если на вход дизъюнктора поступает хотя бы один сигнал равный $1$, то выходе тоже будет сигнал $1$.

Роль базовых логических элементов в создании схем играют ещё два логических элемента: И-НЕ и ИЛИ-НЕ.

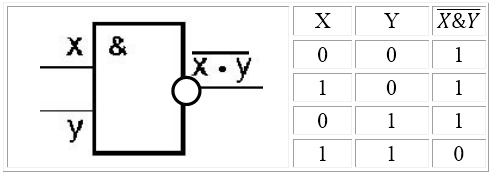
Логический элемент И-НЕ (отрицание конъюнкции) выполняет логическую функцию штрих Шеффера. Операция бинарная, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается следующим образом:

Логический элемент ИЛИ-НЕ (отрицание дизъюнкции) выполняет логическую функцию стрелка Пирса. Тоже бинарная операция, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается так:

Функциональные схемы

Сигнал, который вырабатывает один логический элемент, можно подать на вход другого элемента. Это даст возможность образовать цепочку из отдельных логических элементов – функциональную схему.

Функциональная (логическая) схема – это схема, которая выполняет определённую функцию и состоит из базовых логических элементов. Проанализировав фунциональную схему, можно понять, как работает логическое устройство, то есть ответить на вопрос, какую же функцию она выполняет. А чтобы описать функциональную схему, нужна структурная формула.

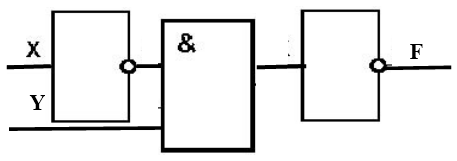
Как по заданной функциональной схеме записать структурную формулу?

Элемент И осуществляет конъюнкцию $bar$ и $Y$, над результатом в элементе НЕ выполняется операция отрицания, то есть вычисляется значение выражения

Записали, что структурной формулой данной функциональной схемы является формула

Для функциональной схемы нужно составить таблицу значений сигналов на входах и выходах схемы, по которой можно понять, какую функцию выполняет данная схема, – таблицу истинности.

Составим таблицу истинности для вышеприведённой схемы. Количество столбцов таблицы равно суммарному количеству входов и выходов нужной схемы. Итого $5$ столбцов. Количество строк таблицы равно $2^n$, где $n$ – количество входов (здесь два), строк $4$.

Обработка любой информации на компьютере − выполнение процессором различных арифметических и логических операций. Для этого в составе процессора есть арифметико-логическое устройство (АЛУ), которое состоит из ряда устройств, построенных на логических элементах, рассмотренных выше. Главными устройствами являются триггеры, полусумматоры, сумматоры, шифраторы, дешифраторы, счетчики, регистры.

Конструируется логическое устройство по следующему алгоритму:

1. по заданным условиям работы проектируемого узла (т.е. по соответствию его входных и выходных сигналов) строится таблица истинности;
2. конструируется логическая функция данного узла по таблице истинности, выполняется при необходимости её преобразование (упрощение), если cоставляется функциональная схема проектируемого узла по формуле логической функции;
3. реализуется полученная схема.

Источник

Логические основы работы компьютера

Логические основы работы компьютера

Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.

Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.

Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».

Логический элемент «НЕ» (инвертор)

Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.

У этого элемента один вход и один выход. На функциональных схемах он обозначается:

Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.

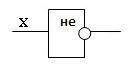
Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx

Логический элемент «И» (конъюнктор)

Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.

Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:

Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.

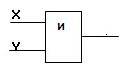
Проверь соответствие логического элемента «И» логическому элементу «И». Воспользуйся тренажером Логические элементы.xlsx

Логический элемент «ИЛИ» (дизъюнктор)

Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:

Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.

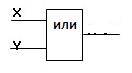
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.

Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.

Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ». Воспользуйся тренажером Логические элементы.xlsx

Пример 1.
Составьте логическую схему для логического выражения: F=A / B / A.

2. Две логические операции: 1-/, 2-/.

Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А/В/ ¬(В/А). Вычислить значения выражения для А=1,В=0.

1. Переменных две: А и В; 1 4 3 2

2. Логических операций три: / и две /; А/В/ ¬ (В/ А).

3. Схему строим слева направо в соответствии с порядком логических операций:

4. Вычислим значение выражения: F=1 / 0 / ¬(0 / 1)=0

Источник

Функциональные схемы

В данной презентации рассмотрены основные принципы построения функциональных схем из базовых логических элементов. Применяется на занятиях по Дискретной математики, информатики.

Просмотр содержимого документа
«Функциональные схемы»

Построение функциональных схем

Преподаватель информатики Кузнецкого филиала ГАПОУ ПО ПМПК

Коткова Наталья Геннадьевна

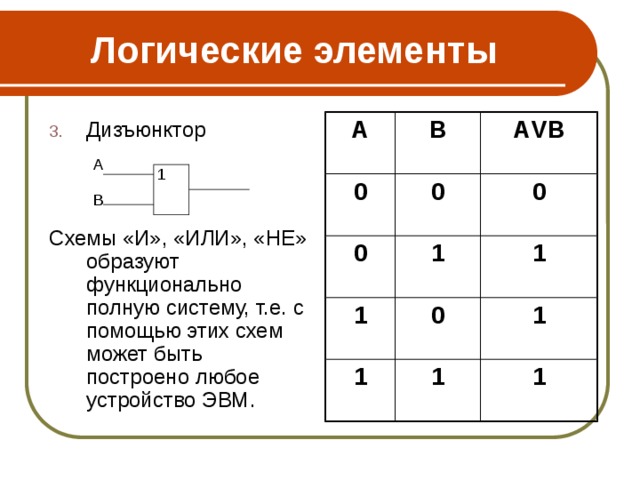
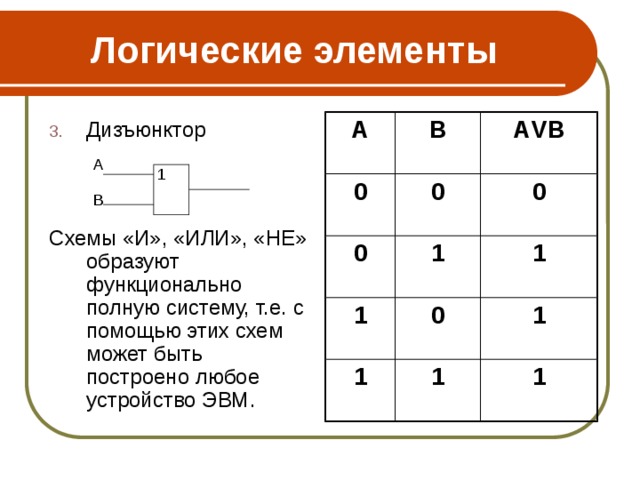
• Дизъюнкция

Комбинационная логическая схема

Комбинационной логической схемой называется цифровая схема, в которой выходные сигналы определяются только теми сигналами, которые поступают на вход схемы в тот же момент времени.

Схемы «И», «ИЛИ», «НЕ» образуют функционально полную систему, т.е. с помощью этих схем может быть построено любое устройство ЭВМ.

Построение функциональных логических схем логических устройств

• Цепочка из логических элементов, в которой выходы одних элементов являются входами других, называется логическим устройством
• Схема соединения логических элементов, реализующая логическую функцию, называется функциональнойсхемой .
• Формой описания функции, реализуемой логическим устройством, является структурнаяформула .

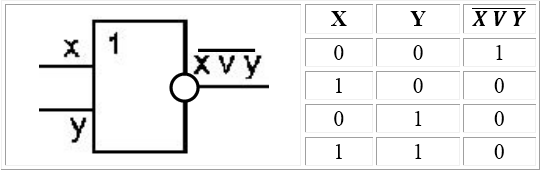
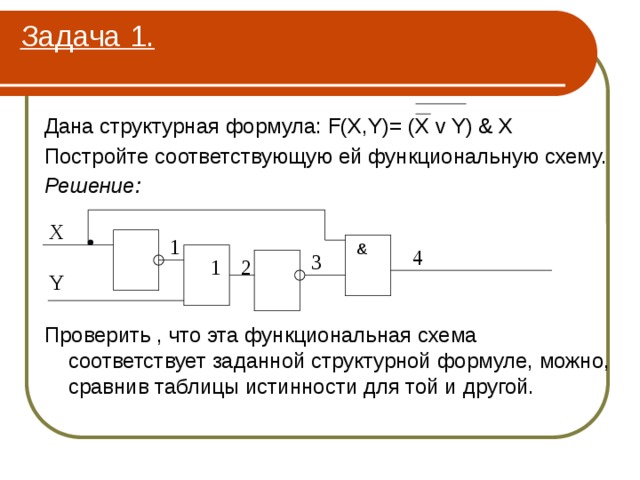
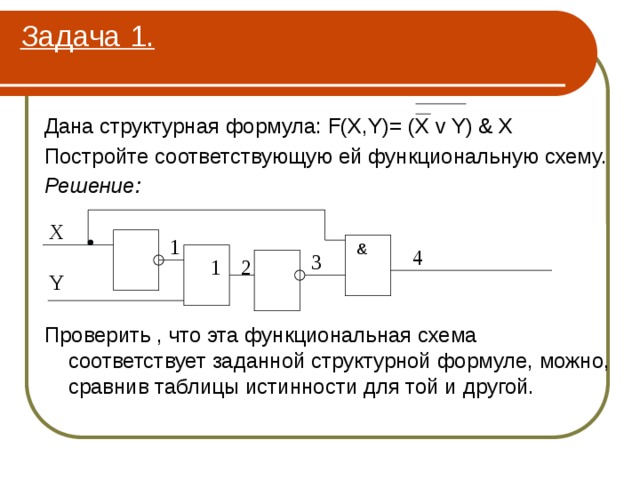
Дана структурная формула: F(X,Y)= (X v Y) & X

Постройте соответствующую ей функциональную схему.

Проверить , что эта функциональная схема соответствует заданной структурной формуле, можно, сравнив таблицы истинности для той и другой.

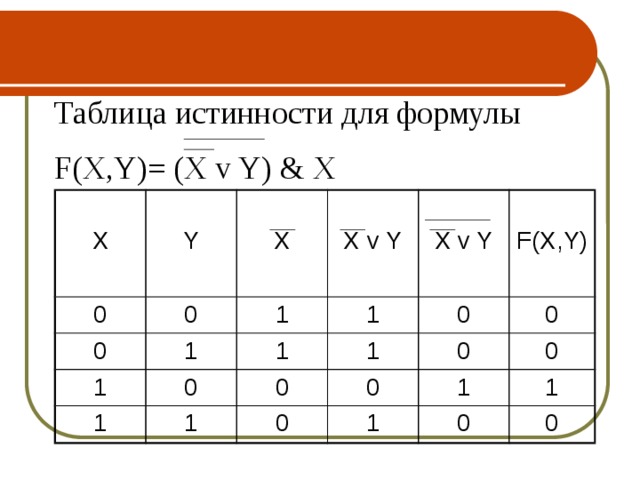
Таблица истинности для формулы

Схемы «И», «ИЛИ», «НЕ» образуют функционально полную систему, т.е. с помощью этих схем может быть построено любое устройство ЭВМ.

Построение функциональных логических схем логических устройств

• Цепочка из логических элементов, в которой выходы одних элементов являются входами других, называется логическим устройством
• Схема соединения логических элементов, реализующая логическую функцию, называется функциональнойсхемой .
• Формой описания функции, реализуемой логическим устройством, является структурнаяформула .

Дана структурная формула: F(X,Y)= (X v Y) & X

Постройте соответствующую ей функциональную схему.

Проверить , что эта функциональная схема соответствует заданной структурной формуле, можно, сравнив таблицы истинности для той и другой.

Источник

Основные направления прикладного использования логики в информатике

1. написание компьютерных программ и их верификация.
2. при проектировании вычислительных устройств используется как теоретический инструмент.
3. Использование логических операций в электронных микросхемах в качестве базовых.
4. логический подход к представлению и решению различных практических задач с использованием вычислительной техники.

Работу большинства вычислительных устройств, которые существуют в настоящее время, прекрасно описывает алгебра логики, разработанная Джорджем Булем. К таким устройствам относятся триггеры, сумматоры, группы переключателей, Кроме того булева алгебра и компьютеры связаны между собой при помощи используемой в ЭВМ двоичной системы счисления. Поэтому в устройствах компьютера можно хранить и преобразовывать и значения логических переменных, и числа.

Логические элементы имеют один (инвертор) или несколько входов, на которые подаются электрические сигналы, обозначаемые условно $0$, если сигнал отсутствует, и $1$, если электрический сигнал имеется. Выход у логических элементов один, откуда снимается новый, преобразованный электрический сигнал.

«Логика и компьютер» 👇

Все электронные схемы компьютера могут быть реализованы с помощью трёх базовых логических элементов И, ИЛИ, НЕ.

Логический элемент НЕ (инвертор). Простейший логический элемент, реализующий функцию отрицания (инверсию). Унарный элемент – элемент, у которого один вход и один выход.

На функциональных схемах обозначается

Если на вход инвертора подаётся $1$, то на выходе реализуется $0$ и наоборот.

Логический элемент И (конъюнктор) реализует умножение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:

Если на входе конъюнктора все входные сигналы имеют значение $1$, то на выходе тоже будет сигнал $1$, в противном случае на выходе будет сигнал $0$.

Логический элемент ИЛИ (дизъюнктор) реализует сложение двух или более логических значений, т.е. имеет два или более входов и один выход. На функциональных схемах обозначается:

Если на вход дизъюнктора поступает хотя бы один сигнал равный $1$, то выходе тоже будет сигнал $1$.

Роль базовых логических элементов в создании схем играют ещё два логических элемента: И-НЕ и ИЛИ-НЕ.

Логический элемент И-НЕ (отрицание конъюнкции) выполняет логическую функцию штрих Шеффера. Операция бинарная, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается следующим образом:

Логический элемент ИЛИ-НЕ (отрицание дизъюнкции) выполняет логическую функцию стрелка Пирса. Тоже бинарная операция, поэтому имеет, как минимум, два входа. На функциональных схемах обозначается так:

Функциональные схемы

Сигнал, который вырабатывает один логический элемент, можно подать на вход другого элемента. Это даст возможность образовать цепочку из отдельных логических элементов – функциональную схему.

Как по заданной функциональной схеме записать структурную формулу?

Элемент И осуществляет конъюнкцию $bar{X}$ и $Y$, над результатом в элементе НЕ выполняется операция отрицания, то есть вычисляется значение выражения

Записали, что структурной формулой данной функциональной схемы является формула

Для функциональной схемы нужно составить таблицу значений сигналов на входах и выходах схемы, по которой можно понять, какую функцию выполняет данная схема, – таблицу истинности.

Составим таблицу истинности для вышеприведённой схемы. Количество столбцов таблицы равно суммарному количеству входов и выходов нужной схемы. Итого $5$ столбцов. Количество строк таблицы равно $2^n$, где $n$ – количество входов (здесь два), строк $4$.

Обработка любой информации на компьютере − выполнение процессором различных арифметических и логических операций. Для этого в составе процессора есть арифметико-логическое устройство (АЛУ), которое состоит из ряда устройств, построенных на логических элементах, рассмотренных выше. Главными устройствами являются триггеры, полусумматоры, сумматоры, шифраторы, дешифраторы, счетчики, регистры.

Конструируется логическое устройство по следующему алгоритму:

1. по заданным условиям работы проектируемого узла (т.е. по соответствию его входных и выходных сигналов) строится таблица истинности;
2. конструируется логическая функция данного узла по таблице истинности, выполняется при необходимости её преобразование (упрощение), если cоставляется функциональная схема проектируемого узла по формуле логической функции;
3. реализуется полученная схема.

1. Построение функциональных логических схем по заданным функциям

При
построении отдельных узлов компьютера
довольно часто необходимо решить
проблему построения функциональных
логических схем по заданным функциям.
Для этого достаточно условиться, что
истинное высказывание соответствует
тому, что цепь проводит ток, а ложное –
цепь разорвана.

Логические
операции конъюнкции, дизъюнкции,
инверсии реализуются в ЭВМ с помощью
следующих элементарных схем.

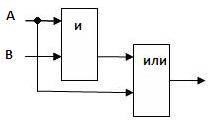
Конъюнкция –
логический элемент «и»:

Этот
элемент выполняет операцию логического
умножения (конъюнкция): f
= x₁
x₂
x₃
…x_n
; и имеет n
входов и один выход.

Дизъюнкция –
логический элемент «или»:

Этот
элемент выполняет операцию логического
сложения (дизъюнкция): f
= x₁
x₂
x₃
…x_n
; и имеет n
входов и один выход.

Инверсия –
логический элемент «не»:

Этот
элемент выполняет операцию логического
отрицания (инверсии): f
=
;
и имеет один вход и один выход.

Сложные функциональные
схемы можно конструировать из основных
логических элементов, используя основные
законы булевой алгебры

2. Пример выполнения контрольного задания

Задание:

Дана
функция,

1. Составить
   функциональную логическую схему по
   данной функции.

2. Упростить
   логическую функцию (используя законы
   булевой алгебры) и выполнить проверку
   преобразования таблицей истинности.

3. Составить
   функциональную логическую схему по
   упрощенной функции.

Выполнение:

1. Составим таблицу
   истинности для заданной функции:

x	y
0	0	1	1	1	0	0	1	1
0	1	1	0	0	1	1	0	0
1	0	0	1	1	0	1	0	0
1	1	0	0	1	0	1	0	0

1. Составим
   функциональную логическую схему по
   заданной функции:

1. Упростим заданную
   функцию, используя законы булевой
   алгебры:

а) по закону де
Моргана – 9

б) по закону
идемпотентности – 13

в) закон отрицание
отрицания – 1

г) закон
дистрибутивности – 6

д) свойства 1 и 0 –
19

е) свойства 1 и 0 –
16

Таким образом,
упрощенная функция имеет вид:

4. Составим таблицу истинности для
упрощенной функции:

x	y
0	0	1	1	1
0	1	1	0	0
1	0	0	1	0
1	1	0	0	0

Таким образом,
сравнивая таблицы истинности для
исходной и упрощенной функций (их
последние столбцы) делаем вывод о
правильности проведенных преобразований.

5. Составим
функциональную логическую схему по
упрощенной функции:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Функциональные схемы
  – электронные схемы, реализованные по принципу замыкания и размыкания контактов реле. Скорость срабатывания электронных схем в тысячи раз быстрее, чем скорость аналогичных релейно-контактных схем.

• 

  2 слайд

  Функциональные элементы (вентили)
  Электронное устройство, получая значение истинности отдельных простых высказываний (1 – наличие сигнала, 0 – отсутствие) могут выдавать значения истинности конъюнкции, дизъюнкции, отрицания. Эти электронные схемы называют функциональными элементами (вентили).

• 

  3 слайд

  1. Элемент И – конъюнктор
  имеет два или более входов и один выход.
  На выходе сигнал появляется тогда и только тогда, когда на все входы поданы сигналы.
  х
  у
  х  у
  х & у
  &
  х  у
  х · у
  х
  у
  И
  Обозначение:

• 

  4 слайд

  2. Элемент ИЛИ – дизъюнктор
  имеет два или более входов и один выход.
  На выходе сигнал появляется тогда, когда хотя бы на один вход подан сигнал.
  х
  у
  х  у
  х + у
  1
  х
  у
  х  у
  х + у
  или
  Обозначение:

• 

  5 слайд

  3. Элемент НЕ – инвертор
  имеет один вход и один выход.
  Сигнал на выходе, когда на входе нет сигнала и наоборот.
  Обозначение:
  х
  х
  не
  х
  х

• 

  6 слайд

  Из функциональных элементов, соединяя их между собой можно составлять функциональные схемы, реализующие сложные логические формулы. Каждой логической формуле можно поставить в соответствие функциональную схему.
  х
  z
  1
  y
  z = x + y
  Например:

• 

  7 слайд

  Пример 1. Составить функциональную схему, реализующую логическую формулу:
  Анализ:
  два входа;
  один выход;
  в функциональной схеме столько элементов, сколько операций в формуле – три операции: , , .
  F(x,y) = (x  y)  x = (x + y) · x
  х
  1
  y
  (x  y)  x
  &
  x
  x+y

• 

  8 слайд

  Задание: составить функциональную схему, реализующую логическую высказывание:

  «Я обязательно поеду на футбольный матч, если достану билет или меня пригласит товарищ и если не будет дождя».

• 

  9 слайд

  Пример 1. Условия работы будущей схемы заданы таблицей истинности:

• 

  10 слайд

  Синтез функциональной схемы одноразрядного двоичного сумматора на два входа
  0
  0
  +
  0
  0
  1
  +
  1
  1
  0
  +
  1
  1
  1
  +
  10
  X
  Y
  +
  PS
  В общем виде:
  Х, Y – входы:
  S – соответствует значению суммы в данном разряде;
  Р – перенос в старший разряд.
  Условия работы будущей схемы заключим в таблицу истинности:
  X
  Y
  +
  PS

• 

  11 слайд

  Логические формулы для функций P(x,y) и S(x,y) :
  P(x,y) = x · y
  S(x,y) = x · y + x · y
  х
  1
  y
  &
  &
  &
  P(x,y)
  S(x,y)
  Функциональная схема должна представлять собой устройство с двумя входами X, Y и двумя выходами P, S.
  Схематически:
  
  x
  y
  p
  s
  y
  x
  x · y
  y · x

• 

  12 слайд

  Сконструированный двоичный сумматор может быть использован лишь в разряде единиц – нет третьего входа для единицы переноса из младшего разряда.
  Для сложения в следующих разрядах нужны сумматоры на три входа.

• 

  13 слайд

  Двоичное сложение на многоразрядном сумматоре
  +
  Xn
  Xi
  X1X0
  . . .
  . . .
  Yn
  Yi
  Y1Y0
  . . .
  . . .
  Sn
  Si
  S1S0
  Sn+1
  . . .
  . . .
  Xi
  Yi
  Si
  Pi
  Pi -1
  +
  Обозначения:
  Xi – значение i-го разряда слагаемого Х;
  Yi – значение i-го разряда слагаемого Y;
  Pi – 1` – значение переноса из соседнего младшего разряда;
  Pi – значение переноса в соседний старший разряд;
  Si – значение разряда суммы;

• 

  14 слайд

  Логические функции Si, Pi от xi, yi, pi-1 задаются таблицей двоичного сложения:
  Si = x·y·p + x·y·p + x·y·p + x·y·p
  Pi = x·y·p + x·y·p + x·y·p + x·y·p

• 

  15 слайд

  Одноразрядный двоичный сумматор на три входа
  х
  1
  y
  &
  &
  &
  Pi
  Si
  &
  &
  1
  pi-1
  1
  Схематически:
  
  Xi
  Yi
  Pi
  Si
  Pi-1

• 

  16 слайд

  Последовательно соединяя несколько одноразрядных сумматоров на три входа (выход Pi одного со входом Pi-1 другого), можно составить многоразрядные двоичные сумматоры, осуществляющие двоичное сложение многоразрядных чисел.
  5
  x5
  y5
  p5
  s5
  2
  x2
  y2
  p2
  s2
  3
  x3
  y3
  p3
  s3
  4
  x4
  y4
  p4
  s4
  1
  x1
  y1
  p1
  s1
  s6
  Пятиразрядный двоичный сумматор

• 

  17 слайд

  5
  x5
  y5
  p5
  s5
  2
  x2
  y2
  p2
  s2
  3
  x3
  y3
  p3
  s3
  4
  x4
  y4
  p4
  s4
  1
  x1
  y1
  p1
  s1
  s6
  Пример. Сложим два двоичных числа х = 11110 и y = 11011 на пятиразрядном сумматоре
  5
  1
  1
  1
  2
  1
  1
  1
  0
  3
  1
  0
  1
  0
  4
  1
  1
  1
  1
  1
  0
  1
  0
  1
  1
  5
  x5
  y5
  p5
  s5
  2
  x2
  y2
  p2
  s2
  3
  x3
  y3
  p3
  s3
  4
  x4
  y4
  p4
  s4
  1
  0
  1
  0
  1
  s6
  5
  x5
  y5
  p5
  s5
  2
  1
  1
  1
  0
  3
  x3
  y3
  p3
  s3
  4
  x4
  y4
  p4
  s4
  1
  0
  1
  0
  1
  s6
  Сложение на многоразрядном сумматоре начинается с разряда единиц, т.е. на первый сумматор на вход х1 – сигнал 0, на вход у1 – сигнал 1. В результате преобразования этих сигналов функциональной схемой 1 на выходе s1 – появится сигнал 1 на выходе р1 – сигнал 0.
  Затем сложение производится на втором одноразрядном сумматоре на вход которого подаются сигналы: на вход х2 – сигнал 1, на вход у2 – сигнал 1, на р1 – сигнал 0. В результате преобразования этих сигналов функциональной схемой 2 на выходе s2 – появится сигнал 0 на выходе р2 – сигнал 1.
  И так далее.
  Но так как в нашем пятиразрядном сумматоре нет 6-го одноразрядного сумматора, то, чтобы не пропало значение переноса в шестой разряд (вырабатывается в пятом разряде), этот выход целесообразно сделать шестым разрядом суммы.

• 

  18 слайд

  Другие арифметические операции (*, /) выполняются с помощью функциональных схем, в основе которых лежит сумматор, реализующий сложение со сдвигом.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 258 129 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Основы туризма и гостеприимства»

• Курс повышения квалификации «Основы местного самоуправления и муниципальной службы»

• Курс повышения квалификации «Организация научно-исследовательской работы студентов в соответствии с требованиями ФГОС»

• Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»

• Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»

• Курс повышения квалификации «Этика делового общения»

• Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»

• Курс профессиональной переподготовки «Управление ресурсами информационных технологий»

• Курс повышения квалификации «Источники финансов»

• Курс повышения квалификации «Мировая экономика и международные экономические отношения»

• Курс профессиональной переподготовки «Организация маркетинговой деятельности»

• Курс профессиональной переподготовки «Стандартизация и метрология»

Раздел 5. Функциональные схемы

Раздел 5. Функциональные схемы Основные логические элементы функциональных схем Логические элементы — устройства, предназначенные для обработки информации в цифровой форме. Элемент “И” (AND) или “конъюнктор” Элемент “ИЛИ” (OR) или “дизъюнктор” Элемент “НЕ” (NOT) или “инвертор” Элемент “И-НЕ” (NAND) Элемент “ИЛИ-НЕ” (NOR) Для того, чтобы понять как работают данные логические элементы, нужно нарисовать таблицу, в которой будут перечислены состояния на выходе при любой комбинации входных сигналов. Такая таблица называется «таблица истинности». Таблицы истинности широко применяются в цифровой технике для описания работы логических схем. Сумматор и триггер     Арифметико-логическое устройство процессора (АЛУ) обязательно содержит в своем составе такие элементы как сумматоры. Эти схемы позволяют складывать двоичные числа. Как происходит сложение? Допустим, требуется сложить двоичные числа 1001 и 0011. Сначала складываем младшие разряды (последние цифры): 1+1=10. Т.е. в младшем разряде будет 0, а единица – это перенос в старший разряд. Далее: 0 + 1 + 1(от переноса) = 10, т.е. в данном разряде снова запишется 0, а единица уйдет в старший разряд. На третьем шаге: 0 + 0 + 1(от переноса) = 1. В итоге сумма равна 1100. Полусумматор     Теперь не будем обращать внимание на перенос из предыдущего разряда и рассмотрим только, как формируется сумма текущего разряда. Если были даны две единицы или два нуля, то сумма текущего разряда равна 0. Если одно из двух слагаемых равно единице, то сумма равна единице. Получить такие результаты можно при использовании вентиля ИСКЛЮЧАЮЩЕГО ИЛИ. Перенос единицы в следующий разряд происходит, если два слагаемых равны единице. И это реализуемо вентилем И. Тогда сложение в пределах одного разряда (без учета возможной пришедшей единицы из младшего разряда) можно реализовать изображенной ниже схемой, которая называется полусумматором. У полусумматора два входа (для слагаемых) и два выхода (для суммы и переноса). На схеме изображен полусумматор, состоящий из вентилей ИСКЛЮЧАЮЩЕЕ ИЛИ и И. Сумматор В отличие от полусумматора сумматор учитывает перенос из предыдущего разряда, поэтому имеет не два, а три входа. Чтобы учесть перенос приходится схему усложнять. По-сути она получается, состоящей из двух полусумматоров. Рассмотрим один из случаев. Требуется сложить 0 и 1, а также 1 из переноса. Сначала определяем сумму текущего разряда. Судя по левой схеме ИСКЛЮЧАЮЩЕЕ ИЛИ, куда входят a и b, на выходе получаем единицу. В следующее ИСКЛЮЧАЮЩЕЕ ИЛИ уже входят две единицы. Следовательно, сумма будет равна 0. Теперь смотрим, что происходит с переносом. В один вентиль И входят 0 и 1 (a и b). Получаем 0. Во второй вентиль (правее) заходят две единицы, что дает 1. Проход через вентиль ИЛИ нуля от первого И и единицы от второго И дает нам 1. Проверим работу схемы простым сложением 0 + 1 + 1 = 10. Т.е. 0 остается в текущем разряде, и единица переходит в старший. Следовательно, логическая схема работает верно. Работу данной схемы при всех возможных входных значениях можно описать следующей таблицей истинности. Примеры заданий на анализ и синтез функциональных схем     Для построения функциональных схем необходимо знать как обозначаются логические операции.     Анализом называется построение формулы алгебры логики (если необходимо – ее таблицы истинности) по заданной функциональной схеме.     Пример.     Записать формулу по данной функциональной схеме.     Внимательно смотрим на схему и смотрим сколько всего входных параметров, в данном случае их 2 – это X и Y, идем далее по схеме, X получает обратное значение НЕ(X), далее НЕ(Х) и Y образуют дизъюнкцию, формулу записываем следующим образом:      Синтезом функциональной схемы по заданной формуле называют построение структуры функциональной схемы, соответствующей заданной формуле алгебры логики.     Пример.     Построить функциональную схему по данной формуле.     Смотрим на формулу и выясняем сколько элементов содержится в формуле, в данном случае их также 2 – это X и Y, рисуем две точки на небольшом расстоянии друг от друга, одну подписываем X, другую – Y. Далее смотрим и замечаем, что нам нужно получить отрицание Y, соответственно от точки Y ведем небольшой отрезок и рисуем отрицание, т.е. прямоугольник с кружочком на выходе, X у нас без отрицания, поэтому просто строим после отрицания Y конъюкцию, т.е. прямоугольник с амперсандом внутри, и подводим к конъюкции отрезок из точки X. Список источников