Как составить функциональную зависимость

Нормализация. Функциональные зависимости атрибутов. Примеры. Построение схем функциональных зависимостей

Перед изучением данной темы рекомендуется ознакомиться с темой:

• Первая нормальная форма. Приведение таблицы к первой нормальной форме. Примеры

---

Содержание

• 1. Понятие функциональной зависимости. Определение. Примеры
• 2. Степени функциональной зависимости. Классификация
• 3. Частичная зависимость. Примеры
• 4. Полная функциональная зависимость. Примеры
• 5. Примеры транзитивной зависимости
• 6. Примеры многозначной зависимости
• 7. Задача. Построить схему функциональных зависимостей между атрибутами отношения
• 8. Задача. Построить схему функциональных зависимостей между атрибутами отношения
• 9. Понятие независимых атрибутов. Примеры
• Связанные темы

---

Поиск на других ресурсах:

1. Понятие функциональной зависимости. Определение. Примеры

После того, как таблица приведена к первой нормальной форме 1НФ, нужно определить функциональную зависимость между атрибутами (полями, столбцами) таблицы. Это необходимо для обеспечения максимально-возможной рациональности в построении таблиц базы данных.

Функциональная зависимость — это связь, которая может возникнуть между сущностями, хранящимися в базе данных. Если сущность A функционально определяет сущность B, то такую зависимость принято обозначать следующим образом:

A → B

здесь

• A – детерминант отношения;
• B – зависимая часть.

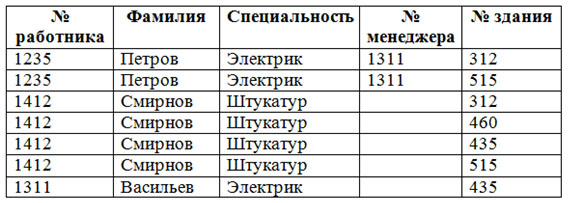
Пример 1. Пусть дано отношение, которое определяет должностные оклады работников некоторого предприятия.

В вышеприведенной таблице оклад работника определяется должностью, которую он занимает. Если работник переходит на другую должность, то меняется и его оклад. Итак, атрибут Должность функционально определяет атрибут Оклад. В символической форме такая зависимость обозначается следующим образом

Должность → Оклад

здесь Должность – детерминант, Оклад – зависимая часть.

Пример 2. Демонстрируется зависимость атрибута от составного (композитного) ключа. На рисунке 1 изображена таблица выпуска различных моделей автомобилей в разные годы.

Ключом отношения являются атрибуты Марка—Модель—Год выпуска. Атрибут «Количество выпущенных моделей» зависит от ключа.

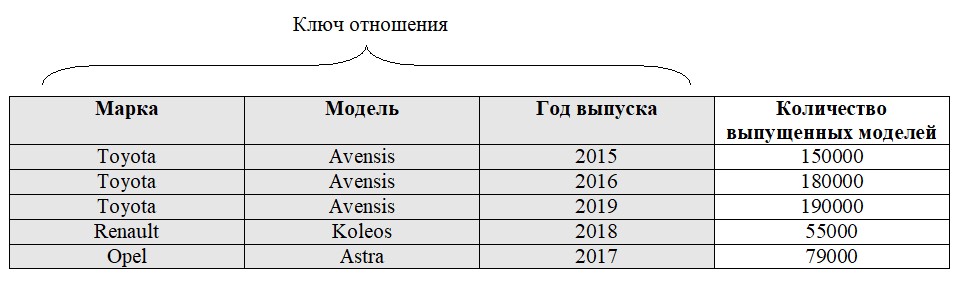
Рисунок 1. Функциональная зависимость атрибута «Количество выпущенных моделей» от ключа

  ⇑

2. Степени функциональной зависимости. Классификация

Различают следующие степени функциональной зависимости между атрибутами:

• частичная зависимость. Эта зависимость может возникать в случаях, когда таблица содержит составной ключ. Составной ключ — это ключ таблицы, который состоит из нескольких атрибутов. Если ключ состоит из одного атрибута, то этот ключ является простым. При частичной зависимости один атрибут таблицы является зависимым от части ключа, то есть от отдельного атрибута, входящего в ключ отношения;
• полная зависимость. Это случай, когда между атрибутами существует зависимость друг от друга;
• транзитивная зависимость. Это зависимость, когда два атрибута связаны между собой через третий атрибут. Этот третий атрибут выступает посредником;
• многозначная зависимость. Это случай, когда одному значению одного атрибута соответствует несколько значений другого атрибута.

  ⇑

3. Частичная зависимость. Примеры

Пример 1. Пусть дана следующая таблица.

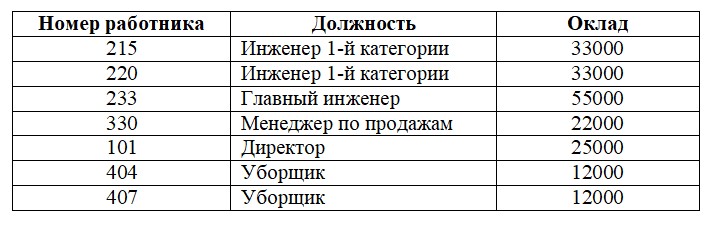
Пусть в таблице первичным ключом выбрано комбинацию атрибутов Номер работника — Должность. Этот ключ является составным. Между составным ключом Номер работника — Должность и атрибутом Оклад существует функциональная зависимость. Это объясняется тем, что оклад работника зависит от занимаемой должности. Символически такую зависимость можно обозначить так: Должность → Оклад.

Поскольку атрибут Оклад зависит только от части ключа (атрибута Должность) а не от всего ключа (Номер работника — Должность), то эта функциональная зависимость является частичной.

Вывод: отдельный атрибут Оклад зависит от определенной части составного ключа, которым является пара атрибутов Номер работника — Должность.

Рисунок 2 схематически отображает частичную зависимость.

Рисунок 2. Частичная зависимость атрибута Оклад от ключа отношения

Пример 2. Пусть дана таблица учета проведенных занятий в учебном заведении.

Для обеспечения уникальности, ключом отношения выбрано атрибуты «Номер аудитории» — «Номер занятия» — «Дата» — «Преподаватель«. Поскольку, за преподавателем закреплена конкретная дисциплина, то атрибут Дисциплина является зависимым от атрибута Преподаватель. Это значит, что атрибут Дисциплина зависим от части ключа отношения, так как атрибут Преподаватель является частью ключа отношения. На рисунке 3 показана эта зависимость.

Рисунок 3. Частичная зависимость атрибута Дисциплина от ключа отношения

  ⇑

4. Полная функциональная зависимость. Примеры

Полная функциональная зависимость между двумя атрибутами — это случай, когда между двумя атрибутами A и B является прямая (A→B) и обратная (B→A) зависимость. При полной функциональной зависимости одному значению атрибута A соответствует только одно значение атрибута B. И, наоборот, одному значению атрибута B соответствует значение атрибута A.
Полная функциональная зависимость между двумя атрибутами A и B обозначается A↔B.

Пример 1. Пусть дана база данных учета учебного процесса, таблица которой содержит атрибуты

• Год — учебный год;
• Курс — курс обучения, на котором учится некоторый студент (группа).

Фрагмент таблицы базы данных следующий

Между этими атрибутами существует полная зависимость. Это означает, что за учебным годом можно определить курс, на котором учится студент. И, наоборот, по курсу обучения можно определить учебный год (при условии, что студент успешно сдал все сессии и не имеет задолженности по дисциплине «Организация баз данных и знаний» 🙂.

На схеме зависимостей такая связь обозначается следующим образом

Рисунок 4. Полная зависимость между атрибутами Год и Курс

Пример 2. Связь между идентификационным номером и именем гражданина. По имени гражданина можно определить идентификационный номер. И, наоборот, по идентификационному номеру можно определить имя гражданина.

  ⇑

5. Примеры транзитивной зависимости

Пример 1. Задана база данных, содержащая информацию о ходе учебного процесса в учебном заведении. В отношении (таблице) используются атрибуты (поля), имеющие транзитивные зависимости.

Между атрибутами Преподаватель и Группа существует транзитивная зависимость (рисунок 5).

Рисунок 5. Транзитивная зависимость между атрибутами Преподаватель и Группа

Рассуждения. За каждым преподавателем закреплена дисциплина. То есть атрибут Дисциплина функционально зависим от атрибута Преподаватель. Согласно учебному плану, каждая группа имеет перечень дисциплин, которые она должна изучить. По дисциплине можно определить группу (или несколько групп), в которых эта дисциплина преподается. Например, дисциплины компьютерного цикла (Базы данных) будут изучать группы компьютерных специальностей. Поэтому, между дисциплиной и группой также существует функциональная зависимость.

Поскольку, за каждой дисциплиной закреплен конкретный преподаватель, то между атрибутами Преподаватель и Группа существует транзитивная зависимость (Преподаватель преподает дисциплину в группе).

Пример 2. Пусть задана таблица начислений стипендии для студентов некоторой группы. Студенты могут учиться на госзаказе (бюджет) или по контракту.

От студента зависит вид договора на обучение: бюджет или контракт. Поэтому возникает функциональная зависимость между атрибутами Студент и Вид договора (рисунок 6).

Рисунок 6. Функциональная зависимость между атрибутами Студент и Вид договора

Вид договора влияет на размер стипендии. Если студент учится по контракту, то стипендия не начисляется. По размеру стипендии нельзя определить вид договора, поскольку студент может учиться на бюджете и не получать стипендию в связи с плохой успеваемостью. Поэтому, между атрибутами Вид договора и Стипендия существует следующая функциональная зависимость (рисунок 7).

Рисунок 7. Функциональная зависимость между атрибутами Вид договора и Стипендия

Значит между атрибутами Студент и Стипендия существует транзитивная зависимость (рисунок 8).

Рисунок 8. Транзитивная зависимость между атрибутами Студент и Стипендия

  ⇑

6. Примеры многозначной зависимости

Пример 1. В учебном заведении преподаватель может преподавать не одну а несколько родственных дисциплин.

Между атрибутами Преподаватель и Дисциплина существует многозначная зависимость, потому что одному значению атрибута Преподаватель соответствует несколько значений атрибута Дисциплина. В данном примере принимается договоренность что одну дисциплину не может преподавать несколько преподавателей.

Пример 2. Задана таблица стоимости новых автомобилей.

Между атрибутами Марка и Модель существует многозначная зависимость. Это объясняется тем, что для одной марки (Renault) может существовать несколько значений моделей (Logan, Megane, Koleos).

  ⇑

7. Задача. Построить схему функциональных зависимостей между атрибутами отношения

Условие задачи. Задана таблица базы данных «Учет товаров в автомагазине», которая приведена к первой нормальной форме 1НФ. Таблица определяет товары, поступающие на склад и имеет следующую структуру

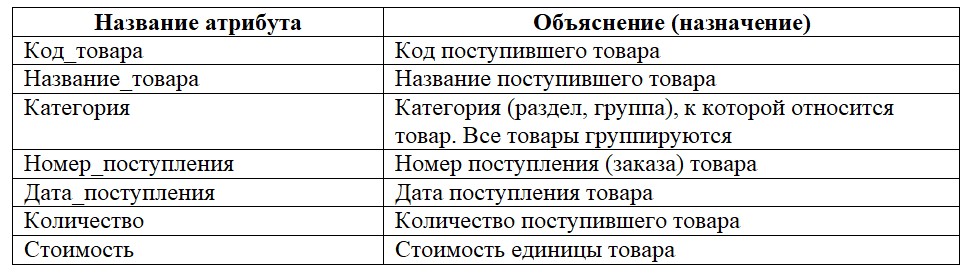
Нужно построить схему зависимостей между атрибутами.

Решение. Схема зависимостей между атрибутами таблицы учета поступивших товаров на складе изображена на рисунке 9.

Рисунок 9. Схема зависимостей между атрибутами

  ⇑

8. Задача. Построить схему функциональных зависимостей между атрибутами отношения

Задано таблицу базы данных магазина, которая отображает учет автозапчастей (товаров). Структура таблицы следующая

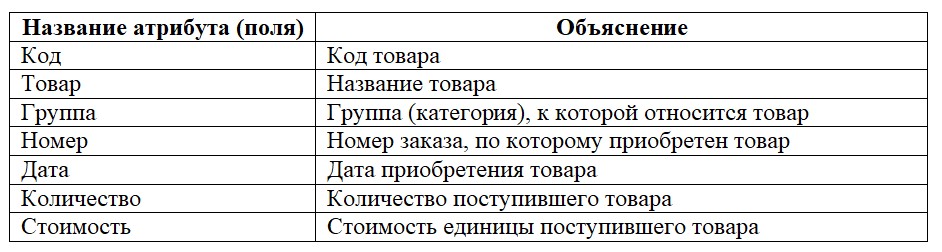
Атрибуты Код, Товар, Группа, Номер и Дата определяют ключ отношения. Поскольку товар с тем же кодом может быть получен несколько раз (в разные даты и в разные номера заказов), то выбор ключа с одним атрибутом Код нецелесообразен.

Последовательность рассуждений при построении схемы функциональных зависимостей следующая.
Товар поступает в магазин на основании заказа для которого фиксируется номер и дата. Каждый поступивший товар идентифицируется кодом и названием поступления. Значит, имеем зависимость атрибутов Код, Товар от атрибутов Номер, Дата.
Товары группируются в группы (категории). Например, для магазина автозапчастей такими категориями товаров могут быть Шины, Аккумуляторы, Трансмиссия и тому подобное. Следовательно, возникает функциональная зависимость Группа → Название.
Полученный товар поступает в определенном количестве и имеет стоимость. Значит, атрибуты Количество и Стоимость функционально зависимы от заказанного товара (пары атрибутов Код—Товар).
С учетом изложенных соображений, схема функциональных зависимостей изображена на рисунке 10.

Рисунок 10. Схема функциональных зависимостей. Учет автозапчастей в магазине

  ⇑

9. Понятие независимых атрибутов. Примеры

Между отдельными атрибутами базы данных могут отсутствовать какие-либо функциональные зависимости. Такие атрибуты называются независимыми друг от друга.

Пример. Задана таблица с данными о преподавателе.

В вышеприведенной таблице нет функциональной зависимости между следующими атрибутами:

• Стаж и Дисциплина. Обозначается как Стаж ¬= Дисциплина;
• Адрес — Дисципліна. Обозначается Адрес ¬= Дисциплина;
• Стаж — Адрес. Обозначается Стаж ¬= Адрес.

  ⇑

---

Связанные темы

• Нормализация. Понятие и необходимость применения. Аномалии модификации. Примеры
• Первая нормальная форма. Приведение таблицы к первой нормальной форме. Примеры

  ⇑

---

Функциональная зависимость, которая также известна как нетривиальная зависимость, возникает, когда A-> B выполняется, где B не является подмножеством A. В отношении, если атрибут B не является подмножеством атрибута A, то он рассматривается как нетривиальный зависимость.

Компания	Исполнительный директор	Возраст
Microsoft	Сатья Наделла	51
Google	Сундар Пичаи	46
яблоко	Тим Кук	57

Пример:

(Компания} -> {Генеральный директор} (если мы знаем Компанию, мы знаем имя генерального директора)

Но генеральный директор не является частью Компании, и, следовательно, это нетривиальная функциональная зависимость.

Транзитив – это тип функциональной зависимости, который возникает, когда t косвенно формируется двумя функциональными зависимостями.

Пример:

Компания	Исполнительный директор	Возраст
Microsoft	Сатья Наделла	51
Google	Сундар Пичаи	46
Алибаба	Джек Ма	54

{Company} -> {CEO} (если мы знаем компанию, мы знаем имя ее генерального директора)

{CEO} -> {Age} Если мы знаем генерального директора, мы знаем Age

Поэтому согласно правилу правила переходной зависимости:

{Company} -> {Age} должно иметь место, это имеет смысл, потому что, если мы знаем название компании, мы можем знать его возраст.

Примечание. Необходимо помнить, что транзитивная зависимость может иметь место только в отношении трех или более атрибутов.

Нормализация – это метод организации данных в базе данных, который помогает избежать аномалии избыточности, вставки, обновления и удаления данных. Это процесс анализа схем отношений на основе их различных функциональных зависимостей и первичного ключа.

Нормализация присуща теории реляционных баз данных. Это может привести к дублированию одних и тех же данных в базе данных, что может привести к созданию дополнительных таблиц.

Функциона́льная зави́симость — бинарное отношение между подмножествами атрибутов отношения в реляционной базе данных. Концепция функциональной зависимости лежит в основе многих вопросов, связанных с проектированием таких баз данных.

Определения[править | править код]

Функциональная зависимость[править | править код]

Пусть дано некоторое отношение со схемой (заголовком) , и  — некоторые подмножества множества атрибутов отношения . Множество функционально зависит от (обозначается ) тогда и только тогда, когда каждое значение множества связано в точности с одним значением множества .

Другими словами, если два кортежа совпадают по значениям в , то они совпадают и по значениям в .

В этом случае  называют детерминантом,  — зависимой частью.

Функциональная зависимость называется тривиальной, если зависимая часть является подмножеством детерминанта:

Замыкание множества зависимостей[править | править код]

Одни функциональные зависимости могут подразумевать другие функциональные зависимости. Например, функциональная зависимость,

.

Множество всех функциональных зависимостей, которые подразумеваются данным множеством функциональных зависимостей называется замыканием множества .

Замыкание множества атрибутов[править | править код]

Пусть  — некоторое множество атрибутов отношения , а  — множество функциональных зависимостей этого отношения. Замыканием множества атрибутов в пределах называется такое множество всех атрибутов отношения , что функциональная зависимость является членом замыкания .

Неприводимые множества зависимостей[править | править код]

Пусть и  — некоторые множества функциональных зависимостей.

Вычисление замыканий[править | править код]

Правила вывода Армстронга[править | править код]

В 1974 году Вильям Армстронг предложил набор правил вывода новых функциональных зависимостей на основе данных.

Пусть у нас есть отношение и множества атрибутов . Для сокращения записи вместо будем писать просто .

Правила вывода Армстронга полны (используя их, можно вывести все остальные функциональные зависимости, подразумеваемые данным множеством) и надежны («лишних» функциональных зависимостей вывести нельзя: выведенная функциональная зависимость справедлива везде, где справедливы исходные функциональные зависимости (из которых она была выведена)).

Кроме того, из данных правил довольно просто выводятся несколько дополнительных правил, упрощающих задачу вывода функциональных зависимостей.

Теорема: Функциональная зависимость выводима из данного множества функциональных зависимостей по правилам вывода Армстронга тогда и только тогда, когда .

Замыкание множества атрибутов[править | править код]

Если применять правила из предыдущего раздела до тех пор, пока создание новых функциональных зависимостей не прекратится само собой, то мы получим замыкание для заданного множества функциональных зависимостей. На практике редко требуется вычислять это замыкание само по себе, чаще всего нам гораздо интереснее узнать, будет ли та или иная функциональная зависимость входить в замыкание. Для этого нам достаточно вычислить замыкание детерминанта. Для этого существует довольно простой алгоритм.

1. Пусть  — множество атрибутов, которое в конечном счете станет замыканием.
2. Осуществляем поиск функциональных зависимостей вида , где , а . Зависимую часть каждой найденной зависимости добавляем в .
3. Повторяем пункт 2, пока ко множеству будет невозможно добавить атрибуты.
4. Множество , к которому невозможно добавить атрибуты и будет замыканием.

Применение[править | править код]

См. также[править | править код]

• Реляционная модель данных
• Проектирование баз данных
• Нормальная форма
• Многозначная зависимость — обобщение функциональной зависимости.

Литература[править | править код]

• К. Дж. Дейт. Введение в системы баз данных = Introduction to Database Systems. — 8-е изд. — М.: «Вильямс», 2006. — С. 1328. — ISBN 0-321-19784-4.

Функциональная зависимость

Реляционная БД содержит семантическую и структурную информацию. Структурой БД определяет число и вид включенных в нее отношений и связи типа «один-ко-многим», которые существуют между кортежами этих отношений. Семантической частью описывается множество функциональных зависимостей, которые существуют между атрибутами этих отношений.

Функциональную зависимость (ФЗ) обозначают $А to В$. Обратим внимание, что А и В могут быть не только единичными атрибутами, но и группами, которые составлены из нескольких атрибутов одного отношения.

Говорят, что функциональные зависимости являются связями типа «один-ко-многим», которые существуют внутри отношения.

С помощью функциональных зависимостей можно накладывать на реляционную схему дополнительные ограничения. Основной идеей является то, что значением одного атрибута в кортеже однозначно определяется значение другого атрибута.

К примеру, в каждом кортеже на рисунке 1 Фамилия однозначно определяется № работника; Специальность однозначно определяется № работника. Данные функциональные зависимости записывают в виде:

ФЗ: № работника $to$ фамилия,
ФЗ: № работника $to$ специальность.

«Функциональные зависимости» 👇

Другими словами функциональная зависимость определяется следующим образом:

Знак $to$ читают «функционально определяет».

Данное определение можно применить также в случае, когда А и В являются множеством столбцов, а не просто отдельными столбцами.

Детерминантом всегда является ключ таблицы, т.к. его значением однозначно определяется значение каждого атрибута таблицы.

Типы функциональных зависимостей

Не все функциональные зависимости являются желательными.

Схема базы данных без избыточных функциональных зависимостей считается корректной. В обратном случае необходимо прибегнуть к процедуре разложения (декомпозиции) существующего множества отношений. При этом множество, которое создается, будет содержать большее количество отношений, являющиеся проекциями отношений исходного множества.

Существует еще несколько видов функциональной зависимости.

Транзитивная функциональная зависимость. Пусть А, В, С – атрибуты какого-либо отношения. При этом $А to В$ и $В to С$ и отсутствует обратное соответствие, то есть $С not to В$ и $В not to А$. В таком случае С транзитивно зависит от А.

Многозначная зависимость. Пусть А, В, С – атрибуты некоторого отношения R. В данном отношении R существует многозначная зависимость $R.А to R.В$ лишь в том случае, когда множество значений В, которое соответствует паре значений А и С, зависит только от А и не зависит от С.

Функциональные зависимости.

Функциональные
зависимости описывают ограничения,
которые связаны не с конкретными
значениями атрибута, а с тем, совпадают
ли определенные компоненты кортежей.

Пусть

– схема отношения, а

– подмножества

(множество атрибутов). Говорят, что X
функционально определяет Y
(Y функционально зависит от
X), и обозначается

,
если в любом отношении R не существует
2-х кортежей, компоненты которых совпадают
по всем атрибутам, принадлежащим

,
но не совпадают по одному или более
атрибутам, принадлежащим Y.

Функциональные
зависимости возникают различными
способами:

1. Если, например,

   является ключом, то

   
   .

2. 

   –

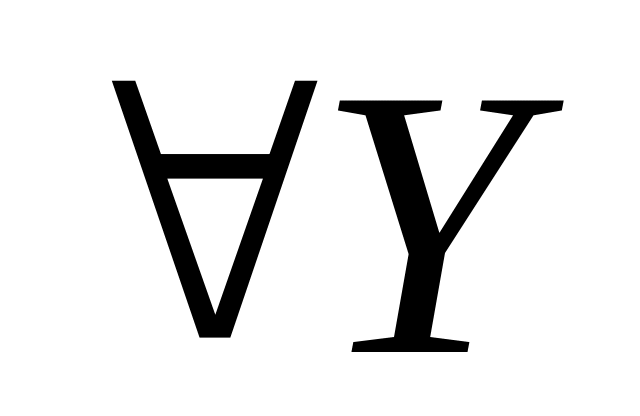
   есть отображение
   

   набора объектов
   

   к набору
   
   .
   Среди

   есть атрибуты, образующие ключ

   для

   ,
   и ключ
   

   для

   ,
   то справедливо

   .

3. и
   

   для
   
   .

Если
заданы функциональные зависимости, то
СУБД будет:

а) поддерживать
ограничения целостности;

б) более эффективно будет реализовываться
отношение, однако при этом будет
невозможно хранение некоторой информации.
Например, Имя

Телефон; то не может быть 2-х телефонов
для одного человека.

В связи с введением
функциональной зависимости можно дать
другое определение ключа:

Если

– схема отношения с атрибутами

и множество функциональных зависимостей

,
а

подмножество

,
то X называется ключом отношения
R, если

1. 
   ,
   где
   

   – замыкание множества функциональных
   зависимостей;

2. Ни для какого
   собственного подмножества
   
   .
   F⁺ – все функциональные
   зависимости, которые могут быть получены
   для данного отношения с использованием
   правил вывода.

Правила
вывода называются аксиомами
функциональной зависимости; пусть
задана схема отношения

с полным множеством атрибутов

и множеством функциональных зависимостей

,
связывающем только атрибуты из

.

1˚. аксиома рефлексивности:

Это правило дает тривиальные зависимости,
т.е. зависимости, правая часть которых
содержится в левой части. Его использование
не зависит от

.

2˚. аксиома пополнения:

3˚. аксиома транзитивности:

Пример: R(индекс,
город, адрес)

F
:
индекс → город

город, адрес →
индекс

F
⁺:
индекс, адрес → город, адрес

город, адрес →
индекс, город, адрес

индекс, адрес
→ индекс, город, адрес

Рассмотренные
аксиомы являются надежными, т.е. приводят
к истинным заключениям. Другие правила
вывода, которые являются следствием из
1˚-3˚:

4˚. правило объединения:

5˚. правило декомпозиции:

(вытекает
из 1˚, 3˚).

6˚. правило
псевдотранзитивности:

Правило
объединения и декомпозиции порождают
важное следствие:

Если

– атрибуты, то зависимость

справедлива т. и т.т., когда

.

Не
существует алгоритма для нахождения
множества функциональной зависимости.

Покрытие множества зависимостей.

Пусть

и

– множества функциональных зависимостей.
Будем считать, что

и

эквивалентны, если

.
В этом случае говорят, что

покрывает

и, наоборот,

покрывает

.

Лемма: Каждое
множество функциональных зависимостей
F покрывается некоторым множеством
функциональных зависимостей

,
в которых ни одна из правых частей не
состоит более чем из одного атрибута.

Теорема: Каждое
множество функциональных зависимостей
F эквивалентно некоторому минимальному
множеству

.

Говорят, что множество
функциональных зависимостей F
минимально, если:

1. правая часть каждой
   зависимости в F состоит только из
   одного атрибута;

2. ни для какой
   зависимости
   

   в F множество
   

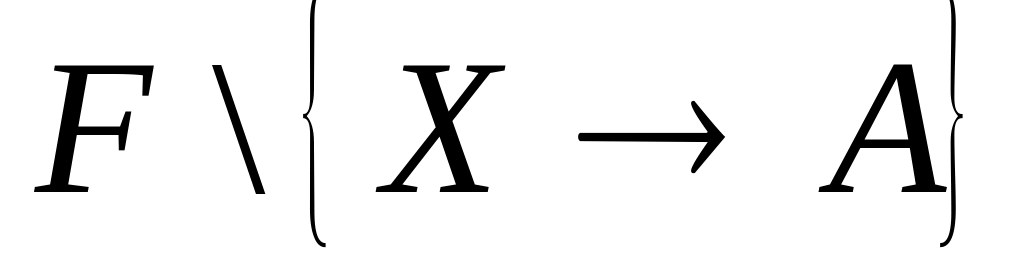
   не эквивалентно F;

3. ни для какой
   функциональной зависимости

   в F и собственного подмножества
   
   ,
   множества
   

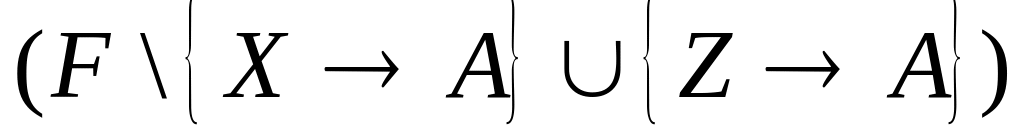
   и F не эквивалентны.

В общем
случае для множества функциональных
зависимостей можем построить минимальное.

Замыкание
множества атрибутов относительно
множества функциональных зависимостей.
Пусть F – множество функциональных
зависимостей на множестве

,
и пусть

,
тогда

(замыкание X относительно F) есть
множество атрибутов А таких, что
зависимость

может быть выведена из F по аксиомам
1˚-3˚.

Лемма1: Функциональная
зависимость

следует из аксиом вывода, если

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #