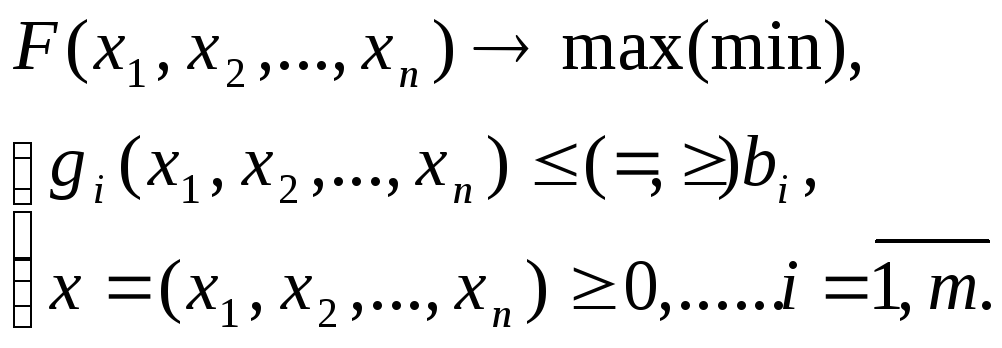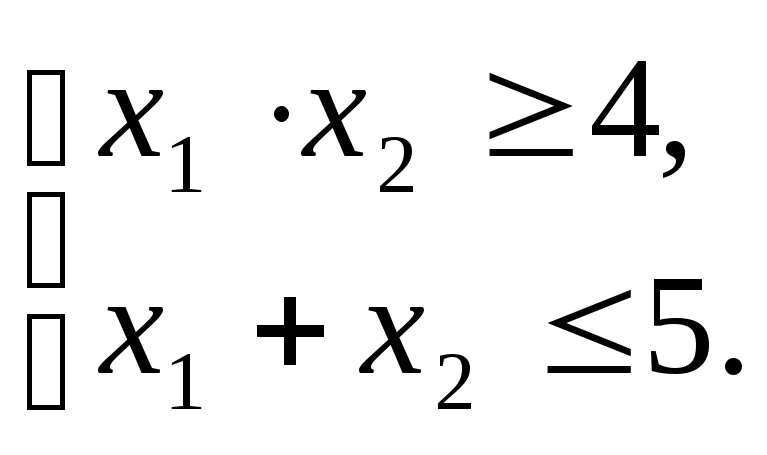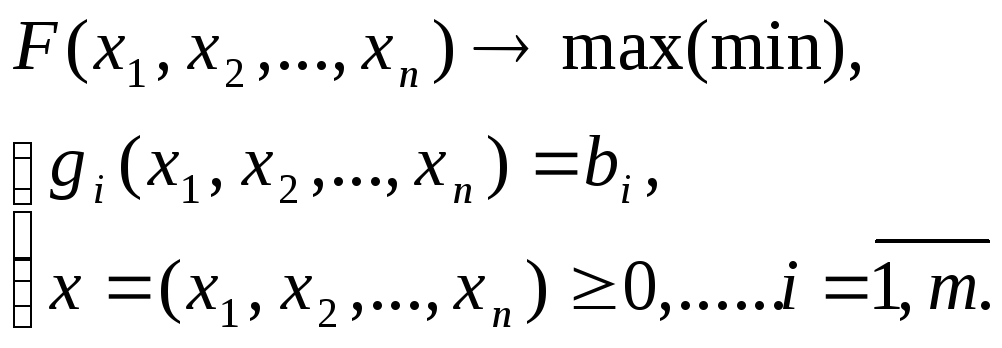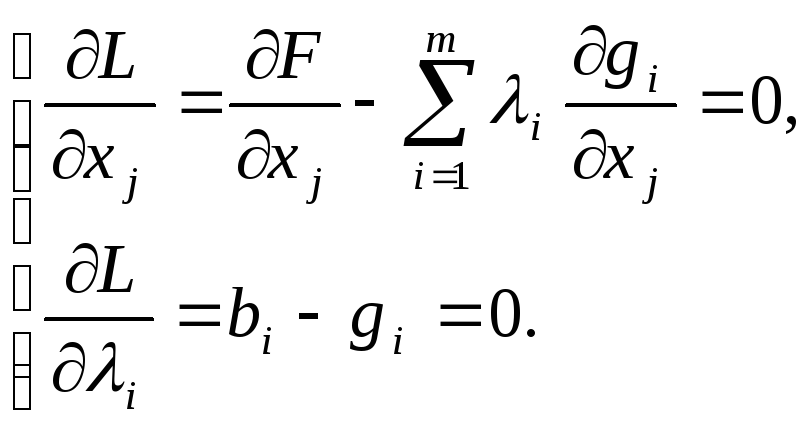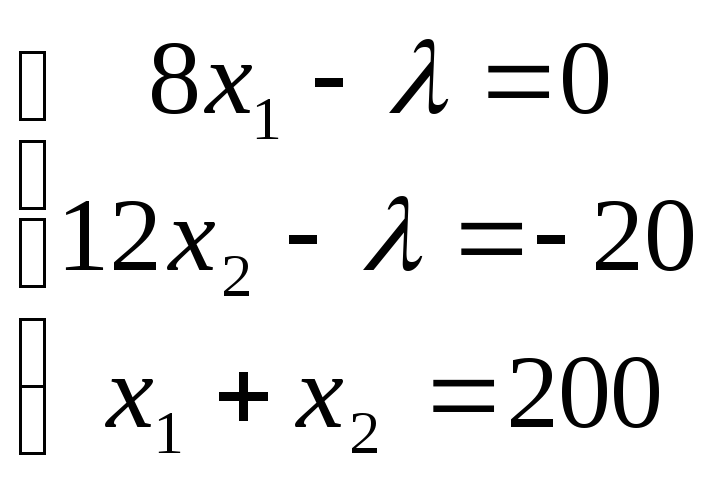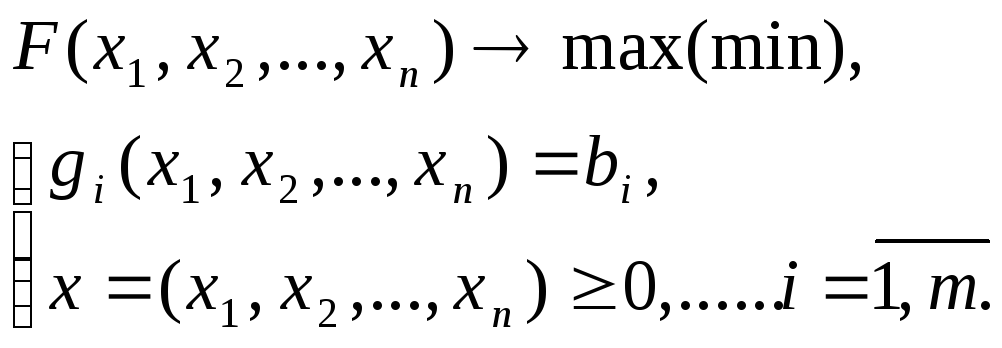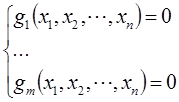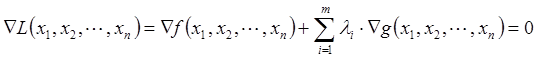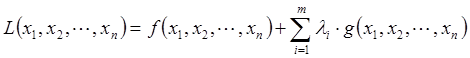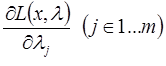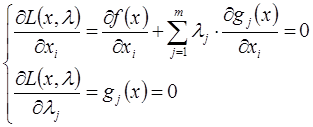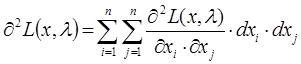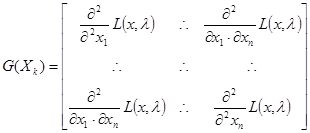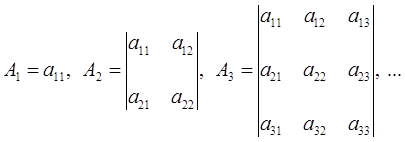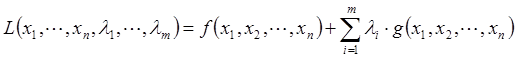Как составить функцию лагранжа

Условный экстремум. Метод множителей Лагранжа. Первая часть.

Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $varphi (x,y)=0$.

Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие $varphi(x,y)=0$. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует $y=psi(x)$, то подставив $y=psi(x)$ в $z=f(x,y)$, получим функцию одной переменной $z=fleft(x,psi(x)right)$. В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.

Метод множителей Лагранжа для функций двух переменных.

Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+lambdavarphi(x,y)$ (параметр $lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:

$$
left { begin{aligned}
& frac{partial F}{partial x}=0;\
& frac{partial F}{partial y}=0;\
& varphi (x,y)=0.
end{aligned} right.
$$

Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F < 0$, то условный максимум.

Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: $varphi_{x}^{‘}dx+varphi_{y}^{‘}dy=0$, $dy=-frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dx$, поэтому в любой стационарной точке имеем:

$$d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=F_{xx}^{”}dx^2+2F_{xy}^{”}dxleft( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)+F_{yy}^{”}left( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)^2=\
=-frac{dx^2}{left(varphi_{y}^{‘} right)^2}cdotleft( -(varphi_{y}^{‘})^2 F_{xx}^{”}+2varphi_{x}^{‘}varphi_{y}^{‘}F_{xy}^{”}-(varphi_{x}^{‘})^2 F_{yy}^{”} right)$$

Второй сомножитель (расположенный в скобке) можно представить в такой форме:

$$
H=left| begin{array} {ccc}
0 & varphi_{x}^{‘} & varphi_{y}^{‘}\
varphi_{x}^{‘} & normred{F_{xx}^{”}} & normred{F_{xy}^{”}} \
varphi_{y}^{‘} & normred{F_{xy}^{”}} & normred{F_{yy}^{”}} end{array} right|
$$

Красным цветом выделены элементы определителя $left| begin{array} {cc} F_{xx}^{”} & F_{xy}^{”} \ F_{xy}^{”} & F_{yy}^{”} end{array} right|$, который является гессианом функции Лагранжа. Если $H > 0$, то $d^2F < 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F > 0$, т.е. имеем условный минимум функции $z=f(x,y)$.

Примечание относительно формы записи определителя $H$. показатьскрыть

Алгоритм исследования функции двух переменных на условный экстремум

1. Составить функцию Лагранжа $F(x,y)=f(x,y)+lambdavarphi(x,y)$
2. Решить систему $
   left { begin{aligned}
   & frac{partial F}{partial x}=0;\
   & frac{partial F}{partial y}=0;\
   & varphi (x,y)=0.
   end{aligned} right.$
3. Определить характер экстремума в каждой из найденных в предыдущем пункте стационарных точек. Для этого применить любой из указанных способов:
   • Составить определитель $H$ и выяснить его знак
   • С учетом уравнения связи вычислить знак $d^2F$

Метод множителей Лагранжа для функций n переменных

Допустим, мы имеем функцию $n$ переменных $z=f(x_1,x_2,ldots,x_n)$ и $m$ уравнений связи ($n > m$):

$$varphi_1(x_1,x_2,ldots,x_n)=0; ; varphi_2(x_1,x_2,ldots,x_n)=0,ldots,varphi_m(x_1,x_2,ldots,x_n)=0.$$

Обозначив множители Лагранжа как $lambda_1,lambda_2,ldots,lambda_m$, составим функцию Лагранжа:

$$F(x_1,x_2,ldots,x_n,lambda_1,lambda_2,ldots,lambda_m)=f+lambda_1varphi_1+lambda_2varphi_2+ldots+lambda_mvarphi_m$$

Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:

$$left{begin{aligned}
& frac{partial F}{partial x_i}=0; (i=overline{1,n})\
& varphi_j=0; (j=overline{1,m})
end{aligned} right.$$

Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F < 0$, – то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:

Определитель матрицы

$$left| begin{array} {ccccc} frac{partial^2F}{partial x_{1}^{2}} & frac{partial^2F}{partial x_{1}partial x_{2}} & frac{partial^2F}{partial x_{1}partial x_{3}} &ldots & frac{partial^2F}{partial x_{1}partial x_{n}}\
frac{partial^2F}{partial x_{2}partial x_1} & frac{partial^2F}{partial x_{2}^{2}} & frac{partial^2F}{partial x_{2}partial x_{3}} &ldots & frac{partial^2F}{partial x_{2}partial x_{n}}\
frac{partial^2F}{partial x_{3} partial x_{1}} & frac{partial^2F}{partial x_{3}partial x_{2}} & frac{partial^2F}{partial x_{3}^{2}} &ldots & frac{partial^2F}{partial x_{3}partial x_{n}}\
ldots & ldots & ldots &ldots & ldots\
frac{partial^2F}{partial x_{n}partial x_{1}} & frac{partial^2F}{partial x_{n}partial x_{2}} & frac{partial^2F}{partial x_{n}partial x_{3}} &ldots & frac{partial^2F}{partial x_{n}^{2}}\
end{array} right|,$$

выделенной в матрице $L$ красным цветом, есть гессиан функции Лагранжа. Используем следующее правило:

• Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ матрицы $L$ совпадают с знаком $(-1)^m$, то исследуемая стационарная точка является точкой условного минимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.
• Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ чередуются, причём знак минора $H_{2m+1}$ совпадает с знаком числа $(-1)^{m+1}$, то исследуемая стационарная точка является точкой условного максимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.

Пример №1

Найти условный экстремум функции $z(x,y)=x+3y$ при условии $x^2+y^2=10$.

Решение

Геометрическая интерпретация данной задачи такова: требуется найти наибольшее и наименьшее значение аппликаты плоскости $z=x+3y$ для точек ее пересечения с цилиндром $x^2+y^2=10$.

Выразить одну переменную через другую из уравнения связи и подставить ее в функцию $z(x,y)=x+3y$ несколько затруднительно, поэтому будем использовать метод Лагранжа.

Обозначив $varphi(x,y)=x^2+y^2-10$, составим функцию Лагранжа:

$$
F(x,y)=z(x,y)+lambda varphi(x,y)=x+3y+lambda(x^2+y^2-10);\
frac{partial F}{partial x}=1+2lambda x; frac{partial F}{partial y}=3+2lambda y.
$$

Запишем систему уравнений для определения стационарных точек функции Лагранжа:

$$
left { begin{aligned}
& 1+2lambda x=0;\
& 3+2lambda y=0;\
& x^2+y^2-10=0.
end{aligned} right.
$$

Если предположить $lambda=0$, то первое уравнение станет таким: $1=0$. Полученное противоречие говорит о том, что $lambdaneq 0$. При условии $lambdaneq 0$ из первого и второго уравнений имеем: $x=-frac{1}{2lambda}$, $y=-frac{3}{2lambda}$. Подставляя полученные значения в третье уравнение, получим:

$$

left( -frac{1}{2lambda} right)^2+left( -frac{3}{2lambda} right)^2-10=0;\
frac{1}{4lambda^2}+frac{9}{4lambda^2}=10; lambda^2=frac{1}{4}; left[ begin{aligned} & lambda_1=-frac{1}{2};\ & lambda_2=frac{1}{2}. end{aligned} right.\
begin{aligned}
& lambda_1=-frac{1}{2}; ; x_1=-frac{1}{2lambda_1}=1; ; y_1=-frac{3}{2lambda_1}=3;\
& lambda_2=frac{1}{2}; ; x_2=-frac{1}{2lambda_2}=-1; ; y_2=-frac{3}{2lambda_2}=-3.end{aligned}
$$

Итак, система имеет два решения: $x_1=1;; y_1=3;; lambda_1=-frac{1}{2}$ и $x_2=-1;; y_2=-3;; lambda_2=frac{1}{2}$. Выясним характер экстремума в каждой стационарной точке: $M_1(1;3)$ и $M_2(-1;-3)$. Для этого вычислим определитель $H$ в каждой из точек.

$$
varphi_{x}^{‘}=2x;; varphi_{y}^{‘}=2y;; F_{xx}^{”}=2lambda;; F_{xy}^{”}=0;; F_{yy}^{”}=2lambda.\

H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{”} & F_{xy}^{”} \ varphi_{y}^{‘} & F_{xy}^{”} & F_{yy}^{”} end{array} right|=
left| begin{array} {ccc} 0 & 2x & 2y\ 2x & 2lambda & 0 \ 2y & 0 & 2lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|
$$

В точке $M_1(1;3)$ получим:

$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & 1 & 3\ 1 & -1/2 & 0 \ 3 & 0 & -1/2 end{array} right|=40 > 0.$$

Следовательно, в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_{max}=z(1;3)=10$.

Аналогично, в точке $M_2(-1;-3)$ найдем:

$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & -1 & -3\ -1 & 1/2 & 0 \ -3 & 0 & 1/2 end{array} right|=-40$$

Так как $H < 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{min}=z(-1;-3)=-10$.

Отмечу, что вместо вычисления значения определителя $H$ в каждой точке, гораздо удобнее раскрыть его в общем виде. Дабы не загромождать текст подробностями, этот способ скрою под примечание.

Запись определителя $H$ в общем виде. показатьскрыть

Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:

$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=2lambda left( dx^2+dy^2right)
$$

Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $left( dx right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $lambda_1=-frac{1}{2}$ получим $d^2F < 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.

Ответ: в точке $(-1;-3)$ функция имеет условный минимум, $z_{min}=-10$. В точке $(1;3)$ функция имеет условный максимум, $z_{max}=10$.

Пример №2

Найти условный экстремум функции $z(x,y)=3y^3+4x^2-xy$ при условии $x+y=0$.

Решение

Первый способ (метод множителей Лагранжа)

Обозначив $varphi(x,y)=x+y$ составим функцию Лагранжа:

$$F(x,y)=z(x,y)+lambda varphi(x,y)=3y^3+4x^2-xy+lambda(x+y).$$

$$
frac{partial F}{partial x}=8x-y+lambda; ; frac{partial F}{partial y}=9y^2-x+lambda.\

left { begin{aligned} & 8x-y+lambda=0;\ & 9y^2-x+lambda=0; \ & x+y=0. end{aligned} right.

$$

Решив систему, получим: $x_1=0$, $y_1=0$, $lambda_1=0$ и $x_2=frac{10}{9}$, $y_2=-frac{10}{9}$, $lambda_2=-10$. Имеем две стационарные точки: $M_1(0;0)$ и $M_2 left(frac{10}{9};-frac{10}{9} right)$. Выясним характер экстремума в каждой стационарной точке с использованием определителя $H$.

$$
H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{”} & F_{xy}^{”} \ varphi_{y}^{‘} & F_{xy}^{”} & F_{yy}^{”} end{array} right|=
left| begin{array} {ccc} 0 & 1 & 1\ 1 & 8 & -1 \ 1 & -1 & 18y end{array} right|=-10-18y
$$

В точке $M_1(0;0)$ $H=-10-18cdot 0=-10 < 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{min}=0$. В точке $M_2left(frac{10}{9};-frac{10}{9}right)$ $H=10 > 0$, посему в данной точке функция имеет условный максимум, $z_{max}=frac{500}{243}$.

Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:

$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=8dx^2-2dxdy+18ydy^2
$$

Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.

$$
d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2
$$

Так как $ d^2F Bigr|_{M_1}=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F Bigr|_{M_2}=-10 dx^2 < 0$, т.е. $M_2left(frac{10}{9}; -frac{10}{9} right)$ – точка условного максимума.

Второй способ

Из уравнения связи $x+y=0$ получим: $y=-x$. Подставив $y=-x$ в функцию $z(x,y)=3y^3+4x^2-xy$, получим некоторую функцию переменной $x$. Обозначим эту функцию как $u(x)$:

$$
u(x)=z(x,-x)=3cdot(-x)^3+4x^2-xcdot(-x)=-3x^3+5x^2.
$$

Таким образом задачу о нахождении условного экстремума функции двух переменных мы свели к задаче определения экстремума функции одной переменной.

$$
u_{x}^{‘}=-9x^2+10x;\
-9x^2+10x=0; ; xcdot(-9x+10)=0;\
x_1=0; ; y_1=-x_1=0;\
x_2=frac{10}{9}; ; y_2=-x_2=-frac{10}{9}.
$$

Получили точки $M_1(0;0)$ и $M_2left(frac{10}{9}; -frac{10}{9}right)$. Дальнейшее исследование известно из курса дифференциального исчисления функций одной переменой. Исследуя знак $u_{xx}^{”}$ в каждой стационарной точке или проверяя смену знака $u_{x}^{‘}$ в найденных точках, получим те же выводы, что и при решении первым способом. Например, проверим знак $u_{xx}^{”}$:

$$u_{xx}^{”}=-18x+10;\
u_{xx}^{”}(M_1)=10;;u_{xx}^{”}(M_2)=-10.$$

Так как $u_{xx}^{”}(M_1)>0$, то $M_1$ – точка минимума функции $u(x)$, при этом $u_{min}=u(0)=0$. Так как $u_{xx}^{”}(M_2)<0$, то $M_2$ – точка максимума функции $u(x)$, причём $u_{max}=uleft(frac{10}{9}right)=frac{500}{243}$.

Значения функции $u(x)$ при заданном условии связи совпадают с значениями функции $z(x,y)$, т.е. найденные экстремумы функции $u(x)$ и есть искомые условные экстремумы функции $z(x,y)$.

Ответ: в точке $(0;0)$ функция имеет условный минимум, $z_{min}=0$. В точке $left(frac{10}{9}; -frac{10}{9} right)$ функция имеет условный максимум, $z_{max}=frac{500}{243}$.

Рассмотрим еще один пример, в котором характер экстремума выясним посредством определения знака $d^2F$.

Пример №3

Найти наибольшее и наименьшее значения функции $z=5xy-4$, если переменные $x$ и $y$ положительны и удовлетворяют уравнению связи $frac{x^2}{8}+frac{y^2}{2}-1=0$.

Решение

Составим функцию Лагранжа: $F=5xy-4+lambda left( frac{x^2}{8}+frac{y^2}{2}-1 right)$. Найдем стационарные точки функции Лагранжа:

$$
F_{x}^{‘}=5y+frac{lambda x}{4}; ; F_{y}^{‘}=5x+lambda y.\

left { begin{aligned}
& 5y+frac{lambda x}{4}=0;\
& 5x+lambda y=0;\
& frac{x^2}{8}+frac{y^2}{2}-1=0;\
& x > 0; ; y > 0.
end{aligned} right.
$$

Все дальнейшие преобразования осуществляются с учетом $x > 0; ; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $lambda=-frac{5x}{y}$ и подставим найденное значение в первое уравнение: $5y-frac{5x}{y}cdot frac{x}{4}=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $frac{4y^2}{8}+frac{y^2}{2}-1=0$, $y^2=1$, $y=1$.

Так как $y=1$, то $x=2$, $lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.

$$
F_{xx}^{”}=frac{lambda}{4}; ; F_{xy}^{”}=5; ; F_{yy}^{”}=lambda.
$$

Так как $frac{x^2}{8}+frac{y^2}{2}-1=0$, то:

$$
dleft( frac{x^2}{8}+frac{y^2}{2}-1right)=0; ; dleft( frac{x^2}{8} right)+dleft( frac{y^2}{2} right)=0; ; frac{x}{4}dx+ydy=0; ; dy=-frac{xdx}{4y}.
$$

В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $lambda=-10$, получив при этом:

$$
F_{xx}^{”}=frac{-5}{2}; ; F_{xy}^{”}=-10; ; dy=-frac{dx}{2}.\

d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=-frac{5}{2}dx^2+10dxcdot left(-frac{dx}{2} right)-10cdot left(-frac{dx}{2} right)^2=\
=-frac{5}{2}dx^2-5dx^2-frac{5}{2}dx^2=-10dx^2.

$$

Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:

$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=frac{lambda}{4}dx^2+10cdot dxcdot frac{-xdx}{4y} +lambdacdot left(-frac{xdx}{4y} right)^2=\
=frac{lambda}{4}dx^2-frac{5x}{2y}dx^2+lambda cdot frac{x^2dx^2}{16y^2}=left( frac{lambda}{4}-frac{5x}{2y}+frac{lambda cdot x^2}{16y^2} right)cdot dx^2
$$

Подставляя $x=2$, $y=1$, $lambda=-10$, получим:

$$
d^2 F=left( frac{-10}{4}-frac{10}{2}-frac{10 cdot 4}{16} right)cdot dx^2=-10dx^2.
$$

Так как $d^2F=-10cdot dx^2 < 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{max}=10-4=6$.

Ответ: в точке $(2;1)$ функция имеет условный максимум, $z_{max}=6$.

В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.

Функция Лагранжа и метод множителей Лагранжа

Краткая теория

---

Метод множителей Лагранжа является классическим методом
решения задач математического программирования (в частности выпуклого). К
сожалению, при практическом применении метода могут встретиться значительные
вычислительные трудности, сужающие область его использования. Мы рассматриваем
здесь метод Лагранжа главным образом потому, что он является аппаратом, активно
используемым для обоснования различных современных численных методов, широко
применяемых на практике. Что же касается функции Лагранжа и множителей
Лагранжа, то они играют самостоятельную и исключительно важную роль в теории и
приложениях не только математического программирования.

Рассмотрим классическую задачу оптимизации:

Среди ограничений этой задачи нет
неравенств, нет условий неотрицательности переменных,
их дискретности,

 и функции

 и

 непрерывны и имеют частные производные
по крайней мере второго порядка.

Классический подход к решению задачи дает систему уравнений
(необходимые условия), которым должна удовлетворять точка

,
доставляющая функции

 локальный экстремум на множестве точек, удовлетворяющих
ограничениям (для задачи выпуклого программирования найденная точка

 будет одновременно и точкой глобального
экстремума).

Предположим, что в точке

 функция (1) имеет локальный условный экстремум
и ранг матрицы

 равен

.
Тогда необходимые условия запишутся в виде:

где

есть функция Лагранжа;

 –
множители Лагранжа.

Существуют также и достаточные условия, при выполнении
которых решение системы уравнений (3) определяет точку экстремума функции

.
Этот вопрос решается на основании исследования знака второго дифференциала
функции Лагранжа. Однако достаточные условия представляют главным образом
теоретический интерес.

Можно указать следующий порядок решения задачи (1), (2)
методом множителей Лагранжа:

1) составить функцию Лагранжа (4);

2) найти частные производные функции Лагранжа по всем
переменным

 и приравнять их

нулю. Тем самым будет получена система (3,
состоящая из

 уравнений. Решить полученную
систему (если это окажется возможным!) и найти таким
образом все стационарные точки функции Лагранжа;

3) из стационарных точек, взятых без координат

 выбрать точки, в которых функция

 имеет условные локальные экстремумы при
наличии ограничений (2). Этот выбор осуществляется, например, с применением
достаточных условий локального экстремума. Часто исследование упрощается, если использовать конкретные условия задачи.

Пример решения задачи

---

Задача

Фирма
реализует автомобили двумя способами: через магазин и через торговых агентов.
При реализации

 автомобилей через магазин расходы на
реализацию составляют

 у.е., а при продаже

 автомобилей через торговых агентов расходы
составляют

 у.е. Найти оптимальный способ реализации
автомобилей, минимизирующий суммарные расходы, если общее число предназначенных
для продажи автомобилей составляет 200 штук.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Составим
математическую модель задачи.

Пусть

 и

 – число автомобилей, реализуемых первым и
вторым способом.

Целевая
функция

(суммарные
издержки минимизируются).

Ограничения
задачи:

Математическая
модель задачи имеет вид:

Для
решения задачи применим метод множителей Лагранжа.

Функция
Лагранжа имеет вид:

Найдем
частные производные по

 и

 и приравняем их к нулю. Получим следующую
систему уравнений:

Решая
систему, найдем:

Составим
определитель из частных производных 2-го порядка для функции

 по

 и

:

Следовательно,
в силу достаточного условия существования условного экстремума, функция

 в точке

 имеет экстремум.

Так как

, то в полученной точке
функция

 имеет условный минимум.

Итак,
оптимальное решение:

Экстремальное значение целевой функции:

Ответ: Нужно продать 99 автомобилей через магазин и 101
автомобиль через торговых агентов, при этом расходы минимизируются и составляют
20398 у.е.

Метод множителей Лагранжа, применяемый для решения задач математического программирования (в частности, линейного программирования) — метод нахождения условного экстремума функции , где , относительно ограничений , где меняется от единицы до .

Описание метода[править | править код]

где .

Обоснование[править | править код]

Нижеприведенное обоснование метода множителей Лагранжа не является его строгим доказательством. Оно содержит эвристические рассуждения, помогающие понять геометрический смысл метода.

Двумерный случай[править | править код]

Пусть требуется найти экстремум функции при условии, заданном уравнением .

Будем считать, что

1) функция непрерывно дифференцируема,

2) функция непрерывно дифференцируема, с частными производными, не равными нулю одновременно, то есть уравнение задаёт гладкую кривую из обыкновенных точек на плоскости .

3) кривая не проходит через точки, в которых градиент обращается в .

Нарисуем на плоскости линии уровня функции (то есть кривые ). Из геометрических соображений следует, что точкой (возможно — точками) условного экстремума функции может быть только точка касания кривой и некоторой линии уровня, то есть точкой, в которой касательная к и касательная к этой линии уровня — совпадают. Действительно, если в некоторой точке кривая пересекает линию уровня трансверсально (то есть под некоторым ненулевым углом), то при движении по кривой из точки можно попасть как на линии уровня, соответствующие значению, большему , так и на линии уровня, соответствующие значению, меньшему . Следовательно, такая точка не может быть точкой экстремума.

Тем самым, необходимым условием экстремума в рассматриваемом случае будет совпадение касательных. Чтобы записать его в аналитической форме, заметим, что оно эквивалентно параллельности градиентов функций и в данной точке, поскольку вектор градиента перпендикулярен касательной к линии уровня. Это условие выражается в следующей форме:

где  — некоторое число, отличное от нуля, и являющееся множителем Лагранжа.

Рассмотрим теперь функцию Лагранжа , зависящую от и :

Необходимым условием её экстремума является равенство нулю градиента . В соответствии с правилами дифференцирования оно записывается в виде

В полученной системе первые два уравнения эквивалентны необходимому условию локального экстремума (1), а третье — уравнению . Из неё можно найти . При этом , поскольку в противном случае градиент функции обращается в нуль в точке , что противоречит предположениям.

Замечание. Найденные таким способом точки могут и не являться точками условного экстремума  — записанное дифференциальное условие носит необходимый, но не достаточный характер.

Вышеприведённые рассуждения о нахождении условного экстремума с помощью вспомогательной функции составляют
основу метода множителей Лагранжа и обобщаются на случай произвольного числа переменных и уравнений, задающих условия.

На основе метода множителей Лагранжа можно получить достаточные условия условного экстремума, требующие анализа (в простейшем случае) вторых производных функции Лагранжа .

Применение[править | править код]

• Метод множителей Лагранжа применяется при решении задач нелинейного программирования, возникающих во многих областях (например, в экономике).
• Основной метод решения задачи об оптимизации качества кодирования аудио и видео информации при заданном среднем битрейте (см. Оптимизация искажений  (англ.) (рус.).

См. также[править | править код]

• Математическое программирование
• Линейное программирование
• Условия Каруша — Куна — Таккера

Литература[править | править код]

• Акулич И.Л. Глава 3. Задачи нелинейного программирования // Математическое программирование в примерах и задачах. — М.: Высшая школа, 1986. — 319 с. — ISBN 5-06-002663-9..
• Зорич В. А. Математический анализ. Часть 1. — изд. 2-е, испр. и доп. — М.: ФАЗИС, 1997.
• Протасов В. Ю. Максимумы и минимумы в геометрии. — М.: МЦНМО. — 56 с. — (Библиотека «Математическое просвещение», выпуск 31).

Лекция 5.

Задача нелинейного
программирования.

Метод множителей
Лагранжа

Вопросы:

1. Постановка
задачи и ее особенности

2. Функция Лагранжа

3. Метод множителей
Лагранжа

4. Экономический
смысл множителей Лагранжа

1. Постановка
задачи и ее особенности

Задача математического программирования

в которой либо целевая функция, либо
ограничения, либо и то и другое нелинейны,
называется задачей нелинейного
программирования.

Нелинейные задачи составляют широкий
класс настолько сложных задач, что до
сих пор невозможно разработать общие
методы, подобные симплекс-методу в
линейном программировании, которые
позволяли бы решить любые нелинейные
задачи. Все возможные методы решения
задач нелинейного программирования
можно разделить на два больших класса:
точные и приближенные методы решения.
Точные методы позволяют определить
решение для некоторых более узких задач,
прежде всего задач с выпуклыми (вогнутыми)
функциями F(x) и g_i(x).
Приближенные (итерационные) методы
позволяют решить практически любую
задачу нелинейного программирования,
однако, имеют свои недостатки: скорость
сходимости (число шагов), точность и др.

Рассмотрим некоторые особенности задач
нелинейного программирования на примере
задач с двумя неизвестными. Так же, как
и в линейном программировании, они
допускают графическое решение.

Пример 1.

Решение

1. Построим допустимую область.

2. Построим линию уровня F(x)
= Const.

Это окружность с центром в т. О₁(4;
6) и радиусом R = 2.

3. Увеличивая R (следовательно, и F), можно
получить точки min F
и max F.
Это будут

т. А – т. минимума и т. В, т.С – точки
локальных максимумов.

4. Координаты т. А находят из условия
перпендикулярности (АО₁) и 2-й
границы:

А(24/13; 36/13)

F_min =
196/13.

B(1; 0)

F_B =
45

C(6; 0)

F_C =
40

т. В – точка максимума и F_max
= 45.

Точка минимума не является вершиной
допустимой области, а лежит на границе.

Пример 2. Та же допустимая область,
а

Минимум F = 0 достигается
в т. О₁(4; 1)

Точка минимума лежит внутри

допустимой области.

Минимум F = 25 достигается в т. А(0;
4)

Пример 3.
.

Решение

1. Допустимая область.

(1) гипербола х₂ = 4/х₁

(2)

2. Линия уровня F(x)
= Const = 0

–
парабола, …

3. т. А – т. max: А(4; 1),
.

т. В – т. min – определяется
приближенно
,
В(1,5; 2,67).

Точка минимума является точкой касания
границы и линии уровня.

2. Функция Лагранжа

Пусть дана задача математического
программирования

где функции F(x) и g(x)
непрерывные вместе со своими частными
производными. Эта задача является
классической задачей на условный
экстремум. Чтобы ее решить используют
функцию Лагранжа.

Функцией Лагранжа называют функцию

,

где
–
множители Лагранжа.

Определим стационарные точки функции
Лагранжа. Необходимые условия:

.
(1)

Заметим, что вторая группа уравнений
совпадает с ограничениями задачи. А
если эти условия выполняются, то L(x,
)
= F(x).
Таким образом, решение системы (1) является
не только стационарной точкой L(x,),
но и стационарной точкой F(x),
удовлетворяющей ограничениям задачи.
Следовательно, решив систему (1), находят
все точки, в которых целевая функция
может иметь экстремум.

Существуют и достаточные условия,
определяющие точки максимума или
минимума или отсутствие экстремума.
Эти условия определяются знаком второго
дифференциала.

3. Метод множителей
Лагранжа

1. Составить функцию Лагранжа.

2. Найти

и приравнять нулю.

3. Решая систему (1), находят точки, в
которых F(x) может иметь экстремум.

4. Среди точек, подозрительных на
экстремум, находят такие, в которых

достигается экстремум, и вычисляют
значения F(x) в этих точках.

5. Определяют точки максимума и
минимума.

Пример. На двух предприятиях отрасли
необходимо изготовить 200 изделий
некоторой продукции. Затраты, связанные
с производством х₁ изделий на
первом предприятии, равны 4х₁²
руб., а затраты, обусловленные изготовлением
х₂ изделий на втором предприятии,
составляют 20х₂ + 6х₂²
руб. Определить, сколько изделий на
каждом из предприятий следует произвести,
чтобы общие затраты, обусловленные
изготовлением необходимой продукции,
были минимальны.

Решение

1. Составим математическую модель.

.

1. Составим функцию Лагранжа

3.
;

;

.

4.

,
,
.

Замечание. Метод множителей Лагранжа
можно применять и в случае, когда
ограничения заданы в виде неравенств.
При этом следует сначала найти точки
безусловного экстремума и среди них
выбрать те, которые удовлетворяют
ограничениям задачи, затем определить
точки, удовлетворяющие системе (1).

4. Экономический
смысл множителей Лагранжа

Пусть дана задача

Точка экстремума х*, F(x*)
= F*. Если значения
b_i могут
изменяться, то х* зависит от b_i:
х*_j
= x_j(b)
и

(2)

С другой стороны, из ограничений следует

(3)

(Если k-е ограничение
дифференцируется по b_i,
то = 0)

Кроме того, в точке экстремума выполняются
условия (1). Откуда

.

Подставив это выражение и (3) в (2), получим

.

Если интерпретировать F доход или
стоимость, b_i
– как затраты некоторых ресурсов, то
множители Лагранжа будут показывать,
как изменится максимальный доход (или
минимальная стоимость), если количество
ресурса i-го вида увеличится на единицу.

Соседние файлы в папке Модуль 2

• #
• #
• #
• #

Метод множителей Лагранжа (в англ. литературе «LaGrange’s method of undetermined multipliers») ˗ это численный метод решения оптимизационных задач, который позволяет определить «условный» экстремум целевой функции (минимальное или максимальное значение)

при наличии заданных ограничений на ее переменные в виде равенств (т.е. определена область допустимых значений) 

 ˗ это значения аргумента функции (управляемые параметры) на вещественной области при котором значение функции стремится к экстремуму. Применение названия «условный» экстремум связано с тем, что на переменные наложено дополнительное условие, которое ограничивает область допустимых значений при поиске экстремума функции.

Метод множителей Лагранжа позволяет задачу поиска условного экстремума целевой функции на множестве допустимых значений преобразовать к задаче безусловной оптимизации функции.

В случае если функции  и  непрерывны вместе со своими частными производными, то существуют такие переменные λ не равные одновременно нулю, при которых выполняется следующее условие:

Таким образом, в соответствии с методом множителей Лагранжа для поиска экстремума целевой функции на множестве допустимых значений составляю функцию Лагранжа L(х, λ), которую в дальнейшем оптимизируют:

где λ ˗ вектор дополнительных переменных, называемых неопределенными множителями Лагранжа.

Таким образом, задача нахождения условного экстремума функции f(x) свелась к задаче поиска безусловного экстремума функции L(x, λ).

Далее в соответствии с методом определяют частные производные функции Лагранжа:

 и 

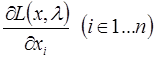
Необходимое условие экстремума функции Лагранжа задается системой уравнений (система состоит из «n + m» уравнений):

Решение данной системы уравнений позволяет определить аргументы функции (Х), при которых значение функции L(x, λ), а также значение целевой функции f(x) соответствуют экстремуму.

Величина множителей Лагранжа (λ) имеет практический интерес в случае, если ограничения представлены в форме со свободным членом уравнения (константой). В этом случае можно рассматривать дальнейшее (увеличение/уменьшение) значения целевой функции за счет изменения значения константы в системе уравнения . Таким образом, множитель Лагранжа характеризует скорость изменения максимума целевой функции при изменении ограничивающей константы.

Существует несколько способов определения характера экстремума полученной функции:

Первый способ: Пусть  – координаты точки экстремума, а  – соответствующее значение целевой функции. Берется точка , близкая к точке , и вычисляется значение целевой функции :

– Если , то в точке  имеет место максимум.

– Если , то в точке  имеет место минимум.

Второй способ: Достаточным условием, из которого можно выяснить характер экстремума, является знак второго дифференциала функции Лагранжа. Второй дифференциал функции Лагранжа определяется следующим образом:

Если в заданной точке , то целевая функция f(x) имеет в данной точке условный минимум, если же , то целевая функция f(x) имеет в данной точке условный максимум.

Третий способ: Также характер экстремума функции можно выяснить рассмотрев гессиан функции Лагранжа. Матрица Гессе представляет собой симметричную квадратную матрицу вторых частных производных функции в точке , в которой элементы матрицы симметричны относительно главной диагонали.

Для определения типа экстремума (максимум или минимум функции) можно воспользоваться правилом Сильвестра:

1. Для того, чтобы второй дифференциал функции Лагранжа был знакоположителен  необходимо, чтобы угловые миноры функции были положительными . При таких условиях функция в этой точке имеет минимум.

2. Для того, чтобы второй дифференциал функции Лагранжа был знакоотрицателен , необходимо, чтобы угловые миноры функции чередовались, причем первый элемент матрицы должен быть отрицательнsv . При таких условиях функция в этой точке имеет максимум.

Под угловым минором понимаем минор, расположенный в первых k строках и k столбцах исходной матрицы.

Основное практическое значение метода Лагранжа заключается в том, что он позволяет перейти от условной оптимизации к безусловной и, соответственно, расширить арсенал доступных методов решения задачи. Однако задача решения системы уравнений, к которой сводится данный метод, в общем случае не проще исходной задачи поиска экстремума. Такие методы называются непрямыми. Их применение объясняется необходимостью получить решение экстремальной задачи в аналитической форме (допустим, для тех или иных теоретических выкладок). При решении конкретных практических задач обычно используются прямые методы, основанные на итеративных процессах вычисления и сравнения значений оптимизируемых функций.

Методика расчета

1 шаг: Определяем функцию Лагранжа из заданной целевой функции и системы ограничений:

2 шаг: Определение аналитических соотношений (в символьном виде) для поиска безусловного экстремума функции L(x, λ).

3 шаг: Решаем полученную систему линейных или нелинейных  уравнений, используя соответствующие методы решения.

4 шаг: Определяем характер экстремума (максимум или минимум целевой функции) по любому из представленных выше методов.