Как составить функцию плотности вероятности - Сайт, где вы сможете решить свои вопросы

2.4.3. Функция ПЛОТНОСТИ распределения вероятностей

или дифференциальная функция распределения. Она представляет собой производную функции распределения: .

Примечание: для дискретной случайной величины такой функции не существует

В нашем примере:

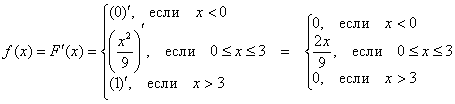
то есть, всё очень просто – берём производную от каждого куска, и порядок.

Но настоящий порядок состоит в том, что несобственный интеграл от с пределами интегрирования от «минус» до «плюс» бесконечности:

– равен единице, и строго единице. В противном случае перед нами не функция плотности, и если эта функция была найдена как производная, то – не является функцией распределения (несмотря на какие бы то ни было другие признаки).

Проверим «подлинность» наших функций. Если случайная величина принимает значения из конечного промежутка, то всё дело сводится к вычислению определённого интеграла. В силу свойства аддитивности, делим интеграл на 3 части:

Совершенно понятно, что левый и правый интегралы равны нулю и нам осталось вычислить средний интеграл:
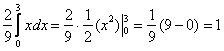, что и требовалось проверить.

С вероятностной точки зрения это означает, что случайная величина достоверно примет одно из значений отрезка . Геометрически же это значит, что площадь между осью и графиком равна единице, и в данном случае речь идёт о площади треугольника . Сторона является фрагментом прямой и для её построения достаточно найти точку :

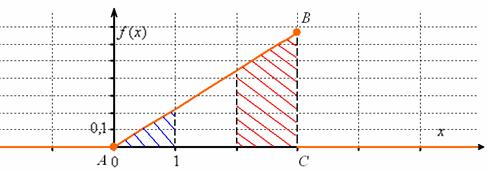
Ну вот, теперь всё наглядно – где бОльшая площадь, там и сконцентрированы более вероятные значения.

Так как функция плотности «собирает под собой» вероятности, то она неотрицательна и её график не может располагаться ниже оси . В общем случае функция разрывна (смотрим, где «жирные» оранжевые точки!).

Теперь разберём весьма любопытный факт: поскольку действительных чисел несчётно много, то вероятность того, что случайная величина примет какое-то конкретное значение стремится к нулю. И поэтому вероятности рассчитывают не для отдельно взятых точек, а для целых промежутков (пусть даже очень малых). Как вы правильно догадываетесь:
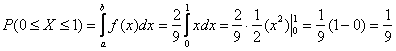(синяя площадь на чертеже) – вероятность того, что случайная величина примет значение из отрезка ;
(красная площадь) – вероятность того, что случайная величина примет значение из отрезка .

По той причине, что отдельно взятые значения можно не принимать во внимание, с помощью этих же интегралов рассчитываются и вероятности по интервалам и полуинтервалам, в частности:

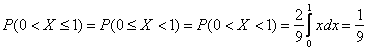
Этим же объяснятся аналогичная «вольность» с функцией .
Возможно, кто-то спросит: а зачем считать интегралы, если есть функция ?

А дело в том, что во многих задачах непрерывная случайная величина ИЗНАЧАЛЬНО задана функцией плотности распределения, которая ТОЖЕ однозначно определяет случайную величину. Но, как вариант, можно сначала найти функцию (с помощью тех же интегралов), после чего использовать «лёгкий способ» бросить курить отыскания вероятностей. Впрочем, об этом чуть позже:

Задача 105
Непрерывная случайная величина задана своей функцией распределения:

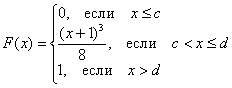
Найти значения и функцию . Проверить, что действительно является функцией плотности распределения. Вычислить вероятности . Построить графики .

Тренируемся самостоятельно! Если возникнут затруднения, то внимательно перечитайте вышеизложенный материал. Краткое решение и ответ в конце книги.

Вообще, типовые задачи на непрерывную случайную величину можно разделить на 2 большие группы:

1) когда дана функция , 2) когда дана функция .

В первом случае не составляет особых трудностей отыскать функцию плотности распределения – почти всегда производные не то что простЫ, а примитивны (в чём мы только что убедились). Но вот когда НСВ задана функцией , то нахождение функции распределения – есть более кропотливый процесс:
Задача 106
Непрерывная случайная величина задана функцией плотности распределения:

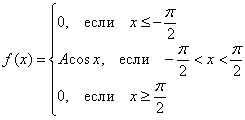
Найти значение и составить функцию распределения вероятностей . Вычислить .
Построить графики .

Решение: найдём константу . Это классика (в подавляющем большинстве задач вам не предложат готовую функцию плотности). Используем свойство .
В данном случае:

На практике нулевые интегралы можно опускать, а константу сразу выносить за знак интеграла:
(*)
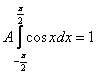Пользуясь чётностью подынтегральной функции, вычислим интеграл:
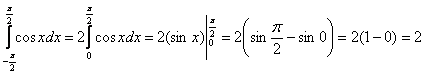и подставим результат в уравнение (*):
, откуда выразим

Таким образом, функция плотности распределения:

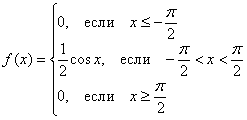
Выполним проверку, а именно, вычислим тот же самый интеграл, но уже с известной константой. Для разнообразия я не буду пользоваться чётностью:
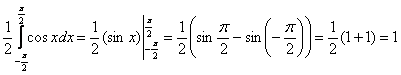, отлично.

Обратите внимание, что только при и только при этом значении предложенная в условии функция является функцией плотности распределения. Ну и тут не лишним будет проконтролировать, что на интервале , т.е. условие неотрицательности действительно выполнено. Доверяй условию, да проверяй 😉 Не раз и не два мне встречались функции, которые в принципе не могли быть плотностью, что говорило об опечатках или о невнимательности авторов задач.

Теперь начинается самое интересное. Функции распределения вероятностей – есть интеграл:

Так как состоит из трёх кусков, то решение разобьётся на 3 шага:

1) На промежутке , поэтому:

2) На интервале , и мы прицепляем следующий вагончик:

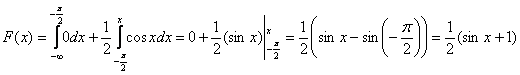
При подстановке верхнего предела интегрирования можно считать, что вместо «икс» мы подставляем «икс». Если же возник вопрос с пределом нижним, то вспоминаем график синуса либо его нечётность: .

3) И, наконец, на , и детский паровозик отправляется в путь:

Внимание! А вот в этом задании нулевые интегралы пропускать НЕ НАДО. Чтобы показать своё понимание функции распределения 😉 К тому же, они могут оказаться вовсе не нулевыми, и тогда придётся иметь дело с интегралами несобственными. И такой пример я обязательно разберу ниже.

Записываем наши достижения под единую скобку:

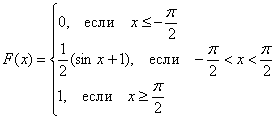
С высокой вероятностью всё правильно, но, тем не менее, устно возьмём производную: 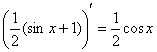, а также «прозвоним» точки «стыка»:

Правильность решения можно проконтролировать и в ходе построения графика, но, во-первых, он не всегда требуется, а во-вторых, до сего момента можно успеть «наломать дров». Ибо вероятности попадания чаще находят с помощью функции распределения:

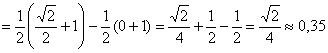– вероятность того, что случайная величина примет значение из промежутка

Второй способ состоит в вычислении интеграла:
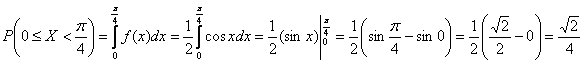что, кстати, не труднее. И проверочка заодно получилась.

Выполним чертежи. График представляет собой косинусоиду, сжатую вдоль ординат в 2 раза. Тот редкий случай, когда функция плотности непрерывна:

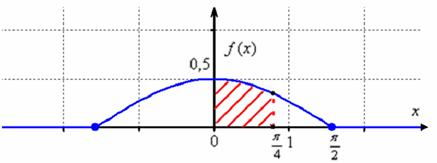
Значение численно равно заштрихованной площади – это я специально нарисовал, чтобы напомнить вероятностный смысл плотности функции распределения. И вся площадь под «дугой» равна единице, то есть, достоверным является тот факт, что случайная величина примет значение из интервала . Заметьте, что значения по условию, невозможны.
Осталось изобразить функцию распределения. График представляет собой синусоиду, сжатую в 2 раза вдоль оси ординат и сдвинутую на вверх:

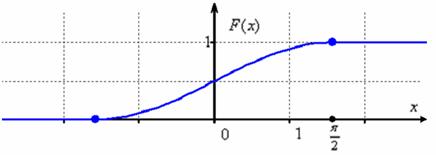
В принципе, тут можно было не заморачиваться преобразованием графиков, а найти несколько опорных точек и догадаться, как выглядит кривая (тригонометрическая таблица в помощь). Но «любительский» подход чреват тем, что график получится принципиально не точным. Так, в нашем примере в точке существует перегиб графика функции , и велик риск неверно отобразить его выпуклость / вогнутость.

Чертежи желательно расположить так, чтобы оси ординат (вертикальные оси) лежали ровненько одна под другой. Это будет хорошим тоном.

И я так чувствую, вам уже не терпится проверить свои силы. Как водится, пример попроще:

Задача 107
Задана плотность распределения вероятностей непрерывной случайной величины :

Требуется:

1) определить коэффициент ;
2) найти функцию распределения ;
3) построить графики ;
4) найти вероятность того, что примет значение из промежутка

и задачка поинтереснее:

Задача 108
Непрерывная случайная величина задана плотностью распределения вероятностей:

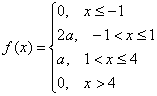
Найти значение и построить график плотности распределения. Найти функцию распределения вероятностей и построить её график. Вычислить вероятность .

Дерзайте! Свериться с решением можно внизу книги.

Следует отметить, что все эти задачи реально предлагают студентам-заочникам, и поэтому я не предлагаю вам ничего необычного.

И в заключение параграфа обещанные случаи с несобственными интегралами:

Задача 109
Непрерывная случайная величина задана своей плотностью распределения:

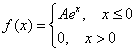
Найти коэффициент и функцию распределения . Построить графики.

Решение: по свойству функции плотности распределения:

В данной задаче состоит из 2 частей, поэтому:

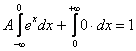
Правый интеграл равен нулю, а вот левый – есть «живой» несобственный интеграл с бесконечным нижним пределом:

Таким образом, наше уравнение превратилось в готовый результат:

и функция плотности:

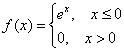
Функция , как нетрудно понять, отыскивается в 2 шага:

1) На промежутке , следовательно:
– вот такая вот у нас замечательная экспонента. Как птица Феникс.

2) На интервале и:
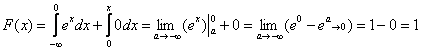, что и должно получиться.

Для построения графиков найдём пару опорных точек: и аккуратно прочертим кусочки экспонент с причитающимися дополнениями:

Заметьте, что теоретически случайная величина может принять сколь угодно большое по модулю отрицательное значение, и ось абсцисс является горизонтальной асимптотой для обоих графиков при .

В соответствующей статье сайта я рассмотрел ещё более интересный пример с функцией , где случайная величина теоретически принимает вообще ВСЕ действительные значения. Но это уже несколько повышенный уровень сложности.

2.4.4. Как вычислить математическое ожидание и дисперсию НСВ?

2.4.2. Вероятность попадания в промежуток

| Оглавление |

Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Плотность распределения вероятностей непрерывной случайной величины

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).

Плотностью распределения вероятностей непрерывной случайной величины

называют функцию

– первую производную от функции распределения

Из этого определения следует, что
функция распределения является первообразной для плотности распределения.

Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.

Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина

примет
значение, принадлежащее интервалу

равна
определенному интегралу от плотности распределения, взятому в пределах от

до

Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу

, равна площади криволинейной трапеции, ограниченной
осью

, кривой распределения

и прямыми

В частности, если

– четная
функция и концы интервала симметричны относительно начала координат, то:

Зная плотность распределения

можно найти
функцию распределения

по формуле:

Свойства плотности распределения

Свойство 1.

Плотность
распределения – неотрицательная функция:

Свойство 2.

Несобственный
интеграл от плотности распределения в пределах от

до

равен единице:

Смежные темы решебника:

Дискретная случайная величина
Непрерывная случайная величина
Интегральная функция распределения вероятностей

Примеры решения задач

Пример 1

Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:

1)
определить коэффициент A;

2) найти
функцию распределения F(x);

3)
схематично построить графики F(x) и f(x);

4) найти
математическое ожидание и дисперсию X;

5) найти
вероятность того, что X примет значение из
интервала (α,β):

α=1; β=1.7

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

1)
Постоянный параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Получаем:

2)
Функцию распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем
отметить, что:

Остается
найти выражение для

, когда

принадлежит
интервалу

Получаем:

3) Построим графики

График плотности распределения

График функции распределения

4)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

5)
Вероятность того, что случайная величина примет значение из интервала

Пример 2

Плотность
распределения вероятности непрерывной случайной величины равна

, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).

Решение

Нормировочный множитель

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

Пример 3

Непрерывная
случайная величина

имеет плотность распределения:

Найти
величину a, вероятность P(X<0) и математическое
ожидание X.

Решение

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Постоянный
параметр

найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности имеет вид:

Вероятность:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Задачи контрольных и самостоятельных работ

Задача 1

Плотность
распределения непрерывной случайной величины X имеет вид:

Найти:

а)
параметр a;

б)
функцию распределения F(x);

в)
вероятность попадания случайной величины X в интервал (6.5; 11);

г)
математическое ожидание M(X) и дисперсию D(X);

Построить
график функций f(x) и F(x).

Задача 2

Задана
функция распределения непрерывной случайной величины:

Найти и
построить график функции плотности распределения вероятностей.

Задача 3

Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).

Задача 4

Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).

α=1,β=2

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Непрерывная
случайная величина

задана плотностью распределения вероятностей.

Требуется
найти:

– функцию
распределения вероятностей;

–
математическое ожидание;

–
дисперсию;

– среднее
квадратическое отклонение;

– вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;

–
построить графики функции распределения и плотности распределения вероятностей.

Задача 6

Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).

Задача 7

Случайная
величина X~N(a,σ)

a=25;
σ=4; α=13; β=30; δ=0.1.

Требуется:

–
составить функцию плотности распределения и построить ее график;

– найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);

– найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.

Задача 8

Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:

Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 9

Случайная
величина X задана функцией распределения вероятностей F(x).

Требуется:

1. Найти
функцию плотности распределения f(x).

2. Найти M(X).

3. Найти
вероятность P(α<X<β)

4.
Построить графики f(x) и F(x).

α=2, β=4.5

Задача 10

Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).

M(X)=-1; D(X)=8

Задача 11

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);

д)
вычислить вероятность попадания в интервал P(a≤x≤b)

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

a=π/4; b=π/3; xp=π/2; p=0.75

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Непрерывная
случайная величина может быть задана
не только с помощью функции распределения.
Введем понятие плотности
вероятности
непрерывной случайной величины.

Рассмотрим
вероятность попадания непрерывной
случайной величины на интервал [х,
х
+ Δх].
Вероятность такого события

P(х
≤ X
≤ х
+ Δх)
= F(х+
Δх)
– F(х),

т.е.
равна приращению функции распределения
F(х)
на этом участке. Тогда вероятность,
приходящаяся на единицу длины, т.е.
средняя плотность вероятности на участке
от х
до х+
Δх,
равна

Переходя к пределу
Δх
→ 0, получим плотность вероятности в
точке х:

представляющую
производную функции распределения
F(х).
Напомним, что для непрерывной случайной
величины F(х)
– дифференцируемая функция.

Определение.
Плотностью
вероятности
(плотностью
распределения)
f(x)
непрерывной
случайной величины Х называется
производная ее функции распределения

f(x)
= F′(x).

(4.8)

Про случайную
величину Х
говорят, что она имеет распределение с
плотностью f(x)
на определенном участке оси абсцисс.

Плотность вероятности
f(x),
как и функция распределения F(x)
является одной из форм закона распределения.
Но в отличие от функции распределения
она существует только для непрерывных
случайных величин.

Плотность вероятности
иногда называют дифференциальной
функцией
или дифференциальным
законом распределения.
График плотности вероятности называется
кривой
распределения.

Пример 4.4.
По данным примера 4.3 найти плотность
вероятности случайной величины Х.

Решение.
Будем находить плотность вероятности
случайной величины как производную от
ее функции распределения f(x)
= F‘(x).

◄

Отметим свойства
плотности вероятности непрерывной
случайной величины.

1.
Плотность
вероятности – неотрицательная функция,
т.е.

f(x)
≥ 0,

(4.9)

как
производная монотонно неубывающей
функции F(x).

2.
Вероятность
попадания непрерывной случайной величины
Х в интервал [α,
β,]
равна
определенному интегралу от ее плотности
вероятности в пределах от α
до β,
т.е.

(4.10)

Геометрически
вероятность попадания в интервал [α,
β,]
равна площади фигуры, ограниченной
сверху кривой распределения и опирающейся
на отрезок [α,
β,]
(рис.4.4).

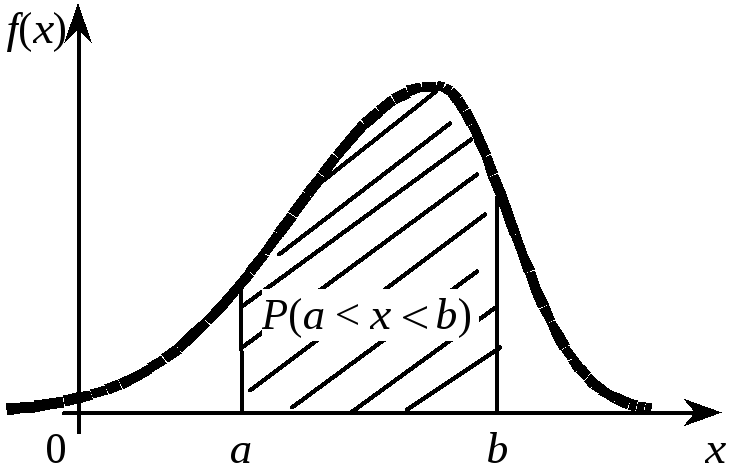
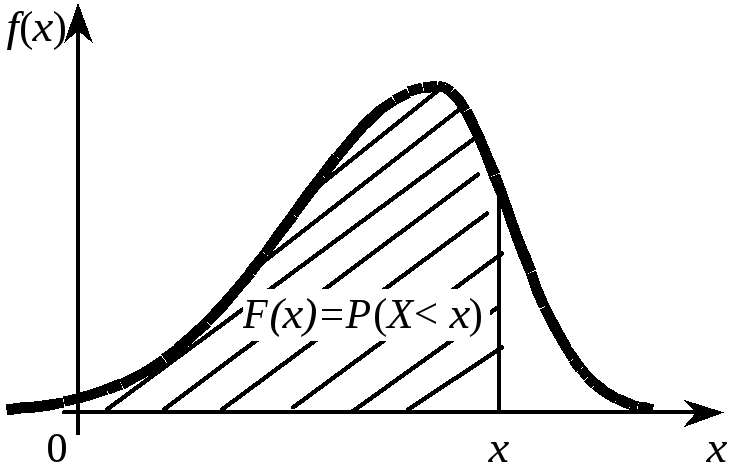
Рис. 4.4 Рис.
4.5

3.
Функция
распределения непрерывной случайной
величины может быть выражен через
плотность вероятности по формуле:

.	(4.11)

Геометрически
функция распределения равна площади
фигуры, ограниченной сверху кривой
распределения и лежащей левее точки х
(рис. 4.5).

4.
Несобственный
интеграл в бесконечных пределах от
плотности вероятности непрерывной
случайной величины равен единице:

.	(4.12)

Геометрически
свойства 1
и 4
плотности вероятности означают, что ее
график – кривая распределения – лежит
не ниже оси абсцисс, а полная площадь
фигуры, ограниченной кривой распределения
и осью абсцисс, равна единице.

Пример 4.5.
Функция f(x)
задана в виде:

Найти: а) значение
А;
б) выражение функции распределения
F(х);
в) вероятность того, что случайная
величина Х
примет значение на отрезке [0; 1].

Решение.
а) Для того, чтобы f(x)
была плотностью вероятности некоторой
случайной величины Х,
она должна быть неотрицательна,
следовательно, неотрицательным должно
быть и значение А.
С учетом свойства 4
находим:

,
откуда А
=
.

б) Функцию
распределения находим, используя
свойство 3:

Если x
≤ 0, то f(x)
= 0 и, следовательно, F(x)
= 0.

Если 0 < x
≤ 2, то f(x)
= х/2
и, следовательно,

Если х
> 2, то f(x)
= 0 и, следовательно

в) Вероятность
того, что случайная величина Х
примет значение на отрезке [0; 1] находим,
используя свойство 2:

=
0,25. ◄

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

В этой статье мы рассмотрим вероятностную массу и функцию плотности вероятности в этом примере. Вы увидите, как понимать и представлять эти функции распределения и их связь с гистограммами. В этом примере мы рассмотрим массу вероятности и функцию плотности вероятности. Вы увидите, как понимать и представлять эти функции распределения и их связь с гистограммами.

Детерминированные процессы дают одинаковые результаты при многократном повторении. Это не относится к случайным величинам, которые описывают случайные события, в которых случайность характеризует процесс.

Это означает, что случайные величины могут принимать различные значения. Как вы можете описать и сравнить эти ценности? Один хороший способ – использовать вероятность того, что произойдет каждый результат.Распределение вероятностей случайной переменной – это функция, которая принимает пространство выборки в качестве входных данных и возвращает вероятности: другими словами, она сопоставляет возможные результаты с их вероятностями. В этом разделе вы узнаете о распределении вероятностей для дискретных и непрерывных переменных.

Вероятностные массовые функции

Функции вероятности дискретных случайных величин называются функциями вероятностных масс (или PMF).Например, предположим, что вы проводите эксперимент по бросанию кости. Вы называете X случайной величиной, соответствующей этому эксперименту. Если исходить из того, что игра справедлива, каждый исход равновероятен: если вы запустите эксперимент большое количество раз, вы получите каждый результат примерно одинаковое количество раз. Здесь есть шесть возможных исходов, поэтому у вас есть один шанс из шести, чтобы вытащить каждое число.

Таким образом, функция вероятностной массы, описывающая X, возвращает 1616 для каждого возможного результата и 0 в противном случае (потому что вы не можете получить что-то другое, кроме 1, 2, 3, 4, 5 или 6).

Вы можете написать

Основы математики для науки о данных: функции плотности вероятности и массы вероятности

и так далее

Свойства вероятностных функций масс.

Не каждую функцию можно рассматривать как функцию массы вероятности. Функция вероятностных масс должна удовлетворять следующим двум условиям:

Функция должна возвращать значения от 0 до 1 для каждого возможного результата:

Сумма вероятностей, соответствующих всем возможным исходам, должна быть равна 1:

Значение x может быть любым действительным числом, потому что значения за пределами области выборки связаны с вероятностью 0. Математически для любого значения x вне области выборки S P (x) = 0.

Моделирование эксперимента с игральными костями

Давайте смоделируем эксперимент с кубиком, используя функцию np.random.randint (low, high, size) из Numpy, которая выводит n (размер) случайных целых чисел от low до high (исключено). Давайте смоделируем 20 бросков кубика:

rolls = np.random.randint(1, 7, 20)
rolls

array([6, 3, 5, …, 6, 5, 1])

Этот массив содержит 20 результатов эксперимента. Назовем X дискретной случайной величиной, соответствующей эксперименту с прокаткой штампа. Функция массы вероятности X определена только для возможных исходов и дает вам вероятность для каждого из них.

Предполагая, что кубик справедлив, у вас должно быть равномерное распределение, то есть равновероятные результаты.

Давайте визуализируем количество каждого результата, полученного вами в случайном эксперименте. Вы можете разделить на количество попыток, чтобы получить вероятность. Давайте воспользуемся plt.stem () из Matplotlib, чтобы визуализировать эти вероятности:

val, counts = np.unique(rolls, return_counts=True)
plt.stem(val, counts/len(rolls), basefmt=”C2-“, use_line_collection=True)

Рис. 1: Вероятностная функция масс случайной величины X, соответствующей прокатке шестигранной матрицы, оцененная из 20 валков.

При равномерном распределении график будет иметь одинаковую высоту для каждого результата (поскольку высота соответствует вероятности, которая одинакова для каждого результата броска кубика). Однако распределение, показанное на рисунке 1, не выглядит однородным. Это потому, что вы недостаточно повторили эксперимент: вероятности сохранятся, если вы повторите эксперимент большое количество раз (теоретически, бесконечное количество раз).

Увеличим количество испытаний:

throws = np.random.randint(1, 7, 100000)
val, counts = np.unique(throws, return_counts=True)
plt.stem(val, counts/len(throws), basefmt=”C2-“, use_line_collection=True)

Рис. 2: Вероятностная функция массы случайной величины X, соответствующая эксперименту по прокатке в штампе, рассчитанная на основе 100 000 валков.

При достаточном количестве испытаний функция массы вероятности, показанная на рисунке 2, выглядит однородной. Это подчеркивает важность количества испытаний с точки зрения частотной вероятности.

Функции плотности вероятности

С непрерывными переменными существует бесконечное количество возможных результатов (ограниченное количеством десятичных знаков, которые вы используете). Например, если вы рисуете число от 0 до 1, вы можете получить результат, например, 0,413949834. Вероятность выпадения каждого числа стремится к нулю: если вы разделите что-либо на очень большое число (количество возможных результатов), результат будет очень маленьким, близким к нулю. Это не очень помогает при описании случайных величин.

Лучше учитывать вероятность получения определенного числа в диапазоне значений. Ось Y функций плотности вероятности не является вероятностью. Это называется плотностью вероятности или просто плотностью. Таким образом, распределения вероятностей для непрерывных переменных называются функциями плотности вероятности (или PDF).

Интеграл от функции плотности вероятности по определенному интервалу дает вам вероятность того, что случайная величина примет значение в этом интервале. Таким образом, эта вероятность определяется площадью под кривой в этом интервале (как вы можете видеть в Essential Math for Data Science).

Обозначение

Здесь я буду обозначать функции плотности вероятности строчной буквой p. Например, функция p (x) дает вам плотность, соответствующую значению x.

пример

Давайте рассмотрим пример функции плотности вероятности. Вы можете случайным образом извлечь данные из нормального распределения, используя функцию Numpy np.random.normal (более подробную информацию о нормальном распределении вы найдете в Essential Math for Data Science).

Вы можете выбрать параметры нормального распределения (среднее и стандартное отклонение) и количество выборок. Давайте создадим переменные данные из 1000 значений, выбранных случайным образом из нормального распределения со средним значением 0,3 и стандартным отклонением 0,1.

np.random.seed(123)
data = np.random.normal(0.3, 0.1, 1000)

Давайте посмотрим на форму распределения с помощью гистограммы. Функция plt.hist () возвращает точные значения x- и y-координат гистограммы. Давайте сохраним это в переменной с именем hist для последующего использования:

hist = plt.hist(data, bins=13, range=(-0.3, 1))

Рисунок 3: Гистограмма данных, полученных из нормального распределения. По оси X отложено значение элемента в векторе, а по оси Y – количество элементов (количество), находящихся в соответствующем диапазоне.

Гистограммы

Гистограммы показывают, как распределяются значения. Это способ моделирования распределения вероятностей с использованием конечного числа значений из распределения. Поскольку мы имеем дело с непрерывными распределениями, эта гистограмма соответствует количеству значений для определенных интервалов (интервалы зависят от бинов параметров в функции hist ()).

Например, на рисунке 3 показано, что в интервале (0,2, 0,3) содержится около 347 элементов. Каждый интервал соответствует ширине 0,1, поскольку мы использовали 13 интервалов для представления данных в диапазоне от -0,3 до 1.

Давайте внимательнее посмотрим на распределение с большим количеством корзин. Вы можете использовать плотность параметра, чтобы ось Y соответствовала плотности вероятности вместо количества значений в каждой ячейке:

hist = plt.hist(data, bins=24, range=(-0.2, 1), density=True)

Рисунок 4: Гистограмма с использованием 30 интервалов и плотности вместо количества.

На рисунке 4 видно, что на этой гистограмме больше интервалов (24 вместо 13). Это означает, что теперь ширина каждого бункера меньше. Ось ординат тоже находится в другом масштабе: она соответствует плотности, а не счетчику значений, как раньше.

Чтобы рассчитать вероятность получить значение в определенном диапазоне от плотности, вам нужно использовать площадь под кривой. В случае гистограмм это площадь столбцов.

Возьмем пример с полосой от 0,2 до 0,25, связанной со следующей плотностью:

print(f”Density: {hist[0][8].round(4)}”)
print(f”Range x: from {hist[1][8].round(4)} to {hist[1][9].round(4)}”)

Density: 2.8
Range x: from 0.2 to 0.25

Поскольку существует 24 ячейки, а диапазон возможных результатов составляет от -0,2 до 1, каждая полоса соответствует диапазону

В нашем примере высота полосы (от 0,2 до 0,25) составляет около 2,8, поэтому площадь этой полосы равна 2.8. 0.05.=0.14. Это означает, что вероятность получить значение от 0,2 до 0,25 составляет около 0,14, или 14%.

Вы видели, что сумма вероятностей должна быть равна единице, поэтому сумма площадей столбца должна быть равна единице. Давайте проверим это: вы можете взять вектор, содержащий плотности (hist [0]), и умножить его на ширину полосы (0,05):

(hist[0] * 0.05).sum().round(4)

1.0

Все хорошо: сумма вероятностей равна единице.

От гистограмм к непрерывным функциям плотности вероятности

Гистограммы представляют собой разделенную на интервалы версию функции плотности вероятности. На рисунке 5 показано представление истинной функции плотности вероятности. Заштрихованная синим область на рисунке соответствует вероятности получения числа от 0 до 0,2 (область под кривой от 0 до 0,2).

Рис. 5. Вероятность выпадения числа от 0 до 0,2 – это выделенная область под кривой.

Свойства функций плотности вероятности

Как и функции массы вероятности, функции плотности вероятности должны удовлетворять некоторым требованиям. Во-первых, он должен возвращать только неотрицательные значения. Математически написано:

Второе требование – общая площадь под кривой функции плотности вероятности должна быть равна 1:

В этой части, посвященной распределению вероятностей, вы видели, что функции массы вероятности предназначены для дискретных переменных, а функции плотности вероятности – для непрерывных переменных.Имейте в виду, что значения на оси y функций вероятности и массы – это вероятности, что не относится к функциям плотности вероятности. Посмотрите на значения плотности (например, на рисунке 4): они могут быть больше единицы, что показывает, что они не являются вероятностями.

Hadrien Jean – специалист по машинному обучению. Он имеет докторскую степень в области когнитивных наук в Ecole Normale Superieure в Париже, где он проводил исследования слухового восприятия, используя поведенческие и электрофизиологические данные. Ранее он работал в отрасли, где создавал конвейеры глубокого обучения для обработки речи. На стыке науки о данных и окружающей среды он работает над проектами по оценке биоразнообразия с использованием глубокого обучения применительно к аудиозаписям. Он также периодически создает контент и преподает в Le Wagon (учебный курс по науке о данных) и пишет статьи в своем блоге (hadrienj.github.io).

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 августа 2021 года; проверки требуют 7 правок.

Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются^{[источник не указан 1062 дня]} и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).

Прикладное описание понятия[править | править код]

Плотность распределения одномерной непрерывной случайной величины — это числовая функция f(x) , отношение ${displaystyle f(x_{1})/f(x_{2})}$ значений которой в точках $x_{1}$ и $x_{2}$ задаёт отношение вероятностей попаданий величины в узкие интервалы равной ширины ${displaystyle [x_{1},x_{1}+Delta x]}$ и ${displaystyle [x_{2},x_{2}+Delta x]}$ вблизи данных точек.

Плотность распределения неотрицательна при любом и нормирована, то есть

${displaystyle int _{-infty }^{+infty }f(x),{mbox{d}}x=1}$

При стремлении к функция f(x) стремится к нулю. Размерность плотности распределения всегда обратная к размерности случайной величины — если исчисляется в метрах, то размерностью будет м^-1.

Если в конкретной ситуации известно выражение для f(x) , с его помощью можно вычислить вероятность попадания величины в интервал [a,b] как

${displaystyle P(xi in [a,b])=int _{a}^{b}f(x),{mbox{d}}x}$

Зная плотность вероятности, можно также определить наиболее вероятное значение (моду) случайной величины как максимум f(x) .
Также с помощью плотности вероятности находится среднее значение случайной величины:

${displaystyle Exi =int _{-infty }^{+infty }xf(x),{mbox{d}}x}$

и среднее значение измеримой функции случайной величины:

${displaystyle langle g(xi )rangle =int _{-infty }^{+infty }g(x)f(x),{mbox{d}}x}$

Чтобы перейти к плотности распределения ${displaystyle {f}_{chi }(y)}$ другой случайной величины , нужно взять

${displaystyle {f}_{chi }(y)=f(z^{-1}(y))cdot left|{frac {{mbox{d}}z^{-1}(y)}{{mbox{d}}y}}right|}$

где ${displaystyle z^{-1}(y)}$ — обратная функция по отношению к (предполагается, что z — взаимно однозначное отображение).

Значение плотности распределения $f(x_{1})$ не является вероятностью принять случайной величиной значение $x_{1}$ . Так, вероятность принятия непрерывной случайной величиной значения $x_{1}$ равна нулю. При непрерывном распределении случайной величины вопрос может ставиться о вероятности её попадания в некий диапазон, а не о вероятности реализации её конкретного значения.

Интеграл

${displaystyle int _{-infty }^{x}f(t),{mbox{d}}t=F(x)}$

называют функцией распределения (соответственно, плотность распределения вероятности — это производная функции распределения). Функция является неубывающей и изменяется от 0 при до 1 при .

Самым простым распределением является равномерное распределение на отрезке [a,b] . Для него плотность вероятности равна:

${displaystyle f(x)=left{{begin{matrix}{1 over b-a},&xin [a,b]\0,&xnot in [a,b]end{matrix}}right..}$

Широко известным распределением является «нормальное», оно же гауссово, плотность которого записывается как

${displaystyle f(x)={frac {1}{{sqrt {2pi }}sigma }}exp left[-{frac {(x-mu )^{2}}{2sigma ^{2}}}right]}$

где и sigma — параметры: математическое ожидание и среднеквадратичное отклонение. Другие примеры плотностей распределения — одностороннее лапласовское ():

{displaystyle f(x)=Aexp left[-lambda ,xright],,(xgeq 0)}

и максвелловское ():

${displaystyle f(x)=Ax^{2}exp left[-alpha x^{2}right],,(xgeq 0)}$

В двух последних примерах множитель подбирается в зависимости от параметра lambda или alpha так, чтобы обеспечить нормировку интеграла от плотности вероятности. В случае распределения Лапласа оказывается, что .

Как названные, так и другие распределения широко применяются в физике. Например, в случае распределения Максвелла роль случайной величины обычно играет абсолютная величина скорости молекулы в идеальном газе. При этом для аргумента функции нередко используют тот же символ, что и для рассматриваемой в физической задаче случайной величины (как если бы выше на месте всюду стояло ). Так, в выражении максвелловской плотности распределения пишут не формальную переменную , а символ скорости . В простейших ситуациях такая вольность с обозначениями не приводит к недоразумениям.

Спадающий при стремлении аргумента к +infty или -infty участок графика плотности вероятности f(x) в областях, где ${displaystyle fll f_{max}}$ , называется хвостом. Из упомянутых распределений, нормальное и лапласовское имеют по два хвоста (слева и справа), а максвелловское в выписанном виде — один (справа).

Выше была изложена суть понятия «плотность вероятности». Однако, такое изложение не является строгим — плотность нередко является функцией нескольких величин, в рассуждениях неявно предполагались не всегда гарантируемые непрерывность и дифференцируемость функций и так далее.

Определение плотности вероятности в теории меры[править | править код]

Плотность вероятности можно рассматривать как один из способов задания вероятностной меры на евклидовом пространстве $mathbb {R} ^{n}$ .
Пусть является вероятностной мерой на $mathbb {R} ^{n}$ , то есть определено вероятностное пространство $left(mathbb{R}^n,mathcal{B}(mathbb{R}^n),mathbb{P}right)$ , где $mathcal{B}(mathbb{R}^n)$ обозначает борелевскую σ-алгебру на $mathbb {R} ^{n}$ . Пусть обозначает меру Лебега на $mathbb {R} ^{n}$ .
Вероятность называется абсолютно непрерывной (относительно меры Лебега) (), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:

$forall B in mathcal{B}(mathbb{R}^n),; ( m(B) = 0 ) Rightarrow ( mathbb{P}(B) = 0 ) .$

Если вероятность абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция $fcolonmathbb{R}^n to [0,infty)$ такая, что

$mathbb{P}(B) = intlimits_{B} f(x), dx$

где использовано общепринятое сокращение , и интеграл понимается в смысле Лебега.

В более общем виде, пусть — произвольное измеримое пространство, а и — две меры на этом пространстве. Если найдется неотрицательная , позволяющая выразить меру через меру в виде

то такую функцию называют плотностью меры по мере , или производной Радона-Никодима меры относительно меры , и обозначают

$f=frac{dnu}{dmu}$

Плотность случайной величины[править | править код]

Пусть определено произвольное вероятностное пространство , и $Xcolon Omega to mathbb {R} ^{n}$ случайная величина (или случайный вектор). индуцирует вероятностную меру $mathbb {P} ^{X}$ на $left(mathbb{R}^n,mathcal{B}(mathbb{R}^n)right)$ , называемую распределением случайной величины .

Если распределение $mathbb {P} ^{X}$ абсолютно непрерывно относительно меры Лебега, то его плотность $f_X = frac{dmathbb{P}^X}{dx}$ называется плотностью случайной величины . Сама случайная величина называется абсолютно непрерывной.

Таким образом для абсолютно непрерывной случайной величины имеем:

$mathbb{P}(X in B) = intlimits_{B} f_X(x), dx$

Замечания[править | править код]

Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.

Функция распределения абсолютно непрерывной случайной величины непрерывна и может быть выражена через плотность следующим образом:

$F_X(x_1,ldots, x_n) = mathbb{P}left(X in prodlimits_{i=1}^n (-infty,x_i]right) = intlimits_{-infty}^{x_n} !! ldots !! intlimits_{-infty}^{x_1} f_X(x'_1,ldots, x'_n), dx'_1ldots dx'_n$

В одномерном случае:

$F_X(x) = intlimits_{-infty}^x f_X(x'), dx'$

Если $f_X in C(mathbb{R}^n)$ , то $F_X in mathcal{D}(mathbb{R}^n)$ , и

$frac{partial^n}{partial x_1 ldots partial x_n} F_X(x_1,ldots, x_n) = f_X(x_1,ldots, x_n)$

В одномерном случае:

$frac{d}{dx} F_X(x) = f_X(x)$

Математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в виде:

$mathbb{E}[g(X)] = intlimits_{mathbb{R}^n} g(x) , mathbb{P}^X(dx) = intlimits_{mathbb{R}^n} g(x), f_X(x), dx$

где $gcolon mathbb{R}^n to mathbb{R}$ — борелевская функция, так что определено и конечно.

Плотность преобразования случайной величины[править | править код]

Пусть $Xcolon Omega to mathbb {R} ^{n}$ — абсолютно непрерывная случайная величина, и $gcolonmathbb{R}^n to mathbb{R}^n$ — инъективная непрерывно дифференцируемая функция такая, что $J_g(x) not=0,; forall xin mathbb{R}^n$ , где J_g(x) — якобиан функции в точке . Тогда случайная величина также абсолютно непрерывна, и её плотность имеет вид:

$f_Y(y) = f_Xleft(g^{-1}(y)right) vert J_{g^{-1}}(y) vert$

В одномерном случае:

$f_Y(y) = f_Xleft(g^{-1}(y)right) leftvert frac{dg^{-1}}{dy}(y)rightvert$

Свойства плотности вероятности[править | править код]

Интеграл от плотности по всему пространству равен единице:

$mathbb{P}left(mathbb{R}^nright) = intlimits_{mathbb{R}^n} f(x), dx = 1$

Обратно, если f(x) — неотрицательная почти всюду функция, такая что $intlimits_{mathbb{R}^n}f(x), dx = 1$ , то существует абсолютно непрерывная вероятностная мера на $mathbb {R} ^{n}$ такая, что f(x) является её плотностью.

Замена меры в интеграле Лебега:

$intlimits_{mathbb{R}^n} varphi(x), mathbb{P}(dx) = intlimits_{mathbb{R}^n}varphi(x), f(x), dx$

где ${displaystyle varphi ::mathbb {R} ^{n}to mathbb {R} }$ любая борелевская функция, интегрируемая относительно вероятностной меры .

Примеры абсолютно непрерывных распределений[править | править код]

Бета-распределение
Гамма-распределение
Гиперэкспоненциальное распределение
Двумерное нормальное распределение
Логнормальное распределение
Многомерное нормальное распределение
Непрерывное равномерное распределение
Нормальное распределение
Обобщённое гиперболическое распределение
Полукруговой закон Вигнера
Распределение variance-gamma
Распределение Вейбулла
Распределение Гомпертца
Распределение Колмогорова
Распределение копулы
Распределение Коши
Распределение Лапласа
Распределение Накагами
Распределение Парето
Распределение Пирсона
Распределение Райса
Распределение Рэлея
Распределение Стьюдента
Распределение Трейси — Видома
Распределение Фишера
Распределение хи-квадрат
Частотное распределение
Экспоненциальное распределение

См. также[править | править код]

Распределение вероятностей
Сингулярное распределение
Функция вероятности

Литература[править | править код]

Плотность вероятности // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.

Источник

2.4.3. Функция ПЛОТНОСТИ распределения вероятностей

Плотность распределения вероятностей непрерывной случайной величины

Краткая теория

Свойства плотности распределения

Примеры решения задач

Пример 1

Пример 2

Пример 3

Задачи контрольных и самостоятельных работ

Вероятностные массовые функции

Свойства вероятностных функций масс.

Моделирование эксперимента с игральными костями

Функции плотности вероятности

Гистограммы

От гистограмм к непрерывным функциям плотности вероятности

Свойства функций плотности вероятности

Прикладное описание понятия[править | править код]

Определение плотности вероятности в теории меры[править | править код]

Плотность случайной величины[править | править код]

Замечания[править | править код]

Плотность преобразования случайной величины[править | править код]

Свойства плотности вероятности[править | править код]

Примеры абсолютно непрерывных распределений[править | править код]

См. также[править | править код]

Литература[править | править код]

Вам также может понравиться

Как найти баланс на yota

Как найти приращение функции по производной

Как найти метонимию в предложении

Добавить комментарий Отменить ответ