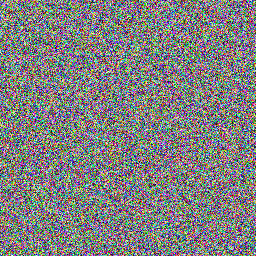
Я работаю программистом в игровой студии IT Territory, а с недавних пор перешел на направление экспериментальных проектов, где мы проверяем на прототипах различные геймплейные гипотезы. И работая над одним из прототипов мы столкнулись с задачей генерации случайных чисел. Я хотел бы поделиться с вами полученным опытом: расскажу о псевдогенераторах случайных чисел, об альтернативе в виде хеш-функции, покажу, как её можно оптимизировать, и опишу комбинированные подходы, которые мы применяли в проекте.
Случайными числами пользовались с самого зарождения математики. Сегодня их применяют во всевозможных научных изысканиях, при проверке математических теорем, в статистике и т.д. Также случайные числа широко используются в игровой индустрии для генерирования 3D-моделей, текстур и целых миров. Их применяют для создания вариативности поведения в играх и приложениях.
Есть разные способы получения случайных чисел. Самый простой и понятный — это словари: мы предварительно собираем и сохраняем набор чисел и по мере надобности берём их по очереди.
К первым техническим способам получения случайных чисел можно отнести различные генераторы с использованием энтропии. Это устройства, основанные на физических свойствах, например, емкости конденсатора, шуме радиоволн, длительности нажатия на кнопку и так далее. Хоть такие числа действительно будут случайными, у таких способов отсутствует важный критерий — повторяемость.
Сегодня мы с вами поговорим о генераторах псевдослучайных чисел — вычисляемых функциях. К ним предъявляются следующие требования:
-
Длинный период. Любой генератор рано или поздно начинает повторяться, и чем позже это случится, тем лучше, тем непредсказуемее будет результат.
-
Портируемость алгоритма на различные системы.
-
Скорость получения последовательности. Чем быстрее, тем лучше.
-
Повторяемость результата. Это очень важный показатель. От него зависят все компьютерные игры, которые используют генераторы миров и различные системы с аналогичной функциональностью. Воспроизводимость даёт нам общий контент для всех, то есть мы можем генерировать на отдельных клиентах одинаковое содержимое. Также мы можем генерировать контент на лету в зависимости от входных данных, например, от местоположения игрока в мире. Ещё повторяемость случайных чисел используется для сохранения конкретного контента в виде зерна. То есть мы можем держать у себя только какое-то число или массив чисел, на основе которых будут генерироваться нужные нам параметры для заранее отобранного контента.
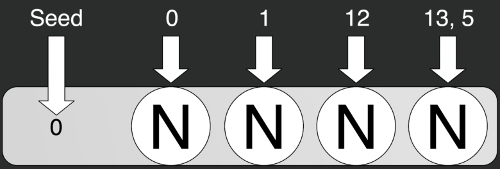
Зерно
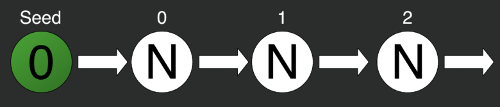
Зерно — это основа генерирования. Оно представляет собой число или вектор чисел, который мы отправляем при инициализации генератора.
var random = new Random(0);
var rn0 = random.Next();
var rn1 = random.Next();
var rn2 = random.Next();На иллюстрации просто инициализирован стандартный генератор случайных чисел из стандартной библиотеки C#. При инициализации отправляем в него некоторое число — seed (зерно), — в данном случае это 0. Затем по очереди берём по одному числу методом Next. Но тут мы столкнёмся с первой проблемой: генерирование всегда будет последовательным. Мы не можем получить сразу i-тый элемент последовательности. Для получения второго элемента последовательности необходимо сначала задать зерно, потом вычислить нулевой элемент, за ним первый и только потом уже второй, третий и i-й.
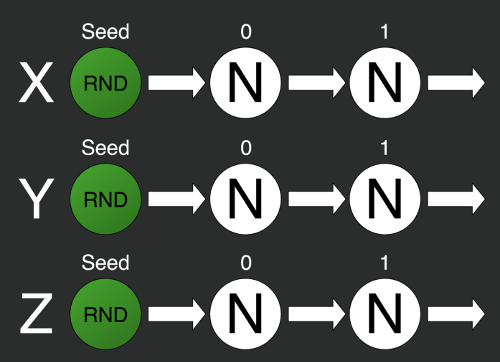
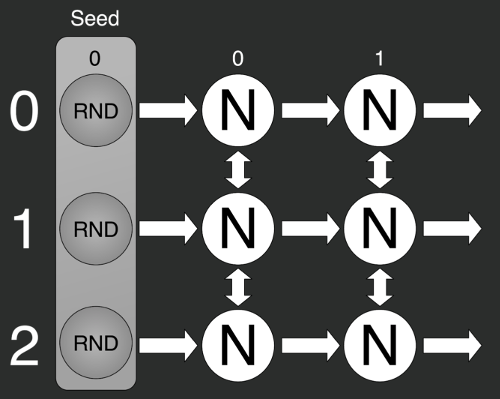
Решить эту проблему можно будет с помощью разделения одного генератора на несколько отдельных.
var X = 0;
var Y = 1;
var Z = 2;
var rs0 = new Random(X);
var rs1 = new Random(Y);
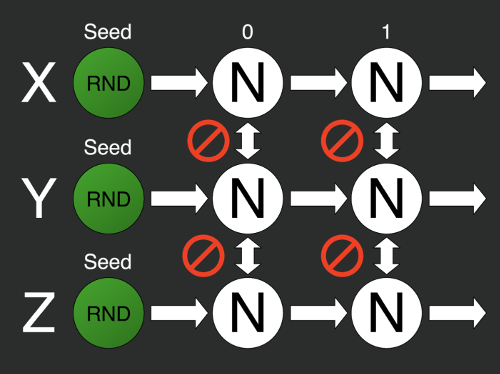
var rs2 = new Random(Z);То есть берём несколько генераторов и задаём им разные зёрна. Но тут мы можем столкнуться со второй проблемой: нельзя гарантировать случайность i-тых элементов разных последовательностей с разными зёрнами.
На иллюстрации изображён результат генерирования нулевого элемента последовательности с помощью стандартной библиотекой C#. Мы постепенно меняли зерно от 0 до N.
Качество генератора
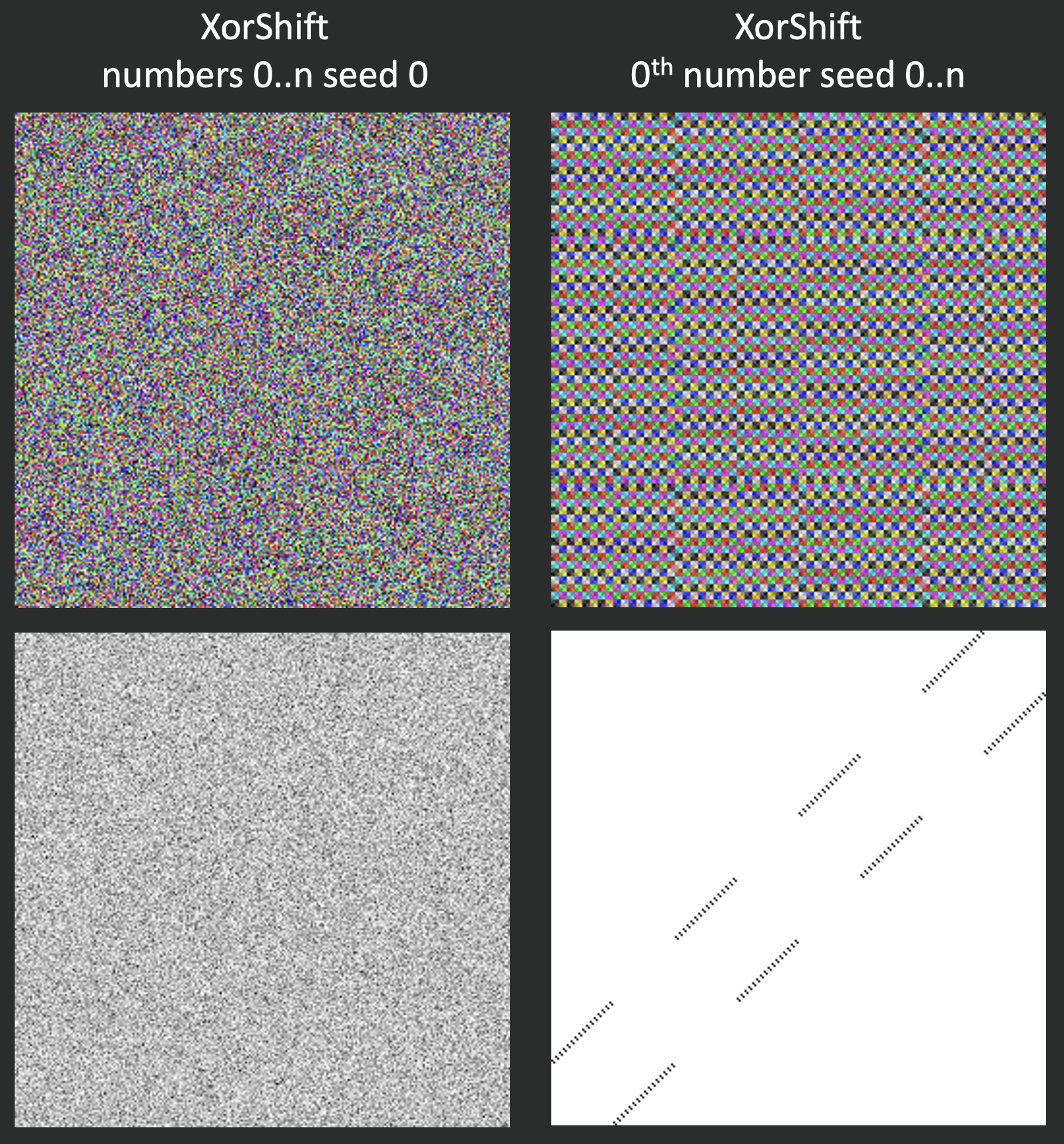
Предлагаю оценивать качество генератора с помощью изображений разного типа. Первый тип — это просто сгенерированная последовательность, который мы визуализируем с помощью первых трёх байтов полученного числа, конвертированных в RGB-представление.
private static uint GetBytePart(uint i, int byteIndex)
{
return ((i >> (8 * byteIndex)) % 256 + 256) % 256;
}
public static Color GetColor(uint i)
{
float r = GetBytePart(i, 0) / 255f;
float g = GetBytePart(i, 1) / 255f;
float b = GetBytePart(i, 2) / 255f;
return new Color(r, g, b);
}Второй тип изображений — это пространственная интерпретация сгенерированной последовательности. Мы берём первые два бита числа (Х и Y), затем считаем количество попаданий в заданные точки и при визуализации вычитаем из 1 отношение количества попаданий в конкретный пиксель к максимальному количеству попаданий в какой-то другой пиксель. Черные пиксели — это точка, куда мы попадаем чаще всего, а белые — куда мы либо почти, либо совсем не попали.
var max = 0;
for (var i = 0; i < ints.Length; i += 2)
{
var x = GetBytePart(ints[i], ByteIndex);
var y = GetBytePart(ints[i + 1], ByteIndex);
var value = coords[x, y];
value++;
max = Mathf.Max(value, max);
coords[x, y] = value;
}Сравнение генераторов
Стандартные средства C#
Ниже я сравнил стандартный генератор из библиотеки С# и линейную последовательность. Первый столбец слева — это случайная последовательность от 0 до N в рамках одного зерна. В центре вверху показаны нулевые элементы случайных последовательностей при разных зёрнах от 0 до N. Вторая линейная последовательность — это числа от 0 до N, которые я визуализировал нашим алгоритмом.
В рамках одного зерна генератор действительно создаёт случайное число. Но при этом для i-тых элементов последовательностей с разным зерном прослеживается паттерн, который схож с паттерном линейной последовательности.
Линейный конгруэнтный генератор (LCG)
Давайте рассмотрим другие алгоритмы. Деррик Генри в 1949 году создал линейный конгруэнтный генератор, который подбирает некие коэффициенты и с их помощью выполняет возведения в степень со сдвигом.
const long randMax = 4294967296;
state = 214013 * state + 2531011;
state ^= state >> 15;
return (uint) (state % randMax);При генерировании с одним зерном паттерн нигде не образуется. Но при использовании i-тых элементов в последовательностях с различными зёрнами паттерн начинает прослеживаться. Причём его вид будет зависеть исключительно от коэффициентов, которые мы подобрали для генератора. Например, есть частный случай линейного конгруэнтного генератора — Randu.
const long randMax = 2147483648;
state = 65539 * state + 0;
return (uint) (state % randMax);Этот генератор страшен тем, что умножает одно большое число на другое и берёт остаток от деления на 231. В результате формируется вот такая красивая картинка.
XorShift
Давайте теперь посмотрим на более свежую разработку — XorShift. Этот алгоритм просто выполняет операцию Xor и сдвигает байт в несколько раз. У него тоже будет прослеживаться паттерн для i-тых элементов последовательностей.
state ^= state << 13;
state ^= state >> 17;
state ^= state << 5;
return state;Вихрь Мерсенна
Неужели не существует генераторов без паттерна? Такой генератор есть — это вихрь Мерсенна. У этого алгоритма очень большой период, из-за чего появление паттерна на некотором количестве чисел физически невозможно. Однако и сложность этого алгоритма достаточно велика, в двух словах его не объяснить.
ulong x;
if (mti >= NN)
{
// generate NN words at one time
for (var i = 0; i < NN - MM; i++)
{
x = (mt[i] & UM) | (mt[i + 1] & LM);
mt[i] = mt[i + MM]
^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
}
for (var i = NN - MM; i < NN - 1; i++)
{
x = (mt[i] & UM) | (mt[i + 1] & LM);
mt[i] = mt[i + (MM - NN)]
^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
}
x = (mt[NN - 1] & UM) | (mt[0] & LM);
mt[NN - 1] = mt[MM - 1]
^ (x >> 1) ^ MAG01[(int) (x & 0x1L)];
mti = 0;
}
x = mt[mti++];
x ^= (x >> 29) & 0x5555555555555555L;
x ^= (x << 17) & 0x71d67fffeda60000L;
x ^= (x << 37) & 0xfff7eee000000000L;
x ^= x >> 43;
return x;Unity — Random
Из других разработок стоит упомянуть генератор от компании Unity — Random, который используется в наборе стандартных библиотек для работы с Unity. При использовании первых элементов последовательности для разных зёрен у него будет прослеживаться паттерн, но при увеличении индекса паттерн исчезает и получается действительно случайная последовательность.
Перемешанный конгруэнтный генератор (PCG)
Противоположностью юнитёвского Random’a является перемешанный конгруэнтный генератор. Его особенность в том, что для первых элементов с различными зёрнами отсутствует ярко выраженный паттерн. Но при увеличении индекса он всё же возникает.
Длительность последовательного генерирования
Это важная характеристика генераторов. В таблице приведена длительность для алгоритмов в миллисекундах. Замеры проводились на моём MacBook Pro 2019 года.
|
0..n |
0 seed 0..n |
100 seed 0..n |
|
|
Вихрь Мерсенна |
11 |
1870 |
2673 |
|
Random (C#) |
30 |
842 |
1364 |
|
LCG |
10 |
28 |
699 |
|
XorShift |
7 |
26 |
420 |
|
Unity Random |
20 |
40 |
1455 |
|
PCG |
18 |
60 |
1448 |
Вихрь Мерсенна работает дольше всего, но даёт качественный результат. Стандартный генератор Random из библиотеки C# подходит для задач, в которых случайность вторична и не имеет какой-то значимой роли, то есть его можно использовать в рамках одного зерна. LCG (линейный конгруэнтный генератор) — это уже более серьёзный алгоритм, но требуется время на подбор нужных коэффициентов, чтобы получить адекватный паттерн. XorShift — самый быстрый алгоритм из всех рассмотренных. Его можно использовать там, где нужно быстро получить случайное значение, но помните про ярко выраженный паттерн с повторяющимся значением. Unity Random и PCG (перемешанный конгруэнтный генератор) сопоставимы по длительности работы, поэтому в разных ситуациях мы можем менять их местами: для длительных последовательностей использовать Unity, а для коротких — PCG.
Альтернатива генераторам — хеш-функции
Хеш-функции (функции свёртки) по определённому алгоритму преобразуют массив входных данных произвольной длины в строку заданной длины. Они позволяют быстрее искать данные, это свойство используется в хеш-таблицах. Также для хеш-функций характерна равномерность распределения, так называемый лавинный эффект. Это означает, что изменение малого количества битов во входном тексте приведёт к лавинообразному и сильному изменению значений выходного массива битов. То есть все выходные биты зависят от каждого входного бита.
Требования к генераторам на основе хеш-функций предъявляются те же самые, что и к простым генераторам, кроме длительности получения последовательности. Дело в том, что такому генератору можно отправить на вход одновременно зерно и требуемое состояние, потому что хеш-функции принимают на вход массивы данных.
Вот пример использования хеш-функции: можно либо создать конкретный класс, отправить туда зерно и постепенно запрашивать только конкретные состояния, либо написать статичную функцию, и отправить туда сразу и зерно, и конкретное состояние. Слева показан алгоритм работы MD5 из стандартной библиотеки C#.
var hash = new Hash(0);
var rn0 = hash.GetHash(0);
var rn1 = hash.GetHash(1);
var rn2 = hash.GetHash(12);
var rn3 = hash.GetHash(13, 5);
var rn4 = Hash.GetHash(0, 0);
var rn5 = Hash.GetHash(0, 1);
var rn6 = Hash.GetHash(0, 12);
var rn7 = Hash.GetHash(0, 13, 5);Сделать генератор на основе хеш-функции можно так. Непосредственно при инициализации генератора задаём зерно, увеличиваем счётчик на 1 при запросе следующего значения и выводим результат хеша по зерну и счётчику.
class HashRandom
{
private int seed;
private int counter;
public HashRandom(int seed)
{
this.seed = seed;
}
public uint Next()
{
return Hash.GetHash(seed, counter++);
}
}Одни из самых популярных хеш-функций — это MurMur3 и WangHash.
MurMur3 не создаёт паттернов при использованиии i-тых элементов разных последовательностей при разных зёрнах. У WangHash статистические показатели образуют заметный паттерн. Но любую функцию можно прогнать через себя два раза и получить улучшенные показатели, как это показано в правом крайнем столбце WangDoubleHash.
Также сегодня активно развивается и набирает популярность алгоритм xxHash.
Забегая вперёд, скажу, что мы выбрали этот генератор для наших проектов и активно его используем.
Длительность последовательного генерирования у всех хеш-функций примерно одинакова. Однако у MD5 эта характеристика заметно отличается, но не потому, что алгоритм плохой, а потому что в стандартной реализации MD5 много разных состояний, которые влияют на быстродействие алгоритма.
|
0..n |
0 seed 0..n |
|
|
MurMur3 |
9 |
32 |
|
WangHash |
8 |
31 |
|
xxHash |
8 |
32 |
|
WangDoubleHash |
9 |
|
|
MD5 |
202 |
Оптимизация хеш-функций
Этот инструмент создавался для других целей — свёртки целых сообщений, поэтому на вход они принимают массивы данных. Лучше оптимизировать хеш-функции для задач генерирования случайных чисел, ведь нам достаточно подать два простых числа — зерно и счётчик.
Что нужно сделать для оптимизации:
-
Убрать функцию включения хвоста. Это операция вставки недостающих элементов в конец массива для хеш-функции. Если его длина меньше требуемой для хеширования, недостающие элементы заполняются определёнными значениями, обычно нулями.
-
Перевести обработку данных с типа byte на тип int.
-
Избавиться от конвертирования массива byte в одно число int.
Мы можем взять такую реализацию алгоритма xxHash:
uint h32;
var index = 0;
var len = buf.Length;
if (len >= 16)
{
var limit = len - 16;
var v1 = seed + P1 + P2;
var v2 = seed + P2;
var v3 = seed + 0;
var v4 = seed - P1;
do
{
v1 = SubHash(v1, buf, index);
index += 4;
v2 = SubHash(v2, buf, index);
index += 4;
v3 = SubHash(v3, buf, index);
index += 4;
v4 = SubHash(v4, buf, index); index += 4;
} while (index <= limit);
h32 = Rot32(v1, 1) + Rot32(v2, 7) + Rot32(v3, 12) + Rot32(v4, 18);
}
else
{
h32 = seed + P5;
}
h32 += (uint) len;
while (index <= len — 4)
{
h32 += BitConverter.ToUInt32(buf, index) * P3;
h32 = Rot32(h32, 17) * P4;
index += 4;
}
while (index < len)
{
h32 += buf[index] * P5;
h32 = Rot32(h32, 11) * P1;
index++;
}
h32 ^= h32 >> 15;
h32 *= P2;
h32 ^= h32 >> 13;
h32 *= P3;
h32 ^= h32 >> 16;
return h32;
И уменьшить до такой:
public static uint GetHash(int buf, uint seed)
{
var h32 = seed + P5;
h32 += 4U;
h32 += (uint) buf * P3;
h32 = Rot32(h32, 17) * P4;
h32 ^= h32 >> 15;
h32 *= P2;
h32 ^= h32 >> 13;
h32 *= P3;
h32 ^= h32 >> 16;
return h32;
}Здесь Р1, Р2, Р3, Р4, Р5 — стандартные коэффициенты алгоритма xxHash.
Комбинированные подходы
Комбинированные подходы бывают двух типов:
-
Сочетание хеш-функции и генератора случайных чисел.
-
Иерархические генераторы.
С первым всё предельно просто: берём хеш-функцию и получаем с её помощью зёрна, которые отправляем в другие генераторы. Слева показан результат работы комбинации стандартного Random из библиотеки C#, зёрна которому мы создавали с помощью хеш-функций.
Второй подход гораздо интереснее. Мы его используем в ситуациях, когда нам необходимо генерировать группы последовательностей, например, ботов для тестирования.
Сначала генерируем зёрна, а затем отправляем их в генераторы ботов. Первое число, полученное из генератора, мы используем как индекс для массива из ников игроков. Второе число будет зерном для генерирования истории матчей. Третье у нас используется для генерирования истории турнира. И т.п.
В этой иерархии могут применяться разные генераторы. Например, когда нам необходимо создать какую-то короткую последовательность, мы использовали перемешанный конгруэнтный генератор. А когда нам нужно было создать длинную историю матча, то использовали генератор Unity.
Мы разобрали наиболее популярные алгоритмы генераторов псевдослучайных чисел, рассмотрели альтернативу в виде хеш-функций, узнали, как их оптимизировать и прошлись по комбинированным подходам к генерированию псевдослучайных чисел. Надеюсь, что вам это было полезно!
JavaScript, Node.JS
Рекомендация: подборка платных и бесплатных курсов таргетированной рекламе – https://katalog-kursov.ru/
Вы когда-нибудь задумывались, как работает Math.random()? Что такое случайное число и как оно получается? А представьте вопрос на собеседовании?—?напишите свой генератор случайных чисел в пару строк кода. И так, что же это такое, случайность и возможно ли ее предсказать?
Меня очень увлекают различные IT головоломки и задачки и генератор случайных чисел — одна из таких задачек. Обычно в своем телеграм канале я разбираю всякие головоломки и разные задачи с собеседований. Задача про генератор случайных чисел набрала большую популярность и мне захотелось увековечить ее в недрах одного из авторитетных источников информации — то бишь здесь, на Хабре.
Данный материал будет полезен всем тем фронтендерам и Node.js разработчикам, кто на острие технологий и хочет попасть в блокчейн проект/стартап, где вопросы про безопасность и криптографию, хотя бы на базовом уровне, спрашивают даже у фронтендеров.
Генератор псевдослучайных чисел и генератор случайных чисел
Для того, чтобы получить что-то случайное, нам нужен источник энтропии, источник некого хаоса из который мы будем использовать для генерации случайности.
Этот источник используется для накопления энтропии с последующим получением из неё начального значения (initial value, seed), которое необходимо генераторам случайных чисел (ГСЧ) для формирования случайных чисел.
Генератор ПсевдоСлучайных Чисел использует единственное начальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел всегда формирует случайное число, имея в начале высококачественную случайную величину, которая берется из различных источников энтропии.
Энтропия?—?это мера беспорядка. Информационная энтропия?—?мера неопределённости или непредсказуемости информации.
Выходит, что чтобы создать псевдослучайную последовательность нам нужен алгоритм, который будет генерить некоторую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не менее, давайте пофантазируем, как бы могли написать свой генератор случайных чисел, если бы у нас не было Math.random()
ГПСЧ имеет некоторый алгоритм, который можно воспроизвести.
ГСЧ?—?это получение чисел полностью из какого либо шума, возможность просчитать который стремится к нулю. При этом в ГСЧ есть определенные алгоритмы для выравнивания распределения.
Придумываем свой алгоритм ГПСЧ
Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG)?—?алгоритм, порождающий последовательность чисел, элементы которой почти независимы друг от друга и подчиняются заданному распределению (обычно равномерному).
Мы можем взять последовательность каких-то чисел и брать от них модуль числа. Самый простой пример, который приходит в голову. Нам нужно подумать, какую последовательность взять и модуль от чего. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:
function* rand() {
const n = 100;
const mod = 2;
let i = 0;
while (true) {
yield i % mod;
if (i++ > n) i = 0;
}
}
let i = 0;
for (let x of rand()) {
if (i++ > 100) break;
console.log(x);
}
Эта функция генерит нам последовательность 01010101010101… и назвать ее даже псевдослучайной никак нельзя. Чтобы генератор был случайным, он должен проходить тест на следующий бит. Но у нас не стоит такой задачи. Тем не менее даже без всяких тестов мы можем предсказать следующую последовательность, значит такой алгоритм в лоб не подходит, но мы в нужном направлении.
А что если взять какую-то известную, но нелинейную последовательность, например число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже подумать на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с какой-то неизвестной точки. Пример такого алгоритма, с последовательностью на базе PI и с изменяемым модулем:
const vector = [...Math.PI.toFixed(48).replace('.','')];
function* rand() {
for (let i=3; i<1000; i++) {
if (i > 99) i = 2;
for (let n=0; n<vector.length; n++) {
yield (vector[n] % i);
}
}
}
Но в JS число PI можно вывести только до 48 знака и не более. Поэтому предсказать такую последовательность все так же легко и каждый запуск такого генератора будет выдавать всегда одни и те же числа. Но наш генератор уже стал показывать числа от 0 до 9.
Мы получили генератор чисел от 0 до 9, но распределение очень неравномерное и каждый раз он будет генерировать одну и ту же последовательность.
Мы можем взять не число Pi, а время в числовом представлении и это число рассматривать как последовательность цифр, причем для того, чтобы каждый раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш алгоритм нашего ГПСЧ будет выглядеть так:
function* rand() {
let newNumVector = () => [...(+new Date)+''].reverse();
let vector = newNumVector();
let i=2;
while (true) {
if (i++ > 99) i = 2;
let n=-1;
while (++n < vector.length) yield (vector[n] % i);
vector = newNumVector();
}
}
// TEST:
let i = 0;
for (let x of rand()) {
if (i++ > 100) break;
console.log(x)
}
Вот это уже похоже на генератор псевдослучайных чисел. И тот же Math.random()?—?это ГПСЧ, про него мы поговорим чуть позже. При этом у нас каждый раз первое число получается разным.
Собственно на этих простых примерах можно понять как работают более сложные генераторы случайных числе. И есть даже готовые алгоритмы. Для примера разберем один из них?—?это Линейный конгруэнтный ГПСЧ(LCPRNG).
Линейный конгруэнтный ГПСЧ
Линейный конгруэнтный ГПСЧ(LCPRNG)?—?это распространённый метод для генерации псевдослучайных чисел. Он не обладает криптографической стойкостью. Этот метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой формулой. Получаемая последовательность зависит от выбора стартового числа?—?т.е. seed. При разных значениях seed получаются различные последовательности случайных чисел. Пример реализации такого алгоритма на JavaScript:
const a = 45;
const c = 21;
const m = 67;
var seed = 2;
const rand = () => seed = (a * seed + c) % m;
for(let i=0; i<30; i++)
console.log( rand() )
Многие языки программирования используют LСPRNG (но не именно такой алгоритм(!)).
Как говорилось выше, такую последовательность можно предсказать. Так зачем нам ГПСЧ? Если говорить про безопасность, то ГПСЧ?—?это проблема. Если говорить про другие задачи, то эти свойства?—?могут сыграть в плюс. Например для различных спец эффектов и анимаций графики может понадобиться частый вызов random. И вот тут важны распределение значений и перформанс! Секурные алгоритмы не могут похвастать скоростью работы.
Еще одно свойство?—?воспроизводимость. Некоторые реализации позволяют задать seed, и это очень полезно, если последовательность должна повторяться. Воспроизведение нужно в тестах, например. И еще много других вещей существует, для которых не нужен безопасный ГСЧ.
Как устроен Math.random()
Метод Math.random() возвращает псевдослучайное число с плавающей запятой из диапазона [0, 1), то есть, от 0 (включительно) до 1 (но не включая 1), которое затем можно отмасштабировать до нужного диапазона. Реализация сама выбирает начальное зерно для алгоритма генерации случайных чисел; оно не может быть выбрано или сброшено пользователем.
Как устроен алгоритм Math.random()?—?интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:
uint32_t state0 = 1;
uint32_t state1 = 2;
uint32_t mwc1616() {
state0 = 18030 * (state0 & 0xffff) + (state0 >> 16);
state1 = 30903 * (state1 & 0xffff) + (state1 >> 16);
return (state0 << 16) + (state1 & 0xffff);
}Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.
Предсказываем Math.random()
Чем это было чревато? Есть такой квест: alf.nu/ReturnTrue
В нем есть задача:
{
let rand = Math.random();
function random4(x) {
return rand === x;
}
}
random4(???)
Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:
random4(function(){var A=18030,B=36969,F=65535,Z=16,M=Math,I=M.imul,c=M.random,M=M.pow(2,32),k,d,g=c()*M,h=c()*M;for(k=0;F^k&&(c=I(A,g>>>Z)+k++)&F^h>>>Z;);for(k=0;F^k&&(d=I(B,g&F)+k++)&F^h&F;);for(k=2;k—;g=c<<Z|d&F)c=c/A|c%A<<Z,d=d/B|d%B<<Z;return(g<0?g+M:g)/M}())
Этот код работал в 70% случаев для Chrome < 49 и Node.js < 5. Рома Дворнов, как всегда, показал чудеса магии, которая не что иное, как глубокое понимание внутренних механизмов браузеров. Я все жду, когда Роман сделает доклад на основе этих событий или напишет более подробную статью.
Что здесь происходит? Все дело в том, что алгоритм можно предсказать. Чтобы это было нагляднее, можно сгенерировать картинку случайных пикселей. На сайте есть такой генератор. Вот что было, когда в браузере был алгоритм MWC1616:
Видите эти равномерности на левом слайде? Изображение показывает проблему с распределением значений. На картинке слева видно, что значения местами сильно группируются, а местами выпадают большие фрагменты. Как следствие?—?числа можно предсказать.
Выходит что мы можем отреверсить Math.random() и предсказать, какое было загадано число на основе того, что получили в данный момент времени. Для этого получаем два значения через Math.random(). Затем вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние можем предсказывать следующие значения Math.random() при этом не меняя внутреннее состояние. Меняем код так так, чтобы вместо следующего возвращалось предыдущее значение. Собственно все это и описано в коде-решении для задачи random4. Но потом алгоритм изменили (подробности читайте в спеке). Его можно будет сломать, как только у нас в JS появится нормальная работа с 64 битными числами. Но это уже будет другая история.
Новый алгоритм выглядит так:
uint64_t state0 = 1;
uint64_t state1 = 2;
uint64_t xorshift128plus() {
uint64_t s1 = state0;
uint64_t s0 = state1;
state0 = s0;
s1 ^= s1 << 23;
s1 ^= s1 >> 17;
s1 ^= s0;
s1 ^= s0 >> 26;
state1 = s1;
return state0 + state1;
}
Его все так же можно будет просчитать и предсказать. Но пока у нас нет “длинной математики” в JS. Можно попробовать через TypedArray сделать или использовать специальные библиотеки. Возможно кто-то однажды снова напишет предсказатель. Возможно это будешь ты, читатель. Кто знает 😉
Сrypto Random Values
Метод Math.random() не предоставляет криптографически стойкие случайные числа. Не используйте его ни для чего, связанного с безопасностью. Вместо него используйте Web Crypto API (API криптографии в вебе) и более точный метод window.crypto.getRandomValues().
Пример генерации случайного числа:
let [rvalue] = crypto.getRandomValues(new Uint8Array(1));
console.log( rvalue )
Но, в отличие от ГПСЧ Math.random(), этот метод очень ресурсоемкий. Дело в том, что данный генератор использует системные вызовы в ОС, чтобы получить доступ к источникам энтропии (мак адрес, цпу, температуре, etc…).
Содержание:развернуть
- Как работают случайные числа
- Модуль random
-
Случайные целые числа (int)
-
Случайные вещественные числа (float)
-
Случайные элементы из последовательности
-
Управление генератором
-
Вероятностное распределение
- Best practices
-
Случайная задержка (random sleep)
-
Случайны элемент из списка (с учетом веса)
-
Случайный пароль
Случайные числа применяются в программировании в разных случаях, например, для моделирования процессов и в видеоиграх. Для начала разберёмся, какую последовательность можно назвать случайной.
Случайной последовательностью называют набор элементов, полученных таким образом, что любой элемент их этого набора никак не связан ни с каким другим элементом. При этом в программировании обычно последовательность не является строго случайной — в ней для генерации следующего элемента используется предыдущий.
Как работают случайные числа
Полностью случайные числа генерируются истинным генератором случайных чисел (TRNG). Их можно получить, например, бросанием кубика или доставанием шаров из урны. Так как подобных устройств нет в компьютере, то в нем можно получить только “псевдослучайные” числа.
В Python, как и во всех остальных языках программирования, используется генератор псевдослучайных чисел, который выдает как будто случайные, но воспроизводимые числа.
Чтобы понять, как работают генераторы псевдослучайных чисел, рассмотрим работу одного из первых подобных генераторов. Его алгоритм работы был разработан Нейманом. В нем первое число возводят в квадрат, а потом из полученного результата берут средние цифры. Например, первое число 281, возводим его в квадрат, получаем 78961 и берем три цифры, находящиеся в середине – 896. После этого для генерации следующего числа используем 896.
Модуль random
В модуле random реализованы различные генераторы псевдослучайных чисел. Здесь присутствуют методы, с помощью которых можно получить равномерное, Гауссовское, бета и гамма распределения и другие функции. Практически все они зависят от метода random(). В Python, в качестве основного, используется генератор псевдослучайных чисел Mersenne Twister, который выдает 53-х битные вещественные числа.
👉 Как использовать: чтобы начать использовать встроенные генераторы случайных чисел, нужно сначала подключить модуль рандом:
import random
После этого можно вызывать методы модуля random:
random.randint(0, 125)
В модуле random существуют методы для генерации целых чисел, с плавающей точкой, для работы с последовательностями. Кроме этого существуют функции для управления генератором и генерации различных последовательностей. Рассмотрим основные из этих методов.
Случайные целые числа (int)
Перечислим основные функции, которые есть в модуле random для выдачи случайных целых чисел.
randint
Функция randint(a, b) получает на вход два целых числа и возвращает случайное значение из диапазона [a, b] (a и b входят в этот диапазон).
import random
random_number = random.randint(0, 125)
print(random_number)
> 113
randrange
В функцию randrange(start, stop[, step]) передают три целых числа:
start– начало диапазона (входит в последовательность);stop– конец диапазона (в последовательность не входит);step– шаг генерации (если на его месте написать 0, получим ошибку “ValueError”).
На выходе функция выдает случайное число в заданном диапазоне.
import random
random_number = random.randrange(1, 100, 2)
print(random_number)
> 43
Случайные вещественные числа (float)
Перечислим функции, которые выдают вещественные числа.
random
Функция random() выдает вещественные числа, в диапазоне [0.0, 1.0) (включая 0.0, но не включая 1.0).
import random
random_number = random.random()
print(random_number)
> 0.47673250896173136
uniform
Сгенерировать число с плавающей точкой можно с помощью функции uniform(a, b). При этом полученное число будет в диапазоне [a, b) или [a, b] (a входит в диапазон, а вхождение b зависит от округления).
import random
random_number = random.uniform(7.3, 10.5)
print(random_number)
> 10.320165816501492
Случайные элементы из последовательности
В модуле random языка Python есть несколько функций, которые можно применять для работы с последовательностями.
choice
С помощью функции choice(seq) можно выбрать один элемент из набора данных. В качестве единственного аргумента в функцию передаётся последовательность. Если последовательность будет пустой (то есть в ней не будет ни одного элемента), получим ошибку “IndexError”.
import random
seq = [10, 11, 12, 13, 14, 15]
random_element = random.choice(seq)
print(random_element)
> 12
choices
С помощью функции choices(seq [, weights, cum_weights, k]) можно выбрать 1 или несколько элементов из набора данных. weights, cum_weights и k — необязательные параметры.
weights— список относительных весов;cum_weights— список кумулятивных (совокупных) весов, например weights [10, 5, 30, 5] эквивалентен cum_weights [10, 15, 45, 50].k— длина возвращаемого списка (она может быть больше длины переданной последовательности и элементы могут дублироваться).
import random
seq = [1, 2, 3, 4, 5, 6]
random_elements = random.choices(seq, weights=[20, 1.1, 1, 2.1, 10, 1], k=4)
print(random_elements)
> [5, 1, 1, 5]
shuffle
Перемешать элементы набора данных можно с помощью функции shuffle(x[, random]).
х— последовательность;random(необязательный параметр) — задает метод вероятностных распределений. Этот параметр не рекомендуется использовать в версии Python 3.9, а в версии 3.11 его поддержка будет прекращена.
shuffle перемешивает переданную последовательность, и возвращает None.
import random
seq = ["Cappuccino", "Latte", "Espresso", "Americano"]
random.shuffle(seq)
print(seq)
> ['Espresso', 'Americano', 'Latte', 'Cappuccino']
sample
Чтобы выбрать какое-то количество элементов из набора данных можно воспользоваться функцией sample(х, k).
х— последовательность;k— количество элементов новой подпоследовательности.
На выходе получаем k уникальных случайных элементов из последовательности.
Если в исходной последовательности есть неуникальные (повторяющиеся) элементы, то каждый их них может появиться в новом списке.
import random
seq = [10, 11, 12, 11, 14, 11]
random_seq = random.sample(seq, 4)
print(random_seq)
> [10, 11, 11, 14]
Управление генератором
Генерация чисел в Python не совсем случайна и зависит от состояния генератора случайных чисел. Рассмотрим функции, с помощью которых можно управлять состоянием этого генератора.
getstate
Метод getstate() модуля random возвращает объект, в котором записано текущим состояние генератора случайных чисел. Его можно использовать для восстановления состояния генератора. Эта функция не имеет параметров.
import random
print(random.getstate())
> (3, (2147483648, 3570748448, 2839542888, 4273933825, 4291584237, ...
setstate
Метод setstate(state) применяется для восстановления состояния генератора случайных чисел. Обычно его используют совместно с методом getstate(). В качестве параметра в функцию передается объект состояния генератора, полученный, например, с помощью функции getstate().
import random
state = random.getstate() # сохраняем текущее состояние генератора
random_number_1 = random.random() # получаем случайное число
print(random_number_1)
# > 0.42164837822065193 # первое случайное число
random_number_2 = random.random()
print(random_number_2)
# > 0.2486825504535808 # второе случайное число
random.setstate(state) # восстанавливаем состояние генератора
random_number_3 = random.random() # снова генерируем число
print(random_number_3)
# > 0.42164837822065193 # новое число равное первому, сгенерированному с тем же состояние генератора
seed
Генератору случайных чисел нужно число, основываясь на котором он сможет начать генерировать случайные значения.
Задать начальное значение можно с помощью метода seed(a=None, version=2).
а— начальное число, с которого начинается генерация. Этот параметр не обязательный. Если он не задан, используется текущее системное время (или доступный механизм генерации, предоставляемый ОС);version— стратегия интерпретации первого аргумента. По умолчанию используется версия 2, при которой str, bytes и bytearray преобразуются в int. Версия 1 (используется для совместимости со старыми версиями Python) и в ней для str и bytes генерирует более узкий диапазон начальных значений.
Вероятностное распределение
В теории вероятностей важную роль играет понятие распределение вероятностей. Оно показывает с какой вероятность может наступить каждое из возможных событий. С его помощью можно моделировать как наступление дискретных событий (например, бросание монеты, количество телефонных разговоров за неделю, количество пассажиров в автобусе), так и непрерывных (например, длительность разговора, количество осадков за год, расход электричества за месяц).
Для наглядности рассмотрим самое распространенное нормальное распределение вероятностей. На рисунке ниже приведена кривая нормального распределения.
В модуле random существуют функции, которые позволяют использовать различные методы вероятностных распределений:
triangular(a, b, mode)— генерирует случайное вещественное число, находящееся в диапазоне от a до b. По умолчанию эти параметры равны: а = 0, b = 1. Третий параметр mode задает среднюю точку вероятности распределения. (подробнее про треугольное распределение тут).betavariate(alpha, beta)— генерирует случайные числа соответствующие параметрам бета-распределения. Возвращаемые значения лежат в диапазоне от 0 до 1.expovariate(lambd)— можно получить случайные значения, соответствующие экспоненциальному распределению. Если lambd положительное, то на выходе будут значения от 0 до +∞, а если отрицательное, то от -∞ до 0.gammavariate(alpha, beta)— на выходе получаются случайные числа, соответствующие гамма распределению. Параметры alpha и beta, передаваемые в функцию должны быть больше 0.gauss(mu, sigma)— на выходе получаются случайные числа, которые соответствуют Гауссовому распределению. В этот метод передаются два параметра: mu — среднее значение и sigma — среднеквадратичное отклонение.lognormvariate(mu, sigma)— генерирует случайные значения соответствующие логарифму нормального распределения. То есть если вычислить натуральный логарифм полученного распределения, то в результате получится нормальное распределение с параметрами mu (среднее) и sigma (среднеквадратичное отклонение).normalvariate(mu, sigma)— предназначен для генерации случайных значений подчиняющихся закону нормального распределения. В качестве параметров передаются: mu — среднее распределения и sigma — стандартное отклонение.vonmisesvariate(mu, kappa)— используется для возврата случайного числа с плавающей запятой с распределением фон Мизеса (или круговым нормальным распределением).paretovariate(alpha)— выдает случайные числа, соответствующие распределению Парето. Параметр alpha задает форму.weibullvariate(alpha, beta)— Значения, выдаваемые weibullvariate соответствуют распределению Вейбулла. Параметр alpha задает масштаб, а beta форму.
💭 Ознакомиться со всеми функциями модуля random можно на официальном сайте Python в разделе документация.
Best practices
Приведем несколько примеров использования случайных чисел.
Случайная задержка (random sleep)
Иногда необходимо сделать так, чтобы программа работала с задержками. Например, это актуально при парсинге сайта (при частых запросах некоторые сайты могут вас банить).
import random
import time
page_list = ["site.ru/page1", "site.ru/page2", "site.ru/page3"]
for page in page_list:
#
# some actions
#
time.sleep(random.randint(1, 3)) # задержка от 1 до 3 секунд
💭 Для имитации действий человека можно использовать random.uniform(1, 3) — это добавит случайные миллисекунды к вашим задержкам.
Случайны элемент из списка (с учетом веса)
Дано: веб-сайт. В базе данных 4 баннера, к каждому баннеру указан вес (приоритет к показу).
Необходимо рандомно показывать на сайте 1 баннер, в зависимости от его веса.
import random
# данные из БД
hero_banners = [
{
"id": 1,
"name": "SupermanBanner",
"weight": 5,
},
{
"id": 2,
"name": "BatmanBanner",
"weight": 40,
},
{
"id": 3,
"name": "FlashBanner",
"weight": 5,
},
{
"id": 4,
"name": "AquamanBanner",
"weight": 40,
}
]
banner_weights = [banner['weight'] for banner in hero_banners]
my_banner = random.choices(hero_banners, banner_weights)[0]
print(my_banner)
> {'id': 2, 'name': 'BatmanBanner', 'weight': 40}
Случайный пароль
С помощью генератора случайных чисел можно создавать пароли. Например, сгенерировать стойкий пароль можно так:
import random
import string
pwd_length = 0
while pwd_length < 12:
pwd_length = int(input('Укажите длину пароля (от 12 символов): '))
# набор данных (заглавные и строчные буквы, цифры, символы пунктуации)
UPPERCASE_CHARACTERS = string.ascii_uppercase
LOWERCASE_CHARACTERS = string.ascii_lowercase
DIGITS = string.digits
SYMBOLS = string.punctuation
# весь набор
combined_list = UPPERCASE_CHARACTERS + LOWERCASE_CHARACTERS + DIGITS + SYMBOLS
# случайный элемент из каждого набора
rand_upper = random.choice(UPPERCASE_CHARACTERS)
rand_lower = random.choice(LOWERCASE_CHARACTERS)
rand_digit = random.choice(DIGITS)
rand_symbol = random.choice(SYMBOLS)
#
temp_pwd = random.sample(combined_list, pwd_length - 4) + [rand_upper, rand_lower, rand_digit, rand_symbol]
random.shuffle(temp_pwd)
password = "".join(temp_pwd)
print(password)
> Укажите длину пароля (от 12 символов): 12
> JFyc;6-ICxuQ
В данном примере будет сгенерирован пароль, содержащий минимум 12 символов, среди которых точно будет маленькая буква, большая буква, цифра и символ.
Методы модуля random позволяют получить случайные данные с использованием Mersenne Twister. Однако имейте в виду, что данный способ не является криптографически безопасным (для генерирования паролей есть более надежные варианты).
Кроме модуля random, в Python существуют альтернативные модули, позволяющие получить случайное значения:
- numpy.random — как
random, но для массивов; - os — в состав входит
urandom()[криптографически безопасный]; - secrets — модуль для генерации безопасных случайных чисел, байтов и строк [криптографически безопасный];
- uuid — содержит нескольких функций для создания 128-битных идентификаторов [криптографически безопасный].
Что такое случайность в компьютере? Как происходит генерация случайных чисел? В этой статье мы постарались дать простые ответы на эти вопросы.
В программном обеспечении, да и в технике в целом существует необходимость в воспроизводимой случайности: числа и картинки, которые кажутся случайными, на самом деле сгенерированы определённым алгоритмом. Это называется псевдослучайностью, и мы рассмотрим простые способы создания псевдослучайных чисел. В конце статьи мы сформулируем простую теорему для создания этих, казалось бы, случайных чисел.
Определение того, что именно является случайностью, может быть довольно сложной задачей. Существуют тесты (например, колмогоровская сложность), которые могут дать вам точное значение того, насколько случайна та или иная последовательность. Но мы не будем заморачиваться, а просто попробуем создать последовательность чисел, которые будут казаться несвязанными между собой.
Часто требуется не просто одно число, а несколько случайных чисел, генерируюемых непрерывно. Следовательно, учитывая начальное значение, нам нужно создать другие случайные числа. Это начальное значение называется семенем, и позже мы увидим, как его получить. А пока давайте сконцентрируемся на создании других случайных значений.
Создание случайных чисел из семени
Один из подходов может заключаться в том, чтобы применить какую-то безумную математическую формулу к семени, а затем исказить её настолько, что число на выходе будет казаться непредсказуемым, а после взять его как семя для следующей итерации. Вопрос только в том, как должна выглядеть эта функция искажения.
Давайте поэкспериментируем с этой идеей и посмотрим, куда она нас приведёт.
Функция искажения будет принимать одно значение, а возвращать другое. Назовём её R.
R(Input) -> Output
Начнём с того, что R – это простая функция, которая всего лишь прибавляет единицу.
R(x) = x + 1
Если значение нашего семени 1, то R создаст ряд 1, 2, 3, 4, … Выглядит совсем не случайно, но мы дойдём до этого. Пусть теперь R добавляет константу вместо 1.
R(x) = x + c
Если с равняется, например, 7, то мы получим ряд 1, 8, 15, 22, … Всё ещё не то. Очевидно, что мы упускаем то, что числа не должны только увеличиваться, они должны быть разбросаны по какому-то диапазону. Нам нужно, чтобы наша последовательность возвращалась в начало – круг из чисел!
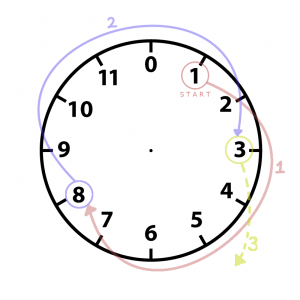
Числовой круг
Посмотрим на циферблат часов: наш ряд начинается с 1 и идёт по кругу до 12. Но поскольку мы работаем с компьютером, пусть вместо 12 будет 0.
Теперь начиная с 1 снова будем прибавлять 7. Прогресс! Мы видим, что после 12 наш ряд начинает повторяться, независимо от того, с какого числа начать.
Здесь мы получаем очень важно свойство: если наш цикл состоит из n элементов, то максимальное число элементов, которые мы можем получить перед тем, как они начнут повторяться это n.
Теперь давайте переделаем функцию R так, чтобы она соответствовала нашей логике. Ограничить длину цикла можно с помощью оператора модуля или оператора остатка от деления.
R(x) = (x + c) % m
На этом этапе вы можете заметить, что некоторые числа не подходят для c. Если c = 4, и мы начали с 1, наша последовательность была бы 1, 5, 9, 1, 5, 9, 1, 5, 9, … что нам конечно же не подходит, потому что эта последовательность абсолютно не случайная. Становится понятно, что числа, которые мы выбираем для длины цикла и длины прыжка должны быть связаны особым образом.
Если вы попробуете несколько разных значений, то сможете увидеть одно свойство: m и с должны быть взаимно простыми.
До сих пор мы делали “прыжки” за счёт добавления, но что если использовать умножение? Умножим х на константу a.
R(x) = (ax + c) % m
Свойства, которым должно подчиняться а, чтобы образовался полный цикл, немного более специфичны. Чтобы создать верный цикл:
- (а – 1) должно делиться на все простые множители m
- (а – 1) должно делиться на 4, если m делится на 4
Эти свойства вместе с правилом, что m и с должны быть взаимно простыми составляют теорему Халла-Добелла. Мы не будем рассматривать её доказательство, но если бы вы взяли кучу разных значений для разных констант, то могли бы прийти к тому же выводу.
Выбор семени
Настало время поговорить о самом интересном: выборе первоначального семени. Мы могли бы сделать его константой. Это может пригодиться в тех случаях, когда вам нужны случайные числа, но при этом нужно, чтобы при каждом запуске программы они были одинаковые. Например, создание одинаковой карты для каждой игры.
Еще один способ – это получать семя из нового источника каждый раз при запуске программы, как в системных часах. Это пригодится в случае, когда нужно общее рандомное число, как в программе с бросанием кубика.
Конечный результат
Когда мы применяем функцию к её результату несколько раз, мы получаем рекуррентное соотношение. Давайте запишем нашу формулу с использованием рекурсии:
x(n) = (a * x(n - 1) + c) % m
Где начальное значение х – это семя, а – множитель, с – константа, m – оператор остатка от деления.
То, что мы сделали, называется линейным конгруэнтным методом. Он очень часто используется, потому что он прост в реализации и вычисления выполняются быстро.
В разных языках программирования реализация линейного конгруэнтного метода отличается, то есть меняются значения констант. Например, функция случайных чисел в libc (стандартная библиотека С для Linux) использует m = 2 ^ 32, a = 1664525 и c = 1013904223. Такие компиляторы, как gcc, обычно используют эти значения.
Заключительные замечания
Существуют и другие алгоритмы генерации случайных чисел, но линейный конгруэнтный метод считается классическим и лёгким для понимания. Если вы хотите глубже изучить данную тему, то обратите внимание на книгу Random Numbers Generators, в которой приведены элегантные доказательства линейного конгруэнтного метода.
Генерация случайных чисел имеет множество приложений в области информатики и особенно важна для криптографии.
На этом всё, спасибо что прочитали!
Оригинал статьи
В данной статье мы рассмотрим процесс генерации случайных данных и чисел в Python. Для этого будет использован модуль random и некоторые другие доступные модули. В Python модуль random реализует генератор псевдослучайных чисел для различных распределений, включая целые и вещественные числа с плавающей запятой.
Содержание
- Как использовать модуль random в Python
- Генерация случайных чисел в Python
- Выбор случайного элемента из списка
- Python функции модуля random
- Случайное целое число — randint(a, b)
- Генерация случайного целого числа — randrange()
- Выбор случайного элемента из списка choice()
- Метод sample(population, k)
- Случайные элементы из списка — choices()
- Генератор псевдослучайных чисел — seed()
- Перемешивание данных — shuffle()
- Генерации числа с плавающей запятой — uniform()
- triangular(low, high, mode)
- Генератор случайной строки в Python
- Криптографическая зашита генератора случайных данных в Python
- getstate() и setstate() в генераторе случайных данных Python
- Состояние генератора getstate()
- Восстанавливает внутреннее состояние генератора — setstate()
- Зачем нужны функции getstate() и setstate()
- Numpy.random — Генератор псевдослучайных чисел
- Генерация случайного n-мерного массива вещественных чисел
- Генерация случайного n-мерного массива целых чисел
- Выбор случайного элемента из массива чисел или последовательности
- Генерация случайных универсально уникальных ID
- Игра в кости с использованием модуля random в Python
Список методов модуля random в Python:
| Метод | Описание |
|---|---|
| seed() | Инициализация генератора случайных чисел |
| getstate() | Возвращает текущее внутренне состояние (state) генератора случайных чисел |
| setstate() | Восстанавливает внутреннее состояние (state) генератора случайных чисел |
| getrandbits() | Возвращает число, которое представляет собой случайные биты |
| randrange() | Возвращает случайное число в пределах заданного промежутка |
| randint() | Возвращает случайное число в пределах заданного промежутка |
| choice() | Возвращает случайный элемент заданной последовательности |
| choices() | Возвращает список со случайной выборкой из заданной последовательности |
| shuffle() | Берет последовательность и возвращает ее в перемешанном состоянии |
| sample() | Возвращает заданную выборку последовательности |
| random() | Возвращает случайное вещественное число в промежутке от 0 до 1 |
| uniform() | Возвращает случайное вещественное число в указанном промежутке |
| triangular() | Возвращает случайное вещественное число в промежутке между двумя заданными параметрами. Также можно использовать параметр mode для уточнения середины между указанными параметрами |
| betavariate() | Возвращает случайное вещественное число в промежутке между 0 и 1, основываясь на Бета-распределении, которое используется в статистике |
| expovariate() | Возвращает случайное вещественное число в промежутке между 0 и 1, или же между 0 и -1, когда параметр отрицательный. За основу берется Экспоненциальное распределение, которое используется в статистике |
| gammavariate() | Возвращает случайное вещественное число в промежутке между 0 и 1, основываясь на Гамма-распределении, которое используется в статистике |
| gauss() | Возвращает случайное вещественное число в промежутке между 0 и 1, основываясь на Гауссовом распределении, которое используется в теории вероятности |
| lognormvariate() | Возвращает случайное вещественное число в промежутке между 0 и 1, основываясь на Логнормальном распределении, которое используется в теории вероятности |
| normalvariate() | Возвращает случайное вещественное число в промежутке между 0 и 1, основываясь на Нормальном распределении, которое используется в теории вероятности |
| vonmisesvariate() | Возвращает случайное вещественное число в промежутке между 0 и 1, основываясь на распределении фон Мизеса, которое используется в направленной статистике |
| paretovariate() | Возвращает случайное вещественное число в промежутке между 0 и 1, основываясь на распределении Парето, которое используется в теории вероятности |
| weibullvariate() | Возвращает случайное вещественное число в промежутке между 0 и 1, основываясь на распределении Вейбулла, которое используется в статистике |
Цели данной статьи
Далее представлен список основных операций, которые будут описаны в руководстве:
- Генерация случайных чисел для различных распределений, которые включают целые и вещественные числа с плавающей запятой;
- Случайная выборка нескольких элементов последовательности
population; - Функции модуля random;
- Перемешивание элементов последовательности. Seed в генераторе случайных данных;
- Генерация случайных строки и паролей;
- Криптографическое обеспечение безопасности генератора случайных данных при помощи использования модуля secrets. Обеспечение безопасности токенов, ключей безопасности и URL;
- Способ настройки работы генератора случайных данных;
- Использование
numpy.randomдля генерации случайных массивов; - Использование модуля
UUIDдля генерации уникальных ID.
В статье также даются ссылки на некоторые другие тексты сайта, связанные с рассматриваемой темой.
Для достижения перечисленных выше задач модуль random будет использовать разнообразные функции. Способы использования данных функций будут описаны в следующих разделах статьи.
Есть вопросы по Python?
На нашем форуме вы можете задать любой вопрос и получить ответ от всего нашего сообщества!
Telegram Чат & Канал
Вступите в наш дружный чат по Python и начните общение с единомышленниками! Станьте частью большого сообщества!
Паблик VK
Одно из самых больших сообществ по Python в социальной сети ВК. Видео уроки и книги для вас!
В самом начале работы необходимо импортировать модуль random в программу. Только после этого его можно будет полноценно использовать. Оператор для импорта модуля random выглядит следующим образом:
Теперь рассмотрим использование самого модуля random на простом примере:
|
import random print(“Вывод случайного числа при помощи использования random.random()”) print(random.random()) |
Вывод:
|
Вывод случайного числа при помощи использования random.random() 0.9461613475266107 |
Как видите, в результате мы получили 0.9461613475266107. У вас, конечно, выйдет другое случайно число.
random()является базовой функцией модуляrandom;- Почти все функции модуля
randomзависят от базовой функцииrandom(); random()возвращает следующее случайное число с плавающей запятой в промежутке[0.0, 1.0].
Перед разбором функций модуля random давайте рассмотрим основные сферы их применения.
Генерация случайных чисел в Python
Давайте рассмотрим самый популярный случай использования модуля random — генерацию случайного числа. Для получения случайного целого числа в Python используется функция randint().
Для генерации случайных целых чисел можно использовать следующие две функции:
randint()randrange()
В следующем примере показано, как получить случайно сгенерированное число в промежутке между 0 и 9.
|
from random import randint print(“Вывод случайного целого числа “, randint(0, 9)) print(“Вывод случайного целого числа “, randrange(0, 10, 2)) |
Вывод:
|
Вывод случайного целого числа 5 Вывод случайного целого числа 2 |
В следующих разделах статьи будут рассмотрены некоторые другие способы генерации случайного числа в Python.
Выбор случайного элемента из списка Python
Предположим, вам дан python список городов, и вы хотите вывести на экран случайно выбранный элемент из списка городов. Посмотрим, как это можно сделать:
|
import random city_list = [‘New York’, ‘Los Angeles’, ‘Chicago’, ‘Houston’, ‘Philadelphia’] print(“Выбор случайного города из списка – “, random.choice(city_list)) |
Вывод:
|
Выбор случайного города из списка – Houston |
Python функции модуля random
Рассмотрим разнообразные функции, доступные в модуле random.
Случайное целое число — randint(a, b) модуль random
- Возвращает случайное целое число
Number, такое чтоa <= Number <= b; randint(a,b)работает только с целыми числами;- Функция
randint(a,b)принимает только два параметра, оба обязательны; - Полученное в результате случайно число больше или равно
a, а также меньше или равноb.
Пример использования random.randint() в Python:
|
import random print(“Использование random.randint() для генерации случайного целого числа”) print(random.randint(0, 5)) print(random.randint(0, 5)) |
Вывод:
|
Использование random.randint() для генерации случайного целого числа 4 2 |
Генерация случайного целого числа — randrange() модуль random
Метод random.randrange() используется для генерации случайного целого числа в пределах заданного промежутка. Скажем, для получения любого числа в диапазоне между 10 и 50.
Шаг показывает разницу между каждым числом заданной последовательности. Шаг по умолчанию равен 1, однако его значение можно изменить.
Пример использования random.randrange() в Python:
|
import random print(“Генерация случайного числа в пределах заданного промежутка”) print(random.randrange(10, 50, 5)) print(random.randrange(10, 50, 5)) |
Вывод:
|
Генерация случайного числа в пределах заданного промежутка 10 15 |
Выбор случайного элемента из списка choice() модуль random
Метод random.choice() используется для выбора случайного элемента из списка. Набор может быть представлен в виде списка или python строки. Метод возвращает один случайный элемент последовательности.
Пример использования random.choice() в Python:
|
import random list = [55, 66, 77, 88, 99] print(“random.choice используется для выбора случайного элемента из списка – “, random.choice(list)) |
Вывод:
|
random.choice используется для выбора случайного элемента из списка – 55 |
Метод sample(population, k) из модуля random
Метод random.sample() используется, когда требуется выбрать несколько элементов из заданной последовательности population.
- Метод
sample()возвращает список уникальных элементов, которые были выбраны из последовательностиpopulation. Итоговое количество элементов зависит от значенияk; - Значение в
populationможет быть представлено в виде списка или любой другой последовательности.
Пример использования random.sample() в Python:
|
import random list = [2, 5, 8, 9, 12] print (“random.sample() “, random.sample(list,3)) |
Вывод:
|
random.sample() [5, 12, 2] |
Случайные элементы из списка — choices() модуль random
random.choices(population, weights=None, *, cum_weights=None, k=1)- Метод
random.choices()используется, когда требуется выбрать несколько случайных элементов из заданной последовательности. - Метод
choices()был введен в версии Python 3.6. Он также позволяет повторять несколько раз один и тот же элемент.
Пример использования random.choices() в Python:
|
import random # Выборка с заменой list = [20, 30, 40, 50 ,60, 70, 80, 90] sampling = random.choices(list, k=5) print(“Выборка с методом choices “, sampling) |
Вывод:
|
Выборка с методом choices [30, 20, 40, 50, 40] |
Генератор псевдослучайных чисел — seed() модуль random
- Метод
seed()используется для инициализации генератора псевдослучайных чисел в Python; - Модуль
randomиспользует значение изseed, или отправной точки как основу для генерации случайного числа. Если значенияseedнет в наличии, тогда система будет отталкиваться от текущего времени.
Пример использования random.seed() в Python:
|
import random random.seed(6) print(“Случайное число с семенем “,random.random()) print(“Случайное число с семенем “,random.random()) |
Вывод:
|
Random number with seed 0.793340083761663 Random number with seed 0.793340083761663 |
Перемешивание данных — shuffle() из модуля random
Метод random.shuffle() используется для перемешивания данных списка или другой последовательности. Метод shuffle() смешивает элементы списка на месте. Самый показательный пример использования — тасование карт.
Пример использования random.shuffle() в Python:
|
list = [2, 5, 8, 9, 12] random.shuffle(list) print (“Вывод перемешанного списка “, list) |
Вывод:
|
Вывод перемешанного списка [8, 9, 2, 12, 5] |
Генерации числа с плавающей запятой — uniform() модуль random
random.uniform()используется для генерации числа с плавающей запятой в пределах заданного промежутка- Значение конечной точки может включаться в диапазон, но это не обязательно. Все зависит от округления значения числа с плавающей запятой;
- Метод может, например, сгенерировать случайно вещественное число в промежутке между 10.5 и 25.5.
Пример использования random.uniform() в Python:
|
import random print(“Число с плавающей точкой в пределах заданного промежутка”) print(random.uniform(10.5, 25.5)) |
Вывод:
|
Число с плавающей точкой в пределах заданного промежутка 22.095283175159786 |
triangular(low, high, mode) из модуля random
Функция random.triangular() возвращает случайное вещественное число N с плавающей запятой, которое соответствует условию lower <= N <= upper, а также уточняющему значению mode.
Значение нижнего предела по умолчанию равно нулю, в верхнего — единице. Кроме того, пик аргумента по умолчанию установлен на середине границ, что обеспечивает симметричное распределение.
Функция random.triangular() используется в генерации случайных чисел для треугольного распределения с целью использования полученных значений в симуляции. Это значит, что в при генерации значения применяется треугольное распределение вероятности.
Пример использования random.triangular() в Python:
|
import random print(“Число с плавающей точкой через triangular”) print(random.triangular(10.5, 25.5, 5.5)) |
Вывод:
|
Число с плавающей точкой через triangular 16.7421565549115 |
Генератор случайной строки в Python
В данном разделе будет подробно расписано, как сгенерировать случайную строку фиксированной длины в Python.
Основные аспекты раздела:
- Генерация случайной строки фиксированной длины;
- Получение случайной алфавитно-цифровой строки, среди элементов которой будут как буквы, так и числа;
- Генерация случайного пароля, который будет содержать буквы, цифры и специальный символы.
Криптографическая зашита генератора случайных данных в Python
Случайно сгенерированные числа и данные, полученные при помощи модуля random в Python, лишены криптографической защиты. Следовательно, возникает вопрос — как добиться надежной генерации случайных чисел?
Криптографически надежный генератор псевдослучайных чисел представляет собой генератор чисел, который обладает особенностями, что делают его подходящим для использования в криптографических приложениях, где безопасность данных имеет первостепенное значение.
- Все функции криптографически надежного генератора возвращают полученные случайным образом байты;
- Значение случайных байтов, полученных в результате использования функции, зависит от источников ОС.
- Качество генерации также зависит от случайных источников ОС.
Для обеспечения криптографической надежности генерации случайных чисел можно использовать следующие подходы:
- Применение модуля secrets для защиты случайных данных;
- Использование из модуля os
os.urandom(); - Использование класса
random.SystemRandom.
Пример криптографически надежной генерации данных в Python:
|
import random import secrets number = random.SystemRandom().random() print(“Надежное число “, number) print(“Надежный токен байтов”, secrets.token_bytes(16)) |
Вывод:
|
Надежное число 0.11139538267693572 Надежный токен байтов b‘xaexa0x91*.xb6xa1x05=xf7+>r;Yxc3’ |
getstate() и setstate() в генераторе случайных данных Python
Функции getstate() и setstate() модуля random позволяют зафиксировать текущее внутреннее состояние генератора.
Используя данные функции, можно сгенерировать одинаковое количество чисел или последовательностей данных.
Состояние генератора getstate() модуль random
Функция getstate() возвращает определенный объект, зафиксировав текущее внутреннее состояние генератора случайных данных. Данное состояние передается методу setstate() для восстановления полученного состояния в качестве текущего.
На заметку: Изменив значение текущего состояния на значение предыдущего, мы можем получить случайные данные вновь. Например, если вы хотите получить аналогичную выборку вновь, можно использовать данные функции.
Восстанавливает внутреннее состояние генератора — setstate() модуль random
Функция setstate() восстанавливает внутреннее состояние генератора и передает его состоянию объекта. Это значит, что вновь будет использован тот же параметр состояния state. Объект state может быть получен при помощи вызова функции getstate().
Зачем нужны функции getstate() и setstate() ?
Если вы получили предыдущее состояние и восстановили его, тогда вы сможете оперировать одними и теми же случайными данными раз за разом. Помните, что использовать другую функцию random в данном случае нельзя. Также нельзя изменить значения заданных параметров. Сделав это, вы измените значение состояния state.
Для закрепления понимания принципов работы getstate() и setstate() в генераторе случайных данных Python рассмотрим следующий пример:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
import random number_list = [3, 6, 9, 12, 15, 18, 21, 24, 27, 30] print(“Первая выборка “, random.sample(number_list,k=5)) # хранит текущее состояние в объекте state state = random.getstate() print(“Вторая выборка “, random.sample(number_list,k=5)) # Восстанавливает состояние state, используя setstate random.setstate(state) #Теперь будет выведен тот же список второй выборки print(“Третья выборка “, random.sample(number_list,k=5)) # Восстанавливает текущее состояние state random.setstate(state) # Вновь будет выведен тот же список второй выборки print(“Четвертая выборка “, random.sample(number_list,k=5)) |
Вывод:
|
Первая выборка [18, 15, 30, 9, 6] Вторая выборка [27, 15, 12, 9, 6] Третья выборка [27, 15, 12, 9, 6] Четвертая выборка [27, 15, 12, 9, 6] |
Как можно заметить в результате вывода — мы получили одинаковые наборы данных. Это произошло из-за сброса генератора случайных данных.
Numpy.random — Генератор псевдослучайных чисел
PRNG является англоязычным акронимом, который расшифровывается как «pseudorandom number generator» — генератор псевдослучайных чисел. Известно, что в Python модуль random можно использовать для генерации случайных скалярных числовых значений и данных.
- Для генерации массива случайных чисел необходимо использовать
numpy.random(); - В модуле numpy есть пакет
numpy.random, который содержит обширный набор функций для генерации случайных n-мерных массивов для различных распределений.
Рассмотрим несколько примеров использования numpy.random в Python.
Генерация случайного n-мерного массива вещественных чисел
- Использование
numpy.random.rand()для генерации n-мерного массива случайных вещественных чисел в пределах[0.0, 1.0) - Использование
numpy.random.uniform()для генерации n-мерного массива случайных вещественных чисел в пределах[low, high)
|
import numpy random_float_array = numpy.random.rand(2, 2) print(“2 X 2 массив случайных вещественных чисел в [0.0, 1.0] n”, random_float_array,“n”) random_float_array = numpy.random.uniform(25.5, 99.5, size=(3, 2)) print(“3 X 2 массив случайных вещественных чисел в [25.5, 99.5] n”, random_float_array,“n”) |
Вывод:
|
2 X 2 массив случайных вещественных чисел в [0.0, 1.0] [[0.08938593 0.89085866] [0.47307169 0.41401363]] 3 X 2 массив случайных вещественных чисел в [25.5, 99.5] [[55.4057854 65.60206715] [91.62185404 84.16144062] [44.348252 27.28381058]] |
Генерация случайного n-мерного массива целых чисел
Для генерации случайного n-мерного массива целых чисел используется numpy.random.random_integers():
|
import numpy random_integer_array = numpy.random.random_integers(1, 10, 5) print(“1-мерный массив случайных целых чисел n”, random_integer_array,“n”) random_integer_array = numpy.random.random_integers(1, 10, size=(3, 2)) print(“2-мерный массив случайных целых чисел n”, random_integer_array) |
Вывод:
|
1–мерный массив случайных целых чисел [10 1 4 2 1] 2–мерный массив случайных целых чисел [[ 2 6] [ 9 10] [ 3 6]] |
Выбор случайного элемента из массива чисел или последовательности
- Использование
numpy.random.choice()для генерации случайной выборки; - Использование данного метода для получения одного или нескольких случайных чисел из n-мерного массива с заменой или без нее.
Рассмотрим следующий пример:
|
import numpy array =[10, 20, 30, 40, 50, 20, 40] single_random_choice = numpy.random.choice(array, size=1) print(“один случайный выбор из массива 1-D”, single_random_choice) multiple_random_choice = numpy.random.choice(array, size=3, replace=False) print(“несколько случайных выборов из массива 1-D без замены”, multiple_random_choice) multiple_random_choice = numpy.random.choice(array, size=3, replace=True) print(“несколько случайных выборов из массива 1-D с заменой”, multiple_random_choice) |
Вывод:
|
один случайный выбор из массива 1–D [40] несколько случайных выборов из массива 1–D без замены [10 40 50] несколько случайных выборов из массива 1–D с заменой [20 20 10] |
В будущих статьях будут описаны другие функции пакета random из nympy и способы их использования.
Генерация случайных универсально уникальных ID
Модуль Python UUID предоставляет неизменяемые UUID объекты. UUID является универсально уникальным идентификатором.
У модуля есть функции для генерации всех версий UUID. Используя функцию uuid.uuid4(), можно получить случайно сгенерированное уникальное ID длиной в 128 битов, которое к тому же является криптографически надежным.
Полученные уникальные ID используются для идентификации документов, пользователей, ресурсов и любой другой информации на компьютерных системах.
Пример использования uuid.uuid4() в Python:
|
import uuid # получить уникальный UUID safeId = uuid.uuid4() print(“безопасный уникальный id “, safeId) |
Вывод:
|
безопасный уникальный id fb62463a–cd93–4f54–91ab–72a2e2697aff |
Игра в кости с использованием модуля random в Python
Далее представлен код простой игры в кости, которая поможет понять принцип работы функций модуля random. В игре два участника и два кубика.
- Участники по очереди бросают кубики, предварительно встряхнув их;
- Алгоритм высчитывает сумму значений кубиков каждого участника и добавляет полученный результат на доску с результатами;
- Участник, у которого в результате большее количество очков, выигрывает.
Код программы для игры в кости Python:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
import random PlayerOne = “Анна” PlayerTwo = “Алекс” AnnaScore = 0 AlexScore = 0 # У каждого кубика шесть возможных значений diceOne = [1, 2, 3, 4, 5, 6] diceTwo = [1, 2, 3, 4, 5, 6] def playDiceGame(): “””Оба участника, Анна и Алекс, бросают кубик, используя метод shuffle””” for i in range(5): #оба кубика встряхиваются 5 раз random.shuffle(diceOne) random.shuffle(diceTwo) firstNumber = random.choice(diceOne) # использование метода choice для выбора случайного значения SecondNumber = random.choice(diceTwo) return firstNumber + SecondNumber print(“Игра в кости использует модуль randomn”) #Давайте сыграем в кости три раза for i in range(3): # определим, кто будет бросать кости первым AlexTossNumber = random.randint(1, 100) # генерация случайного числа от 1 до 100, включая 100 AnnaTossNumber = random.randrange(1, 101, 1) # генерация случайного числа от 1 до 100, не включая 101 if( AlexTossNumber > AnnaTossNumber): print(“Алекс выиграл жеребьевку.”) AlexScore = playDiceGame() AnnaScore = playDiceGame() else: print(“Анна выиграла жеребьевку.”) AnnaScore = playDiceGame() AlexScore = playDiceGame() if(AlexScore > AnnaScore): print (“Алекс выиграл игру в кости. Финальный счет Алекса:”, AlexScore, “Финальный счет Анны:”, AnnaScore, “n”) else: print(“Анна выиграла игру в кости. Финальный счет Анны:”, AnnaScore, “Финальный счет Алекса:”, AlexScore, “n”) |
Вывод:
|
Игра в кости использует модуль random Анна выиграла жеребьевку. Анна выиграла игру в кости. Финальный счет Анны: 5 Финальный счет Алекса: 2 Анна выиграла жеребьевку. Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 2 Алекс выиграл жеребьевку. Анна выиграла игру в кости. Финальный счет Анны: 10 Финальный счет Алекса: 8 |
Вот и все. Оставить комментарии можете в секции ниже.
Являюсь администратором нескольких порталов по обучению языков программирования Python, Golang и Kotlin. В составе небольшой команды единомышленников, мы занимаемся популяризацией языков программирования на русскоязычную аудиторию. Большая часть статей была адаптирована нами на русский язык и распространяется бесплатно.
E-mail: vasile.buldumac@ati.utm.md
Образование
Universitatea Tehnică a Moldovei (utm.md)
- 2014 — 2018 Технический Университет Молдовы, ИТ-Инженер. Тема дипломной работы «Автоматизация покупки и продажи криптовалюты используя технический анализ»
- 2018 — 2020 Технический Университет Молдовы, Магистр, Магистерская диссертация «Идентификация человека в киберпространстве по фотографии лица»