Как составить гистограмму математика

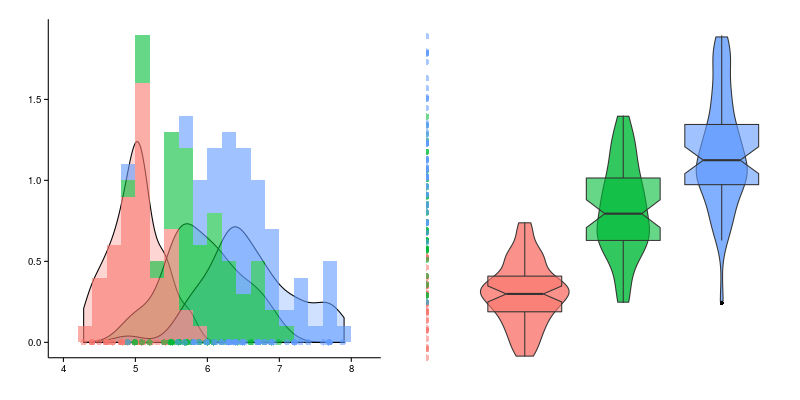
Построение полигона, гистограммы, кумуляты, огивы

Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.

• Полигон
• Гистограмма
• Кумулята и огива

Полигон

---

Полигоном частот называют
ломаную, отрезки которой соединяют точки

. Для построения полигона частот на оси
абсцисс откладывают варианты

, а на оси ординат – соответствующие им
частоты

. Такие точки

 соединяют
отрезками прямых и получают полигон частот.

Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки

. Для построения полигона относительных
частот на оси абсцисс откладывают варианты

, а на оси ординат – соответствующие им
относительные частоты (частости)

. Такие точки

 соединяют
отрезками прямых и получают полигон частот.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

---

Пример 1

Построить полигон частот и
полигон относительных частот (частостей):

Решение

Вычислим относительные
частоты (частости):

Полигон частот

Полигон относительных частот

В случае интервального ряда для
построения полигона в качестве

 берутся середины интервалов.

Гистограмма

---

В случае интервального
статистического распределения целесообразно построить гистограмму.

Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною

, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты 

. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.

В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте

, а в случае неравных интервалов высота
равна плотности относительной частоты

.

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

---

Пример 2

Построить гистограмму
частот и относительных частот (частостей)

Гистограмма частот

Гистограмма относительных частот

---

Пример 3

Построить гистограмму
частот (случай неравных интервалов).

Решение

Вычислим плотности
частоты:

Гистограмма частот

Кроме этой задачи на другой странице сайта есть

пример построения полигона и гистограммы на одном графике для интервального вариационного ряда

Кумулята и огива

---

При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.

Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву.  То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.

---

Пример 4

Построить кумулятивную
кривую:

Решение

Вычислим накопленные
частоты:

Кумулятивная кривая

Была ли эта статья полезной?

Для
наглядности строят различные графики
статистического распределения, например,
гистограмму.

Гистограмма
частот — ступенчатая фигура, состоящая
из прямоугольников, основаниями которых
служат интервалы длиной h, а высота
которых равны отношению n_i/h, где
все наблюдаемые значения разбивают на
несколько интервалов длиною h и находят
значение n_i как сумму частот тех
вариант, которые попали в i-интервал.

Для
построения гистограммы частот на оси
абсцисс откладывают интервалы, а высота
каждого столбика равна n_i/h.

Площадь
i-прямоугольника равна = (n_i/h)
·
h , т. е.
сумме частот тех значений, которые
попали в этот i-интервал.

n_i/h
h

Площадь
всей гистограммы равна количеству
выборки n (сумме всех частот n_i)

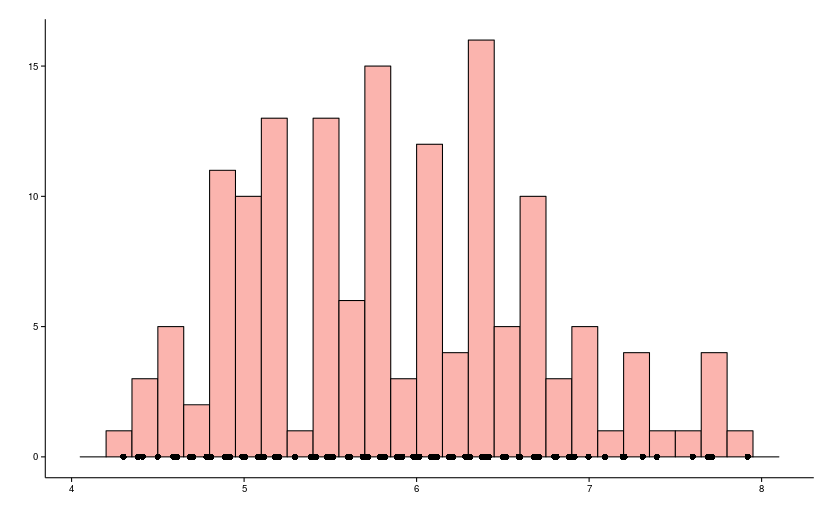
Пример:
построить гистограмму частот распределения:
в 1м столбце указан интервал, а во 2м —
сумма частот вариант:

Интервал h	Частоты ni
2-5	9
5-8	10
8-11	25
11-14	6

Строим
еще одну колонку, в которой укажем
высоту. Как написано выше, высота у нас
равна n_i/h,
и то, и другое нам известно. Интервал
(h) равен 3 (это можно проследить: 2-5=3,
8-5=3, 11-8=3 и т. д.). Итак, строим:

Интервал h	Частоты ni	Высота ni/h
2-5	9	Равно 9:3=3
5-8	10	Равно 10:3=3,3
8-11	25	Равно 25:3=8,3
11-14	6	Равно 6:3=2

Посчитаем
сумму частот (это будет площадь
гистограммы):

складываем
все n_i =
9+10+25+6= 50

Строим
гистограмму:

8

,3

3,3

3

2

2
5 8 11 14

Ось х — интервалы.

Ось
у — высота (тот столбик, который мы
рассчитывали сами)

30. Свойства статистических оценок параметров распределения: несмещённость, эффективность, состоятельность.

Пусть
требуется изучить количественный
признак ГС. В распоряжении исследователя
имеется выборка объемом n
этого количественного признака

;

; … ;

Рассматривая
эти наблюдения как независимые случайные
величины

;

; … ;

можно сказать, что найти СТАТИСТИЧЕСКУЮ
ОЦЕНКУ НЕИЗВЕСТНОГО ПАРАМЕТРА это
значит найти функцию от наблюдаемых
значений, которая и дает приближенное
значение оцениваемого параметра.

Для
того, чтобы статистические оценки давали
хорошие приближения оцениваемых
параметров, они должны удовлетворять
некоторым требованиям.

Пусть


– статистическая оценка неизвестного
параметра

(«тета»)

1. ОПР
   – НЕСМЕЩЁННОЙ называют статистическую
   оценку
   
   математическое ожидание которой равно
   оцениваемому параметру при любом объеме
   выборки т.е.
   

   ОПР
   – СМЕЩЁННОЙ называют оценку, математическое
   ожидание которой не равно оцениваемому
   параметру.

Оценка
должна быть несмещенной.

1. ОПР
   – ЭФФЕКТИВНОЙ называют статистическую
   оценку, которая имеет наименьшую
   возможную дисперсию (при заданном
   объеме выборки n)

2. ОПР
   – СОСТОЯТЕЛЬНОЙ называют статистическую
   оценку, которая при
   
   стремится к оцениваемому параметру.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Гистограмма и ящик с усами на пальцах

В этой заметке я хочу описать два типа графиков для одномерных данных, а именно

• гистограмма
• ящик с усами

Рассмотрим произвольную выборку вещественных чисел , будем обозначать порядковую статистику , такую что .

Гистограмма

Скорее всего все поменять этот тип графика из школьной или университетской программы, который выглядит приблизительно так как на картинке.

Прежде всего необходимо помнить, что значения входной выборки располагаются по оси x, а по оси y располагается число раз, которое данное значение встретилось (назовем их отсчеты). Гистограмма позволяет огрубить и сделать набор данных более компактным, при этом не умаляя его специфичность.
Важными характеристиками гистограммы являются следующие:

• число столбцов (которые называются bins или bars)
• абсолютные или плотностные отсчеты по оси y
• как сгруппированы данные

Столбцы

В подавляющем большинстве случаев гистограмма определена на отрезке , где — исходная выборка, вспомогательные константы, округляющие до ближайших “читаемых” чисел, которые в каждом случае зависят от масштаба и, обычно, это делители десятки в масштабе исходных данных. Если вдруг стало интересно, как ставить отсечки в данных, то можно посмотреть ссылку: R (pretty).

Так же обычно гистограммы делят отрезок I на подотрезки равной длины и, вот, выбор числа отрезков является искусством, хотя можно привести несколько формул:

• Правило Стёрджеса (Не фотограф).
• Правило Скотта.
• Правило Фридмана-Дьякониса.

где — число столбцов, — размер исходной выборки, — оценка стандартного отклонения, — интерквартильное расстояние, которое еще встретится ниже.

Так же можно отметить несколько правил здравого смысла:

• хорошо чтобы в большинстве столбцов было больше одного исходного значения
• каждый столбец гистограммы требует хотя бы одного пикселя по ширине, и в целом ограничение “не более 200” столбцов достаточно распространено

В противном случае, если число столбцов избыточно, а исходных данных мало, гистограмма будет напоминать штрих-код, как например на рисунке ниже.

Ось Y

Гистограммы бывают в абсолютных значениях, когда по оси y откладывается количество элементов исходной выборки попавших в каждый из интервалов, и в относительных, когда сумма столбцов нормируются на единицу, в этом случае гистограмма является оценкой плотности распределения и с точки зрения графика меняется лишь масштаб.

Так как обычная гистограмма является оценкой плотности, то мы можем суммировать столбцы и получить оценку функции вероятности следующим образом: . Два следующих графика построены по одним и тем же данным, слева не нормализованная гистограмма, справа аккумулированные значения нормализованной гистограммы.

Группировка данных

До сих пор был рассмотрен случай, когда у нас есть характеристика, на которую мы просто хотим взглянуть, обычно намного более интересно сравнивать поведение одной и той же характеристики для различных подгрупп. В таком случае гистограмма будет иметь следующий вид.

В данном случае, ширина каждого столбца для каждой группы уменьшается пропорционально числу групп и слегка сдвигаются друг относительно друга, в качестве альтернативы можно рассмотреть полупрозрачное перекрытие, которое будет выглядеть следующим образом для тех же данных.

В сухом остатке

Для отрисовки гистограммы необходимо определить

• Число столбцов
• Нужна ли нормализация и аккумулирование данных
• Способ отображения различных групп

Для отрисовки гистограммы для каждой группы требуется хранить следующие значения:

Диаграмма размаха

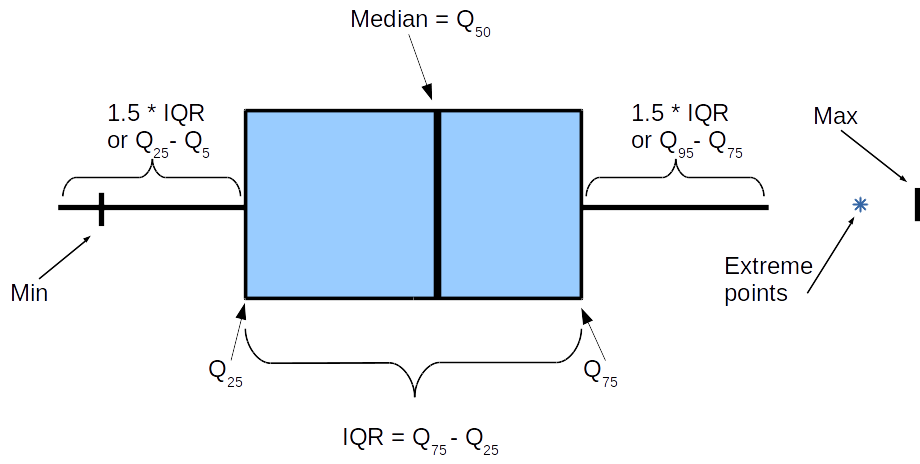
“Ящик с усами” не имеет официально устоявшегося названия, а называть его “ящиком с усами“ у меня язык не поворачивается, тем более когда ящиков несколько, а диаграмма размаха хоть и не очень частотное, но более благозвучное название. Приведем пример трех ящиков слева отображены соответствующие значения исходных данных (не являются частью диаграммы размаха). Прежде всего необходимо отметить, что в случае диаграмм размаха, исходная характеристика откладывается по оси Y, а ось X условна и представляет собой группирующую переменную.

Чтобы нарисовать ящик для одной группы про исходные данные необходимо знать всего три характеристики:

• Первый квартиль
• Медиану
• Третий квартиль

Иногда к “обязательному” набору добавляют следующие дополнительные:

Таким образом, ящик с усами в разрезе будет выглядеть следующим образом.

Некоторые моменты требуют пояснения. Ящик, то есть объект между и , практически везде ограничен этими значениями, а вот “усы” могут различаться и если вас действительно интересуют числа, необходимо уточнять, что имеется в виду в каждом отдельном случае. Самое важное это длина усов: исходим из того, что она .

Отметки минимума и максимума часто опускаются, экстремальные точки, то есть выходящие за пределы усов тоже опускаются либо рисуются точками или звездочками. В зависимости от структуры данных желание отрисовывать экстремальные значения может значительно увеличить объем данных для отрисовки диаграммы размаха.

Магическое число появилось в работе Тьюки Exploratory Data Analysis (1977) и причина его появления не очень ясна, но с тех времен ничего не менялось, многие инструменты предлагают его в качестве значения по умолчанию, но позволяют выставлять произвольное, вплоть до нуля, в этом случае, “усы” будут покрывать весь отрезок от минимального до максимального значений исходных данных.

Есть предположение, что возникло следующим образом. Ширина усов составляет , известно, что для симметричных распределений совпадает с абсолютным отклонением от медианы (MAD), которая в свою очередь, является оценкой дисперсии с коэффициентом . А значит, , мы получаем не безызвестные 3 сигмы влево, 3 сигмы вправо.
Иногда в качестве концов усов предлагается интервал , в таком случае очевидно, что всегда (если исходных данных больше 20) должны получаться точки, не попадающие внутрь интервала и поэтому их обычно игнорируют при таком подходе.

В сухом остатке

Для отрисовки “диаграммы размаха” необходимо определить:

• способ группировки данных
• длину усов
• нужно ли отмечать экстремальные значения

Для отрисовки “ящика с усами” для одной группы требуется всего 3 числа.

Класс 7

Предмет: Вероятность и статистика

Тема: «Построение
гистограмм. Шаги группировки. Решение задач»

Тип урока: изучение нового материала

Цель урока: представление данных в виде
гистограммы.

Задачи: научиться строить и анализировать гистограммы,
подбирать подходящий шаг группировки.

Актуализация опорных данных

Повторить:

– Что такое выборка, ранжированный ряд,
размах, частота, относительная частота, гистограмма.

– Привести примеры для чего используют
гистограммы (например:

1. Анализ продаж, выручки или поставок по
различным срезам:
● по периодам времени;
● по регионам;
● по филиалам/подразделениям;
● по товарам/услугам.

2. Маркетинговый анализ:
● эффективность коммуникативных акций по каналам;
● аналитика затрат на рекламу;
● количество проведенных активностей и их полезность.

3. Финансовый анализ:
● планы и динамика по выручке и прибыли;
● учет приходов и расходов денежных средств;
● количество денег на счетах.
4. Анализ производственных процессов:
● отслеживание складских запасов;
● эффективность использования мощностей;
● учет отгрузок и поставок.

5. Статистический и социодемографический
анализ, а также многое другое.

Изучение нового материала

Шаги группировки.

1 шаг.  Элементы выборки объемом n элементов
расположить в ранжированный ряд (по возрастанию или убыванию)

2 шаг.  Вычислить
размах R (разность между минимальным и максимальным значением случайной
величины):

R=x_max-x_min

3 шаг.  Разбить
вариационный ряд на k непересекающихся интервалов

Можно воспользоваться следующими
рекомендациями

Объем выборки	Число интервалов
25-40	5-6
41-60	6-8
61-100	7-10
101-200	8-12
Более 200	10-15

4 шаг.  Определить
длину одного интервала:

b=R/k

5 шаг.  5. Определить границы каждого интервала.

6 шаг.  Определить
частоты – количество ni элементов выборки, попавших в i-й интервал (элемент,
совпадающий с правой границей интервала, относится к последующему интервалу)

Наряду с частотами одновременно подсчитываются также
относительные частоты и
процент случаев относительно общего объема выборки

Полученные результаты сводятся в таблицу, называемую таблицей
частот группированной выборки.

7 шаг.  По
данным таблицы построить гистограмму.

(по горизонтальной оси – интервалы выборки, по
вертикальной оси частота или относительная частота)

8 шаг.  Описание гистограммы:

· общего количества обследованных.

· минимального и максимального значения анализируемой
величины, (с указанием в скольких процентов случаев)

· наиболее часто и редко встречающегося значения анализируемой
величины (с указанием в скольких процентов случаев)

· в каких пределах в основном лежит анализируемая величина.

· дайте качественную оценку функции плотности распределения
данной случайной величины (нормальное или отличное от нормального).

Первичное закрепление материала

Задание 1.   Результаты измерения
пульса у 25 обследованных.

70;   75;   63;   64;   72;   77;   80;   85;   79;   64;  
63;   60;   55;   56;   58;   58;   73;   72;   65;   65;   66;   68;   69;  
66;   68.

1)Элементы выборки расположим в ранжированный ряд (по
возрастанию)

55;   56;   58;   58;   60;   63;   63;   64;   64;   65;  
65;   66;   66;   68;   68;   69;   70;   72;   72;   73;   75;   77;   79;  
80;   85.

2) Вычислим размах R

R = x_max – x_min = 85 – 55 = 30 (уд./мин)

3) Разобьем вариационный ряд на k непересекающихся интервалов
(воспользуемся таблицей)

У нас 25 объектов выбираем к = 6(столбцов)

4)Определяем длину одного интервала b = R/к = 30 ׃
6 = 5 (уд./мин)

5)Определим границы каждого интервала.

Первый интервал начинается с минимального значения  55уд./мин,
заканчивается 55+5=60

Второй интервал начинается с 60уд./мин, заканчивается
60+5=65уд./мин

И т.д.

6) Строим частотную таблицу

№ столбца	Интервалы измерений пульса	Частота ni	Относительная частота (%)
1	55 ≤ х < 60	4	16
2	60 ≤ х < 65	5	20
3	65 ≤ х < 70	7	28
4	70 ≤ х < 75	4	16
5	75 ≤ х < 80	3	12
6	80 ≤ х ≤ 85	2	8

(частоту считаем в ранжированном ряду)

7) По данным таблицы строим гистограмму

8)Описываем гистограмму:

– Общее количество обследованных  25.

– Минимальное значение пульса лежит в пределах от 55 до
60уд./мин

– Максимальное значение пульса лежит в пределах от 80 до
85уд./мин

– Наиболее часто встречающийся пульс в пределах 65 – 70уд./мин
(28% случаев)

– Наиболее редко встречающийся пульс в пределах 80 – 85уд./мин
(8% случаев)

– Тахикардия ( ˃80уд./мин) наблюдается в 8% случаев

– Брадикардия (< 60уд.мин) наблюдается в 16% случаев

Задание 2.

Опрос потребления йогурта различными возрастными категориями.
Опрошено 100 человек.

Найти относительную частоту потребления йогурта разными
возрастными категориями

Построить гистограмму.

Описать гистограмму.

№ столбца	Интервалы измерений Возраст опрошенных	Частота ni	Относительная частота (%)
1	Менее 10	5
2	10 ≤ х < 20	15
3	20 ≤ х < 30	40
4	30 ≤ х < 40	25
5	40 ≤ х < 50	9
6	50 ≤ х ≤ 60	6

Домашнее задание

Задание 1.

         Ниже приведены результаты 25 измерений напряжения (в
вольтах) в бытовой электросети. Все измерения были сделаны днём в случайно
выбранные моменты времени. Ранее уже говорилось о том, что напряжение в сети
подвержено случайной изменчивости в силу многих факторов.

225 В,     227 В,     225 В,    
228 В,     225 В,

228 В,     218 В,     217 В,    
218 В,     220 В,

223 В,     225 В,     216 В,    
222 В,     224 В,

220 В,     218 В,     221 В,    
220 В,     216 В,

214 В,     219 В,     231 В,     228
В,     227 В.

Разобрать шаги группировки, построить частотную таблицу,
построить гистограмму, описать гистограмму