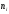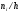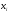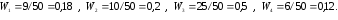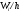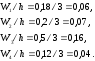Построение полигона, гистограммы, кумуляты, огивы
Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.
- Полигон
- Гистограмма
- Кумулята и огива
Полигон
Полигоном частот называют
ломаную, отрезки которой соединяют точки
. Для построения полигона частот на оси
абсцисс откладывают варианты
, а на оси ординат – соответствующие им
частоты
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки
. Для построения полигона относительных
частот на оси абсцисс откладывают варианты
, а на оси ординат – соответствующие им
относительные частоты (частости)
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 1
Построить полигон частот и
полигон относительных частот (частостей):
Решение
Вычислим относительные
частоты (частости):
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.
Гистограмма
В случае интервального
статистического распределения целесообразно построить гистограмму.
Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною
, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты
. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.
В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте
, а в случае неравных интервалов высота
равна плотности относительной частоты
.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 2
Построить гистограмму
частот и относительных частот (частостей)
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).
Решение
Вычислим плотности
частоты:
Гистограмма частот
Кроме этой задачи на другой странице сайта есть
пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.
Пример 4
Построить кумулятивную
кривую:
Решение
Вычислим накопленные
частоты:
Кумулятивная кривая
Постройка полигона и гистограммы частот
Содержание:
- Что такое полигон и гистограмма частот
- Как построить полигон частот
- Как построить гистограмму частот
- Чему равна площадь гистограммы частот
- Примеры создания полигона и гистограммы в задачах
Что такое полигон и гистограмма частот
Для наглядного представления ряда распределения используют полигон и гистограмму частот.
Определение
Полигон частот – это ломаная, соединяющая точки (x1, n1), (x2, n2),…, (xk, nk), где xi – это варианты или наблюдаемые значения, а ni – частота вариантов.
Существует также полигон относительных частот, представляющий собой ломаную, которая образуется при соединении точек (x1, W1), (x2, W2),…, (xk, Wk). Величина W является отношением частоты данного варианта к объему выборочной совокупности и имеет вид:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
(W_i=frac{n_i}n)
где n – это объем выборки.
Гистограмму используют в случае непрерывного признака.
Определение
Гистограмма частот – это фигура в виде ступеней – прямоугольников, в основании которых лежат частичные интервалы длины h, а высотами служат Wi.
Для гистограммы относительных частот основанием прямоугольников ступенчатой фигуры служат частичные интервалы длины h, а высотами – отношение Wi/h.
Как построить полигон частот
Полигон частот строится следующим образом. На оси абсцисс отмечают наблюдения значения x, на оси ординат откладывают соответствующие xi частоты ni. Точки с координатами (xi, ni), соединенные прямыми отрезками, составляют ломаную – полигон частот.
Пример
Полигон частот для выборки со следующими значениями:
xi 92, 94, 95, 96, 97, 98.
ni 1, 2, 2, 3, 1, 1.
Как построить гистограмму частот
Алгоритм построения гистограммы частот такой: на оси OX отмечаются частичные интервалы h, затем над отложенными значениями проводятся отрезки, параллельные оси OY, на расстоянии отношения плотности частоты ni/h.
Пример гистограммы частот при частичном интервале h, равном 3.
Сумма частот вариант h: 2–5, 5–8, 8–11, 11–14.
Плотность частоты ni/h: 3,3; 8,3.
Чему равна площадь гистограммы частот
Площадь отдельного прямоугольника гистограммы равна сумме частот интервала i и имеет вид:
(frac{n_ih}h=n_i)
Площадь всей гистограммы складывается из всех частот, значит, она равна объему выборки.
Примеры создания полигона и гистограммы в задачах
Задача 1
Успеваемость студентов по дисциплине «Высшая математика» представлена в виде баллов:
Баллы, x: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Количество студентов, n: 1, 1, 2, 3, 4, 4, 6, 5, 3, 3, 2, 1.
Нужно построить полигон частот по этим данным.
Решение
На основе представленной информации строим точки и соединяем их отрезками прямой. Следует заметить, что точки с координатами (0; 0) и (13; 0), которые располагаются на оси OX, имеют своими абсциссами числа на 1 меньшее и большее, чем абсциссы наиболее левой и наиболее правой точек соответственно. Полигон частот выглядит так:
Задача 2
По итогам контрольной работы по биологии среди учеников 9-го класса получена информация о доступности вопросов тестирования (отношение количества учеников, верно ответивших на вопросы, к общему числу учащихся, написавших данную работу). Результаты:
Доступность вопросов, x (%): 25–35, 35–45, 45–55, 55–65, 75–85, 85–95.
Количество вопросов, n: 1, 1, 5, 7, 7, 3, 1.
Всего в контрольной работе было 25 вопросов.
Необходимо построить гистограмму по этому ряду распределения.
Решение
Отмечаем на оси абсцисс 7 отрезков длиной 10. Эти отрезки будут основанием прямоугольников с высотами 1, 1, 5, 7, 7, 3, 1. Ступенчатая фигура, полученная в результате перечисленных действий, является искомой гистограммой.
§ 2. Введение в визуализацию данных
Как правило, использование списков данных – не самый лучший способ
представить данные в вашей работе потому что мы не можем получить много
информации о них просто взглянув на список. Есть и более удобные способы
и в этой статье мы рассмотрим 3 из них на примере следующей выборки:
30 студентов СПбГАУ набрали на интернет-тестировании следующее
количество баллов:
86
80
25
77
73
76
100
90
69
93
90
83
70
73
73
70
90
83
71
95
40
58
68
69
100
78
87
97
92
74
Листостебельная диаграмма
Одним из простейших способов как-то визуализировать данные являются
листостебельные диаграммы (stem and leaf diagrams). Для нашего
примера мы можем построить такую диаграмму:
2
5
3
4
0
5
8
6
9
8
9
7
7
3
6
0
3
3
0
1
8
4
8
6
0
3
3
7
9
0
3
0
0
5
7
2
10
0
0
Эта диаграмма состоит из стебля – чисел, стоящих слева от
вертикальной линии, которые представляют собой десятки и
листьев – соответствующих чисел справа от линии, которые являются
единицами. В общем случае, стебель строят из редко меняющихся разрядов
(десятков в нашем случае), а листья – из тех разрядов, которые меняются
часто (в нашем случае это единицы). Из такой диаграммы мы сможем быстро
получить некую информацию, например, мы видим что 2 студента набрали
максимальное количество баллов, а 3 написали тест меньше, чем на 60
баллов.
Мы также можем построить
сортированную листостебельную диаграмму (sorted stem and leaf diagram)
– она строится точно так же как и обычная, но её листья отсортированны в
проядке возрастания. Для нашего примера:
2
5
3
4
0
5
8
6
8
9
9
7
0
0
1
3
3
3
4
6
7
8
8
0
3
3
6
7
9
0
0
0
2
3
5
7
10
0
0
Такие диаграммы могут быть довольно гибкими: например мы можем разбить
элементы стебля на более мелкие диапазоны. Так, разобьём значение 80 на
два (80-84 и 85-89):
8
0
3
3
8
6
7
Как построить листостебельную диаграмму по шагам:
- Определите часто и редко меняющиеся разряды в ваших данных
- Выпишите редко меняющиеся разряды слева от линии
- Выпишите часто меняющиеся разряды справа от линии
Гистограмма частот
Листостебельная диаграмма непрактична для большой выборки, поэтому можно
использовать
гистограмму частот (frequency histogram). Сначала мы выделяем
группы каких-либо значений, например значения из примера выше мы можем
сгруппировать так:
группа
0
10
20
30
40
50
60
70
80
90
100
значения
0-9
10-19
20-29
30-39
40-49
50-59
60-69
70-79
80-89
90-99
100
Затем подсчитываем частоту для каждой группы (то есть строим таблицу
частот для групп):
x
0
10
20
30
40
50
60
70
80
90
100
f
0
0
1
0
1
1
3
10
5
7
2
И строим диаграмму частот, отмечая группы по оси
x
, а их частоты – по оси
y
:
Этот способ может быть применён к любому количественному набору данных.
Вы можете создавать группы на своё усмотрение, например, разделить
группу 80 на две: 80 и 85.
Как построить гистограмму частот по шагам:
- Сгруппируйте данные
- Постройте таблицу частот для групп
-
Постройте гистограмму, отметив по оси
x
группы, а по оси
y
частоты
Гистограмма относительных частот
До этого момента мы работали с
абсолютными частотами (absolute frequency) то есть количеством
вхождений элемента в набор данных (в случае с частотами группы –
количеством значений, входящих в группу), но мы также можем работать и с
относительными частотами.
Относительная частота (relative frequency),
ω
– отношение частоты элемента к размеру выборки или генеральной
совокупности
Мы можем построить таблицу относительных частот для нашего примера:
x
0
10
20
30
40
50
60
70
80
90
100
ω
0
0
0.033
0
0.033
0.033
0.01
0.333
0.167
0.233
0.067
И строим гистограмму, на этот раз отмечая по оси y уже относительные
частоты:
Как вы можете заметить, пропорции столбиков и общий вид гистограммы не
отличается от гистограммы абсолютных частот – изменяются лишь числа на
оси
y
.
Тем не менее, гистограмма относительных частот позволяет нам
моментально оценить какую часть данных занимает та или иная группа.
Также как и при построении гистограммы частот, при построении
гистограммы относительных частот выбор количества групп обычно зависит
от размера выборки или генеральной совокупности. Чем больше размер, тем
больше групп мы можем выделить.
Как построить гистограмму относительных частот по шагам:
- Сгруппируйте данные
- Постройте таблицу частот для групп
- Постройте таблицу относительных частот для групп
-
Постройте гистограмму, отметив по оси
x
группы, а по оси
y
– относительные частоты
Для
наглядности строят различные графики
статистического распределения, в
частности, полигон и гистограмму.
Определение.
Полигоном
частот называют ломаную, отрезки которой
соединяют точки (x1,
n1),
(x2,
n2),
…, (xk,
nk).
Для
построения полигона частот на оси
абсцисс откладывают варианты xi,
а на оси ординат – соответствующие им
частоты ni.
Точки (xi,
ni)
соединяют отрезками прямых и получают
полигон частот.
Определение.
Полигоном
относительных частот
называют ломаную, отрезки которой
соединяют точки (x1,
w1),
(x2,
w2),
…, (xk,
wk).
Для
построения полигона частот на оси
абсцисс откладывают варианты xi,
а на оси ординат wi.
Точки (xi,
wi)
соединяют отрезками прямых и получают
полигон относительных частот.
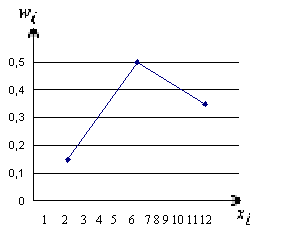
На
рисунке изображен полигон относительных
частот следующего распределения:
|
x |
1,5 |
3,5 |
5,5 |
7,5 |
|
w |
0,1 |
0,2 |
0,4 |
0,3 |
Рис.
6. Полигон относительных частот.
В
случае непрерывного признака целесообразно
строить гистограмму, для чего интервал,
в котором заключены все наблюдаемые
значения признака, разбивают на несколько
частичных интервалов длинной h
и находят для каждого частичного
интервала ni
–
сумму частот вариант, попавших в i-ый
интервал.
Определение.
Гистограммой
частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длиною h,
а высоты равны отношению
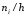
Рис.
7. Гистограмма частот.
Для
построения гистограммы частот на оси
абсцисс откладывают частичные интервалы,
а над ними проводят отрезки, параллельные
оси абсцисс, на расстоянии
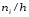
Площадь
i-го
частичного прямоугольника равна
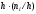
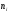
интервала; следовательно, площадь
гистограммы частот равна сумме всех
частот, то есть объему выборки n.
На
рисунке 2 изображена гистограмма частот
распределения объема n=100,
приведенного в таблице 1.
|
Частичный
длиною |
Сумма |
Плотность |
|
5 |
4 |
0,8 |
|
10 |
6 |
1,2 |
|
15 |
16 |
3,2 |
|
20 |
36 |
7,2 |
|
25 |
24 |
4,8 |
|
30 |
10 |
2,0 |
|
34 |
4 |
0,8 |
Определение.
Гистограммой
относительных частот
называют ступенчатую фигуру, состоящую
из прямоугольников, основаниями которых
служат частичные интервалы длинною h,
а высоты равны отношению
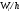
Для
построения гистограммы относительных
частот на оси абсцисс откладывают
частичные интервалы, а над ними проводят
отрезки, параллельные оси абсцисс на
расстоянии
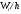
Площадьi-го
частичного прямоугольника равна
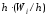
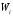
попавших вi-й
интервал. Следовательно, площадь
гистограммы относительных частот равна
сумме всех относительных частот, то
есть единице.
Примеры.
-
В
результате выборки получена следующая
таблица распределения частот.
|
|
2 |
6 |
12 |
|
|
3 |
10 |
7 |
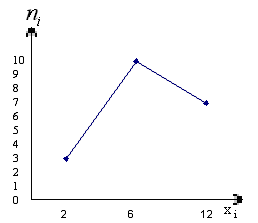
Построить
полигоны частот и относительных частот
распределения.
Для
начала построим полигон частот.
Рис.
8. Полигон частот.
Чтобы
построить полигон относительных частот
найдем относительные частоты, для чего
разделим частоты на объем выборки n.
n
=
3
+
10
+
7
=
20.
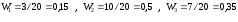
Получаем
|
|
2 |
6 |
12 |
|
|
0,15 |
0,50 |
0,35 |
Построим
полигон относительных частот.
Рис.
9. Полигон относительных частот.
2.
Построить гистограммы частот и
относительных частот распределения.
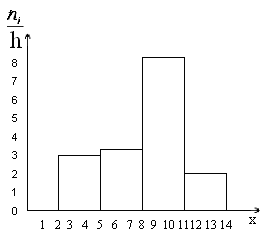
Найдем
плотность частоты
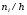
|
Частичный
длиною |
Сумма |
Плотность |
|
2 |
9 |
3 |
|
5 |
10 |
3,3 |
|
8 |
25 |
8,3 |
|
11 |
6 |
2 |
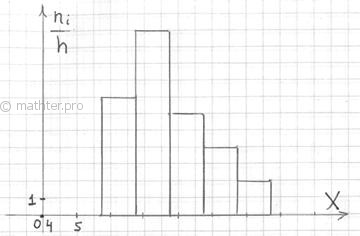
Построим
гистограмму частот.
Рис.
10. Гистограмма частот.
Чтобы
построить гистограмму относительных
частот, нужно найти относительные
частоты. Для этого найдем объем выборки
n.
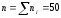
Теперь
найдем относительные частоты
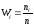
Получим:
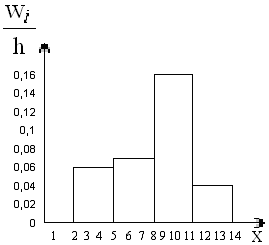
|
Частичный |
Сумма |
Плотность |
|
2 |
0,18 |
0,06 |
|
5 |
0,2 |
0,07 |
|
8 |
0,5 |
0,16 |
|
11 |
0,12 |
0,04 |
Плотности
частот
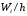
= 3.
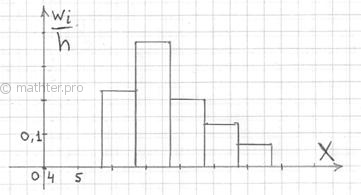
Построим
гистограмму относительных частот.
Рис.11.
Гистограмма относительных частот.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2.2.1. Гистограмма частот
– это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов (данные задачи), а высота –
соответствующим плотностям частот:
при этом вполне допустимо использовать нестандартную шкалу по оси абсцисс, в данном случае я начал нумерацию с четырёх. Площадь гистограммы частот в точности равна объёму совокупности: . В нашем случае
и плотности
совпали с самими частотами
, таким образом:
2.2.2. Гистограмма относительных частот
– это фигура, состоящая из прямоугольников, ширина которых равна длинам частичных интервалов, а высота –
соответствующим плотностям относительных частот:
Площадь такой гистограммы равна единице: , и это статистический аналог функции плотности распределения непрерывной
случайной величины.
Построенный чертёж даёт наглядное и весьма точное представление о распределении цен на ботинки по всей генеральной
совокупности. При условии, что выборка представительна.
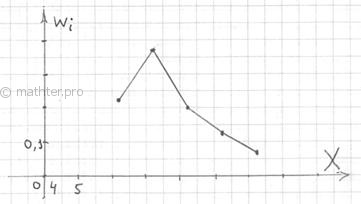
И для ИВР чаще всего требуется построить гистограмму именно относительных частот. А вместе с ней нередко и полигон
таковых частот. Без проблем, полигон относительных частот – это ломаная, соединяющая соседние точки
, где
– середины интервалов:
По сути, здесь мы приблизили интервальный
ряд дискретным, выбрав в качестве вариант середины интервалов. Это важнейший принцип и метод,
который неоднократно встретится нам в будущем.
Большим достоинством приведённого решения является тот факт, что многие вычисления здесь устные, а если вы помните, как
делить «столбиком», то можно обойтись даже без калькулятора. Вот она где притаилась, смерть Терминатора 🙂 😉
Автоматизируем решение в Экселе (видео на Ютуб).
И бонус:


| Оглавление |