Построение графов для чайников: пошаговый гайд
Время на прочтение
7 мин
Количество просмотров 54K
Ранее мы публиковали пост, где с помощью графов проводили анализ сообществ в Точках кипения из разных городов России. Теперь хотим рассказать, как строить такие графы и проводить их анализ.
Под катом — пошаговая инструкция для тех, кто давно хотел разобраться с визуализацией графов и ждал подходящего случая.
1. Выбор гипотезы
Если попытаться визуализировать хотя бы что-то, бездумно загрузив данные в программу построения графов, результат вас не порадует. Поэтому сначала сформулируйте для себя, что хотите узнать с помощью графов, и придумайте жизнеспособную гипотезу.
Для этого разберитесь, какие данные у вас уже есть, что из них можно представить «объектами», а что – «связями» между ними. Обычно объектов значительно меньше, чем связей — можно таким образом проверять себя.
Наш тестовый пример мы готовили совместно с командой Точки кипения из Томска. Соответственно, все данные для анализа по мероприятиям и их участникам у нас будут именно оттуда. Нам стало интересно, сформировалось ли из участников этих мероприятий сообщество и как оно выглядит с точки зрения принадлежности участников к бизнесу, университетам и власти.
Мы предположили, что люди, которые посетили одно и то же мероприятие, связаны друг с другом. Причем чем чаще они присутствовали на мероприятиях совместно, тем сильнее связь.
Во втором случае мы решили узнать, как соотносится принадлежность участников к одному из «нетов» (наших ключевых направлений) с интересующими их сквозными технологиями. Равномерно ли распределение, есть ли «горячие темы»? Для этого анализа мы взяли данные по участникам мероприятий из 200 томских технологических компаний.
В принципе, даже таких первичных формулировок гипотез достаточно, чтобы перейти ко второму шагу.
2. Подготовка данных
Теперь, когда вы определились с тем, что хотите узнать, возьмите весь массив данных, посмотрите, какая информация об «объектах» хранится, выкиньте все лишнее и добавьте недостающее. Если данные распределены по нескольким источникам, предварительно соберите все в одну кучу, убрав дубли.
Поясню на примере. У нас были данные об участниках 650 мероприятий. Это, условно говоря, 650 эксель-таблиц с ~23000 записей в них, содержащих поля «Leader ID», «Должность», «Организация». Для постройки графа достаточно одного уникального идентификатора (тут, к счастью, такой есть – это Leader ID) и признака, привязывающего каждого участника к одной из трех рассматриваемых сфер: власти, бизнесу или университетам. И этой информации у нас еще нет.
Чтобы получить ее, можно пойти напролом: в каждом из 650 файлов убрать лишние столбцы и добавить новое поле, заполнить его значениями для каждой строки, например: «1» для власти, «2» для бизнеса и «3» для образования и науки. А можно сначала объединить все 650 файлов в один большой список, убрать дубли и только после этого добавлять новые значения. В первом случае такая работа займет 1-2 месяца. Во втором — 1-2 недели.
Вообще при добавлении новых атрибутов старайтесь предварительно группировать данные. Например, можно отсортировать участников по компаниям/организациям и скопом выставлять признак.
Готовим данные дальше. Для их загрузки в большинство программ визуализации потребуется создать два файла: один — с перечнем вершин, второй — со списком ребер.
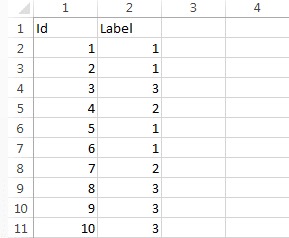
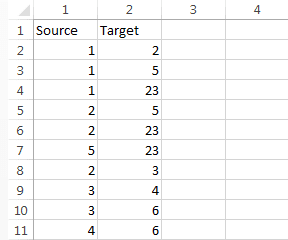
Файл вершин в нашем случае содержал два столбца: Id — номер вершины и Label — тип. Файл ребер содержал также два столбца: Source — id начальной вершины, Target — id конечной вершины.
Как превратить данные о том, что участники 1, 2, 5 и 23 посетили одно мероприятие, в ребра? Необходимо создать шесть строк и отметить связь каждого участника с каждым: 1 и 2, 1 и 5, 1 и 23, 2 и 5, 2 и 23, 5 и 23.
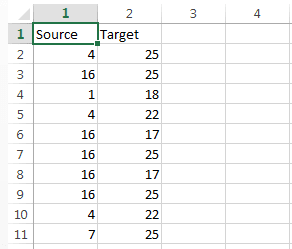
Во втором нашем примере таблицы выглядели так:
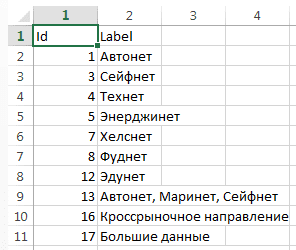
В качестве вершин перечислены как рынки, так и сквозные технологии. Если, скажем, представитель компании, относящейся к рынку «Технет» (ID=4), посетил мероприятие по теме «Большие данные и ИИ» (ID=17), в таблицу ребер заносим ребро (строку), соединяющее эти вершины (Source=4, Target=17).
Этап подготовки данных – это самая трудоемкая часть процесса, но наберитесь терпения.
3. Визуализация графа
Итак, таблицы с данными подготовлены, можно искать средство для их представления в виде графа. Для визуализации мы использовали программу Gephi — мощный опенсорсный инструмент, способный обрабатывать графы с сотнями тысяч вершин и связей. Скачать его можно с официального сайта.
Скриншоты я буду делать со второго проекта, в котором было небольшое число вершин и связей, чтобы все было максимально понятно.
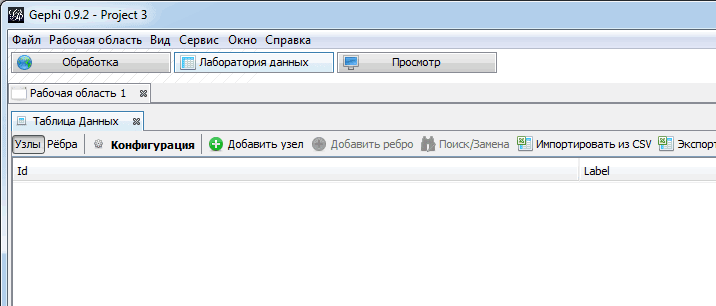
Первым делом нам надо загрузить таблицы с вершинами и ребрами. Для этого выбираем пункт «Импортировать из CSV» из меню раздела «Лаборатория данных».
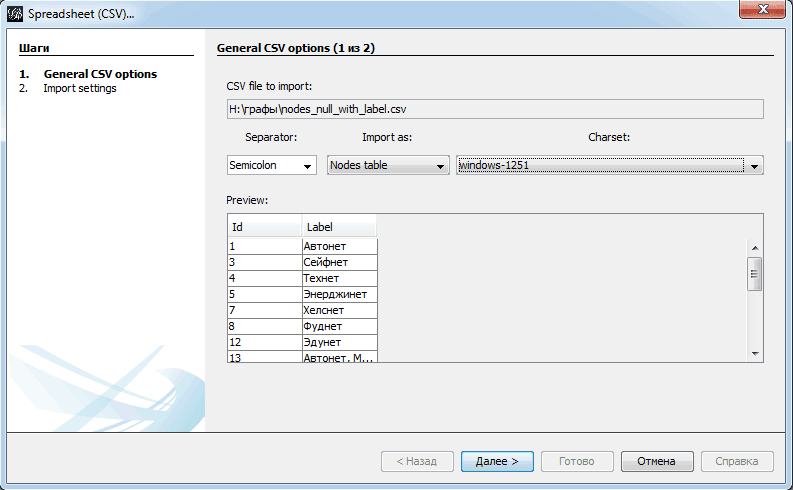
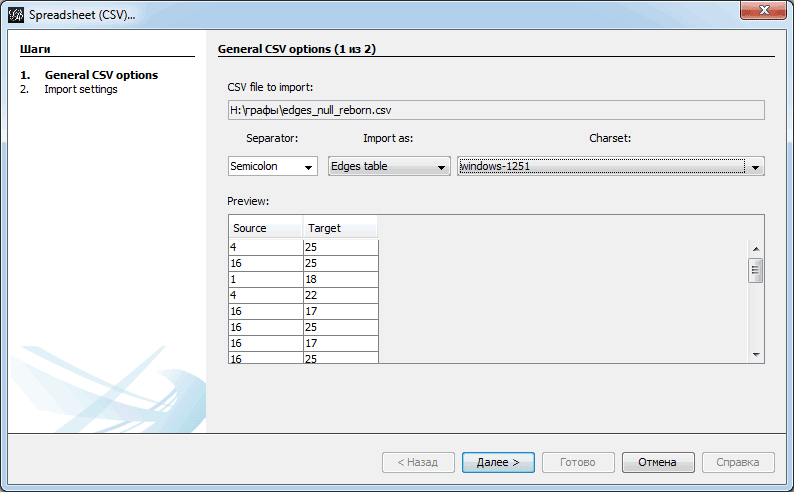
Сначала грузим файл с вершинами. На первом экране формы указываем, что импортируем именно вершины, и проверяем, чтобы программа правильно определила кодировку подписей.
На третьей форме «Отчет об импорте» важно указать тип графа. У нас он не ориентирован.
Похожим образом грузим ребра. В первом окне указываем, что это файл с ребрами, и также проверяем кодировку.
Важный момент ждет нас в третьем окне «Отчет об импорте». Тут важно указать не только то, что граф не ориентирован, но и подгрузить ребра в то же рабочее пространство, что и вершины. Поэтому выбираем пункт «Append to existing workplace».
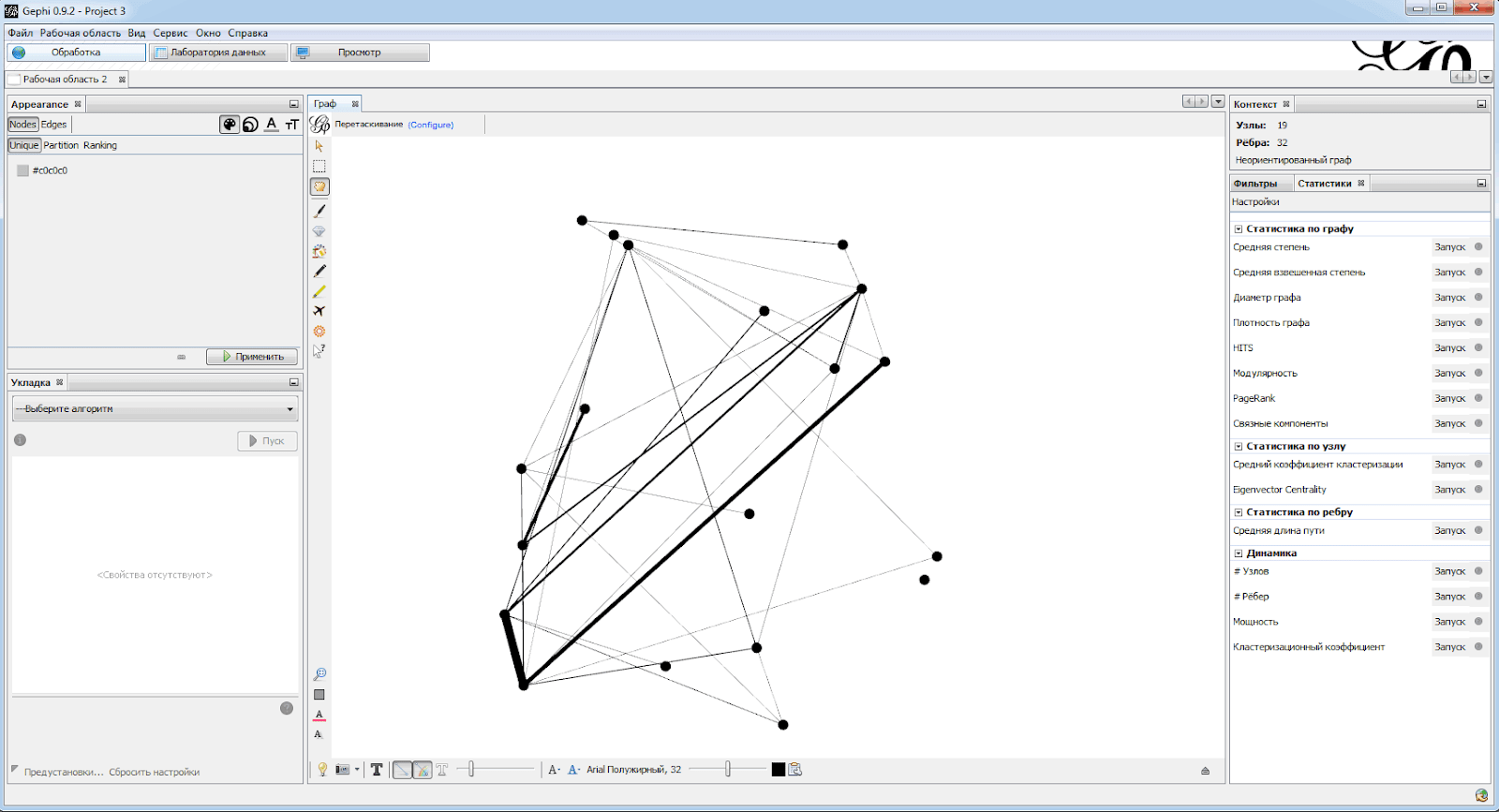
В результате перед нами предстанет граф примерно вот в таком виде (закладка «Обработка»):
Итак, ребра имеют разную толщину в зависимости от количества связей между вершинами. Посмотреть, какой вес стал у каждого ребра, можно на закладке «Лаборатория данных» в свойствах ребер в столбце Weight.
Что здесь плохо: все вершины имеют один размер и расположены абсолютно произвольно. На закладке «Обработка» мы это исправим. Сначала в верхнем левом окне выбираем Nodes и жмем на пиктограммку с кругами («Размер»). Далее выбираем пункт Ranking — он позволяет задать размер вершины в зависимости от какого-либо параметра. У нас есть возможность выбрать только один параметр — Degree (степень), который показывает, сколько ребер выходят из вершины. Выбираем минимальный и максимальный размер кружочка и жмем кнопку «Применить». Здесь же, если выбрать другие пиктограммки, можно настроить цвет маркера вершины и цвет ребер. Теперь граф уже более нагляден.
Следующее, что нужно сделать, — распутать граф. Это можно сделать вручную, двигая вершины, а можно использовать алгоритмы укладки, которые реализованы в Gephi.
Чего мы добиваемся правильной укладкой? Максимальной наглядности. Чем меньше на графе наложений вершин и ребер, чем меньше пересечений ребер, тем лучше. Также неплохо было бы, чтобы смежные вершины были расположены поближе друг к другу, а несмежные —подальше друг от друга. Ну и все было распределено по видимой области, а не сжато в одну кучу.
Как это сделать в Gephi? Левое нижнее окно «Укладка» содержит самые популярные алгоритмы укладки, построенные на силовых аналогиях. Представьте, что вершины — это заряженные шарики, который отталкиваются друг от друга, но при этом некоторые скреплены чем-то, похожим на пружинки. Если задать соответствующие силы и «отпустить» граф, вершины разбегутся на максимально допустимые пружинками расстояния.
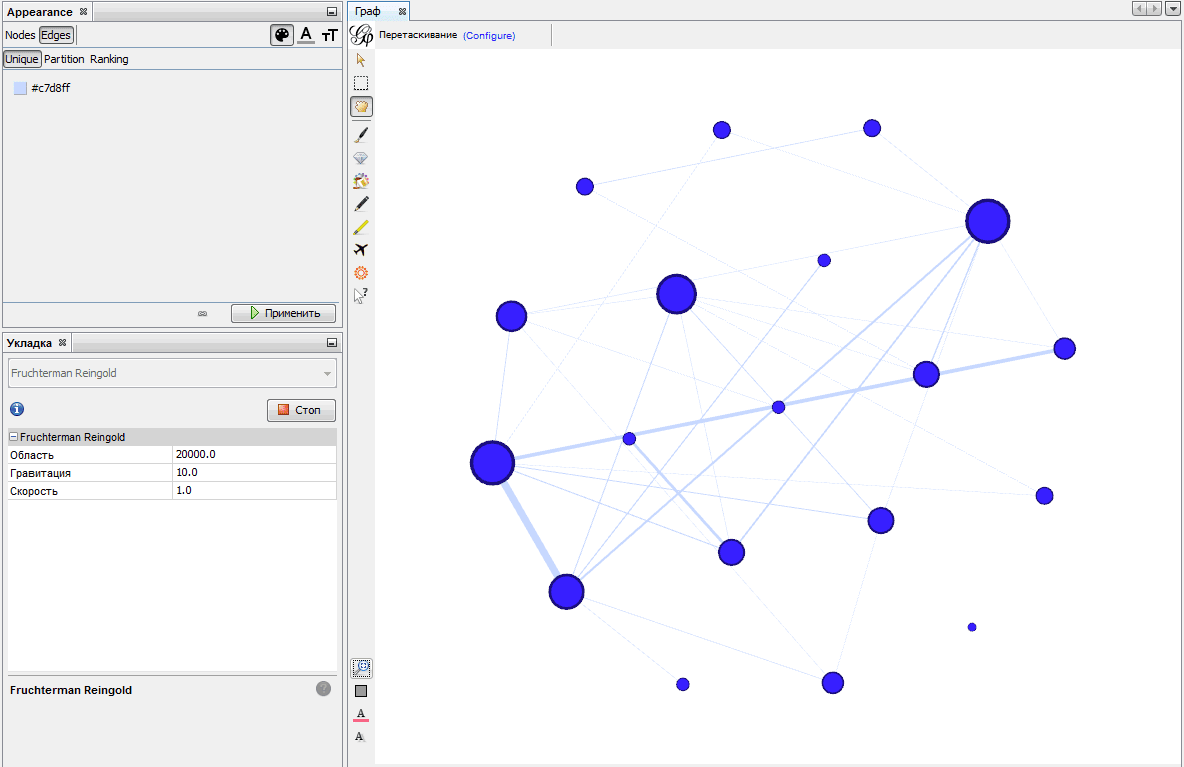
Наиболее равномерную картину дает алгоритм Фрюхтермана и Рейнгольда. Выберите Fruchterman Reingold из выпадающего меню и задайте размер области построения. Нажмите кнопку «Исполнить». Получится что-то вроде этого:
Можно помочь алгоритму и, не останавливая его, поперетаскивать некоторые вершины, стараясь распутать граф. Но помните, что здесь нет кнопки «Отменить», вернуться к прежнему расположению вершин уже не удастся. Поэтому сохраняйте новые версии проекта перед каждым рискованным изменением.
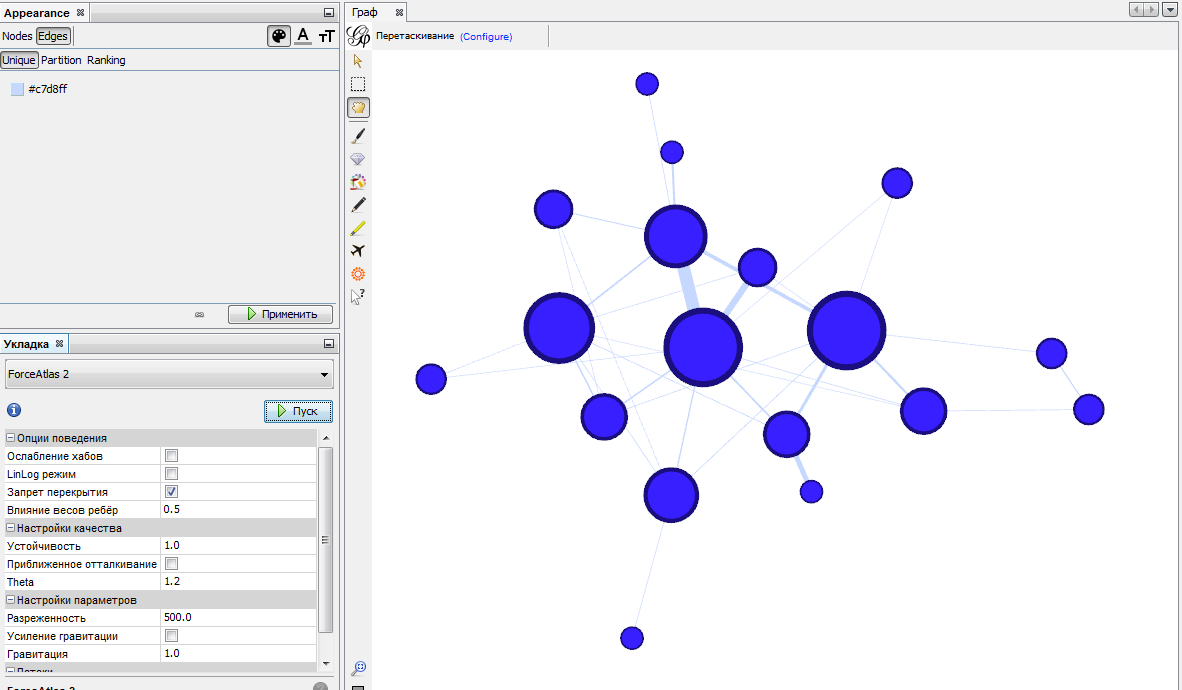
Еще один полезный алгоритм — Force Atlas 2. Он представляет граф в виде металлических колец, связанных между собой пружинами. Деформированные пружины приводят систему в движение, она колеблется и в конце концов принимает устойчивое положение. Этот алгоритм хорош для визуализаций, подчеркивающих структуру группы и выделяющих подмножества с высокой степенью взаимодействия.
Этот алгоритм имеет большое количество настроек. Рассмотрим наиболее важные. «Запрет перекрытия» запрещает вершинам перекрывать друг друга. Разреженность увеличивает расстояние между вершинами, делая граф более читаемым. Также более воздушным граф делает уменьшение влияния весов ребер на взаимное расположение вершин.
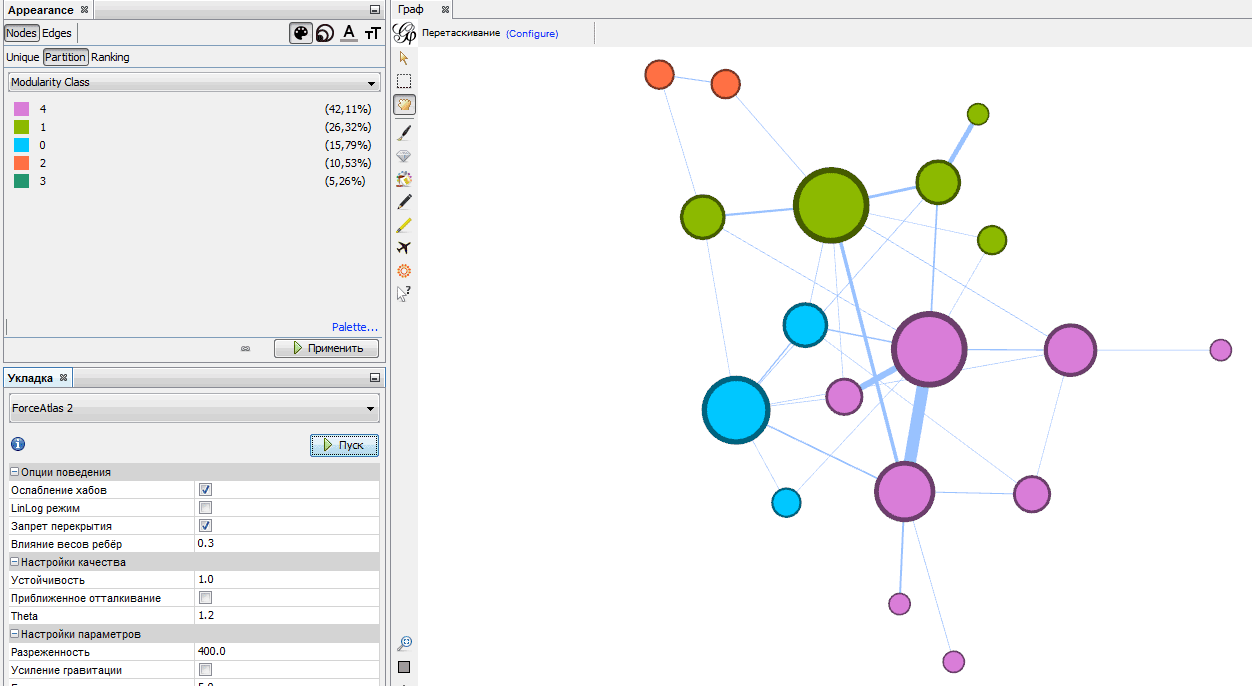
Поигравшись с настройками, получим такой граф:
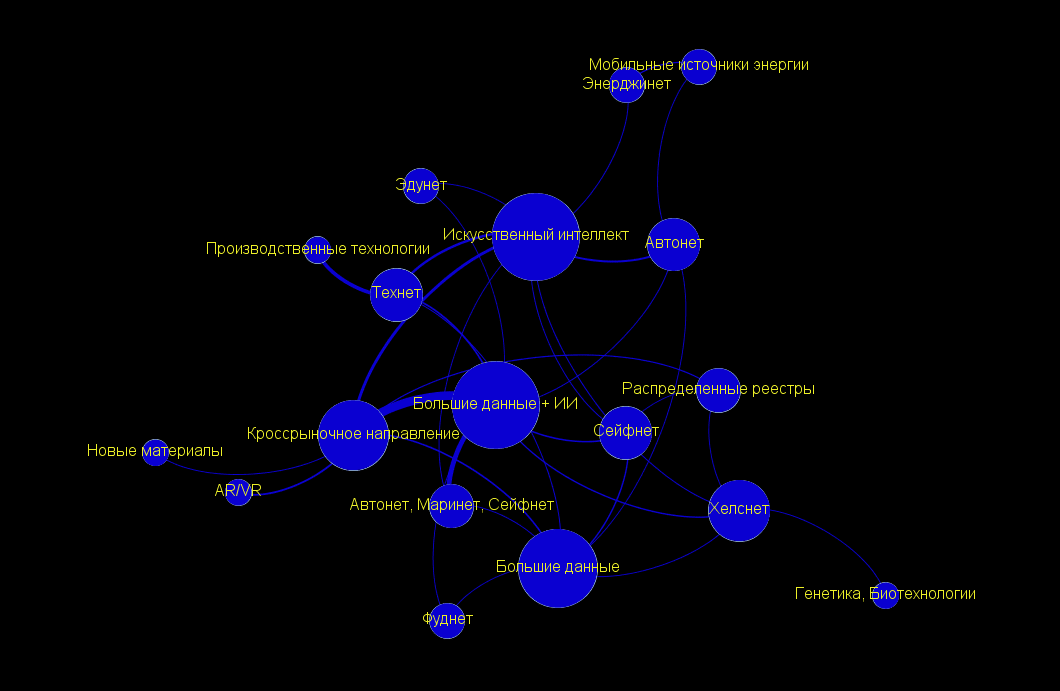
Получив граф в том виде, который вас устраивает, переходите к финальной обработке. Это закладка «Просмотр». Здесь мы можем задать, например, отрисовку графа кривыми ребрами, которая минимизирует наложение вершин на чужие ребра. Можем включить подписи вершин, задав размер и цвет шрифта. Наконец, поменять фон подложки. Например, так:
Для того чтобы сохранить получившийся рисунок, нажмите на надпись «Экспорт SVG/PDF/PNG в левом нижнем углу окна. Также отдельно не забудьте сохранить сам проект через верхнее меню «Файл» — «Сохранить проект».
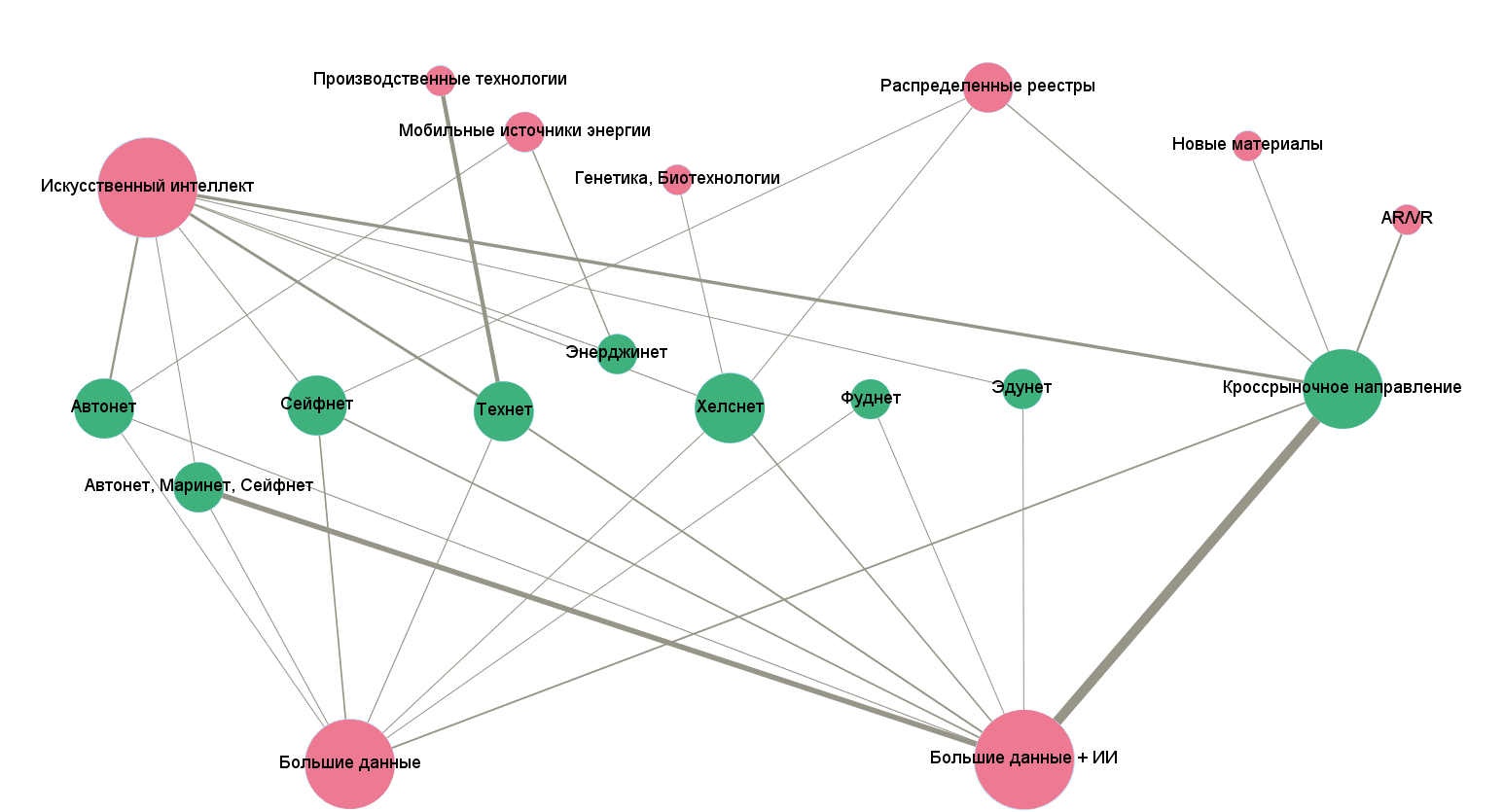
В нашем случае принципиально было выделить взаимосвязь сквозных технологий с рынками НТИ, для чего мы вручную выстроили все рынки в одну линию в центре и разместили все остальное сверху и снизу. Получился вот такой граф. Все-таки для решения конкретных задач без ручной расстановки вершин обойтись не удалось.
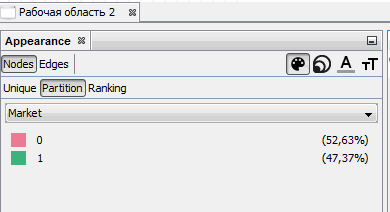
Вы, наверное, думаете, как нам удалось раскрасить вершины в разный цвет? Есть одна хитрость. Можно перейти в закладку «Лаборатория данных», создать там новый столбец в вершинах, назвав его «Market». И заполнить для каждой вершины значениями: 1 если это рынок НТИ, 0 — если сквозная технология. Затем достаточно перейти в «Обработку», выбрать пиктограммку в виде палитры, Nodes — Partition, а в качестве разделителя — наш новый атрибут Market.
Для более сложных построений, когда требуется выделить кластеры и закрасить их разными цветами, в Gephi используется богатый арсенал статистических расчетов, результаты которых можно использовать для раздельной окраски. Находятся эти расчеты в правом столбце вкладки «Обработка».
Например, нажав кнопку «Запуск» возле расчета «Модулярность», вы узнаете оценку уровня кластеризации вашего графа. Если после этого выставить цвет вершин в зависимости от Modularity Class, появится симпатичная картинка наподобие такой:
Если вы хотите еще больше узнать о возможностях Gephi, стоит почитать руководство по работе с программой от Мартина Гранджина http://www.martingrandjean.ch/gephi-introduction/.
4. Анализ результата
Итак, вы получили итоговую визуализацию графа. Что она вам дает? Во-первых, это красиво, ее можно вставить в презентацию, показать знакомым или сделать заставкой на рабочем столе. Во-вторых, по ней вы можете понять, насколько сложной и многокластерной структурой является рассматриваемая вами предметная область. В-третьих, обратите внимание на самые крупные вершины и на самые жирные связи. Это особенные элементы, на которых все держится.
Так, построив граф экспертного сообщества, посещающего мероприятия в Точке кипения, мы сразу обнаружили участников, которые с наибольшей вероятностью выполняют роль суперконнекторов. Они являлись «вершинами», через которые кластеры объединялись в единое целое. А во втором случае мы увидели, как выглядит концентрация специалистов из томских компаний с точки зрения их принадлежности к рынку и сквозной цифровой технологии, на которую они делают ставку. Это косвенно говорит об уровне технологических компетенций и экспертизы региона.
Помощь графов в понимании окружающей действительности реально велика, так что не поленитесь и попробуйте создать собственную визуализацию данных. Это совсем не сложно, но порой трудозатратно.
|
ИП Ширмамедов Учебный центр “Центриум” |
|
|
РАЗРАБОТКА ЗАНЯТИЯ по по |
|
|
Разработал: |
Матвеев Дмитрий Николаевич, преподаватель информационных дисциплин |
|
Москва, |
ЭТАПЫ УЧЕБНОГО ЗАНЯТИЯ
|
№ |
Наименование |
План. |
|
1. |
Организационный |
5 |
|
2. |
Актуализация |
15 |
|
3. |
Изучение |
35 |
|
4. |
Первичное |
30 |
|
5. |
Проверка |
30 |
|
6. |
Выводы, |
4 |
|
7. |
Домашнее |
1 |
Лекционный
материал
Что такое нагруженный граф?
На
прошлых занятиях мы познакомились с тем, что же такое граф, узнали, какой граф
называется ориентированным и порешали задачи на уже готовом графе. Сегодня же
мы познакомимся с новым типом графов, а именно с нагруженным графом.
Нагруженный
граф – это такой граф, у которого каждому ребру сопоставлено определенное число.
Чаще
всего, в задачах ОГЭ и ЕГЭ это число обозначает расстояние от одной вершины до
другой, или время, за которое можно пройти от одной вершины до другой.
Пример
нагруженного графа:
Кратчайшее расстояние (время) от стартового до конечного пункта?
В задачах мы
постоянно будем сталкиваться с вопросом определения кратчайшего расстояния от
одного пункта до другого. Давайте разберемся, что же это значит.
Кратчайшим
называется минимальное из множества всех возможных расстояние (время), за
которое можно добраться от одного пункта до другого.
Единственная
проблема заключается в том, что на практике нам редко будет дан уже готовый
нагруженный граф. Чаще всего нам будет необходимо его построить с помощью
данных, указанных в таблице.
Рассмотрим конкретный пример:
Между
населенными пунктами А, Б, В, Г, Е, Ж, З построены дороги, протяженность
которых указана в таблице (Если числа в ячейке нет, это значит, что прямая
дорога между этими населенными пунктами отсутствует). Передвигаться можно
только по построенным дорогам. Определите длину кратчайшего расстояния между
пунктами А и З.
Давайте сначала
разберёмся как читать эту таблицу. На самом деле она симметрична относительно линии
из крестиков (это отражает то, что длина из условного пункта А в условный пункт
Б равна длине из пункта Б в пункт А, и что граф не является ориентированным,
т.е. двигаться можно в обе стороны). А дальше читаем по строчкам. Берем строчку
А и видим, что числа стоят на пересечении со столбцами Б (28), В (20) и Г (28).
Это значит то, что из А ведут дороги в Б, В, Г и им соответствует данные длины,
и так далее.
Дальше строим
граф.
При построении
графа нужно учесть некоторые вещи:
1)
Рёбра графа не должны пересекаться ни в коем случае!
(Они могут пересекаться, но вы запутаетесь при решении гарантированно)
2)
Точки, в которые приходит больше всего дорог,
должны стоять примерно в центре графа (это скорее рекомендация)
Попробуем построить граф по этой
таблице и получаем такую картину:
Дальше просто
анализируем наш граф и избавляемся от дорог, которые заведомо нам не выгодны,
т.е. слишком длинные. В конечном итоге мы должны зачеркнуть практически все
дороги, чтобы у нас остался один единственный верный путь.
Тут мы можем
избавиться от дороги АБ (можно пройти АВБ), от дорог ВБ и БЕ (можно пройти ВЕ),
от дороги ВЖ (можно пройти ВЕЖ). И у нас остается два пути, через верх и через
низ.
Подсчитываем оба
варианта и видим, что через верх длина будет 42, а через низ 43. Делаем вывод,
что через верх идти выгодней
Значит ответ на эту
задачу: 42.
Еще пример:
Найти
кратчайшее расстояние от пункта А до пункта З.
Получаем следующий граф:
Преобразовываем этот граф, убирая все лишние
дороги:
Ответ на эту задачу: 19
Практическая
работа №3
Тема: Построение собственного графа при анализе таблиц
Цель работы: Отработка
полученных на уроке навыков
Задания к работе:
1) Найдите кратчайшее расстояние от пункта А до пункта Ж
2) Найдите кратчайшее расстояние от пункта А до пункта К
3) Найдите кратчайшее расстояние от пункта А до пункта Н
4) Найдите кратчайшее расстояние от пункта А до пункта К
5) Найдите кратчайшее расстояние от пункта А до пункта М
Самостоятельная
работа №3
Тема: Построение собственного графа при анализе таблиц
Цель работы: Оценивание
приобретенных на уроке навыков
Задания к работе:
1) Найдите кратчайшее расстояние от пункта А до пункта F
2) Найдите кратчайшее расстояние от пункта А до пункта М
3) Найдите кратчайшее расстояние от пункта A до
пункта L
4) Найдите кратчайшее расстояние от пункта А до пункта К
5) Найдите кратчайшее расстояние от пункта А до пункта Н
Графы в информатике являются способом определения отношений в совокупности элементов. Это основные объекты изучения теории графов.
Базовые определения
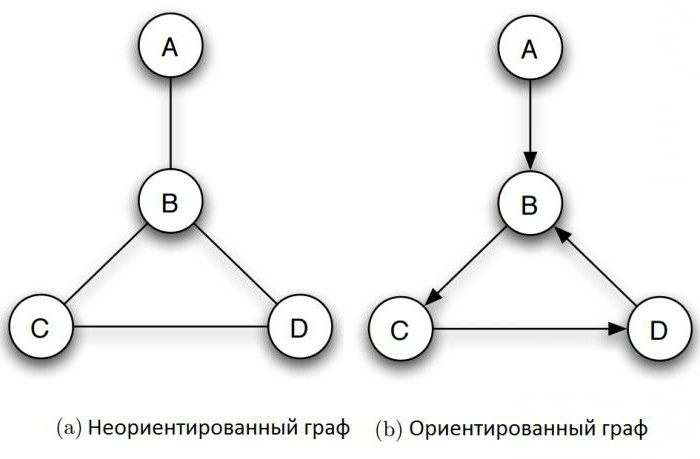
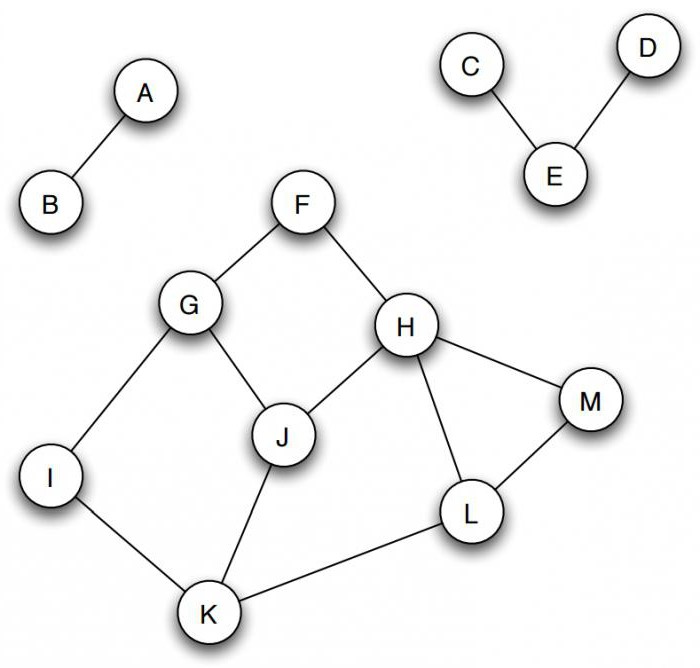
Из чего состоит граф в информатике? Он включает множество объектов, называемых вершинами или узлами, некоторые пары которых связаны т. н. ребрами. Например, граф на рисунке (а) состоит из четырех узлов, обозначенных А, В, С, и D, из которых B соединен с каждой из трех других вершин ребрами, а C и D также соединены. Два узла являются соседними, если они соединены ребром. На рисунке показан типичный способ того, как строить графы по информатике. Круги представляют вершины, а линии, соединяющие каждую их пару, являются ребрами.
Какой граф называется неориентированным в информатике? У него отношения между двумя концами ребра являются симметричными. Ребро просто соединяет их друг с другом. Во многих случаях, однако, необходимо выразить асимметричные отношения – например, то, что A указывает на B, но не наоборот. Этой цели служит определение графа в информатике, по-прежнему состоящего из набора узлов вместе с набором ориентированных ребер. Каждое ориентированное ребро представляет собой связь между вершинами, направление которой имеет значение. Направленные графы изображают так, как показано на рисунке (b), ребра их представлены стрелками. Когда требуется подчеркнуть, что граф ненаправленный, его называют неориентированным.
Модели сетей
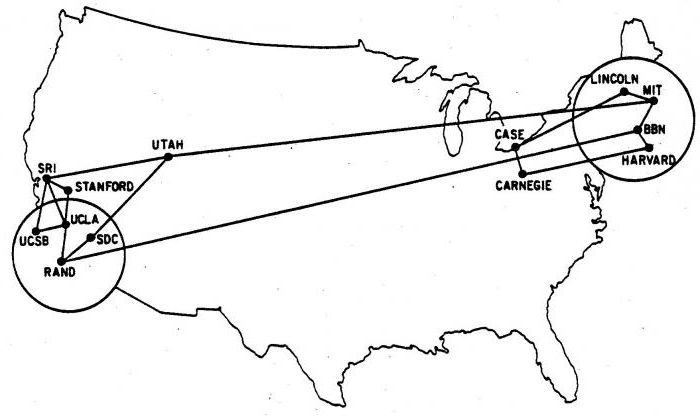
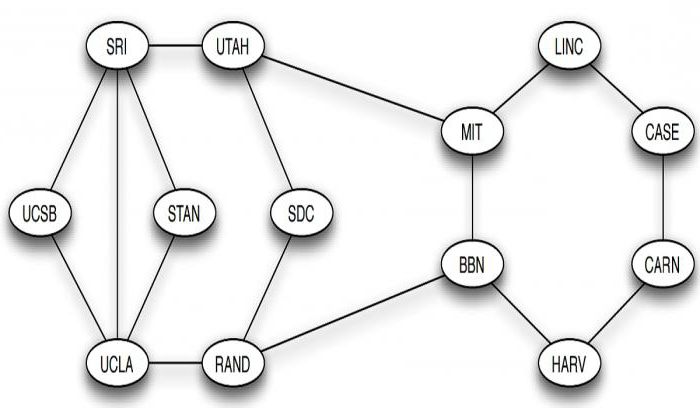
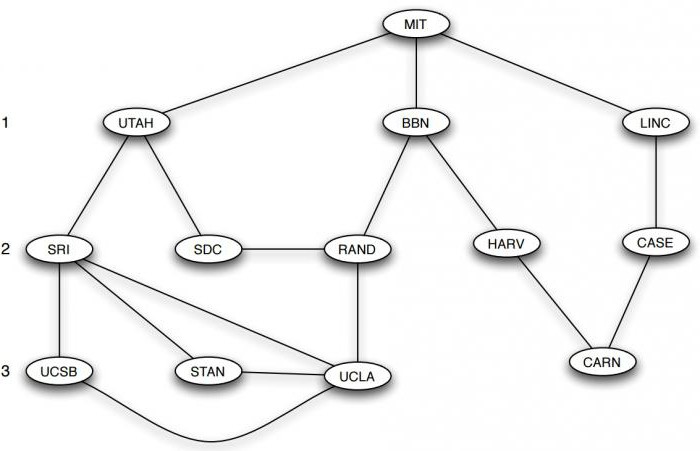
Графы в информатике служат математической моделью сетевых структур. На следующем рисунке представлена структура интернета, тогда носившего название ARPANET, в декабре 1970 года, когда она имела лишь 13 точек. Узлы представляют собой вычислительные центры, а ребра соединяют две вершины с прямой связью между ними. Если не обращать внимания на наложенную карту США, остальная часть изображения является 13-узловым графом, подобным предыдущим. При этом действительное расположение вершин несущественно. Важно, какие узлы соединены друг с другом.
Применение графов в информатике позволяет представить, как вещи либо физически, либо логически связаны между собой в сетевой структуре. 13-узловой ARPANET является примером коммуникационной сети, в которой вершины-компьютеры или другие устройства могут передавать сообщения, а ребра представляют собой прямые линии связи, по которым информация может быть передана.
Маршруты
Хотя графы применяются во многих различных областях, они обладают общими чертами. Теория графов (информатика) включает, возможно, важнейшую из них – идею о том, что вещи часто перемещаются по ребрам, последовательно переходя от узла к узлу, будь то пассажир нескольких авиарейсов или информация, передаваемая от человека к человеку в социальной сети, либо пользователь компьютера, последовательно посещающий ряд веб-страниц, следуя по ссылкам.
Эта идея мотивирует определение маршрута как последовательности вершин, связанных между собой ребрами. Иногда возникает необходимость рассматривать маршрут, содержащий не только узлы, но и последовательность ребер, их соединяющих. Например, последовательность вершин MIT, BBN, RAND, UCLA является маршрутом в графе интернета ARPANET. Прохождение узлов и ребер может быть повторным. Например, SRI, STAN, UCLA, SRI, UTAH, MIT также является маршрутом. Путь, в котором ребра не повторяются, называется цепью. Если же не повторяются узлы, то он носит название простой цепи.
Циклы
Особенно важные виды графов в информатике – это циклы, которые представляют собой кольцевую структуру, такую как последовательность узлов LINC, CASE, CARN, HARV, BBN, MIT, LINC. Маршруты с, по крайней мере, тремя ребрами, у которых первый и последний узел одинаковы, а остальные различны, представляют собой циклические графы в информатике.
Примеры: цикл SRI, STAN, UCLA, SRI является самым коротким, а SRI, STAN, UCLA, RAND, BBN, UTAH, SRI значительно больше.
Фактически каждое ребро графа ARPANET принадлежит к циклу. Это было сделано намеренно: если какое-либо из них выйдет из строя, останется возможность перехода из одного узла в другой. Циклы в системах коммуникации и транспорта присутствуют для обеспечения избыточности – они предусматривают альтернативные маршруты по другому пути цикла. В социальной сети тоже часто заметны циклы. Когда вы обнаружите, например, что близкий школьный друг кузена вашей жены на самом деле работает с вашим братом, то это является циклом, который состоит из вас, вашей жены, ее двоюродного брата, его школьного друга, его сотрудника (т. е. вашего брата) и, наконец, снова вас.
Связный граф: определение (информатика)
Естественно задаться вопросом, можно ли из каждого узла попасть в любой другой узел. Граф связный, если между каждой парой вершин существует маршрут. Например, сеть ARPANET – связный граф. То же можно сказать и о большинстве коммуникационных и транспортных сетей, так как их цель состоит в том, чтобы направлять трафик от одного узла к другому.
С другой стороны, нет никаких априорных оснований ожидать того, что данные виды графов в информатике широко распространены. Например, в социальной сети несложно представить двух людей, не связанных между собой.
Компоненты
Если графы в информатике не связаны, то они естественным образом распадаются на набор связанных фрагментов, групп узлов, которые являются изолированными и не пересекающимися. Например, на рисунке изображены три таких части: первая – А и В, вторая – C, D и Е, и третья состоит из оставшихся вершин.
Компоненты связности графа представляют собой подмножество узлов, у которых:
- каждая вершина подгруппы имеет маршрут к любой другой;
- подмножество не является частью некоторого большего набора, в котором каждый узел имеет маршрут к любому другому.
Когда графы в информатике разделяются на их компоненты, то это является лишь начальным способом описания их структуры. В рамках данного компонента может быть богатая внутренняя структура, важная для интерпретации сети. Например, формальным методом определения важности узла является определение того, на сколько частей разделится граф, если узел будет убран.
Максимальная компонента
Существует метод качественной оценки компонентов связности. Например, есть всемирная социальная сеть со связями между двумя людьми, если они являются друзьями.
Связная ли она? Вероятно, нет. Связность – довольно хрупкое свойство, и поведение одного узла (или небольшого их набора) может свести ее на нет. Например, один человек без каких-либо живых друзей будет компонентом, состоящим из единственной вершины, и, следовательно, граф не будет связным. Или отдаленный тропический остров, состоящий из людей, которые не имеют никакого контакта с внешним миром, также будет небольшой компонентой сети, что подтверждает ее несвязность.
Глобальная сеть друзей
Но есть еще кое-что. Например, читатель популярной книги имеет друзей, выросших в других странах, и составляет с ними одну компоненту. Если принять во внимание родителей этих друзей и их друзей, то все эти люди также находятся в той же компоненте, хотя они никогда не слышали о читателе, говорят на другом языке и рядом с ним никогда не были. Таким образом, хотя глобальная сеть дружбы – не связная, читатель будет входить в компонент очень большого размера, проникающий во все части мира, включающий в себя людей из самых разных слоев и, фактически, содержащий значительную часть населения земного шара.
То же имеет место и в сетевых наборах данных – большие, сложные сети часто имеют максимальную компоненту, которая включает значительную часть всех узлов. Более того, когда сеть содержит максимальную компоненту, она почти всегда только одна. Чтобы понять, почему, следует вернуться к примеру с глобальной сетью дружбы и попробовать вообразить наличие двух максимальных компонент, каждая из которых включает миллионы людей. Потребуется наличие единственного ребра от кого-то из первой компоненты ко второй, чтобы две максимальные компоненты слились в одну. Так как ребро единственное, то в большинстве случаев невероятно, чтобы оно не образовалось, и, следовательно, две максимальные компоненты в реальных сетях никогда не наблюдаются.
В некоторых редких случаях, когда две максимальные компоненты сосуществовали в течение длительного время в реальной сети, их объединение было неожиданным, драматическим, и, в конечном итоге, имело катастрофические последствия.
Катастрофа слияния компонент
Например, после прибытия европейских исследователей в цивилизации Западного полушария примерно полтысячелетия назад произошел глобальный катаклизм. С точки зрения сети это выглядело так: пять тысяч лет глобальная социальная сеть, вероятно, состояла из двух гигантских компонент – одной в Северной и Южной Америке, а другой – в Евразии. По этой причине технологии развивалась независимо в двух компонентах, и, что еще хуже, так же развивались и болезни человека и т. д. Когда две компоненты, наконец, вошли в контакт, технологии и заболевания одной быстро и катастрофически переполнили вторую.
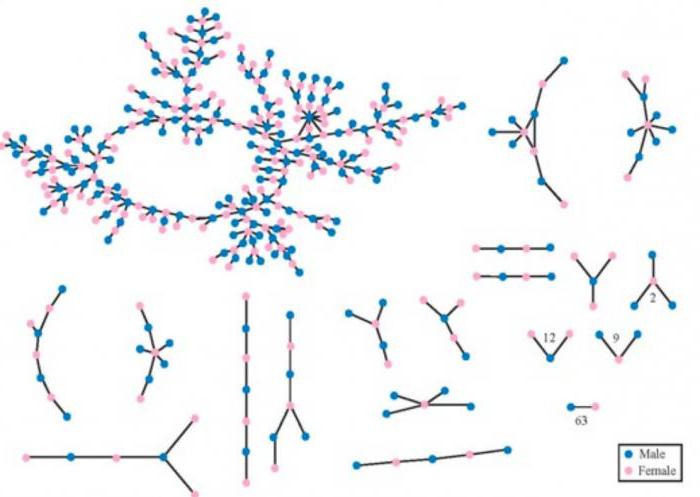
Американская средняя школа
Понятие максимальных компонент полезно для рассуждений о сетях и в гораздо меньших размерах. Интересный пример представляет собой граф, иллюстрирующий романтические отношения в американской средней школе за 18-месячный период. Тот факт, что он содержит максимальную компоненту, имеет важное значение, когда речь заходит о распространении заболеваний, передаваемых половым путем, что и являлось целью проведенного исследования. Ученики, возможно, имели лишь одного партнера за этот период времени, но, тем не менее, не осознавая этого, были частью максимальной компоненты и, следовательно, частью многих маршрутов потенциальной передачи. Эти структуры отражают отношения, которые, возможно, давно закончилась, но они связывают индивидуумов в цепях слишком долго, чтобы стать предметом пристального внимания и сплетен. Тем не менее, они реальны: как социальные факты это невидимые, но логически вытекающие макроструктуры, возникшие как продукт индивидуального посредничества.
Расстояние и поиск в ширину
В дополнение к сведениям о том, связаны ли два узла маршрутом, теория графов в информатике позволяет узнать и о его длине – в транспорте, связи или при распространении новостей и заболеваний, а также о том, проходит ли он через несколько вершин или множество.
Для этого следует определить длину маршрута, равную числу шагов, которые он содержит от начала до конца, т. е. число ребер в последовательности, которая его составляет. Например, маршрут MIT, BBN, RAND, UCLA имеет длину 3, а MIT, UTAH – 1. Используя длину пути, можно говорить о том, расположены ли два узла в графе близко друг к другу или далеко: расстояние между двумя вершинами определяется как длина самого короткого пути между ними. Например, расстояние между LINC и SRI равно 3, хотя, чтобы убедиться в этом, следует удостовериться в отсутствии длины, равной 1 или 2, между ними.
Алгоритм поиска в ширину
Для небольших графов расстояние между двумя узлами подсчитать легко. Но для сложных появляется необходимость в систематическом методе определения расстояний.
Самым естественным способом это сделать и, следовательно, наиболее эффективным, является следующий (на примере глобальной сети друзей):
- Все друзья объявляются находящимися на расстоянии 1.
- Все друзья друзей (не считая уже отмеченных) объявляются находящимися на расстоянии 2.
- Все их друзья (опять же, не считая помеченных людей) объявляются удаленными на расстояние 3.
Продолжая таким образом, поиск проводят в последующих слоях, каждый из которых – на единицу дальше предыдущего. Каждый новый слой составляется из узлов, которые еще не участвовали в предыдущих, и которые входят в ребро с вершиной предыдущего слоя.
Эта техника называется поиском в ширину, так как она выполняет поиск по графу наружу от начального узла, в первую очередь охватывая ближайшие. В дополнение к предоставлению способа определения расстояния, она может служить полезной концептуальной основой для организации структуры графа, а также того, как построить граф по информатике, располагая вершины на основании их расстояния от фиксированной начальной точки.
Поиск в ширину может быть применен не только к сети друзей, но и к любому графу.
Мир тесен
Если вернуться к глобальной сети друзей, можно увидеть, что аргумент, объясняющий принадлежность к максимальной компоненте, на самом деле утверждает нечто большее: не только у читателя есть маршруты к друзьям, связывающие его со значительной долей населения земного шара, но эти маршруты на удивление коротки.
Эта идея получила название «феномена тесного мира»: мир кажется маленьким, если думать о том, какой короткий маршрут связывает любых двух людей.
Теория «шести рукопожатий» впервые экспериментально исследовалась Стенли Милгрэмом и его коллегами в 1960-е годы. Не имея какого-либо набора данных социальных сетей и с бюджетом в 680 долларов он решил проверить популярную идею. С этой целью он попросил 296 случайно отобранных инициаторов попробовать отослать письмо биржевому брокеру, который жил в пригороде Бостона. Инициаторам были даны некоторые личные данные о цели (включая адрес и профессию), и они должны были переслать письмо лицу, которого они знали по имени, с теми же инструкциями, чтобы оно достигло цели как можно быстрее. Каждое письмо прошло через руки ряда друзей и образовало цепочку, замыкавшуюся на биржевом брокере за пределами Бостона.
Среди 64 цепочек, достигших цели, средняя длина равнялась шести, что подтвердило число, названное два десятилетия ранее в названии пьесы Джона Гэра.
Несмотря на все недочеты этого исследования, эксперимент продемонстрировал один из важнейших аспектов нашего понимания социальных сетей. В последующие годы из него был сделан более широкий вывод: социальные сети, как правило, имеют очень короткие маршруты между произвольными парами людей. И даже если такие опосредованные связи с руководителями предприятий и политическими лидерами не окупаются на ежедневной основе, существование таких коротких маршрутов играет большую роль в скорости распространения информации, болезней и других видов заражения в обществе, а также в возможностях доступа, которые социальная сеть предоставляет людям с совершенно противоположными качествами.
Информатика. Учебник для 9 класса (по учебнику К. Ю. Полякова, Е.А. Еремина, базовый уровень)
§17. Графы.
Что такое граф?
Ключевые слова:
• граф • вершина • ребро • матрица смежности • степень вершины • связный граф • взвешенный граф • весовая матрица • ориентированный граф • оптимальный путь • количество путей
Давайте подумаем, как можно наглядно представить такую информацию:
От пос. Васюки три дороги идут в Солнцево, Грибное и Ягодное. Между Солнцевом и Грибным и между Грибным и Ягодным также есть дороги. Кроме того, есть дорога, которая идет из Грибного в лес и возвращается обратно в Грибное.
Нарисуйте в тетради схему дорог по этому описанию.
Можно, например, нарисовать такую схему (рис. 3.17, а).

Рис. 3.17
В информатике для исследования таких схем используют графы.
Граф — это набор вершин (узлов) и связей между ними — рёбер.
Граф, соответствующий нашей схеме дорог, показан на рис. 3.17, б, для краткости населённые пункты обозначены латинскими буквами.
Матрица смежности графа
Для хранения информации об узлах и связях показанного выше графа можно использовать таблицу такого вида (рис. 3.18).

Рис. 3.18
Единица на пересечении строки А и столбца В означает, что между вершинами А и В есть связь. Ноль указывает на то, что связи нет. Такая таблица называется матрицей смежности. Она симметрична относительно главной диагонали (см. закрашенные клетки в таблице).
Исследуйте матрицу смежности и сравните её с графом на рис. 3.17, б. Что означает единица на пересечении столбца С и строки С?
В этом графе есть петля — ребро, которое начинается и заканчивается в одной и той же вершине.
Степенью вершины называют количество рёбер, с которыми связана вершина. При этом петля считается дважды (с вершиной связаны оба конца ребра!).
Подсчитайте по матрице смежности, сколько ребёр в графе. Определите степени всех вершин. Как вы рассуждали?
Строго говоря, граф — это математический объект, а не рисунок. Конечно, его можно нарисовать на плоскости (например, как на рис. 3.17, б), но матрица смежности не даёт никакой информации о том, как именно располагать вершины друг относительно друга. Для таблицы, приведённой выше, возможны, например, такие варианты (рис. 3.19).

Рис. 3.19
Нарисуйте по матрице смежности (рис. 3.20) два разных изображения графа.

Рис. 3.20
Граф имеет 4 вершины, причём каждая вершина связана рёбрами со всеми остальными. Нарисуйте этот граф. Сколько всего рёбер в этом графе?
Граф имеет N вершин, причём каждая вершина связана рёбрами со всеми остальными. Сколько всего рёбер в этом графе?
Граф имеет 4 ребра. Чему равна сумма степеней вершин в этом графе? Зависит ли она от количества вершин?
Граф имеет N рёбер. Чему равна сумма степеней вершин в этом графе?
Попробуйте нарисовать граф с пятью вершинами, где все вершины имеют степень 3. Получилось ли у вас? Почему?
Связный граф
В графе на рис. 3.17, б все вершины связаны: между любой парой вершин существует путь — последовательность вершин, в которой каждая следующая связана ребром с предыдущей. Такой граф называется связным.
Связный граф — это граф, между любыми вершинами которого существует путь.
Теперь представьте себе, что дороги Васюки-Солнцево, Васю- ки-Грибное и Грибное-Ягодное завалило снегом (или размыло дождём) так, что по ним ни пройти, ни проехать (рис. 3.21).

Рис. 3.21
Эту схему тоже можно считать графом (она соответствует определению), но в таком графе есть две несвязанные части, каждая из которых — связный граф. Такие части называют компонентами связности.
Постройте матрицу смежности графа, изображённого на рис. 3.21.
Граф имеет 4 вершины и две компоненты связности. Какое наибольшее количество рёбер может быть в этом графе, если в нём нет петель? Нарисуйте этот граф.
Вспоминая материал предыдущего параграфа, можно сделать вывод, что дерево — это частный случай связного графа. Но у него есть одно важное свойство — в дереве нет замкнутых путей — циклов, т. е. путей, которые начинаются и заканчиваются в одной и той же вершине.
Найдите все циклы в графе на рис. 3.17.
Дерево — это связный граф, в котором нет циклов.
Взвешенный граф
Если в нашем примере нас заинтересует не только наличие дорог между посёлками, но ещё и расстояния между ними, каждой связи нужно сопоставить число — вес ребра (рис. 3.22).

Рис. 3.22
Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра.
Весом может быть не только расстояние, но и, например, стоимость проезда или другая величина.
Как хранить информацию о таком графе? Ответ напрашивается сам собой — нужно в таблицу записывать не 1 или 0, а вес ребра. Если связи между двумя узлами нет, на бумаге можно оставить ячейку таблицы пустой, а при хранении в памяти компьютера записывать в неё условный код, например, число -1 или очень большое число. Такая таблица называется весовой матрицей, потому что содержит веса рёбер. В данном случае она выглядит так (рис. 3.23).

Рис. 3.23
Так же как и матрица смежности, весовая матрица симметрична относительно диагонали.
Что означают пустые ячейки в весовой матрице?
Как по весовой матрице сразу определить, сколько рёбер в графе?
Определите по весовой матрице (рис. 3.24) длины путей ADBEC, ABDCE, DEBAC. Как вы рассуждали?

Рис. 3.24
Оптимальный путь в графе
Для того чтобы определить оптимальный (наилучший) путь между двумя вершинами графа, нужно ввести какой-то числовой показатель, по которому можно сравнивать пути — определять, какой из них лучше. Обычно для оценки пути используют сумму весов ребёр, входящих в этот путь. Например, при поиске кратчайшего пути чем меньше это значение, тем лучше.
Какие показатели вы используете в жизни для определения оптимального пути? Всегда ли самый короткий путь — самый лучший?
Если в графе немного узлов, по весовой матрице можно легко определить оптимальный путь из одной вершины в другую простым перебором вариантов. Рассмотрим граф, заданный весовой матрицей на рис. 3.25 (числа определяют стоимость поездки между соседними пунктами).

Рис. 3.25
Найдём наилучший путь из А в В — такой, при котором общая стоимость поездки минимальная.
Для решения задачи будем строить дерево перебора вариантов. Видим, что из пункта А напрямую

Рис. 3.26
Числа около рёбер обозначают стоимость поездки по этому участку, а индексы у названий узлов показывают общую стоимость проезда в данный узел из узла А. Теперь разберём варианты дальнейшего движения из узла С I tM lt;pb р (рис. 3.27).

Рис. 3.27
Почему, на ваш взгляд, на схеме не показана возможность движения из С в А?
Видим, что из С сразу можно попасть в В, стоимость проезда в этом случае равна 7.
Почему нельзя на этом остановиться, ведь путь из А в В найден?
Проверяя пути через узел В, выясняем, что можно сократить стоимость до 6 (рис. 3.28)

Рис. 3.28
Нужно ли исследовать дальше путь, содержащий цепочку ACED? Сравните стоимость этого пути и стоимость уже найденного пути из А в В.
Аналогично строим вторую часть схемы (рис. 3.29).

Рис. 3.29
Таким образом, оптимальный (наилучший) путь — ADEB, его стоимость — 3.
Нужно ли проверять пути ACED и ADEC, не дошедшие до узла В? Могут ли они улучшить результат?
Конечно, для более сложных графов метод перебора работает очень долго, поэтому используются более совершенные (но значительно более сложные) методы.
Ориентированный граф
Наверное, вы заметили, что при изображении деревьев, которые описывают иерархию (подчинение), мы ставили стрелки от верхних уровней к нижним. Это означает, что для каждого ребра указывается направление, и двигаться можно только по стрелкам, но не наоборот.
Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление.
Орграф может служить, например, моделью системы дорог с односторонним движением. Матрица смежности и весовая матрица для орграфа уже не обязательно будут симметричными.
На схеме на рис. 3.30 всего две дороги с двусторонним движением, по остальным можно ехать только в одну сторону.

Рис. 3.30
Рёбра в орграфе называют дугами. Дуга, в отличие от ребра, имеет начало и конец.
Нарисуйте граф по весовой матрице, показанной на рис. 3.31. С помощью дерева перебора найдите все возможные пути из вершины А в вершину Е, не проходящие дважды через одну и ту же вершину, и стоимости проезда по каждому из этих путей. Определите оптимальный путь из вершины А в вершину Е.

Рис. 3.31
Количество путей
Определим количество возможных путей из вершины А в вершину К для ориентированного графа, показанного на рис. 3.32.

Рис. 3.32
Так как граф ориентированный, переходить в другую вершину можно только по стрелкам.
В графе на рис. 3.32 есть одна начальная вершина А, из которой дуги только выходят. Такая вершина называется истоком. Вершина, в которую дуги только входят (и ни одна не выходит), называется конечной вершиной или стоком. В нашем графе сток — это вершина К.
По весовой матрице на рис. 3.31 найдите исток и сток в графе. Как вы рассуждали?
Будем двигаться по стрелкам от начальной вершины А. Около каждой вершины запишем количество возможных путей из вершины А в эту вершину. В вершину А существует единственный путь — пустой (никуда не ехать). Найдём все вершины, в которые можно приехать только из А: это вершины Б и Г, записываем около них количество путей 1 (рис. 3.33).

Рис. 3.33
Теперь ищем вершины, в которые можно попасть только из уже отмеченных вершин. Например, в вершину В есть один путь из А напрямую, а также по одному пути через Б и Г (так как эти вершины отмечены числом 1). Общее количество путей из А в Б равно сумме отметок предыдущих вершин: для вершины В получаем 3 пути. В вершину Ж можно попасть только из Г, поэтому число путей в Г и Ж совпадает (рис. 3.34).

Рис. 3.34
В вершину Д идёт один путь через Б и три пути через В, поэтому общее число путей — 4. Аналогично получаем 4 пути в вершину Е: 3 пути через В и один через Ж (рис. 3.35).

Рис. 3.35
Далее находим один путь из А в И (только через Ж) и 4 пути из А в 3 (все через Д). В конечную вершину К можно приехать через вершины Д (4 пути), 3 (4 пути), Е (4 пути) и И (1 путь), таким образом, общее количество различных путей равно 13 (рис. 3.36).

Рис. 3.36
Выводы
• Граф — это набор вершин (узлов) и связей между ними — рёбер.
• Матрица смежности — это таблица, в которой единица на пересечении строки и столбца обозначает ребро между соответствующими вершинами, а ноль — отсутствие ребра.
• Связный граф — это граф, между любыми вершинами которого существует путь.
• Цикл — это замкнутый путь в графе.
• Дерево — это связный граф, в котором нет циклов.
• Взвешенный граф — это граф, с каждым ребром которого связано некоторое число — вес ребра. Взвешенный граф описывается весовой матрицей.
• Ориентированный граф (орграф) — это граф, в котором каждое ребро имеет направление. Рёбра орграфа называют дугами. Матрица смежности и весовая матрица орграфа могут быть несимметричными.
Нарисуйте в тетради интеллект-карту этого параграфа.
Вопросы и задания
1. Можно ли сказать, что лес (множество деревьев) — это граф? Почему?
2. Как по матрице смежности определить, есть ли петли в графе?
3. Как по весовой матрице определить длину пути в графе?
4. Когда для представления данных используются орграфы? Приведите примеры.
5. Выполните по указанию учителя задания в рабочей тетради.
Подготовьте сообщение
а) «Задача о Кёнигсбергских мостах»
б) «Решение логических задач с помощью графов»
Оглавление
§16. Списки и деревья.
§17. Графы.
§18. Игровые стратегии.
На уроке рассмотрен материал для подготовки к огэ по информатике, 4 задание разбор
Содержание:
- Объяснение 4 задания ОГЭ по информатике
- Поиск кратчайшего пути (перебор)
- ОГЭ информатика разбор задания 4
- Актуальное
- Тренировочные
4-е задание: «Формальные описания реальных объектов и процессов»
Уровень сложности — базовый,
Максимальный балл — 1,
Примерное время выполнения — 3 минуты.
* до 2020 г — это задание № 3 ОГЭ
Графы
Иногда очень трудно структурировать информацию описанными структурами из-за сложных «взаимоотношений» между объектами. Тогда можно использовать графы:
Граф – это набор вершин и связей между ними, называющихся рёбрами:
Граф, отображающий дороги между поселками
Матрица и список смежности
Связный граф – это граф, между любыми вершинами которого существует путь.
Связный граф
Дерево – это связный граф без циклов (замкнутых участков).
Дерево — связный граф без циклов
Взвешенные графы и весовая матрица
У взвешенных графов указан «вес ребра»:
Из взвешенных графов получается весовая матрица, обратное преобразование тоже возможно.
Весовая матрица
Поиск кратчайшего пути (перебор)
Определение кратчайшего пути между пунктами A и D
- В заданиях ОГЭ этой темы чаще всего используются две информационные модели — таблицы и схемы.
- Информация в таблице строится по следующим правилам: на пересечении строки и столбца находится информация, характеризующая комбинацию этой строки и столбца.
- На схеме информация строится по следующему правилу: если между объектами схемы имеется связь, то она отображается линией, соединяющей названия этих объектов на схеме.
ОГЭ информатика разбор задания 4
Подробный видеоразбор по ОГЭ 4 задания:
📹 Видеорешение на RuTube здесь
Актуальное
Рассмотрим, как решать 4 задание по информатике ОГЭ.
Разбор задания 4.5. Демонстрационный вариант ОГЭ 2022 г ФИПИ:
Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.
Определите длину кратчайшего пути между пунктами A и Е, проходящего через пункт С.
Передвигаться можно только по дорогам, протяжённость которых указана в таблице. Каждый пункт можно посетить только один раз.
✍ Решение:
- Построим дерево протяженности дорог, на ветвях будем отображать протяженность. Учтем, что каждая ветвь, должна включить узел пересечения с С:
Ответ: 8
Разбор задания 4.6
Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых (в километрах) приведена в таблице.
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 5 | 8 | 4 | 1 | ||
| B | 5 | 3 | 3 | 4 | ||
| C | 8 | 3 | 2 | 15 | ||
| D | 4 | 2 | 4 | 12 | ||
| E | 1 | 3 | 4 | 7 | ||
| F | 4 | 15 | 12 | 7 |
Определите длину кратчайшего пути между пунктами A и F, проходящего через пункт С.
Передвигаться можно только по дорогам, протяжённость которых указана в таблице. Каждый пункт можно посетить только один раз.
✍ Решение:
- Найдём все варианты маршрутов из
AвF, проходящих через пунктС, и выберем самый короткий. - Пройдемся по таблице построчно слева-направо сверху-вниз:
A—B—C—D—E--F: длина маршрута 25 км. A—B—C—D--F: длина маршрута 29 км. A—B—C--F: длина маршрута 28 км. пропустим B: A—C--F: длина маршрута 23 км. A—C—D—E--F: длина маршрута 20 км. пропустим и D: A—C—E--F: длина маршрута 16 км. пропустим и E: A—C—D--F: длина маршрута 24 км. A—C--F: длина маршрута 23 км. поменяем следование маршрута, исключая пункты с большим числом км: A—C—B--F: длина маршрута 15 км. A—D—С—B--F: длина маршрута 13 км.
A—D—С—B--F. Длина маршрута 13 км.Ответ: 13
Тренировочные
Разбор задания 4.1:
В таблице приведена стоимость перевозок между соседними железнодорожными станциями, укажите схему, соответствующую таблице:
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 2 | 7 | 4 | ||
| B | 2 | ||||
| C | 7 | 3 | 5 | ||
| D | 3 | 3 | |||
| E | 4 | 5 | 3 |
✍ Решение:
- Необходимо рассмотреть каждую схему и подсчитать количество ребер, выходящих из каждой вершины. В скобках будем указывать соответствующую данному «ребру» стоимость:
1 схема:
A: B(2), C(7), E(4) B: A(2), C(4) Здесь уже можно остановиться, т.к. для вершины B по схеме два ребра, а по таблице одно значение (B->A=2 )
2 схема:
A: B(2), C(7), E(4) B: A(2) C: A(7), D(5), E(3) Здесь уже можно остановиться, т.к. для вершины C стоимость по схеме и по таблице различается: по схеме C->D = 5, а по таблице на пересечении C и D цифра 3.
3 схема:
A: B(2), C(7), E(4) B: A(2) C: A(7), D(3), E(5) D: C(3), E(3) E: A(4), C(5), D(3) Данные на схеме полностью совпадают с табличными!
Ответ: 3
Разбор задания 4.2:
На схеме приведена стоимость перевозок между соседними железнодорожными станциями, укажите таблицу, соответствующую схеме:
1.
|
2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.
|
4.
|
Подобные задания для тренировки
✍ Решение:
- Необходимо рассмотреть каждую таблицу и подсчитать количество пересечений для каждой строки, т.е. для каждой ж.д. станции. В скобках будем указывать соответствующую данной станции стоимость:
1 таблица:
A: B(3), E(2), F(2) Здесь уже можно остановиться, т.к. для станции A по схеме два ребра у вершины А, а по таблице уже три значения
2 таблица:
A: B(3), F(2) B: A(3), C(3), E(5), F(4) C: B(3), D(2), E(5) D: C(2), E(3) F: A(2), B(4) Данные на схеме полностью совпадают с табличными!
Ответ: 2
Разбор задания 4.3:
В таблице приведена стоимость перевозок между соседними железнодорожными станциями. Укажите таблицу, для которой минимальное расстояние от точки A до точки F больше 8.
1.
|
2.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3.
|
4.
|
✍ Решение:
- Для каждой из таблиц построим дерево перевозок, на ветвях будем отображать суммарную стоимость:
- По дереву 1-й таблицы видно, что каждая из ветвей в результате возвращает сумму большую 8. То есть таблица 1 соответствует искомому результату.
1 таблица:
Ответ: 1
Разбор задания 4.4:
Между населёнными пунктами А, В, С, D, Е, F построены дороги, протяжённость которых (в километрах) приведена в таблице:
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| A | 5 | 5 | 4 | |||
| B | 5 | 2 | ||||
| C | 5 | 2 | 1 | |||
| D | 4 | 1 | 3 | |||
| E | 1 | 1 | ||||
| F | 1 | 3 | 1 |
Определите длину кратчайшего пути между пунктами А и F. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.
1) 5
2) 6
3) 7
4) 8
Подобные задания для тренировки
✍ Решение:
- Решать такое задание лучше с помощью дерева:
- Среди приведенных ответов кратчайший путь, равный 6 км, находится под номером 2.
Ответ: 2