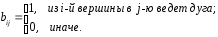Построение графов для чайников: пошаговый гайд
Время на прочтение
7 мин
Количество просмотров 54K
Ранее мы публиковали пост, где с помощью графов проводили анализ сообществ в Точках кипения из разных городов России. Теперь хотим рассказать, как строить такие графы и проводить их анализ.
Под катом — пошаговая инструкция для тех, кто давно хотел разобраться с визуализацией графов и ждал подходящего случая.
1. Выбор гипотезы
Если попытаться визуализировать хотя бы что-то, бездумно загрузив данные в программу построения графов, результат вас не порадует. Поэтому сначала сформулируйте для себя, что хотите узнать с помощью графов, и придумайте жизнеспособную гипотезу.
Для этого разберитесь, какие данные у вас уже есть, что из них можно представить «объектами», а что – «связями» между ними. Обычно объектов значительно меньше, чем связей — можно таким образом проверять себя.
Наш тестовый пример мы готовили совместно с командой Точки кипения из Томска. Соответственно, все данные для анализа по мероприятиям и их участникам у нас будут именно оттуда. Нам стало интересно, сформировалось ли из участников этих мероприятий сообщество и как оно выглядит с точки зрения принадлежности участников к бизнесу, университетам и власти.
Мы предположили, что люди, которые посетили одно и то же мероприятие, связаны друг с другом. Причем чем чаще они присутствовали на мероприятиях совместно, тем сильнее связь.
Во втором случае мы решили узнать, как соотносится принадлежность участников к одному из «нетов» (наших ключевых направлений) с интересующими их сквозными технологиями. Равномерно ли распределение, есть ли «горячие темы»? Для этого анализа мы взяли данные по участникам мероприятий из 200 томских технологических компаний.
В принципе, даже таких первичных формулировок гипотез достаточно, чтобы перейти ко второму шагу.
2. Подготовка данных
Теперь, когда вы определились с тем, что хотите узнать, возьмите весь массив данных, посмотрите, какая информация об «объектах» хранится, выкиньте все лишнее и добавьте недостающее. Если данные распределены по нескольким источникам, предварительно соберите все в одну кучу, убрав дубли.
Поясню на примере. У нас были данные об участниках 650 мероприятий. Это, условно говоря, 650 эксель-таблиц с ~23000 записей в них, содержащих поля «Leader ID», «Должность», «Организация». Для постройки графа достаточно одного уникального идентификатора (тут, к счастью, такой есть – это Leader ID) и признака, привязывающего каждого участника к одной из трех рассматриваемых сфер: власти, бизнесу или университетам. И этой информации у нас еще нет.
Чтобы получить ее, можно пойти напролом: в каждом из 650 файлов убрать лишние столбцы и добавить новое поле, заполнить его значениями для каждой строки, например: «1» для власти, «2» для бизнеса и «3» для образования и науки. А можно сначала объединить все 650 файлов в один большой список, убрать дубли и только после этого добавлять новые значения. В первом случае такая работа займет 1-2 месяца. Во втором — 1-2 недели.
Вообще при добавлении новых атрибутов старайтесь предварительно группировать данные. Например, можно отсортировать участников по компаниям/организациям и скопом выставлять признак.
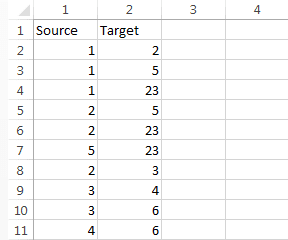
Готовим данные дальше. Для их загрузки в большинство программ визуализации потребуется создать два файла: один — с перечнем вершин, второй — со списком ребер.
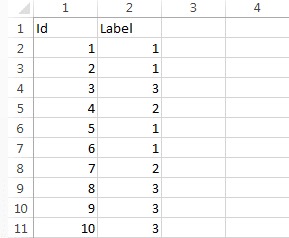
Файл вершин в нашем случае содержал два столбца: Id — номер вершины и Label — тип. Файл ребер содержал также два столбца: Source — id начальной вершины, Target — id конечной вершины.
Как превратить данные о том, что участники 1, 2, 5 и 23 посетили одно мероприятие, в ребра? Необходимо создать шесть строк и отметить связь каждого участника с каждым: 1 и 2, 1 и 5, 1 и 23, 2 и 5, 2 и 23, 5 и 23.
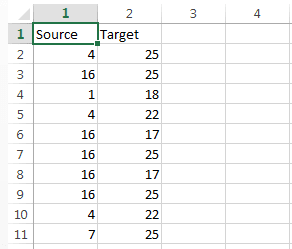
Во втором нашем примере таблицы выглядели так:
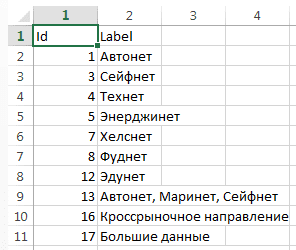
В качестве вершин перечислены как рынки, так и сквозные технологии. Если, скажем, представитель компании, относящейся к рынку «Технет» (ID=4), посетил мероприятие по теме «Большие данные и ИИ» (ID=17), в таблицу ребер заносим ребро (строку), соединяющее эти вершины (Source=4, Target=17).
Этап подготовки данных – это самая трудоемкая часть процесса, но наберитесь терпения.
3. Визуализация графа
Итак, таблицы с данными подготовлены, можно искать средство для их представления в виде графа. Для визуализации мы использовали программу Gephi — мощный опенсорсный инструмент, способный обрабатывать графы с сотнями тысяч вершин и связей. Скачать его можно с официального сайта.
Скриншоты я буду делать со второго проекта, в котором было небольшое число вершин и связей, чтобы все было максимально понятно.
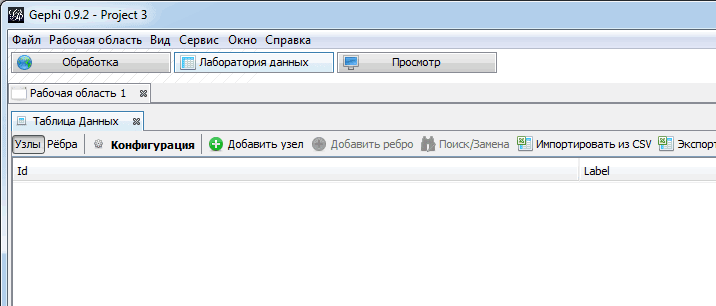
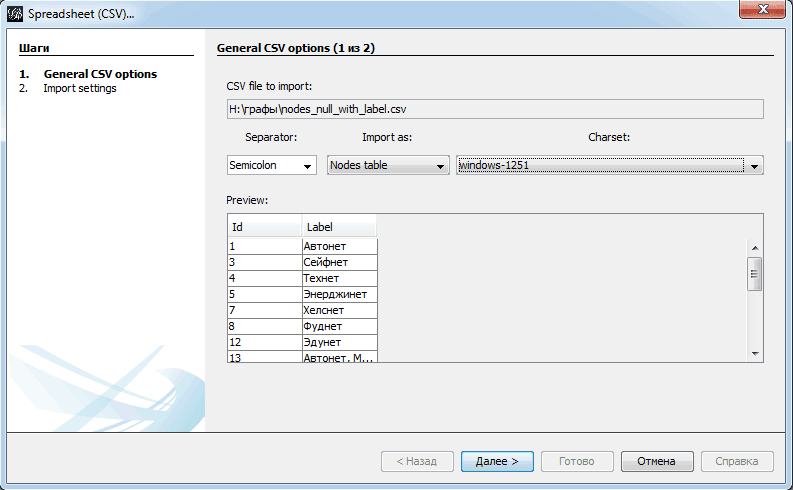
Первым делом нам надо загрузить таблицы с вершинами и ребрами. Для этого выбираем пункт «Импортировать из CSV» из меню раздела «Лаборатория данных».
Сначала грузим файл с вершинами. На первом экране формы указываем, что импортируем именно вершины, и проверяем, чтобы программа правильно определила кодировку подписей.
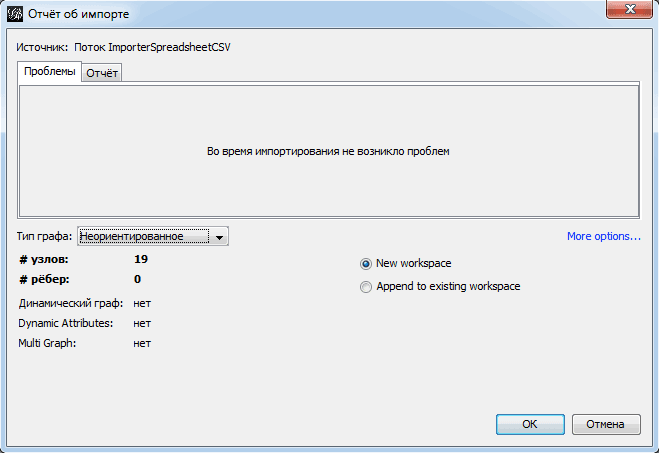
На третьей форме «Отчет об импорте» важно указать тип графа. У нас он не ориентирован.
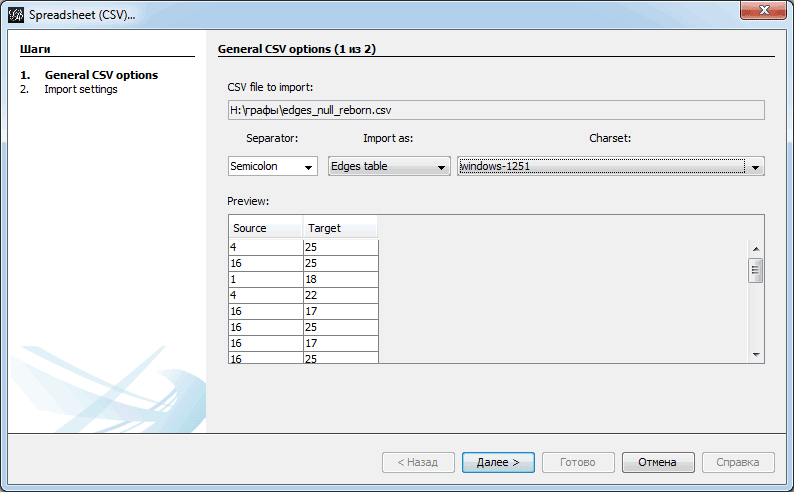
Похожим образом грузим ребра. В первом окне указываем, что это файл с ребрами, и также проверяем кодировку.
Важный момент ждет нас в третьем окне «Отчет об импорте». Тут важно указать не только то, что граф не ориентирован, но и подгрузить ребра в то же рабочее пространство, что и вершины. Поэтому выбираем пункт «Append to existing workplace».
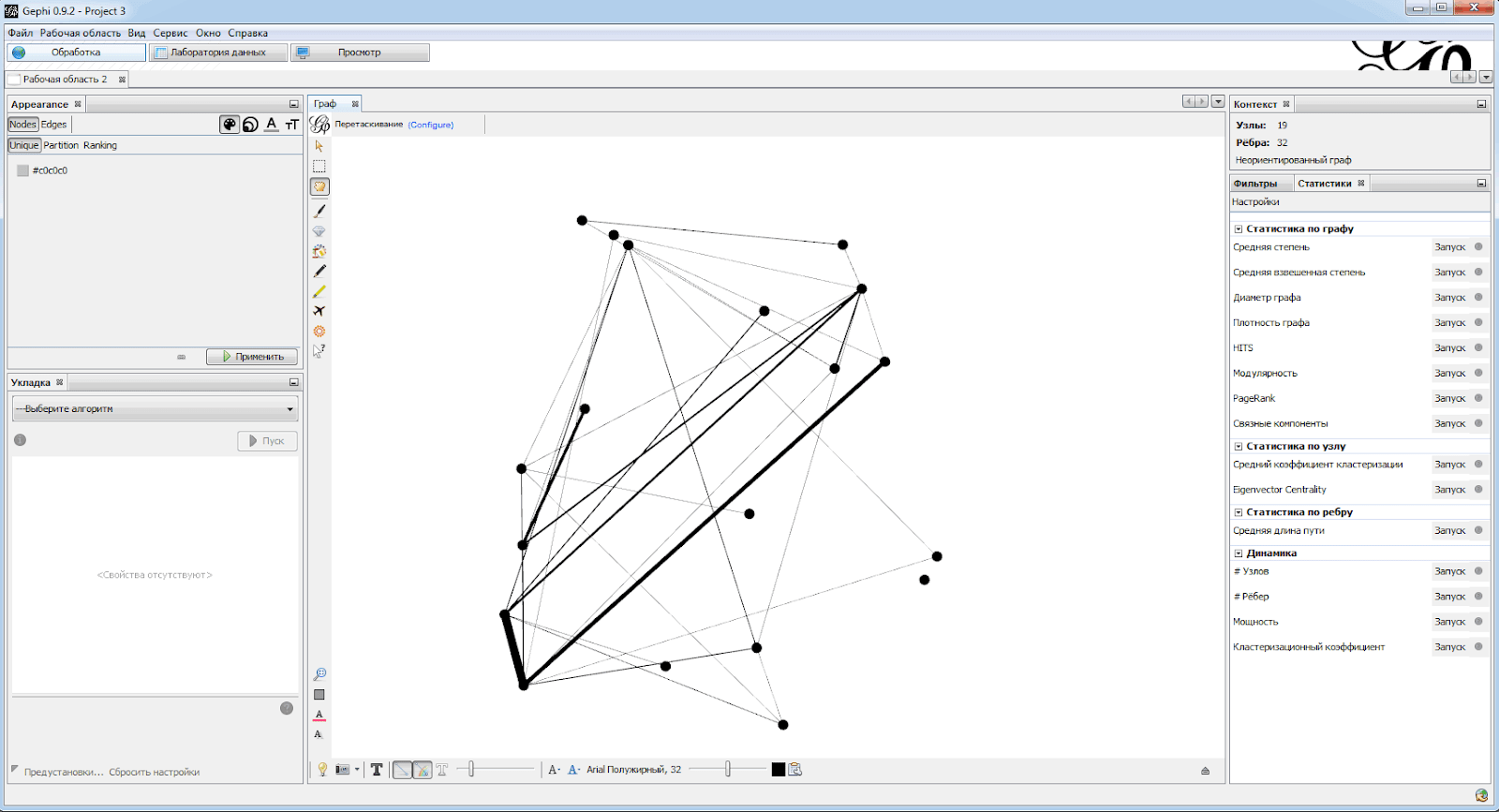
В результате перед нами предстанет граф примерно вот в таком виде (закладка «Обработка»):
Итак, ребра имеют разную толщину в зависимости от количества связей между вершинами. Посмотреть, какой вес стал у каждого ребра, можно на закладке «Лаборатория данных» в свойствах ребер в столбце Weight.
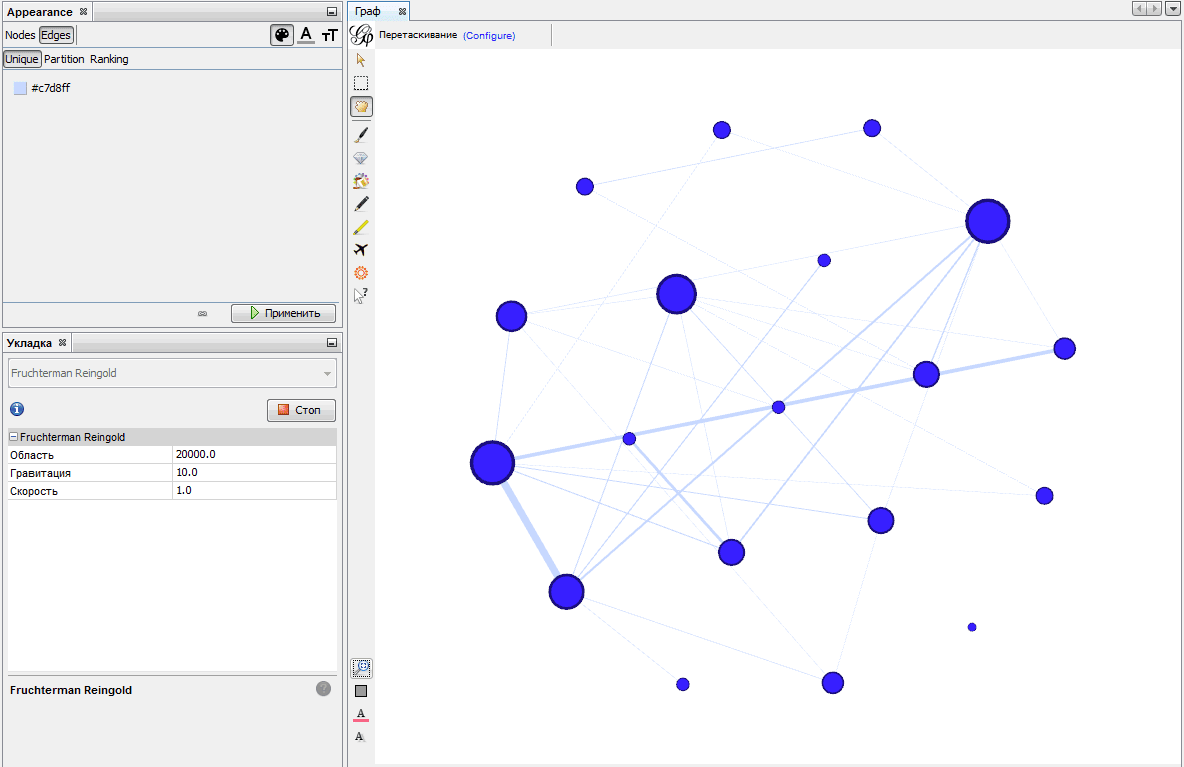
Что здесь плохо: все вершины имеют один размер и расположены абсолютно произвольно. На закладке «Обработка» мы это исправим. Сначала в верхнем левом окне выбираем Nodes и жмем на пиктограммку с кругами («Размер»). Далее выбираем пункт Ranking — он позволяет задать размер вершины в зависимости от какого-либо параметра. У нас есть возможность выбрать только один параметр — Degree (степень), который показывает, сколько ребер выходят из вершины. Выбираем минимальный и максимальный размер кружочка и жмем кнопку «Применить». Здесь же, если выбрать другие пиктограммки, можно настроить цвет маркера вершины и цвет ребер. Теперь граф уже более нагляден.
Следующее, что нужно сделать, — распутать граф. Это можно сделать вручную, двигая вершины, а можно использовать алгоритмы укладки, которые реализованы в Gephi.
Чего мы добиваемся правильной укладкой? Максимальной наглядности. Чем меньше на графе наложений вершин и ребер, чем меньше пересечений ребер, тем лучше. Также неплохо было бы, чтобы смежные вершины были расположены поближе друг к другу, а несмежные —подальше друг от друга. Ну и все было распределено по видимой области, а не сжато в одну кучу.
Как это сделать в Gephi? Левое нижнее окно «Укладка» содержит самые популярные алгоритмы укладки, построенные на силовых аналогиях. Представьте, что вершины — это заряженные шарики, который отталкиваются друг от друга, но при этом некоторые скреплены чем-то, похожим на пружинки. Если задать соответствующие силы и «отпустить» граф, вершины разбегутся на максимально допустимые пружинками расстояния.
Наиболее равномерную картину дает алгоритм Фрюхтермана и Рейнгольда. Выберите Fruchterman Reingold из выпадающего меню и задайте размер области построения. Нажмите кнопку «Исполнить». Получится что-то вроде этого:
Можно помочь алгоритму и, не останавливая его, поперетаскивать некоторые вершины, стараясь распутать граф. Но помните, что здесь нет кнопки «Отменить», вернуться к прежнему расположению вершин уже не удастся. Поэтому сохраняйте новые версии проекта перед каждым рискованным изменением.
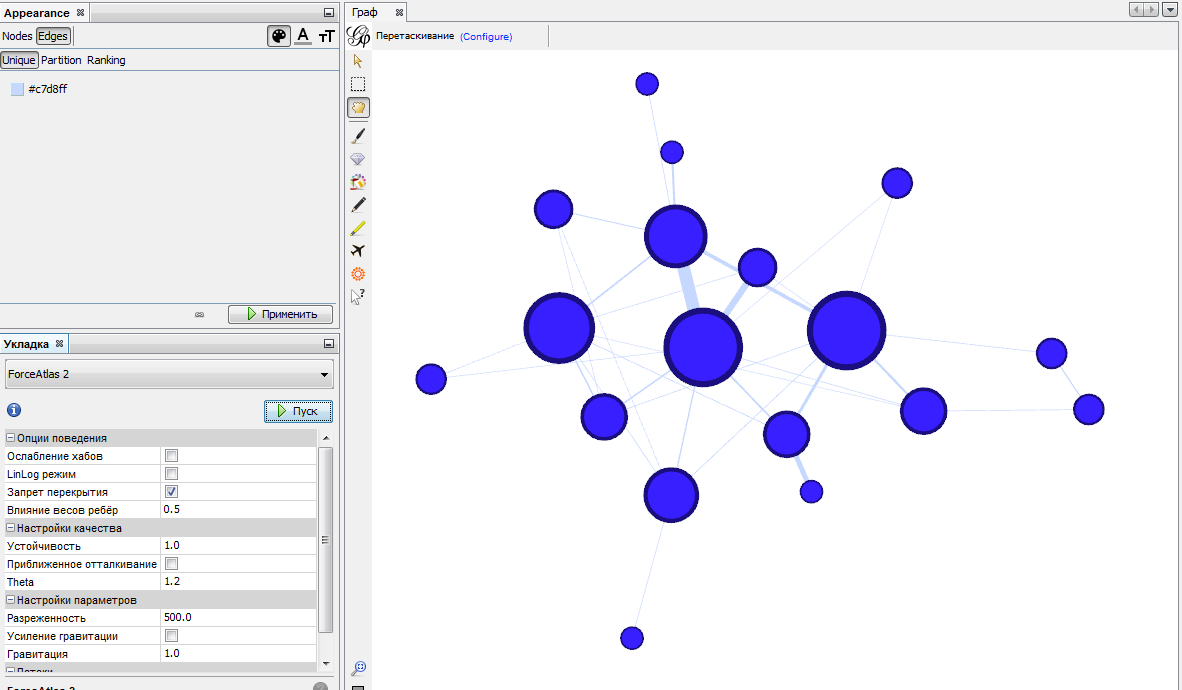
Еще один полезный алгоритм — Force Atlas 2. Он представляет граф в виде металлических колец, связанных между собой пружинами. Деформированные пружины приводят систему в движение, она колеблется и в конце концов принимает устойчивое положение. Этот алгоритм хорош для визуализаций, подчеркивающих структуру группы и выделяющих подмножества с высокой степенью взаимодействия.
Этот алгоритм имеет большое количество настроек. Рассмотрим наиболее важные. «Запрет перекрытия» запрещает вершинам перекрывать друг друга. Разреженность увеличивает расстояние между вершинами, делая граф более читаемым. Также более воздушным граф делает уменьшение влияния весов ребер на взаимное расположение вершин.
Поигравшись с настройками, получим такой граф:
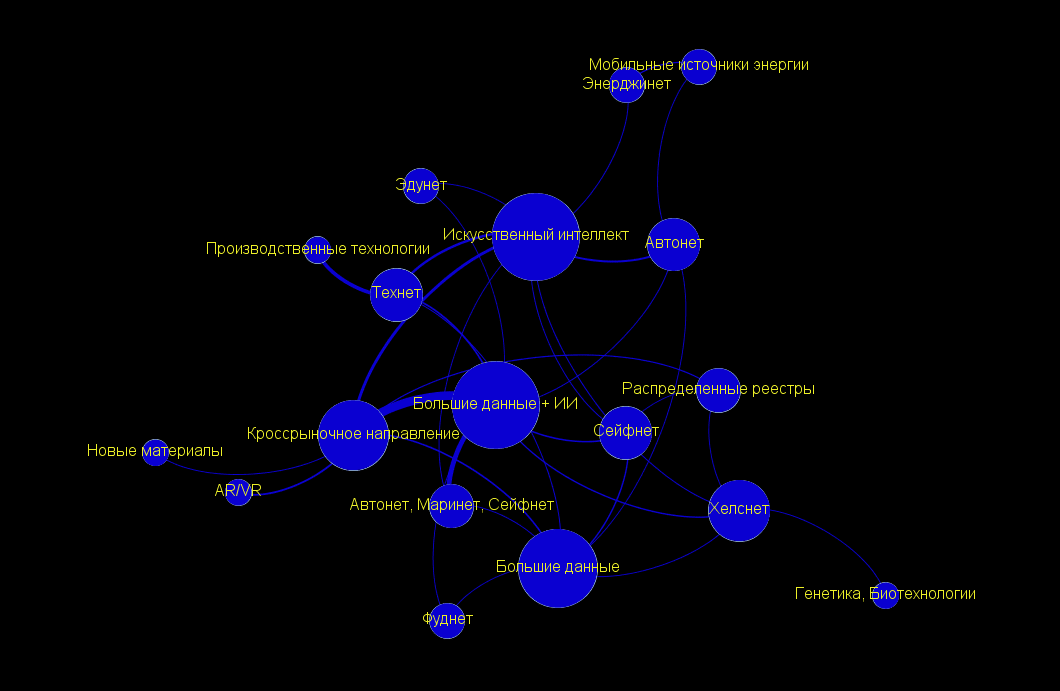
Получив граф в том виде, который вас устраивает, переходите к финальной обработке. Это закладка «Просмотр». Здесь мы можем задать, например, отрисовку графа кривыми ребрами, которая минимизирует наложение вершин на чужие ребра. Можем включить подписи вершин, задав размер и цвет шрифта. Наконец, поменять фон подложки. Например, так:
Для того чтобы сохранить получившийся рисунок, нажмите на надпись «Экспорт SVG/PDF/PNG в левом нижнем углу окна. Также отдельно не забудьте сохранить сам проект через верхнее меню «Файл» — «Сохранить проект».
В нашем случае принципиально было выделить взаимосвязь сквозных технологий с рынками НТИ, для чего мы вручную выстроили все рынки в одну линию в центре и разместили все остальное сверху и снизу. Получился вот такой граф. Все-таки для решения конкретных задач без ручной расстановки вершин обойтись не удалось.
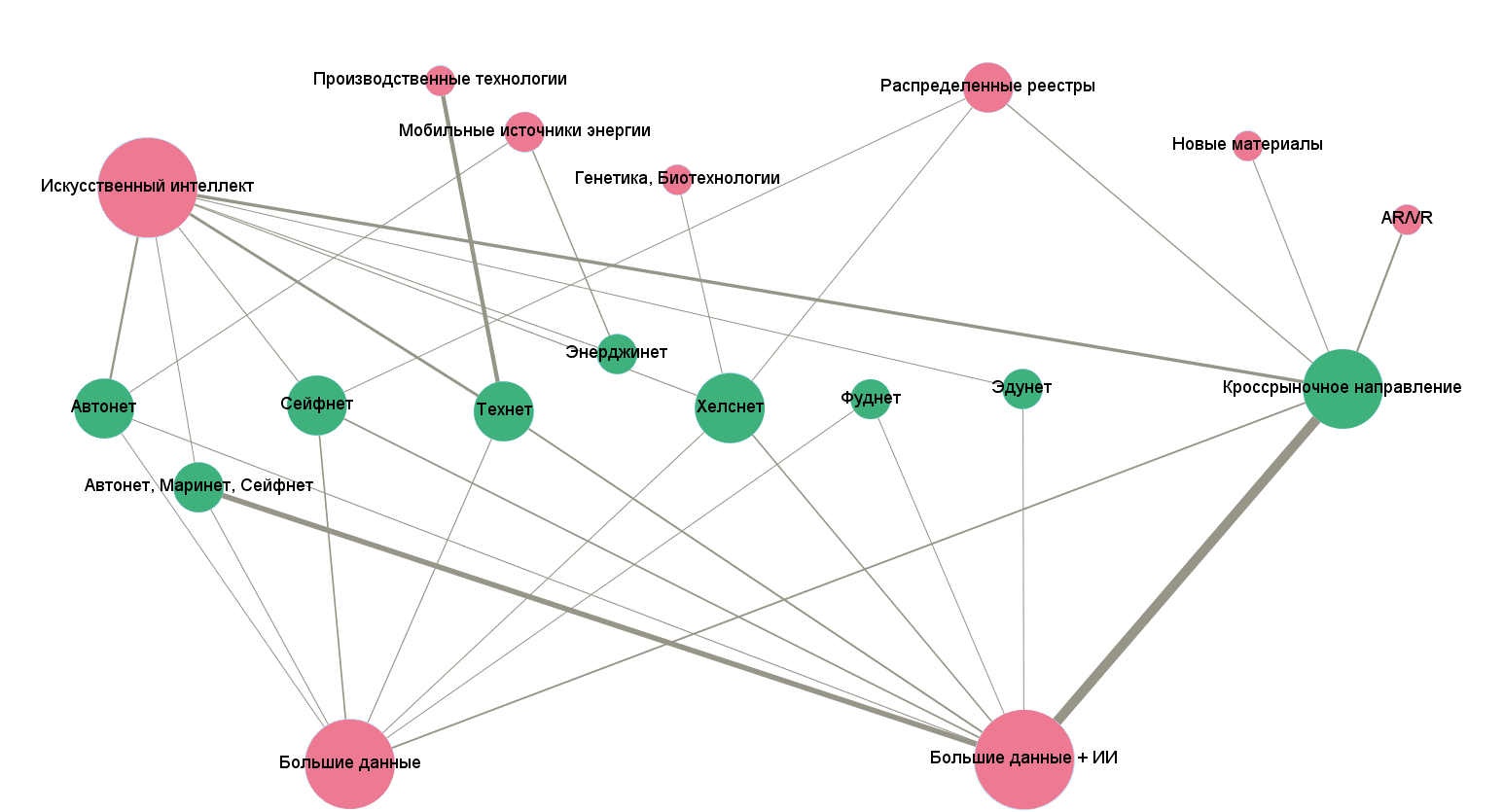
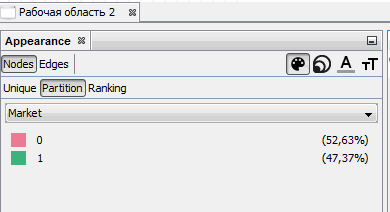
Вы, наверное, думаете, как нам удалось раскрасить вершины в разный цвет? Есть одна хитрость. Можно перейти в закладку «Лаборатория данных», создать там новый столбец в вершинах, назвав его «Market». И заполнить для каждой вершины значениями: 1 если это рынок НТИ, 0 — если сквозная технология. Затем достаточно перейти в «Обработку», выбрать пиктограммку в виде палитры, Nodes — Partition, а в качестве разделителя — наш новый атрибут Market.
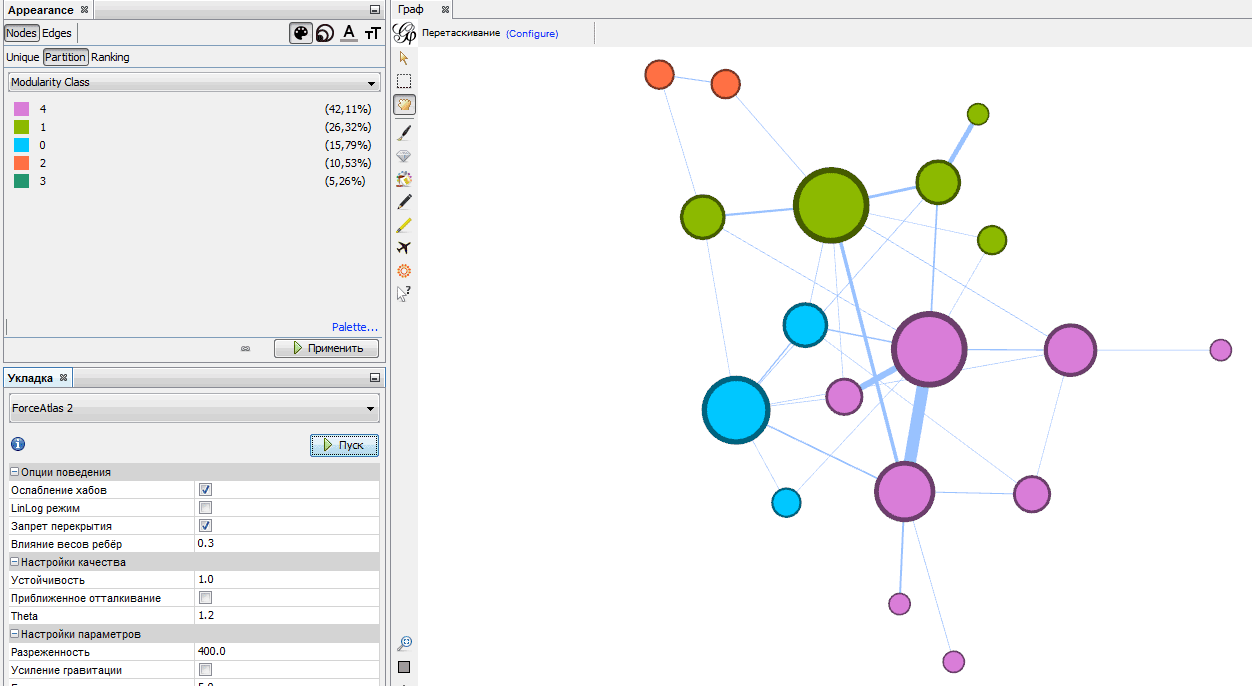
Для более сложных построений, когда требуется выделить кластеры и закрасить их разными цветами, в Gephi используется богатый арсенал статистических расчетов, результаты которых можно использовать для раздельной окраски. Находятся эти расчеты в правом столбце вкладки «Обработка».
Например, нажав кнопку «Запуск» возле расчета «Модулярность», вы узнаете оценку уровня кластеризации вашего графа. Если после этого выставить цвет вершин в зависимости от Modularity Class, появится симпатичная картинка наподобие такой:
Если вы хотите еще больше узнать о возможностях Gephi, стоит почитать руководство по работе с программой от Мартина Гранджина http://www.martingrandjean.ch/gephi-introduction/.
4. Анализ результата
Итак, вы получили итоговую визуализацию графа. Что она вам дает? Во-первых, это красиво, ее можно вставить в презентацию, показать знакомым или сделать заставкой на рабочем столе. Во-вторых, по ней вы можете понять, насколько сложной и многокластерной структурой является рассматриваемая вами предметная область. В-третьих, обратите внимание на самые крупные вершины и на самые жирные связи. Это особенные элементы, на которых все держится.
Так, построив граф экспертного сообщества, посещающего мероприятия в Точке кипения, мы сразу обнаружили участников, которые с наибольшей вероятностью выполняют роль суперконнекторов. Они являлись «вершинами», через которые кластеры объединялись в единое целое. А во втором случае мы увидели, как выглядит концентрация специалистов из томских компаний с точки зрения их принадлежности к рынку и сквозной цифровой технологии, на которую они делают ставку. Это косвенно говорит об уровне технологических компетенций и экспертизы региона.
Помощь графов в понимании окружающей действительности реально велика, так что не поленитесь и попробуйте создать собственную визуализацию данных. Это совсем не сложно, но порой трудозатратно.
1. Методические рекомендации к теме
“Графы”.
Понятие графа целесообразно вводить после
того, как разобрано несколько задач, подобных
задаче 1, решающее соображение в которых –
графическое представление. Важно, чтобы ученики
сразу осознали, что один и тот же граф может быть
нарисован разными способами. Строгое
определение графа, на мой взгляд, давать не нужно,
т.к. оно слишком громоздко и это только затруднит
обсуждение. На первых порах хватит и
интуитивного понятия. При обсуждении понятия
изоморфизма можно решить несколько упражнений
на определение изоморфных и неизоморфных графов.
Одно из центральных мест темы – теорема о
четности числа нечетных вершин. Важно, чтобы
ученики до конца разобрались в ее доказательстве
и научились применять к решению задач. При
разборе нескольких задач рекомендую не
ссылаться на теорему, а фактически повторять ее
доказательство. Чрезвычайно важно также понятие
связности графа. Содержательным соображением
здесь является рассмотрение компоненты
связности, на это необходимо обратить особое
внимание. Эйлеровы графы – тема почти игровая.
Первая и главная цель, которую нужно
преследовать при изучении графов, –научить
школьников видеть граф в условии задачи и
грамотно переводить условие на язык теории
графов. Не стоят рассказывать обе всем на
нескольких занятиях подряд. Лучше разнести
занятия по времени на 2–3 учебных года. (Прилагается
разработка занятия “Понятие графа. Применение
графов к решению задач” в 6 классе).
2. Теоретический материал к теме
“Графы”.
Введение
Графы – замечательные математические объекты,
с их помощью можно решать очень много различных,
внешне не похожих друг на друга задач. В
математике существует целый раздел – теория
графов, который изучает графы, их свойства и
применение. Мы же обсудим только самые основные
понятия, свойства графов и некоторые способы
решения задач.
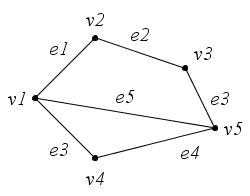
Понятие графа
Рассмотрим две задачи.
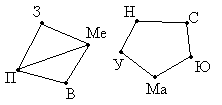
Задача 1. Между девятью планетами
солнечной системы установлено космическое
сообщение. Рейсовые ракеты летают по следующим
маршрутам: Земля – Меркурий; Плутон – Венера;
Земля – Плутон; Плутон – Меркурий; Меркурий –
Вене; Уран – Нептун; Нептун – Сатурн; Сатурн –
Юпитер; Юпитер – Марс и Марс – Уран. Можно ли
долететь на рейсовых ракетах с Земли до Марса ?
Решение: Нарисуем схему условия: планеты
изобразим точками, а маршруты ракет – линиями.
Теперь сразу видно, что долететь с Земли до
Марса нельзя.
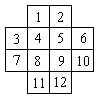
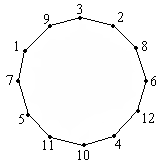
Задача 2. Доска имеет форму двойного
креста, который получается, если из квадрата 4×4
убрать угловые клетки.
Можно ли обойти ее ходом шахматного коня и
вернуться на исходную клетку, побывав на всех
клетках ровно по одному разу ?
Решение: Занумеруем последовательно
клетки доски:
А теперь с помощью рисунка покажем, что такой
обход таблицы, как указано в условии, возможен:
Мы рассмотрели две непохожие задачи. Однако
решения этих двух задач объединяет общая идея –
графическое представление решения. При этом и
картинки, нарисованные для каждой задачи,
оказались похожими: каждая картинка – это
несколько точек, некоторые из которых соединены
линиями.
Такие картинки и называются графами. Точки
при этом называются вершинами, а линии – ребрами
графа. Заметим, что не каждая картинка такого
вида будет называться графом. Например. если вас
попросят нарисовать в тетради пятиугольник, то
такой рисунок графом не будет. Будем называть что
рисунок такого вида, как в предыдущих задачах,
графом, если есть какая-то конкретная задача для
которой такой рисунок построен.
Другое замечание касается вида графа.
Попробуйте проверить, что граф для одной и той же
задачи можно нарисовать разными способами; и
наоборот для разных задач можно нарисовать
одинаковые по виду графы. Здесь важно лишь то,
какие вершины соединены друг с другом, а какие –
нет. Например, граф для задачи 1 можно нарисовать
по-другому:
Такие одинаковые, но по-разному нарисованные
графы, называются изоморфными.
Степени вершин и подсчет числа ребер графа
Запишем еще одно определение: Степенью вершины
графа называется количество выходящих из нее
ребер. В связи с этим, вершина, имеющая четную
степень, называется четной вершиной,
соответственно, вершина, имеющая нечетную
степень, называется нечетной вершиной.
С понятием степени вершины связана одна из
основных теорем теории графов –теорема о
честности числа нечетных вершин. Докажем ее мы
немного позднее, а сначала для иллюстрации
рассмотрим задачу.
Задача 3. В городе Маленьком 15
телефонов. Можно ли их соединить проводами так,
чтобы каждый телефон был соединен ровно с пятью
другими ?
Решение: Допустим, что такое соединение
телефонов возможно. Тогда представим себе граф, в
котором вершины обозначают телефоны, а ребра –
провода, их соединяющие. Подсчитаем, сколько
всего получится проводов. К каждому телефону
подключено ровно 5 проводов, т.е. степень каждой
вершины нашего графа – 5. Чтобы найти число
проводов, надо просуммировать степени всех
вершин графа и полученный результат разделить на
2 (т.к. каждый провод имеет два конца, то при
суммировании степеней каждый провод будет взят 2
раза). Но тогда количество проводов получится
разным . Но это число не
целое. Значит наше предположение о том, что можно
соединить каждый телефон ровно с пятью другими,
оказалось неверным.
Ответ. Соединить телефоны таким образом
невозможно.
Теорема: Любой граф содержит четное
число нечетных вершин.
Доказательство: Количество ребер графа
равно половине суммы степеней его вершин. Так как
количество ребер должно быть целым числом, то
сумма степеней вершин должна быть четной. А это
возможно только в том случае, если граф содержит
четное число нечетных вершин.
Связность графа
Есть еще одно важное понятие, относящееся к
графам – понятие связности.
Граф называется связным, если из любые две
его вершины можно соединить путем, т.е.
непрерывной последовательностью ребер.
Существует целый ряд задач, решение которых
основано на понятии связности графа.
Задача 4. В стране Семерка 15 городов,
каждый из городов соединен дорогами не менее, чем
с семью другими. Докажите, что из каждого города
модно добраться в любой другой.
Доказательство: Рассмотрим два
произвольных А и В города и допустим, что между
ними нет пути. Каждый из них соединен дорогами не
менее, чем с семью другими, причем нет такого
города, который был бы соединен с обоими
рассматриваемыми городами (в противном случае
существовал бы путь из A в B). Нарисуем часть графа,
соответствующую этим городам:
Теперь явно видно, что мы получили не менее
различных 16 городов, что противоречит условию
задачи. Значит утверждение доказано от
противного.
Если принять во внимание предыдущее
определение, то утверждение задачи можно
переформулировать и по-другому: “Доказать, что
граф дорог страны Семерка связен.”
Теперь вы знаете, как выглядит связный граф.
Несвязный граф имеет вид нескольких “кусков”,
каждый из которых – либо отдельная вершина без
ребер, либо связный граф. Пример несвязного графа
вы видите на рисунке:
Каждый такой отдельный кусок называется компонентой
связности графа. Каждая компонента связности
представляет собой связный граф и для нее
выполняются все утверждения, которые мы доказали
для связных графов. Рассмотрим пример задачи, в
которой используется компонента связности:
Задача 5. В Тридевятом царстве только
один вид транспорта – ковер-самолет. Из столицы
выходит 21 ковролиния, из города Дальний – одна, а
из всех остальных городов, – по 20. Докажите, что
из столицы можно долететь в город Дальний.
Доказательство: Понятно, что если
нарисовать граф ковролиний Царства, то он может
быть несвязным. Рассмотрим компоненту связности,
которая включает в себя столицу Царства. Из
столицы выходит 21 ковролиния, а из любых других
городов, кроме города Дальний – по 20, поэтому,
чтобы выполнялся закон о четном числе нечетных
вершин необходимо, чтобы и город Дальний входил в
эту же самую компоненту связности. А так как
компонента связности – связный граф, то из
столицы существует путь по ковролиниям до города
Дальний, что и требовалось доказать.
Графы Эйлера
Вы наверняка сталкивались с задачами, в которых
требуется нарисовать какую-либо фигуру не
отрывая карандаш от бумаги и проводя каждую
линию только один раз. Оказывается, что такая
задача не всегда разрешима, т.е. существуют
фигуры, которые указанным способом нарисовать
нельзя. Вопрос разрешимости таких задач также
входит в теорию графов. Впервые его исследовал в
1736 году великий немецкий математик Леонард
Эйлер, решая задачу о Кенигсбергских мостах.
Поэтому графы, которые можно нарисовать
указанным способом, называются Эйлеровыми
графами.
Задача 6. Можно ли нарисовать
изображенный на рисунке граф не отрывая карандаш
от бумаги и проводя каждое ребро ровно один раз ?
Решение. Если мы будем рисовать граф так,
как сказано в условии, то в каждую вершину, кроме
начальной и конечной, мы войдем столько же раз,
сколько выйдем из нее. То есть все вершины графа,
кроме двух должны быть четными. В нашем же графе
имеется три нечетные вершины, поэтому его нельзя
нарисовать указанным в условии способом.
Сейчас мы доказали теорему об Эйлеровых графах:
Теорема: Эйлеров граф должен иметь не
более двух нечетных вершин.
И в заключение – задача о Кенигсбергских
мостах.
Задача 7. На рисунке изображена схема
мостов города Кенигсберга.
Можно ли совершить прогулку так, чтобы пройти
по каждому мосту ровно 1 раз?
3. Задачи к теме “Графы”
Понятие графа.
1. На квадратной доске 3×3 расставлены 4 коня так,
как показано на рис.1. Можно ли сделав несколько
ходов конями, переставить их в положение,
показанное на рис.2?
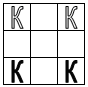
Рис. 1 |
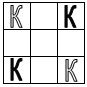
Рис. 2 |
Решение. Занумеруем клетки доски, как
показано на рисунке:
Каждой клетке поставим в соответствие точку на
плоскости и, если из одной клетки можно попасть в
другую ходом шахматного коня, то соответствующие
точки соединим линией. Исходная и требуемая
расстановки коней показаны на рисунках:
При любой последовательности ходов конями
порядок их следования, очевидно, измениться не
может. Поэтому переставить коней требуемым
образом невозможно.
2. В стране Цифра есть 9 городов с названиями 1, 2,
3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два
города соединены авиалинией в том и только в том
случае, если двузначное число, образованное
названиями городов, делится на 3. Можно ли
долететь по воздуху из города 1 в город 9 ?
Решение. Поставив в соответствие каждому
городу точку и соединив точки линией, если сумма
цифр делится на 3, получим граф, в котором цифры 3,
5, 9 связаны между собой, но не связаны с
остальными. Значит долететь из города 1 в город 9
нельзя.
Степени вершин и подсчет числа ребер.
3. В государстве 100 городов к из каждого города
выходит 4 дороги. Сколько всего дорог в
государстве.
Решение. Подсчитаем общее количество
выходящих городов дорог – 100 . 4 =
400. Однако при таком подсчете каждая дорога
посчитана 2 раза – она выходит из одного города и
входит в другой. Значит всего дорог в два раза
меньше, т.е. 200.
4. В классе 30 человек. Может ли быть так, что 9
человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5
друзей ?
Ответ. Нет (теорема о четности числа
нечетных вершин).
5. У короля 19 вассалов. Может ли оказаться так,
что у каждого вассала 1, 5 или 9 соседей ?
Ответ. Нет, не может.
6. Может ли в государстве, в котором из каждого
города выходит ровно 3 дороги, быть ровно 100 дорог?
Решение. Подсчитаем число городов. Число
дорог равно числу городов х, умноженному на 3
(число выходящих из каждого города дорог) и
разделенному на 2 (см. задачу 3). Тогда 100 = Зх/2 =>
Зх=200, чего не может быть при натуральном х. Значит
100 дорог в таком государстве быть не может.
7. Докажите, что число людей, живших когда-либо
на Земле и сделавших нечетное число рукопожатий,
четно.
Доказательство непосредственно следует из
теоремы о четности числа нечетных вершин графа.
Связность.
8. В стране из каждого города выходит 100 дорог и
из каждого города можно добраться до любого
другого. Одну дорогу закрыли на ремонт. Докажите,
что и теперь из любого города можно добраться до
любого другого.
Доказательство. Рассмотрим компоненту
связности, в которую входит один из городов,
дорогу между которыми закрыли. По теореме о
четности числа нечетных вершин в нее входит и
второй город. А значит по-прежнему можно найти
маршрут и добраться из одного из этих городов в
другой.
Графы Эйлера.
9. Имеется группа островов, соединенных мостами
так, что от каждого острова можно добраться до
любого другого. Турист обошел все острова, пройдя
по каждому мосту розно 1 раз. На острове
Троекратном он побывал трижды. Сколько мостов
ведет с Троекратного, если турист
а) не с него начал и не на нем закончил?
б) с него начал, но не на нем закончил?
в) с него начал и на нем закончил?
10. На рисунке изображен парк, разделенный на
несколько частей заборами. Можно ли прогуляться
по парку и его окрестностям так, чтобы перелезть
через каждый забор розно 1 раз?
Графы в информатике являются способом определения отношений в совокупности элементов. Это основные объекты изучения теории графов.
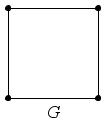
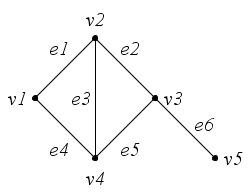
Базовые определения
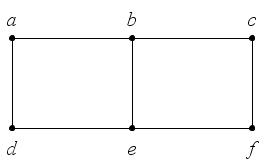
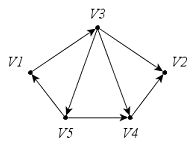
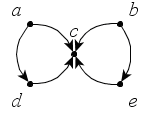
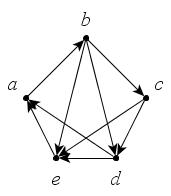
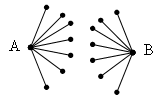
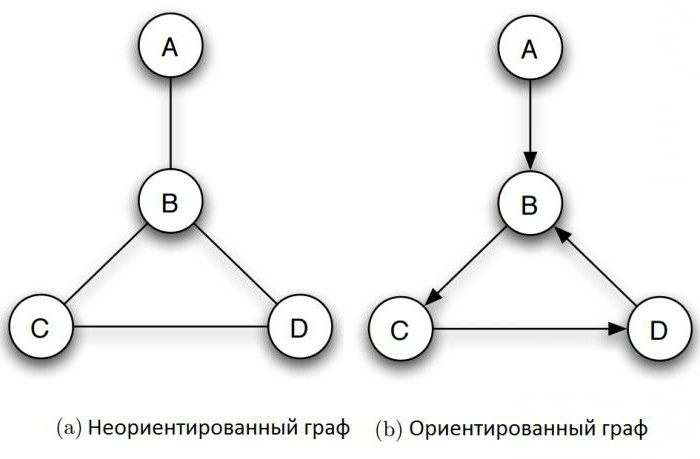
Из чего состоит граф в информатике? Он включает множество объектов, называемых вершинами или узлами, некоторые пары которых связаны т. н. ребрами. Например, граф на рисунке (а) состоит из четырех узлов, обозначенных А, В, С, и D, из которых B соединен с каждой из трех других вершин ребрами, а C и D также соединены. Два узла являются соседними, если они соединены ребром. На рисунке показан типичный способ того, как строить графы по информатике. Круги представляют вершины, а линии, соединяющие каждую их пару, являются ребрами.
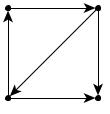
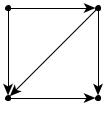
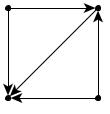
Какой граф называется неориентированным в информатике? У него отношения между двумя концами ребра являются симметричными. Ребро просто соединяет их друг с другом. Во многих случаях, однако, необходимо выразить асимметричные отношения – например, то, что A указывает на B, но не наоборот. Этой цели служит определение графа в информатике, по-прежнему состоящего из набора узлов вместе с набором ориентированных ребер. Каждое ориентированное ребро представляет собой связь между вершинами, направление которой имеет значение. Направленные графы изображают так, как показано на рисунке (b), ребра их представлены стрелками. Когда требуется подчеркнуть, что граф ненаправленный, его называют неориентированным.
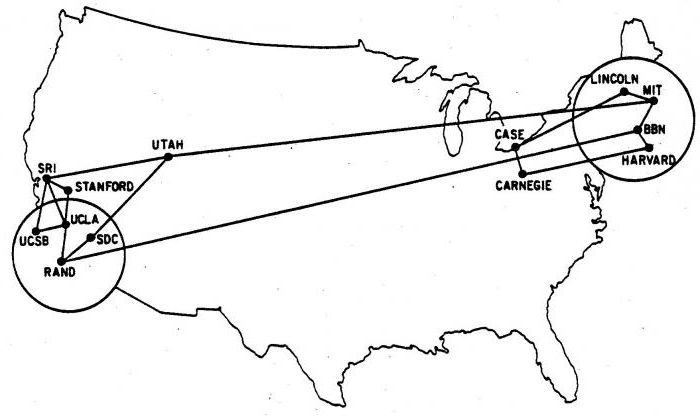
Модели сетей
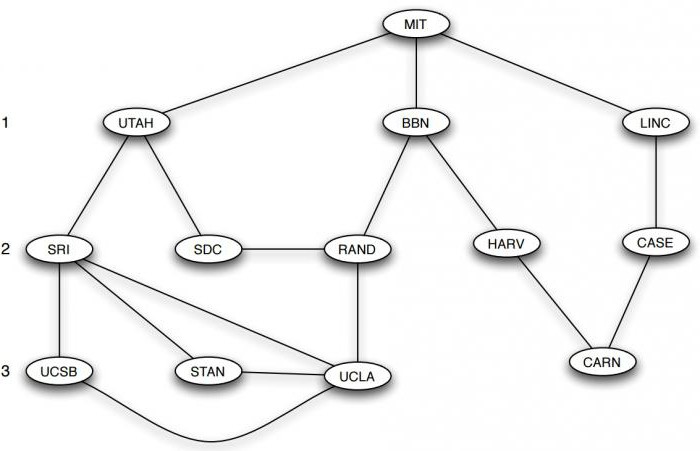
Графы в информатике служат математической моделью сетевых структур. На следующем рисунке представлена структура интернета, тогда носившего название ARPANET, в декабре 1970 года, когда она имела лишь 13 точек. Узлы представляют собой вычислительные центры, а ребра соединяют две вершины с прямой связью между ними. Если не обращать внимания на наложенную карту США, остальная часть изображения является 13-узловым графом, подобным предыдущим. При этом действительное расположение вершин несущественно. Важно, какие узлы соединены друг с другом.
Применение графов в информатике позволяет представить, как вещи либо физически, либо логически связаны между собой в сетевой структуре. 13-узловой ARPANET является примером коммуникационной сети, в которой вершины-компьютеры или другие устройства могут передавать сообщения, а ребра представляют собой прямые линии связи, по которым информация может быть передана.
Маршруты
Хотя графы применяются во многих различных областях, они обладают общими чертами. Теория графов (информатика) включает, возможно, важнейшую из них – идею о том, что вещи часто перемещаются по ребрам, последовательно переходя от узла к узлу, будь то пассажир нескольких авиарейсов или информация, передаваемая от человека к человеку в социальной сети, либо пользователь компьютера, последовательно посещающий ряд веб-страниц, следуя по ссылкам.
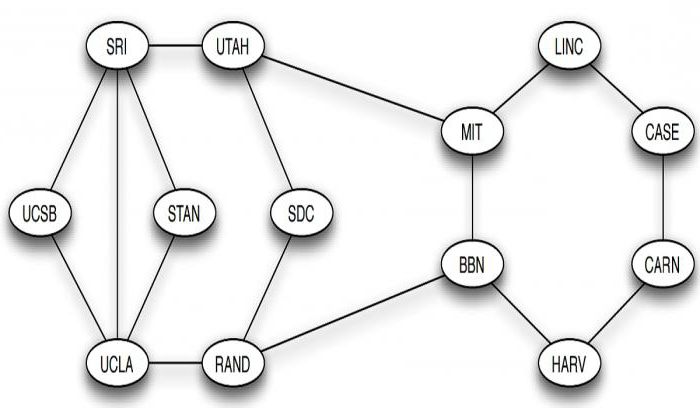
Эта идея мотивирует определение маршрута как последовательности вершин, связанных между собой ребрами. Иногда возникает необходимость рассматривать маршрут, содержащий не только узлы, но и последовательность ребер, их соединяющих. Например, последовательность вершин MIT, BBN, RAND, UCLA является маршрутом в графе интернета ARPANET. Прохождение узлов и ребер может быть повторным. Например, SRI, STAN, UCLA, SRI, UTAH, MIT также является маршрутом. Путь, в котором ребра не повторяются, называется цепью. Если же не повторяются узлы, то он носит название простой цепи.
Циклы
Особенно важные виды графов в информатике – это циклы, которые представляют собой кольцевую структуру, такую как последовательность узлов LINC, CASE, CARN, HARV, BBN, MIT, LINC. Маршруты с, по крайней мере, тремя ребрами, у которых первый и последний узел одинаковы, а остальные различны, представляют собой циклические графы в информатике.
Примеры: цикл SRI, STAN, UCLA, SRI является самым коротким, а SRI, STAN, UCLA, RAND, BBN, UTAH, SRI значительно больше.
Фактически каждое ребро графа ARPANET принадлежит к циклу. Это было сделано намеренно: если какое-либо из них выйдет из строя, останется возможность перехода из одного узла в другой. Циклы в системах коммуникации и транспорта присутствуют для обеспечения избыточности – они предусматривают альтернативные маршруты по другому пути цикла. В социальной сети тоже часто заметны циклы. Когда вы обнаружите, например, что близкий школьный друг кузена вашей жены на самом деле работает с вашим братом, то это является циклом, который состоит из вас, вашей жены, ее двоюродного брата, его школьного друга, его сотрудника (т. е. вашего брата) и, наконец, снова вас.
Связный граф: определение (информатика)
Естественно задаться вопросом, можно ли из каждого узла попасть в любой другой узел. Граф связный, если между каждой парой вершин существует маршрут. Например, сеть ARPANET – связный граф. То же можно сказать и о большинстве коммуникационных и транспортных сетей, так как их цель состоит в том, чтобы направлять трафик от одного узла к другому.
С другой стороны, нет никаких априорных оснований ожидать того, что данные виды графов в информатике широко распространены. Например, в социальной сети несложно представить двух людей, не связанных между собой.
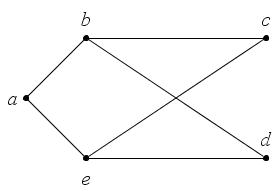
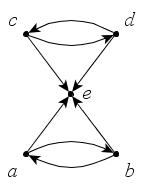
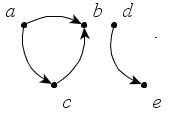
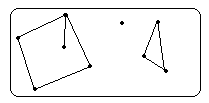
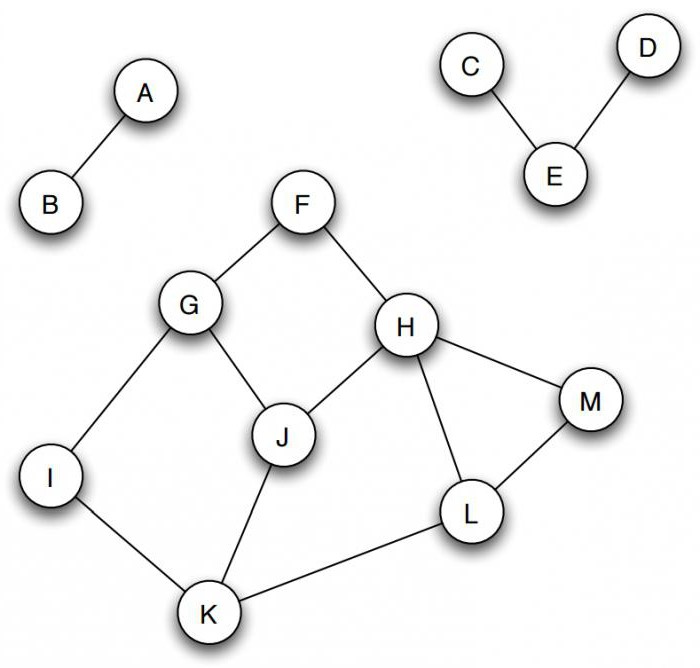
Компоненты
Если графы в информатике не связаны, то они естественным образом распадаются на набор связанных фрагментов, групп узлов, которые являются изолированными и не пересекающимися. Например, на рисунке изображены три таких части: первая – А и В, вторая – C, D и Е, и третья состоит из оставшихся вершин.
Компоненты связности графа представляют собой подмножество узлов, у которых:
- каждая вершина подгруппы имеет маршрут к любой другой;
- подмножество не является частью некоторого большего набора, в котором каждый узел имеет маршрут к любому другому.
Когда графы в информатике разделяются на их компоненты, то это является лишь начальным способом описания их структуры. В рамках данного компонента может быть богатая внутренняя структура, важная для интерпретации сети. Например, формальным методом определения важности узла является определение того, на сколько частей разделится граф, если узел будет убран.
Максимальная компонента
Существует метод качественной оценки компонентов связности. Например, есть всемирная социальная сеть со связями между двумя людьми, если они являются друзьями.
Связная ли она? Вероятно, нет. Связность – довольно хрупкое свойство, и поведение одного узла (или небольшого их набора) может свести ее на нет. Например, один человек без каких-либо живых друзей будет компонентом, состоящим из единственной вершины, и, следовательно, граф не будет связным. Или отдаленный тропический остров, состоящий из людей, которые не имеют никакого контакта с внешним миром, также будет небольшой компонентой сети, что подтверждает ее несвязность.
Глобальная сеть друзей
Но есть еще кое-что. Например, читатель популярной книги имеет друзей, выросших в других странах, и составляет с ними одну компоненту. Если принять во внимание родителей этих друзей и их друзей, то все эти люди также находятся в той же компоненте, хотя они никогда не слышали о читателе, говорят на другом языке и рядом с ним никогда не были. Таким образом, хотя глобальная сеть дружбы – не связная, читатель будет входить в компонент очень большого размера, проникающий во все части мира, включающий в себя людей из самых разных слоев и, фактически, содержащий значительную часть населения земного шара.
То же имеет место и в сетевых наборах данных – большие, сложные сети часто имеют максимальную компоненту, которая включает значительную часть всех узлов. Более того, когда сеть содержит максимальную компоненту, она почти всегда только одна. Чтобы понять, почему, следует вернуться к примеру с глобальной сетью дружбы и попробовать вообразить наличие двух максимальных компонент, каждая из которых включает миллионы людей. Потребуется наличие единственного ребра от кого-то из первой компоненты ко второй, чтобы две максимальные компоненты слились в одну. Так как ребро единственное, то в большинстве случаев невероятно, чтобы оно не образовалось, и, следовательно, две максимальные компоненты в реальных сетях никогда не наблюдаются.
В некоторых редких случаях, когда две максимальные компоненты сосуществовали в течение длительного время в реальной сети, их объединение было неожиданным, драматическим, и, в конечном итоге, имело катастрофические последствия.
Катастрофа слияния компонент
Например, после прибытия европейских исследователей в цивилизации Западного полушария примерно полтысячелетия назад произошел глобальный катаклизм. С точки зрения сети это выглядело так: пять тысяч лет глобальная социальная сеть, вероятно, состояла из двух гигантских компонент – одной в Северной и Южной Америке, а другой – в Евразии. По этой причине технологии развивалась независимо в двух компонентах, и, что еще хуже, так же развивались и болезни человека и т. д. Когда две компоненты, наконец, вошли в контакт, технологии и заболевания одной быстро и катастрофически переполнили вторую.
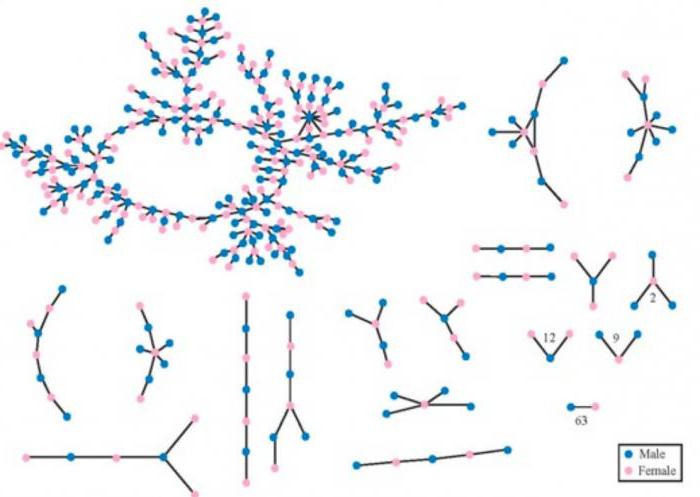
Американская средняя школа
Понятие максимальных компонент полезно для рассуждений о сетях и в гораздо меньших размерах. Интересный пример представляет собой граф, иллюстрирующий романтические отношения в американской средней школе за 18-месячный период. Тот факт, что он содержит максимальную компоненту, имеет важное значение, когда речь заходит о распространении заболеваний, передаваемых половым путем, что и являлось целью проведенного исследования. Ученики, возможно, имели лишь одного партнера за этот период времени, но, тем не менее, не осознавая этого, были частью максимальной компоненты и, следовательно, частью многих маршрутов потенциальной передачи. Эти структуры отражают отношения, которые, возможно, давно закончилась, но они связывают индивидуумов в цепях слишком долго, чтобы стать предметом пристального внимания и сплетен. Тем не менее, они реальны: как социальные факты это невидимые, но логически вытекающие макроструктуры, возникшие как продукт индивидуального посредничества.
Расстояние и поиск в ширину
В дополнение к сведениям о том, связаны ли два узла маршрутом, теория графов в информатике позволяет узнать и о его длине – в транспорте, связи или при распространении новостей и заболеваний, а также о том, проходит ли он через несколько вершин или множество.
Для этого следует определить длину маршрута, равную числу шагов, которые он содержит от начала до конца, т. е. число ребер в последовательности, которая его составляет. Например, маршрут MIT, BBN, RAND, UCLA имеет длину 3, а MIT, UTAH – 1. Используя длину пути, можно говорить о том, расположены ли два узла в графе близко друг к другу или далеко: расстояние между двумя вершинами определяется как длина самого короткого пути между ними. Например, расстояние между LINC и SRI равно 3, хотя, чтобы убедиться в этом, следует удостовериться в отсутствии длины, равной 1 или 2, между ними.
Алгоритм поиска в ширину
Для небольших графов расстояние между двумя узлами подсчитать легко. Но для сложных появляется необходимость в систематическом методе определения расстояний.
Самым естественным способом это сделать и, следовательно, наиболее эффективным, является следующий (на примере глобальной сети друзей):
- Все друзья объявляются находящимися на расстоянии 1.
- Все друзья друзей (не считая уже отмеченных) объявляются находящимися на расстоянии 2.
- Все их друзья (опять же, не считая помеченных людей) объявляются удаленными на расстояние 3.
Продолжая таким образом, поиск проводят в последующих слоях, каждый из которых – на единицу дальше предыдущего. Каждый новый слой составляется из узлов, которые еще не участвовали в предыдущих, и которые входят в ребро с вершиной предыдущего слоя.
Эта техника называется поиском в ширину, так как она выполняет поиск по графу наружу от начального узла, в первую очередь охватывая ближайшие. В дополнение к предоставлению способа определения расстояния, она может служить полезной концептуальной основой для организации структуры графа, а также того, как построить граф по информатике, располагая вершины на основании их расстояния от фиксированной начальной точки.
Поиск в ширину может быть применен не только к сети друзей, но и к любому графу.
Мир тесен
Если вернуться к глобальной сети друзей, можно увидеть, что аргумент, объясняющий принадлежность к максимальной компоненте, на самом деле утверждает нечто большее: не только у читателя есть маршруты к друзьям, связывающие его со значительной долей населения земного шара, но эти маршруты на удивление коротки.
Эта идея получила название «феномена тесного мира»: мир кажется маленьким, если думать о том, какой короткий маршрут связывает любых двух людей.
Теория «шести рукопожатий» впервые экспериментально исследовалась Стенли Милгрэмом и его коллегами в 1960-е годы. Не имея какого-либо набора данных социальных сетей и с бюджетом в 680 долларов он решил проверить популярную идею. С этой целью он попросил 296 случайно отобранных инициаторов попробовать отослать письмо биржевому брокеру, который жил в пригороде Бостона. Инициаторам были даны некоторые личные данные о цели (включая адрес и профессию), и они должны были переслать письмо лицу, которого они знали по имени, с теми же инструкциями, чтобы оно достигло цели как можно быстрее. Каждое письмо прошло через руки ряда друзей и образовало цепочку, замыкавшуюся на биржевом брокере за пределами Бостона.
Среди 64 цепочек, достигших цели, средняя длина равнялась шести, что подтвердило число, названное два десятилетия ранее в названии пьесы Джона Гэра.
Несмотря на все недочеты этого исследования, эксперимент продемонстрировал один из важнейших аспектов нашего понимания социальных сетей. В последующие годы из него был сделан более широкий вывод: социальные сети, как правило, имеют очень короткие маршруты между произвольными парами людей. И даже если такие опосредованные связи с руководителями предприятий и политическими лидерами не окупаются на ежедневной основе, существование таких коротких маршрутов играет большую роль в скорости распространения информации, болезней и других видов заражения в обществе, а также в возможностях доступа, которые социальная сеть предоставляет людям с совершенно противоположными качествами.
В
подразд. 3.1 мы уже познакомились с двумя
способами описания графов: в
виде задания двух множеств вершин
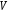
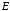
графическим
способом.
Рассмотрим
другие способы задания графов.
-
Матрица
инцидентности
.
Пусть
дан граф
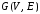
где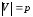
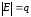
инцидентности имеет размер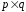
Для
неориентированного графа она имеет вид
Для
орграфа
Замечание
1. Если
граф без петель, то в матрице смежности
по главной диагонали стоят нули.
Пример
1. Составьте
матрицы инцидентности для следующих
графов (рис. 26, а,
б).
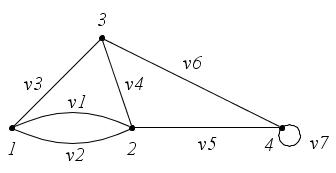
а
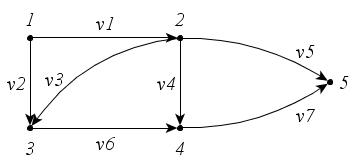
б
Рис.
26
Решение:
а)

б)
В
каждом столбце матрицы инцидентности
неориентированного или ориентированного
графа только два элемента отличны от
нуля (или один, если ребро является
петлей). Для матрицы инцидентности
ориентированного графа либо столбец
содержит один элемент, равный 1, либо
один элемент, равный
либо столбец нулевой.
Отношение
инцидентности можно еще задать списком
ребер графа. Каждая строка этого списка
соответствует ребру, в котором записаны
номера вершин, инцидентных ему.
2.
Матрица смежности
Пусть
дан граф
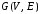
где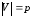
смежности отражает смежность вершин и
имеет размер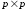
Для
неориентированного графа она имеет вид
Для
орграфа
Для
неориентированного мультиграфа значение
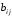
и j-й
вершинам, для ориентированного графа
этот элемент матрицы смежности равен
количеству ребер с началом в i-й
вершине и концом в j-й.
Таким образом, матрица смежности
неориентированного графа симметрична,
а ориентированного – не обязательно
симметрична.
Пример
2.
Найдите матрицы смежности для графов
(рис. 27, а,
б).
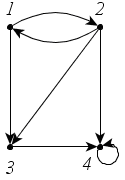
б
а
Рис.
27
Решение
а)
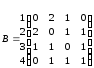
б)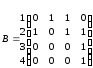
Замечание
2. Для
неориентированного графа матрица
смежности симметричная.
Пример
3.
Нарисуйте граф
c
множеством вершин
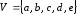
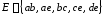
Найдите его матрицу смежности.
Решение
Изображение
графа
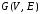
Так
как у графа пять вершин, то матрица
смежности будет
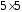
Рис.
28
Вопросы
и задачи для самостоятельного решения
1.
Перечислите способы представления
графов. Дайте понятия матриц смежности
и инцидентности.
2.
Постройте граф по данной матрице
смежности:
3.
Для следующих графов найдите матрицы
инцидентности и смежности (рис. 29, a,
б):
а
б
Рис.
29
-
Пронумеруйте
вершины и ребра орграфов (рис. 30, а,
б).
Найдите для них матрицы инцидентности
и смежности. -
Можно
ли нарисовать, не отрывая карандаша от
бумаги и не проходя ни по одному их
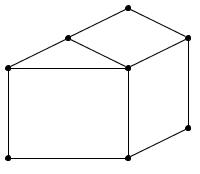
отрезков дважды, «домики с крышами»
(рис. 31, а,
б,
в,
г,
д)?
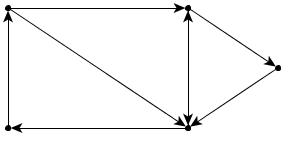
а
б
Рис.
30
б
а
в
д
г
Рис.
31
3.3. Связность графов
Определение
1.
Граф (орграф)
графа (орграфа)
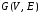
если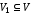
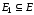
Будем
использовать обозначение
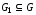
аналогичное обозначению включения для
множеств.
Определение
2. Если
хотя бы одно из указанных двух включений
в определении 1 строгое, то
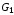
подграфом
графа.
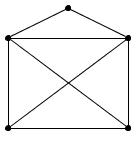
Например,
графы
на рис. 32 являются подграфами графа на
рис. 33.
Рис.
32
Рис.
33
Определение
3. Подграф
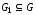
подграфом,
если он не является собственным подграфом
никакого другого подграфа
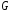
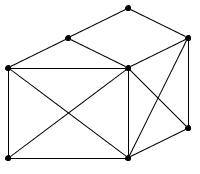
Например,
на
рис. 34 графы
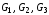
причем они также являются собственными
подграфами.
Рис.
34
Определение
4.
Граф называется связным,
если любую пару его вершин соединяет
какой-нибудь маршрут, в противном случае
граф называется несвязным.
Например,
граф
на рис. 33 является связным.
Определение
5.
Орграф называется сильно
связным,
если для любых двух его вершин



Если существует путь из вершины
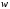
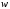

то орграф –односторонне
связан.
Орграф называется слабо
связным,
если в графе
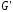

(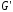
орграфа после отмены ориентации ребер).
Определение
6.
Орграф, не являющийся слабо связным,
называется несвязным.
Например,
на
рис. 35: а
–
сильная
связность; б
– односторонняя связность; в
– слабая связность.
а
б
в
Рис.
35
Определение
7.
Компонентой
связности
графа
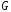
являющийся подграфом никакого другого
связного подграфа графа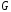
Определение
8.
Компонентой
сильной связности (слабой
связности)
орграфа
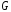
являющийся подграфом никакого другогоcильного
(слабого) связного подграфа графа
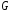
а
б
Рис.
36
Например,
граф, изображенный на рис. 36, а,
имеет
две компоненты связности (рис. 36, б).
Орграф
(рис. 37, а)
имеет три компоненты связности (рис.
37, б).
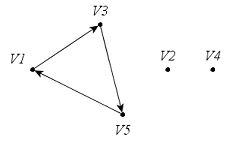
а
б
Рис.
37
Теорема.
Пусть
дан граф
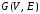
у которого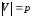
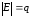
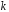
Тогда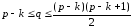
Следствие.
Если
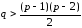
то граф связен.
Вопросы
и задачи для самостоятельного решения
-
Сформулируйте
понятие связного графа (орграфа). -
Для
графов, изображенных на рис. 38, а,
б,
постройте по четыре подграфа.
а
б
Рис.
38
-
Определите
связные орграфы. Какие из них являются
сильно связными (рис. 39)?
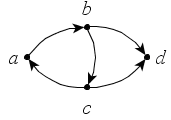
а
б
в
Рис.
39
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #






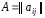 .
.