Как составить граф структуру

Структура данных графа

представляет собой набор узлов, которые имеют данные и связаны с другими узлами.

Давайте попробуем понять это на примере. На facebook все является узлом. Сюда входят пользователь, фотография, альбом, событие, группа, страница, комментарий, история, видео, ссылка, примечание … все, что имеет данные, является узлом.

Каждое отношение – это ребро от одного узла к другому. Публикуете ли вы фотографию, присоединяетесь ли к группе, например, к странице и т. д. Для этих отношений создается новое ребро.

Тогда весь facebook – это совокупность узлов и ребер. Это потому, что facebook использует структуру данных графа для хранения своих данных.

Точнее,

граф

– это структура данных (V, E), которая состоит из:

• Коллекция вершин V.
• Набор ребер E, представленный в виде упорядоченных пар вершин (u, v).

Представлен граф

V = {0, 1, 2, 3}
E = {(0,1), (0,2), (0,3), (1,2)}
G = {V, E}


  Терминология графа

 




     Смежность.

    

    Говорят, что вершина смежна с другой вершиной, если есть ребро, соединяющее их.

    

    Вершины 2 и 3 не являются смежными, потому что между ними нет ребра.
   




     Путь.

    

    Последовательность ребер, которая позволяет вам перейти от вершины A к вершине B, называется путем.

    

    0-1, 1-2 и 0-2 являются путями от вершины 0 до вершины 2.
   




     Ориентированный граф.

    

    Граф, в котором есть ребро (u, v) не обязательно означает, что также имеется ребро (v, u). Ребра в таком графике представлены стрелками, чтобы показать направление ребра.
   



  Способы представления графа

 

  Графы обычно представлены двумя способами:
 



  


                       
  





  1. Матрица смежности

 


   Матрица смежности

  

  – это двумерный (2D) массив V x V вершин. Каждая строка и столбец представляют вершину.
 

  Если значение любого элемента a[i][j] равно 1, это означает, что существует ребро, соединяющее вершину i и вершину j.
 

  Матрица смежности для графа, который мы создали выше.
 


  Поскольку это неориентированный граф, для ребра (0,2) нам также нужно отметить ребро (2,0), делая матрицу смежности симметричной относительно диагонали.
 

  Поиск ребер (проверка, существует ли ребро между вершиной A и вершиной B), чрезвычайно быстр в представлении матрицы смежности, но мы должны зарезервировать пространство для каждой возможной связи между всеми вершинами (V x V), поэтому для этого требуется больше места.
 

  2. Список смежности

 


   Список смежности

  

  представляет собой граф в виде массива связанного списка.
 



  


                       
  





  Индекс массива представляет вершину, и каждый элемент в его связанном списке представляет другие вершины, которые образуют ребро с вершиной.
 

  Список смежности для графа, который мы создали в первом примере, выглядит следующим образом:
 


  Список смежности эффективен с точки зрения хранения, потому что нам нужно хранить только значения для ребер. Для графа с миллионами вершин это может означать много сэкономленного пространства.
 

  Операции над графами

 

  Наиболее распространенные операции над графами:
 


   Проверьте, присутствует ли элемент в графе.
  

   Обход графа.
  

   Добавить элементы (вершины, ребра) в граф.
  

   Нахождение пути от одной вершины к другой.
  

Построение графов для чайников: пошаговый гайд

Ранее мы публиковали пост, где с помощью графов проводили анализ сообществ в Точках кипения из разных городов России. Теперь хотим рассказать, как строить такие графы и проводить их анализ.

Под катом — пошаговая инструкция для тех, кто давно хотел разобраться с визуализацией графов и ждал подходящего случая.

1. Выбор гипотезы

Если попытаться визуализировать хотя бы что-то, бездумно загрузив данные в программу построения графов, результат вас не порадует. Поэтому сначала сформулируйте для себя, что хотите узнать с помощью графов, и придумайте жизнеспособную гипотезу.

Для этого разберитесь, какие данные у вас уже есть, что из них можно представить «объектами», а что – «связями» между ними. Обычно объектов значительно меньше, чем связей — можно таким образом проверять себя.

Наш тестовый пример мы готовили совместно с командой Точки кипения из Томска. Соответственно, все данные для анализа по мероприятиям и их участникам у нас будут именно оттуда. Нам стало интересно, сформировалось ли из участников этих мероприятий сообщество и как оно выглядит с точки зрения принадлежности участников к бизнесу, университетам и власти.

Мы предположили, что люди, которые посетили одно и то же мероприятие, связаны друг с другом. Причем чем чаще они присутствовали на мероприятиях совместно, тем сильнее связь.
Во втором случае мы решили узнать, как соотносится принадлежность участников к одному из «нетов» (наших ключевых направлений) с интересующими их сквозными технологиями. Равномерно ли распределение, есть ли «горячие темы»? Для этого анализа мы взяли данные по участникам мероприятий из 200 томских технологических компаний.

В принципе, даже таких первичных формулировок гипотез достаточно, чтобы перейти ко второму шагу.

2. Подготовка данных

Теперь, когда вы определились с тем, что хотите узнать, возьмите весь массив данных, посмотрите, какая информация об «объектах» хранится, выкиньте все лишнее и добавьте недостающее. Если данные распределены по нескольким источникам, предварительно соберите все в одну кучу, убрав дубли.

Поясню на примере. У нас были данные об участниках 650 мероприятий. Это, условно говоря, 650 эксель-таблиц с ~23000 записей в них, содержащих поля «Leader ID», «Должность», «Организация». Для постройки графа достаточно одного уникального идентификатора (тут, к счастью, такой есть – это Leader ID) и признака, привязывающего каждого участника к одной из трех рассматриваемых сфер: власти, бизнесу или университетам. И этой информации у нас еще нет.

Чтобы получить ее, можно пойти напролом: в каждом из 650 файлов убрать лишние столбцы и добавить новое поле, заполнить его значениями для каждой строки, например: «1» для власти, «2» для бизнеса и «3» для образования и науки. А можно сначала объединить все 650 файлов в один большой список, убрать дубли и только после этого добавлять новые значения. В первом случае такая работа займет 1-2 месяца. Во втором — 1-2 недели.

Вообще при добавлении новых атрибутов старайтесь предварительно группировать данные. Например, можно отсортировать участников по компаниям/организациям и скопом выставлять признак.

Готовим данные дальше. Для их загрузки в большинство программ визуализации потребуется создать два файла: один — с перечнем вершин, второй — со списком ребер.

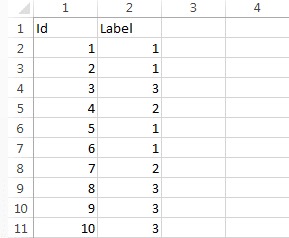
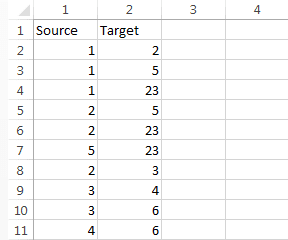
Файл вершин в нашем случае содержал два столбца: Id — номер вершины и Label — тип. Файл ребер содержал также два столбца: Source — id начальной вершины, Target — id конечной вершины.

Как превратить данные о том, что участники 1, 2, 5 и 23 посетили одно мероприятие, в ребра? Необходимо создать шесть строк и отметить связь каждого участника с каждым: 1 и 2, 1 и 5, 1 и 23, 2 и 5, 2 и 23, 5 и 23.

Во втором нашем примере таблицы выглядели так:

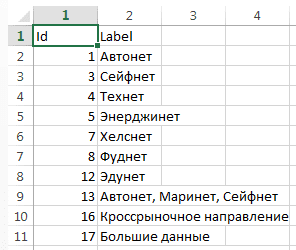
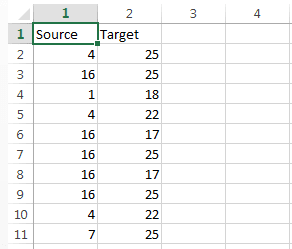
В качестве вершин перечислены как рынки, так и сквозные технологии. Если, скажем, представитель компании, относящейся к рынку «Технет» (ID=4), посетил мероприятие по теме «Большие данные и ИИ» (ID=17), в таблицу ребер заносим ребро (строку), соединяющее эти вершины (Source=4, Target=17).

Этап подготовки данных – это самая трудоемкая часть процесса, но наберитесь терпения.

3. Визуализация графа

Итак, таблицы с данными подготовлены, можно искать средство для их представления в виде графа. Для визуализации мы использовали программу Gephi — мощный опенсорсный инструмент, способный обрабатывать графы с сотнями тысяч вершин и связей. Скачать его можно с официального сайта.

Скриншоты я буду делать со второго проекта, в котором было небольшое число вершин и связей, чтобы все было максимально понятно.

Первым делом нам надо загрузить таблицы с вершинами и ребрами. Для этого выбираем пункт «Импортировать из CSV» из меню раздела «Лаборатория данных».

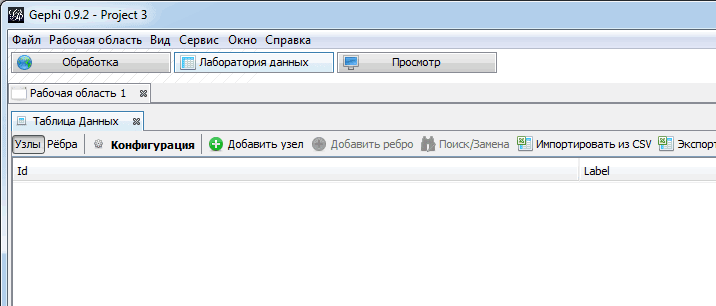
Сначала грузим файл с вершинами. На первом экране формы указываем, что импортируем именно вершины, и проверяем, чтобы программа правильно определила кодировку подписей.

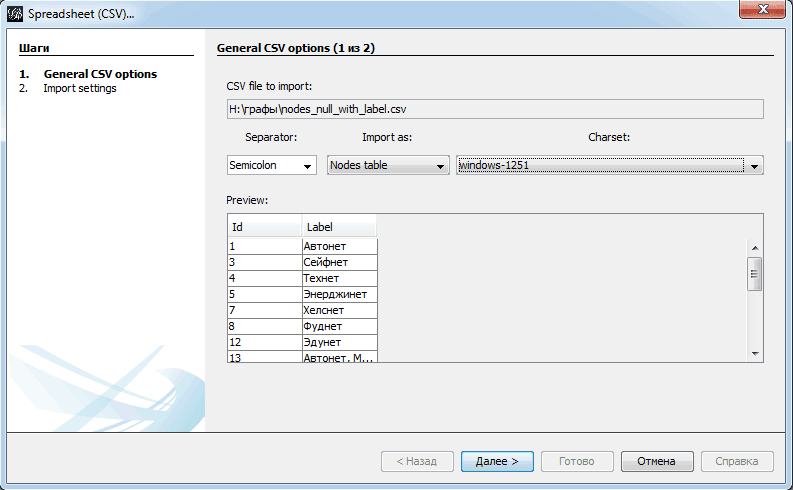
На третьей форме «Отчет об импорте» важно указать тип графа. У нас он не ориентирован.

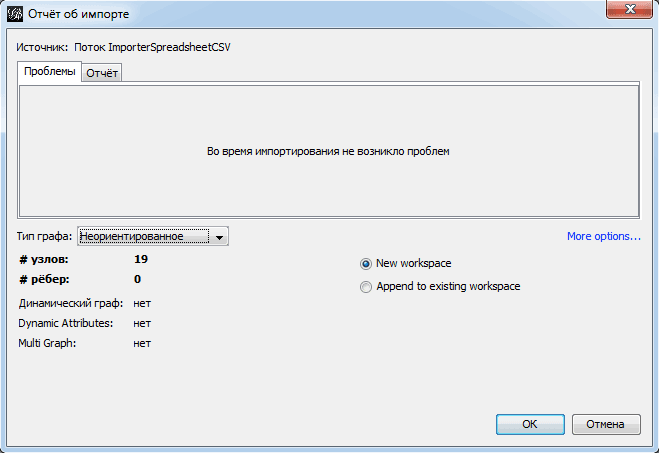
Похожим образом грузим ребра. В первом окне указываем, что это файл с ребрами, и также проверяем кодировку.

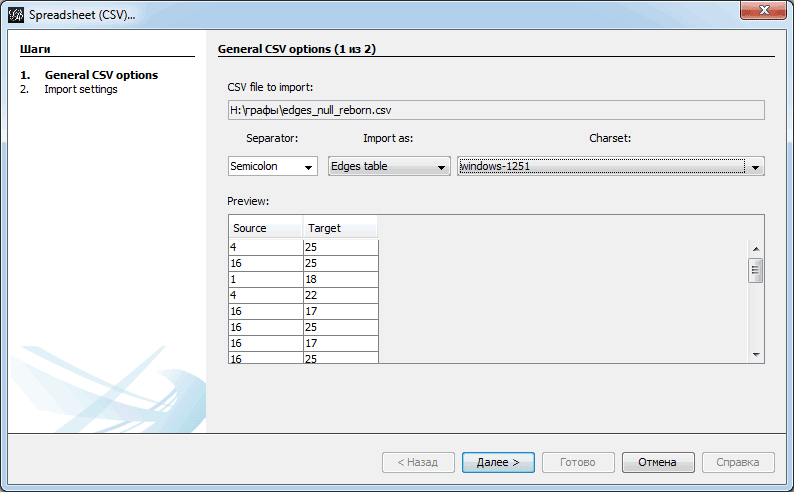
Важный момент ждет нас в третьем окне «Отчет об импорте». Тут важно указать не только то, что граф не ориентирован, но и подгрузить ребра в то же рабочее пространство, что и вершины. Поэтому выбираем пункт «Append to existing workplace».

В результате перед нами предстанет граф примерно вот в таком виде (закладка «Обработка»):

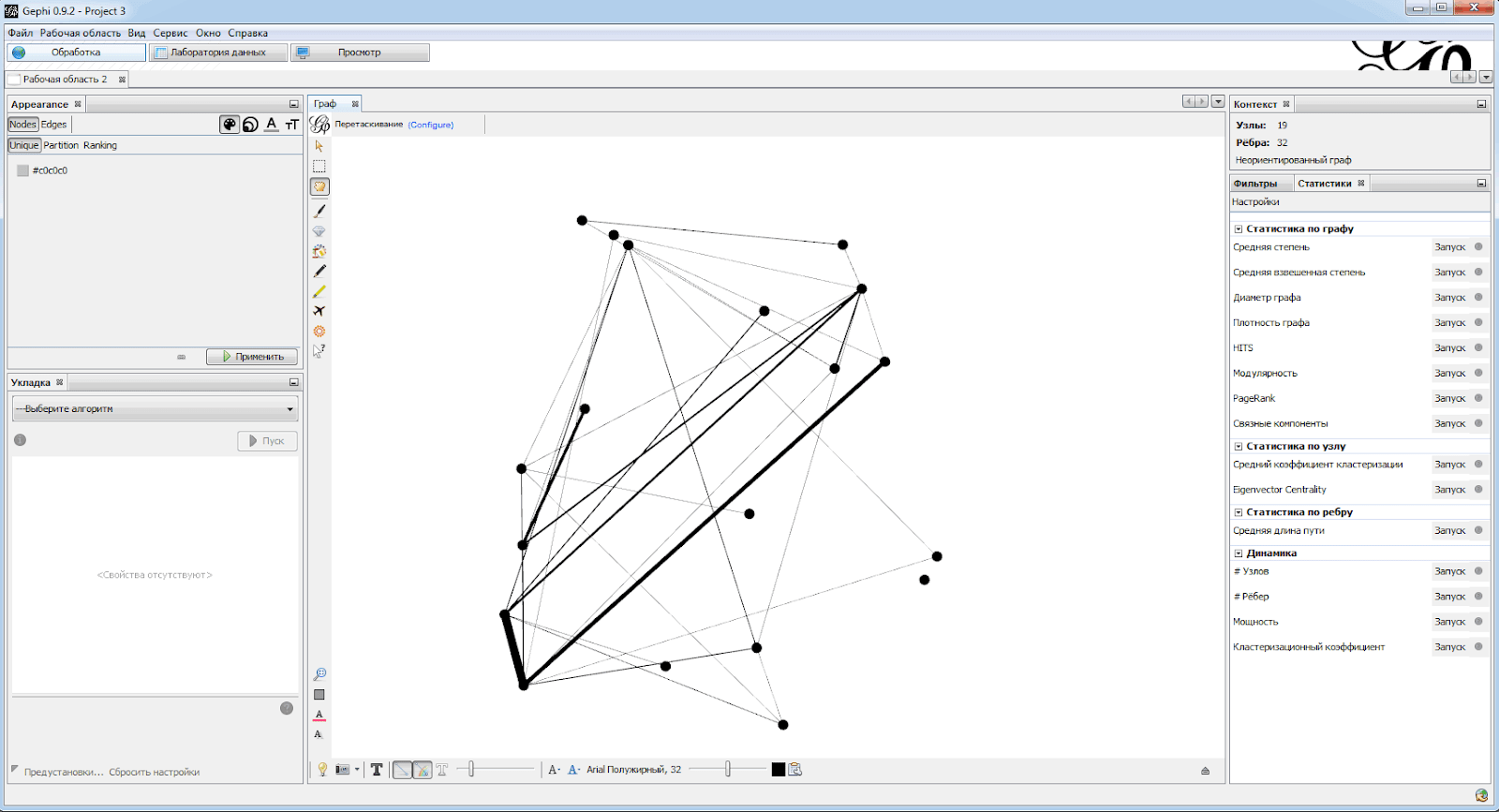
Итак, ребра имеют разную толщину в зависимости от количества связей между вершинами. Посмотреть, какой вес стал у каждого ребра, можно на закладке «Лаборатория данных» в свойствах ребер в столбце Weight.

Что здесь плохо: все вершины имеют один размер и расположены абсолютно произвольно. На закладке «Обработка» мы это исправим. Сначала в верхнем левом окне выбираем Nodes и жмем на пиктограммку с кругами («Размер»). Далее выбираем пункт Ranking — он позволяет задать размер вершины в зависимости от какого-либо параметра. У нас есть возможность выбрать только один параметр — Degree (степень), который показывает, сколько ребер выходят из вершины. Выбираем минимальный и максимальный размер кружочка и жмем кнопку «Применить». Здесь же, если выбрать другие пиктограммки, можно настроить цвет маркера вершины и цвет ребер. Теперь граф уже более нагляден.

Следующее, что нужно сделать, — распутать граф. Это можно сделать вручную, двигая вершины, а можно использовать алгоритмы укладки, которые реализованы в Gephi.

Чего мы добиваемся правильной укладкой? Максимальной наглядности. Чем меньше на графе наложений вершин и ребер, чем меньше пересечений ребер, тем лучше. Также неплохо было бы, чтобы смежные вершины были расположены поближе друг к другу, а несмежные —подальше друг от друга. Ну и все было распределено по видимой области, а не сжато в одну кучу.

Как это сделать в Gephi? Левое нижнее окно «Укладка» содержит самые популярные алгоритмы укладки, построенные на силовых аналогиях. Представьте, что вершины — это заряженные шарики, который отталкиваются друг от друга, но при этом некоторые скреплены чем-то, похожим на пружинки. Если задать соответствующие силы и «отпустить» граф, вершины разбегутся на максимально допустимые пружинками расстояния.

Наиболее равномерную картину дает алгоритм Фрюхтермана и Рейнгольда. Выберите Fruchterman Reingold из выпадающего меню и задайте размер области построения. Нажмите кнопку «Исполнить». Получится что-то вроде этого:

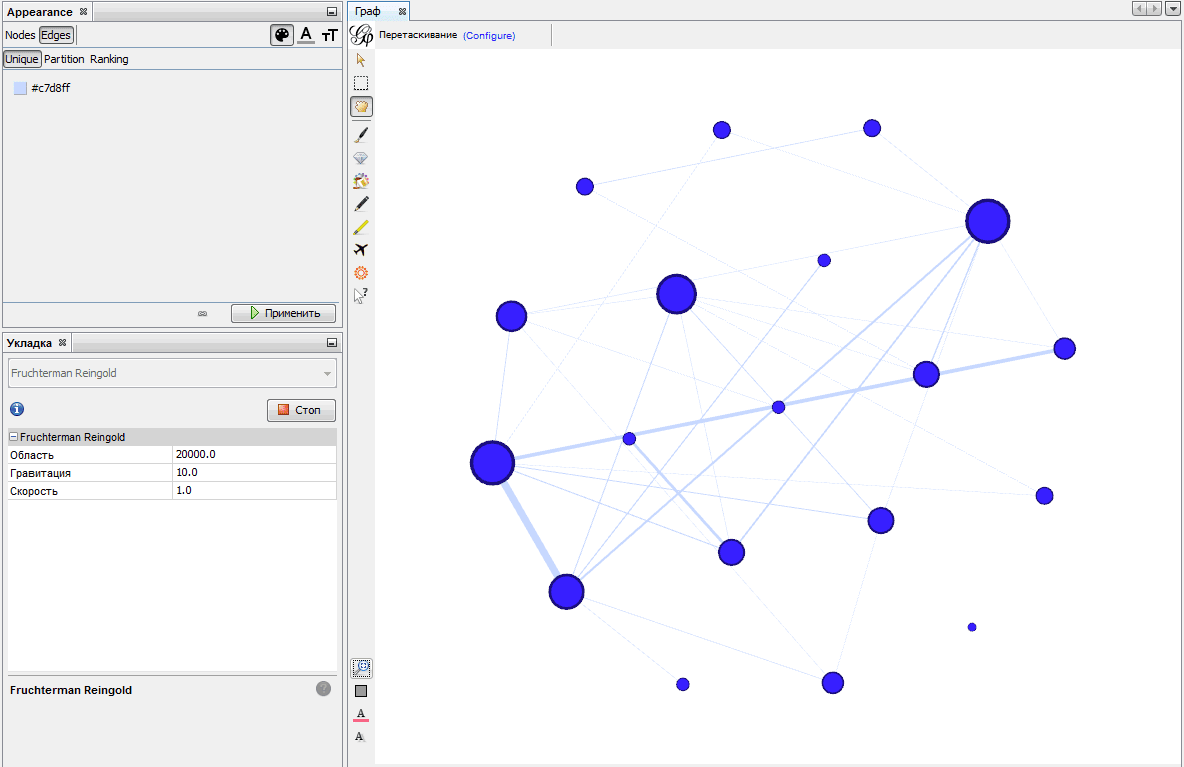
Можно помочь алгоритму и, не останавливая его, поперетаскивать некоторые вершины, стараясь распутать граф. Но помните, что здесь нет кнопки «Отменить», вернуться к прежнему расположению вершин уже не удастся. Поэтому сохраняйте новые версии проекта перед каждым рискованным изменением.

Еще один полезный алгоритм — Force Atlas 2. Он представляет граф в виде металлических колец, связанных между собой пружинами. Деформированные пружины приводят систему в движение, она колеблется и в конце концов принимает устойчивое положение. Этот алгоритм хорош для визуализаций, подчеркивающих структуру группы и выделяющих подмножества с высокой степенью взаимодействия.

Этот алгоритм имеет большое количество настроек. Рассмотрим наиболее важные. «Запрет перекрытия» запрещает вершинам перекрывать друг друга. Разреженность увеличивает расстояние между вершинами, делая граф более читаемым. Также более воздушным граф делает уменьшение влияния весов ребер на взаимное расположение вершин.

Поигравшись с настройками, получим такой граф:

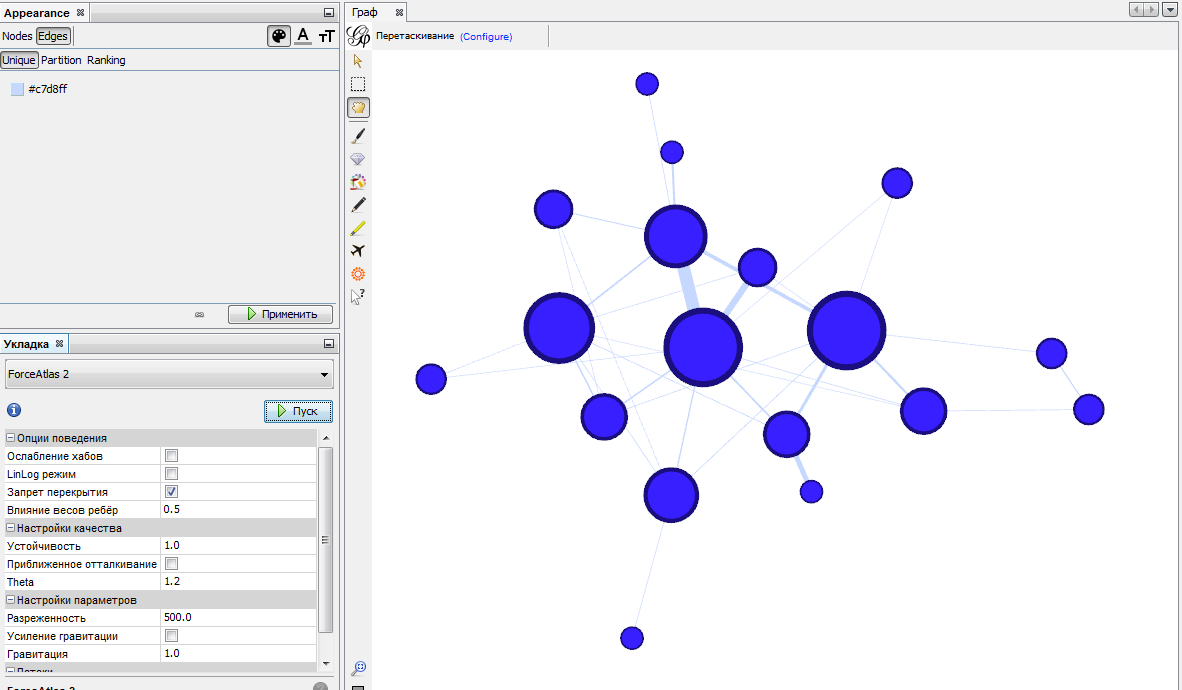
Получив граф в том виде, который вас устраивает, переходите к финальной обработке. Это закладка «Просмотр». Здесь мы можем задать, например, отрисовку графа кривыми ребрами, которая минимизирует наложение вершин на чужие ребра. Можем включить подписи вершин, задав размер и цвет шрифта. Наконец, поменять фон подложки. Например, так:

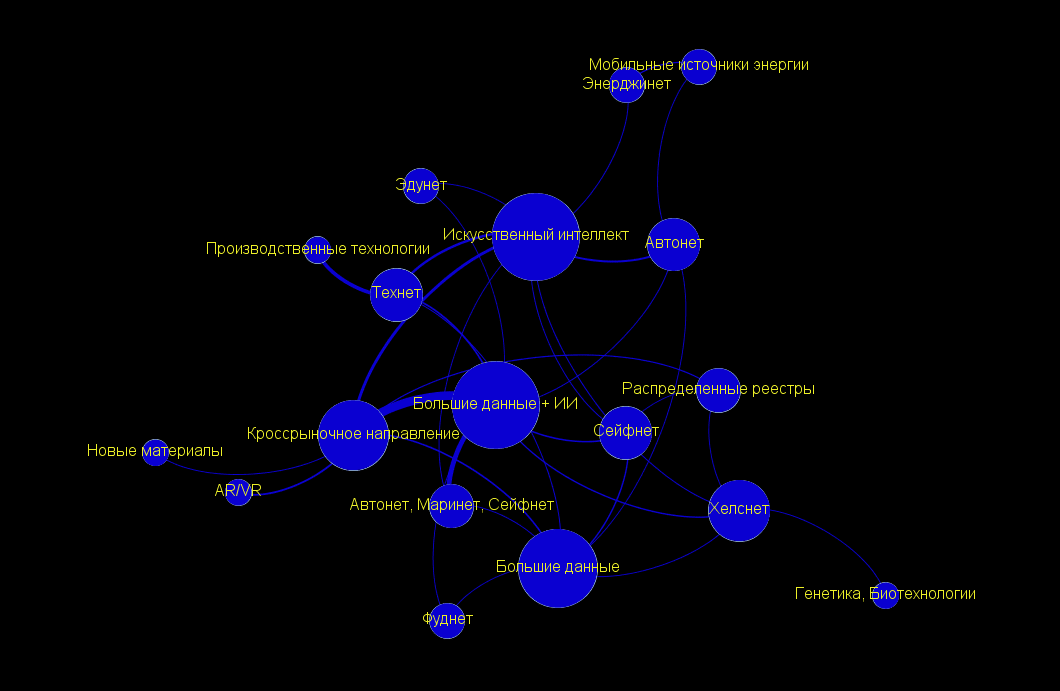
Для того чтобы сохранить получившийся рисунок, нажмите на надпись «Экспорт SVG/PDF/PNG в левом нижнем углу окна. Также отдельно не забудьте сохранить сам проект через верхнее меню «Файл» — «Сохранить проект».

В нашем случае принципиально было выделить взаимосвязь сквозных технологий с рынками НТИ, для чего мы вручную выстроили все рынки в одну линию в центре и разместили все остальное сверху и снизу. Получился вот такой граф. Все-таки для решения конкретных задач без ручной расстановки вершин обойтись не удалось.

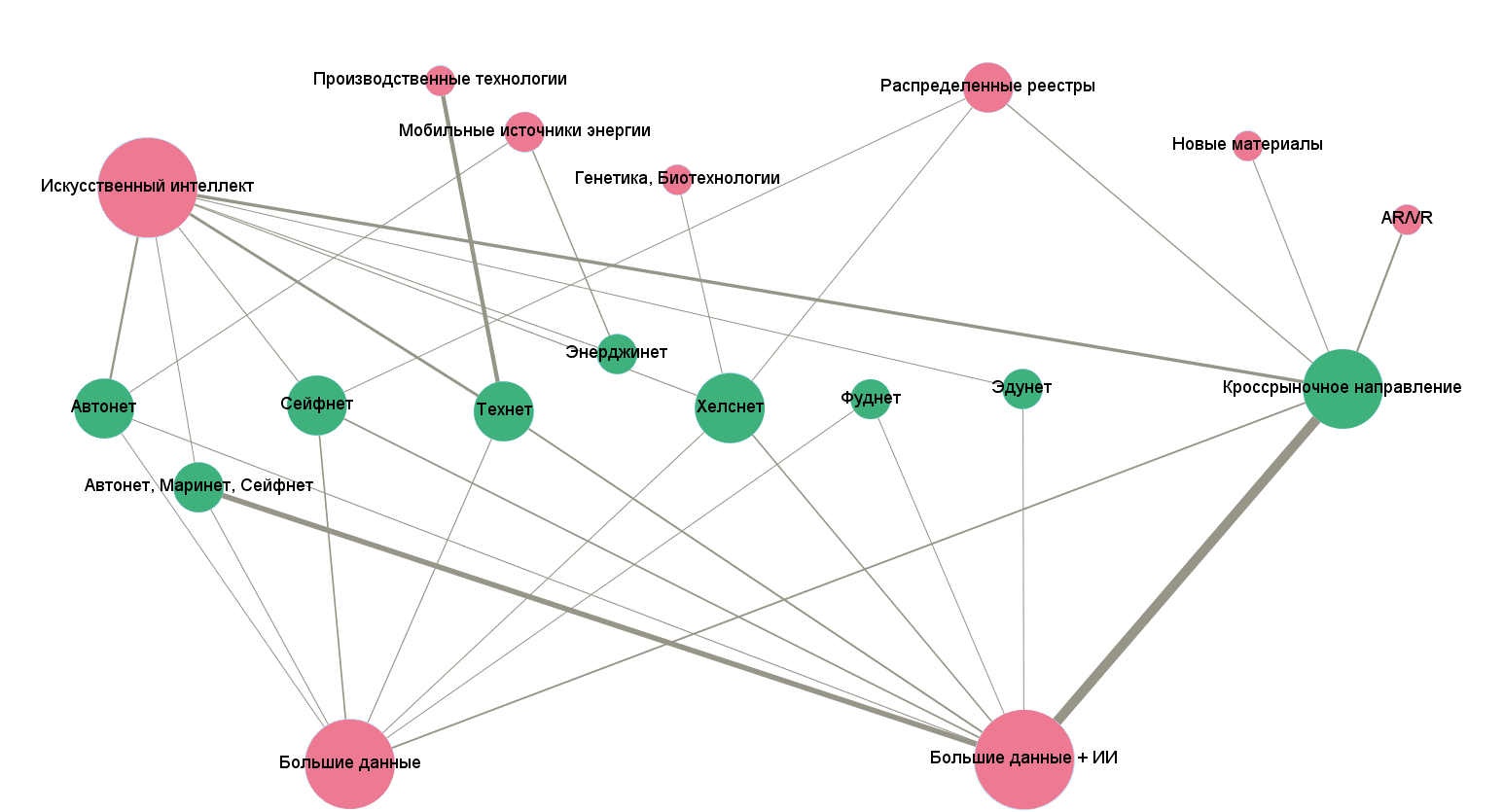
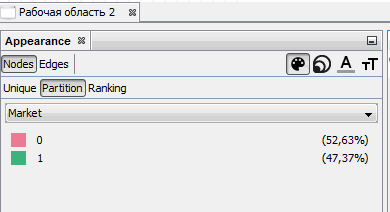
Вы, наверное, думаете, как нам удалось раскрасить вершины в разный цвет? Есть одна хитрость. Можно перейти в закладку «Лаборатория данных», создать там новый столбец в вершинах, назвав его «Market». И заполнить для каждой вершины значениями: 1 если это рынок НТИ, 0 — если сквозная технология. Затем достаточно перейти в «Обработку», выбрать пиктограммку в виде палитры, Nodes — Partition, а в качестве разделителя — наш новый атрибут Market.

Для более сложных построений, когда требуется выделить кластеры и закрасить их разными цветами, в Gephi используется богатый арсенал статистических расчетов, результаты которых можно использовать для раздельной окраски. Находятся эти расчеты в правом столбце вкладки «Обработка».

Например, нажав кнопку «Запуск» возле расчета «Модулярность», вы узнаете оценку уровня кластеризации вашего графа. Если после этого выставить цвет вершин в зависимости от Modularity Class, появится симпатичная картинка наподобие такой:

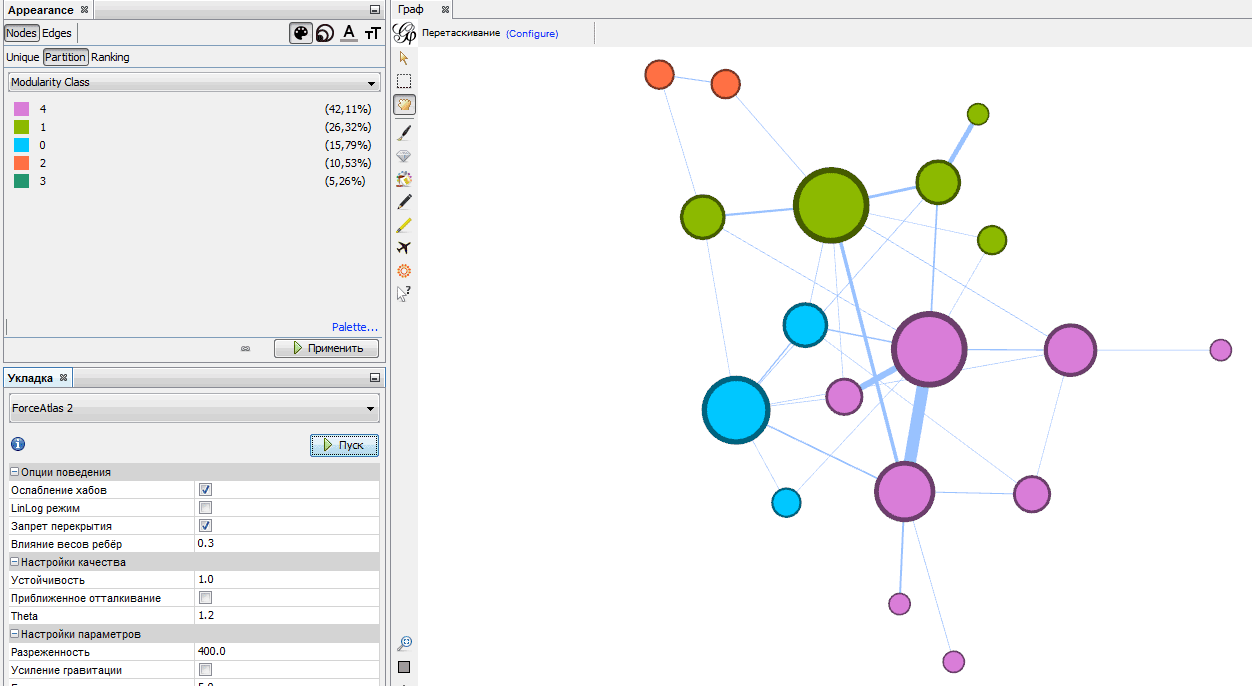
Если вы хотите еще больше узнать о возможностях Gephi, стоит почитать руководство по работе с программой от Мартина Гранджина http://www.martingrandjean.ch/gephi-introduction/.

4. Анализ результата

Итак, вы получили итоговую визуализацию графа. Что она вам дает? Во-первых, это красиво, ее можно вставить в презентацию, показать знакомым или сделать заставкой на рабочем столе. Во-вторых, по ней вы можете понять, насколько сложной и многокластерной структурой является рассматриваемая вами предметная область. В-третьих, обратите внимание на самые крупные вершины и на самые жирные связи. Это особенные элементы, на которых все держится.
Так, построив граф экспертного сообщества, посещающего мероприятия в Точке кипения, мы сразу обнаружили участников, которые с наибольшей вероятностью выполняют роль суперконнекторов. Они являлись «вершинами», через которые кластеры объединялись в единое целое. А во втором случае мы увидели, как выглядит концентрация специалистов из томских компаний с точки зрения их принадлежности к рынку и сквозной цифровой технологии, на которую они делают ставку. Это косвенно говорит об уровне технологических компетенций и экспертизы региона.

Помощь графов в понимании окружающей действительности реально велика, так что не поленитесь и попробуйте создать собственную визуализацию данных. Это совсем не сложно, но порой трудозатратно.

Это вторая часть моей статьи о графах в серии статей о структурах данных. В первой части мы узнали о терминологии графов, типах графов и некоторых реальных применениях графовых структур данных. В этой части цикла мы рассмотрим представление графов, а также построим граф в коде Javascript.

Представление графов

Представление графов связано с тем, как графы могут быть записаны/реализованы в коде. Два наиболее распространенных способа представления графа — через список смежности или матрицу смежности

Список смежности

Список смежности очень прост: это список всех вершин со списком их ребер (смежных вершин). Список может быть любой линейной или итерируемой структурой данных (массивы, карты, связанные списки, очереди). Ниже приведены примеры графов, использующих список смежности.

Направленный граф

Неориентированный граф

Взвешенный граф

Плюсы

• При использовании на разреженных графах (графы с небольшим количеством ребер между вершинами) он занимает мало памяти.

• Его легко понять и реализовать.

• Он быстро создает и удаляет ребра и вершины.

Минусы

• Он менее эффективен по времени при проверке смежности вершин друг с другом.

Матрица смежности

Матрица смежности — это квадратная матрица, строки и столбцы которой равны количеству вершин в графе, а ребра представлены пересечениями между строками и столбцами. Ребра обозначаются цифрой 1, если они есть, и 0, если их нет. Взвешенные ребра обозначаются их весом. Ниже приведены примеры графов, использующих матрицу смежности.

Направленный граф

Неориентированный граф

Взвешенный граф

На приведенных выше изображениях видно, что пересечения AxA, BxB, CxC, DxD и ExE все равны 0; это потому, что в этих графах нет самопетли. Самопетля — это вершина в графе, которая указывает на саму себя.

Плюсы

• Очень экономит время при работе с плотными или полными графами (графы с большим количеством ребер между вершинами называются плотными, а графы со всеми возможными ребрами — полными).

Минусы

• Медленно создает и удаляет ребра и вершины.

• Он намного сложнее, чем список смежности.

• При использовании для разреженных графов (большинство графов являются разреженными) занимает мало памяти.

Реализация на Javascript

Мы будем строить граф, используя представление списка смежности. Наш граф может быть взвешенным, направленным или неориентированным. Наши методы построения графа будут следующими:

• AddVertex: Добавить вершину в граф.
• RemoveVertex: Удалить вершину.
• CreateEdge: добавить ребро между двумя вершинами.
• DeleteEdge: удалить ребро между двумя вершинами.
• IsPresent: Проверить, существует ли вершина.

Графы состоят из вершин/узлов, поэтому давайте сначала создадим конструктор узлов, а затем перейдем к конструктору графов.

class Node {
  constructor(value) {
    (this.value = value),
    (this.edgeList = {});

  }
  addEdge(node, weight) {
    this.edgeList[node.value] = weight ? weight : 0;
  }

  removeEdge(node) {
    delete this.edgeList[node.value];
  }
}

Пояснение

Наши узлы будут иметь два свойства и методы.

• Свойство value будет хранить значение нашего узла.
• Свойство edgeList хранит ребра нашего узла.
• AddEdge — это метод, который добавляет ребро и вес в список edgeList узла. Значение узла, переданное в addEdge, используется как ключ, а вес — как значение. если вес не задан, мы устанавливаем его равным 0.
• DeleteEdge — это метод для удаления ребра из списка edgeList. Он использует значение переданного ему узла, чтобы получить к нему доступ и удалить его.

Теперь давайте рассмотрим наш конструктор графа и то, как работают наши различные методы.

class Graph {
  constructor(type) {
    (this.nodes = new Map()), 
    (this.directed = type ? type : false);

  }
  addVertex(value) {
    let node = new Node(value);
    this.nodes.set(value, node);
  }

  removeVertex(value) {
    let vertex = this.nodes.get(value);
    if (vertex) {
      for (const node of this.nodes.values()) {
        node.removeEdge(vertex);
      }
    }
    return vertex;
  }

  createEdge(startNode, endNode, weight) {
    let startVertex = this.nodes.get(startNode);
    let endVertex = this.nodes.get(endNode);

    if (startVertex && endVertex) {
      startVertex.addEdge(endVertex, weight);

      if (!this.directed) {
        endVertex.addEdge(startVertex, weight);
      }
    }else {
      console.log("non-existent vertex passed")
    }
  }

  deleteEdge(startNode, endNode) {
    let startVertex = this.nodes.get(startNode);
    let endVertex = this.nodes.get(endNode);

    startVertex.removeEdge(endVertex);
    endVertex.removeEdge(startVertex)
  }

  getVertex(value){
    return this.nodes.get(value)
  }

  isPresent(value){
    return this.nodes.has(value)
  }
}

Пояснение

Наш граф будет иметь два свойства: объект Map для хранения вершин/узлов и булево значение для определения типа графа — направленный или ненаправленный. Если при вызове функции передается true, то это направленный граф, в противном случае — ненаправленный.

  addVertex(value) {
    let node = new Node(value);
    this.nodes.set(value, node);
  }

• AddVertex — это наш первый метод. Он просто принимает значение и создает вершину, которую добавляет в объект Map графа.

 removeVertex(value) {
    let vertex = this.nodes.get(value);
    if (vertex) {
      for (const node of this.nodes.values()) {
        node.removeEdge(vertex);
      }
    }
    this.nodes.delete(value);
    return vertex;
  }

• Метод removeVertex удаляет вершину из графа. Она принимает значение и проверяет, существует ли она в графе, если существует, то она проходит по объекту карты вершин и удаляет вершину из списка edgeList всех вершин, а затем удаляет ее из объекта карты вершин.

  createEdge(startNode, endNode, weight) {
    let startVertex = this.nodes.get(startNode);
    let endVertex = this.nodes.get(endNode);

    if (startVertex && endVertex) {
      startVertex.addEdge(endVertex, weight);
      if (!this.directed) {
        endVertex.addEdge(startVertex, weight);
      }
    }else {
      console.log("non-existent vertex passed")
    }
  }

• Метод createEdge создает ребро в графе; при вызове он принимает 3 параметра, начальную и конечную вершины, а также вес ребра. Сначала проверяется, присутствуют ли обе вершины в узле, если да, то вызывается addEdge на начальной вершине и передается конечная вершина и вес. если граф неориентированный, то вызывается addEdge на конечной вершине и передается начальная вершина и вес. если одна из вершин не существует, мы сообщаем об этом пользователю.

  deleteEdge(startNode, endNode) {
    let startVertex = this.nodes.get(startNode);
    let endVertex = this.nodes.get(endNode);

    startVertex.removeEdge(endVertex);
    endVertex.removeEdge(startVertex)
  }

• Метод deleteEdge удаляет ребро из графа, но не вершины. При вызове он принимает два параметра: начальную и конечную вершины/узлы и вызывает метод removeEdge для обоих.

  getVertex(value){
    return this.nodes.get(value)
  }

• Метод getVertex возвращает вершину из объекта карты вершин.

 isPresent(value){
    return this.nodes.has(value)
  }

• Метод isPresent просто проверяет, существует ли вершина/вершина в объекте nodes Map, и возвращает булево значение.

Заключение

Код для этой статьи можно найти здесь. Графы — очень сложная и полезная структура данных, если вы хотите узнать больше о графах, посмотрите это видео, спасибо за чтение и до встречи.

1.

Уважаемые коллеги!
Напоминаем Вам о правилах просмотра презентаций.
1.Для точного движения по маршруту
пользуйтесь управляющими кнопками.
изложения
темы
2.Переходить от слайда к слайду можно при помощи щелчка левой
клавишей мыши.
3.Возвращаться из слайдов – сносок (т.е слайдов разъясняющих
какое-то понятие) лучше через кнопку «Назад» или «Домой»
4.Если Вы допустили ошибку или по другой причине нуждаетесь
в возвращении к уже прочитанному, воспользуйтесь правой
клавишей мыши и в появившемся окне обозначьте действие
«Назад».
НАЗАД
ДОМОЙ
Желаем продуктивного усвоения информации.
Авторы.

2. ТЕХНИКА ФОРМИРОВАНИЯ ГРАФ ЛОГИЧЕСКИХ СТРУКТУР

Простые правила позволят вам быстро и эффективно освоить технику формирования граф
логических структур любой темы. Они следующие:
1. Прочитайте внимательно несколько раз исследуемый материал.
?
2. Выпишите все имеющиеся в этом материале учебные элементы.
?
3. Определите их степень новизны
и составьте таблицу учебных элементов таким
?
образом, более общие понятия определялись более узкими (соловей это птица, но не всегда
птица – это только соловей. Соловей – более узкое понятие, чем птица.) и, с другой стороны
элементы более новые определялись более известными, понятными нам. Для построения граф
используйте логику таблицы учебных элементов.
4. Практически всегда тема является центром ГРАФ СТРУКТУРЫ. От темы и следует
«разветвлять граф». При подборе темы нужно быть крайне внимательным, так как можно тему
слишком расширить, хотя этого и не требуется, или сузить, что не позволит раскрыть всё новое в
учебном материале.
Вообще процесс формирования Графа логической структуры сводится к двум
противоположным мыслительным процессам – объединению информации по признакам и
разделению её по признакам.
Далее

3. Под исследуемым материалом подразумевается любой материал, любой дисциплины и вообще любая прочитываемая информация.

В качестве примера используем данный текст.
«Через тонкую дверную щель пробивались поразительные запахи, от которых
кошачью душу Барсика просто выворачивало наизнанку, хотелось немедленно просочиться и
добраться наконец до вон тех карасиков, лежащих на большом блюде, утопающих в сметане.
Или не плохо было бы вкусить парной колбаски, сосисочек или вон того окорока. В голове
Барсика всё перевернулось, в животе что-то ёкнуло и он, зная о предстоящей трёпке и
игнорируя её, рванул на кухню…»
Нелепо было бы озаглавить рассказ, а ,следовательно, и граф структуру очень широко:
«Срыв нервной деятельности животных в условиях стресса» или , «Вещи, продукты и животные
на нашей кухне», или же – «Пищевая, перерабатывающая отрасли человеческой деятельности и
их влияние на активность домашних животный». Понятно, что так ставить вопросы исходя из
информации текста не корректно. Но возникает вопрос: «А что корректно?». В этом то и
трудность формирования граф. Можно сузить понятия: «Виды мяса» или «Чем пахнет кухня».
Однако, такое узкое название темы мешает полно её раскрыть. Вообще, дать название теме ,
рассказу, отрывку очень не просто. По существу это означает поставить вопрос, отвечая на
который придётся воспроизвести текст и чем полнее приходится его воспроизводить, тем точнее
название. Если название темы предполагает достаточность частичного воспроизведения текста,
то название сужено, если требует дополнительной информации, находящейся вне текста, то
название слишком широко. Иногда требуется формирование подтем внутри текста, это позволяет
усваивать информацию, дробно, но в виде системы.
Достаточно задать более узкие вопросы и подтемы высвечиваются: «Проблемы Барсика»,
«Продукты кухни,» «Возможные запахи». Это позволяет создать структуру логических связей
как внутри подтем, так и между ними, что и будет раскрытием общей темы.

4.

Что такое «признак»? ( В некоторых источниках это понятие обозначается как «основание».) В
широком смысле «признак» – свойство, которым явления, предметы похожи друг на друга и
отличаются друг от друга.
Пример. Все шарообразные тела схожи, но именно этим свойством своей формы они
отличаются от всех кубообразных тел, которые сами именно своей кубообразностью похожи.
Всегда можно подобрать учебные элементы, которые схожи какими то признаками или отличаются
другими: Мы стараемся приобрести вещь, идём в магазин за покупкой. Допустим, мы решили
приобрести рубашку. Мы безошибочно находим нужный вид товара, так как рубашка имеет только
ей свойственные признаки – это верхняя одежда, имеет ворот, более или менее выраженный
рукав, застёгивающиеся полы, ( схожие признаки), но мы не покупаем первое, что попадает в
наши руки, а выбираем в соответствии с нашим вкусом и необходимым размером определённого цвета, с карманами или без,ушитыми или более свободными,
т.е. в
соответствии с необходимыми нам свойствами, которые отличают приглянувшуюся нам вещь.
Можно в любых двух предметах найти сходные или отличные свойства. Даже две идеально
одинакового диаметра начерченные на листе бумаги окружности отличаются уже тем, что по
отношению к нам находятся одна правее, другая левее или ближе и дальше, выше и ниже и т.д. и
т.п. При известном усердии можно отыскать неограниченное количество признаков как схожести,
так и отличия.
Попробуем на примере с Барсиком сформировать граф структуру.

5.

Основные трудности – дать название.
Именно оно отражает смысловое содержание
рассказа.
А каков же смысл?
Справедливо было бы назвать рассказ
«Искушение» Попробуем на основе такого
вывода всё же составить структуру.
Искушение
(Свойствами пищи)
Запахом
Внешним
видом
?
Вместо знака вопроса и вставить-то нечего. Следовательно вот и
закончился наш граф структуры. Наверное название подкачало. А как
быть? Если поставить вопрос «Виды продуктов на кухне», куда тогда
девать Барсика с его аппетитами?
Попробуем ещё расширить вопрос.

6.

Озаглавим рассказ следующим
образом: «Внутренняя борьба в душе
Барсика»
Иногда во имя полноты раскрытия темы приходится жертвовать краткостью названия её. В
нашем случае получилось нечто подобное.
Внутренняя борьба в душе Барсика
Положительные
результаты «набега»
на кухню
Утоление
голода
Удовлетворение
Отрицательные
результаты «набега»
Трёпка
?
кошачьего самолюбия
Снова появился вопросительный знак. Нам не хватает ни знаний ни фантазии для
расширения графа. Мы не смогли отыскать однородные учебные элементы и продолжить
схему. Правда, есть слабое оправдание нашим неудачам: неоднородность по качествам
элементов, их «неакадемичность». Попробуем исправить ситуацию.

7.

Для наглядности приведём технику формирования граф
структуры информации, взятой из лекций по анатомии.
Выберем тему «СИНАПСЫ».
«Синапсом называется функциональное соединение между рабочей клеткой и
нервным
окончанием.
Синапсы
бывают
адренергические,
холинэргические,
возбуждающие,
тормозящие,
электрические,
химические,
центральные,
аксосоматические, аксодендрические, аксоаксональные, периферические, нервномышечные, нервно-железистые.»
Этот отрывок мал по объёму, но у него существенные отличия – он
«академичен»,
однороден по составу
в нём последовательно изложены
обучающие элементы
Есть и определённые трудности, так как текст содержит учебные элементы разной степени новизны,
но не все они имеют определение через более знакомые понятия.. Тем не менее ОБУЧАЮЩАЯ
значимость данной информации такова, что неминуемо побуждает к творческому
поиску
определений. Требуется «порыться» в учебниках прежде чем составить полноценную граф структуру
темы.
Далее

8.

Что понимается под «академичностью».
Язык науки должен быть более «сухим», менее эмоциональным, более
точным. Передаваемый материал в научных работах редко содержит
выражения эмоций, то есть с
точки зрения науки информацию
бесполезную, пустую. Знания, передаваемые другим людям науки или
учащимся, опираются на категории мышления данной науки. С точки
зрения анатомии и физиологии выражение «нам мышцы нужны для
жизни» неинформативно, хотя и эмоционально. Оно не объясняет какие
анатомические структуры реализуют данную потребность(анатомия), и
как они это делают(физиология).
С точки зрения анатомии и физиологии а более академична и,
следовательно, более информативна следующая фраза.- «Мышца, как
орган имеет в основе своей структуры белок миозин, который во время
функции уменьшает свою длину в следствии перераспределения
электрического заряда и скольжения его составных вдоль друг друга, что
приводит к уменьшению длины (сокращению) всей мышцы. Это
обусловливает активность мышц – их способность перемещать костные
рычаги, осуществляя движения в суставах и тем самым обеспечивать
жизненно важную потребность организма в движении»
НАЗАД

9.

1.Сначала расположите по центру листа тему графа (вдруг вы
захотите расширять граф в четырёх и более направлениях)
2.Для наглядности обведите слово овалом или
прямоугольником.
Далее поставьте вопрос на каком основании или по какому
признаку вы делите данное понятие на более простые
По
в
ид
ум
ед
и
ат
ор
а
По
ю
ви
т
йс
де
СИНАПСЫ
П
ос
ле
до
ва
т
ел
ь
Далее
но
гр ст
аф ь ф
а. ор
ми
ро
ва
н
ия
По способу передачи
возбуждения

10.

П
ос
ле
до
Далее смело подставляем значения
ва
т
ел
ь
но
гр ст
аф ь ф
а. ор
ми
ро
адренергические
возбуждающие
тормозящие
холинэргические
По
в
ид
ум
ед
и
ат
ор
а
По
ю
ви
т
йс
де
СИНАПСЫ
По способу передачи
возбуждения
электрические
Далее
химические
ва
н
ия

11.

П
ос
ле
до
Хорошая наглядность получается при
обозначении логических связей стрелками
но
гр ст
аф ь ф
а. ор
ми
ро
Информация графа позволяет расширить его за счёт углубления
понятия «химические синапсы» . Для этого тоже нужно задать
вопрос: «По какому признаку делятся химические синапсы?» Отвечаем на этот вопрос и расширяем граф.
адренергические
возбуждающие
тормозящие
ию
холинэргические
йств
мед
иат
ора
Аксодендрические
По способу передачи
возбуждения
Использовав оставшиеся элементы, завершим граф.
ия
Аксоаксональные
СИНАПСЫ
электрические
ва
н
Аксосоматические
о де
вид
у
По п
По
Далее
ва
т
ел
ь
Центральные
ока
л
о
П
химические
ац
ли з
ии
Периферические
Нервно-мышечные
Нервно-железистые

12.

Вы познакомились
с техникой формирования
графов логических структур
Достоинства графов в
структурировании материала
несомненна.
Граф лаконичен, нагляден.
Информативен.
Однако, одним из его самых больших
недостатков является трудоёмкость
формирования.
Многолетняя практика работы с графами,
положительные результаты этого опыта
в том числе и в контролирующем
качестве при изучении
большинства тем анатомии и
физиологии позволяют надеяться
на его полезность и эффективность
в повышении выживаемости знаний.

13.

Уважаемый коллега, Вы просмотрели
презентацию, которая позволила Вам
ознакомиться с техникой составления граф
логических структур. Желаем удачного
творчества.
Автор Журавлёв О.А.
Если вы желаете вернуться для повторения
материала, нажмите кнопку «Назад»
НАЗАД