Как составить графическую модель математика 2 класс

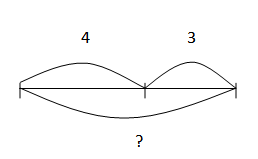
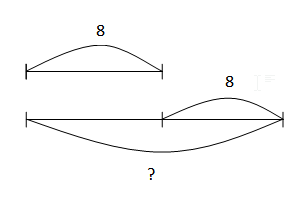
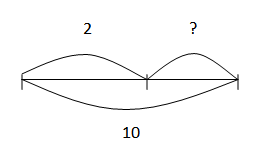
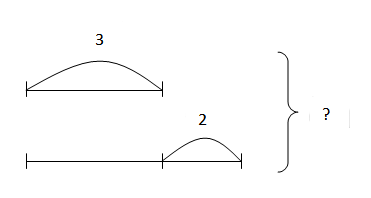
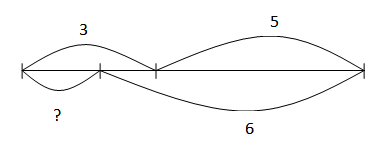
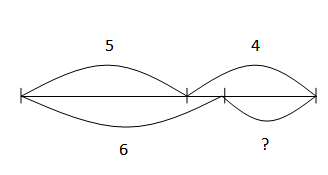
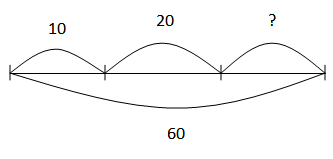
Составь графическую модель и реши уравнения:
21 : x = 3

x : 8 = 3
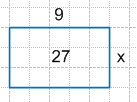
9 * x = 27

Муниципальное автономное общеобразовательное учреждение

«Светлинская средняя  общеобразовательная школа №2»

Графическое моделирование текстовых задач

на уроках математики в начальной школе

Методическая разработка

Головиной Оксаны Иосифовны,

учителя начальных классов

МАОУ «Светлинская СОШ №2»

Содержание

                                                                       
                                 Стр.

Введение………………………………………………….…………………….   3-4

      Глава I……………………………………………………………………  5-9

1.1
 Моделирование – процесс
построения моделей

 для  познавательных целей………………………………………   5

1.2
 Психологический аспект
использования моделирования

 на уроках математики……………………………………………    6

1.3
 Графические модели
текстовых задач………………………….    7-8

1.4
  Развивающая роль
графического моделирования

  в обучении математике…………………………………………..   9

Глава II…………………………………………………………………    10-16

        2.1 Графическое моделирование: этапы работы…………………      10-12            

        2.2 Применение графического моделирования

        при решении текстовых задач………………………………..   13- 17

Заключение……………………………………..………………………    18-19

Список литературы……………………………………………………    20

      Приложение……………………………………………………………  
 21-26

Введение

Современная система образования, в том числе стандарты
второго поколения, ориентированы на подготовку обучающихся к самостоятельному
активному освоению мира, его творческому преобразованию, поэтому одним из
важнейших направлений педагогики сегодня является формирование личности
школьника, способной творчески освоить сложности жизни. Различные аспекты этой
темы рассматриваются в трудах ученых: Л. Выготского, В.П. Зинченко,
Д.С.Лихачева и других. Формирование личности – это последовательное изменение и
усложнение системы отношений к окружающему миру, природе, труду, другим людям и
к себе. Именно в детском возрасте в личности закладываются важнейшие ее
качества, и происходит «переход психологии научения к психологии решения задач».

ФГОС начального общего образования выдвигает новые
требования к подготовке младшего школьника. Особого внимания заслуживает
направление, связанное с формированием метапредметной готовности учащихся,
которая предполагает овладение компетенциями, составляющими основу умения
учиться. К подобным компетенциям относится способность применять различные
средства представления информации для создания моделей изучаемых объектов и
процессов, схем решения учебных и практических задач. Таким образом, можно
вести речь о целенаправленном развитии у учащихся умений, связанных с
применением моделей и моделирования. Очевидно, что именно математика обладает
тем потенциалом, благодаря которому эти умения формируются и совершенствуются.  

Решение текстовых задач – важная составляющая курса математики
начальной школы. Умение решать текстовые задачи является одним из основных
показателей уровня математического развития младшего школьника. Однако практика
показывает, что решение текстовых задач представляет большие трудности для
обучающихся, так как дети не все хорошо ориентируются в тексте задачи, в ее
условии и требовании.

Как же действовать в этой ситуации учителю? Приёмом,
позволяющим научить детей решению текстовых задач, является метод моделирования.
Мы считаем, что система работы над текстовыми задачами методом моделирования
открывает новые возможности для развития интереса к математике, логического
мышления младших школьников. На необходимость использования моделирования в
учебной деятельности указали в своих работах психологи П.Я.Гальперин,
В.В.Давыдов, Л.В Занков, Н.И.Непомнящая и др.

В Федеральном Государственном образовательном
стандарте начального общего образования во главу угла поставлено формирование
универсальных учебных действий, обеспечивающих школьникам умение учиться,
способность к саморазвитию и самосовершенствованию. Младший школьный возраст
является началом формирования учебных действий у детей. Особую группу
общеучебных универсальных действий составляют знаково-символические действия,
которые обеспечивают конкретные способы преобразования учебного материала,
представляют действия  моделирования, выполняющие функции отображения
учебного материала; выделения существенного; отрыва от конкретных ситуативных
значений; формирования обобщенных знаний. Это действия:
– моделирование – преобразование объекта из чувственной формы в модель, где
выделены существенные характеристики объекта (пространственно-графическую или
знаково-символическую);

–  преобразование модели – изменение модели с
целью выявления общих законов, определяющих данную предметную область.

Для того чтобы вооружить учащихся моделированием как
способом познания, нужно, чтобы школьники сами строили модели, сами изучали
какие-либо объекты, явления с помощью моделирования. Известно несколько видов
моделирования. Чтобы сузить рамки содержания  темы, остановимся на одном из них
– графическом моделировании.

Целью работы является  разработка
системы приемов графического моделирования и применение этих приёмов в практике
учебной работы.

Задачи:

·         
Рассмотреть графические
модели, включить их в практическую работу с детьми;

·         
Подобрать различные виды
упражнений  по обучению графическому моделированию

·         
Систематизировать приемы
графического моделирования, учитывая опыт учителей начальной школы.

  Глава I.

1.1  Моделирование
– процесс построения моделей  для  познавательных целей

В методической науке существуют разные определения моделирования.
«Моделирование – процесс построения моделей для каких-либо познавательных
целей. Модель – это объект или система, исследование которой служит средством
для получения знаний о другом объекте – оригинале». (Л.М.Фридман, К.Н.Волков)

В философском энциклопедическом словаре моделирование
рассматривается как метод познания. Его сущность заключается в следующем: для
познания объекта строятся и изучаются модели этого объекта, отображающие
реальность. [13]

И.Б. Новиков дает следующее определение:
«Моделирование –   практическое или теоретическое исследование объекта. При  исследовании
непосредственно изучается не интересующий нас объект, а вспомогательная
искусственная или естественная система, находящаяся в некотором объективном
соответствии с познаваемым объектом, способная его замещать в определенном
отношении и дающая при его исследовании, в конечном итоге, новую информацию о
самом моделируемом объекте».  

В школьной практике изучения математики моделирование
применяется достаточно широко. Но об этом будет сказано ниже.

Моделирование – это действие,  которое выносится и за пределы
младшего школьного возраста и в дальнейшие виды деятельности человека и выходит
на новый уровень своего развития. С помощью моделирования можно вести изучение
от простого – к сложному, от незнакомого – к знакомому, то есть сделать объект
доступным для тщательного изучения.

Какую же практическую пользу принесёт
обучающимся овладение методом моделирования?

Во-первых, введение в содержание обучения понятий
модели и  моделирования существенно меняет отношение учащихся к учебному
предмету, делает их учебную деятельность более осмысленной и более
продуктивной, приводит к ощущению успешности.

Во-вторых, целенаправленное и систематическое обучение
методу моделирования приближает младших школьников к методам научного познания,
обеспечивает их интеллектуальное развитие.

В-третьих, моделирование является средством развития логического
мышления обучающихся, повышает мыслительную активность.

1.2 Психологический аспект использования
моделирования

        на уроках математики

Психология, изучая действия человека, направленные на
познание окружающего мира, рассматривает моделирование с позиции познающего
субъекта. С этой точки зрения графическое моделирование рассматривается как
процесс или деятельность субъекта по построению графической модели для одной из
определённых целей, а именно с целью замещения, представления, интерпретации,
исследования объекта изучения. Модельное отношение тогда является тройственным.
В него входят оригинал, его модель и субъект, выбравший или построивший эту
модель. Появление субъекта, или исследователя, в сложной структуре процесса
моделирования в какой-то мере предопределило развитие моделирования как
содержания и средства обучения.

Психологами доказано, что моделирование имеет
принципиальное значение для учебной деятельности. Важнейшим результатом
психологических исследований для методической науки стал вывод о том, что уже
в младшем школьном возрасте дети способны выполнять действие моделирования с
целью изучения данных им объектов. Всевозможные аспекты процесса применения
моделирования рассматривались на разных этапах развития начального образования.
Однако графическое моделирование преимущественно связывали с проблемой обучения
решению текстовых задач. Овладевая графическим моделированием, учащиеся овладевают
 подходами к решению текстовых задач. 

         1.3. Графические модели текстовых задач

Текстовая задача – это словесная модель проблемной ситуации. Чтобы
решить задачу, надо перевести ее на язык математических действий, т.е.
построить математическую модель. Математической моделью  текстовой
задачи является выражение (либо запись по действиям или уравнение) если    Перевод
текста с естественного языка на математический – сложный процесс. Чтобы
облегчить его – строят вспомогательные модели. Тогда процесс решения задачи
можно рассматривать
как переход от одной модели к другой: от словесной модели к  вспомогательной,
от нее – к математической, на которой и происходит решение задачи. Математическая
модель – это описание какого–либо реального процесса на математическом
языке. [10]

Такой подход к решению задач разделяют психологи. Они
считают, что процесс решения задач – это процесс поиска системы моделей. Каждая
модель выступает как одна из форм отражения сущности задачи, а преобразование
ее идет по пути постепенного обобщения, абстрагирования и, в конечном счете,
построение ее математической модели. Итак, чтобы решить задачу, т.е. перейти к
ее математической модели, необходимо построить промежуточную – вспомогательную
модель.

Вспомогательная модель – это и есть графическая модель. Под  графической
моделью можно понимать такое реализованное с помощью графического действия
изображение, которое не только воспроизводит объект исследования, его отдельные
свойства и отношения, но и позволяет осуществить их дальнейшее изучение.

В структуре любой задачи выделяют:

1. Предметную область, т. е. объекты, о которых идет речь в задаче.

2. Отношения,   которые   связывают объекты предметной области.

3. Требование задачи.

          Объекты задачи и
отношения между ними составляют условие задачи. Напри­мер, в задаче:

«Лида нарисовала 5 домиков, а
Вова – на 4 домика больше. Сколько домиков нарисовал Вова?» — объектами
являются:

1)
количество домиков, нарисованных Лидой (это известный объект в задаче);
количество домиков, нарисованных Вовой (это неизвестный объект в задаче и
согласно требованию искомый).

2) Связывает объекты отношение «больше на».

3) Вопрос

Структуру задачи можно представить с помощью графических
моделей

Рассмотрим некоторые виды
графических моделей на примере одной задачи.

 «Катя
нарисовала 5 деревьев, а  Вова – на 3 дерева больше. Сколько нарисовал  Вова?».

Рисунок:    К.   ♣ ♣ ♣ ♣ ♣

          В.  ♣ ♣ ♣ ♣
♣ ♣ ♣ ♣ 

                                  

                                                
?

Условный рисунок: К.   

                           В.                  

                                                       
 ?

Чертеж:                     5д.                           

          К.                                   3д.

          В.

                                 ?

Схематический чертеж:

                           5д.

         К.

                                            
3 д.

                                              

         В. 

                                  
?

          Наибольшую
сложность в процессе решения текстовой задачи представляет перевод текста с
естественного языка на математический. Чтобы облегчить эту процедуру, строят
вспомогательные модели – схемы, таблицы и другие. Тогда процесс решения задачи
можно рассматривать как переход от одной модели к другой: от словесной модели
реальной ситуации, представленной в задаче, к вспомогательной (схемы, таблицы,
рисунки и так далее); от неё – к математической, на которой и происходит
решение задачи.

Как
отмечает Л.Ш. Левенберг, «… рисунки, схемы и чертежи не только помогают
учащимся в сознательном выявлении скрытых зависимостей между величинами, но и
побуждает активно мыслить, искать наиболее рациональные пути решения задач,
помогает не только усваивать знания, но и овладевать умением применять их».

Для графических моделей характерны следующие особенности:

– наглядность данных моделей;

– возможность
сохранять информацию для дальнейшего изучения и   преобразования;

– организация внутренней психической деятельности учеников;

– указание способов организации действий учащихся;

– открытие нового знания, скрытого при поверхностном анализе объекта
исследования.

1.4. Развивающая роль графического
моделирования

                  в обучении математике

Рассмотрение теоретических основ применения графических моделей в
обучении математике позволяет не только ещё раз подчеркнуть их роль в развитии
младших школьников, но и помогает выделить некоторые  условия использования
графического моделирования как содержания и средства обучения. Среди них:

– систематическая и целенаправленная подготовка учащихся к
моделированию;

– применение моделирования при решении широкого круга математических
задач на различных этапах усвоения математического содержания;

– формирование у школьника осмысленного отношения к моделированию, в котором
он как исследователь играет главную роль, выбирая средство для построения
модели, определяя цель применения, интерпретируя результаты изучения модели;

– преимущественное использование учебных заданий на сопоставление,
создание, преобразование, исследование, интерпретацию моделей, а также открытие новой
информации, неявно представленной в условии математической задачи.

         Начиная с первых дней обучения в школе, ученикам
систематически  предлагаются  задания, в процессе выполнения которых у них
постепенно накапливается опыт перевода обычного текста и аналитических
выражений на язык графических изображений и обратно. Только в этом случае 
графические модели могут стать эффективным средством обучения решения задач с
использованием моделирования. Из сказанного не следует, что при решении каждой
задачи обязательно нужно строить графическую модель. Она является
вспомогательным средством, и ее использование ни в коем случае не должно вести
к ослаблению работы по формированию умения решать задачи с помощью логических
рассуждений, проводимых и без опоры на непосредственное зрительное восприятие
графического изображения.

На современном этапе образования под развивающим
обучением понимается обучение младших школьников общим приемам умственной
деятельности, а на уроках математике – общим приемам по усвоению математических
понятий. Данный процесс можно реализовать в традиционной системе обучения при
решении математических задач, используя метод моделирования. Он дополняет
учебную работу школьников поисковой деятельностью, помогает формированию таких
приемов умственной деятельности как абстрагирование, анализ, синтез; развивает
математическое мышление. Моделирование задач позволяет младшим школьникам
подняться на достаточно высокую ступеньку абстрактности: все второстепенные
детали опущены, выбор действия производится только из логики происходящих
изменений.

 

 

Глава II

2.1. Графическое моделирование: этапы работы

За основу взят УМК «Школа России» (программа по
математике М.И. Моро, М..А. Бантовой, Г.В. Бельтюковой). Важным является усовершенствование
общих приемов умственной деятельности (наблюдения, анализа,
сравнения, синтеза, обобщения, дедуктивному и индуктивному умозаключению и
т.д.). Мною также анализировались учебники Н.Б. Истоминой (УМК «Гармония»),
И.И. Аргинской (развивающая система Л.В. Занкова), Л.Г. Петерсон (УМК «2000»).
Заложенная в них концепция целенаправленной и систематической работы по
формированию приемов умственной деятельности: анализа и синтеза, сравнения,
классификации, аналогии и обобщения в процессе усвоения математического
содержания показалась мне очень важной для любого ребенка, с какой бы
математической подготовкой он не пришел бы в первый класс и по какой бы системе
не обучался.

Графическое моделирование заключается в том, что для
исследования какого-либо объекта (в нашем случае текстовой задачи) выбирают
(или строят) другой объект, в каком-то отношении подобный тому, который
исследуют. Построенный новый объект изучают, с его помощью решают
исследовательские задачи, а затем результат переносят на первоначальный объект.

В графическом моделировании выделяется ряд этапов:

1.     предварительный анализ текста
задачи;

2.     перевод текста на
знаково-символический язык, который осуществляеся графическими средствами;

3.     построение модели;

4.     работа с моделью;

5.     соотнесение результатов,
полученных на модели, с реальностью (с текстами).

Каждый компонент деятельности
моделирования имеет свое содержание со своим составом операций и средствами,
которые согласно психологическим исследованиям должны стать самостоятельным предметом
усвоения. 

Предварительный анализ включает ряд приемов. Это прежде всего
проведение семантического анализа текста. Он предполагает работу над отдельными
словами, терминами, перефразирование, переформулирование текста. Другим приемом
анализа текста, ведущего к пониманию его смысла, являются постановка вопросов,
определенный способ чтения текста. В литературе выделена система вопросов,
ведущих к осмыслению текста. Одним из приемов анализа, ведущих к пониманию
текста, является выделение «смысловых опорных пунктов» текста, которые
способствуют выделению структуры текста.

В общей деятельности моделирования
действие анализа является подготовительным этапом для осуществления действия
перевода и построения модели. 
Для приобретения опыта в семантическом и математическом анализе текстов задач (простых
и составных) используются следующие задания (Приложение 1)

Эти задания позволяют школьникам сделать
первые шаги в ос­мыслении структуры задачи.

Перевод текста на знаково-символический язык делает обозримыми связи и отношения,
скрытые в тексте, и способствует тем самым поиску и нахождению решения.
Эффективность перевода текста определяется видом используемых знаково-символических
средств. 

При создании
различного типа моделей очень важно выделить, какая информация должна быть
включена в модель, какие средства (символы, знаки) будут употребляться для
каждой выделенной составляющей текста, какие из них должны иметь одинаковую
символику, а какие – различную. В процессе построения модели и работе с ней
проводится анализ текста и перевод на математический язык: выделяются
известные, неизвестные объекты, величины, отношения между ними, основные и
промежуточные вопросы. 
Построению графической модели следует специально учить детей.

Для этого можно использовать следующую «Памятку» (Приложение 2).

Чтобы проверить, все ли данные задачи отражены на модели, можно
прочитать задачу, показывая, все на модели.

Работа с моделью. Вынесение во внешний план элементов задачи и их
отношений, настолько обнажает связи и зависимости между величинами в задаче,
что иногда перевод сразу ведет к открытию решения. Однако во многих задачах
перевод текста на язык графики является только началом анализа, для решения
задачи требуется дальнейшая работа со схемами. Именно здесь возникает
необходимость формирования у учащихся умения работать с моделями,
преобразовывать их. При этом необходимо иметь в виду, что уровень графической
подготовки при построении модели и работе с ней (согласно психологическим
исследованиям) определяется главным образом не степенью владения им техникой
выполнения графического изображения, а тем, насколько он готов к мысленным
преобразованиям образно-знаковых моделей, насколько подвижно его образное
мышление. 

Работа с моделью может вестись в двух направлениях:

а) достраивание схемы, исходя из логического выведения, расшифровки
данных задачи;

б) видоизменение
схемы, ее переконструирование. 
В процессе обучения графическому моделированию можно использовать следующие задания
и вопросы (Приложение 3)

Наряду с выше изложенным, учитель должен помнить, что одного
составления модели к задаче недостаточно. Следует включить и обратные задания,
а именно: составление текстов различных задач по модели, на выбор нужной модели
к данной задаче, на нахождение ошибок в модели и др., что будет способствовать
развитию творческого мышления каждого ребенка (Приложение 4).

Постоянное
использование этих заданий дает хорошие результаты, способствует формированию
умения  решать задачи.

Соотнесение
результатов работы на модели с текстом.

 Моделирование
осуществляется для того, чтобы получить новые данные о реальности или ее
описании, поэтому необходимым моментом деятельности моделирования является соотнесение
результатов с текстом.

Из
практики известно, что учащиеся после решения задачи так или иначе проверяют
свои ответы для доказательства того, что полученные ответы удовлетворяют
условиям и требованиям задачи. Однако это соотнесение результатов с текстом
задачи не есть только проверка ответа задачи, соотнесение его с требованиями.
Принципиально важным при проверке ответов решения задачи для деятельности
моделирования является не столько выявление правильности (точности) ответа,
сколько соотнесение данных, полученных на модели с ее описанием в тексте. 

На
уроках использую модель работы над задачей по  системе  Занкова (Приложение 5)

Графическое моделирование – это замена действий с обычными предметами
действия с их уменьшенными образцами, моделями, муляжами, макетами, а также их
графическими заменителями: рисунками, чертежами, схемами и т.п.

Но чтобы получить желаемый результат, надо помнить:

• Работа должна быть систематической; 
• Модель должна возникать на глазах детей;
• Необходимо поощрять желание детей выполнить краткую запись;
• Проверять  правильность выполнения модели;
• Сравнивать разные способы, выявлять  рациональный.

2.2      Применение графического
моделирования при решении текстовых задач

Уровень опыта по степени новизны состоит в комбинировании элементов известных методик
(опорные схемы С.Н. Лысенковой, технология развивающего обучения Л.В. Занкова,
графическое моделирование из системы  Н.Б.Истоминой).

Рассмотрим, как можно использовать метод моделирования
при решении задач.

Работа по моделированию начинается с 1
класса. Сначала задачи моделируются с помощью рисунков и схематических
рисунков.

Задача №1:

«У мальчика было 3 красных мяча и 2 синих. Сколько
всего мячей было у мальчика?»

                             ?

Задача №2:

«У Маши было 6 яблок. Она отдала Тане 2
яблока. Сколько яблок осталось у Маши?»

                            ?

Задача №3

«В первый день для ремонта школы привезли
на 4-х машинах по 10 бревен. Сколько всего бревен привезли за эти два дня?»
Если записать ее кратко в таком виде:

1д. – 28б.             

                                               
?

2д. – на 4 маш. по 10б.     

Такая
модель не отражает жизненной ситуации с достаточной наглядностью, что приводит
к ошибкам в решении задачи. Поэтому необходимо
смоделировать ее условие в виде схематического рисунка:

1д.-  

                                                                 ?

2 д. –

Такая модель отражает математическую ситуацию более
наглядно. По ней даже слабый ученик сможет записать решение, если не
так:

28 + 10 * 4 = 68
(б.), то хотя бы так:

1)     10+10+10+10 = 40(6.)

2)     28 + 40 = 68(6.)

Ответ: 68 бревен.

Задача №4

«В совхозе работают 37 трактористов,
шоферов на 8 больше, чем трактористов, а комбайнеров на 5 меньше, чем шоферов.
Сколько комбайнеров работает в совхозе?» Обычная краткая запись этой задачи
выглядит так:

Т. – 37 ч.

Ш. – на 8 больше, чем трактористов

К. – ? – на 5 меньше, чем шоферов

Такая запись
при первичном анализе этой задачи нерациональна, так как не раскрывает
наглядно взаимоотношении величин и не помогает в выборе действий.

На уроке с учениками
мы смоделировали задачу по другому.

Такая
модель дает наглядное представление об отношениях между данными и искомыми в задаче. Анализируя задачу, дети выясняют, что шоферов на 8 больше, чем трактористов, т.е. их
столько же да еще 8. поэтому отрезок на схеме, изображающий численность
шоферов, они начертят большей длины, чем
отрезок, изображающий численность трактористов. А так как численность
комбайнеров на 5 меньше, чем шоферов, т.е. их столько же, но без 5, то и
отрезок, показывающий численность комбайнеров, должен быть меньше отрезка,
показывающего численность шоферов. При таком моделировании выбор действия будет
понятным и обоснованным.

Задача №5

«В
трех одинаковых ящиках 21 кг апельсинов. Сколько килограммов апельсин в 8 таких
ящиках?»

Масса апельсинов в 1 ящике	Количество ящиков	Общая масса
? одинаковая                     ?	3 шт.  8 шт.	21 кг                   ? кг

Таблица – это тоже модель задачи, но более абстрактная,
чем схематический рисунок или чертеж. Она предполагает уже хорошее знание
учащимися взаимозависимостей пропорциональных величин, так как сама таблица
этих зависимостей не показывает. Поэтому при первичном знакомстве с такой
задачей таблица мало помогает представить математическую ситуацию и выбрать
нужное действие.

При
первичном знакомстве с этой задачей моделируем ее условие в виде схематического
рисунка или чертежа.

 

               21 кг

                              
?

      или                                      
 

                           
                          

                                                                           
Масса апельсин одного ящика

                    
21 кг   

                     

 

                                                               
?

По такой модели путь
решения задачи понятен всем учащимся: чтобы узнать, сколько килограммов
апельсин в 8 ящиках, нужно знать, сколько килограммов апельсин в одном ящике.

Задача №6

«В швейной
мастерской было 240 м. ситца. Когда сшили несколько платьев, расходуя на каждое
по 3 м, то в мастерской осталось 90 м ситца. Сколько платьев сшили?»

При
первичном анализе этой задачи используем графическую модель, в виде
схемы:

                                               240
м

 

расход на каждое платье по 3
м.

                                                                                       
осталось 90 м.

Сшили платьев – ?

Особенно
большую роль играет моделирование при решении задач на движение. При этом
модели должны создавать сами учащиеся под руководством учителя. Рассмотрим
пример такого моделирования.

Задача №7

 «Из
двух городов, находящихся на расстоянии 520
км, одновременно вышли навстречу друг другу два поезда, которые встретились
через 4 ч. Один поезд шел со скоростью 60 кмч. С какой скоростью шел второй поезд?»

Вызванный
ученик, повторяя содержание задачи, под наблюдением класса моделирует описанную
в ней жизненную ситуацию. Расстояния между городами он изображает в виде
отрезка. Направление встречного движения показывает стрелками, а место встречи
обозначает флажком, число часов движения каждого поезда отмечает вертикальными
штрихами на схеме, а также обозначает цифрами расстояние между городами и
скорость движения первого поезда.

Решение
задачи детям было предложено записать самостоятельно. Учащиеся решили задачу
двумя способами:

I
способ: (520 – 60 * 4) : 4 = 70 (км/ч)            II способ:  520 : 4 – 60 = 70
(км/ч)           

Такое
моделирование, когда модель возникает на глазах у детей, имеет явное
преимущество перед применением готовых рисунков и схем.

Решение
задачи разными способами создает предпосылки для формирования у обучающихся
умения находить свой оригинальный способ решения задачи,  содействует
воспитанию стремления вести самостоятельно поиск решения новой задачи.

Итогом
обучения построению и осмыслению схематического чертежа является
самостоятельное моделирование задач учащимися.                                          

Каждая модель имеет преимущества
и недостатки, универсальной модели нет; каждая значима при решении определенных
задач, необходимо обучать  детей составлению различных моделей и развивает 
умение видеть целесообразность или нецелесообразность использования
определенной модели (то есть выбирать нужную модель при решении конкретной
задачи).

И.И. Аргинская, автор учебника «Математика» по
развивающей системе обучения Л.В.
Занкова пишет: «Необходимо помнить, что краткая запись условия не самоцель, а
только средство, помогающее решению задачи, и каждый ребёнок может использовать
то, что ему действительно помогает достигнуть конечного результата, а не то,
что ему в этом мешает».

Заключение

В ходе работы с графическими моделями мы убедились, что  графические модели
являются эффективным средством поиска решения задачи. В процессе решения
детям приходится переходить от одной формы записи к другой и  находить среди
них оптимальную. Процесс графического  моделирования текстовой задачи повышает
мыслительную активность детей, способствует развитию вариативности мышления, а
значит, делает решение задач более приятным  и интересным.

Чтобы самостоятельно решать задачи, ученик должен освоить различные
виды моделей, научиться выбирать модель, соответствующую предложенной задаче, и
переходить от одной модели к другой. Для того чтобы вооружить учащихся
моделированием как способом познания, нужно, чтобы школьники сами строили
модели, сами изучали какие-либо объекты, явления с помощью моделирования.

 Использование графического моделирования при решении текстовых задач
обеспечит более качественный анализ задачи, осознанный поиск ее решения,
обоснованный выбор арифметических действий и предупредит многие ошибки в
решении задач. Модель задачи может быть использована для составления и решения
обратных задач.

Таким образом, обучение
с применением графического моделирования

·       
повышает активность
мыслительной деятельности учащихся;

·       
помогает
понять задачу;

·       
осознать выбор
действия;

·       
найти
самостоятельно рациональный путь решения;

·       
установить
способ проверки.

Вывод: в целом полученные результаты дают основание предположить, что опыт
работы по графическому моделированию текстовых задач на уроках математики имеет
практическую значимость для повышения качества образовательного процесса. И наша работа имеет конкретную учебную
направленность и может быть использована в практической деятельности другими
педагогами.

Литература

1.    
Алексеева Л.Л.
«Планируемые результаты начального общего образования» (Стандарты второго поколения):
–  М.: Просвещение, 2009 г.

2.    
Аргинская И.И., Дмитриева
Н.Я.Обучаем по системе Л.В. Занкова: – М.: Просвещение, 1993
г.

3.     Асмолов А.Г., Бурменская Г.В.,
Володарская И.А. Как проектировать универсальные учебные действия  в начальной
школе: от действия к мысли: пособие для учителя: – М: Просвещение,  2008
г.

4.    
Зайцева С.А. Решение составных задач на уроках математики: –  Москва:
Чистые пруды, 2006 г.

5.    
Н.Б.Истомина. Методика обучения математике в начальных классах. Учебное
пособие: – Москва: Издательство, 1998 г.

6.    
Н.Б.Истомина. Учимся решать задачи: – Москва: Линна-Пресс, 2005 г.

7.    
Лавриненко Т.А. Как научить детей решать задачи: Методические
рекомендации для учителей начальных классов: – Саратов: «Лицей», 2000
г.

8.    
Муртазина Н.А. Теоретические основы применения графического
моделирования при обучении младших школьников математике. Начальная школа 2012
г. № 3

9.    
Мустафаева Ф.Ф. Некоторые методические вопросы использования
графических изображений при изучении математики. Начальная школа.  -2009 г.
№11. с. 92-95

10. Ожегов С.И.,
Шведова Н.Ю. Толковый словарь русского языка: – Издательства «Азъ», 1992
г.

11. Пичугин С.С 
Графическое моделирование в работе над текстовой задачей. Начальная школа, 2009
г. №9 с. 41-45

12.
Федеральный
государственный общеобразовательный стандарт начального общего образования

13.
Фролова И.Т. Философский
словарь: – М.: Политиздат, 1991 г.

14. Шадрина И.В.
Использование графических моделей для разъяснения смысла арифметических
действий. Начальная школа, 1991 г. №12.  с. 56-58

15.
Интернет – ресурсы

     http://www.openclass.ru/

     http://festival.1september.ru/

     http://standart.edu.ru/

     http://www.proshkolu.ru/

Приложение
1

·         
Чем похожи тексты задач? Чем отличаются?

а)
На одном проводе сидели ласточки, а на другом —  7 воробьев. Сколько всего
сидело птиц на проводах?

б) На одном проводе сидело 9 ласточек, а
на другом 7 воробьев. Сколько всего   сидело птиц на проводах?

·         
Подумай! Будут ли эти тексты задачами?

а)
На одной тарелке 3 огурца, а на другой – 4. Сколько помидоров на двух тарелках?

б)
На клумбе росло 5 тюльпанов и 3 розы. Сколько тюльпанов росло клумбе?

·         
Подумай! На какие вопросы можно ответить, пользуясь этим услови­ем:

От
проволоки длиной 15 дм отрезали сначала 2 дм, потом еще 4 дм.

а)
Сколько всего дециметров проволоки отрезали?

б)
На сколько дециметров меньше отрезали в первый раз, чем во вто­рой?

в)
 На сколько дециметров проволока стала короче?

г)
Сколько дециметров проволоки осталось?

·                    
Подбери условия к данному вопросу и реши задачу.

Сколько всего детей занимается в студии?

а)  В
студии 30 детей, из них 16 мальчиков.

б)  В
студии мальчики и девочки. Мальчиков на 7 меньше, чем девочек.

в)  В
студии 8 мальчиков и 20 девочек.

г)  В
студии 8 мальчиков, а девочек на 2 больше.

д)  В
студии занимаются 8 мальчиков, а девочек на 2 меньше.

Приложение 2

                       
Памятка

    1. Что будем
изображать?

    2. Как будем
изображать?

    3. Что в первую
очередь будем изображать?

    4. Как числа,
данные в задаче, помогут построить модель?

    5. Как расположим
модель?

    6. Как на модели
обозначим данные?

    7. Что теперь
полезно изобразить (до тех пор, пока не будут отражены все данные и все
отношения между данными и искомыми параметрами)?

    8. Как на модели
обозначим вопрос задачи?

Приложение 3

·         
Сделай рисунок (чертеж)
данной задачи.

Мотоциклист ехал 3 ч со средней скоростью 60
км.ч и 2 ч со средней скоростью 70 км.ч. Какое расстояние он проехал за все
это время?

·         
Я прочитаю две задачи, а
вы определите, к какой из них полезно сделать рисунок (чертеж).

1) Посадили 12 тюльпанов, по 6
тюльпанов в каждом ряду. Сколько получилось рядов тюльпанов?

2)  У Вовы  27 открыток, а  у Олега в 3 раза меньше,  чем
у Вовы. Сколько открыток у Вовы?

·         
Прочитайте
задачу, показывая все данные на чертеже (рисунке).

·         
Объясните, как построили
чертеж (рисунок) к задаче.

·         
Соответствует ли рисунок
(чертеж) задаче?

·         
Что в нем лишнее (чего в
нем недостает)?

·         
Что нужно сделать, чтобы
рисунок (чертеж) соответствовал задаче?

Приложение 4

·                   
Составьте
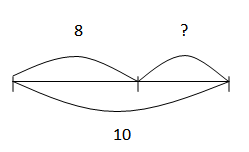
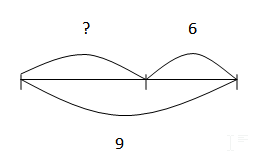
текст задачи для данной модели.

                           6

                 ?

• Подбери нужную
  схему к задаче.

В
портфеле лежит 14 тетрадей в клетку и 9 тетрадей в линейку. Сколько всего
тетрадей лежит в портфеле?

                              
?                                                                    14 т.

               
14 т.              9т.                                          ?                        9
т.

• Выберите из
  предложенных задач ту, которая соответствует предложенной модели. Объясни
  свой выбор.

                            90
ящ.

                 ?                    50
ящ.      

а)
На базе было несколько ящиков, после того как 50 ящиков увезли, осталось 90
ящиков. Сколько ящиков было на базе?

б) На базе было 90 ящиков, оттуда увезли 50 ящиков.
Сколько ящиков осталось?

• Заполните схему – заготовку
  данными задачи.

     Сколько красных яблок положили в вазу, если всего в нее положили 8
яблок, из них зеленых – 3?

 

• Найдите  ошибки в схеме.

 На ветке сидело несколько
птиц. После того как 5 птиц улетели, их осталось 9.   Сколько птиц сидело на
ветке?

             9 п.              ?                                                                          
                                  

                     5 п.

• Завершите построение схемы.

Курица легче зайца на 4
кг, а заяц легче собаки на 8 кг. На сколько собака тяжелее курицы? На сколько
курица легче собаки?

К.

З.

С.

• Измени текст задачи в соответствии с вопросом,
  указанным на схеме.

Расстояние
между городами 720 км. Автобус в первый день проехал 300
км, а во второй день 212 км. Сколько километров ему осталось проехать в третий
день?

• Рассмотри схему подумай, на какой вопрос   можно
  ответить, пользуясь данным условием.

          Коля выше Пети на 20
см, а Петя выше Вовы на 7 см.  

20 см

К.  

                                                    7
см

П.

В.

Приложение 5

Модель работы над задачей	Алгоритм решения задачи для ученика
	1.     Читаю задачу… 2.     В задаче говорится… 3.     Мне известно… 4.     Надо узнать… 5.     Читаю по частям, составляю краткую запись… 6.     Рассказываю по краткой записи… 7.     Составляю план решения задачи… 8.     Решаю… 9.     Пишу ответ…. 10. Проверяю…       11. Ищу другой способ решения задачи…

В одной из своих статей я рассказывала о том, как научить ребенка составлять схематический чертёж к задачам на сложение и вычитание. Сегодня я расскажу о том, как составлять схематический чертёж к задачам на умножение и деление.

Пример 1

Бабушка испекла 10 пирожков с вишней, а пирожков с капустой она испекла в 4 раза больше. Сколько пирожков с капустой испекла бабушка?

Напомню, что, при составлении чертежа, мы используем понятия “целое” и “части”. При умножении целое – это результат (произведение), а при делении целым является делимое (то число, которое мы делим).

В данной задаче целым будет количество пирожков с капустой. Поэтому показываем, что наше целое состоит из нескольких одинаковых частей (количество пирожков с вишней).

Пример 2

Бабушка испекла 9 пирожков с капустой, а пирожков с вишней – в 3 раза меньше. Сколько пирожков с вишней испекла бабушка?

Пример 3

Бабушка испекла 30 пирожков с капустой и 10 пирожков с вишней. Во сколько раз пирожков с капустой больше, чем пирожков с вишней?

Пример 4

На столе стоят 3 тарелки. На каждой тарелке по 2 пирожных. Сколько всего пирожных?

В схеме к этой задаче нам надо показать, что количество пирожных в одной тарелке повторяется несколько раз.

Пример 5

16 слив разложили на тарелки, по 2 сливы на каждую. Сколько потребовалось тарелок?

А в этой задаче мы показываем, что в числе 16 содержится несколько раз по 2.

Схема к этой задаче будет такая:

Пример 6

В связке было 15 бананов. Третью часть бананов съел папа. Сколько бананов осталось?

В схеме к этой задаче мы показываем, что все количество бананов состоит из трёх одинаковых частей. Одну из этих частей съели, а две остались.

Делитесь своим мнением в комментариях, подписывайтесь на мой канал

Педагогический опыт

«Метод моделирования

при решении текстовых задач»

Москвичева

Наталья Станиславовна

Учитель начальных классов

«Математике должно учить в школе

 еще с той целью, чтобы познания,

здесь приобретаемые, были достаточными

 для обыкновенных потребностей в жизни»

И.Л. Лобачевский

ИНФОРМАЦИЯ ОБ ОПЫТЕ

1.Актуальность педагогического опыта

С самого начала своей педагогической деятельности я задавалась вопросом “Почему многие дети не умеют решать текстовые задачи, более того панически боятся их?”. Первые шаги при решении простых задач, казалось бы, не вызывают у учащихся затруднений. Однако в дальнейшем самостоятельное решение составных задач оказывается не по силам многим ученикам, и от класса к классу эти учащиеся испытывают все большие трудности.

Причина же возникающих затруднений состоит, прежде всего, в том, что у учащихся не сформировано в достаточной мере умение анализировать текст задачи, правильно выделять известное и неизвестное, устанавливать их взаимосвязь, которая является основой выбора действия для решения задачи. Все перечисленное и составляет общее умение работы над задачей.

Современная школа должна формировать целостную систему универсальных учебных действий, то есть ключевые компетенции. Обучение сегодня рассматривается не как простая трансляция знаний от учителя к ученику, а как сотрудничество. И в образовательном процессе начинают преобладать методы работы, обеспечивающие становление самостоятельной творческой личности, готовой к восприятию и решению инновационных задач.

Но для того, чтобы ребёнок умел учиться, умел добывать необходимую информацию, анализировать её, уместно и умело применять её, нужно совершенствовать его мыслительные способности, которые позволили бы ему мыслить более продуктивно. Ведь именно благодаря способности человека мыслить решаются трудные задачи, делаются открытия, появляются изобретения.

Таким образом, обнаруживаются противоречия между возрастающим объемом информации, который предлагается обучающимся, и недостаточным включением самих обучающихся в познавательный процесс; между современными требованиями к подготовке выпускников начальной школы и сложившейся системой обучения младших школьников.

Разрешение этих противоречий и обусловило выбор темы: «Метод моделирования при решении текстовых задач».

Я считаю, что богатые возможности для развития интереса к математике, логического мышления младших школьников открывает система работы над текстовыми задачами методом моделирования.

2.Методологическая база педагогического опыта

Вопросы использования моделирования как метода научного познания довольно широко освещены в философской литературе (К.Б. Батораев, Б.А. Глинский, Б.С. Грязнов, Б.С. Дынин, К.Е Морозов, А.И. Уемов, В.А. Штофф и др.). Анализ работ перечисленных авторов позволяет сделать вывод, что моделирование как метод научного познания в науке используется с давних времен. Однако проблема использования моделирования в обучении разрабатывается в психолого-дидактических исследованиях лишь в последние десятилетия. В работах Л.И. Айдаровой, В.В. Давыдова, А.К. Марковой, Н.Г. Салминой, Л.М. Фридмана, А.А. Шибанова, Е.В. Чудиновой, Д.Б. Эльконина и других авторов рассматриваются различные аспекты проблемы использования моделей и моделирования в учебном процессе.

Условно можно выделить два основных направления в исследованиях по использованию моделирования в обучении:

• Первое направление посвящено вопросам влияния моделирования на умственное развитие ученика (А.А. Венгер, П.Я Гальперин, В.В. Давыдов, Н.Г. Салмина, Д.Б. Эльконин).
• Второе направление исследований затрагивает в основном методические аспекты применения моделирования в учебном процессе (Л.И. Айдарова, А.В. Белошистая, А.У Варданян, ГА. Варданян, СИ. Волкова, Я. Дадоджанов, А.К. Маркова, Г.И. Минская).

Анализ проведенных исследований позволяет констатировать высокую оценку со стороны исследователей продуктивности моделирования как для усвоения учебного материала по конкретной дисциплине, так и для умственного развития школьников. Учеными признается, что использование моделирования в обучении усиливает его развивающий эффект.

Опыт направлен на то, чтобы обеспечить положительную динамику в развитии умения решать текстовые задачи посредством метода моделирования.

Для реализации цели необходимо решение следующих задач:

1. Систематически применять существующий методический подход к обучению решению задач.
2. Формировать у обучающихся через уроки математики умение моделировать.
3. Разработать и ввести в педагогическую практику уроки с использованием метода моделирования.

На современном этапе образования под развивающим обучением понимается обучение младших школьников общим приемам умственной деятельности, а на уроках математики – общим приемам по усвоению математических понятий. Метод моделирования дополняет учебную работу школьников поисковой деятельностью, помогает формированию таких приемов умственной деятельности как абстрагирование, анализ, синтез, развивает математическое мышление.

Моделирование задач позволяет младшим школьникам подняться на достаточно высокую ступеньку абстрактности: все второстепенные детали опущены, выбор действия производится только из логики происходящих изменений.

Благодаря моделированию, математические связи и зависимости приобретают для учеников смысл, а в процессе его использования происходит углубление и развитие математического мышления учащихся. Поэтому моделирование – это один из ведущих методов обучения решению задач и важное средство познания действительности.

3. Ожидаемые результаты

Реализация данной работы, направлена на формирование способности моделирования, даст возможность учащимся получить высокие предметные результаты и освоить универсальные учебные действия.

№пп	УУД	Результат:
1	Личностные универсальные учебные действия	Будет сформирована: – внутренняя позиция учащегося; – адекватная мотивация учебной деятельности; – ориентация на моральные нормы и их выполнение.
2	Регулятивные универсальные учебные действия	Овладеют: – способностью принимать и сохранять учебную задачу; – планировать реализацию задачи; – контролировать и оценивать свои действия; – вносить коррективы в выполнение действий.
3	Познавательные универсальные учебные действия	Научатся: – воспринимать и анализировать тексты, знаково-символические средства, в том числе овладеют действием моделирования, спектром логических действий и операций, общими приемами решения текстовых задач.
4	Коммуникативные универсальные учебные действия	Приобретут: – умения учитывать позицию собеседника; – организовывать сотрудничество и кооперацию с учителем и сверстниками; – адекватно воспринимать и передавать информацию; – отображать предметное содержание и условия деятельности в сообщениях, важнейшими компонентами которых являются тексты.

Кроме этого предполагается повышение уровня сформированности умения решать текстовые задачи при помощи моделирования на уроках математики по возрастам:

1 класс

Учащиеся должны уметь:

• сравнивать величины, записывать результаты сравнения с помощью отрезков, с помощью буквенных формул;
• использовать знаково-символические средства (чертежи, формулы, схемы) представления информации при решении задачи;
• работать с модельными средствами (знаковыми, графическими, словесными) в рамках изученного материала;
• строить графические модели арифметических действий (сложения и вычитания) и осуществлять переход от этих моделей к буквенным формулам и обратно;
• моделировать разностное отношение и отношение «частей и целого» с помощью чертежа и формул;
• находить целое или части по чертежу, формуле;
• переходить от одного вида модели (графической, знаковой) к другой;
• подбирать величины к заданной формуле;
• правильно выполнять построение (отмеривание) величины по схеме;
• строить числовую прямую, выбирая подходящие направление, начало и шаг;
• моделировать отношения величин с помощью чертежей и стрелочных схем;
• составлять по моделям текстовые задачи и математические выражения.

Программа для 1 класса (по Л.М. Фридман)

Понятия, которыми должны овладеть учащиеся	Подготовительные упражнения	Виды задач, решаемые в данном классе
1. Представление о задаче. 2. Вопрос (требование) задачи. 3. Известные (данные) значения величин. 4. Искомое значение величины. 5. Слова-признаки соотношений сложения и вычитания.	1. Расчленение текста простой задачи на условие и требование (вопрос). 2. Построение схематической модели простых задач на сложение и вычитание. 3. Составление простых задач на сложение и вычитание: а) по заданному условию; б) по заданному вопросу.	1. Простые задачи вида равенства и неравенства. 2. Простые разрешаемые задачи на сложение и вычитание. 3. Косвенные простые задачи на сложение и вычитание.

2 класс

Учащиеся должны уметь:

• моделировать разностное отношение и отношение «частей и целого» с помощью чертежа и формул;
• использовать знаково-символические средства (чертежи, формулы, схемы) представления информации при решении задачи;
• работать с модельными средствами (знаковыми, графическими, словесными) в рамках изученного материала;
• строить графические модели арифметических действий (сложения и вычитания) и осуществлять переход от этих моделей к буквенным формулам и обратно;
• переводить информацию из графического или формализованного (символьного) представления в текстовое, и наоборот;
• находить целое или части по чертежу, формуле;
• переходить от одного вида модели (графической, знаковой) к другой;
• подбирать величины к заданной формуле;
• по схеме отмерить величину, используя промежуточную мерку, измерить данную величину с помощью промежуточной мерки и представить результат измерения в виде схемы;
• записывать результат измерения системой мерок;
• моделировать отношения величин с помощью чертежей и стрелочных схем;
• описывать процессы с помощью специальных таблиц;
• составлять по моделям текстовые задачи и математические выражения;
• описывать действия умножения и деления с помощью треугольной схемы.

Понятия, которыми должны овладеть учащиеся	Подготовительные упражнения	Виды задач, решаемые в данном классе
1. Слова-признаки соотношения разностного сравнения. 2. Слова-признаки перехода от одной единицы счета или измерения к другой. 3. Слова-признаки разбиения целого на равные части.	1. Составление задачи, обратной данной. 2. Построение схематичной и графической модели задач. 3. Составление текста задачи по ее модели. 4. Составление задач по результатам наблюдений, измерений. 5. Подбор данных к заданному вопросу и подбор вопроса к заданным данным.	1.Простые задачи соотношения: а) разностного соотношения; б) перехода от одной единицы счета или измерения к другой; в) разбиения целого на равные части. 2. Сложные открытые задачи из двух соотношений.

3 класс

Учащиеся должны уметь:

• использовать знаково-символические средства (чертежи, формулы, схемы) представления информации при решении задачи;
• работать с модельными средствами (знаковыми, графическими, словесными) в рамках изученного материала;
• строить графические модели всех арифметических действий и осуществлять переход от этих моделей к буквенным формулам и обратно;
• переводить информацию из графического или формализованного (символьного) представления в текстовое, и наоборот;
• переходить от одного вида модели (графической, знаковой) к другой;
• подбирать величины к заданной формуле;
• анализировать задачи с однородными величинами и моделировать результаты анализа на моделях (чертежах и схемах);
• составлять по моделям текстовые задачи и математические выражения;
• читать чертежи и схемы, выполнять по ним вычисления;
• составлять выражения по чертежам и схемах, вычислять значения буквенных выражений при заданных значениях букв.

Понятия, которыми должны овладеть учащиеся	Подготовительные упражнения	Виды задач, решаемые в данном классе
Повторение и углубление понятий, изученных в предыдущих классах. Вспомогательная и решающая модели задачи. Вычислительная формула задачи. Стоимость – количество – цена. Путь – время – скорость.  Уравнение, корень уравнения.	Составление вычислительной формулы для решения сложной открытой задачи, когда дано ее решение по вопросам. Составление всех обратных задач для сложной задачи из 2-4 соотношений.	Решение сложных открытых задач, состоящих из 2-4 соотношений с помощью составления вычислительной формулы. Решение задач с неопределенными неизвестными разными методами. Решение сложных задач с помощью составления уравнения разными методами. Решение задач геометрического содержания.

4 класс

Учащиеся должны уметь:

• использовать знаково-символические средства (чертежи, формулы, схемы) представления информации при решении задачи
• работать с модельными средствами (знаковыми, графическими, словесными) в рамках изученного материала;
• строить графические модели всех арифметических действий и осуществлять переход от этих моделей к буквенным формулам и обратно;
• переводить информацию из графического или формализованного (символьного) представления в текстовое, и наоборот;
• переходить от одного вида модели (графической, знаковой) к другой;
• подбирать величины к заданной формуле;
• моделировать отношения величин с помощью чертежей и стрелочных схем;
• описывать процессы с помощью специальных таблиц;
• подбирать, составлять задания на работу с моделями, их конструирование, а также осуществление различных переходов между ними;
• составлять по моделям текстовые задачи и математические выражения;
• представлять результаты анализа на моделях (чертежах, схемах, таблицах);
• читать чертежи, схемы, таблицы, диаграммы, выполнять по ним вычисления;
• моделировать и разрешать реальные ситуации, требующие умения находить геометрические величины;
• составлять выражения по чертежам и схемам, вычислять значения буквенных выражений при заданных значениях букв.

Понятия, которыми должны овладеть учащиеся	Подготовительные упражнения	Виды задач, решаемые в данном классе
Повторение и углубленное овладение всеми основными понятиями, изученными в предыдущих классах. Функции задач в жизненной практике людей. Сложение и вычитание скоростей. Собственная скорость лодки и скорость течения, скорость по течению и против течения реки. Сущность решения задачи и этапы процесса решения.	Составление задач по данным других учебных предметов и по краеведческим и другим реальным материалам.	Решение сложных задач по материалам других учебных предметов и реальным данным краеведческого и другого реального материала. Задачи, связанные со сложением и вычитанием скоростей. Задачи геометрического содержания, данные для которых получены непосредственным измерением. Графическое решение задач.

Учитель должен:

– владеть методом формирования у обучающихся умения моделирования при решении текстовых задач.

        4. Описание деятельностного аспекта

В соответствии с поставленными целями и задачами использую на уроках математики при решении задач особые знаково-символические средства – модели, однозначно отображающие структуру задачи и достаточно простые для усвоения младшими школьниками.

«Моделирование – процесс построения моделей для каких-либо познавательных целей. Модель – это объект или система, исследование которой служит средством для получения знаний о другом объекте – оригинале или прототипе модели». (Л. М. Фридман, К. Н. Волков).

Другими словами, изображение условия задачи при помощи символов и знаков, позволяет выделить логические связи и установить закономерности.

Классификация моделей

Исходя из общей классификации моделей, я использую в своей работе таблицу «Моделирование текстовых задач»:

 

Согласна с коллегами, которые утверждают, что освоение моделей – это трудная для обучающихся работа. Причем трудности связаны не с абстрактным характером модели, а с тем, что, моделируя, обучающиеся отображают сущность рассматриваемых в задаче объектов и отношений между ними.

Поэтому обучение моделированию веду целенаправленно, соблюдая ряд условий:

• начинаю работу с подготовительных упражнений по моделированию: на первых этапах знакомлю учащихся с «ключевыми» словами в тексте задачи (Приложение 3);
• применяю метод моделирования при изучении математических понятий;
• веду работу по усвоению знаково-символического языка, на котором строится модель;
• систематически провожу работу по освоению моделей тех отношений, которые рассматриваются в задачах (Приложение 4).

Каждая модель выступает как одна из форм отображения сущности задачи, помогающая детям выстроить логическую цепочку умозаключений, приводящих к конечному результату. При анализе данной задачи детям предлагается сразу несколько моделей, для того, чтобы познакомить с разными видами моделирования, во-первых. И, во-вторых, дети почти сразу определяют какая модель им «ближе». Причем делают это индивидуально, выбирая самый оптимальный вариант для себя, что дает положительный результат. При таком подходе развивается творческое мышление, активизируется мыслительная деятельность, нет закомплексованности, если вдруг предложенная модель не будет «принята» ребенком. И, что самое главное, такая работа при решении сложных задач приводит к многообразию способов решения, причем дети делают это самостоятельно.

Виды моделей:

1. Использование чертежа при решении простых задач

Для развития математических представлений, умения анализировать, обобщать предлагаю следующие задачи.

а) Задача (1 кл.). В вазе лежит всего 10 яблок, из них одно зеленое, а остальные красные. Сколько красных яблок в вазе?

     10

  1

Моделируя задачу таким способом, детям предоставляется возможность работать в дальнейшем с большими числовыми данными, в условии задачи могут быть использованы буквенные выражения.

Опыт показывает, что, используя графическое моделирование простых задач, дети без особых трудностей, естественно переходят к решению задач в два действия.

Действенным средством для поиска решения задачи служит и схематический чертеж. Кроме того, обоснование учеником своих действий при построении чертежа способствует развитию умения рассуждать, учит последовательно и аргументировано излагать свои мысли.

б) Моделирование текстовой задачи в виде отрезка продолжаю и в следующих классах.

Пример моделирования нестандартной текстовой задачи в виде отрезка.

Задача. На чемпионате в школе по игре в шахматы Сережа сыграл 12 партий. Когда у него спросили, сколько же партий он выиграл, Сережа ответил: “Две партии я проиграл, а из остальных на каждые две партии вничью у меня 3 выигранных”. Сколько шахматных побед у Сережи?

Модель данной задачи.

В данном случае графическая иллюстрация заставляет детей мыслить логически и последовательно.

2. Предметное моделирование

Изобрази с помощью кружков красного и белого цвета то, о чем говорится в задаче: “У дома 3 клумбы и у школы столько же клумб. Сколько всего клумб у дома и школы?” Что обозначают кружки красного цвета? Кружки желтого цвета?

Данный процесс моделирования предлагаю детям для закрепления умения строить предметные модели.

3. Схематический рисунок

Задача (1 кл.). У хозяйки 9 кур, а уток на 4 больше.

Обозначь каждую птицу кругом и покажи на рисунке сколько уток у хозяйки.

Маша сделала такой рисунок:

А Миша такой:

Кто прав: Маша или Миша?

При помощи задач такого вида активизирую мыслительную деятельность обучающихся и создаю условия для осознания той ситуации, которая представлена в виде текста.

4. Математическое моделирование (формулы)

Задача. У мальчика 50 копеек. Яблоко стоит а копеек, а груша к копеек. О чем мальчик думает при выполнении каждого из следующих действий.

50-а 50:к а+к 50-а·3 50-а-к (а+к)·2

а-к 50-к а·4 50-(а+к) (50-а)·к а·9-50

(К каждому выражению нужно поставить вопрос).

Мой опыт работы подтверждает целенаправленность такого приема решения задач. Детей увлекает такая творческая работа. Они с интересом включаются в поисковую деятельность.

5. Информационная модель (таблица, график, диаграмма)

Задача. Отец старше сына в 4 раза, через 20 лет он будет старше сына в 2 раза. Сколько лет отцу?

Отец	Сын	Возраст через 20лет (отец)	Возраст через 20лет (сын)	Вывод
20 24 28 32 36 40	5 6 7 8 9 10	40 44 48 52 56 60	25 26 27 28 29 30	Нет Нет Нет Нет Нет В 2 раза

Данная модель позволяет решать задачи способом перебора. Детям особенно нравится работа с такими моделями. Так как привлекает собой большим количеством чисел и при видимой сложности решается без особых затруднений.

5. Выводы и результаты работы

по моделированию задач на уроках математики:

Целенаправленная работа по развитию математического мышления при помощи метода моделирования на уроках в начальной школе позволяет школьникам достичь значительных успехов.

При поступлении в 1 класс школьники не проходят никакого отбора, обучаются все с учётом индивидуальных особенностей и склонностей.  В сентябре 2015 я начала работать в 1 «В» классе. В октябре была проведена диагностика по методике Л.Ф.Тихомировой и А.В.Басова на выявления уровня интеллектуального развития младших школьников. Результаты диагностики показали, что сформировалось несколько различных групп. Из 28 учащихся класса имеют:

 высокий уровень – 8%  обучающихся;

 нормальный уровень – 24% обучающихся;

 ниже среднего – 32% обучающихся;

 низкий – 36% обучающихся.

Исходя из данных диагностики, можно сделать вывод, что 68% детей с низким уровнем развития.

В результате внедрения в процесс обучения математического моделирования мы достигли следующих результатов:

– у большинства обучающихся сформировалась положительная мотивация к изучению математики;

– более эффективно формируется навык творческого подхода к решению практических задач;

– создаются предпосылки для более осознанного изучения математики;

– более эффективно развиваются ключевые компетентности;

– учащиеся стали ощущать себя успешными и уверенными, возросла степень их психологического комфорта на уроках.

Накопленный опыт показывает, что развивающие функции моделирования текстовых задач способствуют активизации мыслительной деятельности обучающихся на уроках математики, так как работа с моделями помогает включить их в активную умственную деятельность. Кроме того, изучение темы идет более быстрым темпом и обеспечивает осознанное усвоение материала, т.к. работа с моделями доступна обучающимся младшего школьного возраста, опора на модель обеспечивает самостоятельное выполнение заданий, заданий творческого характера.

Решение текстовых задач – не самоцель, а средство для того чтобы учащиеся овладели разумным общим подходом к решению любых задач, которые им могут встретиться в жизни.

Приложение 1

Подготовительные упражнения для моделирования задач.

1. Обозначить на чертеже числа из рассказов.

а) в одном ведре было а кг яблок, а в другом е кг.

б) в одном ведре было р кг яблок, а в другом на в кг меньше.

2. Построить модель отношения «больше на» и определить способ нахождения большей величины.

а) в парке росло 150 берез и несколько лип. Лип было на 30 больше, чем берез. Сколько было лип?

3. Составь по чертежу задачу о покупке красных и синих шаров. Одну задачу составь со словом «больше», другую со словом «меньше». Реши задачи.

                   9                

а)        

                                               ?

                               23

                                 23

б)

                                               

                                               9

        

                          ?

4.Какой чертеж будешь использовать, решая задачу: «В книге 36 страниц. Это на 17 страниц больше, чем во второй книге. Сколько страниц во второй книге?»

            36            17                             36            ?                                             17

а)         б)        в)

               

                      ?                                      17                                           36                  

                     36

г)

             

                               17                      

 

               ?

5. Какой могла быть модель, если решение задачи было таким: 18+13,
17 – 10 ?

7. Как нужно изменить чертеж, если вопрос задачи будет таким: «На сколько больше ящиков с помидорами, чем с огурцами, привезли в магазин?»

               18 ящ.             12 ящ.

                          ?

8. Построй модель к задаче: «В двух коробках 36 карандашей. Сколько карандашей во второй коробке, если в первой их 17?»

9. Запиши в нужные клетки таблицы следующие числа: 57, 75, 44, 74, 55, 77, 47. Какие числа нужно записать в оставшиеся клетки?

д.	ед.	4	5	7
4
5
7

10. Дан чертеж:

                            М

           К                              ?

Как найти величину, обозначенную знаком «?» ? Запишите формулу.

11. Сколько разностей можно составить из чисел 30, 25, 17, 9, если для их составления брать по два числа? Будут ли среди них разности, значение которых равны?

Приложение 2.

Графические модели решения задач по математике.

Задача (1 кл.).

Таня нарисовала 5 домиков, а Сережа на 4 больше. Сколько домиков нарисовал Сережа?

Так для данной задачи, графическая модель может быть выполнена:

1. а) в виде рисунка

Т.

С. 

?

б) в виде условного рисунка

Т.

С. 

?

в) в виде чертежа

           5 д.

Т.

        ?

С.

4 д.

г) в виде схематизированного чертежа

           5 д.

Т.

        ?

С.

4 д.

«КЛЮЧЕВЫЕ» СЛОВА В ТЕКСТЕ ЗАДАЧИ

Разностное отношение

•  на (больше, меньше)        

Кратное отношение

• В … раз (больше, меньше)

Целое из равных частей

• по … в каждом …,

• поровну в каждом ряду …,

• В  одинаковых …,

• … доля …

Приложение 3.

Целое из разных частей

• Было

• Привезли (купили, подарили, приехали, …)

• Стало

• Было

• Уехали (продали, съели, …)

• Осталось

• Было … в одном …,

• Было … во втором …,

• Всего (вместе) …

Приложение 4.

«Таблица отношений величин»

Приложение 5.

Задача. У девочки несколько зеленых шаров и 3 красных. Всего 8 шаров. Сколько зеленых шаров у девочки?

Использование моделей при составлении и решении уравнений позволяет не заучивать правила нахождения неизвестных величин, а самостоятельно открывать, формулировать их через осознание действия в процессе решения задач.

Я убеждена, что, если у младших школьников будет сформирована самостоятельная учебная деятельность, им легче будет обучаться на следующих уровнях системы образования.

В связи с этим использую различные задания для развития самостоятельности обучающихся, активизации их мыслительной деятельности используя метод моделирования задач.

1. Опишите ситуацию с помощью схемы.

а) Было 4 треугольника синего и один красный. Всего 5 треугольников.

б) Было 5 треугольников. Из них 4 синих, а 1 красный.

в) Синих квадратов 2, а красных на 4 больше.

1. Составьте рассказ  по схемам (неизвестна часть и целое)
   
2. Прочитайте и расшифруйте схему (предлагаются модели различного вида).

2. Решение задачи разными способами создает предпосылки для формирования у обучающихся умения находить свой оригинальный способ решения задачи, воспитывает стремление вести самостоятельно поиск решения новой задачи. Широкие возможности в этом плане дают приемы моделирования.

Задача. На швейной фабрике мастер шил одинаковые пальто, израсходовав на них 24 м ткани. Его ученица сшила на 6 пальто меньше, израсходовав на них в 4 раза меньше ткани. Сколько всего пальто сшили мастер и ученица?

Задачу можно решить традиционно – по вопросам (6 действий), находя расход ткани на одно изделие. Но можно решить и другим способом – гораздо быстрее. Из чертежа модели текста задачи следует, что на 3 части приходится 6 пальто, тогда на 1 часть – 2 пальто. Всего – 5 частей (1+4) или 10 пальто (по 2 – 5 раз, 2х5=10).

3. При решении задач осуществляю дифференцированный подход:

Задача. В двух корзинах 75 яблок. Когда из первой взяли 6, а из второй 9, то в корзине осталось яблок поровну. Сколько яблок было в каждой корзине?

Для самостоятельного решения данной задачи в соответствии с уровнем подготовленности детям предлагаю следующие чертежи.

По этим чертежам предлагаю следующие задания:

1. Рассмотри чертеж и реши задачу.
2. Закончи чертеж к задаче. Обозначь на нем данные и искомое и реши задачу.

Я активно использую метод моделирования как основной прием анализа задачи, который помогает обучающимся увидеть задачу в целом и не только понять ее, но и самому найти правильное решение.

При решении текстовых задач действия должны пройти через 3 этапа:

1. Целенаправленно отрабатывается в операциях с объемным предметам или их заменителями;

2. Проговаривается, сначала громко, затем про себя;

3. Переход в умственные действия.

Использую следующие графические схемы.

Задача №1

Дети посадили у школы 6 лип и 4 березы. Сколько всего деревьев посадили дети у школы?

Задача №2

В нашем доме 9 этажей, Это на 4 этажа больше, чем в соседнем. Сколько этажей в соседнем доме?

Задания на выбор модели данной задаче (или наоборот) помогают ученику понять структуру задачи. Как правило, если обучающиеся справляются с данным заданием, то у них не возникает проблем в решении текстовых задач.

Например, я предлагаю выбрать модель к задаче №3 «На ветке сидело несколько птиц. После того как 5 птиц улетели, их осталось 9. Сколько птиц сидело на ветке?»