Как составить график для окружности

Уравнение с двумя переменными и его график. Уравнение окружности

п.1. Понятие уравнения с двумя переменными

Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, (mathrm) – гипербола.

Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.

Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm<frac1x>) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график – ниже).

п.2. Обобщенные правила преобразования графика уравнения

Пусть F(x; y) = 0 – исходный график некоторой функции

Симметричное отображение относительно оси OY

Симметричное отображение относительно оси OX

Центральная симметрия относительно начала координат

Параллельный перенос графика на a единиц вправо

Параллельный перенос графика на a единиц влево

Параллельный перенос графика на b единиц вниз

Параллельный перенос графика на b единиц вверх

Сжатие графика к оси OY в a раз

Сжатие графика к оси OX в b раз

F(x; by) = 0
0 Например:

Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ mathrm <(x-2)^2+(y-1)^2=9>$$

п.4. Примеры

Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm<7>=-frac<2> + 2 > ) – это прямая

б) xy + 4 = 0
Выразим y из уравнения: ( mathrm> ) – это гипербола

в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm=2> )

г) x 2 + 5y – 2 = 0
Выразим y из уравнения: ( mathrm<5>> ) – это парабола

Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm<5>=-frac25|x|+2> )
Строим график для ( mathrm ), а затем отражаем его относительно оси OY в левую полуплоскость.

б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.

в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.

г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).

д) (mathrm<frac<|x-1|><2>+2|y-2|=4>)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.

Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.

Как построить окружность?

Как построить окружность?

Окружностью называется фигура которая состоит из всех точек плоскости равноудаленных от данной точки. Эта точка называется центром окружности.

Радиусом называется любой отрезок соединяющей точку окружности с ее центром.

Чтобы построить окружность необходимо знать уравнение окружности:

(х – а) 2 + (у – b) 2 = R 2

Точка С(а;b) центр окружности, радиус R, х и у – координаты произвольной точки окружности.

И так, чтобы построить окружность необходимо знать цент окружности и радиус. Рассмотрим пример:

Пример №1:
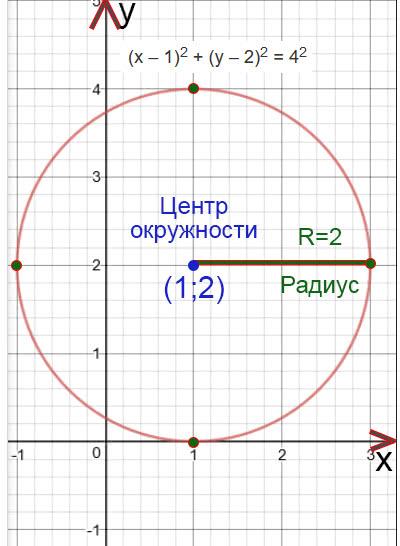
(х – 1) 2 + (у – 2) 2 = 4 2

Найдем центр окружности:
х – 1=0
x=1

Центр окружности будет находится в точке (1;2)

Найдем радиус окружности:
R 2 =4
R 2 =2 2
R=2

Построим окружность. Отметим сначала центр окружности, а потом отложим с четырех сторон (вверх, вниз, влево и право) длину радиуса и отметим эту длину точками. Потом проведем окружность.

Пример №2:
х 2 + (у + 1) 2 =1

Можно представить уравнение окружности ввиде:
(х-0) 2 + (у + 1) 2 =1 2

Найдем центр окружности:
х=0

Центр окружности будет находится в точке (0;–1)

Найдем радиус окружности:
R 2 =1
R 2 =1 2
R=1

Построим окружность.

Подписывайтесь на канал на YOUTUBE и смотрите видео, подготавливайтесь к экзаменам по математике и геометрии с нами.

Построение графиков функций

О чем эта статья:

11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие функции

Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.

Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:

• Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
• Графический способ — наглядно.
• Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
• Словесный способ.

Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.

Например, для функции вида область определения выглядит так

• х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.

Область значений — множество у, то есть это значения, которые может принимать функция.

Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.

Понятие графика функции

Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.

График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.

Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.

Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.

В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.

Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).

Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:

Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.

Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.

Исследование функции

Важные точки графика функции y = f(x):

• стационарные и критические точки;
• точки экстремума;
• нули функции;
• точки разрыва функции.

Стационарные точки — точки, в которых производная функции f(x) равна нулю.

Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.

Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Нули функции — это значения аргумента, при которых функция равна нулю.

Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.

Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:

Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.

Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.

Схема построения графика функции:

1. Найти область определения функции.
2. Найти область допустимых значений функции.
3. Проверить не является ли функция четной или нечетной.
4. Проверить не является ли функция периодической.
5. Найти нули функции.
6. Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
7. Найти асимптоты графика функции.
8. Найти производную функции.
9. Найти критические точки в промежутках возрастания и убывания функции.
10. На основании проведенного исследования построить график функции.

У нас есть отличные курсы по математике для учеников с 1 по 11 классы!

Построение графика функции

Чтобы понять, как строить графики функций, потренируемся на примерах.

Задача 1. Построим график функции

Упростим формулу функции:

при х ≠ -1.

График функции — прямая y = x – 1 с выколотой точкой M (-1; -2).

Задача 2. Построим график функции

Выделим в формуле функции целую часть:

График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции

Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.

Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.

Вспомним, как параметры a, b и c определяют положение параболы.

Ветви вниз, следовательно, a 0.

Точка пересечения с осью Oy — c = 0.

Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.

Ветви вниз, следовательно, a 0.

Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b

Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.

k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.

k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.

k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.

Задача 5. Построить график функции

Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.

Нули функции: 3, 2, 6.

Промежутки знакопостоянства функции определим с помощью метода интервалов.

Вертикальные асимптоты: x = 0, x = 4.

Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.

Вот так выглядит график:

Задача 6. Построить графики функций:

б)

г)

д)

Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.

а)

Преобразование в одно действие типа f(x) + a.

Сдвигаем график вверх на 1:

б)

Преобразование в одно действие типа f(x – a).

Сдвигаем график вправо на 1:

В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x – a), затем сложение f(x) + a.

Сдвигаем график вправо на 1:

Сдвигаем график вверх на 2:

г)

Преобразование в одно действие типа

Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:

д)

Мы видим три преобразования вида f(ax), f (x + a), -f(x).

Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.

Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

[spoiler title=”источники:”]

http://tutomath.ru/uroki/kak-postroit-okruzhnost.html

http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij

[/spoiler]

п.1. Понятие уравнения с двумя переменными

Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x² + 2x – 1 – парабола, (mathrm{y=frac1x}) – гипербола.

Если записать такое выражение: x²(x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.

Все записанные выражения являются уравнениями с двумя переменными.
В общем случае их принято записывать в виде F(x; y) = 0.

Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x² + 2x – y – 1 = 0 – парабола
F(x; y) = (mathrm{frac1x}) – y = 0 – гипербола
F(x; y)=x²(x + y) + y – 1 = 0 – некоторая кривая (график – ниже).

п.2. Обобщенные правила преобразования графика уравнения

Пусть F(x; y) = 0 – исходный график некоторой функции

п.3. Уравнение окружности

Окружность с центром в точке O($x_0, y_0$) и радиусом R в прямоугольной системе координат задаётся уравнением: $$ mathrm{(x-x_0)^2+(y-y_0)^2=R^2} $$

Например:

п.4. Примеры

Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: ( mathrm{y=frac{-2x+14}{7}=-frac{2}{x} + 2 } ) – это прямая

б) xy + 4 = 0
Выразим y из уравнения: ( mathrm{y=frac{-4}{x}} ) – это гипербола

в) ( x+ 2)² + y² = 4
Это – уравнение окружности с центром O(–2; 0), радиусом ( mathrm{R=sqrt{4}=2} )

г) x² + 5y – 2 = 0
Выразим y из уравнения: ( mathrm{y=frac{-x^2+2}{5}} ) – это парабола

Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
( mathrm{y=frac{-2|x|+10}{5}=-frac25|x|+2} )
Строим график для ( mathrm{xgt 0: y=-frac25 x+2} ), а затем отражаем его относительно оси OY в левую полуплоскость.

б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.

в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.

г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).

д) (mathrm{frac{|x-1|}{2}+2|y-2|=4})
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.

Пример 3. Постройте график уравнения:
а) x² + y² + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x² + 4x + 4) + (y² – 6y + 9) – 9 = 0
(x + 2)² + (y – 3)² = 3² – уравнение окружности с центром (–2; 3), радиусом 3.

б) (mathrm{x^2+y^2-x+8y+15frac14=0})
Выделим полные квадраты:
(mathrm{left(x^2-x+frac14right)+(y^2+8y+16)-1=0})
(mathrm{left(x-frac12right)^2+(y+4)^2=1}) – уравнение окружности с центром (mathrm{left(frac12; -4right)}), радиусом 1

На этой странице вы узнаете

• Как найти углы у апельсина?
• Кто сказал “Ты как хочешь, а я уехала!” 

Люди пользуются тригонометрией с древнейших времен. Добывая еду с помощью лука и стрел, человек уже применял знания, которые мы разберем в этой статье.

Единичная тригонометрическая окружность

Единичная тригонометрическая окружность — это окружность с центром в точке (0; 0) на координатной плоскости, радиус которой равен 1

Так как длина всей окружности равна 2π, сделаем вывод, что половина окружности — это π, а четверть — это  π2.

Теперь разделим окружность сначала на восемь частей, а потом ту же окружность на двенадцать частей. Рассчитаем значения полученных точек. 

Заметим, что точка 0 совпадает с точкой 2π. Это означает, что мы сделали один оборот по окружности. Но мы можем продолжать идти так и дальше: тогда эта же точка будет принимать значения 4π, 6π, 8π. 

Движение по тригонометрической окружности можно сравнить с движением по числовой прямой, закрученной в спираль. 

Аналогично можно двигаться и против движения часовой стрелки, но это уже будет отрицательная спираль.

Как записать множество точек, находящихся в одной точке окружности, но на разных витках спирали?

Так как тригонометрические функции — это периодические функции, то и значения в точках будут повторяться с определенным интервалом: то есть с интервалом 2πk, где k принадлежит множеству целых чисел.

Пример:  π + 2πk, k ∈ Z

Теперь рассмотрим значения синусов и косинусов, определенных на окружности точек.

На положительных частях осей они представлены как (frac{1}{2}), (frac{sqrt{2}}{2}), (frac{sqrt{3}}{2}), а на отрицательных —  (-frac{1}{2}), (-frac{sqrt{2}}{2}), (-frac{sqrt{3}}{2}).

Для нахождения значения синуса или косинуса известного угла нужно провести перпендикулярную прямую к прямой, предназначенной этой функции. Значение, в котором она пересечет прямую функции будет являться значением этой тригонометрической функции от известного числа.

Пример:
Нужно узнать чему равно (sin frac{pi}{3})

Сначала найдем (frac{pi}{3}) на окружности, затем проведем перпендикулярную прямую к прямой синусов. Ответом является  значение в точки пересечения.

(sin frac{pi}{3} = frac{sqrt{3}}{2})

Теперь проведём ещё две прямые для обозначения прямых тангенса и котангенса. Отметим на них значения для точек окружности.

Для нахождения значения тангенса или котангенса известного угла нужно провести прямую через точку (0; 0) и это число на окружности. Значение, в котором она пересечет прямую данной функции, будет являться значением этой тригонометрической функции от известного числа.

Пример: 

Нужно узнать чему равно (ctg frac{2 pi}{3})

Сначала найдем (frac{2 pi}{3}) на окружности, затем проведём прямую через (0; 0) и эту точку на окружности. Ответом является  значение в точки пересечения проведенной прямой и прямой котангенсов. 

(ctg frac{2 pi}{3} = -frac{sqrt{3}}{3})

Примеры тригонометрии можно найти и в жизни. Например: когда мы режем морковку, нож находится под углом (frac{pi}{2}) к поверхности доски.

Графики тригонометрических функций

Как уже было сказано ранее, тригонометрические функции — это периодические функции. 

То есть, значения этих функций повторяются через определенный период. Теперь рассмотрим подробнее графики таких функций. 

Находя значения у для разных значений х и соединяя точки, можно получить следующие графики функций.

График y = sin x — синусоида.

График y = cos x — косинусоида.

График y = tgx — тангенсоида.

Важно: тангенсоида никогда не может принимать значения (frac{pi}{2}); (frac{3 pi}{2}); (frac{5 pi}{2}) и т. д. Так как тангенс — это синус делить на косинус, а делить на ноль нельзя, следовательно, косинус не равен нулю. Данные значения отмечены на графике пунктирными линиями.

График y = ctgx — котангенсоида.

Важно: котангенсоида никогда не может принимать значения 0; π; 2π и т. д., так как котангенс — это косинус делить на синус. Делить на ноль нельзя, значит синус не равен нулю.  Данные значения отмечены на графике пунктирными линиями.

Каждую из рассмотренных выше функций можно сдвигать по осям Х и Y и растягивать по оси Y. Давайте рассмотрим такие растяжения и сдвиги.

Коэффициент перед тригонометрической функцией

Чем больше коэффициент перед тригонометрической функцией, тем сильнее она вытягивается по вертикали. 

Рассмотрим на примере синусоиды и тангенсоиды. Косинусоида и котангенсоида растягиваются по аналогии.

Сдвиг по оси Y

График тригонометрической функции сдвигается по оси Y на прибавленную к значению y константу. 

Рассмотрим на примере синусоиды и тангенсоиды. Косинусоида и котангенсоида сдвигаются по аналогии.

Сдвиг по оси Х

График тригонометрической функции сдвигается по оси Х на прибавленную к значению х константу. 

Рассмотрим на примере синусоиды и тангенсоиды. Косинусоида и котангенсоида сдвигаются по аналогии.

Важно: при прибавлении положительной константы — сдвиг влево, при вычитании положительной константы — сдвиг вправо.

Фактчек

• Единичная тригонометрическая окружность — это окружность с центром в точке (0; 0) на координатной плоскости, радиус которой равен 1.
• Один проход по окружности — это 2π.
• Двигаться по окружности можно как в положительную, так и в отрицательную сторону.
• График функции — это представление функции на координатной плоскости.
• Коэффициент перед функцией отвечает за растяжение графика функции вдоль оси Y.
• Константа, прибавляемая к х или y, отвечает за сдвиг функции относительно изначального значения.

Проверь себя

Задание 1.
Чему равно (sin frac{5 pi}{4})?

1. (frac{sqrt{3}}{2})
2. (frac{sqrt{2}}{2})
3. (-frac{sqrt{2}}{2})
4. 1

Задание 2.
Чему равно (cos frac{pi}{3})?

1. 1
2. (frac{1}{2})
3. (-frac{1}{2})
4. (frac{sqrt{3}}{2})

Задание 3.
Чему равно (ctg frac{pi}{2})?

1. 0
2. 1
3. (sqrt{3})
4. (frac{sqrt{2}}{2})

Задание 4.
Куда будет сдвиг (sin(x + frac{4 pi}{3}))?

1. Вправо
2. Влево
3. Вверх
4. Вниз

Задание 5.
Куда будет сдвиг ctg x + 2?

1. Вправо
2. Влево
3. Вниз
4. Вверх

Ответы: 1. — 3; 2. — 2; 3. — 1; 4. — 2; 5. — 4.

Каждое уравнение с
двумя переменными  х  и  у  определяет некоторое множество пар  (х; у)  значений
переменных, которые являются решениями этого уравнения, т. е. задаёт некоторое
отношение между значениями переменной  х  и значениями
переменной  у. График отношения, заданного уравнением с двумя
переменными, или, короче, график уравнения с двумя переменными, есть, как
известно, множество точек плоскости, координаты которых служат решениями
уравнения. Мы знаем, что графиком уравнения вида  ax + by = c,
где  a ≠ 0  или  b ≠ 0,
служит прямая линия, график уравнения вида  

y = ax² +
bx + c (a ≠ 0)   

парабола, график
уравнения вида  

xy = k

гипербола.

На рисунку
изображён график уравнения 

х² + 9у²
= 81.

Кривая такого вида
называется эллипсом.

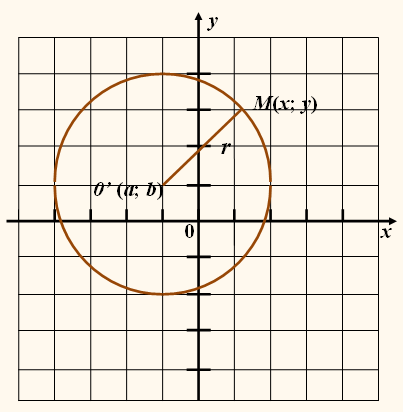
Графиком уравнения

(x – a)² +
(y – b)² =
r²

является окружность на координатной плоскости  хОу  с центром в точке  О’(a; b)  и радиусом 
r (r
> 0).

Уравнением фигуры
на плоскости  в декартовых координатах
называется уравнение с двумя переменными 
х  и  у, которые будут координатами любой точки фигуры. И наоборот:
любые два числа, которые будут решением этого уравнения, будут координатами некоторой
точки фигуры.

Составим уравнение окружности
с центром в точке  А₀(а; b)  и радиусом  R.

Возьмём произвольную
точку  А(х; у)  на окружности. Расстояние от неё до
центра  А₀  равно  R. Квадрат расстояния от точки  А  до  А₀  равен:

(х – a)²
+ (у – b)².

Таким образом, координаты  х, у  каждой точки  А  окружности будут корнями уравнения:

(х – a)²
+ (у – b)² = R².

Наоборот: любая
точка  А, координаты которой будут решениями уравнения, принадлежат окружности, так как расстояние
от неё до точки  А₀  равно  R. Отсюда вытекает, что это уравнение будет уравнением окружности
с центром  А₀  и радиусом 
R.

Обратите внимание, что
когда центром окружности будет начало координат, то уравнение окружности имеет
вид:

х² + у² = R².

ПРИМЕР:

Какая геометрическая фигура задано уравнением ?

х² + у²
+ ах + bу + с = 0.

РЕШЕНИЕ:

видим, что искомая фигура – окружность с центром

ПРИМЕР:

Построить график уравнения:

х² + у²
= 16.

Перепишем уравнение в виде

(х – 0)² + (у – 0)² = 4².

Графиком этого уравнения является окружность с центром в
точке  О(0;
0)  и
радиусом  4.

ПРИМЕР:

Построить график уравнения:

(х – 1)² + (у – 2)² = 9.

Перепишем уравнение в виде

(х – 1)² + (у – 2)² = 3².

Графиком этого уравнения является окружность с центром в
точке  (1;
2)  и
радиусом  3.

ПРИМЕР:

Построить график уравнения:

х² + у²
+ 4х = 0.

Перепишем уравнение в виде

х² +
4х + 4 + у² = 4,

(х + 2)² + у²
= 4,

(х – (–2))² + (у – 0)² = 2²,

Графиком этого уравнения является окружность с центром в
точке  (–2;
0)  и
радиусом  2.

От графиков функций
необходимо отличать графики уравнений.

ПРИМЕР:

На координатной плоскости изображена окружность радиусом  r = 5  с центром в начале координат. Уравнение этой окружности:

х² + у²
= 25.

Можно сказать и так: графиком уравнения 

х² + у²
= 25 

будет окружность, изображённая на рисунку.

А можно график уравнения 

х² + у²
= 25 

считать графиком некоторой функции ? Нет. Если переменные  х  и  у  связаны соотношением 

х² + у²
= 25,

то одному значению 
х = 3  соответствует два
разных значения переменной  у:  4  и  –4.
А соотношение между переменными  х  и  у  только тогда считается функцией, когда каждому
значению  х  из области определения соответствует одно
значение  у.
График уравнения только тогда будет графиком некоторой функции, если каждая
прямая, параллельная оси  у, пересекает
его не больше чем в одной точке.

ПРИМЕР:

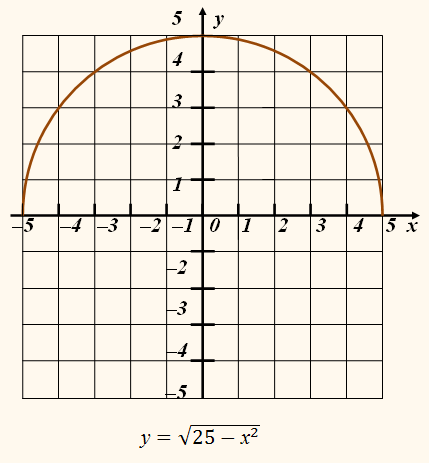
Изображённые на рисунке полуокружности – графики функций

Их объединение – вся окружность – график не функции, а уравнения  

у² = 25 – х², или 

у² +
х² = 25.

Задания к уроку 27