Построение прямой по ее уравнению
Прямая вполне определена, если известны две принадлежащие ей точки. Для того чтобы построить прямую по ее уравнению, надо, пользуясь этим уравнением, найти координаты двух ее точек. Твердо следует помнить, что если точка принадлежит прямой, то координаты этой точки удовлетворяют уравнению прямой.
При практическом построении прямой по ее уравнению наиболее точный график получится тогда, когда координаты взятых для ее построения двух точек – целые числа.
1. Если прямая определена общим уравнением Ax + By + C = 0 и 
 , то для ее построения проще всего определить точки пересечения прямой с координатными осями.
, то для ее построения проще всего определить точки пересечения прямой с координатными осями.
Укажем, как определить координаты точек пересечения прямой с координатными осями. Координаты точки пересечения прямой с осью Ox находят из следующих соображений: ординаты всех точек, расположенных на оси Ox, равны нулю. В уравнении прямой полагают, что y равно нулю, и из полученного уравнения находят x. Найденное значение x и есть абсцисса точки пересечения прямой с осью Ox. Если окажется, что x = a, то координаты точки пересечения прямой с осью Ox будут (a, 0).
Чтобы определить координаты точки пересечения прямой с осью Oy, рассуждают так: абсциссы всех точек, расположенных на оси Oy, равны нулю. Взяв в уравнении прямой x равным нулю, из полученного уравнения определяют y. Найденное значение y и будет ординатой пересечения прямой с осью Oy. Если окажется, например, что y = b, то точка пересечения прямой с осью Oy имеет координаты (0, b).
Пример. Прямая 2x + y – 6 = 0 пересекает ось Ox в точке (3, 0). Действительно, взяв в этом уравнении y = 0, получим для определения x уравнение 2x – 6 = 0, откуда x = 3.
Чтобы определить точку пересечения этой прямой с осью Oy, положим в уравнении прямой x = 0. Получим уравнение y – 6 = 0, из которого следует, что y = 6. Таким образом, прямая пересекает координатные оси в точках (3, 0) и (0, 6).
Если же в общем уравнении прямой C = 0, то прямая, определяемая этим уравнением, проходит через начало координат. Таким образом, уже известна одна ее точка, и для построения прямой остается только найти еще одну ее точку. Абсциссу x этой точки задают произвольно, а ординату y находят из уравнения прямой.
Пример. Прямая 2x – 4y = 0 проходит через начало координат. Вторую точку прямой определим, взяв, например, x = 2. Тогда для определения y получаем уравнение 2*2 – 4y = 0; 4y = 4; y = 1. Итак, прямая 2x – 4y = 0 проходит через точки (0, 0) и (2, 1).
Если прямая задана уравнением y = kx + b с угловым коэффициентом, то из этого уравнения уже известна величина отрезка b, отсекаемого прямой на оси ординат, и для построения прямой остается определить координаты еще только одной точки, принадлежащей этой прямой. Если в уравнении y = kx + b 


 , то легче всего определить координаты точки пересечения прямой с осью Ox. Выше было указано, как это сделать.
, то легче всего определить координаты точки пересечения прямой с осью Ox. Выше было указано, как это сделать.
Если же в уравнении y = kx + b b = 0, то прямая проходит через начало координат, и тем самым уже известна одна принадлежащая ей точка. Чтобы найти еще одну точку, следует дать x любое значение и определить из уравнения прямой значение y, соответствующее этому значению x.
Пример. Прямая 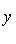

 проходит через начало координат и точку (2, 1), так как при x = 2 из ее уравнения
проходит через начало координат и точку (2, 1), так как при x = 2 из ее уравнения 



 .
.
Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение прямой, проходящей через две данные точки. Угол между двумя прямыми. Условие параллельности и перпендикулярности двух прямых. Определение точки пересечения двух прямых
1. Уравнение прямой, проходящей через данную точку A(x1, y1) в данном направлении, определяемом угловым коэффициентом k,
Это уравнение определяет пучок прямых, проходящих через точку A(x1, y1), которая называется центром пучка.
2. Уравнение прямой, проходящей через две точки: A(x1, y1) и B(x2, y2), записывается так:



 (2)
(2)
Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле
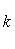


 (3)
(3)
3. Углом между прямыми A и B называется угол, на который надо повернуть первую прямую A вокруг точки пересечения этих прямых против движения часовой стрелки до совпадения ее со второй прямой B. Если две прямые заданы уравнениями с угловым коэффициентом
то угол между ними  определяется по формуле
определяется по формуле



 (5)
(5)
Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой.
Если уравнения прямой заданы в общем виде
угол между ними определяется по формуле



 (7)
(7)
4. Условия параллельности двух прямых:
а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:
б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.



 (9)
(9)
5. Условия перпендикулярности двух прямых:
а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.
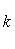
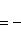

 (10)
(10)
Это условие может быть записано также в виде
б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства
6. Координаты точки пересечения двух прямых находят, решая систему уравнений (6). Прямые (6) пересекаются в том и только в том случае, когда
Как построить прямую? Как построить график прямой или линейной функции?
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ
Для начала определимся с формулой прямой или линейной функции ее записывают по-разному, но смысл от этого не меняется:y=kx+b; y=ax+b; ax+by+c=0;
a и k — называются угловыми коэффициентами, а число b – свободным членом.
Если a>0 или k>0, то график прямой возрастающий;
 y=ax+b, a>0
y=ax+b, a>0
Если a  a
a
Параллельные прямые имеют равные угловые коэффициенты и разные свободные члены b не равно с.
Пусть дано две прямые y=kx+b и y=ax+c, они будут параллельны если k=a
 Признак параллельности прямых a=k
Признак параллельности прямых a=k
Перпендикулярные прямые (это прямые которые пересекаются под 90 градусов), произведение их угловых коэффициентов будет равняться -1.
Пусть дано две прямые y=kx+b и y=ax+c, они будут перпендикулярны если k*a=-1
 Перпендикулярные прямые k*a=-1
Перпендикулярные прямые k*a=-1
b — указывает где график прямой пересекает ось y.

Алгоритм построения прямой.
Что бы построить прямую, нужно найти не менее двух то точек на графике и начертить линейную функцию.
ПРАКТИЧЕСКАЯ ЧАСТЬ
Рассмотрим на примере №1:
берем 2 точки чтобы построить график прямой
x1=0 y1=0+2=2 получили точку (0;2)
x2=1 y2=1+2=3 получили точку (1;3)
Видно что a=1 (график прямой возрастает),
b=2 (график прямой пересекает ось y в точке (0;2))
 y=ax+b, a>0
y=ax+b, a>0
Пример №2:
Среди прямых, заданных уравнениями, укажите пары параллельных прямых: 1) х+у=2; 2) у-х=2; 3) х-у=3; 4) y=1; 5) у=3; 6) 2х+2у+5=0.
Выразим во всех уравнениях y, получим
1) у=2-x; k=-1
2) у=2+x; k=1
3) у=x-3; k=1
4) y=1; k=0
5) у=3; k=0
6) у=-2,5-x; k=-1.
Ответ: Параллельные прямые 1) и 6); 2) и 3); 4) и 5), так как коэффициенты их равны.
График линейной функции, его свойства и формулы

О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х – 2. Значит:
- если х = 0, то у = -2;
- если х = 2, то у = -1;
- если х = 4, то у = 0;
- и т. д.
Для удобства результаты можно оформлять в виде таблицы:
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
- Область определения функции — множество всех действительных чисел.
- Множеством значений функции является множество всех действительных чисел.
- График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
- Функция не имеет ни наибольшего, ни наименьшего значений.
- Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит y = b — четная;
b = 0, k ≠ 0, значит y = kx — нечетная;
b ≠ 0, k ≠ 0, значит y = kx + b — функция общего вида;
b = 0, k = 0, значит y = 0 — как четная, так и нечетная функция. - Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
- График функции пересекает оси координат:
ось абсцисс ОХ — в точке (-b/k, 0);
ось ординат OY — в точке (0; b). - x=-b/k — является нулем функции.
- Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х. - Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0: функция принимает отрицательные значения на промежутке (-∞, – b /k) и положительные значения на промежутке (- b /k, +∞)
При k b /k, +∞) и положительные значения на промежутке (-∞, – b /k). - Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом.
Если k > 0, то этот угол острый, если k
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
- если k > 0, то график наклонен вправо;
- если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
- если b 1 /2x + 3, y = x + 3.
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
Теперь рассмотрим графики функций y = -2x + 3, y = – 1 /2x + 3, y = -x + 3.
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x – 2.
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
- график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
- график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
- график функции y = 2x – 2 (b = -2) пересекает ось OY в точке (0; -2).
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png” style=”height: 600px;”>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=”https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png” style=”height: 600px;”>
Точки пересечения графика функции y = kx + b с осями координат:
- С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b). - С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = – b /k.
Координаты точки пересечения с осью OX: (- b /k; 0)
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
- В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
2 = -4(-3) + b
b = -10 - Таким образом, нам надо построить график функции y = -4x – 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
- Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство. - Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
- Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
[spoiler title=”источники:”]
http://tutomath.ru/uroki/linejnoj-funkcii.html
http://skysmart.ru/articles/mathematic/grafik-linejnoj-funkcii
[/spoiler]
Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».
Важно!

Функцию вида «y = kx + b» называют линейной функцией.
Буквенные множители «k» и «b»
называют
числовыми коэффициентами.
Вместо «k» и «b»
могут стоять любые числа (положительные, отрицательные или дроби).
Другими словами, можно сказать, что «y = kx + b» — это семейство всевозможных функций, где вместо
«k» и «b» стоят числа.
Примеры функций типа «y = kx + b».
- y = 5x + 3
- y = −x + 1
- y = x − 2
- y = 0,5x
Давайте определим для каждой функций выше, чему равны числовые коэффициенты
«k» и
«b».
| Функция | Коэффициент «k» | Коэффициент «b» | ||||
|---|---|---|---|---|---|---|
| y = 5x + 3 | k = 5 | b = 3 | ||||
| y = −x + 1 | k = −1 | b = 1 | ||||
y =
x − 2 |
k =
|
b = −2 | ||||
| y = 0,5x | k = 0,5 | b = 0 |
Обратите особое внимание на функцию «y = 0,5x»
в таблице. Часто совершают ошибку при поиске в ней числового коэффициента «b».
Рассматривая
функцию «y = 0,5x», неверно утверждать, что числового коэффициента
«b» в функции нет.
Числовый коэффициент «b» присутствет в функции типа «y = kx + b» всегда.
В функции «y = 0,5x»
числовый коэффициент «b» равен нулю.
Как построить график линейной функции
«y = kx + b»
Запомните!
![]()
Графиком линейной функции «y = kx + b» является прямая.
Так как графиком функции «y = kx + b»
является прямая линия, функцию называют линейной функцией.
Из геометрии вспомним аксиому (утверждение, которое не требует доказательств),
что через любые две точки можно провести прямую и притом только одну.
Исходя из аксиомы выше следует, что
чтобы построить график функции вида
«у = kx + b» нам достаточно будет найти всего
две точки.
Для примера построим график функции «y = −2x + 1».
Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».
Важно!

Выбирая произвольные числовые значения вместо «x», лучше брать числа
«0» и «1».
С этими числами легко выполнять расчеты.
| x | Расчет «y = −2x + 1» |
|---|---|
| 0 | y(0) = −2 · 0 + 1 = 1 |
| 1 | y(1) = −2 · 1 + 1 = −2 + 1 = −1 |
Полученные значения «x» и «y» — это координаты точек графика функции.
Запишем полученные координаты точек «y = −2x + 1» в таблицу.
| Точка |
Координата по оси «Оx» (абсцисса) |
Координата по оси «Оy» (ордината) |
|---|---|---|
| (·)A | 0 | 1 |
| (·)B | 1 | −1 |
Отметим полученные точки на системе координат.
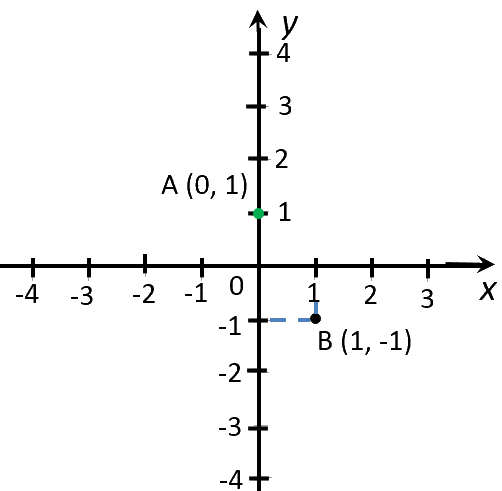
Теперь проведем прямую через отмеченные точки. Эта прямая будет
являться графиком функции «y = −2x + 1».
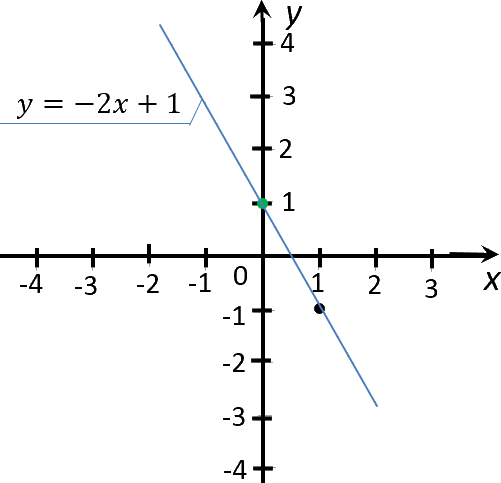
Как решать задачи на
линейную функцию «y = kx + b»
Рассмотрим задачу.
Построить график функции «y = 2x + 3». Найти по графику:
- значение «y» соответствующее значению «x» равному −1; 2; 3; 5;
- значение «x», если значение «y» равно
1; 4; 0; −1.
Вначале построим график функции «y = 2x + 3».
Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = 2x + 3» достаточно найти всего две точки.
Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».
Выполним расчеты и запишем их результаты в таблицу.
| Точка |
Координата по оси «Оx» |
Координата по оси «Оy» |
|---|---|---|
| (·)A | 0 | y(0) = 2 · 0 + 3 = 3 |
| (·)B | 1 | y(1) = 2 ·1 + 3 = 5 |
Отметим полученные точки на прямоугольной системе координат.
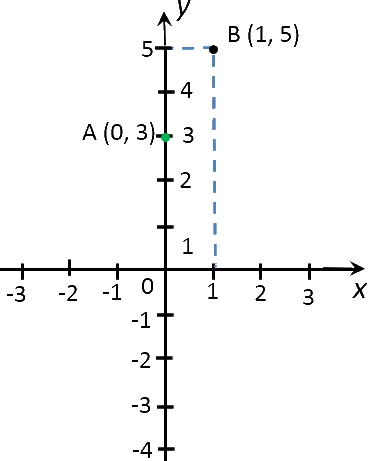
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = 2x + 3».
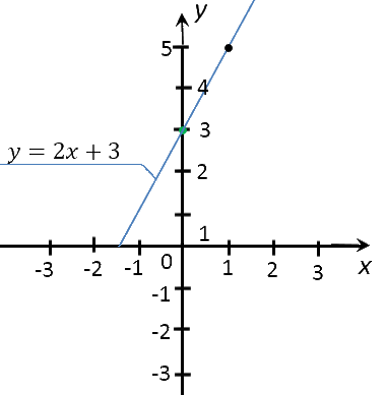
Теперь работаем с построенным графиком функции «y = 2x + 3».
Требуется найти значение «y»,
соответствующее значению «x»,
которое равно −1; 2; 3; 5.
Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».
В этому уроке для решения задачи выше вспомним только основные моменты.
Запомните!
![]()
Чтобы найти значение «y» по известному значению «x» на графике
функции необходимо:
- провести перпендикуляр от оси «Ox»
(ось абсцисс)
из заданного числового значения «x»
до пересечения
с графиком функции; - из полученной точки пересечения перпендикуляра и графика функции провести еще один перпендикуляр к оси
«Oy»
(ось ординат); - полученное числовое значение на оси «Oy» и будет искомым значением.
По правилам выше найдем на построенном ранее графике функции «y = 2x + 3»
необходимые значения функции «y» для
«x» равным −1; 2; 3; 5.
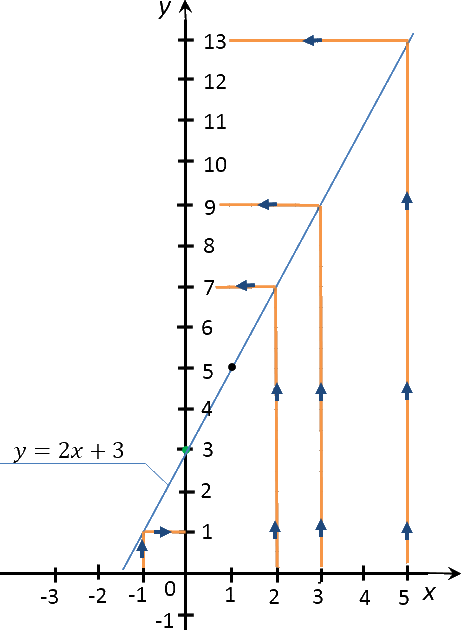
Запишем полученные результаты в таблицу.
| Заданное значение «x» | Полученное с графика значение «y» |
|---|---|
| −1 | 1 |
| 2 | 7 |
| 3 | 9 |
| 5 | 13 |
Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно 1; 4; 0; −1.
Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси
«Oy».
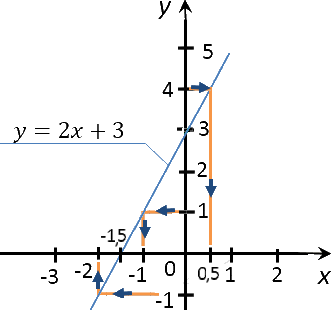
Запишем полученные результаты в таблицу.
| Заданное значение «y» | Полученное с графика значение «x» |
|---|---|
| −1 | −2 |
| 0 | −1,5 |
| 1 | −1 |
| 4 | 0,5 |
Как проверить, проходит ли график через точку
Рассмотрим другое задание.
Не выполняя построения графика функции
«y = 2x −
», выяснить, проходит ли график
через точки с координатами (0;
− ) и (1; −2).
Запомните!
![]()
Чтобы проверить принадлежность точки графику функции нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка
не принадлежит графику функции.
Подставим в функцию
«y = 2x −
»
координаты точки (0;
− ).
− = 2 · 0
−
− =
−
(верно)
Это означает, что график функции «y = 2x −
» проходит через точку с координатами (0;
− ).
Проверим точку с координатами (1; −2).
Также подставим координаты
в функцию «y = 2x −
».
−2 = 2 · 1 −
−2 = 2 −
−2 = 1 −
−2 = 1 (неверно)
Это означает, что график функции «y = 2x −
» не проходит через точку с координатами (1; −2).
Как найти точки пересечения графика с осями
Рассмотрим задачу.
Найти координаты точек пересечения графика функции «y = −1,5x + 3» с осями координат.
Для начала построим график функции «y = −1,5x + 3» и на графике отметим точки пересечения
с осями.
Для построения графика функции найдем координаты двух точек
функции
«y = −1,5x + 3».
Выберем два произвольных числовых значения для «x» и рассчитаем значение
«y» по формуле
функции. Например, для x = 0 и
x = 1.
| Точка |
Координата по оси «Оx» |
Координата по оси «Оy» |
|---|---|---|
| (·)A | 0 | y(0) = −1,5 · 0 + 3 = 3 |
| (·)B | 1 | y(1) = −1,5 · 1 + 3 = 1,5 |
Отметим полученные точки на системе координат и проведем через них прямую.
Тем самым мы построим график функции «y = −1,5x + 3».
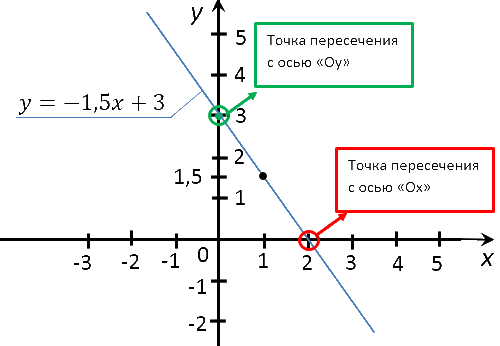
Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.
Запомните!
![]()
Чтобы найти координаты точки пересечения графика функции
с осью
«Oy»
(осью ординат)
нужно:
- приравнять координату точки по оси
«Ox» к нулю
(x = 0); - подставить вместо «x» в формулу функции ноль и найти значение
«y»; - записать полученные координаты точки пересечения с осью
«Oy».
Подставим вместо «x» в формулу функции «y = −1,5x + 3» число ноль.
y(0) = −1,5 · 0 + 3 = 3
(0; 3) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Oy».
Запомните!
![]()
Чтобы найти координаты точки пересечения графика функции
с осью
«Ox»
(осью абсцисс)
нужно:
- приравнять координату точки по оси
«Oy» к нулю
(y = 0); - подставить вместо «y» в формулу функции ноль и найти значение
«x»; - записать полученные координаты точки пересечения с осью
«Oy».
Подставим вместо «y» в формулу функции «y = −1,5x + 3» число ноль.
0 = −1,5x + 3
1,5x = 3 | :(1,5)
x = 3 : 1,5
x = 2
(2; 0) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Ox».
Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните
«правило противоположности».
Важно!

Если нужно найти координаты точки пересечения графика с осью
«Ox», то приравниваем
«y» к нулю.
И наооборот. Если нужно найти координаты точки пересечениа графика с осью
«Oy»,
то приравниваем «x» к нулю.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
19 мая 2023 в 9:06
Михаил Лысенко

Профиль
Благодарили: 0
Сообщений: 1

Михаил Лысенко
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
19 мая 2023 в 13:04
Ответ для Михаил Лысенко
Борис Гуров

Профиль
Благодарили: 1
Сообщений: 28

Борис Гуров
Профиль
Благодарили: 1
Сообщений: 28
Добрый день!
Это квадратичная функция. Они разобраны в другом уроке
0
Спасибо
Ответить
построить график линейной функции:
a)
y=13x+1,x∈−6;3
; b)
y=13x+1,x∈−6;3
.
Составим таблицу значений функции:
| (x) | (-6) | (3) |
| (y) | (-1) | (2) |
Построим на координатной плоскости (xOy) точки ((-6;-1)) и ((3;2)) и
проведём через них прямую.
Далее выделим отрезок, соединяющий построенные точки.
Этот отрезок и есть график линейной функции
y=13x+1,x∈−6;3
.
Точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены тёмными кружочками.

b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)).
Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.

По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.
В случае
a)
y=13x+1,x∈−6;3
, имеем:
yнаиб
(= 2) и
yнаим
(= -1);
b)
y=13x+1,x∈−6;3
, концы отрезка не рассматриваются, поэтому наибольшего и наименьшего значений нет.
Как для графика составить уравнение
Глядя на график прямой, можно без особых сложностей составить ее уравнение. При этом вам могут быть известны две точки, либо нет – в таком случае начинать решение нужно с поиска двух точек, принадлежащих прямой.

Инструкция
Чтобы найти координаты точки, принадлежащей прямой, выберите ее на линии и опустите перпендикулярные линии на оси координат. Определите, какому числу соответствует точка пересечения, пересечение с осью ох – это значение абсциссы, то есть х1, пересечение с осью оу – это ордината, у1.
Постарайтесь выбрать точку, координаты которой можно определить без дробных значений, для удобства и точности расчетов. Для построения уравнения вам нужно как минимум две точки. Найдите координаты еще одной точки, принадлежащей данной прямой (х2, у2).
Подставьте значения координат в уравнение прямой, имеющей общий вид у=kx+b. У вас получится система из двух уравнений у1=kx1+b и y2=kx2+b. Решите эту систему, например, следующим способом.
Выразите b из первого уравнения и подставьте во второе, найдите k, подставьте в любое уравнение и найдите b. Например, решение системы 1=2k+b и 3=5k+b будет выглядеть так: b=1-2k, 3=5k+(1-2k); 3k=2, k=1.5, b=1-2*1,5=-2. Таким образом, уравнение прямой имеет вид y=1,5х-2.
Зная две точки, принадлежащие прямой, попробуйте воспользоваться каноническим уравнением прямой, оно выглядит таким образом: (х – х1)/(х2 – х1)=(у – у1)/(у2 – у1). Подставьте значения (х1;у1) и (х2;у2), упростите. Например, точки (2;3) и (-1;5) принадлежат прямой (х-2)/(-1-2)=(у-3)/(5-3); -3(х-2)=2(у-3); -3х+6=2у-6; 2у=12-3х или у=6-1,5х.
Чтобы найти уравнение функции, имеющей нелинейный график, действуйте так. Просмотрите все стандартные графики y=x^2, y=x^3, y=√x, y=sinx, y=cosx, y=tgx и т.д. Если один из них напоминает вам ваш график, возьмите его за основу.
Начертите на той же оси координат стандартный график функции-основы и найдите его отличия от своего графика. Если график перенесен на несколько единиц вверх или вниз – значит к функции добавлено это число (например, у=sinx+4). Если график перенесен вправо или влево, значит, число добавлено к аргументу (например, у=sin (х+П/2).
Вытянутый график в высоту график говорит о том, что функция аргумента умножена на какое-то число (например, у=2sinx). Если график, напротив, уменьшен в высоту, значит, число перед функцией меньше 1.
Сравните график функции-основы и вашей функции по ширине. Если он более узкий, значит перед х стоит число больше 1, широкий – число меньше 1 (например, у=sin0.5х).
Подставляя в получившееся уравнение функции разные значения х, проверяйте, правильно ли находится значение функции. Если все верно – вы подбрали уравнение функции по графику.
Обратите внимание
Возможно, график соответствует найденному уравнению лишь на определенном отрезке. В таком случае укажите, для каких значений х выполняется полученное равенство.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Вспомним, что такое график функции:
Графиком функции называется множество точек плоскости, абсциссы которых равны значениям аргумента $x$, а ординаты – соответствующим значениям функции $y$.
Как мы уже выяснили, график линейной функции представляет из себя прямую линию.
Построение графиков
Для его построения нет необходимости находить координаты более двух точек. То есть, чтобы построить график линейной функции, достаточно подставить в заданную формулу всего два значения $x$
Значит, нужно:
- Подставить в функцию 2 любых значения $x$ и получить соответствующие значения $y$.
- Мы получили координаты 2 точек. Отметим их на координатной плоскости.
- Проведём через эти 2 точки прямую линию.
Построим график функции $y=2x+1$
Для удобства состоим таблицу значений $x$ и $y$.
| Переменная | Значение 1 | Значение 2 |
|---|---|---|
| $x$ | ||
| $y$ |
Какие $x$ взять? Удобно брать небольшие числа, например $0$ и $1$
| Переменная | Значение 1 | Значение 2 |
|---|---|---|
| $x$ | $color{#3D68EB}0$ | $color{#ED7858}1$ |
| $y$ |
Теперь нужно посчитать $y$. Подставляем по очереди 2 значения $x$ в нашу функцию:
$x=color{#3D68EB}0$
$y=2x+1$
$y=2 cdot 0 + 1 = color{#253f8d}1$
$x=color{#ED7858}1$
$y=2x+1$
$y=2 cdot 1 + 1 = color{#eb3d3d}3$
Вписываем полученные значения в таблицу и отмечаем точки:
| Переменная | Значение 1 | Значение 2 |
|---|---|---|
| $x$ | $color{#3D68EB}0$ | $color{#ED7858}1$ |
| $y$ | $color{#253f8d}1$ | $color{#eb3d3d}3$ |
Проводим через эти точки прямую линию. График готов.
Доведите навык до совершенства с помощью тренажёра построения графиков линейной функции.
