- Определение прямой пропорциональности
- График прямой пропорциональности
- Примеры
Определение прямой пропорциональности
Если машина движется со скоростью 50 км/ч, пройденное расстояние (в километрах) в зависимости от времени (в часах) s = 50t. Время мы определяем как $tgeq0$. Но механика позволяет нам рассчитать не только будущее положение тела, но и прошлое, подставив в формулу $t lt 0$ и запросто «прокрутив» время назад. Поэтому в общем случае, если движение было и остаётся постоянным, мы получаем:
$${left{ begin{array}{c} – infty lt tlt + infty \ s = 50t end{array} right.}$$
Можно представить себе не только отрицательное время («поход в прошлое»). Ещё проще ввести отрицательные координаты: направо идём – координата растёт, становится положительной, поворачиваем налево – уменьшается, становится отрицательной.
В задачах, связанных с экономикой, величины также могут уходить в «плюс» и «минус»: покупки/продажи, кредиты/депозиты, доходы/затраты, прибыли/убытки . Часто эти величины изменяются на какую-то постоянную сумму с течением времени.
Если обобщить формулы, описывающие подобные зависимости, то получаем:
$${left{ begin{array}{c}- infty lt x lt + infty – аргумент, quad любое quad действительное quad число \ k = const ≠ 0 quad – параметр, quad константа \ y = kx quad – функцияend{array} right.}$$
Функция такого вида называется прямой пропорциональностью.
Если $k gt 0$, то чем больше x, тем больше y – функция возрастает.
Если $k lt 0$, то чем больше x, тем больше y – функция убывает.
График прямой пропорциональности
Графиком прямой пропорциональности является прямая, проходящая через начало координат.
Согласно аксиоме планиметрии, через любые две точки можно провести прямую и притом только одну. Значит, положение прямой на плоскости полностью определяется двумя точками . Получаем:
Алгоритм построения графика прямой пропорциональности
- Выбрать произвольное значение аргумента $x_*neq 0$
- Вычислить соответствующее значение функции $y_*=kx_*$
- Отметить на координатной плоскости точку $(x_*,y_* )$
- Провести прямую через начало координат (0;0) и точку $(x_*,y_* )$
Эта прямая – график прямой пропорциональности y=kx.
Например: построим график функции y = 2x

Примеры
Пример 1. Постройте графики прямых пропорциональностей.
Укажите, возрастает или убывает функция.

$k = 1 gt 0$ – функция возрастает

$k = 3 gt 0$ – функция возрастает

$k = frac{1}{3} gt 0$ – функция возрастает

$k = -1 lt 0$ – функция убывает

$k = -2 lt 0$ – функция убывает

$k = -frac{1}{2} lt 0$ – функция убывает
Пример 2. Известно, что график прямой пропорциональности проходит через точку A(5;22). Проходит ли этот график через точки B(7;32,4)и C(9;39,6)?
Точка A определяет коэффициент пропорциональности:
$$ k= frac{y_A}{x_A} = frac{22}{5} = 4,4 $$
При $x = 7:y = 4,4 cdot 7 = 30,8 neq 32,4 Rightarrow$ B не принадлежит графику.
При $x = 9:y = 4,4 cdot 9 = 39,6 Rightarrow C$ принадлежит графику.
Пример 3. Является ли прямой пропорциональностью функция, проходящая через точки:
а) A(1,5;2,75) и B(12;22)

Найдём коэффициенты пропорциональностей для каждой из точек:
$$ k_A = frac{y_A}{x_A} = frac{2,75}{1,5} stackrel{text{ × 4}}{=} frac{11}{6} = frac{15}{6} $$
$$ k_B = frac{y_B}{x_B} = frac{22}{12} = frac{11}{6} = frac{15}{6} $$
$k_A = k_B Rightarrow$ прямая AB $y=1 frac{5}{6} x$ является прямой пропорциональностью.
б) A(3;4,5) и B(5;8)

Найдём коэффициенты пропорциональностей для каждой из точек:
$$ k_A = frac{y_A}{x_A} = frac{2,75}{1,5} = frac{4,5}{3} = 1,5 $$
$$ k_B = frac{y_B}{x_B} = frac{8}{5} = 1,6 $$
$k_A neq k_B Rightarrow$ прямая AB не является прямой пропорциональностью.
Вопросы
занятия:
·
ввести понятие «прямая пропорциональность»;
·
привести примеры, когда прямая пропорциональность встречается в повседневной
жизни;
·
построить график прямой пропорциональности;
·
определить от чего зависит расположение графика в координатной плоскости.
Материал
урока
Давайте
рассмотрим пример.
Пример.
Обратите
внимание, что если переменную t увеличить,
например, в 2 раза, то и переменная H
также
увеличится в 2 раза. То есть:
Также
заметим, что зависимость высоты растения от времени его роста мы задали
формулой вида:
В
рассматриваемом примере: k = 2,5, а переменная t является независимой.
Сформулируем
определение.
Определение.
С
прямой пропорциональностью мы с вами часто встречаемся в повседневной жизни.
Например,
Или,
Теперь
давайте построим график прямой пропорциональности:
Видим,
что все точки лежат на одной прямой, которая проходит через начало координат.
Для убедительности можем даже приложить линейку.
Таким
образом, можем сформулировать определение.
Определение.
Графиком
прямой пропорциональности y = kx является прямая,
проходящая через начало координат.
Нам
известно, что прямая определяется двумя точками. А
значит, для построения графика функции y
= kx достаточно
указать любую точку графика этой функции, которая отличается от точки с координатами:
(0, 0), то есть от начала координат.
Например,
А
теперь посмотрите на рисунок, на котором изображены графики прямой
пропорциональности.
Обратите
внимание, что графики тех функций, которые имеют
положительный коэффициент k расположены в первой и третьей координатных
четвертях, а которые имеют отрицательный коэффициент k
–
во второй и четвёртой четвертях. То есть расположение графика функции y = kx в координатной плоскости зависит от коэффициента
k.
Прямая пропорциональность и её график
Александр Мельник
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение прямой пропорциональности
Для начала напомним следующее определение:
Определение
Две величины называются прямо пропорциональными, если их отношение равно конкретному, отличному от нуля числу, то есть:
[frac{y}{x}=k]
Отсюда мы видим, что $y=kx$.
Определение
Функция вида $y=kx$ называется прямой пропорциональностью.
Прямая пропорциональность является частным случаем линейной функции $y=kx+b$ при $b=0$. Число $k$ называется коэффициентом пропорциональности.
Примером прямой пропорциональности может служить второй закон Ньютона: Ускорение тела прямо пропорционально приложенной к нему силе:
[F=ma]
Здесь масса — коэффициент пропорциональности.
Исследование функции прямой пропорциональности $f(x)=kx$ и её график
Вначале рассмотрим функцию $fleft(xright)=kx$, где $k > 0$.
- Область определения — все числа.
- Область значения — все числа.
- $fleft(-xright)=-kx=-f(x)$. Функция прямой пропорциональности нечетна.
- Функция проходит через начало координат.
- $f’left(xright)={left(kxright)}’=k>0$. Следовательно, данная функция возрастает на всей области определения. Точек экстремума нет.
- $f^{”}left(xright)=k’=0$. Следовательно, функция не имеет точек перегиба.
- ${mathop{lim}_{xto -infty } kx }=-infty $, ${mathop{lim}_{xto +infty } kx }=+infty $
- График (рис. 1).
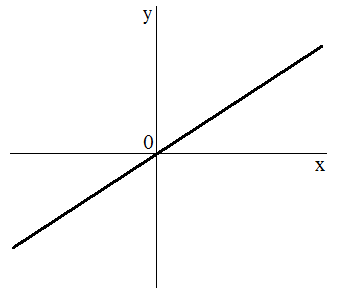
Рис. 1. График функции $y=kx$, при $k>0$
Теперь рассмотрим функцию $fleft(xright)=kx$, где $k
- Область определения — все числа.
- Область значения — все числа.
- $fleft(-xright)=-kx=-f(x)$. Функция прямой пропорциональности нечетна.
- Функция проходит через начало координат.
- $f’left(xright)={left(kxright)}’=k
- $f^{”}left(xright)=k’=0$. Следовательно, функция не имеет точек перегиба.
- ${mathop{lim}_{xto -infty } kx }=+infty $, ${mathop{lim}_{xto +infty } kx }=-infty $
- График (рис. 2).
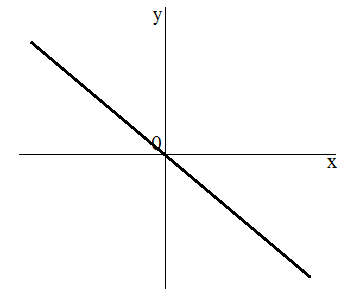
Рис. 2. График функции $y=kx$, при $k
Важно: для построения графика функции $y=kx$ достаточно найти одну, отличную от начала координат точку $left(x_0, y_0right)$ и провести прямую через эту точку и начало координат.
Задачи на построение графиков функции прямой пропорциональности
Сделаем домашку
с вашим ребенком за 380 ₽
Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online
Бесплатное пробное занятие
*количество мест ограничено
Задача 1
Построить график функции $y=-x$
Найдем точку, принадлежащую данной функции. Пусть $x=1$, тогда $y=-1$. Проведем прямую через точки $left(1,-1right) и (0, 0)$. Получим
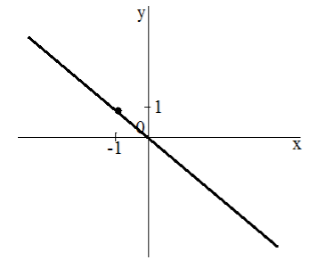
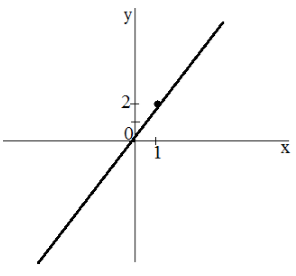
Задача 2
Построить график функции $y=2x$
Найдем точку, принадлежащую данной функции. Пусть $x=1$, тогда $y=2$. Проведем прямую через точки $left(1,2right) и (0, 0)$. Получим
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Дата последнего обновления статьи: 02.02.2023
Прямая пропорциональность — базовые понятия
Определение
Пропорциональностью в алгебре называют зависимость между парой величин, при которой изменение одной из них приводит к изменению другой во столько же раз.
Пропорциональность бывает двух видов:
- прямая;
- обратная.
Пример
Предположим, что скорость движения автомобиля составляет 50 км/ч. По определению, скоростью является расстояние, преодолеваемое за единицу времени. В данном случае транспортное средство проезжает 50 километров в течение 1 часа.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если автомобиль движется в течение еще одного часа с такой же скоростью 50 км/ч, то он преодолеет расстояние в 100 км.
Согласно примеру, увеличение времени в 2 раза сопровождается увеличением пройденного расстояния во столько же раз, то есть в 2 раза. Величины времени и расстояния будут прямо пропорциональными. Они обладают взаимосвязью, которую называют прямой пропорциональностью.
Определение
Прямая пропорциональность – это взаимосвязь между двумя величинами, при которой увеличение одной из них приводит к увеличению другой во столько же раз и, наоборот, при уменьшении одной величины в какое-то число раз, другая величина уменьшается во столько же раз.
Предположим, что вначале водитель планировал проехать 100 км за 2 часа, но после того, как он преодолел 50 км, произошла остановка. В таком случае, уменьшая расстояние в 2 раза, получим, что время уменьшится тоже в 2 раза.
Особенностью прямо пропорциональных величин является стабильность их отношений. Таким образом, во время изменения значений прямо пропорциональных величин, их отношение остается постоянным. Рассмотренная ситуация характеризуется изменением расстояния с 50 км при значении времени в 1 час. Отношение расстояния ко времени равно 50 и определяется формулой:
(frac{50}{1}=50)
После увеличения времени движения автомобиля в 2 раза, оно составит 2 часа. Таким образом, расстояние также увеличилось в 2 раза до 100 км. Отношение 100 км к 2 часам равно числу 50:
(frac{100}{2}=50)
Число 50 представляет собой коэффициент прямой пропорциональности. Эта величина демонстрирует, какое расстояние соответствует одному часу движения. В условиях рассматриваемого примера данный коэффициент является скоростью движения автомобиля, исходя из ее определения.
С помощью прямо пропорциональных характеристик можно составлять пропорции. Например, записанные ранее отношения составляют пропорционально:
(frac{50}{1}=frac{100}{2})
Представленное выражение читают таким образом: 50 км так относятся к 1 часу, как 100 км относятся к 2 часам.
Линейное уравнение относительно двух переменных x и y имеет такой вид:
ax + by + c = 0
(aneq 0)
(bneq 0)
Известно, что график записанного равенства является прямая линия, любая точка на которой имеет два числа в виде координат x и y, то есть абсциссы и ординаты. Каждая точка этой прямой соответствует заданному уравнению. Если выразить y через x, получим:
by = -ax – c
Принимая во внимание, что (bneq 0), можно поделить на него две части выражения:
(y=-frac{a}{b}x-frac{c}{b})
Сделать уравнение более удобным можно с помощью следующих обозначений:
(-frac{a}{b}=k)
(-frac{c}{b}=m)
Таким образом:
y = kx + m
Данным способом была выведена линейная функция y от x в общем виде. В этом случае были применены новые обозначения:
- x — в виде независимой переменной или аргумента;
- y — представляет собой зависимую переменную или функцию;
- k и m — являются параметрами, полностью и однозначно определяющими конкретную линейную функцию.
В том случае, когда m = 0, уравнение примет вид:
y = kx
Данная функция представляет собой прямую пропорциональность. Она определяется с помощью единственного параметра k.
Исследование функции прямой пропорциональности и ее график
Определение
Функция, которая обладает видом y = kx, где k — число (k≠0), является функцией прямой пропорциональности.
Число k представляет собой коэффициент пропорциональности. Переменная y пропорциональна переменной x. Прямая пропорциональность является частным случаем линейной функции
y = kx + m, если m=0
График прямой пропорциональности изображают в виде прямой, которая пересекает начало координат или точку O (0;0). Для того чтобы построить график прямой пропорциональности, требуется взять одну точку, вторая – будет точкой O.
Прямая пропорциональность характеризуется следующими свойствами:
- областью определения является множество действительных чисел: D(y): x∈(-∞;+∞) (или x∈R);
- областью значений является множество действительных чисел: D(y): y∈(-∞;+∞) (или y∈R);
- нуль функции (y=0) при x=0;
- если k>0, функция y = kx возрастает, а при k<0 — убывает;
Если k>0, график функции пересекает первую и третью координатные четверти. Функция будет обладать положительными значениями, если значения аргумента положительные:
y > 0 при x > 0.
Функция будет обладать отрицательными значениями, если значения аргумента отрицательные:
y < 0 при x < 0.
Если k < 0, то функция будет иметь график, проходящий через вторую и четвертую координатную четверть. Функция будет характеризоваться положительными значениями, если значения аргумента отрицательные:
y > 0 при x < 0.
Функция будет характеризоваться отрицательными значениями, если значения аргумента положительные:
y < 0 при x > 0.
Величина k представляет собой угловой коэффициент прямой y = kx. С другой стороны, k является тангенсом угла α, образованного прямой и положительным направлением оси Ох.
В качестве примера можно рассмотреть такие функции:
- y = 2x в виде прямой пропорциональности;
- y = 2x + 1 в виде линейной функции;
- y = 2x – 1 в виде линейной функции.
Можно построить график рассматриваемых функций. Каждая из них обладает коэффициентом k = 2. Для первой функции m = 0, для второй: m = 1, для третьей: m = -1. Данные величины вытекают из стандартной записи линейного уравнения:
y = kx + m
Необходимо представить данные в виде таблицы:
График примет такой вид:
Прямые, которые были построены, параллельны. Это объясняется равенством их угловых коэффициентов. Согласно теореме, если y = kx является графиком прямой пропорциональности, тогда график y = kx + m будет ему параллелен, так как коэффициентом k определяется угол наклона к оси x, и данный коэффициент y функций будет обладать равными значениями.
Примеры задач на прямую пропорциональность
Задача 1
Требуется определить соотношение между угловыми коэффициентами, согласно графику:
Решение:
(k_{1}=frac{y_{1}}{x})
(k_{2}=frac{y_{2}}{x})
x = x;
(y_{1}> y_{2})
Таким образом:
(k_{1}>k_{2})
Ответ: (k_{1}>k_{2})
Задача 2
Требуется построить график прямой пропорциональности при том, что на данном графике есть точка с координатами (2;8).
Решение:
Построить прямую можно через пару точек. Первая будет обладать координатами (0;0), исходя из того, что любой график прямой пропорциональности пересекает точку (0;0). Вторая точка дана в условии задачи (2;8).
Задачу можно решить другим способом. Согласно координатам точки (2;8), получим:
x=2 и y=8
Данные выражения подходят для уравнения вида:
y = kx
Можно подставить известные значения и определить k:
8 = 2k
k = 4
Таким образом, уравнение примет вид:
y = 4x
С помощью данного уравнения можно построить график:

