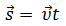Как составить график зависимости пути от времени

Если траектория движения точки известна, то зависимость пути

, пройденного точкой, от истекшего промежутка времени

 дает полное описание этого движения. Мы видели, что для равномерного движения такую зависимость можно дать в виде формулы (9.2). Связь между

 и

 для отдельных моментов времени можно задавать также в виде таблицы, содержащей соответственные значения промежутка времени и пройденного пути. Пусть нам дано, что скорость некоторого равномерного движения равна 2 м/с. Формула (9.2) имеет в этом случае вид

. Составим таблицу пути и времени такого движения:

t, с	1	2	3	4	5	6	…
s, м	2	4	6	8	10	12	…

Зависимость одной величины от другой часто бывает удобно изображать не формулами или таблицами, а графиками, которые более наглядно показывают картину изменения переменных величин и могут облегчать расчеты. Построим график зависимости пройденного пути от времени для рассматриваемого движения. Для этого возьмем две взаимно перпендикулярные прямые — оси координат; одну из них (ось абсцисс) назовем осью времени, а другую (ось ординат) — осью пути. Выберем масштабы для изображения промежутков времени и пути и примем точку пересечения осей за начальный момент и за начальную точку на траектории. Нанесем на осях значения времени и пройденного пути для рассматриваемого движения (рис. 18). Для «привязки» значений пройденного пути к моментам времени проведем из соответственных точек на осях (например, точек 3 с и 6 м) перпендикуляры к осям. Точка пересечения перпендикуляров соответствует одновременно обеим величинам: пути

 и моменту

, — этим способом и достигается «привязка». Такое же построение можно выполнить и для любых других моментов времени и соответственных путей, получая для каждой такой пары значений время — путь одну точку на графике. На рис. 18 выполнено такое построение, заменяющее обе строки таблицы одним рядом точек. Если бы такое построение было выполнено для всех моментов времени, то вместо отдельных точек получилась бы сплошная линия (также показанная на рисунке). Эта линия и называется графиком зависимости пути от времени или, короче, графиком пути.

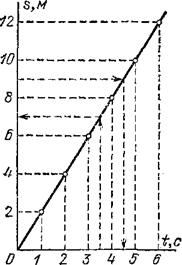
Рис. 18. График пути равномерного движения со скоростью 2 м/с

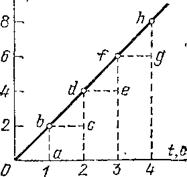
Рис. 19. К упражнению 12.1

В нашем случае график пути оказался прямой линией. Можно показать, что график пути равномерного движения всегда есть прямая линия; и обратно: если график зависимости пути от времени есть прямая линия, то движение равномерно.

Повторяя построение для другой скорости движения, найдем, что точки графика для большей скорости лежат выше, чем соответственные точки графика для меньшей скорости (рис. 20). Таким образом, чем больше скорость равномерного движения, тем круче прямолинейный график пути, т. е. тем больший угол он составляет с осью времени.

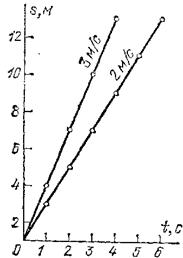
Рис. 20. Графики пути равномерных движений со скоростями 2 и 3 м/с

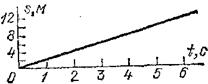
Рис. 21. График того же движения, что на рис. 18, вычерченный в другом масштабе

Наклон графика зависит, конечно, не только от числового значения скорости, но и от выбора масштабов времени и длины. Например, график, изображенный на рис. 21, дает зависимость пути от времени для того же движения, что и график рис. 18, хотя и имеет другой наклон. Отсюда ясно, что сравнивать движения по наклону графиков можно только в том случае, если они вычерчены в одном и том же масштабе.

С помощью графиков пути можно легко решать разные задачи о движении. Для примера на рис. 18 штриховыми линиями показаны построения, необходимые для того, чтобы решить следующие задачи для данного движения: а) найти путь, пройденный за время 3,5 с; б) найти время, за которое пройден путь 9 м. На рисунке графическим путем (штриховые линии) найдены ответы: а) 7 м; б) 4,5 с.

На графиках, описывающих равномерное прямолинейное движение, можно откладывать по оси ординат вместо пути

 координату

 движущейся точки. Такое описание открывает большие возможности. В частности, оно позволяет различать направление движения по отношению к оси

. Кроме того, приняв начало отсчета времени за нуль, можно показать движение точки в более ранние моменты времени, которые следует считать отрицательными.

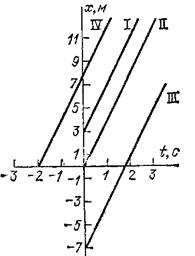
Рис. 22. Графики движений с одной и той же скоростью, но при различных начальных положениях движущейся точки

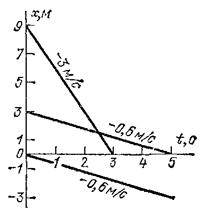
Рис. 23. Графики нескольких движений с отрицательными скоростями

Например, на рис. 22 прямая I есть график движения, происходящего с положительной скоростью 4 м/с (т. е. в направлении оси

), причем в начальный момент движущаяся точка находилась в точке с координатой

 м. Для сравнения на том же рисунке дан график движения, которое происходит с той же скоростью, но при котором в начальный момент движущаяся точка находится в точке с координатой

 (прямая II). Прямая. III соответствует случаю, когда в момент

 движущаяся точка находилась в точке с координатой

 м. Наконец, прямая IV описывает движение в случае, когда движущаяся точка имела координату

 в момент

 с.

Мы видим, что наклоны всех четырех графиков одинаковы: наклон зависит только от скорости движущейся точки, а не от ее начального положения. При изменении начального положения весь график просто переносится параллельно самому себе вдоль оси

 вверх или вниз на соответственное расстояние.

Графики движений, происходящих с отрицательными скоростями (т. е. в направлении, противоположном направлению оси

), показаны на рис. 23. Они представляют собой прямые, наклоненные вниз. Для таких движений координата

 точки с течением времени уменьшается.

12.3.
График пути для точки, движущейся со скоростью

, отсекает на оси ординат отрезок

. Как зависит от времени расстояние

 от начальной точки? Напишите формулу этой зависимости.

12.4.
Точка, движущаяся со скоростью

, в момент

 находится на расстоянии

 от начальной. Как зависит от времени расстояние

?

12.5.
Точка, двигаясь равномерно вдоль оси

, имела координаты

м и

м в моменты времени

с и

с соответственно. Найдите графически, в какой момент точка проходила через начало координат и какова была координата

 в начальный момент. Найдите проекцию скорости на ось

.

12.6.
Найдите при помощи графика пути, когда и на каком расстоянии от точки А автомашину, вышедшую из точки А, догонит вторая автомашина, вышедшая из той же точки через 20 мин после первой, если первая машина движется со скоростью 40 км/ч, а вторая — со скоростью 60 км/ч.

12.7.
Найдите при помощи графика пути, где и когда встретятся автомашины, вышедшие одновременно навстречу друг другу со скоростями 40 и 60 км/ч из пунктов А и В, лежащих на расстоянии 100 км друг от друга.

Графики пути можно строить и для случаев, в которых тело движется равномерно в течение определенного промежутка времени, затем движется равномерно, но с другой скоростью в течение другого промежутка времени, затем снова меняет скорость и т. д. Например, на рис. 26 показан график движения, в котором тело двигалось в течение первого часа со скоростью 20 км/ч, в течение второго часа — со скоростью 40 км/ч и в течение третьего часа — со скоростью 15 км/ч.

12.8.
Постройте график пути для движения, в котором за последовательные часовые промежутки тело имело скорости 10, -5, 0, 2, -7 км/ч. Чему равно суммарное перемещение тела?

I. Механика

Тестирование онлайн

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают

Графики равномерного движения

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) – прямая линия, параллельная оси времени.

Правило определения пути по графику v(t): Численное значение перемещения (пути) – это площадь прямоугольника под графиком скорости.

Зависимость пути от времени. График s(t) – наклонная линия.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Графики равноускоренного движения

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.

Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.

Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

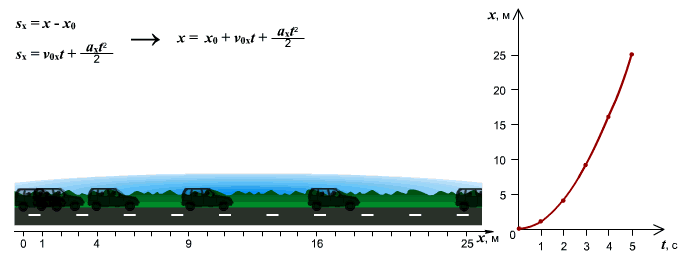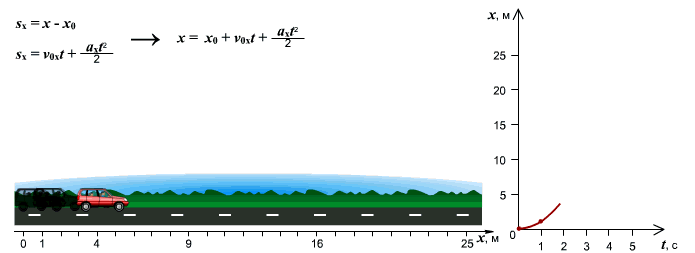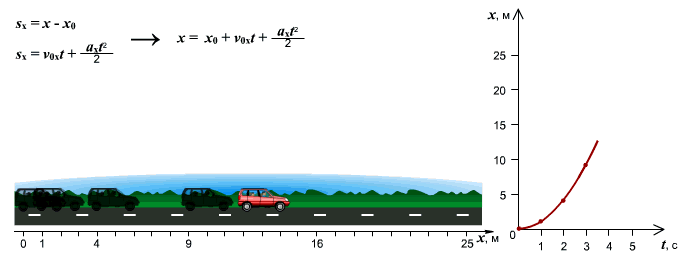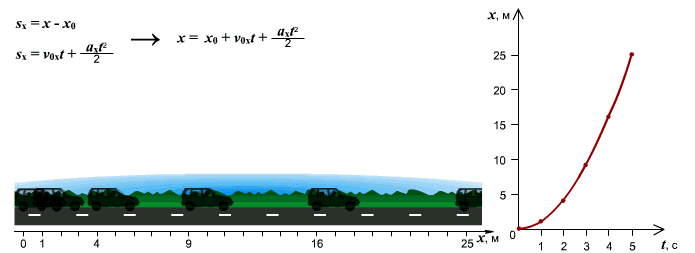
Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.

График движения при . График движения при

График движения при . График движения при

Сравнительная таблица графиков

Если
траектория движения точки известна, то зависимость пути , пройденного точкой, от
истекшего промежутка времени  дает полное описание этого движения.
Мы видели, что для равномерного движения такую зависимость можно дать в виде
формулы (9.2). Связь между  и  для отдельных моментов времени можно
задавать также в виде таблицы, содержащей соответственные значения промежутка
времени и пройденного пути. Пусть нам дано, что скорость некоторого
равномерного движения равна 2 м/с. Формула (9.2) имеет в этом случае вид . Составим таблицу
пути и времени такого движения:

t, с	1	2	3	4	5	6	…
s, м	2	4	6	8	10	12	…

Зависимость
одной величины от другой часто бывает удобно изображать не формулами или
таблицами, а графиками, которые более наглядно показывают картину изменения
переменных величин и могут облегчать расчеты. Построим график зависимости
пройденного пути от времени для рассматриваемого движения. Для этого возьмем
две взаимно перпендикулярные прямые — оси координат; одну из них (ось абсцисс)
назовем осью времени, а другую (ось ординат) — осью пути. Выберем масштабы для
изображения промежутков времени и пути и примем точку пересечения осей за
начальный момент и за начальную точку на траектории. Нанесем на осях значения
времени и пройденного пути для рассматриваемого движения (рис. 18). Для
«привязки» значений пройденного пути к моментам времени проведем из
соответственных точек на осях (например, точек 3 с и 6 м) перпендикуляры к
осям. Точка пересечения перпендикуляров соответствует одновременно обеим
величинам: пути  и
моменту ,
— этим способом и достигается «привязка». Такое же построение можно выполнить и
для любых других моментов времени и соответственных путей, получая для каждой
такой пары значений время — путь одну точку на графике. На рис. 18 выполнено
такое построение, заменяющее обе строки таблицы одним рядом точек. Если бы
такое построение было выполнено для всех моментов времени, то вместо отдельных
точек получилась бы сплошная линия (также показанная на рисунке). Эта линия и
называется графиком зависимости пути от времени или, короче, графиком пути.

Рис.
18. График пути равномерного движения со скоростью 2 м/с

Рис.
19. К упражнению 12.1

В нашем случае
график пути оказался прямой линией. Можно показать, что график пути
равномерного движения всегда есть прямая линия; и обратно: если график
зависимости пути от времени есть прямая линия, то движение равномерно.

Повторяя
построение для другой скорости движения, найдем, что точки графика для большей
скорости лежат выше, чем соответственные точки графика для меньшей скорости
(рис. 20). Таким образом, чем больше скорость равномерного движения, тем круче
прямолинейный график пути, т. е. тем больший угол он составляет с осью времени.

Рис.
20. Графики пути равномерных движений со скоростями 2 и 3 м/с

Рис.
21. График того же движения, что на рис. 18, вычерченный в другом масштабе

Наклон графика
зависит, конечно, не только от числового значения скорости, но и от выбора
масштабов времени и длины. Например, график, изображенный на рис. 21, дает
зависимость пути от времени для того же движения, что и график рис. 18, хотя и
имеет другой наклон. Отсюда ясно, что сравнивать движения по наклону графиков
можно только в том случае, если они вычерчены в одном и том же масштабе.

С помощью
графиков пути можно легко решать разные задачи о движении. Для примера на рис.
18 штриховыми линиями показаны построения, необходимые для того, чтобы решить
следующие задачи для данного движения: а) найти путь, пройденный за время 3,5
с; б) найти время, за которое пройден путь 9 м. На рисунке графическим путем
(штриховые линии) найдены ответы: а) 7 м; б) 4,5 с.

На графиках,
описывающих равномерное прямолинейное движение, можно откладывать по оси
ординат вместо пути  координату  движущейся точки. Такое
описание открывает большие возможности. В частности, оно позволяет различать
направление движения по отношению к оси . Кроме того, приняв начало отсчета
времени за нуль, можно показать движение точки в более ранние моменты времени,
которые следует считать отрицательными.

Рис.
22. Графики движений с одной и той же скоростью, но при различных начальных
положениях движущейся точки

Рис.
23. Графики нескольких движений с отрицательными скоростями

Например, на
рис. 22 прямая I есть график движения, происходящего с положительной скоростью
4 м/с (т. е. в направлении оси ), причем в начальный момент
движущаяся точка находилась в точке с координатой  м. Для сравнения на том же рисунке
дан график движения, которое происходит с той же скоростью, но при котором в
начальный момент движущаяся точка находится в точке с координатой  (прямая II).
Прямая. III соответствует случаю, когда в момент  движущаяся точка находилась в точке
с координатой  м.
Наконец, прямая IV описывает движение в случае, когда движущаяся точка имела
координату  в
момент  с.

Мы видим, что
наклоны всех четырех графиков одинаковы: наклон зависит только от скорости
движущейся точки, а не от ее начального положения. При изменении начального
положения весь график просто переносится параллельно самому себе вдоль оси  вверх или вниз на
соответственное расстояние.

Графики
движений, происходящих с отрицательными скоростями (т. е. в направлении,
противоположном направлению оси ), показаны на рис. 23. Они
представляют собой прямые, наклоненные вниз. Для таких движений координата  точки с течением
времени уменьшается.

12.3. График
пути для точки, движущейся со скоростью , отсекает на оси ординат отрезок . Как зависит от
времени расстояние  от начальной точки? Напишите формулу
этой зависимости.

12.4. Точка,
движущаяся со скоростью , в момент  находится на расстоянии  от начальной. Как
зависит от времени расстояние ?

12.5. Точка,
двигаясь равномерно вдоль оси , имела координаты м и м в моменты
времени с
и с
соответственно. Найдите графически, в какой момент точка проходила через начало
координат и какова была координата  в начальный момент. Найдите проекцию
скорости на ось .

12.6. Найдите
при помощи графика пути, когда и на каком расстоянии от точки А автомашину,
вышедшую из точки А, догонит вторая автомашина, вышедшая из той же точки через
20 мин после первой, если первая машина движется со скоростью 40 км/ч, а вторая
— со скоростью 60 км/ч.

12.7. Найдите
при помощи графика пути, где и когда встретятся автомашины, вышедшие
одновременно навстречу друг другу со скоростями 40 и 60 км/ч из пунктов А и В,
лежащих на расстоянии 100 км друг от друга.

Графики пути
можно строить и для случаев, в которых тело движется равномерно в течение
определенного промежутка времени, затем движется равномерно, но с другой
скоростью в течение другого промежутка времени, затем снова меняет скорость и
т. д. Например, на рис. 26 показан график движения, в котором тело двигалось в
течение первого часа со скоростью 20 км/ч, в течение второго часа — со
скоростью 40 км/ч и в течение третьего часа — со скоростью 15 км/ч.

Задание:
12.8. Постройте график пути для движения, в котором за последовательные
часовые промежутки тело имело скорости 10, -5, 0, 2, -7 км/ч. Чему равно
суммарное перемещение тела?

Цели урока:

обучающая: рассмотреть и сформировать навыки построения графиков зависимости кинематических величин от времени при равномерном и равноускоренном движении; научить учащихся анализировать эти графики; путем решения за­дач закрепить полученные знания на практике;

развивающая: развитие умения наблюдать, анализировать конкретные ситуации; выделять определенные признаки;

воспитывающая: воспитание дисциплины и норм поведения, творческого от­ношения к изучаемому предмету; стимулировать активность учащихся.

Методы:

словесный — беседа;

наглядный — видеоурок, записи на доске;

контролирующий — тестирование или устный (письменный) опрос, решение задач).

Связи:

межпредметные: математика — линейная зависимость, график линейной функции; квадратичная функция и ее график;

внутрипредметные: равномерное и равноускоренное движение.

Ход урока:

1. Организационный этап.

Добрый день. Прежде чем мы приступим к уроку, хотелось бы, чтобы каждый из вас настроился на рабочий лад.

2. Актуализация знаний.

3. Объяснение нового материала.

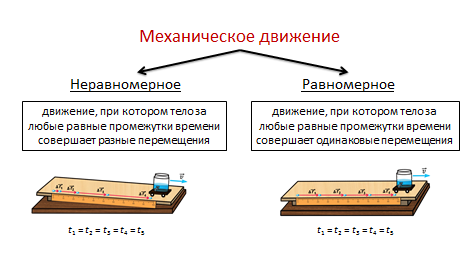
Мы с вами знаем, что механическое движение — это изменение положения тела (или частей тела) в пространстве относительного других тел с течением времени.

В свою очередь механическое движение бывает двух видов — равномерное, при котором тело за любые равные промежутки времени совершает одинаковые перемещения, и неравномерным, при котором тело за любые равные промежутки времени совершает разные перемещения.

Давайте вспомним основные формулы, которые мы выучили для равномерного и неравномерного движения.

Если движение равномерное, то:

1. Скорость тела не меняется с течением времени;

2. Что бы найти скорость тела, необходимо путь, который прошло тело за некоторый промежуток времени, разделить на этот промежуток времени;

3. Уравнение перемещения имеет вид:

4. И  — кинематическое уравнение равномерного движения.

Для равноускоренного:

1. Ускорение тела не изменяется с течением времени;

2. Ускорение есть величина, равная отношению изменения скорости тела, к промежутку времени, в течении которого это изменение произошло

3. Уравнение скорости для равноускоренного движения имеет вид:

4.  — уравнение перемещения для равноускоренного движения;

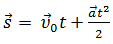
5. — кинематическое уравнение равноускоренного движения.

Для большей наглядности движение можно описывать с помощью графиков.

Рассмотрим зависимость ускорения, которым может обладать тело вследствие своего движения, от времени.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения ускорения тела, полученный график будет выражать зависимость ускорения тела от времени.

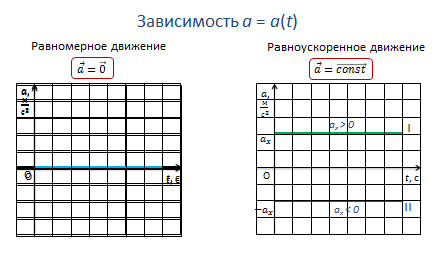
Для равномерного прямолинейного движения график зависимости ускорения от времени имеет вид прямой, которая совпадает с осью времени, т.к. ускорение при равномерном движении равно нулю.

Для равноускоренного движения график ускорения также имеет вид прямой, параллельной оси времени. При этом график располагается над осью времени, если тело движется ускоренно, и под осью времени, если тело движется замедленно.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, а по вертикальной оси ординат — тоже в соответствующем масштабе — значения скорости тела, то мы получим график скорости.

Для равномерного движения график скорости имеет вид прямой, параллельной оси времени. При этом график скорости располагается над осью времени, если тело движется по оси Х, и под осью времени, если тело движется против оси Х.

Такие графики показывают, как изменяется скорость с течением времени, т. е. как скорость зависит от времени. В случае прямолинейного равномерного движения эта «зависимость» состоит в том, что скорость с течением времени не меняется. Поэтому график скорости представляет собой прямую, параллельную оси времени.

По графику скорости тоже можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованного прямоугольника: верхнего, если тело движется в сторону положительного направления, и нижнего — в случае движения тела в отрицательном направлении.

Действительно, площадь прямоугольника равна произведению его сторон: S=ab, где a и b стороны прямоугольника.

Но одна из сторон в определенном масштабе равна времени, а другая — скорости. А их произведение как раз и равно абсолютному значению перемещения тела. При этом перемещение будет положительным, если проекция вектора скорости положительна, и отрицательным, если проекция вектора скорости отрицательна.

При равноускоренном движении тела, происходящем вдоль координатной оси X, скорость с течением времени не остается постоянной, а меняется со временем согласно формуле v = v₀ + at, т. е. скорость является линейной функцией, и поэтому графики скорости имеют вид прямой, наклоненную к оси времени. Причем, чем больше угол наклона, те большую скорость имеет тело. На нашем графике прямая 1 соответствует движению с положительным ускорением (скорость увеличивается) и некоторой начальной скоростью, прямая 2 — движению с отрицательным ускорением (скорость убывает) и начальной скоростью равной нулю.

По графику скорости при равноускоренном движении также можно узнать абсолютное значение перемещения тела за данный промежуток времени. Оно численно равно площади заштрихованной трапеции для тела 1, и прямоугольного треугольника — в противоположном случае. Действительно, например, площадь трапеции равна произведению полу суммы её оснований на высоту. В нашем случае, в определенном масштабе, высота трапеции равна времени, а основания — начальной и конечной скорости.

При этом проекция перемещения для первого тела будет положительной.

Для второго тела, прямоугольного треугольника — половине произведения его катетов. В нашем случае, катеты — это время и конечная скорость тела.

Проекция перемещения — отрицательна.

Теперь рассмотрим зависимость пройденного пути от времени.

Как и в предыдущих случаях, по оси абсцисс мы будем откладывать время, с момента начала движения, а по оси ординат — путь.

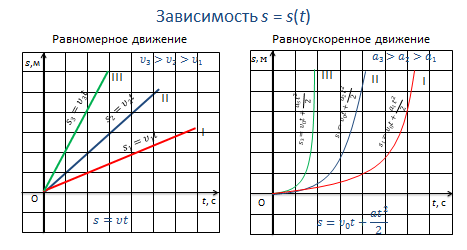
Для равномерного движения график зависимости пути от времени представляет собой прямую линию, т.к. зависимость — линейная.

При этом наклон графика к оси времени зависит от модуля скорости: чем больше скорость, тем больший угол наклона и тем больше скорость движения тела.

При равноускоренном движении графиком будет являться ветка параболы, т.к. зависимость, в этом случае, будет квадратичной. И чем больше ускорение, с которым движется тело, тем сильнее график будет прижиматься к оси ординат.

Теперь перейдем к рассмотрению зависимости перемещения от времени.

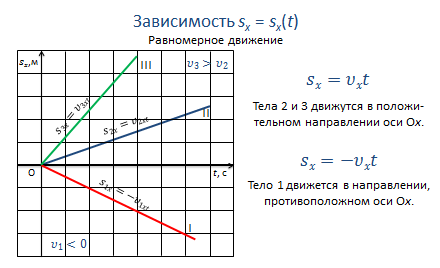
Рассмотрим равномерное движение.

Т.к. при равномерном движении перемещение линейно зависит от времени (s_x = υ_xt), то графиком будет являться прямая линия. Направление и угол наклона графика к оси времени будет зависеть от проекции вектора скорости на координатную ось.

Так, в нашем случае, тела 2 и 3 движутся в положительном направлении оси Х, при этом скорость третьего тела больше скорости второго.

А тело 1 — в направлении, противоположном направлению оси Х, поэтому график располагается под осью времени.

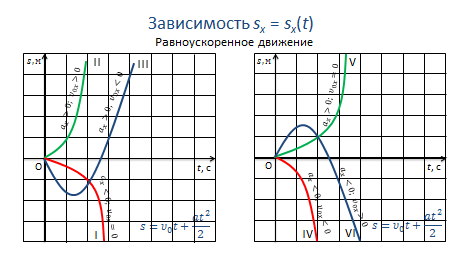
Для равноускоренного движения графиком перемещения является парабола, положение вершины которой зависит от направлений начальной скорости и ускорения.

Для 1-го тела ускорение меньше нуля, начальная скорость равна нулю.

Для 2-го тела ускорение и начальная скорость тела больше нуля.

Для 3-го тела ускорение больше нуля, начальная скорость меньше нуля.

У 4-го тела начальная скорость и ускорение меньше нуля.

Для 5-го тела ускорение больше нуля, а начальная скорость равна нулю.

И, наконец, 6-ое тело двигается замедленно, но с некоторой начальной скоростью.

И последнее, что мы с вами рассмотрим — это зависимость координаты тела от времени.

Если по горизонтальной оси (оси абсцисс) откладывать в определенном масштабе время, прошедшее с начала отсчета времени, а по вертикальной оси (оси ординат) — тоже в соответствующем масштабе — значения координаты тела, полученный график будет выражать зависимость координаты тела от времени (его также называют графиком движения).

Для равноускоренного движения графиком движения, как и в случае перемещения, является парабола, положение вершины которой также зависит от направлений начальной скорости и ускорения.

График равномерного движения представляет собой прямую линию. Это значит, что координата линейно зависит от времени.

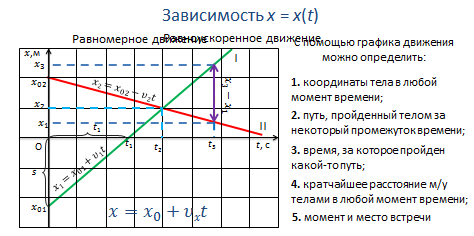
В случае прямолинейного движения тела графики дви­жения дают полное решение за­дачи механики, так как они позволяют найти поло­жение тела в любой момент времени, в том числе и в моменты времени, предшество­вавшие начальному моменту (если предполо­жить, что тело двигалось с такой же ско­ростью и до начала отсчета времени).

С помощью графика движения можно определить:

1. координаты тела в любой момент времени;

2. путь, пройденный телом за некоторый промежуток времени;

3. время, за которое пройден какой-то путь;

4. кратчайшее расстояние м/у телами в любой момент времени;

5. момент и место встречи и т. д.

По виду графиков зависи­мости координаты от времени можно судить и о скорости дви­жения. Ясно, что скорость тем больше, чем круче график, т. е. чем больше угол между ним и осью времени (чем больше этот угол, тем больше изме­нение координаты за одно и то же время).

При этом надо помнить, что график зависимости координаты тела от времени не следует путать с траекторией движения тела — прямой, во всех точках которой тело побывало при своем движении.

4. Этап обобщения и закрепления нового материала

И так, сделаем главный вывод.

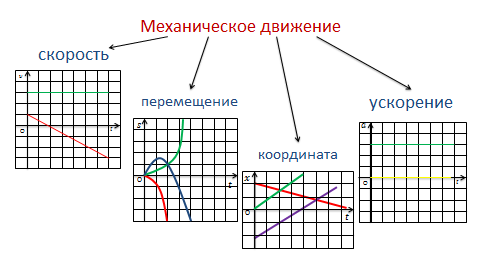
Механическое движение для большей наглядности можно описывать с помощью графиков:

1) Зависимости скорости от времени;

2) Зависимости ускорения от времени;

3) Зависимость координаты тела от времени;

4) И зависимости перемещения тела от времени, в течении которого это перемещение произошло.

5. Рефлексия

Хотелось бы услышать ваши отзывы о сегодняшнем уроке: что вам понравилось, что не понравилось, чем бы хотелось узнать еще.

6. Домашнее задание.

Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.

Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.

Будем отдельно рассматривать:

• движение без ускорения (равномерное), и
• движение с ускорением (неравномерное).

1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec{a} =0).

2). Неравномерное движение — скорость меняется и появляется ускорение.

Пусть ускорение есть и, оно не изменяется: (vec{a} =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:

• Равноускоренное движение — скорость тела увеличивается.
• Равнозамедленное движение — скорость уменьшается.

Примечание: Когда изменяется скорость, всегда появляется ускорение!

Движение будем изображать графически, используя две перпендикулярные оси.

На графиках будем откладывать:

• по горизонтали — время в секундах.
• по вертикали — координаты тела, или проекции скорости и ускорения.

Для каждого вида движения получим три графика. Графики будем называть так:

1. x(t) – зависимость координаты от времени;
2. v(t) – зависимость проекции скорости от времени;
3. a(t) – зависимость проекции ускорения от времени.

Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.

Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют

Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_{0}) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_{0}]

Скорость и ускорение неподвижного тела равны нулю:

[vec{v}=0]

[vec{a}=0]

Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.

Скорость не меняется — движение равномерное

Разберём равномерное движение в направлении оси (рис. 2а).

Начальная координата тела – это точка (x_{0}), а конечная координата — точка (x) на  оси Ox. В точку «x» тело переместится к конечному времени «t».

Красной стрелкой обозначено направление, в котором тело движется.

 Примечание: Тело движется туда, куда направлен вектор его скорости.

Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).

Уравнение, описывающее изменение координаты выглядят так:

[ x  = x_{0} + v cdot t ]

Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:

[ v  = v_{0} = const ]

Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:

[ a = 0 ]

Равномерное движение в направлении противоположном оси

Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).

Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.

Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.

Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.

А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.

Равноускоренное движение в направлении оси, скорость увеличивается

Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.

Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.

Уравнение, которое описывает квадратичное изменение координаты, выглядит так:

[ x = frac{a}{2}cdot t^{2} + v_{0} cdot t + x_{0} ]

Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:

[ v  = v_{0} + a cdot t ]

Ускорение есть (рис. 4г) и оно не меняется:

[ a = const ]

Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.

Примечания:

1). Координата «x» будет изменяться:

• по линейному закону, когда скорость не меняется — остается одной и той же.
• по квадратичному закону, когда скорость будет изменяться (расти, или убывать).

2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.

3). Квадратичный закон – это уравнение второй степени, на графике — парабола.

4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.

Равноускоренное движение против оси

Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).

Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).

Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).

Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec{v}) и (vec{a}) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.

Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.

Скорость уменьшается — движение равнозамедленное

Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).

Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).

Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).

А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).

Равнозамедленное движение против оси

Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).

Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).

Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).

Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.

Выводы

1). Все, что лежит:

• выше оси t – положительное;
• ниже оси t – отрицательное;
• на горизонтальной оси t – равно нулю.

2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).

3). Если скорость не меняется, ускорения нет.

• График x(t) координаты – это прямая линия.
• График v(t) скорости – горизонтальная прямая.
• График a(t) ускорения лежит на оси t.

4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.

• График x(t) координаты – это правая ветвь параболы.
• График v(t) скорости – наклонная прямая.
• График a(t) ускорения – горизонтальная прямая.

5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.

• График x(t) координаты – это левая ветвь параболы.
• График v(t) скорости – наклонная прямая.
• График a(t) ускорения – горизонтальная прямая.