Как составить граничные условия

Предположим, вам надо рассчитать задачу, в которой нагрузка движется таким образом, что в процессе моделирования она пересекает различные конечные элементы и геометрические границы. В таких случаях, помимо прочего вам потребуется задавать граничные условия только к части геометрической границы или описать его срабатывание только при определенных условиях или критериях. В этой заметке мы расскажем, как гибкость COMSOL Multiphysics позволяет решать подобные задачи.

Классификация граничных условий

С математической точки зрения при решении дифференциальных уравнений с частными производными возникает три типа граничных условий (ГУ):условие и задача Дирихле (ГУ первого рода), Неймана (ГУ второго рода) и Робена (ГУ третьего рода). В задаче Дирихле определяется и ограничивается самая искомая переменная. В задаче Неймана граничные условия накладываются на поток, т.е. на производную искомой функции. Задача Робина, по сути, является совокупностью двух предыдущих. В ней на границе области задаётся связь между искомой переменной и ее производной.

В следующей таблице для того, чтобы вновь перейти от математического описания к физическому, представлены конкретные примеры ГУ 1-го, 2-го и 3-го рода для различных физик.

Физика	Условие Дирихле	Условие Неймана	Условие Робина
Механика твердого тела (Solid Mechanics)	Смещение (Displacement)	Усилиe (Traction)	Пружина (Spring)
Теплопередача (Heat Transfer)	Температура (Temperature)	Тепловой поток (Heat flux)	Конвекция (Convection)
Скалярная акустика (Pressure Acoustics)	Звуковое давление (Acoustic pressure)	Нормальная составляющая Акустического ускорения (Normal acceleration)	Импеданс (Impedance)
Электрические токи (Electric Currents)	Фиксированный потенциал (Fixed potential)	Фиксированный ток (Fixed current)	Импеданс (Impedance)

При моделировании с помощью метода конечных элементов (FEM) эти виды граничных условий по-разному влияют на математическую и программную постановку задачи.

Условия Неймана (Neumann Conditions)

Условия Неймана — это «нагрузки». Они записываются в правой части системы уравнений. В COMSOL Multiphysics они представлены как т.н. weak contributions (условия/дополнения в слабой форме), что можно увидеть, предварительно включив опцию Equation View (Отображение уравнений) в Model Builder (Построителе моделей). Так как условия Неймана являются чисто аддитивными дополнениями к правой части, они могу содержать любую функцию различных переменных величин, например, времени, координат или других параметров.

Давайте рассмотрим задачу, в которой круглый источник тепла радиусом R движется в направлении x со скоростью v. Его интенсивность задаётся параболическим распределением с пиковым значением q_0. Математически его можно задать, как

q(x,y,t)=q_0left(1-left(frac{r}{R}right)^2right), quad r=sqrt{(x-vt)^2+y^2}, quad r < R

Очевидно, что в случае подвижной нагрузки невозможно однозначно определить геометрическую границу или область конечно-элементной сетки, на которые в конкретный момент времени будут действовать нагрузка с данным распределением.

Само по себе такое распределение можно описать следующим образом. Так как радиальная координата r будет использоваться два раза, давайте зададим её в качестве переменной. Ниже на скриншотах поэтапно показано, как задать входные данные и сам подвижный источник тепла.

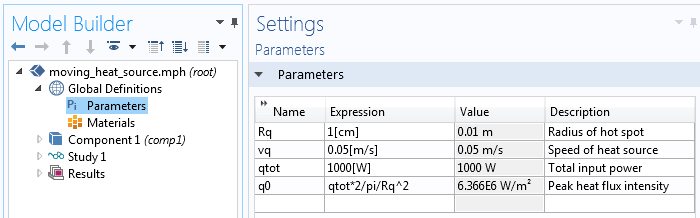
Параметры, описывающие подвижный источник тепла.

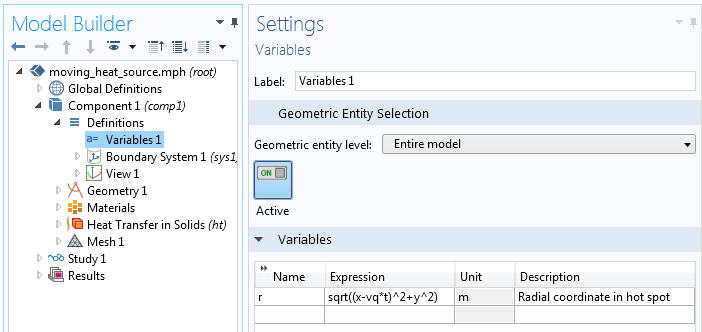
Задание переменной локальной радиальной координаты, в виде математического выражения расстояния от центра подвижного источника тепла.

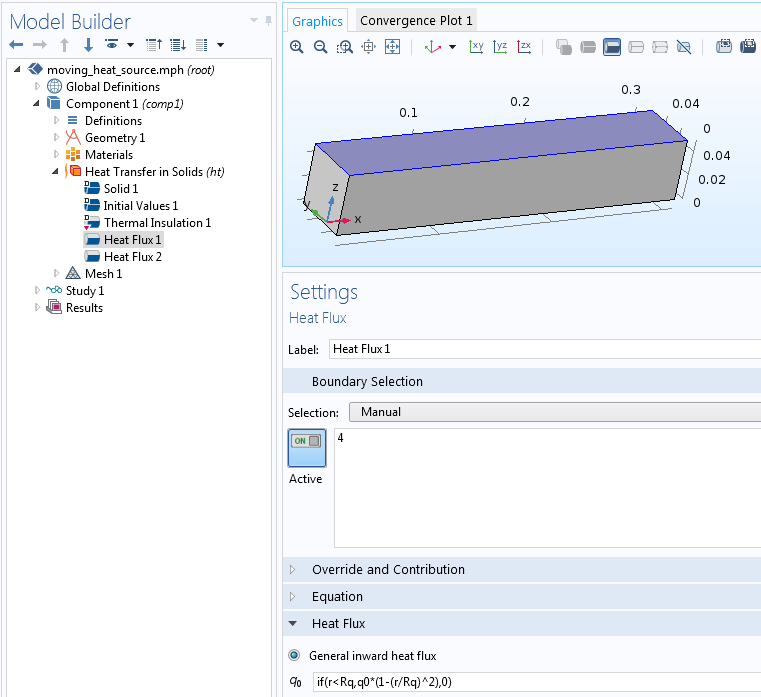
Настройки узла heat flux (тепловой поток).

Результаты расчета во временной области с использованием описанных выше настроек представлены на анимации ниже. Модель симметрична относительно плоскости yz, поэтому фактически расчет идет для половины области, а нагрузка задаётся подвижным полукругом.

Анимация распределения температуры в процессе движения источника тепла.

Условия Дирихле (Dirichlet Conditions)

При использовании граничного условия Дирихле, изначально задаётся зависимая переменная, так что нет необходимости её находить в процессе расчета. Следовательно, уравнения для этих степеней свободы можно исключать из постановки задачи. При этом условия Дирихле изменяют структуру матрицы жёсткости системы уравнений. При просмотре в режиме Equation View в COMSOL Multiphysics, эти условия будут отображаться, как ограничения (constraints).

Предположим, стоит задача смоделировать подвижный точечный источник тепла, температура которого была бы ровно 450 К. Возможно, это немного нереальная “модельная” поставка задачи, но зато она хорошо показывает различия условий Неймана и Дирихле. Если в узле Temperature (Температура) мы зададим аналогичное предыдущему случаю простое выражение ( if(r < R,450[K],0)), то это будет значить, что температура на частях границ, которые не соприкасаются с точечным источником, будет нулевой.

Однако это не то, что нас устроит, т.к. мы хотим лишь отключить условия Дирихле за пределами точечного источника. Для корректной настройки можно прибегнуть к небольшой хитрости. Если записать выражение if(r < R,450[K],ht.Tvar) в качестве значения для температуры, то мы получим желаемый результат (что продемонстрировано на анимации ниже).

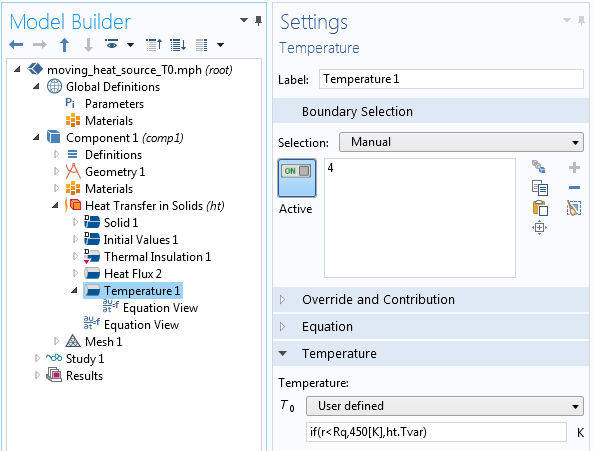
Настройки граничного условия типа Дирихле.

Анимация распределения температуры при движении точечного источника.

Чтобы лучше понять, как это работает, рекомендуем включить режим отображения Equation View и посмотреть на реализацию условий Дирихле (в данном случае, на задание температуры):

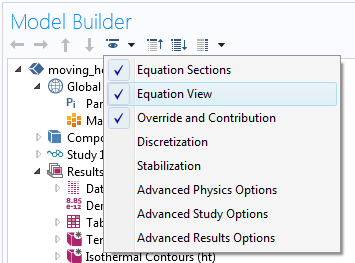
Чтобы включить отображение Equation View, поставьте напротив него галочку.

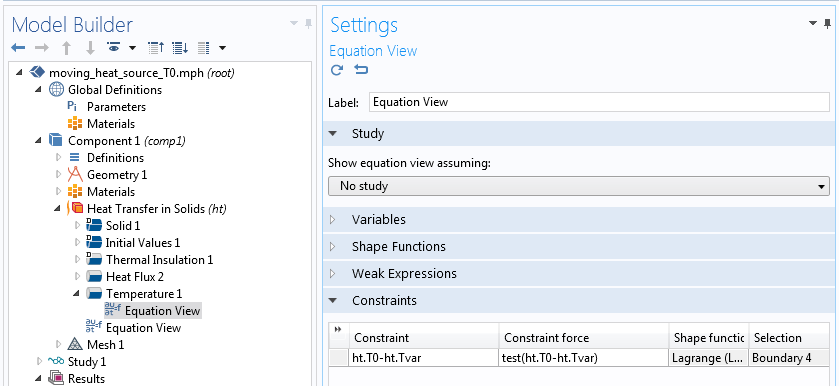
Отображение Equation View для узла Temperature.

Ограничение записано в виде ht.T0-ht.Tvar. Неявно подразумевается, что ht.T0-ht.Tvar = 0. Первое слагаемое — это температура, которую вы задаёте на входе для данного ГУ. Второе — это искомая в интерфейсе температура, записанная в виде переменной. Данное выражение ограничивает температуру заданным значением, пока последнее не станет равным самой этой переменной, т.е. ht.Tvar. В таком выражение в символьной форме становится равным ht.Tvar-ht.Tvar, что эквивалентно нулю. И следовательно, никаких ограничений не накладывается, т.е. 0.

Ограничения в слабой форме (Weak Constraints)

В общем случае в COMSOL Multiphysics условие Дирихле можно задать двумя способами. По умолчанию используется т.н. pointwise constraint (ограничение в точках), как показано выше, однако, также можно использовать т.н. weak constraint (ограничение в слабой форме). В последнем случае уравнения добавляются, а не исключаются. Для обеспечения заданного значения температуры затем добавляются необходимые тепловые потоки в качестве дополнительных степеней свободы (т.н. Lagrange multipliers или множители Лагранжа).

Вы можете использовать фактически тот же прием, о котором говорилось раньше, с небольшим дополнением. Чтобы получить возможность использовать обраничения в слабой форме, нужно предварительно включить опцию Advanced Physics Options (Расширенные физические настройки).

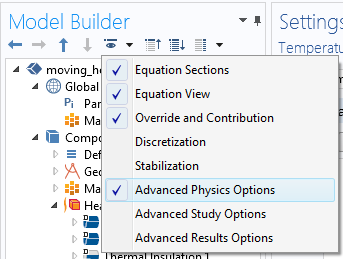
Окно построителя моделей с активированной опцией Advanced Physics Options.

При выставлении в настройках узла галочки в поле «Use weak constraints» (Использовать ограничения в слабой форме) будут добавлены дополнительные степени свободы для множителей Лагранжа. В данном случае, эти степени свободы описаны как T_lm.

Если для задания температуры в узле Temperature использовать вышеупомянутое выражение, то на границе, на которой выключено условие Дирихле, дополнительные степени свободы не повлияют на матрицу жёсткости системы (на частях границы, где ГУ будет “выключено”). Матрица жёсткости при этом станет вырожденной. Чтобы избежать такой ситуации, измените выражение if(r < R,450[K],ht.Tvar) на if(r < R,450[K],ht.Tvar-T_lm*1e-2). Множитель, который используется для переменной T_lm, может варьироваться в зависимости от различных моделей и физических полей, что в общей случае требует небольшого предварительно подбора. Более подробное описание того, почему так происходит и почему работает предложенная выше модификация не входит в рамки данной заметки.

Как в таких случаях пишут в классических монографиях — “оставляем доказательство данной техники читателю в качестве упражнения”.

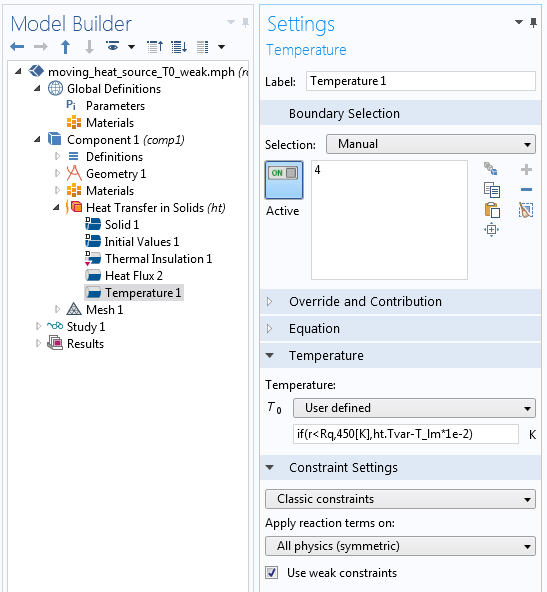
Окно настроек условия Дирихле с логическим критерием срабатывания и использованием обраничений в слабой форме.

Условия Робена (Robin Conditions)

Условия Робена влияют как на матрицу жёсткости, так и на правую часть уравнения. Сама структура матрицы, конечно же, не меняется, но добавляются дополнительные слагаемые к её элементам. Условия Робена в режиме отображения Equation View представлены также в качестве weak contributions, т.е. условий/дополнений в слабой форме. Задание этих условий в качестве функций от времени, пространственных координат и других переменных ничем не отличается от аналогичных техник для условий Неймана.

Интересно отметить, что, при выборе соответствующих значений, фактически можно превращать условия Робена в апроксимированные условия Дирихле или Неймана. Это особенно важно, когда в процессе процессе моделирования необходимо переключаться между различными граничными условиями.

Чтобы создать аналог условия Дирихле, надо задать большое значение «жёсткости», будь то коэффициент жёсткости пружины или коэффициент теплопередачи. В математике это будет являться так называемым методом штрафов (penalty implementation) для условия Дирихле. Чем больше «жёсткость», тем выше точность заданного значения степени свободы. Но есть одно но: слишком высокая жёсткость может привести к неправильному формированию матрицы жёсткости. В задачах теплопередачи, отправной точкой для «высокого» коэффициента теплопередачи alpha может служить выражение

alpha=1000 frac{lambda}{h}

где lambda — коэффициент теплопроводности, а h — характерный размер конечного элемента.

Аналогичный подход может использоваться применительно к другим физическим интерфейсам. Необходимо просто заменить lambda на соответствующее материальное свойство (к примеру, модуль Юнга в механике твёрдых тел). Множитель 1000 — это лишь предположении, которое в дальнейшем можно заменить на 10⁴ или 10⁵.

Если вы хотите использовать задание конвекции для моделирования точечного источника из предыдущего примера, можете воспользоваться настройками, изображёнными на следующем скриншоте. Обратите внимание, что в уравнении используется встроенная переменная h, которая содержит данные о размере элемента.

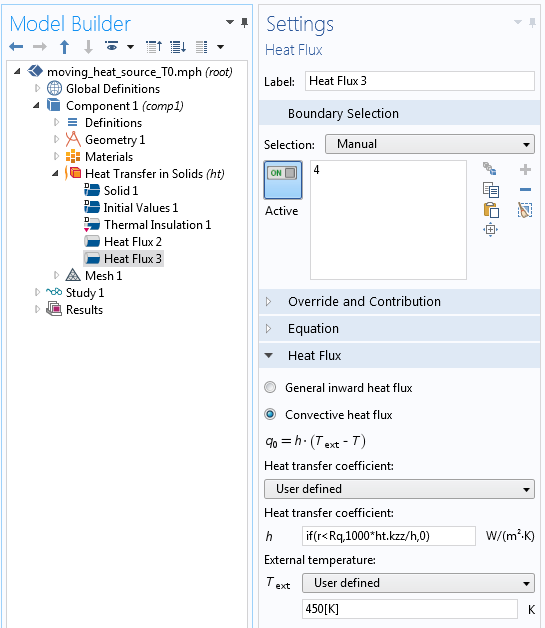
Использование конвекции для задания температуры.

В давние времена, когда я только начал изучать конечно-элементное моделирование, иногда в программах было невозможно задать отличные от нуля перемещения в механике конструкций. Так как такой алгоритм обработки было очень сложно запрограммировать. В таком случае, простейшим решением было использование метода штрафов путём добавления предварительно сжатой жёсткой пружины. Но при этом было также нежелательно делать ее слишком жёсткой; в те дни ещё использовались вычисления с одинарной точностью.

Теперь давайте рассмотрим аппроксимацию условия Неймана. Мы хотим описать тепловой поток, который не зависит от температуры на поверхности. В случае теплопередачи, условие Робена для направленного внутрь теплового потока q будет следующим

q=alpha(T_{textrm{ext}}-T)

где alpha — это коэффициент теплопередачи, T — температура на границе и T_{textrm{ext}} — внешняя температура. То есть, если T_{textrm{ext}} намного больше, чем расчётная температура на поверхности, то q approx alpha T_{textrm{ext}}.

Идея заключается в том, чтобы подобрать произвольный, очень большой T_{textrm{ext}} и рассчитать подходящий коэффициент теплопроводности, как показано ниже.

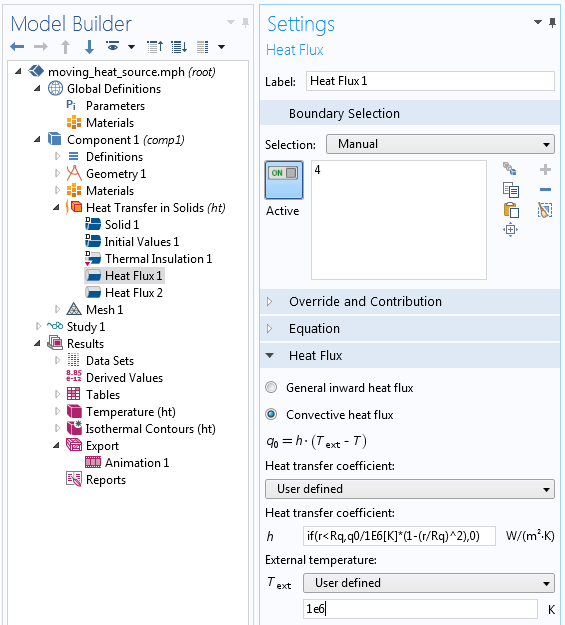
Использование конвекции для задания теплового потока.

Проектировщики используют подобный метод для задания фиксированного значения силы в реальных механических устройствах, к примеру, предварительно сжатой длинной мягкой пружине. Если предварительное сжатие пружины намного больше, чем смещение частей, с которыми она соединяется, то сила будет практически постоянной.

К вопросу про ошибки дискретизации

Когда граничное условие задаётся логическим выражением, наподобие if(r < R,..., то с большой вероятностью граница области, к которой оно применяется, не будет соответствовать граням конечных элементов. В таком случае могут возникнуть ошибки дискретизации.

Для условий Неймана или Робена численное интегрирование выполняется по каждому конечному элементу. Значение функции в элементе вычисляется методом дискретных точек Гаусса (квадратура Гаусса). Если размер конечных элементов больше, чем геометрический размер “нагрузки”, то итоговое количество точек Гаусса, распределённых под нагрузкой, может значительно влиять на результирующую нагрузку. Таким образом, в любой момент времени на участке должно быть несколько элементов, распределённых под нагрузкой.

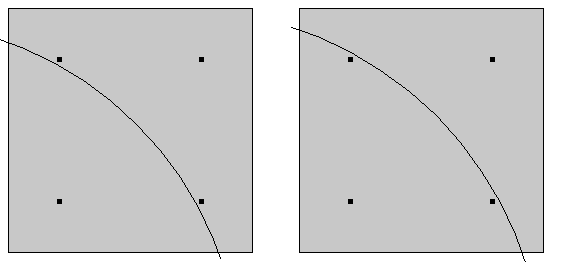
Даже небольшое изменение расположения нагрузки может повлиять на количество точек интегрирования. (На самом деле, количество точек намного больше. Для наглядности мы упростили картину.)

Напротив, условия Дирихле применяются к узлам сетки. На рисунке ниже показано распределение температуры и теплового потока в определённый момент времени. В задаче моделировался подвижный круглый источник с заданной температурой 450 K. На его границе видна тёмная область с температурой порядка 260 K. Поскольку начальная температура и температура окружающей среды равны 293 K, казалось бы, этого не может быть. На самом деле — это численный артефакт, связанный с тем, что не во всех узлах конечных элементов задано условие Дирихле. А при отсутствии непрерывности условий Дирихле, в матрице возможны неопределённости и сингулярности. Эту тему мы подробно обсуждали в предыдущей заметке блога. Сгущение сетки может помочь сократить появление и эффект от данных артефактов.

Зелёными стрелками на рисунке показаны узлы, в которые «входит» тепловой поток как “реакция” на заданную фиксированную температуру. Заданная в модели сетка приводит к достаточно грубой аппроксимации такого полукруга.

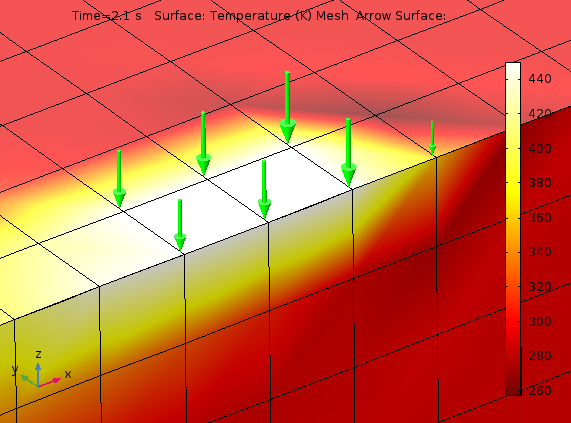
Распределение температуры и направление теплового потока вокруг полукруглого источника температуры.

Задание в граничных условиях зависимостей от решения

Во многих случаях решение может влиять на граничные условия. Как правило, это приводит к нелинейностям, которые автоматически обнаруживаются программным обеспечением COMSOL Multiphysics.

В качестве примера рассмотрим балку, внизу которой расположена точка опоры, препятствующая дальнейшему изгибу. Такую задачу можно сформулировать как задачу Дирихле, добавив физический интерфейс Beam (Балка) и узел Prescribed Displacement/Rotation (Установленное смещение/вращение).

Балка с опорой, ограничивающей перемещение, и распределённой нагрузкой.

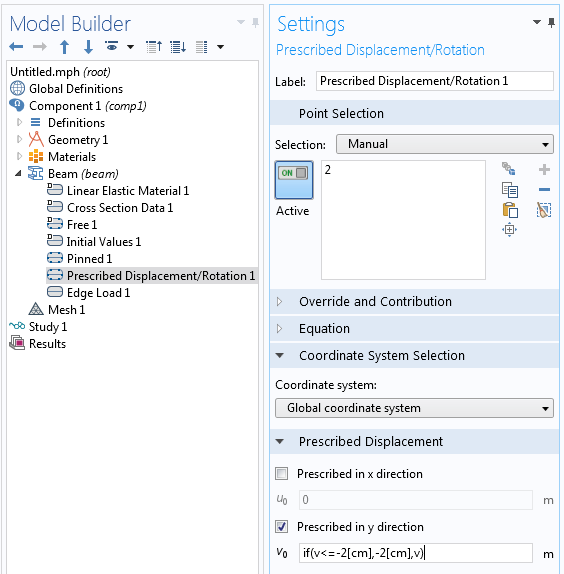
В окне настроек показано, как задать ограничение перемещения балки величиной 2 см.

Расчёт дает ожидаемые результаты. Чем меньше нагрузка, тем симметричнее кривая. При максимальной нагрузке даже меняется изгиб балки. Это немного заметно на графике деформаций, но еще лучше видно на графике изгибающего момента (bending moment).

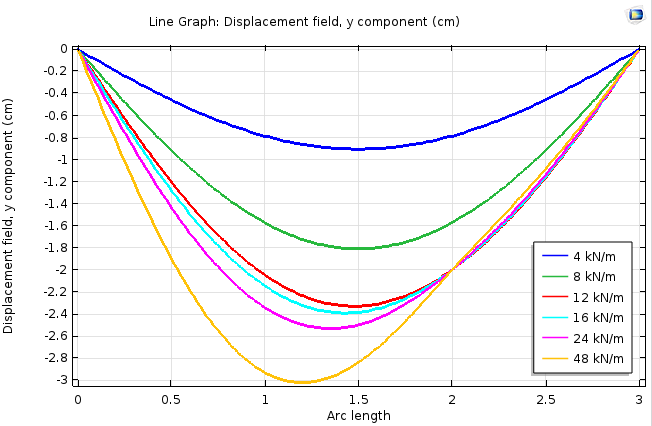
Кривые, демонстрирующие деформации балки по её длине при разных прикладываемых нагрузках.

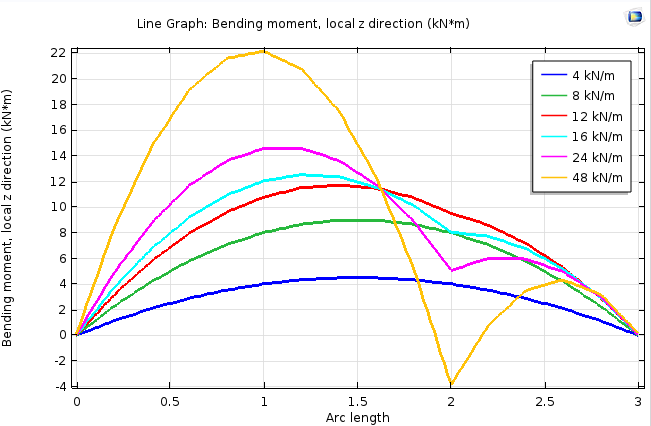
Кривые, демонстрирующие распределение изгибающего момента балки по её длине при разных прикладываемых нагрузках.

Данные настройки модели довольно грубые, что может привести к проблемам со сходимостью при итерационном поиске решения. Для более точной настройки необходимо использовать сильно нелинейную пружину в точке опоры таким образом, чтобы сила реакции была непрерывно дифференцируемой функцией от перемещения. Данный пример похож на доступную в физическом интерфейсе Solid Mechanics реализацию метода штрафов для контактов.

Заключительные положения по использованию продвинутых граничных условий в COMSOL Multiphysics

COMSOL Multiphysics предоставляет очень гибкие инстументы и приемы по настройке нестандартных граничных условий. В этой заметке мы привели лишь несколько примеров того, как можно воспользоваться данными возможностями.

Настоятельно рекомендуем ознакомиться с моделью подвижной нагрузки, которая доступна в качестве учебного примере в Галерее моделей и приложений.

Если у вас есть дополнительные вопросы о задании нестандартных граничных условий в моделях, пожалуйста, не стесняйтесь писать и задавать их нам.

Граничные условия.

• Граничными
  условиями первого рода задается закон
  распределения температуры по поверхности
  объекта в любой точке поверхности и в
  любой момент времени.

• Граничные
  условия второго рода – определяют
  значения плотности теплового потока
  на поверхности объекта в любой точке
  и в любой момент времени.

• Граничные
  условия третьего
  рода
  – определяют температуру жидкости
  омывающей поверхность или закон ее
  изменения и условия теплообмена на
  границах раздела сред. Должна быть
  задана температура и вид теплообмена
  (t_ж,
  t_c,
  …).

• Граничные
  условия четвертого рода – условия на
  границе раздела двух твердых тел.
  Теплота, подведенная к поверхности
  одного тела, передается полностью
  другому телу, имеющему другие
  характеристики.

Совокупность
дифференциального уравнения
теплопроводности и условия однозначности
представляют собой полную математическую
формулировку задачи.

Рассмотрим пример.

Стационарная теплопроводность плоской,
однородной, изотропной, бесконечной
стенки без внутренних источников теплоты
при граничных условиях первого рода.

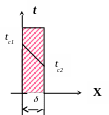
Запишем
уравнение Фурье-Кирхгофа:

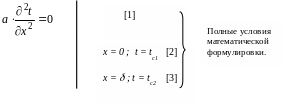
Целью
решения является:

Определение
закона изменения температуры в теле;

Определение
величины теплового потока.

Решается
задача путем интегрирования
дифференциального уравне-ния [1]:

–
температурный градиент этого объекта.

Разделяем
переменные и интегрируем [2]:

Получаем:

t
= C₁x+C₂
[5]
– общее
решение задачи.

Температура
изменяется линейно.

Частное
решение определяется при определении
С₁
и С₂.

При
условии [2]
t_c1
= C₂
[6];

При
условии [3]
t_c2
= C₁

+ t_c1
;

[7];

[8]
– частное решение.

Подставляя
x
можно определить любую температуру.

Вторая
часть задачи решается по закону Фурье.

подставляем
в [7];

[9]
– уравнение плотности теплового потока.

–
термическое
сопротивление стенки.

Таким
образом, плотность теплового потока
при теплопроводности прямопропорциональна
температурному напору и обратнопропорциональна
термическому сопротивлению.

Если
необходимо определить полный тепловой
поток, то:

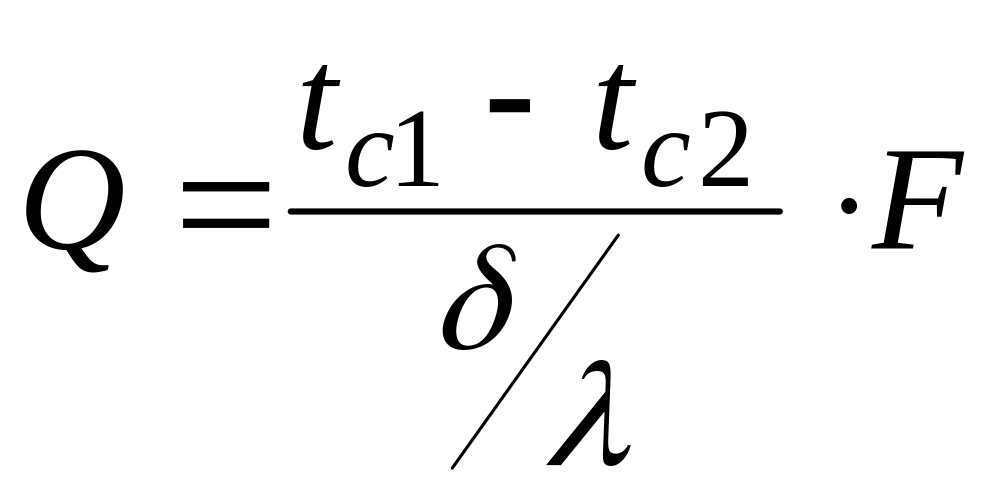
[10].

71

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Раздел 3.   Граничные условия.

 3.1 Неприменимость уравнений Максвелла в дифференциальной

 форме на границе  раздела диэлектрических сред.

Уравнения Максвелла в дифференциальной форме справедливы для описания сред электродинамические параметры, которых либо являются непрерывными функциями координат  поля в линейных средах, электродинамические параметры (e_а,m_а,s) которых не зависят от координат, либо являются непрерывными функциями координат. На практике, чаще всего возникают задачи, в которых присутствуют электродинамические среды, отличающиеся электродинамическими параметрами. На границе раздела сред, где соответствующие параметры меняются скачком, операция дифференцирования, а стало быть, и уравнения Максвелла в дифференциальной форме, незаконна. В этом случае для описания электромагнитного поля при переходе границы раздела сред, используют уравнения Максвелла в интегральной форме.

         Соотношения, которые описывают взаимосвязь векторов электромагнитного поля на границе раздела сред, называют граничными условиями.

Рекомендуемые материалы

3.2. Граничные условия для векторов электрического поля

Условия для нормальных составляющих векторов Е и D.

Поверхностные заряды.

         На границе раздела двух сред, отличающихся объемом и диэлектрической проницаемостью, выделим элементарную площадку DS. Размеры ее настолько малы, что ее можно считать плоской. В пределах площадки нормальная составляющая вектора электрического смещения  на границе раздела в пределах  была распределена равномерно. На  DS, как на основании, построим прямой цилиндр высотой Dh так, чтобы его основания ( и ) находились в различных средах. Единичный вектор – нормаль к основанию  считается положительной, если она из второй среды в первую.

Применим к этому цилиндру 3-тье уравнение Максвелла в интегральной форме: (1)

Полную поверхность представим в виде суммы:

 (2)

Рассмотрим предел для левой части при . Устремим  таким образом, чтобы DS₁ и DS₂ все время были в разных средах. Очевидно, что в пределе DS₁ и DS₂ совпадут с площадкой DS. Учитывая, что направление векторасовпадает с направлением внешней нормали к поверхности цилиндра для слагаемых, в левой части получим следующее предельное соотношение:

 (3)

 (4)

 (5)

Осуществляя предельный переход при  в соотношении (2) с учетом выражения (3), получим: (6).

В данном соотношении следует рассмотреть 2 случая:

1. Пусть, на границе раздела S отсутствуют поверхностные заряды, тогда  при любом конечном значении r^э (объемной плотности заряда) предел справа будет равен нулю и, получим: (7)

Из (7) следует, что при отсутствии поверхностного заряда на границе раздела S нормальная составляющая вектора электрического смещения D_n непрерывна при прохождении границы раздела.

2. Будем полагать, что электрические заряды распределены по поверхности S с поверхностной плотностью .

В этом случае предел в правой части (6) можно преобразовать следующим образом:        .

Равномерное распределение нормальной составляющей вектора D на границе раздела сред в пределах ∆S сопряжено с условием нормального распределения поверхностной плотности заряда в пределах ∆S.

 (8).

Подставляя (8) в (6) получим, что при условии поверхностного распределения заряда граничное условие будет следующим:

 (9)    .

Из (9) следует, что при наличии поверхностных зарядов на границе раздела нормальная компонента вектора D претерпевает разрыв величина которого определяется аовырхностной плотностью электрических зарядов.

Переходя в (7) к напряжениям электрического поля получим:

 или  (10)

Переходя в (9)  к напряжениям электрического поля получим:  (11) – справедливо при наличии поверхностных зарядов. Из (10) и (11) следует, что даже при отсутствии поверхностных зарядов нормальная компонента вектора Е претерпевает разрыв, величина которого определяется соотношением диэлектрических проницаемостей сред. Наличие поверхностных зарядов изменяют величину этого разрыва.

P.S. Поверхностная плотность электрического заряда это удобная идеализация, упрощающая решение задач. Фактически электрический заряд распределен в конечном приграничном слое. Мы прибегаем к понятию плоскости поверхностного заряда, когда нас не интересует значение D в случае заряженного слоя.

3.3.Условия для касательных составляющих вектора E и D

         На границе раздела сред, отличающихся e_а, выделим точку. Проведем через нее нормаль к поверхности S. Через эту нормаль проведем плоскость р.

На линии пересечения плоскостей выделим элементарный отрезок Dl, так, чтобы его можно было считать прямолинейным, и касательная, составляющая Е в I и II средах у границы раздела, была распределена равномерно. Отрезок Dl включает точку, в которой построили единичную нормаль. В этой точке проведем единичный вектор касательный к Dl и единичный вектор перпендикулярный к Dl. В плоскости р построим контур высотой Dh так, чтобы участки контура CD и АВ находились в разных средах. Положительное направление обхода контура ABCD связано с направлением единичной нормали правилом правого винта. Применим к контуру ABCD 2-ое уравнение Максвелла:

           (1)

Представим контур в виде суммы отрезков:

  (2)

Три единичных вектора связаны векторным соотношением. В слагаемых AB и CD векторные элементы dl равны, поэтому их можно заменить:

АВ: 

                                                    CD:

Найдем предел в соотношении (2) при Dh. Высоту уменьшим так, что бы АВ и CD были в разных средах. В пределе они совпадут с отрезком Dl.

так как вектор  в 1 и 2 средах, а также  имеют конечное значение, то

С учетом отмеченных особенностей предельный переход при Dh®0 ,в соотношении (2), приводит к следующему соотношению:                                       

       (3)

На границе раздела сред тангенциальная составляющая напряженности электрического поля непрерывна:  (4)

Тангенциальная компонента вектора электрического смешения претерпевает разрыв, величина которого равна отношению диэлектрической проницаемости сред. Из полученных граничных условий следует, что на границе раздела сред, векторы электрического поля  преломляются.

            

3.4. Граничные условия для векторов магнитного поля.

Условия для нормальных составляющих векторов В и Н.

         Имеется некая граница раздела сред. Выделяем на ней элементарную площадку DS. Размеры малы на столько, что в пределах этой площадки нормальная компонента  распределена равномерно. Строим на основании этой площадки цилиндр.

Применим к цилиндру закон Гаусса

     (1)

        (2)

Во всех этих интегралах направление  совпадает с внешней нормалью к цилиндру. Устремим высоту цилиндра Dh®0 так, чтобы DS₁ и DS₂ находились в разных средах. Тогда:

Так как  имеет конечные значения, то . В итоге получим:

     (3)

    (4)

Из (3) и (4) следует, что нормальная компонента вектора магнитной индукции непрерывна при прохождении границы сред. Тангенциальная компонента вектора напряженности магнитного поля непрерывна только при отсутствии на границе сред поверхностного тока.

В другом случае  компонента Н претерпевает разрыв,  который определяется отношением магнитных проницаемостей сред.

3.5. Условия для касательных составляющих В и Н.

Поверхностный ток.

         Условия для касательных составляющих магнитных векторов выводятся также как и для электрических. Через нормаль проводим плоскость р. На линии пересечения выделяем элемент длины Dl, малый настолько, чтобы в пределах этого участка касательные составляющие  в 1 и 2 средах были распределены равномерно. На этом отрезке строим контур так, чтобы участки контура были в разных средах. Положительное направление обхода контура связано с этими векторами правилом правого винта . Применим к контуру первое уравнение Максвелла в интегральной форме:     (1). Левую часть представим в виде суммы интегралов по участкам контура:

  (2)

 на участках АВ и СD может быть  представлен:

         Устремим Dh®0 так, чтобы участки контура находились в разных средах. Тангенциальная составляющая  распределена равномерно.

         Так как векторы  в 1 и 2 средах, а также вектор  имеют конечную величину, то

         В результате предельного перехода, примененного к соотношению (2), получим

(3)

1. Пусть на границе раздела S отсутствуют поверхностные токи, тогда правая часть соотношения (3) обращается в нуль, получаем                                                 (4)

При отсутствии поверхностных токов тангенциальная компонента  непрерывна при прохождении границы раздела сред.

   2.  Пусть на границе раздела сред S имеются поверхностные токи.

Ðàçäåë1. В этом случае правую часть соотношения (3) можно преобразовать

Плотность поверхностного тока распределена в пределах Dl равномерно (это условие является следствием исходного предположения о равномерном распределении тангенциальной составляющей  в пределах Dl)                         

       

         С учетом приведенных соотношений, предельный переход, выполненный в соотношении (3) приведет к следующему соотношению: 

        (5)

При наличии поверхностных токов на границе раздела тангенциальная составляющая  претерпевает разрыв, величина которого определяется плотностью поверхностного тока. Используя взаимосвязь единичных векторов, соотношение (5) можно переписать в векторной форме:

 (6)

         Соотношения (4), (5), (6) можно переписать для магнитной индукции: (7)                         (8)

         Из соотношений (7), (8) следует, что тангенциальные компоненты вектора магнитной индукции на границе раздела претерпевают разрыв. Наличие поверхностного тока только изменяет величину разрыва, увеличивая или уменьшая ее. Понятие поверхностного тока это удобная идеализация, упрощающая решение задач. Ток протекает в конечном, по величине, слое. Причем  тангенциальная составляющая   непрерывна во всех точках внутри этого слоя, но по разные стороны этого слоя тангенциальная составляющая   имеет различные значения. Поэтому, когда мы переходим к поверхностным токам, мы вынуждены предположить скачкообразное изменение тангенциальной составляющей .

3.6. Полная система граничных условий.

Граничные условия на поверхности идеального проводника

         (1)

Отсутствующие граничные условия являются следствием приведенных, при использовании материальных уравнений                         

         Частный случай, когда на границе раздела отсутствуют поверхностные заряды и поверхностные токи выглядит следующим образом:

    (2)

         Система (1) может быть записана в векторной форме:

  (3)

Соотношения (1) и (3) применимы в самом общем случае. В ряде случаев эти условия могут быть упрощены. Обычно при решении электродинамических задач, в которых присутствуют металлические тела, обычно предполагают, что проводимость этих металлических тел равна бесконечности. Известно, что в идеально проводящих средах электромагнитное поле отсутствует. Упрощенно, это можно показать: закон Ома в дифференциальной форме     

.

    В идеально проводящих средах s =¥. Объемная плотность не может быть равна бесконечности, т.е. вынуждены предположить, что . Пусть идеально проводящей является 2 среда, тогда соотношения (1) и (3) будут выглядеть:

Бесплатная лекция: “2 Общеинфекционный синдром” также доступна.

  (4)

       (5)

Для переменного электромагнитного поля .

2 уравнение Максвелла: , где .

Это получится, если .

         Из соотношений (4) и (5) следует, что на поверхности идеального проводника тангенциальная составляющая   и нормальная  обращаются в нуль.

Начальные и граничные условия

Приведенные уравнения (10)-(12) являются частными случаями общего дифференциального уравнения с частными производными второго порядка. Эти уравнения описывают различные физические явления и процессы. Так уравнение гиперболического вида

описывает процессы, связанные с механическими, электрическими, акустическими и другими видами колебаний. Поэтому это уравнение называют волновым уравнением. В этом уравнении независимые переменные t и x характеризуют временную и пространственную координаты.

Уравнение параболического вида

описывает процессы тепло- и массопереноса, диффузию и другие процессы переноса. В случае изучения процесса теплопереноса его называют уравнением теплопроводности.

Уравнение эллиптического вида

,

называемое уравнением Пуассона, описывает стационарные (установившиеся, т. е не зависящие от времени) процессы, например стационарное температурное поле, потенциальное течение жидкости т. п.

Как и любые дифференциальные уравнения, приведенные уравнения имеют бесконечное множество решений, которые отличаются произвольными функциями (решения обыкновенных дифференциальных уравнений различаются значениями констант). Поэтому для получения единственного решения задают дополнительные условия, которые принято называть условиями однозначности. Они могут содержать в себе информацию о геометрических и физических свойствах исследуемого объекта, его исходном состоянии, о характеристиках воздействия на него объектов внешней среды и т. п.

Задание условий однозначности позволяет выделить конкретный рассматриваемый объект, конкретный процесс из общей группы подобных объектов и процессов. Например, распространение теплоты в заготовке при ее обработке точением, шлифованием или при сварке и других видах обработки, сопровождающихся передачей тепловой энергии, будет описываться одним и тем же уравнением теплопроводности. Однако является очевидным, что при шлифовании или при сварке температура и ее изменение в одних и тех же точках заготовки будет разной и зависеть от многих причин, в частности, какой источник теплоты воздействует на заготовку, какая была температура в точках заготовки до начала обработки и других факторов.

В условиях однозначности выделяют начальные и граничные условия. Начальные условия отражают состояние объекта, процесса или явления на исходный (начальный) момент времени наблюдения t₀ в виде значения искомого решения во всех точках x, y рассматриваемой области объекта, например

или , (13)

где θ(x, y, t₀) – температура в точке x, y рассматриваемой области объекта в момент времени t₀. Обычно принимают t₀ = 0; f(x, y) – известная функция.

В отдельных задачах начальные условия могут содержать в себе также значения производных искомого решения по времени, например, скорость изменения температуры в момент времени t₀ или скорость перемещения рассматриваемого тела в точке x, y.

Граничные условия отражают взаимодействие исследуемого объекта с объектами внешней среды, которое имеет место на ограничивающих его поверхностях. С физической точки зрения это взаимодействие может быть выражено в виде приложения к той или иной части поверхности исследуемого объекта внешней нагрузки (сосредоточенных или распределенных сил), подведения или отводе теплоты и т. п.

Математически вид или признак взаимодействия описывается в форме констант, функциональных зависимостей и т. д., определяющих значения искомого решения на граничных поверхностях объекта, а также нормальных к граничным поверхностям производных искомого решения.

Условия однозначности совместно с дифференциальным уравнением позволяют математически полностью и однозначно отразить конкретный рассматриваемый процесс или явление.

В зависимости от того, какие условия однозначности заданы в математической постановке задачи выделяют три типа задач.

Задача первого типа – это задача Коши, в которой дифференциальное уравнение дополнено только начальными условиями, задающими состояние объекта, процесса или явления на исходный (начальный) момент времени наблюдения. Граничные условия в задаче Коши отсутствуют. Отсутствие граничных условий определено тем, что рассматривается либо неограниченное пространство, либо весьма малый начальный промежуток времени t, при котором влияние границ еще пренебрежимо мало.

Задача Коши формулируется при решении дифференциальных уравнений гиперболического и параболического видов.

Задача второго типа – это задача, в которой нет начальных условий, а заданы только граничные условия. Это условия, в свою очередь, подразделяются обычно на три вида (рода).

Граничным условием первого рода является условие, при котором в точках x, y на границе Г рассматриваемой области искомая функция u(x, y) принимает заданные значения, например

.

Граничным условием второго рода является условие, при котором в точках x, y рассматриваемой области производная по нормали n к граничной поверхности Г (нормальная производная) искомой функции u(x, y) принимает заданные значения, например

.

Граничным условием третьего рода является условие, при котором в точках x, y на границе Г рассматриваемой области задана линейная комбинация искомой функции и ее нормальной производной. Например, при решении задачи определения температурного поля в твердом теле это условие может иметь вид

,

где θ(x, y) – температура в точке x, y на границе Г поверхности рассматриваемого твердого тела; λ – коэффициент теплопроводности материала тела;

α – коэффициент теплоотдачи от поверхности тела; θ_о – температура окружающей среды.

В теплофизике технологических процессов механической обработки деталей часто используются граничные условия четвертого рода. Эти условия возникают тогда, когда рассматриваемое твердое тело находится в беззазорном контакте с другим твердым телом и между ними происходит теплообмен. При граничных условиях четвертого рода, когда контакт между телами идеален, температура в любой точке поверхности соприкосновения как со стороны одного, так ИСО стороны другого тела одна и та же, т. е.

.

Задачи второго типа имеют место тогда, когда состояние объекта исследования рассматривается в моменты времени, достаточно удаленных от начального момента и влиянием начальных условий можно пренебречь. В этих случаях процесс, протекающий в объекте, считается установившимся, стационарным. Постановка задач этого типа может содержать дифференциальное уравнение любого типа.

Задача третьего типа – это так называемая смешанная задача, в которой задаются и начальные и граничные условия. Смешанная задача формулируется для гиперболических и параболических типов уравнений.

Начальные и граничные условия

Здравствуйте, продолжаем нашу рубрику по дифференциальным уравнениям, это уже 2 статья, если вы хотите начать сначала и ознакомиться с видами дифференциальных уравнений, то вам в первую статью.

Введение

Итак, для использования численных методов при решении дифференциального уравнения необходимо дополнительные условия. Если искомая функция(концентрация, температура и т.д) является функцией времени u=u(t), то требуются начальные условия, которые являются значением этой функции в момент времени, принятый за начальный:

Если начальная функция также зависит и от пространственных координат u=u(t,x), то начальное условие характеризуют ее распределение в пространстве в начальный момент времени:

В последнем случае помимо начальных условий требуются еще и граничные условия, которые имеют значения функции u(t,x) на границе изучаемой системы для любого момента времени. Причем, если искомая функция зависит от нескольких пространственных координат, то необходимо задавать граничные условия по каждой из них.

Небольшой пример

Например для следующего уравнения:

• начальное условие
• 2 граничных условия по координате
• 1 граничное условие по координате
• 2 граничных условия по координате

Сразу же возникает вопрос, почему именно так? Так вот, порядок производной определяет количество граничных условий для переменной. Как вы заметили, по y присутствует только первая производная, поэтому и одно граничное условие.

Классификация граничных условий

Для лучшего понимания рассмотрим классификацию на примере уравнения:

будет изменятся от до , соответственно при , будет левая граница, а при , будет правая.

Граничные условия 1-ого рода

Записываются следующим образом:

— функции, зависящие от , как пример:

Граничные условия 2-ого рода

Здесь вместо самих функций используются их первые производные.

Граничные условия 3-ого рода

Смешанные граничные условия

В этом случае левое и правое граничные условия могут быть разных родов:

Заключение

На этом мы подходим к концу нашей статьи. Сегодня мы с вами изучили начальные и граничные условия в дифференциальных уравнениях. Если вам что то осталось непонятным, то это нормально, не пугайтесь. В будущих статьях мы будем еще подробнее разбираться с этими и другими тонкостями, ну а на сегодня это все.

Спасибо, что прочитали статью, если у вас остались вопросы, то задавайте их в комментариях.
И, буду вам очень признателен, если вы вступите в нашу группу вконтакте, ссылка на которую размещена слева вверху под названием сайта.

Определения и понятия теории дифференциальных уравнений

С этой темы мы рекомендуем начинать изучение теории дифференциальных уравнений. В одном разделе мы собрали все основные термины и определения, которые будут применяться при рассмотрении теоретической части. Для того, чтобы облегчить усвоение материала, мы приводим многочисленные примеры.

Дифференциальное уравнение

Дифференциальное уравнение – это уравнение, которое содержит неизвестную функцию под знаком производной или дифференциала.

Обыкновенное дифференциальное уравнение содержит неизвестную функцию, которая является функцией одной переменной. Если же переменных несколько, то мы имеем дело с уравнением в частных производных.

Имеет значение также порядок дифференциального уравнения, за который принимают максимальный порядок производной неизвестной функции дифференциального уравнения.

Обыкновенные дифференциальные уравнения 1 -го, 2 -го и 5 -го порядков:

1 ) y ‘ + 1 = 0 ; 2 ) d 2 y d x 2 + y = x · sin x ; 3 ) y ( 5 ) + y ( 3 ) = a · y , α ∈ R

Уравнения в частных производных 2 -го порядка:

1 ) ∂ 2 u ∂ t 2 = v 2 · ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 + ∂ 2 u ∂ z 2 , u = u ( x , y , z , t ) , v ∈ R ; 2 ) ∂ 2 u ∂ x 2 – ∂ 2 u ∂ y 2 = 0 , u = u ( x , y )

С порядками ДУ разобрались. Далее мы будем в основном рассматривать обыкновенные дифференциальные уравнения n -ого порядка вида F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 или F x , y , d y d x , d 2 y d x 2 , . . . , d n y d x n = 0 , в которых Ф ( x , y ) = 0 – это заданная неявно функция. В тех случаях, когда это будет возможно, неявную функцию мы будем записывать в ее явном представлении y = f ( x ) .

Интегрирование дифференциального уравнения

Интегрирование дифференциального уравнения – это процесс решения этого уравнения.

Решением дифференциального уравнения является функция Ф ( x , y ) = 0 , которая задана неявно и которая обращает данное уравнение в тождество. В некоторых случаях нам нужно будет неявно заданную функцию у выражать через аргумент х явно.

Искать решение дифференциального уравнения мы всегда будем на интервале Х , который задается заранее.

В каких случаях мы будем учитывать интервал Х ? Обычно в условии задач он не упоминается. В этих случаях мы буде искать решение уравнения F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) для всех х , при которых искомая функция у и исходное уравнение будут иметь смысл.

Интеграл дифференциального уравнения – это название решения дифференциального уравнения.

Функции y = ∫ x d x или y = x 2 2 + 1 можно назвать решением дифференциального уравнения y ‘ = x .

У одного дифференциального уравнения может быть множество решений.

Функция y = x 3 3 является решением ДУ y ‘ = x 2 . Если мы подставим полученную функцию в исходное выражение, то получим тождество y ‘ = x 3 3 = 1 3 · 3 x 2 = x 2 .

Вторым решением данного дифференциального уравнения является y = x 3 3 + 1 . Подстановка полученной функции в уравнение также превращает его в тождество.

Общее решение ДУ

Общее решение ДУ – это все множество решений данного дифференциального уравнения.

Также общее решение часто носит название общего интеграла ДУ.

Общее решение дифференциального уравнения y ‘ = x 2 имеет вид y = ∫ x 2 d x или y = x 3 3 + C , где C – произвольная постоянная. Из общего интеграла ДУ y = x 3 3 + C мы можем прийти к двум решениям, которые мы привели в прошлом примере. Для этого нам нужно подставить значения С = 0 и C = 1 .

Частное решение ДУ

Частное решение ДУ – это такое решение, которое удовлетворяет условиям, заданным изначально.

Для ДУ y ‘ = x 2 частным решением, которое будет удовлетворять условию y ( 1 ) = 1 , будет y = x 3 3 + 2 3 . Действительно, y ‘ = x 3 3 + 2 3 ‘ = x 2 и y ( 1 ) = 1 3 3 + 2 3 = 1 .

К числу основных задач из теории дифференциальных уравнений относятся:

• задачи Коши;
• задачи нахождения общего решения ДУ при заданном интервале Х ;
• краевые задачи.

Особенностью задач Коши является наличие начальных условий, которым должно удовлетворять полученное частное решение ДУ. Начальные условия задаются следующим образом:

f ( x 0 ) = f 0 ; f ‘ ( x 0 ) = f 1 ; f ‘ ‘ ( x 0 ) = f 2 ; . . . ; f ( n – 1 ) ( x 0 ) = f n – 1

где f 0 ; f 1 ; f 2 ; . . . ; f n – 1 – это некоторые числа.

Особенностью краевых задач является наличие дополнительных условий в граничных точках x 0 и x 1 , которым должно удовлетворять решение ДУ второго порядка: f ( x 0 ) = f 0 , f ( x 1 ) = f 1 , где f 0 и f 1 – заданные числа. Такие задачи также часто называют граничными задачами.

Линейное обыкновенное ДУ n -ого порядка имеет вид:

f n ( x ) · y ( n ) + f n – 1 ( x ) · y ( n – 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

При этом коэффициенты f 0 ( x ) ; f 1 ( x ) ; f 2 ( x ) ; . . . ; f n ( x ) – это непрерывные функции аргумента х на интервале интегрирования.

Уравнение f n ( x ) · y ( n ) + f n – 1 ( x ) · y ( n – 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x ) будет называться линейным однородным дифференциальным уравнением в том случае, если f ( x ) ≡ 0 . Если нет, то мы будем иметь дело с линейным неоднородным ДУ.

В линейных однородных ДУ коэффициенты f 0 ( x ) = f 0 ; f 1 ( x ) = f 1 ; f 2 ( x ) = f 2 ; . . . ; f n ( x ) = f n могут быть постоянными функциями (некоторыми числами), то мы будем говорить о ЛОДУ с постоянными коэффициентами или ЛНДУ с постоянными коэффициентами. В ЛОДУ с постоянными коэффициентами f ( x ) ≡ 0 , в ЛНДУ с постоянными коэффициентами f ( x ) ненулевая.

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами – это уравнение n -ой степени вида f n · k n + f n – 1 · k n – 1 + . . . + f 1 · k + f 0 = 0 .

Остальные определения мы будем разбирать в других темах по мере изучения теории.

[spoiler title=”источники:”]

http://codetown.ru/differencialnye-uravneniya/conditions/

http://zaochnik.com/spravochnik/matematika/differentsialnye-uravnenija/teorija-differentsialnyh-uravnenij/

[/spoiler]

Макеты страниц