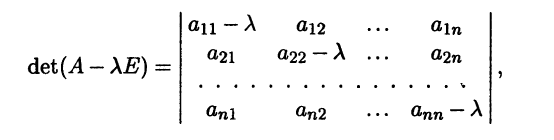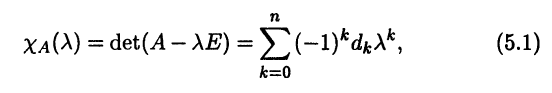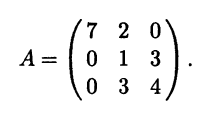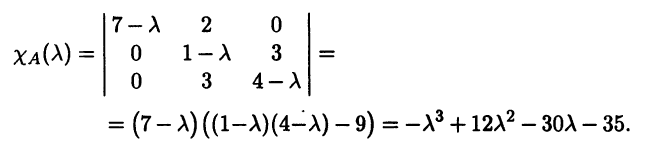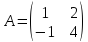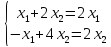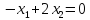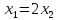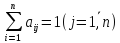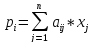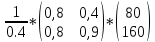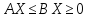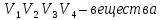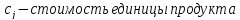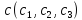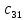Как составить характеристическое уравнение для матрицы

Для произвольной квадратной матрицы А = (a_ij) порядка n рассмотрим определитель

где Е – единичная матрица, а λ – действительное переменное. Относительно переменного λ этот определитель является многочленом степени n и может быть записан в виде

где множители (-l)_k введены для удобства.

Определение 5.1. Многочлен _χA(λ) = det(A – λЕ) называют характеристическим многочленом матрицы А, а уравнение _χA(λ) = 0 – характеристическим уравнением матрицы А.

Пример 5.1. Найдем характеристическое уравнение матрицы

Для этого раскроем определитель:

Итак, характеристическое уравнение заданной матрицы имеет вид -λ³ + 12λ² – 30λ – 35 = 0. #

Квадратную матрицу можно использовать в качестве значе-ния переменного в произвольном многочлене. Тогда значением многочлена от матрицы будет матрица того же порядка, что и исходная [III]. Интерес представляют такие многочлены, значение которых от данной матрицы есть нулевая матрица. Их называют аннулирующими многочленами. Оказывается, что одним из таких аннулирующих многочленов для матрицы является ее характеристический многочлен.

Теорема 5.1 (теорема Кэли – Гамильтона). Для любой квадратной матрицы характеристический многочлен является ее аннулирующим многочленом. #

Выясним, как связаны между собой характеристические многочлены подобных матриц.

Теорема 5.2. Характеристические многочлены (уравнения) подобных матриц совпадают.

◄ Пусть квадратные матрицы A и А’ одного порядка подобны, т.е. существует такая невырожденная матрица Р того же порядка, что А’ = Р^-1АР. Тогда в силу свойств определителей [III] имеем

_χA’(λ) = det (А’ – λЕ) = det(P^-1AP – λР^-1ЕР) = det(P^-1(A – λЕ)Р) = detP^-1 det(A – λE)detP = det(A – λE) = _χA(λ). ►

1. Линейные операции над векторами

2. Базис. Cкалярное произведение

3. Векторное и смешанное произведения векторов

4. Декартова система координат. прямая на плоскости

5. Плоскость в пространстве

6. Прямая в пространстве

7. Кривые второго порядка — I

8. Кривые второго порядка — II

9. Поверхности второго порядка

10. Матрицы и операции с ними

11. Обратная матрица

12. Ранг матрицы

13. Системы линейных алгебраических уравнений

14. Свойства решений однородных и неоднородных СЛАУ

Рассмотрим
квадратную матрицу А (n*n).
Рассмотрим мн-во векторов –столбцов
размерности n.
В рез-те произведение это матрицы на
n-мерный
вектор х получиться также n-мерный
вектор у: АХ=У

Число
α наз-ся собственным значением кв матрицы
А, если найдется вектор х, такой, что ах=
λ х

Пример

Собственное
значение λ
= 5. Собственный вектор (1,1).

Каждый
вектор
где
с – произвольное число, является
собственным вектором матрицы А.

Рассмотрим
для удобства кв матрицу А(2*2) и равно
ах=х.
Или Ах=λех

Ах-
λех=0

0
–нулевая матрица – вектор.

(А-
λе) х = 0

Матричному
уравнению соответствует однородное
уравнение квадратной матрицей (А-λЕ).
По теореме ненулевое решение однородной
системы существует такая и только такая,
когда определитель системы равен 0.

=
0

Теорема.
Собственным значением матрицы является
решение ур-я
.
Это ур-е являетсяхарактеристическим
уравнением
матрицы А. Это многочлен степени n
относительно неизвестной λ.

Собственный
вектор при любом с ≠0, образует базис
пространства R²

Пример.

–
характеристический
многочлен.

λ=2
λ=3

Матрица
имеет 2 собственных значения. Найдем
собственные вектора.

Общее
решение:

(2с,
с), где с – любое действительное число.
То же самое, если λ=3

Замечание:

Собственные
векторы, при любом с≠0, образуют базис
пространства R².

17. Модель международной торговли (линейная модель обмена). Условия сбалансированности.

Предположим,
что n
стран или к-либо других автономных
сообществ людей осуществляют между
собой торговлю. Пусть доход i-ой
страны от торговли составляет х ден.
ед.
– доля дохода, которуюj-ая
страна тратит на закупку товара у i-ой
страны. S
– НД

A
=

Расходы

В
экономической лит-ре наз-ся структурной
матрицей торговли. Ограничимся ситуацией,
когда страна тратит все на покупку
собственных товаров и товаров из других
стран. Тогда (сумма по столбцу)

Произведение

представляет
собой выручку i-ой
страны от продажи товаров j-ой.
Поэтому суммарная выручка

i-ой
страны от продажи товаров на внутреннем
и внешнем рынке:

Сбалансированная
торговля – НД и выручка равны м-у собой.

В
матричном виде: Х(х₁,
х₂,…,
х_n)^т
– вектор доходов.

X=AX

AX=P

18. Межотраслевая модель экономики (модель Леонтьева)

Модель
предполагает, что экономика состоит
из некоторого числа взаимодействующих
отраслей, каждая из которых воображаемо
производит только один вид продукции
и использует только 1 процесс производства.

Предположим,
что имеется n
отраслей. Каждая производит продукции
в точности столько, сколько требуется
для удовлетворения потребностей других
отраслей и рынка.

– кол-во
единиц продукции, произведенной i-ой
отраслью в данном году.

–
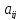
кол-во продукции i-ой
отрасли, необходимой для произ-ва 1 ед
продукции j-ой
отрасли при неизменной технологии. Этот
коэффициент пропорционально зависит
от технологии j-ой
отрасли и наз-ся коэффициентом
прямых затрат.
И сама i-ая
отрасль также использует часть своей
продукции на пр-во. Величина
идущая на потребление, др словами на
свободный рынок, наз-сяпродуктом
конечного потребления.

i-ая
отрасль вырабатывает продукции:

Например,
имеются 3 отрасли;

Объем
продукции (валовой
выпуск?)

В
балансовой модели Леонтьева объем
продукции х складывается из продукции
АХ, идущей на пр-во и потребление.
Определим У:

Тогда:
Х=АХ+У (*)

Уравнение
(*) наз-ют уравнением линейного
межотраслевого баланса.
Оно используется двояко.

В
1 случае известен валовой продукт и
нужно рас-ть вектор конечного потребления.

Во
2 случае уравнение межотраслевого
баланса используется с целью планирования.
Здесь на определенном промежутке времени
известен вектор конечного потребления
и требуется найти вектор валового
выпуска продукции.

Т.о.
в 1 случае:

(ЕХ-АХ)=У
(Е-А)*Х=У

В
случае невыраженности матрицы (Е-А)
получим: Х = (Е-А)^-1
* У

И
во 2 случае: Х = (Е-А)^-1
* У

Пример.

Данные
о работе 2-х фирм приведены в таблице.

Фирма	Поставки фирме
1-й	2-й
1	0,1	0,4
2	0,8	0,2

Пусть
ВВ продукции
.
Найдем вектор конечного потребления.

Решение.

Составим
матрицы задачи Леонтьева.

Подставим
данные в ур-е и получаем:

У=
(Е-А)*Х=

Пример
2. -//-

Пусть
задан вектор конечного потребления..
Требуется найти ВВ продукции Х.

Найдем
обратную матрицу:

(Е-А)^-1
=

Х
= (Е-А)^-1
* У =

=

19.
Построение экономико-математических
моделей и задача линейного программирования.
Задача об использовании ресурсов, задача
о диете, транспортная задача. Графический
метод решения задачи линейного
программирования с 2 переменными.

Задача
линейного программирования состоит в
нахождении такого решения системы
линейных ограничений, для которого ф-я,
рассматриваемая на мн-ве всех решений,
достигает своего наибольшего, либо
наименьшего значения. Другими словами,
в определении такого решения системы
линейных уравнений или неравенств вида:

которые
давали бы максимальную (миним) величину
линейной ф-ции

Задача
об использовании ресурсов. Предприятие
имеет 2 вида ресурсов. В нашем случае
– R₁
и R₂.
В кол-ве b₁
и b₂.
Изготавливаются 2 вида продукции T₁
и T₂.
а_ij
–
расход i
–го сырья на j-ый
вид продукции. Эта инфо задается матрицей
А.

Общий
вид задачи:

Задача
о диете

Для
животноводческого комплекса необходимо
составить такой рацион, который
удовлетворял бы суточным потребностям
животных в тех или иных питательных
веществах, был бы по возможности дешев
и состоял из имеющихся в распоряжении
продуктов.

– сколько
в-ва
находиться
в продукте

A(4*3)

Введем
величины
.

–
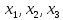
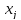
кол-во
продукта
,
которое будет употреблено для смеси.

СХ
– суточная
стоимость рациона

Составим
суточный рацион, который удовлетворял
бы потребностям и был минимальным по
стоимости.

Транспортная
задача

Пусть
необходимо перевезти однородный груз
из пунктов его пр-ва или хранения в
пункты его потребления. При этом ставиться
задача свести к минимуму транспортные
расходы.

Пусть
есть пункты поставки

И
там находиться ед груза:

Пункты
потребления

Их
потребности составляют:

стоимость
перевозки ед товара из
пункта
в

План
перевозок можно задать в таблице:

–
кол-во
груза, которое нужно перевезти из
пункта
в

Если
выполняется условие:
.
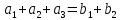
То
задача наз-ся сбалансированной. Поэтому:

Стоимость
перевозки из i-го
пункта в j-ый
равна

Т.о.:
на
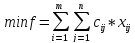
мн-ве решений системы ограничений (*).

В
общем случае, мн-во допустимых решений
представляет собой пересечение
полуплоскостей. Такое мн-во является
выпуклым.

1. В
   случае если эта область является
   многоугольником (ограничено), то
   оптимальное решение всегда сущ-ет.
   Максимальное (минимальное) значение
   ф-ции достигается в какой-либо вершине
   этого многоугольника, т.е достаточно
   определить вершины многоугольника и
   выделить ту из них, для которой значение
   ф-ции является наибольшим (либо
   наименьшим).

2. Если
   мн-во допустимых решений не содержит
   ни одной точки, то задача не имеет
   решений.

3. Если
   образует неограниченную многоугольную
   область то

   1. решение
      находиться в какой-либо вершине области
      решений

   2. заданная
      ф-ция не ограничена сверху (снизу).
      Можно выяснить по расположению линий
      уровня в конкретном случае при изменении
      значений ф-ций.

13.4. ХАРАКТЕРИСТИЧЕСКОЕ УРАВНЕНИИ КВАДРАТНОЙ МАТРИЦЫ

Пусть А = [arsl представляет собой квадратную матрицу гс-го порядка, а I — единичная матрица такого же порядка. Характеристической матрицей для А называется матрица

an — Я а12 • – а1п А —Я1 = «21 а22 — Я . • • 2 п -anl ап2 •• апп – где Я — любой множитель или параметр.

Определитель | А — Я1| матрицы, если его написать в развернутом виде, представляет собой многочлен степени п относительно Я, коэффициенты которого составлены из элементов матрицы [ars]. Член, имеющий наивысшую степень относительно Я, равен (—1)ПЯП, а свободный член равен | А|. Труднее выразить в общем виде коэффициенты при Яп-1, Яп

2, . ит. д. (см. упражнение 3). Если мы приравняем этот характеристический многочлен нулю, получим уравнение степени п относительно Я, корни которого Ях> Я2, . Яп могут быть как вещественными числами, так и попарно сопряженными комплексными числами. Мы получаем таким образом характеристическое уравнение квадратной матрицы А, и его корни называются характеристическими, или скрытыми, корнями, а иногда собственными значениями матрицы А.

Определение. Характеристическим уравнением квадратной матрицы А гс-го порядка называется уравнение

характеристические корни (или собственные значения) которого будут Ях, Я2, . Яп.

Если Яг — характеристический корень этого уравнения, так что | А — ЯД| = 0, то матрица А — ЯД является особенной. Следовательно (см. 13.1), ее строки и столбцы линейно зависимы, и можно подобрать такую систему чисел, из которых не все равны нулю, что если представить их в виде вектора-столбца

Вектор кг называется собственным вектором, соответствующим собственному значению Яг.

Свободным членом характеристического уравнения является |А|. Если матрица А неособенная, то | А| Ф 0, и ни один из характеристических корней не равен нулю. Если же матрица А особенная, то по меньшей мере один из характеристических корней равен нулю. Развивая эту мысль, мы должны доказать, что если ранг матрицы А равен г, то имеется г ненулевых и п — г нулевых характеристических корней.

Пример (а). Матрица А= —1 особенная.

ее ранг равен 2. Характеристическое уравнение этой матрицы после упрощений приводится к многочлену Xs—6А,2Ц-9А = 0, корни которого равны 3, 3 и 0. Существование- одного нулевого корня свидетельствует о том, что ранг матрицы А на единицу меньше 3*

При рассмотрении этого вопроса мы воспользуемся понятием подобных матриц. Будем рассматривать только квадратные матрицы w-го порядка. Матрицы А и В называются подобными, если можно подобрать такую неособенную матрицу Р, что В = РАР”1. Идея доказательства заключается в том, чтобы установить подобие матрицы А и некоторой диагональной матрицы X, а затем показать, что диагональные элементы матрицы X суть характеристические корни матрицы А. Выполнить это довольно сложно; в самом деле,, не всегда осуществима такая «диагонализация» матрицы А. Приведем доказательство для частного случая, взятое из книги Мёрдока [10].

Одну из посылок доказать легко: если матрица А ранга г подобна диагональной матрице X, диагональные элементы которой суть Х2, . то тогда эти элементы представляют собой характеристические корни матрицы А, причем г из них отличны от нуля. Это доказательство распадается на две части.

I. Подобные матрицы имеют один и тот же ранг и одинаковые характеристические корни.

Доказательство. Для подобных матриц А и В (ранг которых одинаков,, см. раздел 12.9) В^РАР”1, и поскольку PIP ^PP ^ I, то

В —XI — PAP”1 — X PIP”1 — Р (А — АЛ) Р1.

Далее, |Р’Ч = 1/|Р|, так что

|В — Я1| = |Р||А—АЛ|| Р”11 = | А — А, 11,

что и требовалось доказать.

Доказательство. Матрица (X — XI) также является диагональной, по ее диагонали расположены элементы (Хг — Х), <К2—Х)>. (Хп — Х). Значит,, характеристическим уравнением этой матрицы будет

что и требовалось доказать.

Из I и II следует, что если матрицы А и X (обе ранга г) подобны,, то матрица А имеет те же характеристические корни, что и матрица X, то есть (А1, Х2, . Хп). Но ранг матрицы X равен г только в том случае,, если г и только г чисел X отличны от нуля.

Задача состоит в том, чтобы «диагонализовать» матрицу А. Рассмотрим здесь только один частный случай – матрица А симметрическая, так что А’ = А. Тогда все характеристические корни матрицы А оказываются вещественными числами. Это представляет значительное упрощение, поскольку отпадают трудности, связанные с наличием комплексных элементов во взятых нами матрицах. Доказывается этот вывод следующим образом. Пусть симметрическая матрица А имеет характеристический корень к = а + ф, а сопряженный ему обозначим через А/ = а — ф. Тогда |А —Л1| = 0. Составим матрицу:

В = (А-Ы) (A-^’I) = A2-2aA + (a2 + P2)I=:(A-aI)2 + p2I,

которая является квадратной матрицей, составленной из вещественных чисел. Эта матрица особенная, поскольку из |А — Я1| = 0 следует, что | В | = 0. Значит, в соответствии с пунктом I раздела 13.2, Вх = 0 для некоторого ненулевого вектора х, а значит, х’Вх = х’0 = 0. Вместе с тем

х’Вх = х’ (А – a I)2 х + х’ Р2 їх.

Легко* видеть, что первое слагаемое правой части, будучи квадратичной формой, неотрицательно; второе слагаемое |32х’1х = (32х’х, разлагая по элемента^ вектора х, можно представить в виде $*(x + xl + .. . +Яп). Значит, если х есть ненулевой вектор, то х’Вх = 0 только в том случае, если равны нулю как первое слагаемое, то есть [ А — al | = 0, так и второе слагаемое, то есть (3 = 0. Следовательно, к = а и представляет собой вещественное число, что и требовалось доказать.

Обозначим вещественные характеристические корни симметрической матрицы А через к1У . кп и построим, используя их, диагональную матрицу.

Для любой симметрической матрицы А можно подобрать такую ортогональную матрицу Р, что Р

АР представляет собой диагональную матрицу X, построенную на характеристических корнях матрицы А. Из Р

гАР = Х следует, что А=Р^Р-1, и что матрица А подобна диагональной матрице X; наша задача тогда решена. Доказывается приведенное выше положение следующим образом.

Пусть ненулевой вектор хг является собственным вектором, соответствующим характеристическому корню kr- матрицы А, то есть (А— А,г1)хг = 0. Следовательно,

Axr = krxr (r = 1, 2, . (1)

Составим из векторов хг (г = 1, 2, . п), взятых в качестве столбцов, матрицу Р. Тогда п уравнений (1) представятся одним матричным уравнением

Транспонируем обе части уравнения (2); поскольку матрицы А и к симметрические, то есть А’ = А и к’ = к, получаем

Следовательно, правые части уравнений (2) и (3) равны между собой:

а это возможно только в том случае, если РР’ = 1, или Р’ = Р-1. Значитг матрица Р ортогональная, и уравнение (2) можно представить в виде:

что и требовалось доказать.

Всю совокупность полученных результатов можно теперь объединить в следующем предложении: Симметрическая матрица А /г-го порядка и ранга г имеет п вещественных характеристических корней, образующих диагональные элементы диагональной матрицы X, подобной матрице А:

А = РЯА”1, где Р — некоторая ортогональная матрйца г характеристических корней отличны от нуля, а п — г нулевые. Продемонстрируем это на следующем примере.

Г 2 -1 -П Матрица А=| —1 2 —1 I симметрическая, ее ранг равен 2;

характеристические корни этой матрицы [см. выше, пример (а)] равны 3, 3 и 0« Рассмотрим матрицу P, ортогональность которой доказана в примере (б) раздела 12.9: Дважды выполнив операцию умножения на А, а затем результат на Р, получим

Р = 1 1 1 ” Г 1 і 0

1 /з 1 , так что Р’ —P г = /2 1 /2 1 у 2

1 /6 1/3 J L/S /з /3 , матриц, т.

[ 3 0 0 1 _ 0 3 0 =х.

о о о J Эта диагональная матрица образована из характеристических корней ^матрицы А« Значит, матрица А преобразована в подобную ей диагональную матрицу X ,с помощью операции

где Р—приведенная выше ортогональная матрица. Отметим, что характеристическому корню 3 соответствует тако,й собственный вектор x = (xv х2, х3), что

Г-1 -і -її (А—ЗІ) х = I —1 —1 —1 х=0.

L—і -і -і J После операции умножения каждый из элементов полученной матрицы оказывается равным —(яі+^г+яз); следовательно, он должен быть равен нулю. Значит, х = (1, —1,0) и х= (1, 1, —2) являются собственными векторами матрицы А. Нужно искать два значения собственных векторов, так как существуют два характеристических корня, равные 3 (кратность равна двум). Возьмем два приведенных выше значения собственных векторов, элементы которых пропорциональны соответственно элементам первого и второго столбцов матрицы Р. Третьему характеристическому корню матрицы А (нулю) соответствует собственный вектор (1, 1, 1), элементы которого пропорциональны элементам третьего столбца матрицы Р.

А)”1 положительна в том

Значительный интерес представляют и квадратные матрицы другого вида, все элементы которых неотрицательны (А>0). Такими матрицами часто пользуются в экономике. Пусть неотрицательная матрица А является и неразложимой — в том смысле, как это понимается в пункте V раздела 12.9. Тогда матрица (И — А) или характеристическое уравнение для матрицы А, обладает рядом свойств, установленных Дебрэ и Герштейном [4]. Если — наибольший из характеристических корней матрицы А, то он и наибольший из корней уравнения |Я1 — А| = 0, первый член которого равен Хп. Следовательно, *если X > Хт, то | XI — А | > 0. Дебрэ и Герштейн первыми сумели показать, что все главные квадратные подматрицы матрицы Х I — А|, то есть такие подматрицы, в которых опущены столбцы и строки одних и тех же номеров, имеют положительные значения определителей в том и только в том

случае, если X > Хт.

Задачи и упражнения

1. Найти характеристические корни матриц

2. Показать, что характеристические корни симметрической пеособепной матрицы j^J * J равны 1 и —1 и что, следовательно, она подобна матрице Х = ^J .

На этом основании показать, что ортогональная матрица Р в равенстве А = РА,Р-1 имеет следующий вид:

Р== 1 1 , Y2 /2 1 1 L/2 /2J 3. Пусть A = [ars] — любая квадратная матрица третьего порядка. Показать, что | А — XI |= — А3+/?!А,2—Рък^-Рз’

а32 а33 а31 Л33

Представить полученный результат в общем виде для квадратной матрицы А любого порядка п.

4. Матрица А является ортогональной (АА’ = 1). Показать, что А-Х1

=0, а следовательно,

Доказать, что если |А — ХД|=0, То справедливо и осли X—характеристический корень ортогональной матрицы, то характеристическим корнем является и І/Х.

[spoiler title=”источники:”][/spoiler]