Хэш-таблицы
Хэш-таблица (перемешанная
таблица, таблица с вычисляемыми адресами)
– это динамическое
множество, поддерживающее операции
добавления, поиска и удаления элемента
и использующее специальные
методы адресации.
Основное
отличие таблиц от других динамических
множеств – вычисление
адреса элемента
по значению ключа.
Идея
хэш-реализации состоит в том, что работа
с одним большим массивом сводится к
работе с некоторым количеством небольших
множеств.

Например,
записная книжка. Страницы книжки помечены
буквами. Страница, помеченная некоторой
буквой, содержит фамилии, начинающиеся
с этой буквы. Большое множество фамилий
разбито на 28 подмножеств. При поиске
книжка сразу открывается на нужной
букве и поиск ускоряется.
В
программировании хэш-таблица –
это структура
данных, которая хранит пары (ключ или
индекс + значение) и с которой выполняются
три операции: добавление новой пары,
поиск и удаление пары по ключу.
Поиск
в хэш-таблицах осуществляется
в два этапа:
первый
шаг – вычисление хэш-функции, которая
преобразует ключ
поиска в табличный адрес:
второй
шаг – процесс разрешения конфликтов
при обработке таких ключей.
Если
разным
значениям
ключей таблицы хэш-функция генерирует
одинаковые
адреса, то говорят, что
возникает коллизия (конфликт,
столкновение).
Хэш-функции
Основное
назначение хэш-функции – поставить в
соответствие различным ключам
по возможности разные
не отрицательные целые
числа.
Хэш-функция
тем лучше,
чем меньше
одинаковых
значений она генерирует.
Хэш-функцию
надо подобрать таким образом, чтобы
выполнялись следующие свойства:
-
хэш-функция
определена на элементах множества и
принимает целые
неотрицательные
значения; -
хэш-функцию
легко
вычислить; -
хэш-функция
может принимать различные
значения приблизительно с равной
вероятностью
(минимизация
коллизий); -
на
близких
значениях
аргумента
хэш-функция
принимает далекие
друг от друга значения.
Чтобы
построить хорошую хэш-функцию надо
знать распределение ключей. Если
распределение ключей известно, то в
идеальном случае, случае плотность
распределения ключей и плотность
распределения значений хэш-функции
должны быть идентичны.
Пусть
p(key)
–
плотность распределения запросов
ключей. Тогда в идеальном случае плотность
распределения запросов входов
таблицыg(H(key))д.
быть такой, чтобы в среднем число
элементов, кот. надо пройти в цепочках
близнецов, было минимальным.
Пример.
Пусть
имеется множество ключей
{0,
1, 4, 5, 6, 7, 8, 9, 15, 20, 30, 40}
и
пусть таблица допускает 4
входа.
Можно
построить хэш-функцию:
h(key)
= key
% 4.
Тогда
получатся следующие адреса
для входов
{0,
1, 2, 3}
таблицы:
-
key
0
1
4
5
6
7
8
9
15
20
30
40
h(key)
0
1
0
1
2
3
0
1
3
0
0
0
-
Номер
входа0
1
2
3
Максимальная
длина цепочки6
3
1
2
%
обращений50
25
8
17
Если
считать, что в среднем при поиске
надо про-смотреть половину
списка, то потребуется пройти примерно
3·0,5+1,5·0,25+0,5·0,08+1·0,17
≈ 2,1 элемента
списка.
Пример
с другой хэш-функцией.

|
key |
0 |
1 |
4 |
5 |
6 |
7 |
8 |
9 |
15 |
20 |
30 |
40 |
|
h(key) |
0 |
0 |
0 |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
|
Номер |
0 |
1 |
2 |
3 |
|
% |
25 |
25 |
25 |
25 |
В
среднем потребуется пройти 4·1,5·0,25
= 1,5 элемента
списка.
Если
это информационно-поисковая система,
то повысится ее производительность при
поиске примерно на 25%.
Методы построения хэш-функций
Модульное
хэширование
Простой,
эффективный и часто используемый метод
хэширования.
Размер
таблицы выбирается в виде простого
числа m
и
вычисляется хэш-функция как остаток
от деления:
h(key)
= key
%
m
key –
целое числовое значение ключа,
m
–
число хэш-значений (входов хэш-таблицы).
Такая
функция называется модульной
и изменяется от 0
до
(m
– 1).
Модульная
хэш-функция
на языке С++:
typedef
int
HashIndexType;
HashIndexType
Hash(int
Key)
{
return
Key
% m;
}
Пример
key
= {1,
3,
56,
4,
32,
40,
23,
7,
41,13,
6,7}
Пусть
m
= 5
h(key)
=
{1, 3, 1, 4, 2, 0, 3, 2, 1, 3, 1, 2}
Важен
выбор m.
Чтобы
получить случайное распределение ключей
надо брать простое
число.
Мультипликативный
метод
Хэш-функция:
h(key)
= [m
(key·A·mod1)]
0
< A
< 1 –
константа.
Число
входов таблицы m
рекомендуется
выбирать как степень числа 2.
В
качестве А
некоторые
авторы
рекомендуют
выбирать золотое сечение: A
= (√5 -1) / 2 ≈
0.618
12mod5
= 2
(остаток от деления 12 на 5).
5,04mod1
=
0,04
(выделяется
дробная часть)
Пример
key
= 123456
m
=10000
A
= 0,6180339887499
= 0,618…
h(key)
=
[10000·(123456·0,618…mod1)]
=
=
[10000·(76500,004…mod1)]
=
=
[10000·0,0041151…]
= [41,151…] = 41
Аддитивный
метод
Используется
для строк
переменной длины (размер таблицы m
равен 256).
typedef
unsigned char HashIndexType;
HashIndexType
Hash(char *str)
{
HashIndexType h = 0;
while
(*str)
h
+= (*str)++;
return
h;
}
Недостаток
аддитивного метода: не различаются
схожие слова и анаграммы, т.е. h(XY)
= h(YX)
Аддитивный
метод,
в котором ключом является символьная
строка. В хеш-функции строка преобразуется
в целое суммированием всех символов и
возвращается остаток от деления
на m (обычно
размер таблицы m =
256).int
h(char
*key,
int
m)
{int
s
= 0;while(*key)s
+= *key++;return
s % m;}Коллизии возникают в строках,
состоящих из одинакового набора символов,
например, abc и cab.Данный
метод можно несколько модифицировать,
получая результат, суммируя только
первый и последний символы строки-ключа.int
h(char
*key,
int
m)
{int
len
= strlen(key),
s
= 0;if(len < 2) // Если длина ключа равна 0 или
1,s
= key[0];
// возвратить key[0]else
s
= key[0]
+ key[len–1];return
s % m;}В этом случае коллизии будут возникать
только в строках, например, abc и amc.
хеш-функция
принимает ключ и вычисляет по нему адрес
в таблице (адресом может быть индекс в
массиве, к которому прикреплены цепочки),
то есть она, например, из строки “abcd”
может получить число 3, а из строки “efgh”
может получить число 7
а
потом первая структура цепочки берётся
через hash[3], или через hash[7]
дальше
идёт поиск по цепочке, пока в цепочке
структур из hash[3] не будет найдено “abcd”,
или в цепочке структур из hash[7] не будет
найдено “efgh”
когда
структура с “abcd” найдена, берутся
и возвращаются остальные её данные, или
она вообще вся возвращается (адрес её),
чтобы можно было остальные данные из
неё взять
а
цепочка структур создаётся потому, что
многие разные ключи, имеют один и тот
же адрес в таблице, то есть, например,
хеш-функция для “abcd” может выдать
3 и для “zxf9” тоже может выдать 3,
таким образом они сцепляются в цепочку,
которая повисает на третьем индексе
массива……
В
массиве H хранятся сами пары ключ-значение.
Алгоритм вставки элемента проверяет
ячейки массива H в некотором порядке до
тех пор, пока не будет найдена первая
свободная ячейка, в которую и будет
записан новый элемент.
Алгоритм
поиска просматривает ячейки хеш-таблицы
в том же самом порядке, что и при вставке,
до тех пор, пока не найдется либо элемент
с искомым ключом, либо свободная ячейка
(что означает отсутствие элемента в
хеш-таблице).
Исключающее
ИЛИ
Используется
для строк переменной длины. Метод
аналогичен аддитивному, но различает
схожие слова. Заключается в том, что к
элементам строки последовательно
применяется операция «исключающее ИЛИ»
typedef
unsigned char HashIndexType;
unsigned
char Rand8[256];
HashIndexType
Hash(char *str)
{
unsigned char h = 0;
while
(*str) h = Rand8[h ^ (*str)++];
return
h;
}
Здесь
Rand8
– таблица
из 256 восьмибитовых случайных чисел.
размер
таблицы
<= 65536
typedef
unsigned short int HashIndexType;
unsigned
char Rand8[256];
HashIndexType
Hash(char *str)
{
HashIndexType h; unsigned char h1, h2;
if
(*str == 0) return 0;
h1
= *str; h2 = *str + 1; str++;
while
(*str)
{
h1 = Rand8[h1 ^ *str]; h2 = Rand8[h2 ^ *str];
str++;
}
h
= ((HashIndexType)h1 << 8) | (HashIndexType)h2;
return
h % HashTableSize }
Универсальное
хэширование
Подразумевает
случайный
выбор хэш-функции из некоторого множества
во время выполнения
программы.
Если
в мультипликативном методе использовать
в качестве А
последовательность случайных
значений вместо фиксированного числа,
то получится универсальная хэш-функция.
Однако
время на генерирование случайных чисел
будет слишком большим.
Можно
использовать псевдослучайные
числа.
//
генератор псевдослучайных чисел
typedef
int
HashIndexType;
HashIndexType
Hash(char
*v, int m)
{
int h, a = 31415, b = 27183;
for(h
= 0; *v
!= 0;
v++, a = a*b % (m – l))
h
= (a*h + *v) % m;
return
(h < 0) ? (h + m) : h;
}
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Хеш-функция, что это такое?
Время на прочтение
8 мин
Количество просмотров 117K

Приветствую уважаемого читателя!
Сегодня я хотел бы рассказать о том, что из себя представляет хеш-функция, коснуться её основных свойств, привести примеры использования и в общих чертах разобрать современный алгоритм хеширования SHA-3, который был опубликован в качестве Федерального Стандарта Обработки Информации США в 2015 году.
Общие сведения
Криптографическая хеш-функция – это математический алгоритм, который отображает данные произвольного размера в битовый массив фиксированного размера.
Результат, производимый хеш-функцией, называется «хеш-суммой» или же просто «хешем», а входные данные часто называют «сообщением».
Для идеальной хеш-функции выполняются следующие условия:
а) хеш-функция является детерминированной, то есть одно и то же сообщение приводит к одному и тому же хеш-значению
b) значение хеш-функции быстро вычисляется для любого сообщения
c) невозможно найти сообщение, которое дает заданное хеш-значение
d) невозможно найти два разных сообщения с одинаковым хеш-значением
e) небольшое изменение в сообщении изменяет хеш настолько сильно, что новое и старое значения кажутся некоррелирующими
Давайте сразу рассмотрим пример воздействия хеш-функции SHA3-256.
Число 256 в названии алгоритма означает, что на выходе мы получим строку фиксированной длины 256 бит независимо от того, какие данные поступят на вход.
На рисунке ниже видно, что на выходе функции мы имеем 64 цифры шестнадцатеричной системы счисления. Переводя это в двоичную систему, получаем желанные 256 бит.
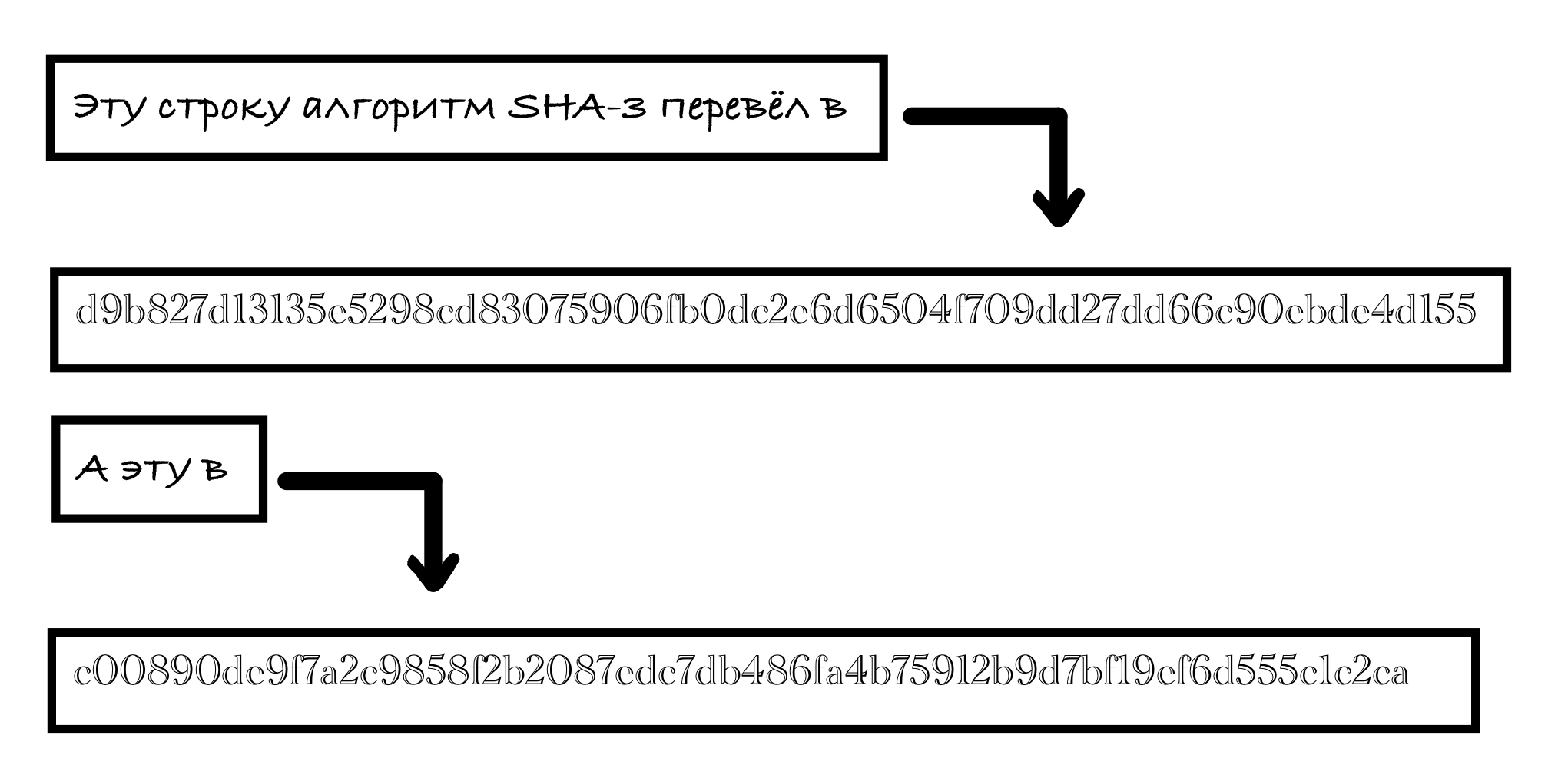
Любой заинтересованный читатель задаст себе вопрос: “А что будет, если на вход подать данные, бинарный код которых во много раз превосходит 256 бит?”
Ответ таков: на выходе получим все те же 256 бит!
Дело в том, что 256 бит – это соответствий, то есть
различных входов имеют свой уникальный хеш.
Чтобы прикинуть, насколько велико это значение, запишем его следующим образом:
Надеюсь, теперь нет сомнений в том, что это очень внушительное число!
Поэтому ничего не мешает нам сопоставлять длинному входному массиву данных массив фиксированной длины.
Свойства
Криптографическая хеш-функция должна уметь противостоять всем известным типам криптоаналитических атак.
В теоретической криптографии уровень безопасности хеш-функции определяется с использованием следующих свойств:
Pre-image resistance
Имея заданное значение h, должно быть сложно найти любое сообщение m такое, что
Second pre-image resistance
Имея заданное входное значение , должно быть сложно найти другое входное значение
такое, что
Collision resistance
Должно быть сложно найти два различных сообщения и
таких, что
Такая пара сообщений и
называется коллизией хеш-функции
Давайте чуть более подробно поговорим о каждом из перечисленных свойств.
Collision resistance. Как уже упоминалось ранее, коллизия происходит, когда разные входные данные производят одинаковый хеш. Таким образом, хеш-функция считается устойчивой к коллизиям до того момента, пока не будет обнаружена пара сообщений, дающая одинаковый выход. Стоит отметить, что коллизии всегда будут существовать для любой хеш-функции по той причине, что возможные входы бесконечны, а количество выходов конечно. Хеш-функция считается устойчивой к коллизиям, когда вероятность обнаружения коллизии настолько мала, что для этого потребуются миллионы лет вычислений.
Несмотря на то, что хеш-функций без коллизий не существует, некоторые из них достаточно надежны и считаются устойчивыми к коллизиям.
Pre-image resistance. Это свойство называют сопротивлением прообразу. Хеш-функция считается защищенной от нахождения прообраза, если существует очень низкая вероятность того, что злоумышленник найдет сообщение, которое сгенерировало заданный хеш. Это свойство является важным для защиты данных, поскольку хеш сообщения может доказать его подлинность без необходимости раскрытия информации. Далее будет приведён простой пример и вы поймете смысл предыдущего предложения.
Second pre-image resistance. Это свойство называют сопротивлением второму прообразу. Для упрощения можно сказать, что это свойство находится где-то посередине между двумя предыдущими. Атака по нахождению второго прообраза происходит, когда злоумышленник находит определенный вход, который генерирует тот же хеш, что и другой вход, который ему уже известен. Другими словами, злоумышленник, зная, что пытается найти
такое, что
Отсюда становится ясно, что атака по нахождению второго прообраза включает в себя поиск коллизии. Поэтому любая хеш-функция, устойчивая к коллизиям, также устойчива к атакам по поиску второго прообраза.
Неформально все эти свойства означают, что злоумышленник не сможет заменить или изменить входные данные, не меняя их хеша.
Таким образом, если два сообщения имеют одинаковый хеш, то можно быть уверенным, что они одинаковые.
В частности, хеш-функция должна вести себя как можно более похоже на случайную функцию, оставаясь при этом детерминированной и эффективно вычислимой.

Применение хеш-функций
Рассмотрим несколько достаточно простых примеров применения хеш-функций:
• Проверка целостности сообщений и файлов
Сравнивая хеш-значения сообщений, вычисленные до и после передачи, можно определить, были ли внесены какие-либо изменения в сообщение или файл.
• Верификация пароля
Проверка пароля обычно использует криптографические хеши. Хранение всех паролей пользователей в виде открытого текста может привести к массовому нарушению безопасности, если файл паролей будет скомпрометирован. Одним из способов уменьшения этой опасности является хранение в базе данных не самих паролей, а их хешей. При выполнении хеширования исходные пароли не могут быть восстановлены из сохраненных хеш-значений, поэтому если вы забыли свой пароль вам предложат сбросить его и придумать новый.
• Цифровая подпись
Подписываемые документы имеют различный объем, поэтому зачастую в схемах ЭП подпись ставится не на сам документ, а на его хеш. Вычисление хеша позволяет выявить малейшие изменения в документе при проверке подписи. Хеширование не входит в состав алгоритма ЭП, поэтому в схеме может быть применена любая надежная хеш-функция.
Предлагаю также рассмотреть следующий бытовой пример:
Алиса ставит перед Бобом сложную математическую задачу и утверждает, что она ее решила. Боб хотел бы попробовать решить задачу сам, но все же хотел бы быть уверенным, что Алиса не блефует. Поэтому Алиса записывает свое решение, вычисляет его хеш и сообщает Бобу (сохраняя решение в секрете). Затем, когда Боб сам придумает решение, Алиса может доказать, что она получила решение раньше Боба. Для этого ей нужно попросить Боба хешировать его решение и проверить, соответствует ли оно хеш-значению, которое она предоставила ему раньше.
Теперь давайте поговорим о SHA-3.

SHA-3
Национальный институт стандартов и технологий (NIST) в течение 2007—2012 провёл конкурс на новую криптографическую хеш-функцию, предназначенную для замены SHA-1 и SHA-2.
Организаторами были опубликованы некоторые критерии, на которых основывался выбор финалистов:
• Безопасность
Способность противостоять атакам злоумышленников
• Производительность и стоимость
Вычислительная эффективность алгоритма и требования к оперативной памяти для программных реализаций, а также количество элементов для аппаратных реализаций
• Гибкость и простота дизайна
Гибкость в эффективной работе на самых разных платформах, гибкость в использовании параллелизма или расширений ISA для достижения более высокой производительности
В финальный тур попали всего 5 алгоритмов:
• BLAKE
• Grøstl
• JH
• Keccak
• Skein
Победителем и новым SHA-3 стал алгоритм Keccak.
Давайте рассмотрим Keccak более подробно.
Keccak
Хеш-функции семейства Keccak построены на основе конструкции криптографической губки, в которой данные сначала «впитываются» в губку, а затем результат Z «отжимается» из губки.
Любая губчатая функция Keccak использует одну из семи перестановок которая обозначается
, где
перестановки представляют собой итерационные конструкции, состоящие из последовательности почти одинаковых раундов. Число раундов
зависит от ширины перестановки и задаётся как
где
В качестве стандарта SHA-3 была выбрана перестановка Keccak-f[1600], для неё количество раундов
Далее будем рассматривать
Давайте сразу введем понятие строки состояния, которая играет важную роль в алгоритме.
Строка состояния представляет собой строку длины 1600 бит, которая делится на и
части, которые называются скоростью и ёмкостью состояния соотвественно.
Соотношение деления зависит от конкретного алгоритма семейства, например, для SHA3-256
В SHA-3 строка состояния S представлена в виде массива слов длины
бит, всего
бит. В Keccak также могут использоваться слова длины
, равные меньшим степеням 2.
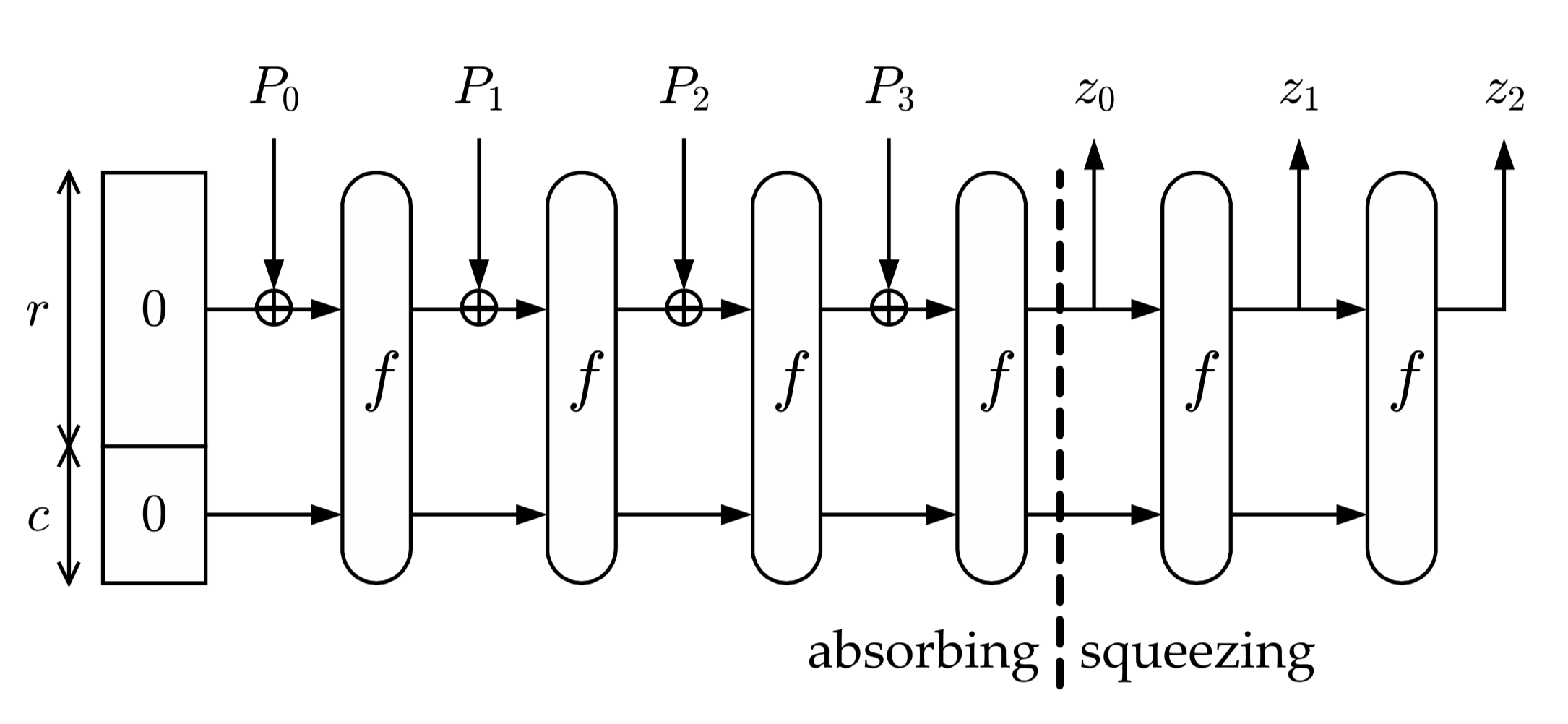
Алгоритм получения хеш-функции можно разделить на несколько этапов:
• С помощью функции дополнения исходное сообщение M дополняется до строки P длины кратной r
• Строка P делится на n блоков длины
• «Впитывание»: каждый блок дополняется нулями до строки длиной
бит (b = r+c) и суммируется по модулю 2 со строкой состояния
, далее результат суммирования подаётся в функцию перестановки
и получается новая строка состояния
, которая опять суммируется по модулю 2 с блоком
и дальше опять подаётся в функцию перестановки
. Перед началом работы криптографической губки все элементы
равны 0.
• «Отжимание»: пока длина результата меньше чем
, где
– количество бит в выходном массиве хеш-функции,
первых бит строки состояния
добавляется к результату
. После каждой такой операции к строке состояния применяется функция перестановок
и данные продолжают «отжиматься» дальше, пока не будет достигнуто значение длины выходных данных
.
Все сразу станет понятно, когда вы посмотрите на картинку ниже:
Функция дополнения
В SHA-3 используется следующий шаблон дополнения 10…1: к сообщению добавляется 1, после него от 0 до r – 1 нулевых бит и в конце добавляется 1.
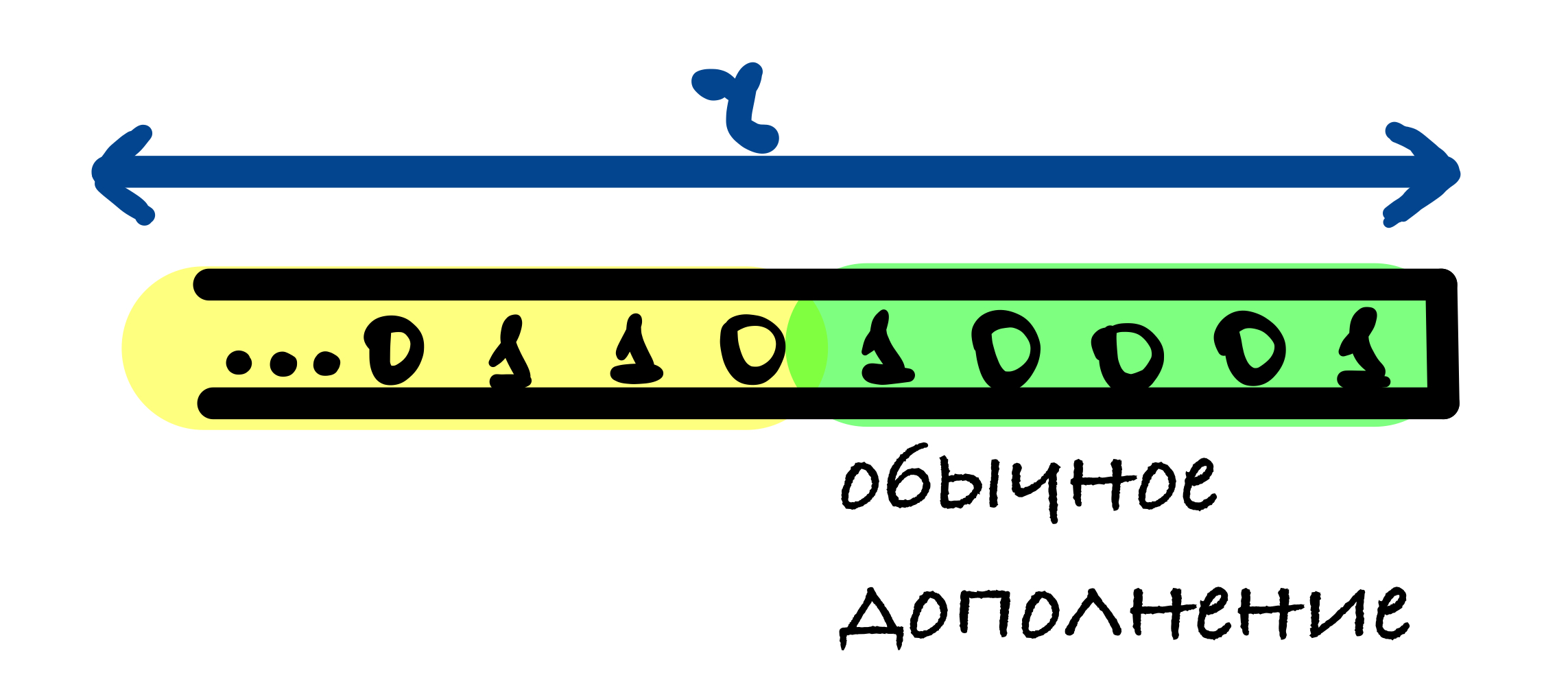
r – 1 нулевых бит может быть добавлено, когда последний блок сообщения имеет длину r – 1 бит. В этом случае последний блок дополняется единицей и к нему добавляется блок, состоящий из r – 1 нулевых бит и единицы в конце.
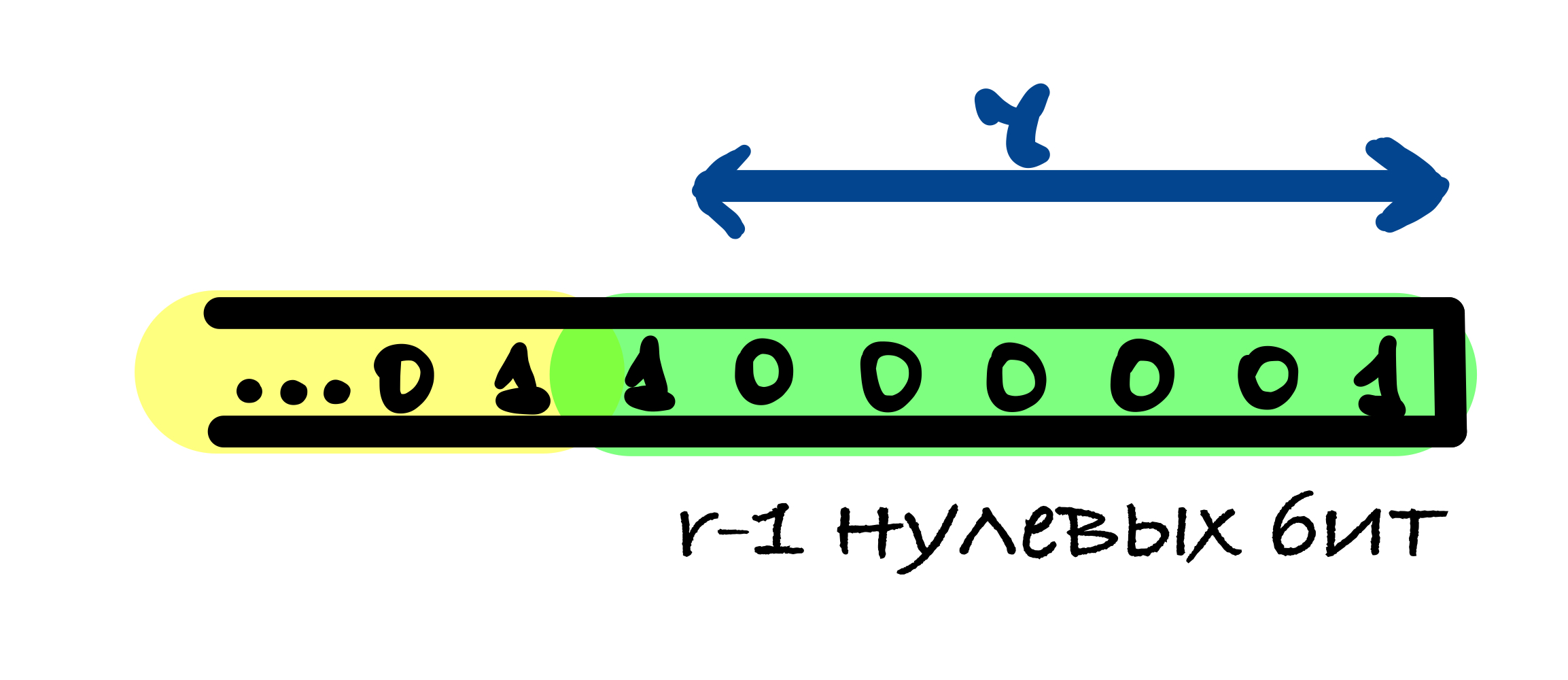
Если длина исходного сообщения M делится на r, то в этом случае к сообщению добавляется блок, начинающийся и оканчивающийся единицами, между которыми находятся r – 2 нулевых бит. Это делается для того, чтобы для сообщения, оканчивающегося последовательностью бит как в функции дополнения, и для сообщения без этих бит значения хеш-функции были различны.
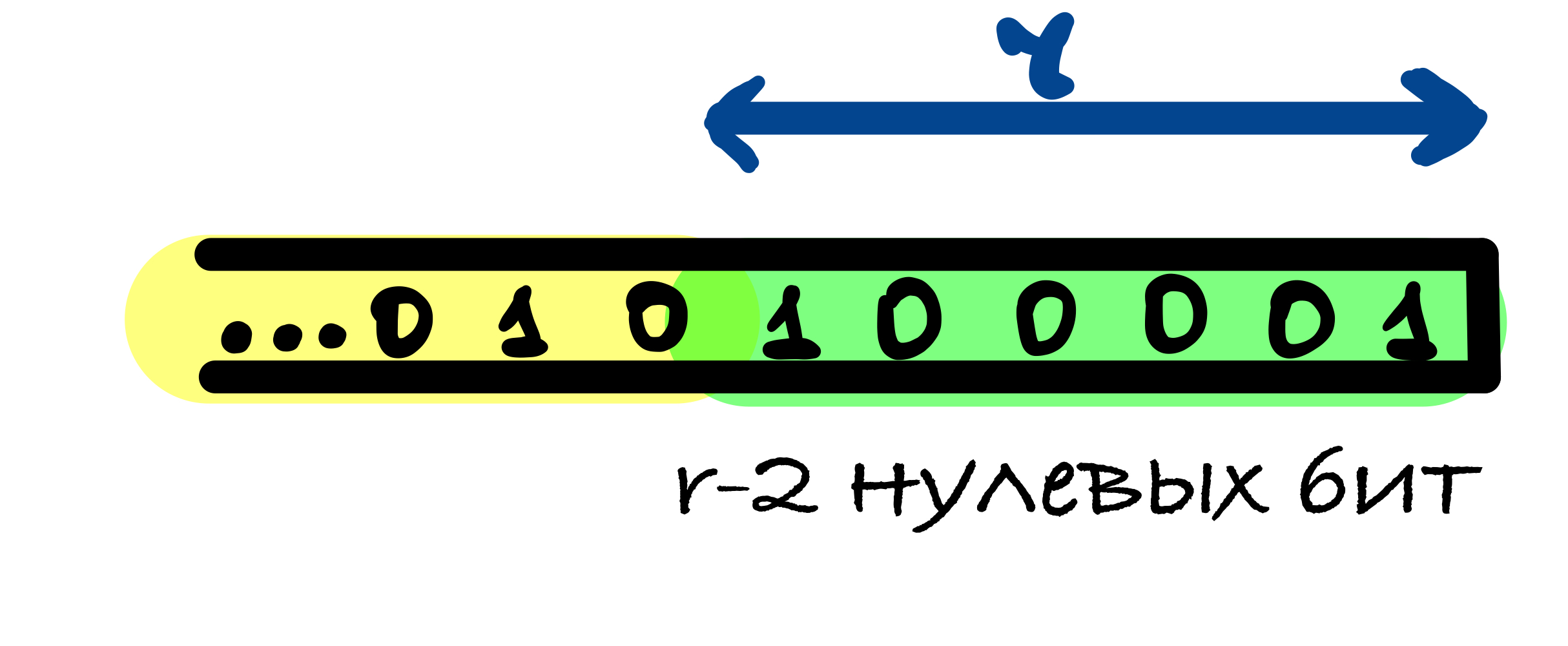
Первый единичный бит в функции дополнения нужен, чтобы результаты хеш-функции от сообщений, отличающихся несколькими нулевыми битами в конце, были различны.
Функция перестановок
Базовая функция перестановки состоит из раундов по пять шагов:
-
Шаг
-
Шаг
-
Шаг
-
Шаг
-
Шаг
Тета, Ро, Пи, Хи, Йота
Далее будем использовать следующие обозначения:
Так как состояние имеет форму массива
, то мы можем обозначить каждый бит состояния как
Обозначим результат преобразования состояния функцией перестановки
Также обозначим функцию, которая выполняет следующее соответствие:
– обычная функция трансляции, которая сопоставляет биту
бит
,
где – длина слова (64 бит в нашем случае)
Я хочу вкратце описать каждый шаг функции перестановок, не вдаваясь в математические свойства каждого.
Шаг
Эффект отображения можно описать следующим образом: оно добавляет к каждому биту
побитовую сумму двух столбцов
и
Схематическое представление функции:
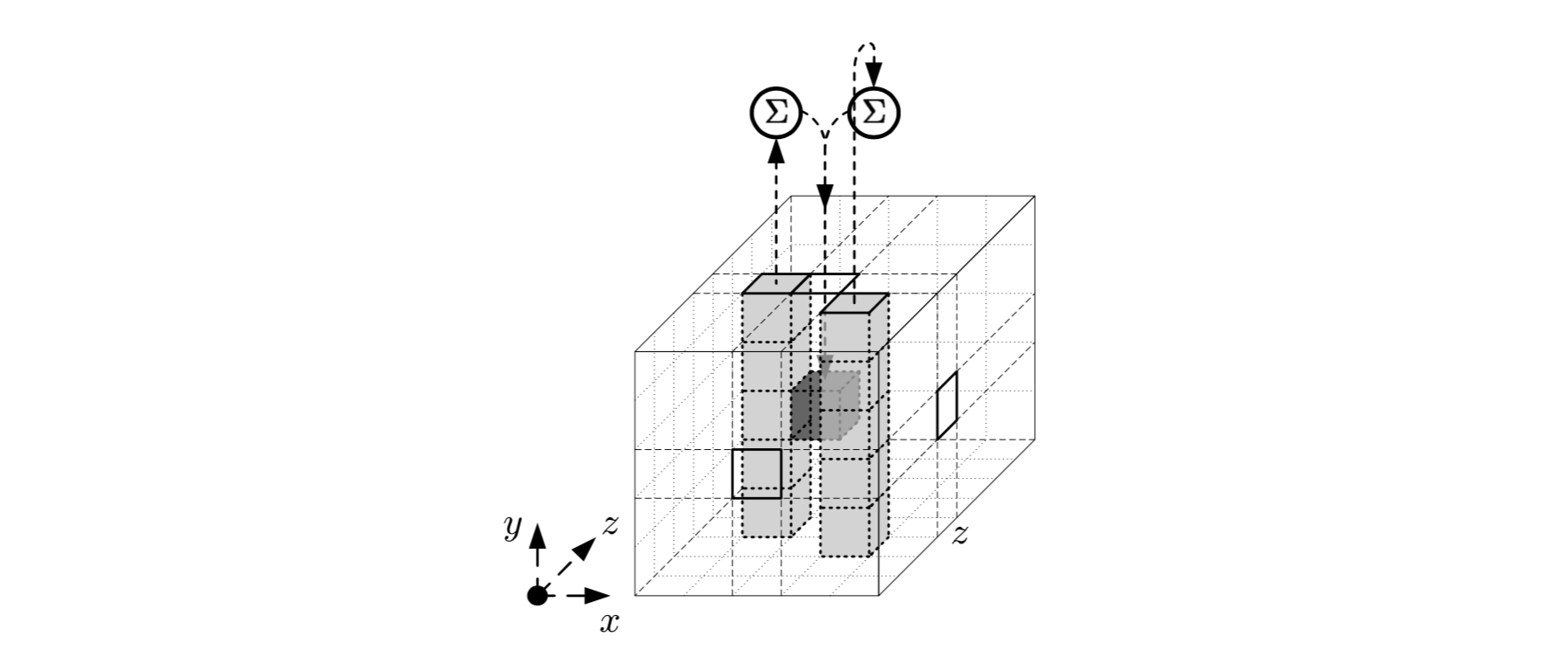
Псевдокод шага:

Шаг
Отображение направлено на трансляции внутри слов (вдоль оси z).
Проще всего его описать псевдокодом и схематическим рисунком:

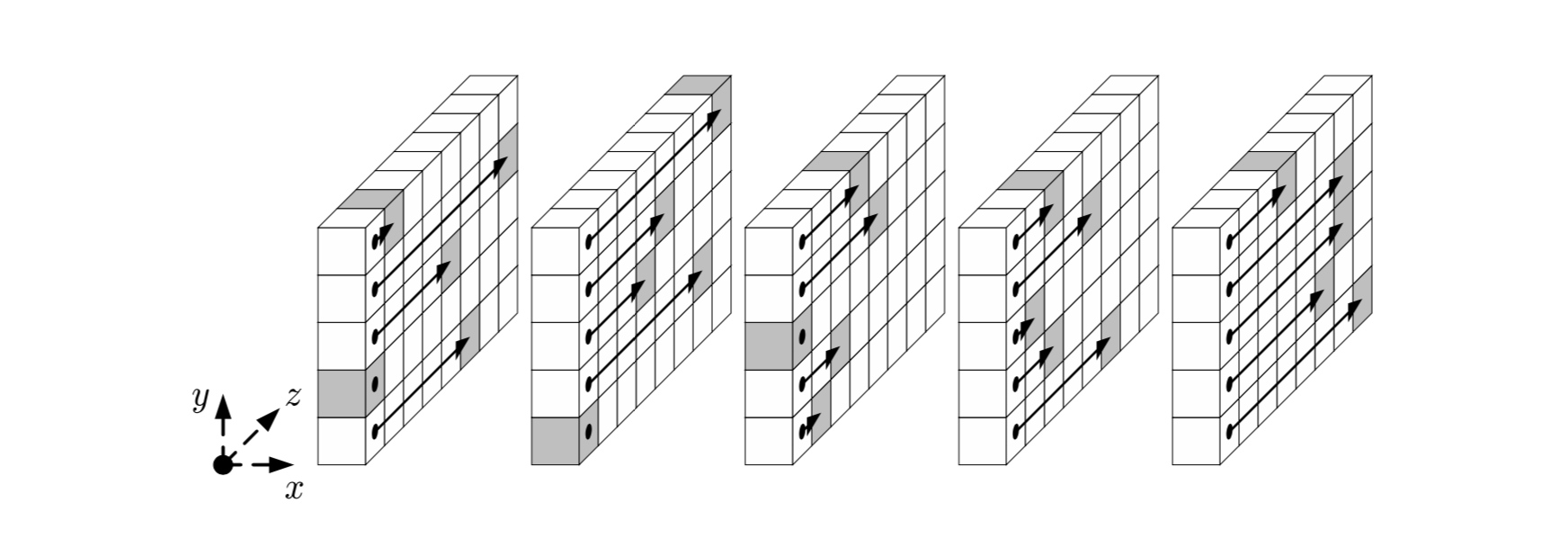
Шаг
Шаг представляется псевдокодом и схематическим рисунком:


Шаг
Шаг является единственный нелинейным преобразованием в
Псевдокод и схематическое представление:

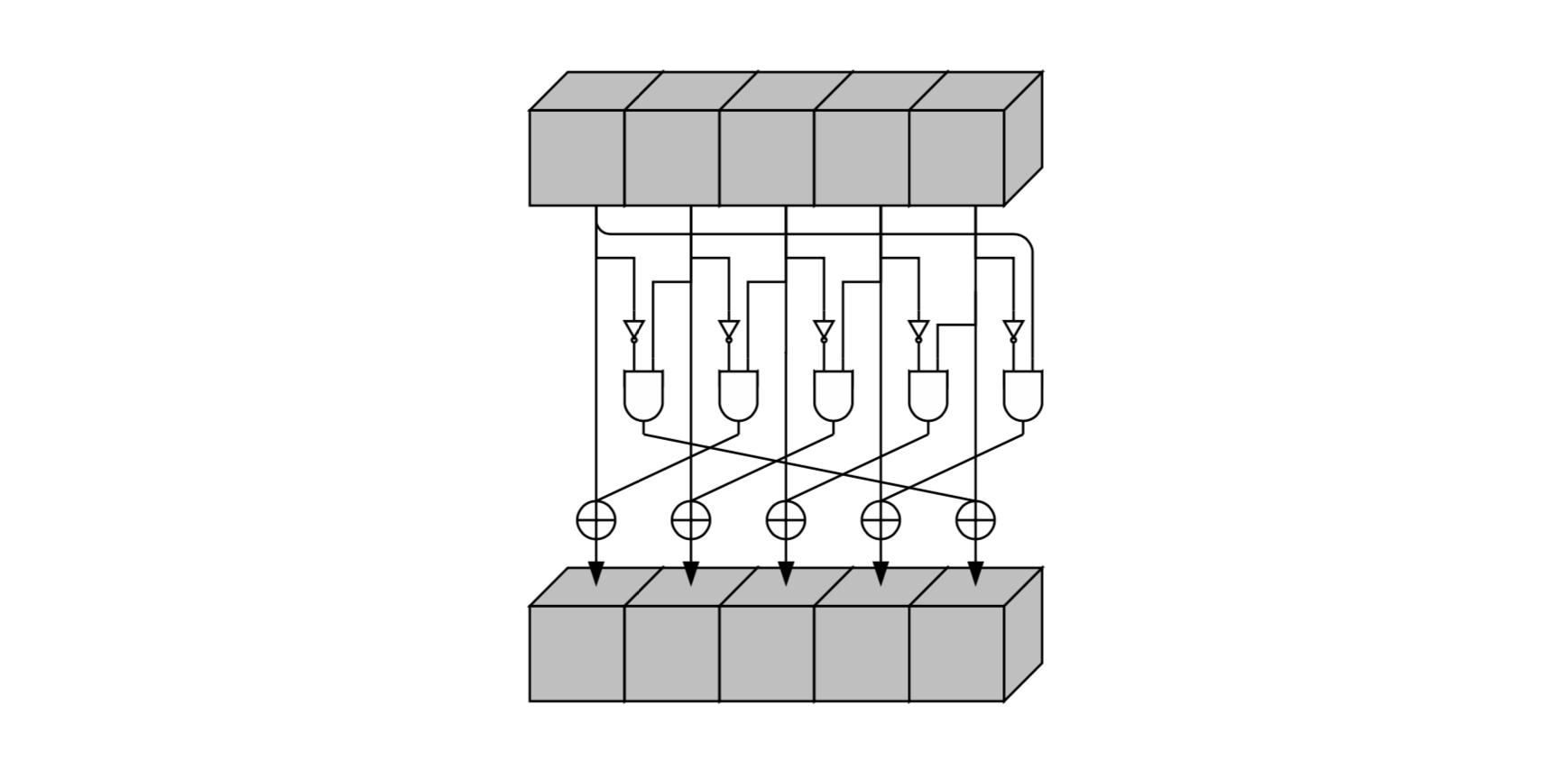
Шаг
Отображение состоит из сложения с раундовыми константами и направлено на нарушение симметрии. Без него все раунды
были бы эквивалентными, что делало бы его подверженным атакам, использующим симметрию. По мере увеличения
раундовые константы добавляют все больше и больше асимметрии.
Ниже приведена таблица раундовых констант для
бит

Все шаги можно объединить вместе и тогда мы получим следующее:


Где константы являются циклическими сдвигами и задаются таблицей:
Итоги
В данной статье я постарался объяснить, что такое хеш-функция и зачем она нужна
Также в общих чертах мной был разобран принцип работы алгоритма SHA-3 Keccak, который является последним стандартизированным алгоритмом семейства Secure Hash Algorithm
Надеюсь, все было понятно и интересно
Всем спасибо за внимание!
Курс по структурам данных: https://stepik.org/a/134212
На прошлом занятии мы в целом
познакомились с работой хэш-таблиц. Теперь пришло время затронуть важный
вопрос, как найти хорошую хэш-функцию? И что значит слово «хорошая»?
Как мы с вами
уже говорили, на вход алгоритма хэширования подается некий ключ, например, «d». На выходе
получаем индекс ячейки массива, куда записывается значение этого ключа:
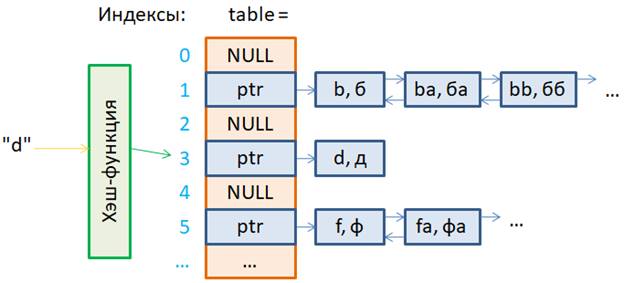
Так вот, в
качестве ключей хэш-таблиц можно использовать любую байтовую
последовательность. На уровне компьютера – это она воспринимается, как конечная
последовательность из целых чисел в диапазоне от 0 до 255 включительно,
например (в соответствии с кодовой таблицей ASCII):
“for” –
“102, 111, 114”
“53$%!”
– “53, 51, 36, 37, 33”
И так для любой
байтовой последовательности. Затем, над этими числами выполняются какие-либо
алгоритмические и математические операции так, чтобы свести все к одному числу k, как правило,
целому и неотрицательному. После этого полученное число передается в качестве
аргумента непосредственно в функцию хэширования, которая возвращает индекс
массива:
i = h(k)
Вот основные этапы
преобразования начального ключа в индекс таблицы при хэшировании. На этом
занятии мы с вами сосредоточимся непосредственно на функции h(k), а ключами
будем считать некие числа k. Вопрос о преобразовании
последовательности байт в число я опущу. Если интересно, то об этих алгоритмах
легко найти информации на просторах Интернета.
Способы построения хэш-функций
Давайте теперь
вернемся к вопросу, что такое хорошая хэш-функция. Как мы с вами уже говорили, она
должна обладать следующими основными свойствами:
- быть
однозначной, то есть, для одного и того же ключа k выдавать одно и
то же значение индекса i (свойство
последовательности); - быстро
вычисляться; - выходные значения
(индексы) i должны
находиться в диапазоне хэш-таблицы (массива); - множество ключей
{k} должны
равномерно распределяться по таблице.
Я думаю, здесь в
целом все понятно, кроме, может быть последнего свойства: зачем требовать от
хэш-функции равномерного распределения ключей по ячейкам таблицы? Смотрите. В
общем случае, мы наперед не знаем, какие ключи k будут подаваться
на вход хэш-функции. Очевидно, что возможное количество этих ключей K много больше
текущего числа ячеек M в хэш-таблице. Значит, хэш-функция h(k) отображает
большее множество K в меньшее M. И как бы мы ни выбирали функцию
h(k), обязательно
будет существовать пара ключей k1, k2, которым
функция h(k) назначит один
и тот же индекс. Лучшее, что мы здесь можем сделать – это минимизировать
вероятность такого события. А это, в свою очередь, приводит к равномерности
распределения хэш-функцией возможных ключей {k} по ячейкам
таблицы. Вот отсюда и появляется последнее требование к хорошей хэш-функции. В
этом случае можно доказать, что средняя длина цепочек в хэш-таблице будет равна
коэффициенту заполнения:
α = n / m,
где n – число
хранимых ключей; m – общее число ячеек в таблице. И алгоритмы
поиска/удаления ключей, в среднем, будут выполняться за:
1 + α
операций. Это среднее
минимальное число, которое может быть достигнуто.
Построение хэш-функции методом деления
Наверное, самое
простое, что мы можем сделать, чтобы преобразовать множество целых
неотрицательных чисел {k} (ключи) в диапазон значений [0; m-1] (индексы
таблицы) – это взять и вычислить остаток от деления операцией:
![]()
Я напомню, что в
языках С++ и Python функция mod реализуется
оператором % следующим образом:
h(k) = k % m
На выходе имеем множество целых значений
в нужном нам диапазоне [0; m-1].
Получается, мы
только что построили простую и универсальную хэш-функцию, которую можно
использовать в любых хэш-таблицах? Давайте проверим, так ли это? Пусть ![]() ,
,
где p – некоторое
натуральное число, например, ![]() . В
. В
итоге, для разных ключей получим следующее распределение:
|
Ключ |
Хэш |
Ключ |
Хэш |
Ключ |
Хэш |
|
111 1011 |
1011 |
0000 |
0101 |
1111 |
0101 |
|
1100 1001 |
1001 |
1000 |
0101 |
1001 |
0101 |
Смотрите, число m=16, фактически,
выделяет последние 4 бита ключа k. И если вдруг так окажется, что все
потенциальные ключи {k}, которые будут сохраняться в
хэш-таблице, имеют одинаковые последние 4 бита, то всем им будет назначен один
и тот же индекс. То есть, мы получим худший случай работы хэш-таблицы.
Чтобы этого
избежать, число m следует выбирать, во-первых, простым
(то, что делится только на самого себя и на единицу), а, во-вторых, как можно
более далеким от степени двойки, то есть, от чисел ![]() . Но
. Но
это, в свою очередь, накладывает определенные ограничения на размер m таблицы, что не очень
удобно, так как размер хэш-таблицы может меняться по мере ее заполнения.
Построение хэш-функции методом умножения
Другой метод умножения
для построения хэш-функций решает эту проблему:
![]()
Здесь A – некоторая
константа, выбранная из диапазона 0 < A < 1 так,
чтобы при умножении k на A формировалось
дробное число, а затем, с помощью операции mod 1 выделяется
эта дробная часть числа. Благодаря этому, мы как бы перемешиваем возможные
значения ключей {k}, формируем случайные числа, зависящие от k, причем, эти
числа находятся в диапазоне [0; 1). Все что нам остается – это расширить
диапазон до [0; m-1] в целых числах. Для этого вещественное число
умножается на m с округлением
до наименьшего целого (оператор ![]() ).
).
Вот
математический смысл этой формулы. В результате, число m теперь можно
выбирать любым и это никак не скажется на качестве работы хэш-функции. Часто ![]() ,
,
где p – натуральное
число. Так как это соответствует динамическому увеличению хэш-таблицы в два
раза, каждый раз, когда она приближается к заполнению.
Здесь только
остается вопрос, как выбрать константу A? Дональд Кнут в
своем известном труде «Искусство программирования» предложил значение этой
константы брать равной:
![]()
Как показала
практика, при таком значении A мультипликативная
хэш-функция h(k) для
произвольных ключей k дает более-менее равномерное распределение.
Другие алгоритмы хэширования
Вообще, как
выбрать конкретный вид хэш-функции для решения той или иной задачи – вопрос
открытый. Например, в практике построения хэш-таблиц также строят хэш-функции на
базе известных алгоритмов из криптографии, например:
- CRC –
циклический
избыточный код; - MD5 –
128-битный
алгоритм хэширования; - SHA –
семейство
алгоритмов хэширования.
Можно предложить
и другие подобные детерминированные алгоритмы, которые переводят
последовательность байт (ключей) в числа с равномерным распределением. А уже
потом, эти числа можно перевести в любой требуемый диапазон индексов хэш-таблицы.
Универсальное хэширование
Итак, мы увидели
каким образом можно выполнять построение хэш-функций. Но как бы хорошо не
работал алгоритм хэширования остается одна важная проблема: для каждой
конкретной функции h(k) всегда можно подобрать такой набор ключей
{k}, что все они
будут располагаться в одной ячейке хэш-таблицы, то есть, для всех них функция
выдаст одно и то же значение. Этим обстоятельством, например, может
воспользоваться злоумышленник, чтобы специально замедлить работу программы. В
любом случае, это некая уязвимость, которую хотелось бы устранить. Давайте
посмотрим, как с этим можно бороться?
Пусть у нас
имеется несколько хеш-функций:
![]()
В целом, они по-разному
распределяют одни и те же ключи по таблице. Тогда, чтобы исключить
предсказуемость распределения набора ключей {k}, мы в момент
создания очередной хэш-таблицы случайным образом выберем одну из хеш-функций и
будем ее использовать для текущей хеш-таблицы. В этом случае, какой бы набор из
ключей {k} ни подавался
на вход алгоритма хеширования, он в разных таблицах будет распределяться
по-разному. А это именно то, что нам и нужно. Таким образом, уязвимость будет
устранена.
Но как
сформировать набор из H хэш-функций? Если мы будем их просто
формировать по методу умножения или деления, или еще как-нибудь, то может
возникнуть ситуация, когда разные хэш-функции для определенного набора ключей {k} будут выдавать
схожие значения индексов. То есть, результаты работы функций окажутся не такими
уж и независимыми. И тогда злоумышленник снова может воспользоваться своей
идеей и подать на вход алгоритма хэширования проблемный набор ключей. Поэтому
мало сформировать множество разных хэш-функций, они должны еще выдавать
независимый набор индексов для одного и того же набора входных значений {k}. Именно такой
набор функций получил название универсального.
Итак, нам нужно
построить универсальный набор хэш-функций, чтобы устранить проблему
предсказуемости распределения ключей по индексам таблицы. Как это сделать? Томас
Кормен в книге «Алгоритмы: построение и анализ» описывает следующий
математический подход. Универсальное множество хэш-функций можно построить по
правилу:
![]()
где p – некоторое
простое число, которое больше размера таблицы m; ![]() ,
, ![]() –
–
целые числа, взятые из указанного диапазона. В результате, всего мы имеем:
![]()
различных
хэш-функций. Причем значение m выбирается произвольным образом, то
есть, размер хэш-таблицы может быть любым, в том числе и ![]() ,
,
где n – натуральное
число.
Далее,
доказывается, что для двух случайных ключей ![]() любая
любая
выбранная хэш-функция выдаст одно и то же значение (индекс) с вероятностью 1/m, где m – размер хэш-таблицы.
То есть, ключи распределяются равномерно.
Таким образом,
если мы хотим реализовать универсальное хэширование, то достаточно определить
простое число p > m, а затем,
случайным образом выбрать значения a и b из их
диапазонов. Эти значения определяют конкретный вид хэш-функции, которая
используется для перевода ключей в индексы таблицы. В результате, злоумышленник
не сможет наперед знать, какая именно будет использована хэш-функция, а значит,
не сможет подготовить проблемный набор ключей {k} для
образования длинных цепочек в хэш-таблице. В этом и состоит идея универсального
хэширования.
Курс по структурам данных: https://stepik.org/a/134212
Видео по теме
Хэширование¶
В предыдущих разделах мы смогли усовершенствовать наши алгоритмы поиска,
используя преимущества информации о том, где элементы хранятся относительно
друг друга. Например, зная, что список упорядочен, мы можем осуществлять поиск
за логарифмическое время, используя бинарный алгоритм. В этом разделе мы
попытаемся пойти ещё на шаг дальше: построить такую структуру данных, в которой
можно будет осуществлять поиск за время (O(1)).
Эту концепцию называют хэшированием.
Теперь нам надо знать больше, чем просто расположение элемента, когда мы ищем
его в коллекции. Если каждый элемент находится там, где ему следует быть, то
поиск может использовать только сравнения для обнаружения присутствия искомого.
Однако, дальше мы увидим, что это, как правило, не единственный выход.
Хэш-таблица – это коллекция элементов, которые сохраняются таким образом,
чтобы позже их было легко найти. Каждая позиция в хэш-таблице (часто называемая
слотом) может содержать собственно элемент и целое число, начинающееся с нуля.
Например, у нас есть слот 0, слот 1, слот 2 и так далее. Первоначально хэш-таблица
не содержит элементов, так что каждый из них пуст. Мы можем сделать реализацию
хэш-таблицы, используя список, в котором каждый элемент инициализирован
специальным значением Python None. Рисунок 4
демонстрирует хэш-таблицу размером (m=11). Другими словами, в ней есть
(m) слотов, пронумерованных от 0 до 10.

Рисунок 4: Хэш-таблица с 11-ю пустыми слотами
Связь между элементом и слотом, в который он кладётся, называется
хэш-функцией. Она принимает любой элемент из коллекции и возвращает целое
число из диапазона имён слотов (от 0 до (m-1)). Предположим, что у нас
есть набор целых чисел 54, 26, 93, 17, 77 и 31. Наша первая хэш-функция, иногда
называемая “методом остатков”, просто берёт элемент и делит его на размер таблицы,
возвращая остаток в качестве хэш-значения ((h(item)=item % 11)).
В таблице 4 представлены все хэш-значения чисел из
нашего примера. Обратите внимание: метод остатков (модульная арифметика) обычно
присутствует в той или иной форме во всех хэш-функциях, поскольку результат
должен лежать в диапазоне имён слотов.
| Элемент | Хэш-значение |
|---|---|
| 54 | 10 |
| 26 | 4 |
| 93 | 5 |
| 17 | 6 |
| 77 | 0 |
| 31 | 9 |
Поскольку хэш-значения могут быть посчитаны, мы можем вставить каждый элемент в
хэш-таблицу на определённое место, как это показано на
рисунке 5. Обратите внимание, что теперь заняты 6 из 11
слотов. Это называется фактором загрузки и обычно обозначается
(lambda = frac {numberofitems}{tablesize}).
В этом примере (lambda = frac {6}{11}).

Рисунок 5: Хэш-таблица с шестью элементами
Теперь, когда мы хотим найти элемент, мы просто используем хэш-функцию, чтобы
вычислить имя слота элемента и затем проверить по таблице его наличие. Эта
операция поиска имеет (O(1)), поскольку на вычисление хэш-значения
требуется константное время, как и на переход по найденному индексу. Если всё
находится там, где ему положено, то мы получаем алгоритм поиска за константное
время.
Возможно, вы уже заметили, что такая техника работает только если каждый элемент
отображается на уникальную позицию в хэш-таблице. Например, если следующим в
нашей коллекции будет элемент 44, то он будет иметь хэш-значение 0
((44 % 11 == 0)). А так как 77 тоже имеет хэш-значение 0, то у нас
проблемы. В соответствии с хэш-функцией два или более элементов должны иметь
один слот. Это называется коллизией (иногда “столкновением”). Очевидно, что
коллизии создают проблемы для техники хэширования. Позднее мы обсудим их в деталях.
Хэш-функции¶
Для заданной коллекции элементов хэш-функция, связывающая каждый из них с
уникальным слотом, называется идеальной хэш-функцией. Если мы знаем, что ни
один элемент коллекции никогда не изменится, то возможно создать идеальную
хэш-функцию (см. упражнения, чтобы узнать об этом больше). К сожалению, для
произвольного набора элементов не существует систематического способа
сконструировать идеальную хэш-функцию. К счастью, для эффективной работы она
нам и не нужна.
Один из способов всегда иметь идеальную хэш-функцию состоит в увеличении размера
хэш-таблицы таким образом, чтобы в ней могло быть размещено каждое из возможных
значений элементов. Таким образом гарантируется уникальность слотов. Хотя такой
подход практичен для малого числа элементов, при возрастании их количества он
перестаёт быть осуществимым. Например, для девятизначных индексов социального
страхования потребуется порядка миллиарда слотов. Даже если мы захотим всего
лишь хранить данные для класса из 25 студентов, то потратим на это чудовищное
количество памяти.
Наша цель: создать хэш-функцию, которая минимизировала бы количество коллизий,
легко считалась и равномерно распределяла элементы в хэш-таблице. Существует
несколько распространённых способов расширить простой метод остатков.
Рассмотрим некоторые из них.
Метод свёртки для создания хэш-функций начинает с деления элемента на
составляющие одинаковой величины (кроме последнего, который может иметь
отличающийся размер). Эти кусочки складываются вместе и дают результирующее
хэш-значение. Например, если наш элемент – телефонный номер 436-555-4601, то мы
можем взять цифры и рабить их на группы по два (43, 65, 55, 46, 01). После
сложения (43+65+55+46+01) мы получим 210. Если предположить, что
хэш-таблица имеет 11 слотов, то нужно выполнить дополнительный шаг, поделив это
число на 11 и взяв остаток. В данном случае (210 % 11) равно 1, так что
телефонный номер 436-555-4601 хэшируется в слот 1. Некоторые методы свёртки идут
на шаг дальше и перед сложением переворачивают каждый из кусочков разбиения.
Для примера выше мы бы получили (43+56+55+64+01 = 219),
что даёт (219 % 11 = 10).
Другая числовая техника для создания хэш-функций называется
методом средних квадратов. Сначала значение элемента возводится в квадрат,
а затем из получившихся в результате цифр выделяется некоторая порция. Например,
если элемент равен 44, то мы прежде вычислим (44 ^{2} = 1,936). Выделив
две средние цифры (93) и выполнив шаг получения остатка, мы получим 5
((93 % 11)). Таблица 5 показывает элементы, к
которым применили оба метода: остатков и средних квадратов. Убедитесь, что
понимаете, как эти значения были получены.
| Элемент | Остаток | Средний квадрат |
|---|---|---|
| 54 | 10 | 3 |
| 26 | 4 | 7 |
| 93 | 5 | 9 |
| 17 | 6 | 8 |
| 77 | 0 | 4 |
| 31 | 9 | 6 |
Мы также можем создать хэш-функцию для символьных элементов (например, строк).
Слово “cat” можно рассматривать, как последовательность кодов его букв.
>>> ord('c') 99 >>> ord('a') 97 >>> ord('t') 116
Затем можно взять эти три кода, сложить их и спользовать метод остатков, чтобы
получить хэш-значение (см. рисунок 6).
Листинг 1 демонстрирует функцию hash, принимающую
строку и размер таблицы и возвращающую хэш-значение из диапазона от 0 до tablesize-1.
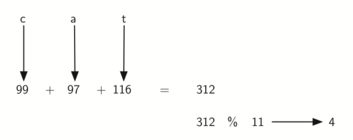
Рисунок 6: Хэширование строки с использованием кодов символов
Листинг 1
def hash(astring, tablesize): sum = 0 for pos in range(len(astring)): sum = sum + ord(astring[pos]) return sum%tablesize
Интересное наблюдение: когда мы используем эту хэш-функцию, анаграммы всегда
будут иметь одинаковое хэш-значение. Чтобы исправить это, следует использовать
позицию символа в качестве веса. Рисунок 7 показывает
один из вариантов использования позиционного значения в качестве весового фактора.
Модификацию функции hash мы оставляем в качестве упражнения.
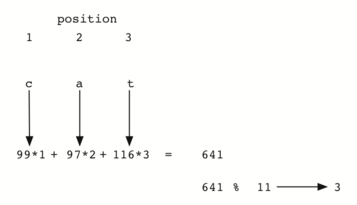
Рисунок 7: Хэширование строки с использованием кодов символов и весов
Вы можете придумать другие числовые способы вычисления хэш-значений для элементов
коллекции. Важно только помнить, что эффекитвная хэш-функция не должна являться
доминирующей частью процессов хранения и поиска. Если она слишком сложна, то
требует много работы на вычисление имени слота. В этом случае проще было бы
использовать последовательный или бинарный поиск, описанные выше. Таким образом,
сама идея хэширования терпит поражение.
Разрешение коллизий¶
Вернёмся к проблеме коллизий. Когда два элемента хэшируются в один слот, нам
требуется систематический метод для размещения в хэш-таблице второго элемента.
Этот процесс называется разрешением коллизии. Как мы утверждали ранее, если
хэш-функция идеальна, то коллизии никогда не произойдёт. Однако, поскольку часто
такое положение дел невозможно, разрешение коллизий становится важной частью
хэширования.
Одним из методов разрешения коллизий является просмотр хэш-таблицы и поиск
другого свободного слота для размещения в нём элемента, создавшего проблему.
Простой способ сделать это – начать с оригинальной позиции хэш-значения и
перемещаться по слотам определённым образом до тех пор, пока не будет найден
пустой. Заметьте: нам может понадобиться вернуться обратно к первому слоту
(циклически), чтобы охватить хэш-таблицу целиком. Этот процесс разрешения
коллизий называется открытой адресацией, поскольку пытается найти следующий
свободный слот (или адрес) в хэш-таблице. Систематически посещая каждый слот по
одному разу, мы действуем в соответствии с техникой открытой адресации,
называемой линейным пробированием.
Рисунок 8 показывает расширенный набор целых элементов
после применения простой хэш-функции метода остатков (54,26,93,17,77,31,44,55,20).
В таблице 4 выше собраны хэш-значения оригинальных
элементов, а на рисунке 5 представлено первоначальное
содержимое хэш-таблицы. Когда мы пытаемся поместить 44 в слот 0, возникает
коллизия. При линейном пробировании мы последовательно – слот за слотом –
просматриваем таблицу, до тех пор, пока не найдём открытую позицию. В данном
случае это оказался слот 1.
В следующий раз 55, которое должно разместиться в слоте 0, будет положено в слот
2 – следующую незанятую позицию. Последнее значение 20 хэшируется в слот 9. Но
поскольку он занят, мы делаем линейное пробирование. Мы посещаем слоты
10, 0, 1, 2 и наконец находим пустой слот на позиции 3.

Рисунок 8: Разрешение коллизий путём линейного пробирования
Поскольку мы построили хэш-таблицу с помощью открытой адресации
(или линейного пробирования), важно использовать тот же метод при поиске элемента.
Предположим, мы хотим найти число 93. Вчисление его хэш-значения даст 5. Обнаружив
в пятом слоте 93, мы вернём True. Но что если мы ищем 20? Теперь хэш-значение
равно 9, а слот 9 содержит 31. Нельзя просто вернуть False, поскольку здесь
могла быть коллизия. Так что мы вынуждены провести последвательный поиск, начиная
с десятой позиции, который закончится, когда найдётся число 20 или пустой слот.
Недостатком линейного пробирования является его склонность к кластеризации:
элементы в таблице группируются. Это означает, что если возникает много коллизий
с одним хэш-значением, то окружающие его слоты при линейном пробировании будут
заполнены. Это начнёт оказывать влияние на вставку других элементов, как мы
наблюдали выше при попытке вставить в таблицу число 20. В итоге, кластер
значений, хэшируемых в 0, должен быть пропущен, чтобы найти вакантное место.
Этот кластер показан на рисунке 9.

Рисунок 9: Кластер элементов для слота 0
Одним из способов иметь дело с кластеризацией является расширение линейного
пробирования таким образом, чтобы вместо последовательного поиска следующего
свободного места мы пропускали слоты, получая таким образом более равномерное
распределение элементов, вызвавших коллизии. Потенциально это уменьшит
возникающую кластеризацию. Рисунок 10 показывает
элементы после разрешения коллизий с использованием пробирования “плюс 3”.
Это означает, что при возникновении коллизии, мы рассматриваем каждый третий
слот до тех пор, пока не найдём пустой.

Рисунок 10: Разрешение коллизий с использованием методики “плюс 3”
Общее название для такого процесса поиска другого слота после коллизии
– повторное хэширование. С помощью простого линейного пробирования повторная
хэш-функция выглядит как (newhashvalue = rehash(oldhashvalue)), где
(rehash(pos) = (pos + 1) % sizeoftable). Повторное хэширование “плюс 3”
может быть определёно как (rehash(pos) = (pos+3) % sizeoftable).
В общем случае: (rehash(pos) = (pos + skip) % sizeoftable). Важно
отметить, что величина “пропуска” должна быть такой, чтобы в конце концов
пройти по всем слотам. В противном случае часть таблицы окажется
неиспользованной. Для обеспечения этого условия часто предполагается,
что размер таблицы является простым числом. Вот почему в примере мы
использовали 11.
Ещё одним вариантом линейного пробирования является квадратичное пробирование.
Вместо использования константного значения “пропуска”, мы используем повторную
хэш-функцию, которая инкрементирует хэш-значение на 1, 3, 5, 7, 9 и так далее.
Это означает, что если первое хэш-значение равно (h), то последующими
будут (h+1), (h+4), (h+9), (h+16) и так далее.
Другими словами, квадратичное пробирование использует пропуск, состоящий из
следующих один за другим полных квадратов. Рисунок 11
демонстрирует значения из нашего примера после использования этой методики.

Рисунок 11: Разрешение коллизий с помощью квадратичного пробирования
Альтернативным методом решения проблемы коллизий является разрешение каждому
слоту содержать ссылку на коллекцию (или цепочку) значений. Цепочки
позволяют множеству элементов занимать одну и ту же позицию в хэш-таблице.
Чем больше элементов хэшируются в одно место, тем сложнее найти элемент в
коллекции. Рисунок 12 показывает, как элементы добавляются
в хэш-таблицу с использованием цепочек для разрешения коллизий.
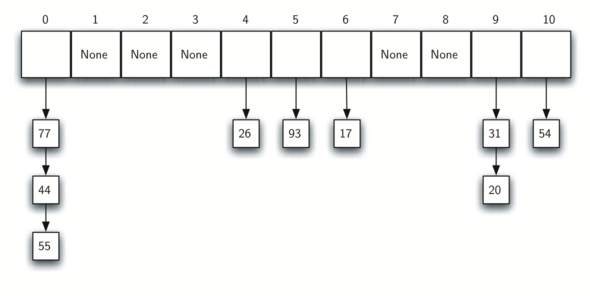
Рисунок 12: Разрешение коллизий с помощью цепочек
Когда мы хотим найти элемент, мы используем хэш-функцию для генерации номера
слота, в котором он должен размещаться. Поскольку каждый слот содержит коллекцию,
мы используем различные техники поиска, чтобы определить, представлен ли он в
ней. Преимуществом данного подхода является вероятность получить гораздо меньше
элементов в каждом слоте, так что поиск будет более эффективным. Более подробный
анализ мы проведём в конце этой главы.
Самопроверка
Q-50: В хэш-таблице размером 13 какой индекс будет связан со следующими двумя
ключами 27, 130?
Q-51: Предположим, у вас есть следующий набор ключей для вставки в хэш-таблицу,
содержащую ровно 11 значений: 113 , 117 , 97 , 100 , 114 , 108 , 116 ,
105 , 99. Что из следующего лучше всего демонстрирует содержимое таблицы
после вставки всех ключей с использованием линейного пробирования?
a) 100, __, __, 113, 114, 105, 116, 117, 97, 108, 99
b) 99, 100, __, 113, 114, __, 116, 117, 105, 97, 108
c) 100, 113, 117, 97, 14, 108, 116, 105, 99, __, __
d) 117, 114, 108, 116, 105, 99, __, __, 97, 100, 113
Реализация абстрактного типа данных Map¶
Одной из наиболее используемых коллекций Python являются словари. Напомним, что
словарь – ассоциативный тип данных, в котором можно хранить пары ключ-значение.
Ключи используются для поиска ассоциативных значений данных. Мы часто называем
эту идею отображением.
Абстрактный тип данных Map можно определить следующим образом.
Его структура – неупорядоченная коллекция ассоциаций между ключами и значениями.
Все ключи уникальны, таким образом поддерживаются отношения “один к одному”
между ключами и значениями. Операции для такого типа данных представлены ниже:
- Map() Создаёт новый пустой экземпляр типа. Возвращает пустую коллекцию
отображений. - put(key, val) Добавляет новую пару ключ-значение в отображение. Если
такой ключ уже имеется, то заменяет старое значение новым. - get(key) Принимает ключ, возвращает соответствующее ему значение из
коллекции или None. - del Удаляет пару ключ-значение из отображения, используя оператор вида
del map[key]. - len() Возвращает количество пар ключ-значение, хранящихся в коллекции.
- in Возвращает True для оператора вида key in map, если данный ключ
присутствует в коллекции, или False в противном случае.
Одним из больших преимуществ словарей является то, что, имея ключ, мы можем
найти ассоциированное с ним значение очень быстро. Для обеспечения надлежащей
скорости требуется реализация, поддерживающая эффективный поиск. Мы можем
использовать список с последовательным или бинарным поиском, но правильнее
будет воспользоваться хэш-таблицей, описанной выше, поскольку поиск элемента в
ней может приближаться к производительности (O(1)).
В листинге 2 мы используем два списка,
чтобы создать класс HashTable, воплощающий абстрактный тип данных Map.
Один список, называемый slots, будет содержать ключи элементов, а
параллельный ему список data – значения данных. Когда мы находим ключ, на
соответствующей позиции в списке с данными будет находиться связанное с ним
значение. Мы будем работать со списком ключей, как с хэш-таблицей, используя
идеи, представленные ранее. Обратите внимание, что первоначальный размер
хэш-таблицы выбран равным 11. Хотя это число произвольно, важно, чтобы оно было
простым. Это сделает алгоритм разрешения коллизий максимально эффективным.
Листинг 2
class HashTable: def __init__(self): self.size = 11 self.slots = [None] * self.size self.data = [None] * self.size
hashfunction реализует простой метод остатков. В качестве техники разрешения
коллизий используется линейное пробирование с функцией повторного хэширования
“плюс 1”. Функция put (см. листинг 3)
предполагает, что в конце-концов найдётся пустой слот, или такой ключ уже
присутствует в self.slots. Она вычисляет оригинальное хэш-значение и, если
слот не пуст, применяет функцию rehash до тех пор, пока не найдёт свободное
место. Если непустой слот уже содержит ключ, старое значение данных будет
заменено на новое.
Листинг 3
def put(self,key,data): hashvalue = self.hashfunction(key,len(self.slots)) if self.slots[hashvalue] == None: self.slots[hashvalue] = key self.data[hashvalue] = data else: if self.slots[hashvalue] == key: self.data[hashvalue] = data #replace else: nextslot = self.rehash(hashvalue,len(self.slots)) while self.slots[nextslot] != None and self.slots[nextslot] != key: nextslot = self.rehash(nextslot,len(self.slots)) if self.slots[nextslot] == None: self.slots[nextslot]=key self.data[nextslot]=data else: self.data[nextslot] = data #replace def hashfunction(self,key,size): return key%size def rehash(self,oldhash,size): return (oldhash+1)%size
Аналогично функция get (см. листинг 4)
начинает с вычисления начального хэш-значения. Если искомая величина не
содержится в этом слоте, то используется rehash для определения следующей
позиции. Обратите внимание: строка 15 гарантирует, что поиск закончится,
проверяя, не вернулись ли мы в начальный слот. Если такое происходит, значит
все возможные слоты исчерпаны, и элемент в коллекции не представлен.
Кончный метод класса HashTable предоставляет для словарей дополнительный
функционал. Мы перегружаем методы __getitem__ и __setitem__, чтобы
получать доступ к элементам с помощью []. Это подразумевает, что созданному
экземпляру HashTable будет доступен знакомый оператор индекса. Оставшиеся
методы мы оставляем в качестве упражнения.
Листинг 4
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
def get(self,key): startslot = self.hashfunction(key,len(self.slots)) data = None stop = False found = False position = startslot while self.slots[position] != None and not found and not stop: if self.slots[position] == key: found = True data = self.data[position] else: position=self.rehash(position,len(self.slots)) if position == startslot: stop = True return data def __getitem__(self,key): return self.get(key) def __setitem__(self,key,data): self.put(key,data) |
Следующая сессия демонстрирует класс HashTable в действии. Сначала мы
создаём хэш-таблицу и сохраняем в неё несколько элементов с целочисленными
ключами и строковыми значениями данных.
>>> H=HashTable() >>> H[54]="cat" >>> H[26]="dog" >>> H[93]="lion" >>> H[17]="tiger" >>> H[77]="bird" >>> H[31]="cow" >>> H[44]="goat" >>> H[55]="pig" >>> H[20]="chicken" >>> H.slots [77, 44, 55, 20, 26, 93, 17, None, None, 31, 54] >>> H.data ['bird', 'goat', 'pig', 'chicken', 'dog', 'lion', 'tiger', None, None, 'cow', 'cat']
Далее мы получаем доступ и изменяем некоторые из элементов в хэш-таблице.
Обратите внимание, что значение с ключом 20 заменяется.
>>> H[20] 'chicken' >>> H[17] 'tiger' >>> H[20]='duck' >>> H[20] 'duck' >>> H.data ['bird', 'goat', 'pig', 'duck', 'dog', 'lion', 'tiger', None, None, 'cow', 'cat'] >> print(H[99]) None
Целиком пример хэш-таблицы можно увидеть в ActiveCode 1.
Пример хэш-таблицы целиком (hashtablecomplete)
Анализ хэширования¶
Как мы заключили выше, в лучшем случае хэширование предоставляет технику поиска
за константное время: (O(1)). Однако, из-за некоторого числа коллизий с
количеством сравнений всё не так просто. Несмотря на то, что полный анализ
хэширования выходит за рамки этого текста, мы можем определить несколько
общеизвестных результатов, аппроксимирующих количество сравнений, необходимое
для поиска элемента.
Наиболее важной частью информации, которую нам надо проанализировать при
использовании хэш-таблицы, является фактор загрузки (lambda).
Концептуально, если (lambda) мало, то вероятность столкновений низкая.
Т.е. элементы вероятнее всего будут находиться в слотах, соответствующих их
хэш-значениям. Если же (lambda) велико, то это означает близость таблицы
к заполнению, т.е. будет возникать всё больше и больше коллизий. Следовательно,
их разрешение будет более сложным, требовать больше сравнений для поиска
свободного слота. В случае цепочек увеличение коллизий означает возрастание
количества элементов в каждой из них.
Как и раньше, мы будем рассматривать результаты удачного и неудачного поиска.
В первом случае, при использовании открытой адресации с линейным пробированием
среднее число сравнений приблизительно равно
(frac{1}{2}left(1+frac{1}{1-lambda}right)).
Во втором – (frac{1}{2}left(1+left(frac{1}{1-lambda}right)^2right)).
Если мы используем цепочки, то среднее количество сравнений будет
(1 + frac {lambda}{2}) для удачного поиска и (lambda) для неудачного.
В этой статье вы познакомитесь с хэш-таблицами и увидите примеры их реализации в Cи, C++, Java и Python.
Хеш-таблица — это структура данных, в которой все элементы хранятся в виде пары ключ-значение, где:
- ключ — уникальное число, которое используется для индексации значений;
- значение — данные, которые с этим ключом связаны.
Хеширование (хеш-функция)
В хеш-таблице обработка новых индексов производится при помощи ключей. А элементы, связанные с этим ключом, сохраняются в индексе. Этот процесс называется хешированием.
Пусть k — ключ, а h(x) — хеш-функция.
Тогда h(k) в результате даст индекс, в котором мы будем хранить элемент, связанный с k.
Коллизии
Когда хеш-функция генерирует один индекс для нескольких ключей, возникает конфликт: неизвестно, какое значение нужно сохранить в этом индексе. Это называется коллизией хеш-таблицы.
Есть несколько методов борьбы с коллизиями:
- метод цепочек;
- метод открытой адресации: линейное и квадратичное зондирование.
1. Метод цепочек
Суть этого метода проста: если хеш-функция выделяет один индекс сразу двум элементам, то храниться они будут в одном и том же индексе, но уже с помощью двусвязного списка.
Если j — ячейка для нескольких элементов, то она содержит указатель на первый элемент списка. Если же j пуста, то она содержит NIL.
Псевдокод операций
chainedHashSearch(T, k)
return T[h(k)]
chainedHashInsert(T, x)
T[h(x.key)] = x
chainedHashDelete(T, x)
T[h(x.key)] = NIL 2. Открытая адресация
В отличие от метода цепочек, в открытой адресации несколько элементов в одной ячейке храниться не могут. Суть этого метода заключается в том, что каждая ячейка либо содержит единственный ключ, либо NIL.
Существует несколько видов открытой адресации:
a) Линейное зондирование
Линейное зондирование решает проблему коллизий с помощью проверки следующей ячейки.
h(k, i) = (h′(k) + i) mod m,
где
i = {0, 1, ….}h'(k)— новая хеш-функция
Если коллизия происходит в h(k, 0), тогда проверяется h(k, 1). То есть значение i увеличивается линейно.
Проблема линейного зондирования заключается в том, что заполняется кластер соседних ячеек. Это приводит к тому, что при вставке нового элемента в хеш-таблицу необходимо проводить полный обход кластера. В результате время выполнения операций с хеш-таблицами увеличивается.
b) Квадратичное зондирование
Работает оно так же, как и линейное — но есть отличие. Оно заключается в том, что расстояние между соседними ячейками больше (больше одного). Это возможно благодаря следующему отношению:
h(k, i) = (h′(k) + c1i + c2i2) mod m,
где
c1иc2— положительные вспомогательные константы,i = {0, 1, ….}
c) Двойное хэширование
Если коллизия возникает после применения хеш-функции h(k), то для поиска следующей ячейки вычисляется другая хеш-функция.
h(k, i) = (h1(k) + ih2(k)) mod m
«Хорошие» хеш-функции
«Хорошие» хеш-функции не уберегут вас от коллизий, но, по крайней мере, сократят их количество.
Ниже мы рассмотрим различные методы определения «качества» хэш-функций.
1. Метод деления
Если k — ключ, а m — размер хеш-таблицы, то хеш-функция h() вычисляется следующим образом:
h(k) = k mod m
Например, если m = 10 и k = 112, то h(k) = 112 mod 10 = 2. То есть значение m не должно быть степенью 2. Это связано с тем, что степени двойки в двоичном формате — 10, 100, 1000… При вычислении k mod m мы всегда будем получать p-биты низшего порядка.
если m = 22, k = 17, тогда h(k) = 17 mod 22 = 10001 mod 100 = 01
если m = 23, k = 17, тогда h(k) = 17 mod 22 = 10001 mod 100 = 001
если m = 24, k = 17, тогда h(k) = 17 mod 22 = 10001 mod 100 = 0001
если m = 2p, тогда h(k) = p биты порядком ниже, чем m2. Метод умножения
h(k) = ⌊m(kA mod 1)⌋,
где
kA mod 1отделяет дробную частьkA;⌊ ⌋округляет значение;A— произвольная константа, значение которой должно находиться между 0 и 1. Оптимальный вариант ≈ (√5-1) / 2, его предложил Дональд Кнут.
3. Универсальное хеширование
В универсальном хешировании хеш-функция выбирается случайным образом и не зависит от ключей.
Где применяются
- Когда необходима постоянная скорость поиска и вставки.
- В криптографических приложениях.
- Когда необходима индексация данных.
Примеры реализации хеш-таблиц в Python, Java, Си и C++
Python
# Реализация хеш-таблицы в Python
hashTable = [[],] * 10
def checkPrime(n):
if n == 1 or n == 0:
return 0
for i in range(2, n//2):
if n % i == 0:
return 0
return 1
def getPrime(n):
if n % 2 == 0:
n = n + 1
while not checkPrime(n):
n += 2
return n
def hashFunction(key):
capacity = getPrime(10)
return key % capacity
def insertData(key, data):
index = hashFunction(key)
hashTable[index] = [key, data]
def removeData(key):
index = hashFunction(key)
hashTable[index] = 0
insertData(123, "apple")
insertData(432, "mango")
insertData(213, "banana")
insertData(654, "guava")
print(hashTable)
removeData(123)
print(hashTable)
Java
// Реализация хеш-таблицы в Java
import java.util.*;
class HashTable {
public static void main(String args[])
{
Hashtable<Integer, Integer>
ht = new Hashtable<Integer, Integer>();
ht.put(123, 432);
ht.put(12, 2345);
ht.put(15, 5643);
ht.put(3, 321);
ht.remove(12);
System.out.println(ht);
}
}
Cи
// Реализация хеш-таблицы в Cи
#include <stdio.h>
#include <stdlib.h>
struct set
{
int key;
int data;
};
struct set *array;
int capacity = 10;
int size = 0;
int hashFunction(int key)
{
return (key % capacity);
}
int checkPrime(int n)
{
int i;
if (n == 1 || n == 0)
{
return 0;
}
for (i = 2; i < n / 2; i++)
{
if (n % i == 0)
{
return 0;
}
}
return 1;
}
int getPrime(int n)
{
if (n % 2 == 0)
{
n++;
}
while (!checkPrime(n))
{
n += 2;
}
return n;
}
void init_array()
{
capacity = getPrime(capacity);
array = (struct set *)malloc(capacity * sizeof(struct set));
for (int i = 0; i < capacity; i++)
{
array[i].key = 0;
array[i].data = 0;
}
}
void insert(int key, int data)
{
int index = hashFunction(key);
if (array[index].data == 0)
{
array[index].key = key;
array[index].data = data;
size++;
printf("n Ключ (%d) вставлен n", key);
}
else if (array[index].key == key)
{
array[index].data = data;
}
else
{
printf("n Возникла коллизия n");
}
}
void remove_element(int key)
{
int index = hashFunction(key);
if (array[index].data == 0)
{
printf("n Данного ключа не существует n");
}
else
{
array[index].key = 0;
array[index].data = 0;
size--;
printf("n Ключ (%d) удален n", key);
}
}
void display()
{
int i;
for (i = 0; i < capacity; i++)
{
if (array[i].data == 0)
{
printf("n array[%d]: / ", i);
}
else
{
printf("n Ключ: %d array[%d]: %d t", array[i].key, i, array[i].data);
}
}
}
int size_of_hashtable()
{
return size;
}
int main()
{
int choice, key, data, n;
int c = 0;
init_array();
do
{
printf("1.Вставить элемент в хэш-таблицу"
"n2.Удалить элемент из хэш-таблицы"
"n3.Узнать размер хэш-таблицы"
"n4.Вывести хэш-таблицу"
"nn Пожалуйста, выберите нужный вариант: ");
scanf("%d", &choice);
switch (choice)
{
case 1:
printf("Введите ключ -:t");
scanf("%d", &key);
printf("Введите данные-:t");
scanf("%d", &data);
insert(key, data);
break;
case 2:
printf("Введите ключ, который хотите удалить-:");
scanf("%d", &key);
remove_element(key);
break;
case 3:
n = size_of_hashtable();
printf("Размер хеш-таблицы-:%dn", n);
break;
case 4:
display();
break;
default:
printf("Неверно введены данныеn");
}
printf("nПродолжить? (Нажмите 1, если да): ");
scanf("%d", &c);
} while (c == 1);
}
C++
// Реализация хеш-таблицы в C++
#include <iostream>
#include <list>
using namespace std;
class HashTable
{
int capacity;
list<int> *table;
public:
HashTable(int V);
void insertItem(int key, int data);
void deleteItem(int key);
int checkPrime(int n)
{
int i;
if (n == 1 || n == 0)
{
return 0;
}
for (i = 2; i < n / 2; i++)
{
if (n % i == 0)
{
return 0;
}
}
return 1;
}
int getPrime(int n)
{
if (n % 2 == 0)
{
n++;
}
while (!checkPrime(n))
{
n += 2;
}
return n;
}
int hashFunction(int key)
{
return (key % capacity);
}
void displayHash();
};
HashTable::HashTable(int c)
{
int size = getPrime(c);
this->capacity = size;
table = new list<int>[capacity];
}
void HashTable::insertItem(int key, int data)
{
int index = hashFunction(key);
table[index].push_back(data);
}
void HashTable::deleteItem(int key)
{
int index = hashFunction(key);
list<int>::iterator i;
for (i = table[index].begin();
i != table[index].end(); i++)
{
if (*i == key)
break;
}
if (i != table[index].end())
table[index].erase(i);
}
void HashTable::displayHash()
{
for (int i = 0; i < capacity; i++)
{
cout << "table[" << i << "]";
for (auto x : table[i])
cout << " --> " << x;
cout << endl;
}
}
int main()
{
int key[] = {231, 321, 212, 321, 433, 262};
int data[] = {123, 432, 523, 43, 423, 111};
int size = sizeof(key) / sizeof(key[0]);
HashTable h(size);
for (int i = 0; i < n; i++)
h.insertItem(key[i], data[i]);
h.deleteItem(12);
h.displayHash();
}
