Хеш-таблицы
Время на прочтение
9 мин
Количество просмотров 190K
Предисловие
Я много раз заглядывал на просторы интернета, нашел много интересных статей о хеш-таблицах, но вразумительного и полного описания того, как они реализованы, так и не нашел. В связи с этим мне просто нетерпелось написать пост на данную, столь интересную, тему.
Возможно, она не столь полезна для опытных программистов, но будет интересна для студентов технических ВУЗов и начинающих программистов-самоучек.

Мотивация использовать хеш-таблицы
Для наглядности рассмотрим стандартные контейнеры и асимптотику их наиболее часто используемых методов.
Все данные при условии хорошо выполненных контейнерах, хорошо подобранных хеш-функциях
Из этой таблицы очень хорошо понятно, почему же стоит использовать хеш-таблицы. Но тогда возникает противоположный вопрос: почему же тогда ими не пользуются постоянно?
Ответ очень прост: как и всегда, невозможно получить все сразу, а именно: и скорость, и память. Хеш-таблицы тяжеловесные, и, хоть они и быстро отвечают на вопросы основных операций, пользоваться ими все время очень затратно.
Понятие хеш-таблицы
Хеш-таблица — это контейнер, который используют, если хотят быстро выполнять операции вставки/удаления/нахождения. В языке C++ хеш-таблицы скрываются под флагом unoredered_set и unordered_map. В Python вы можете использовать стандартную коллекцию set — это тоже хеш-таблица.
Реализация у нее, возможно, и не очевидная, но довольно простая, а главное — как же круто использовать хеш-таблицы, а для этого лучше научиться, как они устроены.
Для начала объяснение в нескольких словах. Мы определяем функцию хеширования, которая по каждому входящему элементу будет определять натуральное число. А уже дальше по этому натуральному числу мы будем класть элемент в (допустим) массив. Тогда имея такую функцию мы можем за O(1) обработать элемент.
Теперь стало понятно, почему же это именно хеш-таблица.
Проблема коллизии
Естественно, возникает вопрос, почему невозможно такое, что мы попадем дважды в одну ячейку массива, ведь представить функцию, которая ставит в сравнение каждому элементу совершенно различные натуральные числа просто невозможно. Именно так возникает проблема коллизии, или проблемы, когда хеш-функция выдает одинаковое натуральное число для разных элементов.
Существует несколько решений данной проблемы: метод цепочек и метод двойного хеширования. В данной статье я постараюсь рассказать о втором методе, как о более красивом и, возможно, более сложном.
Решения проблемы коллизии методом двойного хеширования
Мы будем (как несложно догадаться из названия) использовать две хеш-функции, возвращающие взаимопростые натуральные числа.
Одна хеш-функция (при входе g) будет возвращать натуральное число s, которое будет для нас начальным. То есть первое, что мы сделаем, попробуем поставить элемент g на позицию s в нашем массиве. Но что, если это место уже занято? Именно здесь нам пригодится вторая хеш-функция, которая будет возвращать t — шаг, с которым мы будем в дальнейшем искать место, куда бы поставить элемент g.
Мы будем рассматривать сначала элемент s, потом s + t, затем s + 2*t и т.д. Естественно, чтобы не выйти за границы массива, мы обязаны смотреть на номер элемента по модулю (остатку от деления на размер массива).
Наконец мы объяснили все самые важные моменты, можно перейти к непосредственному написанию кода, где уже можно будет рассмотреть все оставшиеся нюансы. Ну а строгое математическое доказательство корректности использования двойного хеширования можно найти тут.
Реализация хеш-таблицы
Для наглядности будем реализовывать хеш-таблицу, хранящую строки.
Начнем с определения самих хеш-функций, реализуем их методом Горнера. Важным параметром корректности хеш-функции является то, что возвращаемое значение должно быть взаимопросто с размером таблицы. Для уменьшения дублирования кода, будем использовать две структуры, ссылающиеся на реализацию самой хеш-функции.
int HashFunctionHorner(const std::string& s, int table_size, const int key)
{
int hash_result = 0;
for (int i = 0; s[i] != s.size(); ++i)
hash_result = (key * hash_result + s[i]) % table_size;
hash_result = (hash_result * 2 + 1) % table_size;
return hash_result;
}
struct HashFunction1
{
int operator()(const std::string& s, int table_size) const
{
return HashFunctionHorner(s, table_size, table_size - 1); // ключи должны быть взаимопросты, используем числа <размер таблицы> плюс и минус один.
}
};
struct HashFunction2
{
int operator()(const std::string& s, int table_size) const
{
return HashFunctionHorner(s, table_size, table_size + 1);
}
};Чтобы идти дальше, нам необходимо разобраться с проблемой: что же будет, если мы удалим элемент из таблицы? Так вот, его нужно пометить флагом deleted, но просто удалять его безвозвратно нельзя. Ведь если мы так сделаем, то при попытке найти элемент (значение хеш-функции которого совпадет с ее значением у нашего удаленного элемента) мы сразу наткнемся на пустую ячейку. А это значит, что такого элемента и не было никогда, хотя, он лежит, просто где-то дальше в массиве. Это основная сложность использования данного метода решения коллизий.
Помня о данной проблеме построим наш класс.
template <class T, class THash1 = HashFunction1, class THash2 = HashFunction2>
class HashTable
{
static const int default_size = 8; // начальный размер нашей таблицы
constexpr static const double rehash_size = 0.75; // коэффициент, при котором произойдет увеличение таблицы
struct Node
{
T value;
bool state; // если значение флага state = false, значит элемент массива был удален (deleted)
Node(const T& value_) : value(value_), state(true) {}
};
Node** arr; // соответственно в массиве будут хранится структуры Node*
int size; // сколько элементов у нас сейчас в массиве (без учета deleted)
int buffer_size; // размер самого массива, сколько памяти выделено под хранение нашей таблицы
int size_all_non_nullptr; // сколько элементов у нас сейчас в массиве (с учетом deleted)
};На данном этапе мы уже более-менее поняли, что у нас будет храниться в таблице. Переходим к реализации служебных методов.
...
public:
HashTable()
{
buffer_size = default_size;
size = 0;
size_all_non_nullptr = 0;
arr = new Node*[buffer_size];
for (int i = 0; i < buffer_size; ++i)
arr[i] = nullptr; // заполняем nullptr - то есть если значение отсутствует, и никто раньше по этому адресу не обращался
}
~HashTable()
{
for (int i = 0; i < buffer_size; ++i)
if (arr[i])
delete arr[i];
delete[] arr;
}Из необходимых методов осталось еще реализовать динамическое увеличение, расширение массива — метод Resize.
Увеличиваем размер мы стандартно вдвое.
void Resize()
{
int past_buffer_size = buffer_size;
buffer_size *= 2;
size_all_non_nullptr = 0;
size = 0;
Node** arr2 = new Node * [buffer_size];
for (int i = 0; i < buffer_size; ++i)
arr2[i] = nullptr;
std::swap(arr, arr2);
for (int i = 0; i < past_buffer_size; ++i)
{
if (arr2[i] && arr2[i]->state)
Add(arr2[i]->value); // добавляем элементы в новый массив
}
// удаление предыдущего массива
for (int i = 0; i < past_buffer_size; ++i)
if (arr2[i])
delete arr2[i];
delete[] arr2;
}Немаловажным является поддержание асимптотики O(1) стандартных операций. Но что же может повлиять на скорость работы? Наши удаленные элементы (deleted). Ведь, как мы помним, мы ничего не можем с ними сделать, но и окончательно обнулить их не можем. Так что они тянутся за нами огромным балластом. Для ускорения работы нашей хеш-таблицы воспользуемся рехешом (как мы помним, мы уже выделяли под это очень странные переменные).
Теперь воспользуемся ими, если процент реальных элементов массива стал меньше 50, мы производим Rehash, а именно делаем то же самое, что и при увеличении таблицы (resize), но не увеличиваем. Возможно, это звучит глуповато, но попробую сейчас объяснить. Мы вызовем наши хеш-функции от всех элементов, переместим их в новых массив. Но с deleted-элементами это не произойдет, мы не будем их перемещать, и они удалятся вместе со старой таблицей.
Но к чему слова, код все разъяснит:
void Rehash()
{
size_all_non_nullptr = 0;
size = 0;
Node** arr2 = new Node * [buffer_size];
for (int i = 0; i < buffer_size; ++i)
arr2[i] = nullptr;
std::swap(arr, arr2);
for (int i = 0; i < buffer_size; ++i)
{
if (arr2[i] && arr2[i]->state)
Add(arr2[i]->value);
}
// удаление предыдущего массива
for (int i = 0; i < buffer_size; ++i)
if (arr2[i])
delete arr2[i];
delete[] arr2;
}Ну теперь мы уже точно на финальной, хоть и длинной, и полной колючих кустарников, прямой. Нам необходимо реализовать вставку (Add), удаление (Remove) и поиск (Find) элемента.
Начнем с самого простого — метод Find элемент по значению.
bool Find(const T& value, const THash1& hash1 = THash1(), const THash2& hash2 = THash2())
{
int h1 = hash1(value, buffer_size); // значение, отвечающее за начальную позицию
int h2 = hash2(value, buffer_size); // значение, ответственное за "шаг" по таблице
int i = 0;
while (arr[h1] != nullptr && i < buffer_size)
{
if (arr[h1]->value == value && arr[h1]->state)
return true; // такой элемент есть
h1 = (h1 + h2) % buffer_size;
++i; // если у нас i >= buffer_size, значит мы уже обошли абсолютно все ячейки, именно для этого мы считаем i, иначе мы могли бы зациклиться.
}
return false;
}Далее мы реализуем удаление элемента — Remove. Как мы это делаем? Находим элемент (как в методе Find), а затем удаляем, то есть просто меняем значение state на false, но сам Node мы не удаляем.
bool Remove(const T& value, const THash1& hash1 = THash1(), const THash2& hash2 = THash2())
{
int h1 = hash1(value, buffer_size);
int h2 = hash2(value, buffer_size);
int i = 0;
while (arr[h1] != nullptr && i < buffer_size)
{
if (arr[h1]->value == value && arr[h1]->state)
{
arr[h1]->state = false;
--size;
return true;
}
h1 = (h1 + h2) % buffer_size;
++i;
}
return false;
}Ну и последним мы реализуем метод Add. В нем есть несколько очень важных нюансов. Именно здесь мы будем проверять на необходимость рехеша.
Помимо этого в данном методе есть еще одна часть, поддерживающая правильную асимптотику. Это запоминание первого подходящего для вставки элемента (даже если он deleted). Именно туда мы вставим элемент, если в нашей хеш-таблицы нет такого же. Если ни одного deleted-элемента на нашем пути нет, мы создаем новый Node с нашим вставляемым значением.
bool Add(const T& value, const THash1& hash1 = THash1(),const THash2& hash2 = THash2())
{
if (size + 1 > int(rehash_size * buffer_size))
Resize();
else if (size_all_non_nullptr > 2 * size)
Rehash(); // происходит рехеш, так как слишком много deleted-элементов
int h1 = hash1(value, buffer_size);
int h2 = hash2(value, buffer_size);
int i = 0;
int first_deleted = -1; // запоминаем первый подходящий (удаленный) элемент
while (arr[h1] != nullptr && i < buffer_size)
{
if (arr[h1]->value == value && arr[h1]->state)
return false; // такой элемент уже есть, а значит его нельзя вставлять повторно
if (!arr[h1]->state && first_deleted == -1) // находим место для нового элемента
first_deleted = h1;
h1 = (h1 + h2) % buffer_size;
++i;
}
if (first_deleted == -1) // если не нашлось подходящего места, создаем новый Node
{
arr[h1] = new Node(value);
++size_all_non_nullptr; // так как мы заполнили один пробел, не забываем записать, что это место теперь занято
}
else
{
arr[first_deleted]->value = value;
arr[first_deleted]->state = true;
}
++size; // и в любом случае мы увеличили количество элементов
return true;
}В заключение приведу полную реализацию хеш-таблицы.
int HashFunctionHorner(const std::string& s, int table_size, const int key)
{
int hash_result = 0;
for (int i = 0; s[i] != s.size(); ++i)
{
hash_result = (key * hash_result + s[i]) % table_size;
}
hash_result = (hash_result * 2 + 1) % table_size;
return hash_result;
}
struct HashFunction1
{
int operator()(const std::string& s, int table_size) const
{
return HashFunctionHorner(s, table_size, table_size - 1);
}
};
struct HashFunction2
{
int operator()(const std::string& s, int table_size) const
{
return HashFunctionHorner(s, table_size, table_size + 1);
}
};
template <class T, class THash1 = HashFunction1, class THash2 = HashFunction2>
class HashTable
{
static const int default_size = 8;
constexpr static const double rehash_size = 0.75;
struct Node
{
T value;
bool state;
Node(const T& value_) : value(value_), state(true) {}
};
Node** arr;
int size;
int buffer_size;
int size_all_non_nullptr;
void Resize()
{
int past_buffer_size = buffer_size;
buffer_size *= 2;
size_all_non_nullptr = 0;
size = 0;
Node** arr2 = new Node * [buffer_size];
for (int i = 0; i < buffer_size; ++i)
arr2[i] = nullptr;
std::swap(arr, arr2);
for (int i = 0; i < past_buffer_size; ++i)
{
if (arr2[i] && arr2[i]->state)
Add(arr2[i]->value);
}
for (int i = 0; i < past_buffer_size; ++i)
if (arr2[i])
delete arr2[i];
delete[] arr2;
}
void Rehash()
{
size_all_non_nullptr = 0;
size = 0;
Node** arr2 = new Node * [buffer_size];
for (int i = 0; i < buffer_size; ++i)
arr2[i] = nullptr;
std::swap(arr, arr2);
for (int i = 0; i < buffer_size; ++i)
{
if (arr2[i] && arr2[i]->state)
Add(arr2[i]->value);
}
for (int i = 0; i < buffer_size; ++i)
if (arr2[i])
delete arr2[i];
delete[] arr2;
}
public:
HashTable()
{
buffer_size = default_size;
size = 0;
size_all_non_nullptr = 0;
arr = new Node*[buffer_size];
for (int i = 0; i < buffer_size; ++i)
arr[i] = nullptr;
}
~HashTable()
{
for (int i = 0; i < buffer_size; ++i)
if (arr[i])
delete arr[i];
delete[] arr;
}
bool Add(const T& value, const THash1& hash1 = THash1(),const THash2& hash2 = THash2())
{
if (size + 1 > int(rehash_size * buffer_size))
Resize();
else if (size_all_non_nullptr > 2 * size)
Rehash();
int h1 = hash1(value, buffer_size);
int h2 = hash2(value, buffer_size);
int i = 0;
int first_deleted = -1;
while (arr[h1] != nullptr && i < buffer_size)
{
if (arr[h1]->value == value && arr[h1]->state)
return false;
if (!arr[h1]->state && first_deleted == -1)
first_deleted = h1;
h1 = (h1 + h2) % buffer_size;
++i;
}
if (first_deleted == -1)
{
arr[h1] = new Node(value);
++size_all_non_nullptr;
}
else
{
arr[first_deleted]->value = value;
arr[first_deleted]->state = true;
}
++size;
return true;
}
bool Remove(const T& value, const THash1& hash1 = THash1(), const THash2& hash2 = THash2())
{
int h1 = hash1(value, buffer_size);
int h2 = hash2(value, buffer_size);
int i = 0;
while (arr[h1] != nullptr && i < buffer_size)
{
if (arr[h1]->value == value && arr[h1]->state)
{
arr[h1]->state = false;
--size;
return true;
}
h1 = (h1 + h2) % buffer_size;
++i;
}
return false;
}
bool Find(const T& value, const THash1& hash1 = THash1(), const THash2& hash2 = THash2())
{
int h1 = hash1(value, buffer_size);
int h2 = hash2(value, buffer_size);
int i = 0;
while (arr[h1] != nullptr && i < buffer_size)
{
if (arr[h1]->value == value && arr[h1]->state)
return true;
h1 = (h1 + h2) % buffer_size;
++i;
}
return false;
}
};В этой статье вы познакомитесь с хэш-таблицами и увидите примеры их реализации в Cи, C++, Java и Python.
Хеш-таблица — это структура данных, в которой все элементы хранятся в виде пары ключ-значение, где:
- ключ — уникальное число, которое используется для индексации значений;
- значение — данные, которые с этим ключом связаны.
Хеширование (хеш-функция)
В хеш-таблице обработка новых индексов производится при помощи ключей. А элементы, связанные с этим ключом, сохраняются в индексе. Этот процесс называется хешированием.
Пусть k — ключ, а h(x) — хеш-функция.
Тогда h(k) в результате даст индекс, в котором мы будем хранить элемент, связанный с k.
Коллизии
Когда хеш-функция генерирует один индекс для нескольких ключей, возникает конфликт: неизвестно, какое значение нужно сохранить в этом индексе. Это называется коллизией хеш-таблицы.
Есть несколько методов борьбы с коллизиями:
- метод цепочек;
- метод открытой адресации: линейное и квадратичное зондирование.
1. Метод цепочек
Суть этого метода проста: если хеш-функция выделяет один индекс сразу двум элементам, то храниться они будут в одном и том же индексе, но уже с помощью двусвязного списка.
Если j — ячейка для нескольких элементов, то она содержит указатель на первый элемент списка. Если же j пуста, то она содержит NIL.
Псевдокод операций
chainedHashSearch(T, k)
return T[h(k)]
chainedHashInsert(T, x)
T[h(x.key)] = x
chainedHashDelete(T, x)
T[h(x.key)] = NIL 2. Открытая адресация
В отличие от метода цепочек, в открытой адресации несколько элементов в одной ячейке храниться не могут. Суть этого метода заключается в том, что каждая ячейка либо содержит единственный ключ, либо NIL.
Существует несколько видов открытой адресации:
a) Линейное зондирование
Линейное зондирование решает проблему коллизий с помощью проверки следующей ячейки.
h(k, i) = (h′(k) + i) mod m,
где
i = {0, 1, ….}h'(k)— новая хеш-функция
Если коллизия происходит в h(k, 0), тогда проверяется h(k, 1). То есть значение i увеличивается линейно.
Проблема линейного зондирования заключается в том, что заполняется кластер соседних ячеек. Это приводит к тому, что при вставке нового элемента в хеш-таблицу необходимо проводить полный обход кластера. В результате время выполнения операций с хеш-таблицами увеличивается.
b) Квадратичное зондирование
Работает оно так же, как и линейное — но есть отличие. Оно заключается в том, что расстояние между соседними ячейками больше (больше одного). Это возможно благодаря следующему отношению:
h(k, i) = (h′(k) + c1i + c2i2) mod m,
где
c1иc2— положительные вспомогательные константы,i = {0, 1, ….}
c) Двойное хэширование
Если коллизия возникает после применения хеш-функции h(k), то для поиска следующей ячейки вычисляется другая хеш-функция.
h(k, i) = (h1(k) + ih2(k)) mod m
«Хорошие» хеш-функции
«Хорошие» хеш-функции не уберегут вас от коллизий, но, по крайней мере, сократят их количество.
Ниже мы рассмотрим различные методы определения «качества» хэш-функций.
1. Метод деления
Если k — ключ, а m — размер хеш-таблицы, то хеш-функция h() вычисляется следующим образом:
h(k) = k mod m
Например, если m = 10 и k = 112, то h(k) = 112 mod 10 = 2. То есть значение m не должно быть степенью 2. Это связано с тем, что степени двойки в двоичном формате — 10, 100, 1000… При вычислении k mod m мы всегда будем получать p-биты низшего порядка.
если m = 22, k = 17, тогда h(k) = 17 mod 22 = 10001 mod 100 = 01
если m = 23, k = 17, тогда h(k) = 17 mod 22 = 10001 mod 100 = 001
если m = 24, k = 17, тогда h(k) = 17 mod 22 = 10001 mod 100 = 0001
если m = 2p, тогда h(k) = p биты порядком ниже, чем m2. Метод умножения
h(k) = ⌊m(kA mod 1)⌋,
где
kA mod 1отделяет дробную частьkA;⌊ ⌋округляет значение;A— произвольная константа, значение которой должно находиться между 0 и 1. Оптимальный вариант ≈ (√5-1) / 2, его предложил Дональд Кнут.
3. Универсальное хеширование
В универсальном хешировании хеш-функция выбирается случайным образом и не зависит от ключей.
Где применяются
- Когда необходима постоянная скорость поиска и вставки.
- В криптографических приложениях.
- Когда необходима индексация данных.
Примеры реализации хеш-таблиц в Python, Java, Си и C++
Python
# Реализация хеш-таблицы в Python
hashTable = [[],] * 10
def checkPrime(n):
if n == 1 or n == 0:
return 0
for i in range(2, n//2):
if n % i == 0:
return 0
return 1
def getPrime(n):
if n % 2 == 0:
n = n + 1
while not checkPrime(n):
n += 2
return n
def hashFunction(key):
capacity = getPrime(10)
return key % capacity
def insertData(key, data):
index = hashFunction(key)
hashTable[index] = [key, data]
def removeData(key):
index = hashFunction(key)
hashTable[index] = 0
insertData(123, "apple")
insertData(432, "mango")
insertData(213, "banana")
insertData(654, "guava")
print(hashTable)
removeData(123)
print(hashTable)
Java
// Реализация хеш-таблицы в Java
import java.util.*;
class HashTable {
public static void main(String args[])
{
Hashtable<Integer, Integer>
ht = new Hashtable<Integer, Integer>();
ht.put(123, 432);
ht.put(12, 2345);
ht.put(15, 5643);
ht.put(3, 321);
ht.remove(12);
System.out.println(ht);
}
}
Cи
// Реализация хеш-таблицы в Cи
#include <stdio.h>
#include <stdlib.h>
struct set
{
int key;
int data;
};
struct set *array;
int capacity = 10;
int size = 0;
int hashFunction(int key)
{
return (key % capacity);
}
int checkPrime(int n)
{
int i;
if (n == 1 || n == 0)
{
return 0;
}
for (i = 2; i < n / 2; i++)
{
if (n % i == 0)
{
return 0;
}
}
return 1;
}
int getPrime(int n)
{
if (n % 2 == 0)
{
n++;
}
while (!checkPrime(n))
{
n += 2;
}
return n;
}
void init_array()
{
capacity = getPrime(capacity);
array = (struct set *)malloc(capacity * sizeof(struct set));
for (int i = 0; i < capacity; i++)
{
array[i].key = 0;
array[i].data = 0;
}
}
void insert(int key, int data)
{
int index = hashFunction(key);
if (array[index].data == 0)
{
array[index].key = key;
array[index].data = data;
size++;
printf("n Ключ (%d) вставлен n", key);
}
else if (array[index].key == key)
{
array[index].data = data;
}
else
{
printf("n Возникла коллизия n");
}
}
void remove_element(int key)
{
int index = hashFunction(key);
if (array[index].data == 0)
{
printf("n Данного ключа не существует n");
}
else
{
array[index].key = 0;
array[index].data = 0;
size--;
printf("n Ключ (%d) удален n", key);
}
}
void display()
{
int i;
for (i = 0; i < capacity; i++)
{
if (array[i].data == 0)
{
printf("n array[%d]: / ", i);
}
else
{
printf("n Ключ: %d array[%d]: %d t", array[i].key, i, array[i].data);
}
}
}
int size_of_hashtable()
{
return size;
}
int main()
{
int choice, key, data, n;
int c = 0;
init_array();
do
{
printf("1.Вставить элемент в хэш-таблицу"
"n2.Удалить элемент из хэш-таблицы"
"n3.Узнать размер хэш-таблицы"
"n4.Вывести хэш-таблицу"
"nn Пожалуйста, выберите нужный вариант: ");
scanf("%d", &choice);
switch (choice)
{
case 1:
printf("Введите ключ -:t");
scanf("%d", &key);
printf("Введите данные-:t");
scanf("%d", &data);
insert(key, data);
break;
case 2:
printf("Введите ключ, который хотите удалить-:");
scanf("%d", &key);
remove_element(key);
break;
case 3:
n = size_of_hashtable();
printf("Размер хеш-таблицы-:%dn", n);
break;
case 4:
display();
break;
default:
printf("Неверно введены данныеn");
}
printf("nПродолжить? (Нажмите 1, если да): ");
scanf("%d", &c);
} while (c == 1);
}
C++
// Реализация хеш-таблицы в C++
#include <iostream>
#include <list>
using namespace std;
class HashTable
{
int capacity;
list<int> *table;
public:
HashTable(int V);
void insertItem(int key, int data);
void deleteItem(int key);
int checkPrime(int n)
{
int i;
if (n == 1 || n == 0)
{
return 0;
}
for (i = 2; i < n / 2; i++)
{
if (n % i == 0)
{
return 0;
}
}
return 1;
}
int getPrime(int n)
{
if (n % 2 == 0)
{
n++;
}
while (!checkPrime(n))
{
n += 2;
}
return n;
}
int hashFunction(int key)
{
return (key % capacity);
}
void displayHash();
};
HashTable::HashTable(int c)
{
int size = getPrime(c);
this->capacity = size;
table = new list<int>[capacity];
}
void HashTable::insertItem(int key, int data)
{
int index = hashFunction(key);
table[index].push_back(data);
}
void HashTable::deleteItem(int key)
{
int index = hashFunction(key);
list<int>::iterator i;
for (i = table[index].begin();
i != table[index].end(); i++)
{
if (*i == key)
break;
}
if (i != table[index].end())
table[index].erase(i);
}
void HashTable::displayHash()
{
for (int i = 0; i < capacity; i++)
{
cout << "table[" << i << "]";
for (auto x : table[i])
cout << " --> " << x;
cout << endl;
}
}
int main()
{
int key[] = {231, 321, 212, 321, 433, 262};
int data[] = {123, 432, 523, 43, 423, 111};
int size = sizeof(key) / sizeof(key[0]);
HashTable h(size);
for (int i = 0; i < n; i++)
h.insertItem(key[i], data[i]);
h.deleteItem(12);
h.displayHash();
}
21 сентября, 2022 12:24 пп
10 343 views
| Комментариев нет
Development
Хеш-таблица в C/C++ (ассоциативный массив) — это структура данных, которая сопоставляет ключи со значениями и использует хеш-функцию для вычисления индексов ключа.
Индекс хеш-таблицы позволяет нам сохранить значение в соответствующем месте.
Если два разных ключа получают один и тот же индекс, для учета подобных коллизий мы должны использовать другие структуры данных (сегменты).

Главное преимущество использования хеш-таблицы – очень короткое время доступа. Конфликты иногда могут возникать, но шансы практически равны нулю, если выбрать очень хорошую хэш-функцию.
Итак, в среднем временная сложность представляет собой постоянное время доступа O(1) – это называется амортизационной временной сложностью.
C++ STL (стандартная библиотека шаблонов) использует структуру данных std::unordered_map(), которая реализует все эти функции хэш-таблицы.
Однако уметь строить хеш-таблицы с нуля – навык важный и полезный, и именно этим мы займемся в данном мануале.
Давайте разберемся подробнее в деталях реализации таблиц. Любая реализация хеш-таблицы состоит из следующих трех компонентов:
- Хорошая хеш-функция для сопоставления ключей со значениями.
- Структура данных хеш-таблицы, поддерживающая операции вставки, поиска и удаления.
- Структура данных для учета конфликтов ключей
Выбор хэш-функции
Первый шаг — выбрать достаточно хорошую хеш-функцию с низкой вероятностью возникновения коллизии.
Но для иллюстрации в этом мануале мы сделаем все наоборот – выберем плохую функцию и посмотрим, что получится.
В этой статье мы будем работать только со строками (или массивами символов).
Мы будем использовать очень простую хеш-функцию, которая просто суммирует значения ASCII строки. Эта функция позволит нам продемонстрировать, как обрабатывать коллизии.
#define CAPACITY 50000 // Size of the Hash Table
unsigned long hash_function(char* str) {
unsigned long i = 0;
for (int j=0; str[j]; j++)
i += str[j];
return i % CAPACITY;
}
Вы можете проверить эту функцию для разных строк и увидеть, возникают коллизии или нет. Например, строки «Hel» и «Cau» будут конфликтовать, так как они имеют одинаковое значение ASCII.
Примечание: Таблица должна вернуть число в пределах своей емкости. В противном случае мы можем получить доступ к несвязанной области памяти, что приведет к ошибке.
Определение структуры данных хеш-таблицы
Хеш-таблица — это массив элементов, которые сами по себе являются парой {ключ: значение}.
Давайте теперь определим структуру нашего элемента.
typedef struct Ht_item Ht_item;
// Define the Hash Table Item here
struct Ht_item {
char* key;
char* value;
};
Теперь хеш-таблица имеет массив указателей, которые сами ведут на Ht_item, так что получается двойной указатель.
Помимо этого, мы также будем отслеживать количество элементов в хеш-таблице с помощью count и сохранять размер таблицы в size.
typedef struct HashTable HashTable;
// Define the Hash Table here
struct HashTable {
// Contains an array of pointers
// to items
Ht_item** items;
int size;
int count;
};
Создание хеш-таблицы и ее элементов
Чтобы создать в памяти новую хеш-таблицу и ее элементы, нам нужны функции.
Сначала давайте создадим элементы. Это очень просто делается: нам нужно лишь выделить память для ключа и значения и вернуть указатель на элемент.
Ht_item* create_item(char* key, char* value) {
// Creates a pointer to a new hash table item
Ht_item* item = (Ht_item*) malloc (sizeof(Ht_item));
item->key = (char*) malloc (strlen(key) + 1);
item->value = (char*) malloc (strlen(value) + 1);
strcpy(item->key, key);
strcpy(item->value, value);
return item;
}
Теперь давайте напишем код для создания таблицы. Этот код выделяет память для структуры-оболочки HashTable и устанавливает для всех ее элементов значение NULL (поскольку они не используются).
HashTable* create_table(int size) {
// Creates a new HashTable
HashTable* table = (HashTable*) malloc (sizeof(HashTable));
table->size = size;
table->count = 0;
table->items = (Ht_item**) calloc (table->size, sizeof(Ht_item*));
for (int i=0; i<table->size; i++)
table->items[i] = NULL;
return table;
}
Мы почти закончили с этой частью. Как программист C/C++, вы обязаны освобождать выделенную память с помощью malloc(), calloc().
Давайте же напишем функции, которые освобождают элемент и всю таблицу.
void free_item(Ht_item* item) {
// Frees an item
free(item->key);
free(item->value);
free(item);
}
void free_table(HashTable* table) {
// Frees the table
for (int i=0; i<table->size; i++) {
Ht_item* item = table->items[i];
if (item != NULL)
free_item(item);
}
free(table->items);
free(table);
}
Итак, мы завершили работу над нашей функциональной хеш-таблицей. Давайте теперь начнем писать методы insert(), search() и delete().
Вставка в хеш-таблицу
Сейчас мы создадим функцию ht_insert(), которая выполнит задачу вставки за нас.
Она принимает в качестве параметров указатель HashTable, ключ и значение.
void ht_insert(HashTable* table, char* key, char* value);
Далее нужно выполнить определенные шаги, связанные с функцией вставки.
Создать элемент на основе пары {ключ : значение}.
- Вычислить индекс на основе хеш-функции
- Путем сравнения ключа проверить, занят ли данный индекс или еще нет.
- Если он не занят, мы можем напрямую вставить его в index
- В противном случае возникает коллизия, и нам нужно ее обработать
О том, как обрабатывать коллизии, мы поговорим немного позже, после того, как создадим исходную модель.
Первый шаг прост. Мы напрямую вызываем create_item(key, value).
int index = hash_function(key);
Второй и третий шаги для получения индекса используют hash_function(key). Если мы вставляем ключ в первый раз, элемент должен быть NULL. В противном случае либо точная пара «ключ: значение» уже существует, либо это коллизия.
В этом случае мы определяем другую функцию handle_collision(), которая, как следует из названия, обработает эту потенциальную коллизию.
// Create the item
Ht_item* item = create_item(key, value);
// Compute the index
int index = hash_function(key);
Ht_item* current_item = table->items[index];
if (current_item == NULL) {
// Key does not exist.
if (table->count == table->size) {
// Hash Table Full
printf("Insert Error: Hash Table is fulln");
free_item(item);
return;
}
// Insert directly
table->items[index] = item;
table->count++;
}
Давайте рассмотрим первый сценарий, где пара «ключ: значение» уже существует (то есть такой же элемент уже был вставлен в таблицу ранее). В этом случае мы всего лишь должны обновить значение элемента, просто присвоить ему новое значение.
if (current_item == NULL) {
....
....
}else {
// Scenario 1: We only need to update value
if (strcmp(current_item->key, key) == 0) {
strcpy(table->items[index]->value, value);
return;
}
else {
// Scenario 2: Collision
// We will handle case this a bit later
handle_collision(table, item);
return;
}
}
Итак, функция вставки (без коллизий) теперь выглядит примерно так:
void handle_collision(HashTable* table, Ht_item* item) {
}
void ht_insert(HashTable* table, char* key, char* value) {
// Create the item
Ht_item* item = create_item(key, value);
Ht_item* current_item = table->items[index];
if (current_item == NULL) {
// Key does not exist.
if (table->count == table->size) {
// Hash Table Full
printf("Insert Error: Hash Table is fulln");
return;
}
// Insert directly
table->items[index] = item;
table->count++;
}
else {
// Scenario 1: We only need to update value
if (strcmp(current_item->key, key) == 0) {
strcpy(table->items[index]->value, value);
return;
}
else {
// Scenario 2: Collision
// We will handle case this a bit later
handle_collision(table, item);
return;
}
}
}
Поиск элементов в хеш-таблице
Если мы хотим проверить правильность вставки, мы должны определить функцию поиска, которая проверяет, существует ключ или нет, и возвращает соответствующее значение, если он существует.
char* ht_search(HastTable* table, char* key);
Логика очень проста. Функция просто переходит к элементам, котороые не являются NULL, и сравнивает ключ. В противном случае она вернет NULL.
char* ht_search(HashTable* table, char* key) {
// Searches the key in the hashtable
// and returns NULL if it doesn't exist
int index = hash_function(key);
Ht_item* item = table->items[index];
// Ensure that we move to a non NULL item
if (item != NULL) {
if (strcmp(item->key, key) == 0)
return item->value;
}
return NULL;
}
Тестирование базовой модели
Давайте проверим, правильно ли работает то, что мы муже написали. Для этого мы используем программу-драйвер main().
Чтобы проиллюстрировать, как все работает, добавим еще одну функцию print_table(), которая выводит хеш-таблицу.
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define CAPACITY 50000 // Size of the Hash Table
unsigned long hash_function(char* str) {
unsigned long i = 0;
for (int j=0; str[j]; j++)
i += str[j];
return i % CAPACITY;
}
typedef struct Ht_item Ht_item;
// Define the Hash Table Item here
struct Ht_item {
char* key;
char* value;
};
typedef struct HashTable HashTable;
// Define the Hash Table here
struct HashTable {
// Contains an array of pointers
// to items
Ht_item** items;
int size;
int count;
};
Ht_item* create_item(char* key, char* value) {
// Creates a pointer to a new hash table item
Ht_item* item = (Ht_item*) malloc (sizeof(Ht_item));
item->key = (char*) malloc (strlen(key) + 1);
item->value = (char*) malloc (strlen(value) + 1);
strcpy(item->key, key);
strcpy(item->value, value);
return item;
}
HashTable* create_table(int size) {
// Creates a new HashTable
HashTable* table = (HashTable*) malloc (sizeof(HashTable));
table->size = size;
table->count = 0;
table->items = (Ht_item**) calloc (table->size, sizeof(Ht_item*));
for (int i=0; i<table->size; i++)
table->items[i] = NULL;
return table;
}
void free_item(Ht_item* item) {
// Frees an item
free(item->key);
free(item->value);
free(item);
}
void free_table(HashTable* table) {
// Frees the table
for (int i=0; i<table->size; i++) {
Ht_item* item = table->items[i];
if (item != NULL)
free_item(item);
}
free(table->items);
free(table);
}
void handle_collision(HashTable* table, unsigned long index, Ht_item* item) {
}
void ht_insert(HashTable* table, char* key, char* value) {
// Create the item
Ht_item* item = create_item(key, value);
// Compute the index
unsigned long index = hash_function(key);
Ht_item* current_item = table->items[index];
if (current_item == NULL) {
// Key does not exist.
if (table->count == table->size) {
// Hash Table Full
printf("Insert Error: Hash Table is fulln");
// Remove the create item
free_item(item);
return;
}
// Insert directly
table->items[index] = item;
table->count++;
}
else {
// Scenario 1: We only need to update value
if (strcmp(current_item->key, key) == 0) {
strcpy(table->items[index]->value, value);
return;
}
else {
// Scenario 2: Collision
// We will handle case this a bit later
handle_collision(table, index, item);
return;
}
}
}
char* ht_search(HashTable* table, char* key) {
// Searches the key in the hashtable
// and returns NULL if it doesn't exist
int index = hash_function(key);
Ht_item* item = table->items[index];
// Ensure that we move to a non NULL item
if (item != NULL) {
if (strcmp(item->key, key) == 0)
return item->value;
}
return NULL;
}
void print_search(HashTable* table, char* key) {
char* val;
if ((val = ht_search(table, key)) == NULL) {
printf("Key:%s does not existn", key);
return;
}
else {
printf("Key:%s, Value:%sn", key, val);
}
}
void print_table(HashTable* table) {
printf("nHash Tablen-------------------n");
for (int i=0; i<table->size; i++) {
if (table->items[i]) {
printf("Index:%d, Key:%s, Value:%sn", i, table->items[i]->key, table->items[i]->value);
}
}
printf("-------------------nn");
}
int main() {
HashTable* ht = create_table(CAPACITY);
ht_insert(ht, "1", "First address");
ht_insert(ht, "2", "Second address");
print_search(ht, "1");
print_search(ht, "2");
print_search(ht, "3");
print_table(ht);
free_table(ht);
return 0;
}
В результате мы получим:
Key:1, Value:First address Key:2, Value:Second address Key:3 does not exist Hash Table ------------------- Index:49, Key:1, Value:First address Index:50, Key:2, Value:Second address -------------------
Замечательно! Кажется, все работает так, как мы и ожидали. Теперь давайте перейдем к обработке коллизий.
Разрешение коллизий
Существуют различные способы разрешения коллизии. Мы рассмотрим метод под названием «метод цепочек», целью которого является создание независимых цепочек для всех элементов с одинаковым хэш-индексом.
Мы создадим эти цепочки с помощью связных списков.
Всякий раз, когда возникает коллизия, мы добавляем дополнительные элементы, которые конфликтуют с одним и тем же индексом в списке переполненных бакетов. Таким образом, нам не придется удалять какие-либо существующие записи из таблицы.
Поскольку связные списки имеют временную сложность O(n) для вставки, поиска и удаления, при возникновении коллизии время доступа в наихудшем случае тоже будет O(n). Этот метод хорошо подходит для работы с таблицами небольшой емкости.
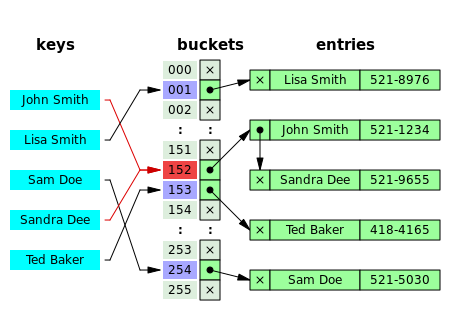
Давайте же приступим к реализации связанного списка.
typedef struct LinkedList LinkedList;
// Define the Linkedlist here
struct LinkedList {
Ht_item* item;
LinkedList* next;
};
LinkedList* allocate_list () {
// Allocates memory for a Linkedlist pointer
LinkedList* list = (LinkedList*) malloc (sizeof(LinkedList));
return list;
}
LinkedList* linkedlist_insert(LinkedList* list, Ht_item* item) {
// Inserts the item onto the Linked List
if (!list) {
LinkedList* head = allocate_list();
head->item = item;
head->next = NULL;
list = head;
return list;
}
else if (list->next == NULL) {
LinkedList* node = allocate_list();
node->item = item;
node->next = NULL;
list->next = node;
return list;
}
LinkedList* temp = list;
while (temp->next->next) {
temp = temp->next;
}
LinkedList* node = allocate_list();
node->item = item;
node->next = NULL;
temp->next = node;
return list;
Ht_item* linkedlist_remove(LinkedList* list) {
// Removes the head from the linked list
// and returns the item of the popped element
if (!list)
return NULL;
if (!list->next)
return NULL;
LinkedList* node = list->next;
LinkedList* temp = list;
temp->next = NULL;
list = node;
Ht_item* it = NULL;
memcpy(temp->item, it, sizeof(Ht_item));
free(temp->item->key);
free(temp->item->value);
free(temp->item);
free(temp);
return it;
}
void free_linkedlist(LinkedList* list) {
LinkedList* temp = list;
while (list) {
temp = list;
list = list->next;
free(temp->item->key);
free(temp->item->value);
free(temp->item);
free(temp);
}
}
Теперь нужно добавить эти списки переполненных бакетов в хеш-таблицу. У каждого элемента должна быть одна такая цепочка, поэтому для всей таблицы мы добавим массив указателей LinkedList.
typedef struct HashTable HashTable;
// Define the Hash Table here
struct HashTable {
// Contains an array of pointers
// to items
Ht_item** items;
LinkedList** overflow_buckets;
int size;
int count;
};
Теперь, когда мы определили overflow_buckets, давайте добавим функции для их создания и удаления. Их также необходимо учитывать в старых функциях create_table() и free_table().
LinkedList** create_overflow_buckets(HashTable* table) {
// Create the overflow buckets; an array of linkedlists
LinkedList** buckets = (LinkedList**) calloc (table->size, sizeof(LinkedList*));
for (int i=0; i<table->size; i++)
buckets[i] = NULL;
return buckets;
}
void free_overflow_buckets(HashTable* table) {
// Free all the overflow bucket lists
LinkedList** buckets = table->overflow_buckets;
for (int i=0; i<table->size; i++)
free_linkedlist(buckets[i]);
free(buckets);
}
HashTable* create_table(int size) {
// Creates a new HashTable
HashTable* table = (HashTable*) malloc (sizeof(HashTable));
table->size = size;
table->count = 0;
table->items = (Ht_item**) calloc (table->size, sizeof(Ht_item*));
for (int i=0; i<table->size; i++)
table->items[i] = NULL;
table->overflow_buckets = create_overflow_buckets(table);
return table;
}
void free_table(HashTable* table) {
// Frees the table
for (int i=0; i<table->size; i++) {
Ht_item* item = table->items[i];
if (item != NULL)
free_item(item);
}
// Free the overflow bucket linked linkedlist and it's items
free_overflow_buckets(table);
free(table->items);
free(table);
}
Теперь перейдем к функции handle_collision().
Здесь есть два сценария. Если список элемента не существует, нам нужно создать такой список и добавить в него элемент.
В противном случае мы можем просто вставить элемент в список.
void handle_collision(HashTable* table, unsigned long index, Ht_item* item) {
LinkedList* head = table->overflow_buckets[index];
if (head == NULL) {
// We need to create the list
head = allocate_list();
head->item = item;
table->overflow_buckets[index] = head;
return;
}
else {
// Insert to the list
table->overflow_buckets[index] = linkedlist_insert(head, item);
return;
}
}
Итак, мы закончили со вставкой, и теперь нам также нужно обновить функцию поиска, так как нам, возможно, потребуется также просмотреть переполненные бакеты.
char* ht_search(HashTable* table, char* key) {
// Searches the key in the hashtable
// and returns NULL if it doesn't exist
int index = hash_function(key);
Ht_item* item = table->items[index];
LinkedList* head = table->overflow_buckets[index];
// Ensure that we move to items which are not NULL
while (item != NULL) {
if (strcmp(item->key, key) == 0)
return item->value;
if (head == NULL)
return NULL;
item = head->item;
head = head->next;
}
return NULL;
Итак, мы учли коллизии в функциях insert() и search(). На данный момент наш код выглядит так:
#include
#include
#include
#define CAPACITY 50000 // Size of the Hash Table
unsigned long hash_function(char* str) {
unsigned long i = 0;
for (int j=0; str[j]; j++)
i += str[j];
return i % CAPACITY;
}
typedef struct Ht_item Ht_item;
// Define the Hash Table Item here
struct Ht_item {
char* key;
char* value;
};
typedef struct LinkedList LinkedList;
// Define the Linkedlist here
struct LinkedList {
Ht_item* item;
LinkedList* next;
};
typedef struct HashTable HashTable;
// Define the Hash Table here
struct HashTable {
// Contains an array of pointers
// to items
Ht_item** items;
LinkedList** overflow_buckets;
int size;
int count;
};
static LinkedList* allocate_list () {
// Allocates memory for a Linkedlist pointer
LinkedList* list = (LinkedList*) malloc (sizeof(LinkedList));
return list;
}
static LinkedList* linkedlist_insert(LinkedList* list, Ht_item* item) {
// Inserts the item onto the Linked List
if (!list) {
LinkedList* head = allocate_list();
head->item = item;
head->next = NULL;
list = head;
return list;
}
else if (list->next == NULL) {
LinkedList* node = allocate_list();
node->item = item;
node->next = NULL;
list->next = node;
return list;
}
LinkedList* temp = list;
while (temp->next->next) {
temp = temp->next;
}
LinkedList* node = allocate_list();
node->item = item;
node->next = NULL;
temp->next = node;
return list;
}
static Ht_item* linkedlist_remove(LinkedList* list) {
// Removes the head from the linked list
// and returns the item of the popped element
if (!list)
return NULL;
if (!list->next)
return NULL;
LinkedList* node = list->next;
LinkedList* temp = list;
temp->next = NULL;
list = node;
Ht_item* it = NULL;
memcpy(temp->item, it, sizeof(Ht_item));
free(temp->item->key);
free(temp->item->value);
free(temp->item);
free(temp);
return it;
}
static void free_linkedlist(LinkedList* list) {
LinkedList* temp = list;
while (list) {
temp = list;
list = list->next;
free(temp->item->key);
free(temp->item->value);
free(temp->item);
free(temp);
}
}
static LinkedList** create_overflow_buckets(HashTable* table) {
// Create the overflow buckets; an array of linkedlists
LinkedList** buckets = (LinkedList**) calloc (table->size, sizeof(LinkedList*));
for (int i=0; isize; i++)
buckets[i] = NULL;
return buckets;
}
static void free_overflow_buckets(HashTable* table) {
// Free all the overflow bucket lists
LinkedList** buckets = table->overflow_buckets;
for (int i=0; isize; i++)
free_linkedlist(buckets[i]);
free(buckets);
}
Ht_item* create_item(char* key, char* value) {
// Creates a pointer to a new hash table item
Ht_item* item = (Ht_item*) malloc (sizeof(Ht_item));
item->key = (char*) malloc (strlen(key) + 1);
item->value = (char*) malloc (strlen(value) + 1);
strcpy(item->key, key);
strcpy(item->value, value);
return item;
}
HashTable* create_table(int size) {
// Creates a new HashTable
HashTable* table = (HashTable*) malloc (sizeof(HashTable));
table->size = size;
table->count = 0;
table->items = (Ht_item**) calloc (table->size, sizeof(Ht_item*));
for (int i=0; isize; i++)
table->items[i] = NULL;
table->overflow_buckets = create_overflow_buckets(table);
return table;
}
void free_item(Ht_item* item) {
// Frees an item
free(item->key);
free(item->value);
free(item);
}
void free_table(HashTable* table) {
// Frees the table
for (int i=0; isize; i++) {
Ht_item* item = table->items[i];
if (item != NULL)
free_item(item);
}
free_overflow_buckets(table);
free(table->items);
free(table);
}
void handle_collision(HashTable* table, unsigned long index, Ht_item* item) {
LinkedList* head = table->overflow_buckets[index];
if (head == NULL) {
// We need to create the list
head = allocate_list();
head->item = item;
table->overflow_buckets[index] = head;
return;
}
else {
// Insert to the list
table->overflow_buckets[index] = linkedlist_insert(head, item);
return;
}
}
void ht_insert(HashTable* table, char* key, char* value) {
// Create the item
Ht_item* item = create_item(key, value);
// Compute the index
unsigned long index = hash_function(key);
Ht_item* current_item = table->items[index];
if (current_item == NULL) {
// Key does not exist.
if (table->count == table->size) {
// Hash Table Full
printf("Insert Error: Hash Table is fulln");
// Remove the create item
free_item(item);
return;
}
// Insert directly
table->items[index] = item;
table->count++;
}
else {
// Scenario 1: We only need to update value
if (strcmp(current_item->key, key) == 0) {
strcpy(table->items[index]->value, value);
return;
}
else {
// Scenario 2: Collision
handle_collision(table, index, item);
return;
}
}
}
char* ht_search(HashTable* table, char* key) {
// Searches the key in the hashtable
// and returns NULL if it doesn't exist
int index = hash_function(key);
Ht_item* item = table->items[index];
LinkedList* head = table->overflow_buckets[index];
// Ensure that we move to items which are not NULL
while (item != NULL) {
if (strcmp(item->key, key) == 0)
return item->value;
if (head == NULL)
return NULL;
item = head->item;
head = head->next;
}
return NULL;
}
void print_search(HashTable* table, char* key) {
char* val;
if ((val = ht_search(table, key)) == NULL) {
printf("%s does not existn", key);
return;
}
else {
printf("Key:%s, Value:%sn", key, val);
}
}
void print_table(HashTable* table) {
printf("n-------------------n");
for (int i=0; isize; i++) {
if (table->items[i]) {
printf("Index:%d, Key:%s, Value:%s", i, table->items[i]->key, table->items[i]->value);
if (table->overflow_buckets[i]) {
printf(" => Overflow Bucket => ");
LinkedList* head = table->overflow_buckets[i];
while (head) {
printf("Key:%s, Value:%s ", head->item->key, head->item->value);
head = head->next;
}
}
printf("n");
}
}
printf("-------------------n");
}
int main() {
HashTable* ht = create_table(CAPACITY);
ht_insert(ht, "1", "First address");
ht_insert(ht, "2", "Second address");
ht_insert(ht, "Hel", "Third address");
ht_insert(ht, "Cau", "Fourth address");
print_search(ht, "1");
print_search(ht, "2");
print_search(ht, "3");
print_search(ht, "Hel");
print_search(ht, "Cau");
print_table(ht);
free_table(ht);
return 0;
}
Удаление из хеш-таблицы
Давайте взглянем на функцию удаления данных из таблицы:
void ht_delete(HashTable* table, char* key);
Эта функция работает аналогично вставке. Нам нужно:
- Вычислить хеш-индекс и получить элемент.
- Если это NULL, нам ничего не нужно делать
- В противном случае, если для этого индекса нет цепочки коллизий, после сравнения ключей нужно просто удалить элемент из таблицы.
- Если цепочка коллизий существует, мы должны удалить этот элемент и соответствующим образом сдвинуть данные.
Мы не будем перечислять здесь слишком много подробностей, так как эта процедура включает только обновление элементов заголовка и освобождение памяти. Предлагаем вам попытаться реализовать это самостоятельно.
Предоставляем вам рабочую версию для сравнения.
void ht_delete(HashTable* table, char* key) {
// Deletes an item from the table
int index = hash_function(key);
Ht_item* item = table->items[index];
LinkedList* head = table->overflow_buckets[index];
if (item == NULL) {
// Does not exist. Return
return;
}
else {
if (head == NULL && strcmp(item->key, key) == 0) {
// No collision chain. Remove the item
// and set table index to NULL
table->items[index] = NULL;
free_item(item);
table->count--;
return;
}
else if (head != NULL) {
// Collision Chain exists
if (strcmp(item->key, key) == 0) {
// Remove this item and set the head of the list
// as the new item
free_item(item);
LinkedList* node = head;
head = head->next;
node->next = NULL;
table->items[index] = create_item(node->item->key, node->item->value);
free_linkedlist(node);
table->overflow_buckets[index] = head;
return;
}
LinkedList* curr = head;
LinkedList* prev = NULL;
while (curr) {
if (strcmp(curr->item->key, key) == 0) {
if (prev == NULL) {
// First element of the chain. Remove the chain
free_linkedlist(head);
table->overflow_buckets[index] = NULL;
return;
}
else {
// This is somewhere in the chain
prev->next = curr->next;
curr->next = NULL;
free_linkedlist(curr);
table->overflow_buckets[index] = head;
return;
}
}
curr = curr->next;
prev = curr;
}
}
}
}
Полный код
Наконец, мы можем посмотреть на полный код программы хеш-таблицы.
#include
#include
#include
#define CAPACITY 50000 // Size of the Hash Table
unsigned long hash_function(char* str) {
unsigned long i = 0;
for (int j=0; str[j]; j++)
i += str[j];
return i % CAPACITY;
}
typedef struct Ht_item Ht_item;
// Define the Hash Table Item here
struct Ht_item {
char* key;
char* value;
};
typedef struct LinkedList LinkedList;
// Define the Linkedlist here
struct LinkedList {
Ht_item* item;
LinkedList* next;
};
typedef struct HashTable HashTable;
// Define the Hash Table here
struct HashTable {
// Contains an array of pointers
// to items
Ht_item** items;
LinkedList** overflow_buckets;
int size;
int count;
};
static LinkedList* allocate_list () {
// Allocates memory for a Linkedlist pointer
LinkedList* list = (LinkedList*) malloc (sizeof(LinkedList));
return list;
}
static LinkedList* linkedlist_insert(LinkedList* list, Ht_item* item) {
// Inserts the item onto the Linked List
if (!list) {
LinkedList* head = allocate_list();
head->item = item;
head->next = NULL;
list = head;
return list;
}
else if (list->next == NULL) {
LinkedList* node = allocate_list();
node->item = item;
node->next = NULL;
list->next = node;
return list;
}
LinkedList* temp = list;
while (temp->next->next) {
temp = temp->next;
}
LinkedList* node = allocate_list();
node->item = item;
node->next = NULL;
temp->next = node;
return list;
}
static Ht_item* linkedlist_remove(LinkedList* list) {
// Removes the head from the linked list
// and returns the item of the popped element
if (!list)
return NULL;
if (!list->next)
return NULL;
LinkedList* node = list->next;
LinkedList* temp = list;
temp->next = NULL;
list = node;
Ht_item* it = NULL;
memcpy(temp->item, it, sizeof(Ht_item));
free(temp->item->key);
free(temp->item->value);
free(temp->item);
free(temp);
return it;
}
static void free_linkedlist(LinkedList* list) {
LinkedList* temp = list;
while (list) {
temp = list;
list = list->next;
free(temp->item->key);
free(temp->item->value);
free(temp->item);
free(temp);
}
}
static LinkedList** create_overflow_buckets(HashTable* table) {
// Create the overflow buckets; an array of linkedlists
LinkedList** buckets = (LinkedList**) calloc (table->size, sizeof(LinkedList*));
for (int i=0; isize; i++)
buckets[i] = NULL;
return buckets;
}
static void free_overflow_buckets(HashTable* table) {
// Free all the overflow bucket lists
LinkedList** buckets = table->overflow_buckets;
for (int i=0; isize; i++)
free_linkedlist(buckets[i]);
free(buckets);
}
Ht_item* create_item(char* key, char* value) {
// Creates a pointer to a new hash table item
Ht_item* item = (Ht_item*) malloc (sizeof(Ht_item));
item->key = (char*) malloc (strlen(key) + 1);
item->value = (char*) malloc (strlen(value) + 1);
strcpy(item->key, key);
strcpy(item->value, value);
return item;
}
HashTable* create_table(int size) {
// Creates a new HashTable
HashTable* table = (HashTable*) malloc (sizeof(HashTable));
table->size = size;
table->count = 0;
table->items = (Ht_item**) calloc (table->size, sizeof(Ht_item*));
for (int i=0; isize; i++)
table->items[i] = NULL;
table->overflow_buckets = create_overflow_buckets(table);
return table;
}
void free_item(Ht_item* item) {
// Frees an item
free(item->key);
free(item->value);
free(item);
}
void free_table(HashTable* table) {
// Frees the table
for (int i=0; isize; i++) {
Ht_item* item = table->items[i];
if (item != NULL)
free_item(item);
}
free_overflow_buckets(table);
free(table->items);
free(table);
}
void handle_collision(HashTable* table, unsigned long index, Ht_item* item) {
LinkedList* head = table->overflow_buckets[index];
if (head == NULL) {
// We need to create the list
head = allocate_list();
head->item = item;
table->overflow_buckets[index] = head;
return;
}
else {
// Insert to the list
table->overflow_buckets[index] = linkedlist_insert(head, item);
return;
}
}
void ht_insert(HashTable* table, char* key, char* value) {
// Create the item
Ht_item* item = create_item(key, value);
// Compute the index
unsigned long index = hash_function(key);
Ht_item* current_item = table->items[index];
if (current_item == NULL) {
// Key does not exist.
if (table->count == table->size) {
// Hash Table Full
printf("Insert Error: Hash Table is fulln");
// Remove the create item
free_item(item);
return;
}
// Insert directly
table->items[index] = item;
table->count++;
}
else {
// Scenario 1: We only need to update value
if (strcmp(current_item->key, key) == 0) {
strcpy(table->items[index]->value, value);
return;
}
else {
// Scenario 2: Collision
handle_collision(table, index, item);
return;
}
}
}
char* ht_search(HashTable* table, char* key) {
// Searches the key in the hashtable
// and returns NULL if it doesn't exist
int index = hash_function(key);
Ht_item* item = table->items[index];
LinkedList* head = table->overflow_buckets[index];
// Ensure that we move to items which are not NULL
while (item != NULL) {
if (strcmp(item->key, key) == 0)
return item->value;
if (head == NULL)
return NULL;
item = head->item;
head = head->next;
}
return NULL;
}
void ht_delete(HashTable* table, char* key) {
// Deletes an item from the table
int index = hash_function(key);
Ht_item* item = table->items[index];
LinkedList* head = table->overflow_buckets[index];
if (item == NULL) {
// Does not exist. Return
return;
}
else {
if (head == NULL && strcmp(item->key, key) == 0) {
// No collision chain. Remove the item
// and set table index to NULL
table->items[index] = NULL;
free_item(item);
table->count--;
return;
}
else if (head != NULL) {
// Collision Chain exists
if (strcmp(item->key, key) == 0) {
// Remove this item and set the head of the list
// as the new item
free_item(item);
LinkedList* node = head;
head = head->next;
node->next = NULL;
table->items[index] = create_item(node->item->key, node->item->value);
free_linkedlist(node);
table->overflow_buckets[index] = head;
return;
}
LinkedList* curr = head;
LinkedList* prev = NULL;
while (curr) {
if (strcmp(curr->item->key, key) == 0) {
if (prev == NULL) {
// First element of the chain. Remove the chain
free_linkedlist(head);
table->overflow_buckets[index] = NULL;
return;
}
else {
// This is somewhere in the chain
prev->next = curr->next;
curr->next = NULL;
free_linkedlist(curr);
table->overflow_buckets[index] = head;
return;
}
}
curr = curr->next;
prev = curr;
}
}
}
}
void print_search(HashTable* table, char* key) {
char* val;
if ((val = ht_search(table, key)) == NULL) {
printf("%s does not existn", key);
return;
}
else {
printf("Key:%s, Value:%sn", key, val);
}
}
void print_table(HashTable* table) {
printf("n-------------------n");
for (int i=0; isize; i++) {
if (table->items[i]) {
printf("Index:%d, Key:%s, Value:%s", i, table->items[i]->key, table->items[i]->value);
if (table->overflow_buckets[i]) {
printf(" => Overflow Bucket => ");
LinkedList* head = table->overflow_buckets[i];
while (head) {
printf("Key:%s, Value:%s ", head->item->key, head->item->value);
head = head->next;
}
}
printf("n");
}
}
printf("-------------------n");
}
int main() {
HashTable* ht = create_table(CAPACITY);
ht_insert(ht, "1", "First address");
ht_insert(ht, "2", "Second address");
ht_insert(ht, "Hel", "Third address");
ht_insert(ht, "Cau", "Fourth address");
print_search(ht, "1");
print_search(ht, "2");
print_search(ht, "3");
print_search(ht, "Hel");
print_search(ht, "Cau"); // Collision!
print_table(ht);
ht_delete(ht, "1");
ht_delete(ht, "Cau");
print_table(ht);
free_table(ht);
return 0;
}
Результат выглядит так:
Key:1, Value:First address
Key:2, Value:Second address
3 does not exist
Key:Hel, Value:Third address
Key:Cau, Value:Fourth address
-------------------
Index:49, Key:1, Value:First address
Index:50, Key:2, Value:Second address
Index:281, Key:Hel, Value:Third address => Overflow Bucket => Key:Cau, Value:Fourth address
-------------------
-------------------
Index:50, Key:2, Value:Second address
Index:281, Key:Hel, Value:Third address
-------------------
Заключение
Надеемся, вы поняли, как можно реализовать хеш-таблицу с нуля на C/C++. Возможно, у вас получилось реализовать ее самостоятельно.
Советуем вам также попробовать на примере полученной таблицы использовать другие алгоритмы обработки коллизий и другие хеш-функции и проверить их производительность.
Скачать код, который мы рассмотрели в этом руководстве, можно на Github Gist.
Читайте также: Сравнение строк в C++: три основных метода
Tags: C++
March 2021
Summary: An explanation of how to implement a simple hash table data structure using the C programming language. I briefly demonstrate linear and binary search, and then design and implement a hash table. My goal is to show that hash table internals are not scary, but – within certain constraints – are easy enough to build from scratch.
Go to: Linear search | Binary search | Hash tables | Implementation | Discussion
Recently I wrote an article that compared a simple program that counts word frequencies across various languages, and one of the things that came up was how C doesn’t have a hash table data structure in its standard library.
There are many things you can do when you realize this: use linear search, use binary search, grab someone else’s hash table implementation, or write your own hash table. Or switch to a richer language. We’re going to take a quick look at linear and binary search, and then learn how to write our own hash table. This is often necessary in C, but it can also be useful if you need a custom hash table when using another language.
Linear search
The simplest option is to use linear search to scan through an array. This is actually not a bad strategy if you’ve only got a few items – in my simple comparison using strings, it’s faster than a hash table lookup up to about 7 items (but unless your program is very performance-sensitive, it’s probably fine up to 20 or 30 items). Linear search also allows you to append new items to the end of the array. With this type of search you’re comparing an average of num_keys/2 items.
Let’s say you’re searching for the key bob in the following array (each item is a string key with an associated integer value):
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Key | foo |
bar |
bazz |
buzz |
bob |
jane |
x |
| Value | 10 | 42 | 36 | 7 | 11 | 100 | 200 |
You simply start at the beginning (foo at index 0) and compare each key. If the key matches what you’re looking for, you’re done. If not, you move to the next slot. Searching for bob takes five steps (indexes 0 through 4).
Here is the algorithm in C (assuming each array item is a string key and integer value):
typedef struct {
char* key;
int value;
} item;
item* linear_search(item* items, size_t size, const char* key) {
for (size_t i=0; i<size; i++) {
if (strcmp(items[i].key, key) == 0) {
return &items[i];
}
}
return NULL;
}
int main(void) {
item items[] = {
{"foo", 10}, {"bar", 42}, {"bazz", 36}, {"buzz", 7},
{"bob", 11}, {"jane", 100}, {"x", 200}};
size_t num_items = sizeof(items) / sizeof(item);
item* found = linear_search(items, num_items, "bob");
if (!found) {
return 1;
}
printf("linear_search: value of 'bob' is %dn", found->value);
return 0;
}
Binary search
Another simple approach is to put the items in an array which is sorted by key, and use binary search to reduce the number of comparisons. This is kind of how we might look something up in a (paper) dictionary.
C even has a bsearch function in its standard library. Binary search is reasonably fast even for hundreds of items (though not as fast as a hash table), because you’re only comparing an average of log(num_keys) items. However, because the array needs to stay sorted, you can’t insert items without copying the rest down, so insertions still require an average of num_keys/2 operations.
Assume we’re looking up bob again (in this pre-sorted array):
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Key | bar |
bazz |
bob |
buzz |
foo |
jane |
x |
| Value | 42 | 36 | 11 | 7 | 10 | 100 | 200 |
With binary search, we start in the middle (buzz), and if the key there is greater than what we’re looking for, we repeat the process with the lower half. If it’s greater, we repeat the process with the higher half. In this case it results in three steps, at indexes 3, 1, 2, and then we have it. This is 3 steps instead of 5, and the improvement over linear search gets (exponentially) better the more items you have.
Here’s how you’d do it in C (with and without bsearch). The definition of the item struct is the same as above.
int cmp(const void* a, const void* b) {
item* item_a = (item*)a;
item* item_b = (item*)b;
return strcmp(item_a->key, item_b->key);
}
item* binary_search(item* items, size_t size, const char* key) {
if (size + size < size) {
return NULL; // size too big; avoid overflow
}
size_t low = 0;
size_t high = size;
while (low < high) {
size_t mid = (low + high) / 2;
int c = strcmp(items[mid].key, key);
if (c == 0) {
return &items[mid];
}
if (c < 0) {
low = mid + 1; // eliminate low half of array
} else {
high = mid; // eliminate high half of array
}
}
// Entire array has been eliminated, key not found.
return NULL;
}
int main(void) {
item items[] = {
{"bar", 42}, {"bazz", 36}, {"bob", 11}, {"buzz", 7},
{"foo", 10}, {"jane", 100}, {"x", 200}};
size_t num_items = sizeof(items) / sizeof(item);
item key = {"bob", 0};
item* found = bsearch(&key, items, num_items, sizeof(item), cmp);
if (found == NULL) {
return 1;
}
printf("bsearch: value of 'bob' is %dn", found->value);
found = binary_search(items, num_items, "bob");
if (found == NULL) {
return 1;
}
printf("binary_search: value of 'bob' is %dn", found->value);
return 0;
}
Note: in binary_search, it would be slightly better to avoid the up-front “half size overflow check” and allow the entire range of size_t. This would mean changing the mid calculation to low + (high-low)/2. However, I’m going to leave the code stand for educational purposes – with the initial overflow check, I don’t think there’s a bug, but it is non-ideal that I’m only allowing half the range of size_t. Not that I’ll be searching a 16 exabyte array on my 64-bit system anytime soon! For further reading, see the article Nearly All Binary Searches and Mergesorts are Broken. Thanks Seth Arnold and Olaf Seibert for the feedback.
Hash tables
Hash tables can seem quite scary: there are a lot of different types, and a ton of different optimizations you can do. However, if you use a simple hash function together with what’s called “linear probing” you can create a decent hash table quite easily.
If you don’t know how a hash table works, here’s a quick refresher. A hash table is a container data structure that allows you to quickly look up a key (often a string) to find its corresponding value (any data type). Under the hood, they’re arrays that are indexed by a hash function of the key.
A hash function turns a key into a random-looking number, and it must always return the same number given the same key. For example, with the hash function we’re going to use (64-bit FNV-1a), the hashes of the keys above are as follows:
| Key | Hash | Hash modulo 16 |
|---|---|---|
bar |
16101355973854746 | 10 |
bazz |
11123581685902069096 | 8 |
bob |
21748447695211092 | 4 |
buzz |
18414333339470238796 | 12 |
foo |
15902901984413996407 | 7 |
jane |
10985288698319103569 | 1 |
x |
12638214688346347271 | 7 (same as foo) |
The reason I’ve shown the hash modulo 16 is because we’re going to start with an array of 16 elements, so we need to limit the hash to the number of elements in the array – the modulo operation divides by 16 and gives the remainder, limiting the array index to the range 0 through 15.
When we insert a value into the hash table, we calculate its hash, modulo by 16, and use that as the array index. So with an array of size 16, we’d insert bar at index 10, bazz at 8, bob at 4, and so on. Let’s insert all the items into our hash table array (except for x – we’ll get to that below):
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Key | . | jane |
. | . | bob |
. | . | foo |
bazz |
. | bar |
. | buzz |
. | . | . |
| Value | . | 100 | . | . | 11 | . | . | 10 | 36 | . | 42 | . | 7 | . | . | . |
To look up a value, we simply fetch array[hash(key) % 16]. If the array size is a power of two, we can use array[hash(key) & 15]. Note how the order of the elements is no longer meaningful.
But what if two keys hash to the same value (after the modulo 16)? Depending on the hash function and the size of the array, this is fairly common. For example, when we try to add x to the array above, its hash modulo 16 is 7. But we already have foo at index 7, so we get a collision.
There are various ways of handling collisions. Traditionally you’d create a hash array of a certain size, and if there was a collision, you’d use a linked list to store the values that hashed to the same index. However, linked lists normally require an extra memory allocation when you add an item, and traversing them means following pointers scattered around in memory, which is relatively slow on modern CPUs.
A simpler and faster way of dealing with collisions is linear probing: if we’re trying to insert an item but there’s one already there, simply move to the next slot. If the next slot is full too, move along again, until you find an empty one, wrapping around to the beginning if you hit the end of the array. (There are other ways of probing than just moving to the next slot, but that’s beyond the scope of this article.) This technique is a lot faster than linked lists, because your CPU’s cache has probably fetched the next items already.
Here’s what the hash table array looks like after adding “collision” x (with value 200). We try index 7 first, but that’s holding foo, so we move to index 8, but that’s holding bazz, so we move again to index 9, and that’s empty, so we insert it there:
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| Key | . | jane |
. | . | bob |
. | . | foo |
bazz |
x |
bar |
. | buzz |
. | . | . |
| Value | . | 100 | . | . | 11 | . | . | 10 | 36 | 200 | 42 | . | 7 | . | . | . |
When the hash table gets too full, we need to allocate a larger array and move the items over. This is absolutely required when the number of items in the hash table has reached the size of the array, but usually you want to do it when the table is half or three-quarters full. If you don’t resize it early enough, collisions will become more and more common, and lookups and inserts will get slower and slower. If you wait till it’s almost full, you’re essentially back to linear search.
With a good hash function, this kind of hash table requires an average of one operation per lookup, plus the time to hash the key (but often the keys are relatively short string).
And that’s it! There’s a huge amount more you can do here, and this just scratches the surface. I’m not going to go into a scientific analysis of big O notation, optimal array sizes, different kinds of probing, and so on. Read Donald Knuth’s TAOCP if you want that level of detail!
Hash table implementation
You can find the code for this implementation in the benhoyt/ht repo on GitHub, in ht.h and ht.c. For what it’s worth, all the code is released under a permissive MIT license.
I got some good feedback from Code Review Stack Exchange that helped clean up a few sharp edges, not the least of which was a memory leak due to how I was calling strdup during the ht_expand step (fixed here). I confirmed the leak using Valgrind, which I should have run earlier. Seth Arnold also gave me some helpful feedback on a draft of this article. Thanks, folks!
API design
First let’s consider what API we want: we need a way to create and destroy a hash table, get the value for a given key, set a value for a given key, get the number of items, and iterate over the items. I’m not aiming for a maximum-efficiency API, but one that is fairly simple to implement.
After a couple of iterations, I settled on the following functions and structs (see ht.h):
// Hash table structure: create with ht_create, free with ht_destroy.
typedef struct ht ht;
// Create hash table and return pointer to it, or NULL if out of memory.
ht* ht_create(void);
// Free memory allocated for hash table, including allocated keys.
void ht_destroy(ht* table);
// Get item with given key (NUL-terminated) from hash table. Return
// value (which was set with ht_set), or NULL if key not found.
void* ht_get(ht* table, const char* key);
// Set item with given key (NUL-terminated) to value (which must not
// be NULL). If not already present in table, key is copied to newly
// allocated memory (keys are freed automatically when ht_destroy is
// called). Return address of copied key, or NULL if out of memory.
const char* ht_set(ht* table, const char* key, void* value);
// Return number of items in hash table.
size_t ht_length(ht* table);
// Hash table iterator: create with ht_iterator, iterate with ht_next.
typedef struct {
const char* key; // current key
void* value; // current value
// Don't use these fields directly.
ht* _table; // reference to hash table being iterated
size_t _index; // current index into ht._entries
} hti;
// Return new hash table iterator (for use with ht_next).
hti ht_iterator(ht* table);
// Move iterator to next item in hash table, update iterator's key
// and value to current item, and return true. If there are no more
// items, return false. Don't call ht_set during iteration.
bool ht_next(hti* it);
A few notes about this API design:
- For simplicity, we use C-style NUL-terminated strings. I know there are more efficient approaches to string handling, but this fits with C’s standard library.
- The
ht_setfunction allocates and copies the key (if inserting for the first time). Usually you don’t want the caller to have to worry about this, or ensuring the key memory stays around. Note thatht_setreturns a pointer to the duplicated key. This is mainly used as an “out of memory” error signal – it returns NULL on failure. - However,
ht_setdoes not copy the value. It’s up to the caller to ensure that the value pointer is valid for the lifetime of the hash table. - Values can’t be NULL. This makes the signature of
ht_getslightly simpler, as you don’t have to distinguish between a NULL value and one that hasn’t been set at all. - The
ht_lengthfunction isn’t strictly necessary, as you can find the length by iterating the table. However, that’s a bit of a pain (and slow), so it’s useful to haveht_length. - There are various ways I could have done iteration. Using an explicit iterator type with a while loop seems simple and natural in C (see the example below). The value returned from
ht_iteratoris a value, not a pointer, both for efficiency and so the caller doesn’t have to free anything. - There’s no
ht_removeto remove an item from the hash table. Removal is the one thing that’s trickier with linear probing (due to the “holes” that are left), but I don’t often need to remove items when using hash tables, so I’ve left that out as an exercise for the reader.
Demo program
Below is a simple program (demo.c) that demonstrates using all the functions of the API. It counts the frequencies of unique, space-separated words from standard input, and prints the results (in an arbitrary order, because the iteration order of our hash table is undefined). It ends by printing the total number of unique words.
// Example:
// $ echo 'foo bar the bar bar bar the' | ./demo
// foo 1
// bar 4
// the 2
// 3
void exit_nomem(void) {
fprintf(stderr, "out of memoryn");
exit(1);
}
int main(void) {
ht* counts = ht_create();
if (counts == NULL) {
exit_nomem();
}
// Read next word from stdin (at most 100 chars long).
char word[101];
while (scanf("%100s", word) != EOF) {
// Look up word.
void* value = ht_get(counts, word);
if (value != NULL) {
// Already exists, increment int that value points to.
int* pcount = (int*)value;
(*pcount)++;
continue;
}
// Word not found, allocate space for new int and set to 1.
int* pcount = malloc(sizeof(int));
if (pcount == NULL) {
exit_nomem();
}
*pcount = 1;
if (ht_set(counts, word, pcount) == NULL) {
exit_nomem();
}
}
// Print out words and frequencies, freeing values as we go.
hti it = ht_iterator(counts);
while (ht_next(&it)) {
printf("%s %dn", it.key, *(int*)it.value);
free(it.value);
}
// Show the number of unique words.
printf("%dn", (int)ht_length(counts));
ht_destroy(counts);
return 0;
}
Now let’s turn to the hash table implementation (ht.c).
Create and destroy
Allocating a new hash table is fairly straight-forward. We start with an initial array capacity of 16 (stored in capacity), meaning it can hold up to 8 items before expanding. There are two allocations, one for the hash table struct itself, and one for the entries array. Note that we use calloc for the entries array, to ensure all the keys are NULL to start with, meaning all slots are empty.
The ht_destroy function frees this memory, but also frees memory from the duplicated keys that were allocated along the way (more on that below).
// Hash table entry (slot may be filled or empty).
typedef struct {
const char* key; // key is NULL if this slot is empty
void* value;
} ht_entry;
// Hash table structure: create with ht_create, free with ht_destroy.
struct ht {
ht_entry* entries; // hash slots
size_t capacity; // size of _entries array
size_t length; // number of items in hash table
};
#define INITIAL_CAPACITY 16 // must not be zero
ht* ht_create(void) {
// Allocate space for hash table struct.
ht* table = malloc(sizeof(ht));
if (table == NULL) {
return NULL;
}
table->length = 0;
table->capacity = INITIAL_CAPACITY;
// Allocate (zero'd) space for entry buckets.
table->entries = calloc(table->capacity, sizeof(ht_entry));
if (table->entries == NULL) {
free(table); // error, free table before we return!
return NULL;
}
return table;
}
void ht_destroy(ht* table) {
// First free allocated keys.
for (size_t i = 0; i < table->capacity; i++) {
free((void*)table->entries[i].key);
}
// Then free entries array and table itself.
free(table->entries);
free(table);
}
Hash function
Next we define our hash function, which is a straight-forward C implementation of the FNV-1a hash algorithm. Note that FNV is not a randomized or cryptographic hash function, so it’s possible for an attacker to create keys with a lot of collisions and cause lookups to slow way down – Python switched away from FNV for this reason. For our use case, however, FNV is simple and fast.
As far as the algorithm goes, FNV-1a simply starts the hash with an “offset” constant, and for each byte in the string, XORs the hash with the byte, and then multiplies it by a big prime number. The offset and prime are carefully chosen by people with PhDs.
We’re using the 64-bit variant, because, well, most computers are 64-bit these days and it seemed like a good idea. You can tell I don’t have one of those PhDs. 🙂 Seriously, though, it seemed better than using the 32-bit version in case we have a very large hash table.
#define FNV_OFFSET 14695981039346656037UL
#define FNV_PRIME 1099511628211UL
// Return 64-bit FNV-1a hash for key (NUL-terminated). See description:
// https://en.wikipedia.org/wiki/Fowler–Noll–Vo_hash_function
static uint64_t hash_key(const char* key) {
uint64_t hash = FNV_OFFSET;
for (const char* p = key; *p; p++) {
hash ^= (uint64_t)(unsigned char)(*p);
hash *= FNV_PRIME;
}
return hash;
}
I won’t be doing a detailed analysis here, but I have included a little statistics program that prints the average probe length of the hash table created from the unique words in the input. The FNV-1a hash algorithm we’re using seems to work well on the list of half a million English words (average probe length 1.40), and also works well with a list of half a million very similar keys like word1, word2, and so on (average probe length 1.38).
Interestingly, when I tried the FNV-1 algorithm (like FNV-1a but with the multiply done before the XOR), the English words still gave an average probe length of 1.43, but the similar keys performed very badly – an average probe length of 5.02. So FNV-1a was a clear winner in my quick tests.
Get
Next let’s look at the ht_get function. First it calculates the hash, modulo the capacity (the size of the entries array), which is done by ANDing with capacity - 1. Using AND is only possible because, as we’ll see below, we’re ensuring our array size is always a power of two, for simplicity.
Then we loop till we find an empty slot, in which case we didn’t find the key. For each non-empty slot, we use strcmp to check whether the key at this slot is the one we’re looking for (it’ll be the first one unless there had been a collision). If not, we move along one slot.
void* ht_get(ht* table, const char* key) {
// AND hash with capacity-1 to ensure it's within entries array.
uint64_t hash = hash_key(key);
size_t index = (size_t)(hash & (uint64_t)(table->capacity - 1));
// Loop till we find an empty entry.
while (table->entries[index].key != NULL) {
if (strcmp(key, table->entries[index].key) == 0) {
// Found key, return value.
return table->entries[index].value;
}
// Key wasn't in this slot, move to next (linear probing).
index++;
if (index >= table->capacity) {
// At end of entries array, wrap around.
index = 0;
}
}
return NULL;
}
Set
The ht_set function is slightly more complicated, because it has to expand the table if there are too many elements. In our implementation, we double the capacity whenever it gets to be half full. This is a little wasteful of memory, but it keeps things very simple.
First, the ht_set function. It simply expands the table if necessary, and then inserts the item:
const char* ht_set(ht* table, const char* key, void* value) {
assert(value != NULL);
if (value == NULL) {
return NULL;
}
// If length will exceed half of current capacity, expand it.
if (table->length >= table->capacity / 2) {
if (!ht_expand(table)) {
return NULL;
}
}
// Set entry and update length.
return ht_set_entry(table->entries, table->capacity, key, value,
&table->length);
}
The guts of the operation is in the ht_set_entry helper function (note how the loop is very similar to the one in ht_get). If the plength argument is non-NULL, it’s being called from ht_set, so we allocate and copy the key and update the length:
// Internal function to set an entry (without expanding table).
static const char* ht_set_entry(ht_entry* entries, size_t capacity,
const char* key, void* value, size_t* plength) {
// AND hash with capacity-1 to ensure it's within entries array.
uint64_t hash = hash_key(key);
size_t index = (size_t)(hash & (uint64_t)(capacity - 1));
// Loop till we find an empty entry.
while (entries[index].key != NULL) {
if (strcmp(key, entries[index].key) == 0) {
// Found key (it already exists), update value.
entries[index].value = value;
return entries[index].key;
}
// Key wasn't in this slot, move to next (linear probing).
index++;
if (index >= capacity) {
// At end of entries array, wrap around.
index = 0;
}
}
// Didn't find key, allocate+copy if needed, then insert it.
if (plength != NULL) {
key = strdup(key);
if (key == NULL) {
return NULL;
}
(*plength)++;
}
entries[index].key = (char*)key;
entries[index].value = value;
return key;
}
What about the ht_expand helper function? It allocates a new entries array of double the current capacity, and uses ht_set_entry with plength NULL to copy the entries over. Even though the hash value is the same, the indexes will be different because the capacity has changed (and the index is hash modulo capacity).
// Expand hash table to twice its current size. Return true on success,
// false if out of memory.
static bool ht_expand(ht* table) {
// Allocate new entries array.
size_t new_capacity = table->capacity * 2;
if (new_capacity < table->capacity) {
return false; // overflow (capacity would be too big)
}
ht_entry* new_entries = calloc(new_capacity, sizeof(ht_entry));
if (new_entries == NULL) {
return false;
}
// Iterate entries, move all non-empty ones to new table's entries.
for (size_t i = 0; i < table->capacity; i++) {
ht_entry entry = table->entries[i];
if (entry.key != NULL) {
ht_set_entry(new_entries, new_capacity, entry.key,
entry.value, NULL);
}
}
// Free old entries array and update this table's details.
free(table->entries);
table->entries = new_entries;
table->capacity = new_capacity;
return true;
}
Length and iteration
The ht_length function is trivial – we update the number of items in _length as we go, so just return that:
size_t ht_length(ht* table) {
return table->length;
}
Iteration is the final piece. To create an iterator, a user will call ht_iterator, and to move to the next item, call ht_next in a loop while it returns true. Here’s how they’re defined:
hti ht_iterator(ht* table) {
hti it;
it._table = table;
it._index = 0;
return it;
}
bool ht_next(hti* it) {
// Loop till we've hit end of entries array.
ht* table = it->_table;
while (it->_index < table->capacity) {
size_t i = it->_index;
it->_index++;
if (table->entries[i].key != NULL) {
// Found next non-empty item, update iterator key and value.
ht_entry entry = table->entries[i];
it->key = entry.key;
it->value = entry.value;
return true;
}
}
return false;
}
Discussion
That’s it – the implementation in ht.c is only about 200 lines of code, including blank lines and comments.
Beware: this is a teaching tool and not a library, so I encourage you to play with it and let me know about any bugs I haven’t found! I would advise against using it without a bunch of further testing, checking edge cases, etc. Remember, this is unsafe C we’re dealing with. Even while writing this I realized I’d used malloc instead of calloc to allocate the entries array, which meant the keys may not have been initialized to NULL.
As I mentioned, I wanted to keep the implementation simple, and wasn’t too worried about performance. However, a quick, non-scientific performance comparison with Go’s map implementation shows that it compares pretty well – with half a million English words, this C version is about 50% slower for lookups and 40% faster for insertion.
Speaking of Go, it’s even easier to write custom hash tables in a language like Go, because you don’t have to worry about handling memory allocation errors or freeing allocated memory. I recently wrote a counter package in Go which implements a similar kind of hash table.
There’s obviously a lot more you could do with the C version. You could focus on safety and reliability by doing various kinds of testing. You could focus on performance, and reduce memory allocations, use a “bump allocator” for the duplicated keys, store short keys inside each item struct, and so on. You could improve the memory usage, and tune _ht_expand to not double in size every time. Or you could add features such as item removal.
After I’d finished writing this, I remembered that Bob Nystrom’s excellent Crafting Interpreters book has a chapter on hash tables. He makes some similar design choices, though his chapter is significantly more in-depth than this article. If I’d remembered his chapter before I started, I probably wouldn’t have written this one!
In any case, I hope you’ve found this useful or interesting. If you spot any bugs or have any feedback, please let me know. You can also go to the discussions on Hacker News, programming Reddit, and Lobsters.
I’d love it if you sponsored me on GitHub – it will motivate me to work on my open source projects and write more good content. Thanks!
Содержание
- Задание
- Введение
- Струра данных
- Метод цепочек
- Метод открытой адресации
- Линейнон пробирование
- Двойное хеширование
- Сравнение
- Формат входных данных
- План выполнения домашнего задания
Задание
Сравнить хэш-таблицы с различными способами разрешения коллизий:
метод цепочек, метод двойного хэширования и метод линейного пробирования.
Введение
Хеширование – преобразование ключей к числам.
Хеш-таблица – массив ключей с особой логикой, состоящей из:
1. Вычисления хеш-функции, которая преобразует ключ поиска в индекс.
2. Разрешения конфликтов, т.к. два и более различных ключа могут преобразовываться в один и тот же индекс массива.
Отношение порядка над ключами не требуется.
Хеш-функция ― преобразование по детерминированному алгоритму входного массива данных произвольной длины (один ключ) в выходную битовую строку фиксированной длины (значение). Результат вычисления хеш-фукнции называют «хешем».
Хеш-функция должна иметь следующие свойства:
- Всегда возвращать один и тот же адрес для одного и того же ключа;
- Не обязательно возвращает разные адреса для разных ключей;
- Использует все адресное пространство с одинаковой вероятностью;
- Быстро вычислять адрес.
Коллизией хеш-функции H называется два различных входных блока данных X и Y таких, что H(x) = H(y).
Структкра данных
Хеш-таблица – структура данных, хранящая ключи в таблице. Индекс ключа вычисляется с помощью хеш-функции. Операции: добавление, удаление, поиск.
Пусть хеш-таблица имеет размер M, количество элементов в хеш-таблице – N.
Число хранимых элементов, делённое на размер массива (число возможных значений хеш-функции), называется коэффициентом заполнения хеш-таблицы (load factor). Обозначим его α = N/M.
Этот коэффициент является важным параметром, от которого зависит среднее время выполнения операций.
Парадокс дней рождений. При вставке в хеш-таблицу размером 365 ячеек всего лишь 23-х элементов вероятность коллизии уже превысит 50 % (если каждый элемент может равновероятно попасть в любую ячейку).
Хеш-таблицы различаются по методу разрешения коллизий.
Основные методы разрешения коллизий:
- Метод цепочек.
- Метод открытой адресации.
Метод цепочек
Каждая ячейка массива является указателем на связный список (цепочку). Коллизии приводят к тому, что появляются цепочки длиной более одного элемента.
Добавление ключа.
- Вычисляем значение хеш-функции добавляемого ключа –
h. - Находим
A[h]– указатель на список ключей. - Вставляем в начало списка (в конец списка дольше). Если запрещено дублировать ключи, то придется просмотреть весь список.
Время работы:
В лучшем случае – O(1).
В худшем случае
– если не требуется проверять наличие дубля, то O(1)
– иначе – O(N)
Удаление ключа.
- Вычисляем значение хеш-функции удаляемого ключа –
h. - Находим
A[h]– указатель на список ключей. - Ищем в списке удаляемый ключ и удаляем его.
Время работы:
В лучшем случае – O(1).
В худшем случае – O(N).
Поиск ключа.
- Вычисляем значение хеш-функции ключа –
h. - Находим
A[h]– указатель на список ключей. - Ищем его в списке.
Время работы:
В лучшем случае – O(1).
В худшем случае – O(N).
Среднее время работы операций поиска, вставки (с проверкой на дубликаты) и удаления в хеш-таблице, реализованной методом цепочек – O(1 + α), где α – коэффициент заполнения таблицы.
Среднее время работы.
Теорема.
Среднее время работы операций поиска, вставки (с
проверкой на дубликаты) и удаления в хеш-таблице, реализованной
методом цепочек – O(1 + α), где α – коэффициент заполнения
таблицы.
Доказательство. Среднее время работы – математическое ожидание
времени работы в зависимости от исходного ключа.
Время работы для обработки одного ключа T(k) зависит от длины
цепочки и равно 1 + Nh(k) , где Ni – длина i-ой цепочки.
Предполагаем, что хеш-функция равномерна, а ключи
равновероятны.
Среднее время работы
Метод открытой адресации
Все элементы хранятся непосредственно в массиве. Каждая запись в массиве содержит либо элемент, либо NIL. При поиске элемента систематически проверяем ячейки до тех пор, пока не найдем искомый элемент или не убедимся в его отсутствии.
При поиске элемента систематически проверяем ячейки до
тех пор, пока не найдем искомый элемент или не убедимся в
его отсутствии.
Вставка ключа.
- Вычисляем значение хеш-функции ключа –
h. - Систематически проверяем ячейки, начиная от
A[h], до тех пор, пока не находим пустую ячейку. - Помещаем вставляемый ключ в найденную ячейку. В п.2 поиск пустой ячейки выполняется в некоторой последовательности. Такая последовательность называется «последовательностью проб».
Последовательность проб зависит от вставляемого в таблицу ключа. Для определения исследуемых ячеек расширим хеш-функцию, включив в нее номер пробы (от 0).
h ∶ U × {0, 1, ... , M − 1} → {0, 1, ... , M − 1 }
Важно, чтобы для каждого ключа k последовательность проб h(k, 0), h(k, 1), ... , h(k, M − 1) представляла собой перестановку множества 0,1, ... , M − 1 , чтобы могли быть просмотрены все ячейки таблицы.
Поиск ключа.
Исследуется та же последовательность, что и в алгоритме вставки ключа. Если при поиске встречается пустая ячейка, поиск завершается неуспешно, поскольку искомый ключ должен был бы быть вставлен в эту ячейку в последовательности проб, и никак не позже нее.
Удаление ключа.
Алгоритм удаления достаточен сложен. Нельзя при удалении ключа из ячейки i просто пометить ее значением NIL. Иначе в последовательности проб для некоторого ключа (или некоторых) возникнет пустая ячейка, что приведет к неправильной работе алгоритма поиска.
Решение. Помечать удаляемые ячейки спец. значением «Deleted». Нужно изменить методы поиска и вставки. В методе вставки проверять «Deleted», вставлять на его место. В методе поиска продолжать поиск при обнаружении «Deleted».
Вычисление последовательности проб.
Желательно, чтобы для различных ключей k последовательность проб h(k, 0), h(k, 1), ... , h(k, M − 1) давала большое количество последовательностей- перестановок множества 0,1,... , M − 1 .
Обычно используются три метода построения h(k, i):
- Линейное пробирование.
- Квадратичное пробирование.
- Двойное хеширование.
Линейное пробирование
h(k, i) = (h′(k) + i) mod M
Основная проблема – кластеризация. Последовательность подряд идущих занятых элементов таблицы быстро увеличивается, образуя кластер. Попадание в элемент кластера при добавлении гарантирует «одинаковую прогулку» для различных ключей и проб. Новый элемент будет добавлен в конец кластера, увеличивая его.
Двойное хеширование
h(k, i) = (h1(k) + ih2(k)) mod M.
Требуется, чтобы последовательность проб содержала все индексы 0, .. , M–1. Для этого все значения h2(k) должны быть взаимно простыми с M.
- M может быть степенью двойки, а
h2(k)всегда возвращать нечетные числа. - M простое, а
h2(k)меньшеM.
Общее количество последовательностей проб O(M^2).
Сравнение
| Лучший случай | В среднемю Метод цепочек. | В среднем. Метод открытой адресации. | Худший случай. | |
|---|---|---|---|---|
| Поиск | O(1) |
O(1 + a) |
O(1 / 1 - a) |
O(n) |
| Вставка | O(1) |
O(1 + a) |
O(1 / 1 - a) |
O(n) |
| Удаление | O(1) |
O(1 + a) |
O(1 / 1 - a) |
O(n) |
Использование хеш-таблиц
Хеширование полезно, когда широкий диапазон возможных значений должен быть сохранен в малом объеме памяти, и нужен способ быстрого, практически произвольного доступа. Хэш-таблицы часто применяются в базах данных, и, особенно, в языковых процессорах типа компиляторов и ассемблеров, где они изящно обслуживают таблицы идентификаторов. В таких приложениях, таблица – наилучшая структура данных.
Использование программы
Для запуска необходиа java версии 1.8 и Apache Maven версии 3.5.0.
Для компиляции необходимо в корне проекта выполнить команду
mvn clean compile assembly:single
А для запуска программы
java -jar HashTable-1.0-SNAPSHOT-jar-with-dependencies.jar <input_file> <output_file>
Оба параметра являются обязательными.
Во время выполнения в консоль будут выведены выполненные команды.
Формат входных данных
Входной файл содержит последовательность команд, т.е. представляет набор строк вида
command [key] [data]
где command — add, delete, search, min, max, print или спец. команда;
key — ключ, целое число;
data — данные, целое число.
Примеры:
add 10 20
search 15
print
min
Команда print отражает внутреннее строение структуры данных. Для хэш-таблицы с методом цепочек вывод команды print будет
иметь следующий вид:
Hash table: [ { 90 240 77 } { 416 } { } { 557 99 } { 246 } { 556 } { 267 } { 947 } ]
{} – отдельная ячейка массива, в которой храниться список ключей.
А для хеш-таблиц с открытой адресацией вывод будет выглядеть так:
Hash table: [ 755 D __ 855 __ 942 __ 346 __ 588 __ 576 ]
__ – пустая ячейка, D – удаленная ячейка.
Формат выходных данных
В выходной файл выводятся результаты исполнения программы.
Команда print должна отражать внутреннее строение структуры данных
Команда search выводит error, в случае, когда значение не было найдено, или значение найденное по ключу в противном случае.
Команда add добавляет значение в таблицу (Ничего не выводит).
Команда delete удаляетя число, или ничего не делает, если значение не было найдено (Ничего не выводит).
Команда min выводит минимальное число в таблице, или empty, если таблица пустая.
Команда max выводит максимальное число в таблице,или empty, если таблица пустая.
Тесты
Было создано три вида тестов. Одни проверяют корректность работы методов каждой хеш-таблицы, вторые для провеки времени выполнения большого числа операций добавления, поиска и удаления.
1.Юнит тесты, проверящие корректность работы методов каждой хеш-таблицы
Тесты находятся в ./src/test/java/tests/
2.Юнит тесты для провеки времени выполнения большого числа операций добавления, поиска и удаления.
Тесты находятся в ./src/test/java/tests/
3.Файлы с входными данными и правильными ответами.
На вход программе подается два файла.
- Входной файл.
- Выходной файл с результатами исполнения программы.
Заитем выходной файл с результатами исполнения программы сравнивается с файлом в котором находятся правильные ответы
Тесты находятся в ./tests/
Подробное описание тестов
1.Простая проверка всех операций кроме print
2.Проверка корректной работы add, delete(удаление элементов по несушествуюшему ключу) и print
3.Проверка корректной работы add, delete(удаление элементов по сушествуюшему ключу) и print
4.Проверка корректной работы search(поиск элементов по несушествуюшему ключу)
5.Проверка корректной работы search(поиск элементов по сушествуюшему ключу)
Сравнение времени работы
Время работы рачитываем тестом с 1000000 операций каждого типа.
Метод цепочек:
Add time: 545
Search time: 354
Delete time: 255
Линейное пробирование:
Add time: 562
Search time: 281
Delete time: 365
Двойное хэштрование:
Add time: 582
Search time: 273
Delete time: 377
Вывод
При использовании открытой адресации двойное хеширование обычно превосходит квадратичное пробирование. Единственным исключением является ситуация, в которой доступен большой объем памяти, а данные не расширяются после создания таблицы; в этом случае линейное пробирование несколько проще реализуется, а при использовании коэффициентов нагрузки менее 0,5 не приводит к заметным потерям производительности.
Если количество элементов, которые будут вставляться в хеш-таблицу, неизвестно на момент ее создания, метод цепочек предпочтительнее открытой адресации. Увеличение коэффициента заполнения при открытой адресации приводит к резкому снижению быстродействия, а с методом цепочек быстродействие убывает всего лишь линейно.
Если не уверены — используйте метод цепочек. У него есть свои недостатки — прежде всего необходимость в дополнительном классе связанного списка, но зато если в список будет внесено больше данных, чем ожидалось изначально, реализация по крайней мере не замедлится до полного паралича.
План выполнения домашнего задания
1.Реализовать хеш-таблицу с методом цепочек
2.Реализовать хеш-таблицу с двойным хешированием
3.Реализовать хеш-таблицу с линейным пробированием
4.Тесты
5.Сравнение производительности и расхода памяти
6.Анализ полученных результатов и вывод
7.???
8.Profit
