Как составить интересную задачу по математике

Качественное образование:
ТРИЗ-педагогика, метод создания задач по математике

В одной из книг известный журналист С. Соловейчик поделился, как рассказывая однажды маленькому мальчику сказку, обратил внимание, что ребенок не столько следит за сюжетом, сколько пытается повторить движения рук взрослого: «Я думал, что учу его сопереживать героям сказки, а на самом деле он учился жестикулировать»…

Т.е. воспитание, впрочем, как и обучение, бывает «видимое», когда мы ставим перед собой конкретные цели и надеемся на их достижение, и «невидимое», когда на самом деле мы достигаем чего-то другого. И нередко эти незаметные, неосознаваемые нами уроки оказываются не только более результативными, но порой могут свести на нет все сознательные усилия.

Например, мы говорим о гендерном равенстве, а ученики на уроке математики решают задачи о том, как «мама испекла 16 пирожков», «мама посадила 18 кустов малины», «бабушка приготовила 50 вареников», «мама подоила Буренку», «мама купила 3 пакета муки», «мама принесла из теплицы огурцы», «мама заготовила 15 л компота», «бабушка высушила 15 кг яблок», «мама купила детям костюмы» и т.д. и т.п.

А где же сильная половина? «Папа с сыновьями катался на трехколесных велосипедах», «папа пошел с сыном в цирк», «папа раздал детям абрикосы»… Нет, конечно, за четыре года обучения школьники могут однажды встретить задачу про то, как «папа принес из магазина 6 кг картофеля», и узнать о том, что «папа с сыном пилили дрова» или «ловили рыбу»…

А как вам такая задача: «Две девочки и мальчик пропололи 18 рядов капусты. Девочки пропололи по 7 рядов. Сколько рядов прополол мальчик?».

Но кроме этого ответа очень хочется узнать, а почему мальчик сделал гораздо меньше девочек?..

Вот и получается, что будущие мужчины с детства привыкают к тому, что домашняя работа не для них…(И может корни проблемы разводов надо искать в школьных учебниках?..)

Мы учим детей быть экономными и хозяйственными, ответственными и добросовестными, активными и любознательными. А на уроке решаем задачи про то, как «поезд опоздал на 70 минут», как «у продавца были 5 спелых и 4 неспелых арбуза», как «по телевизору показали 60 серий фильма и осталось показать еще 40»…

А еще, к сожалению, иногда мы учим по принципу: «Зачем думать, решать нужно!». К примеру: «Велосипедист за 5 часов проехал 70 км. За какое время он проедет 140 км?» (10 часов в седле без остановки — это реально?), «Для ремонта квартиры купили 3 банки краски» (это была квартира кума Тыквы?), «На зиму в сельской школе заготовили 994 кг угля» (речь о современной школе 21 века?)..

Грустно. И совсем непросто потом красивыми и правильными словами из планов воспитательной работы, которые говорятся напрямую в лоб, изменить то, что сформировалось косвенно, изнутри, за пределами нашего педагогического внимания.

Очень хочется надеяться, что новые учебники математики, кото-рых с нетерпением ждут наши школы, смогут избежать подобного рассогласования, когда вслух учим одному, а на самом деле — другому.

Но пока многие учителя выход видят в том, чтобы придумывать задачи самостоятельно. Очень часто в качестве содержания берутся сюжеты из детской литературы, ведь тогда можно «убить двух зайцев»: и задачу интересную решить и книжку еще раз напомнить.

Более того, процесс придумывания представляется довольно легким занятием: берешь сказочных героев, добавляешь числа — и задача готова! Но так ли все просто на самом деле?

Итак, какие типичные ошибки и недочеты можно выявить в «самодельных» задачах:

несоответствие сюжета задачи сказочной основе:

— Кролик три кочана отдал Винни-Пуху…
— Дюймовочка испекла 5 тортов…
— Крошечка-Хаврошечка играла в шахматы…
— вместе с Буратино в автобусе ехало 8 пассажиров…
— у бабы-Яги было 12 банок с вареньем…
— младший брат Элизы читал книгу 7 дней…

несоответствие чисел реальности:

— за три дня белка разгрызла 2835 орешков… (при восьмичасовом рабочем дне это больше ста в час…)
— бесенок бежит со скоростью 280 км/ч… (это средняя скорость пассажирского самолета…)
— сколько попугаев длиной 50 см может проглотить удав длиной 12 м?.. (и от кончика хвоста они в ряд так и укладываются…)
— Белоснежка собрала 128 ромашек, а колокольчиков в три раза больше… (и как она несла такую охапку, и вообще, зачем столько цветов?..)

несоответствие сюжета ценностным ориентирам:

— Соловей-Разбойник 12 богатырей погубил и 9 — покалечил…
— волк сначала съел трех козлят, а потом еще столько же…
— жадной старухе прислуживали 28 дворян, а бояр в 2 раза меньше…
— гуси ущипнули гадкого утенка 12 раз, а куры — на 4 раза больше…
— ведьма варила кости своей дочери 2 часа…
— Карлсон забрал у Малыша 6 булочек и 10 конфет…
— царевна откусила одну четвертую отравленного яблочка…
Пожалуй, довольно.

Вывод однозначный: чтобы придумать интересную задачу со сказочным содержанием нужно знать и соблюдать определенные правила, одного желания недостаточно.

Прежде всего, сюжет сказочной задачи должен соответствовать содержанию сказки-прототипа.

Даже при составлении «обычных» задач, когда ситуация, действия героев, предметы и т.д. задаются, казалось бы, совершенно произвольно, выполняются требования согласования: в магазине делают покупки, а не едят пирожки; при сочинении задачи на движение вряд ли местом действия может быть выбрана библиотека, в школьном дворе ученики сажают березы, а не кактусы и т.д.

Поэтому первым шагом при сочинении задачи на литературной (сказочной) основе будет выделение главных героев произведения и их наиболее характерных действий и признаков.

Например:

«Колобок»:
герои: бабушка, дедушка, Колобок, лиса…
Колобок: убежал, пел песни, встречал зверей…

«Красная шапочка»:
герои: девочка, бабушка, волк, охотники…
Красная шапочка: несла пирожки, собирала цветы, шла по тропинке, разговаривала с волком…

«Незнайка»:
герои: Незнайка, Знайка, коротышки…
Незнайка: сочинял, рисовал, ездил на автомобиле, играл…
Знайка: размышлял, выступал, руководил…

«Снежная Королева»:
герои: Герда, Кай, Снежная королева, принцесса, разбойница…
Герда: искала Кая, была в плену, помогала животным…
Кай: катался на санках, попал во дворец, выкладывал слово…

«Гостья из будущего»:
Герои: Алиса Селезнева, Коля Гераскин, школьники, космические пираты…
Алиса: понимала язык животных, много знала, быстро бегала…
Коля: побывал в будущем, прятался, разоблачал пиратов…

«Гарри Поттер»:
герои: Гарри Поттер, Гермиона, Рони, преподаватели…
Гарри Поттер: имел сову, летал на метле, сражался с Волан-де-Мортом…
Гермиона: старательно училась, любила читать, помогала друзьям…

При этом уже на данном этапе выбор героев и их действий происходит через призму воспитывающего характера обучения: мы не сочиняем задачи, сколько времени нужно Лисе, чтобы съесть Колобка; по какой дорожке волку лучше бежать к дому бабушки, сколько коротышек обидел Незнайка своими стихами, на сколько осколков тролли разбили злое зеркало, сколько раз пираты перевоплощались, на сколько больше подарков получил Дадли, чем Гарри и т.д. То есть сразу же обозначается, на чьей стороне будут ученики и кому они могли бы помогать, сопереживать, подражать…

Далее «гармонию» следует наполнить «алгеброй»: представить сказочный сюжет в виде условия задачи определенного типа.

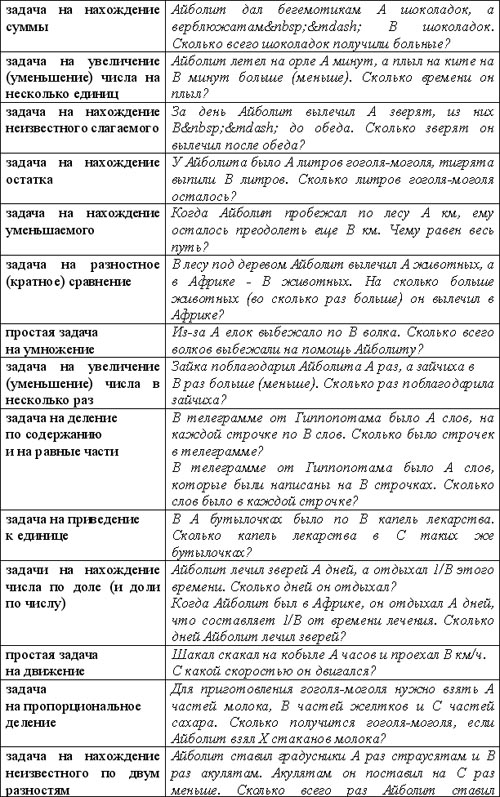
Как это можно сделать, покажем на примере сказки «Доктор Айболит»:

Легко заметить, что представлены не все типы задач, изучаемые в начальных классах (и речь идет не о составных задачах, которые получаются из объединения простых). Не были представлены задачи таких типов как «цена, количество, стоимость», «нахождение площади и периметра», «встречное (обратное, противоположное) движение» и некоторых других.

И это не случайно, ведь сюжет диктует свои правила и ограниче-ния. Если придумать задачу о том, как Айболит совершал покупки или измерял стороны прямоугольников, то это уже будет не сказочная задача, а искусственная, которая вызывает справедливую реакцию детей: «В сказке такого не было!». И в подобных случаях мы получаем не задачу на основе литературного сюжета, а задачу с использованием имен литературных героев (только возникают вопросы: «Зачем, для чего это нужно? Что это дает?»).

Поэтому сказки выбираются не произвольно, а исходя из соответствия их содержания смыслу математических действий. Например: задачи с использованием понятий «цена, количество, стоимость» можно придумывать по сказкам «Сказка о попе и его работнике Балде», «Вот какой Рассеянный»,

«Пеппи Длинныйчулок», «Старик Хоттабыч», «Приключения капитана Врунгеля»; задачи про различные виды движения могут быть придуманы по сказкам «Федорино горе», «Бременские музыканты», «Приключения Нильса с дикими гусями», «Приключения барона Мюнхаузена», «Маугли»; задачи с геометрическим содержанием можно встроить в сюжеты таких сказок, как «Три медведя», «Вершки и корешки», «Волшебник Изумрудного города», «Приключения Гулливера» и др.

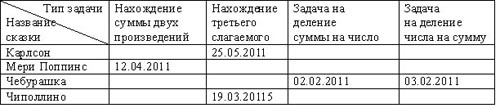
Но здесь возникает следующая проблема: если в 4 классе можно давать практически любой сказочный сюжет и он будет знаком учащимся, то круг чтения первоклассника ограничен как скоростью чтения, так и возрастными особенностями. Для решения данной проблемы рекомендуется использовать таблицу, по одной оси которой откладываются названия известных произведений, а по другой — изучаемые типы задач (они ведь тоже будут отличаться в разных классах). А на пересечении осей можно отмечать, какие задачи уже были составлены.

Пример фрагмента таблицы:

При этом не забываем, что хорошая задача отличается не только соответствием сюжета модели решения, но и «правдоподобностью» используемых числовых данных, которые не всегда определяются соответствующим концерном.

Например, Принцесса на горошине могла спать на 22 перинах, а не на 88 (хотя оба числа в пределах 100), старуха могла захотеть новое корыто длиной 1м 4 дм, а, наоборот, 4 м 1 дм — вряд ли, скорость хромой Серой шейки не может быть больше скорости зайца или лисы и т.д. То есть после того, как задача составлена, необходимо окинуть ее беспристрастным взглядом…

Все? Алгоритм пройден?

Нет. Если мы говорим о творческом процессе, то радость созидания будет гораздо полнее, когда творчество и труд превращаются в сотворчество и сотрудничество.

Уже с первого класса совместно с ребятами можно анализировать сюжет сказки и выбирать, какие из сюжетных линий могли бы стать основой задачи. Также следует обращать внимание учащихся на то, что можно «считать» в рассматриваемом сюжете.

Далее не обязательно предлагать придумывать задачи определенного типа, а можно предложить схему условия или числовое выражение, которое является решением задачи…

Можно проводить конкурсы, кто больше придумает различных задач по одной сказке или кто использует больше сказок, чтобы придумать задачи на одну тему…

Можно «издавать» сборники детских задач и использовать их во время самостоятельных работ…

Можно в качестве домашнего задания дать сочинение задач по прочитанной книге…

Можно проводить комбинированные уроки «внеклассное чтение + математика»…

А наградой за все наши усилия будет восторг класса, перефразировавшего слова поэта: «Что за прелесть эти задачи! Давайте скорее их решать!».

“Обучение – это ремесло, использующее
бесконечное количество маленьких трюков” (Д.Пойа.)

В методической литературе нет общепринятого
определения понятия “занимательность обучения
математике”. Оно считается интуитивно ясным.

Но под занимательностью понимаются те
компоненты занятия (способы подачи учебного
материала, специфические свойства информации и
заданий, связанных с учебным материалом), которые
содержат в себе элементы необычайного,
удивительного, комического, вызывают интерес у
учащихся к учебному предмету и способствуют
созданию положительной эмоциональной
обстановки учения.

Перечислим основные положения, касающиеся
занимательности обучения:

1. “Всю занимательность обучения следует делить
   на “внешнюю” (не связанную с содержанием урока)
   и “внутреннюю”, причем “внутренняя”
   занимательность предпочтительнее “внешней” и
   удельный вес ее должен постепенно
   увеличивается”. (К.Д.Ушинский)
2. Все материалы занимательного характера
   разбиваются на три группы: материалы,
   занимательные по форме; материалы, занимательные
   по содержанию; материалы, занимательные и по
   форме и по содержанию.
3. Основу занимательности, используемой на уроках
   должны составлять задания, непосредственно
   связанные с программным материалом.

Под методикой использования занимательных
заданий понимаются методы, средства и приемы
подачи занимательных задач, занимательные формы
организации обучения.

Первая и основная тенденция состоит в том, что
педагог переносит на урок занимательные
материалы из внеучебной деятельности.

Использование занимательных заданий
целесообразно тогда, когда есть опасность:

• Неприятия учащимися какого-либо учебного
  задания,
• При прохождении сложных тем или при постановке
  трудных задач,
• При изучении материала, подлежащего прочному
  запоминанию,
• При выработке умений и навыков учащихся, когда
  требуется выполнить значительное количество
  однотипных упражнений.

Предпочтение следует отдавать занимательному
материалу, отражающему существенные моменты
изучаемого, а также, занимательным заданиям
неоднократного использования.

Для каждого занимательного материала педагог
должен выяснить: будет ли он занимательным для
учащихся? Будет ли его использование
эффективным?

Необычный учебный материал обладает
некоторыми особенностями по сравнению с обычным.

Схема обычного занятия:

Но иногда полезно нарушать эту схему. Причем
при этом нарушении, ученику приходится
анализировать ситуацию, выделять существенные
моменты, вспоминать правила, проявлять
сообразительность. Анализ ускоряет формирование
навыка и запоминание правил. Эта связь между
заданиями и аналитической деятельностью
учащихся присуща заданиям, составленным с
помощью приемов занимательности.

Их методическая ценность в том, что ребенку
надо глубже вникать в сущность задания, выделять
главные моменты, учитывать связь между
компонентами. Благодаря этому учебный навык, на
формирование которого направлено задание,
вырабатывается быстрее, т.к. он связан с
продуктивной деятельностью ребенка.

Еще одно достоинство многих занимательных
задач заключается в том, что при их решении у
учащихся возникает необходимость менять ход
мыслей на обратный. Как известно, умение менять
ход своей мысли на обратный – ценнейшее качество
ума. Занимательные задания способствуют
формированию гибкости ума, освобождению
мышления от шаблонов.

С помощью приемов занимательности создаются
задания, которые могут служить мостиком от
стандартных задач к нестандартным.

Известно, что учащимся с трудом дается решение
нестандартных заданий. Причин этому много. Одна
из них заключается в том, что переход от
стандартных задач к нестандартным очень резок.
Необходимы переходные задания. Здесь на помощь
учителю и ученикам и приходят занимательные
задания.

Свобода при выполнении занимательных заданий
важна и в методическом отношении. В некоторых
случаях появляется возможность подготавливать
учащихся к формированию умений и навыков. В
других случаях свобода помогает освоению
приемов устной работы.

Таким образом, приемы занимательности часто
связаны с общими проблемами обучения: развитием
приемов мышления, общеучебных умений и навыков и
т.д.

Рассмотрим методические особенности
занимательных заданий, составленных с помощью
некоторых приемов занимательности.

Приемы занимательности, связанные с
подачей задания.

Приемы этой группы дают возможность то или иное
задание облечь в занимательную форму. Рассмотрим
такие приемы.

Логический каркас. Путем логических
заключений требуется выявить из нескольких
утверждений одно верное утверждение.

Пример 1. Известно, что одно из утверждений
о функции f(x)=xⁿ ложно, а два другие истинны.

1. Уравнение xⁿ = 15 имеет одно решение.
2. f(-12)= f(12).
3. Точка А (-2; 40096) принадлежит графику данной
   функции.

Выясните, будет ли данная функция четной.

В ненавязчивой форме проводится знакомство с
дедуктивным методом. Наглядность ситуации
способствует тому, что вывод, сделанный в классе,
понятен практически каждому. Это является первой
ступенькой в понимании дедуктивных рассуждений.
Рассуждения могут проводиться по такой схеме.

Из первого утверждения следует, что функция
нечетная.

Из второго – четная.

Теперь все зависит от третьего утверждения. Так
как (-2)ⁿ = 4096, то n – четное число.

Вывод: функция f(x) является четной.

Пример 2. Из двух равенств одно верное,
другое нет.

352 _* 427 = 150 308

564 _* 376 = 212 064.

Узнайте устно, какое равенство верно, а какое
неверно.

Рассуждения:

Первое равенство – явно неверное, так как при
умножении 2 и 7 цифра единиц произведения должна
равняться 4, а не 8.

Второе равенство – верное. При умножении 4 и 6
цифра единиц произведения равна 4, следовательно,
равенство верное.

Учитель может предложить учащимся самим
составлять логические каркасы. Ученики

вполне подготовлены к интуитивному пониманию
этого метода, принимают его и используют при
решении задач.

Ситуации, создаваемые с помощью этого приема,
помогают также осознать учащимися идею
контрпримера. Действительно, чтобы установить
ложность какого-либо утверждения, достаточно
увидеть ошибку.

Выполнение заданий с помощью приема
“Логический каркас” происходит в интересной,
запоминающейся для учащихся форме, сохраняющей
их полную самостоятельность.

При использовании этого приема учителю надо
тщательно подбирать утверждения, чтобы они
отражали существенные моменты изученного
материала.

Задание с продолжением. Новое задание
получается из предыдущего путем дописывания к
формулировке старого задания одного или
нескольких слов (символов).

Главное достоинство этого задания – экономия
времени на уроке, и возник этот прием как одно из
решений проблемы: сократить время на знакомство
с задачами.

Прочитав условие задания, и вникнув в него,
ученик решает его успешно. Продолжение задачи
заинтересовывает его, к тому же требуется меньше
времени на знакомство с условием. Решение второй
задачи может быть аналогичным решению первой
задачи, а может быть совершенно другим. Если
решение аналогично, то происходит закрепление
приобретенных навыков, если же решение резко
отличается от первого, то необходимо проявить
определенную гибкость ума, чтобы
сориентироваться в данной ситуации.

Рассмотрим различные возможности предъявления
задания с продолжением учащимся. Самый простой
путь: на доске записана задача, ученики решают ее.
Затем учитель дописывает два-три слова или
символа – получается вторая задача; затем,
дописав еще символы, получим третью задачу и т.д.
Когда дети привыкнут к подобным заданиям, можно
использовать такой методический прием. Сразу
записать задачу и все ее продолжения, отделяя
одно от другого чертой. Сколько черточек –
столько и задач.

Со временем можно предлагать ученикам самим
составлять содержательные продолжения задач.
Причем здесь возникают разнообразные
методические возможности. Например, из
нескольких предложений выберите любое и решите
задачу или выберите такое, чтобы получился
данный объект; придумайте общее продолжение для
двух различных задач и т.д.

Пример 1.

1. Запишите функцию, графиком которой является
   парабола,
2. И ее ветви опущены вниз,
3. И она проходит через точку (-1; -8).

Пример 2.

1. Запишите такой четырехчлен, чтобы его можно
   было разложить на множители,
2. И чтобы первый множитель был равен 3х – 2с,
3. А второй 2 х + 7у.

Пример 3.

Запишите степень с основанием с, которую
можно представить:

1. в виде квадрата,
2. и в виде куба,
3. и в виде четвертой степени,
4. и в виде пятой степени.

Приемы занимательности, связанные со
структурой задания.

Найдите ошибку. Ученику предлагается
отыскать ошибку (или ошибки) в решении (или в
ответе) одного или нескольких заданий.

Этот прием давно используется и доказал свою
эффективность с методической точки зрения:
вырабатывается критичность мышления,
развивается самоконтроль ученика. Кроме того
этот метод приучает ребенка к внимательности,
позволяет провести профилактику ошибок.

Прямое указание учащемуся на ошибку, пусть даже
и исправленную, малоэффективно. Лучше сначала
использовать задания, в которых ошибки очевидны.
Потом постепенно переходить к
“замаскированным” ошибкам.

Возможные пути предъявления таких заданий:

• на доске записано несколько утверждений, в том
  числе и неверные, которые надо отыскать и указать
  в них ошибки.
• применение приема “Математический герой”.
• провокация ошибки.

Рассмотрим эти пути подробнее.

Пример 4. Из нескольких равенств несколько
ложных, причем их количество можно сообщить
учащимся, а можно и не сообщать. После каждого
ответа учитель предлагает ученику что-то
изменить в записи, чтобы равенство оказалось
верным. Тут важно предусмотреть различные
способы исправления.

А) 0,9 + (-0,9) = 0;

Б) 0,9 _*  (-0,9) = 0.

Выявлено неверное равенство 0,9 · (-0,9) = 0, ученик
исправляет так 0,9 · (-0,9) = 0,81.

Особый интерес представляют утверждения, в
которых допущено более одной ошибки. Например,
если в равенстве -3,2 · 0,5 = 16 ученики видят только
одну ошибку, то характер ошибки, которую они
называют, дает дополнительную информацию для
учителя.

Пример 5. Даны смежные углы и три утверждения
о них:

1. один из них на 90° больше другого;
2. их градусные меры относятся как 4 : 5;
3. один из них в 3 раза меньше другого.

Одно из этих утверждений противоречит двум
другим. Найдите его.

Рассуждения: “Из первого утверждения следует,
что градусные меры углов 135° и 45°; из второго – 80° и
100°, из третьего – 45° и 135°. Значит, второе
утверждение противоречит другим”.

Пример 6. В арсенале Вити Верхоглядкина
столько ошибок, недочетов, неправильностей,
неверных рассуждений, что ученики каждый раз с
удовольствием их находят. Причем, после разбора
ошибочного решения Вити у самих учащихся ошибки
подобного рода потом встречаются редко.

“Витя Верхоглядки, выполняя домашнее задание,
решил уравнение так:

15х – 30 = 12х – 24

15(х – 2) = 12(х – 2)

15 = 12.

Ответ: решения нет.

В чем его ошибка?”

Задания на нахождение ошибки дают простор
инициативе учащихся. Действительно, решить
задание чаще всего можно одним способом, а
проверить его решение удается часто двумя-тремя.
Причем проверка правильности обычно возможна
только при хорошем владении учебным материалом.
Ошибки учеников провоцируются самим процессом
познания. Возникает мысль: а нельзя ли
попробовать хоть как-то упорядочить этот
процесс?

В некоторых случаях это можно сделать, если
учитель сам специально натолкнет ученика на
ошибку. Встреча с ошибкой будет происходить под
контролем учителя, она будет вскрыта, выявятся
причины ее возникновения. Благодаря яркости
ситуации ученики запомнят свои ошибочные
действия и в дальнейшем стараются не допускать
их. Провокация ошибки есть не что иное, как
учебная задача с подвохом. Учитель строит
учебную ситуацию таким образом, что ученики, как
правило, ошибаются при решении какого-либо
задания.

Пример 7. Предлагается взять любые два их
чисел 12, 42, 51, 69 и составить обыкновенную дробь,
чтобы она была несократимой.

Использование новых мыслительных операций.
Приемы мышления могут быть занимательными для
школьников, которые их только осваивают.
Например, учащимся после окончания начальной
школы вполне доступны рассуждения в один – два
логических шага.

Пример 8. Даны 5 чисел: -9, -2, 6, -3, -5. Выберите из
них такие 4 числа, чтобы их произведение было
положительно. Найдите это произведение.

У всех получается 270. Почему?

Объяснение: так как произведение –
положительное число, то в данном случае все 4
множителя должны быть отрицательными. Значит,
надо перемножить числа -9, -2, -3, -5, а это
произведение равно 270.

Пример 9. Из следующих многочленов:

1. – 6ах – 2х – 15а + 6;
2. 1 + а? + а? + а¹⁰;
3. 35ах – 20х + 21а – 12;
4. 3х + 5а – 6ах – b

только один можно разложить на множители.
Какой? Разложите его на множители.

Решение: 35ах – 20х + 21а – 12 = ( 5х +
3) ( 7а – 4).

Можно рассуждать так.

Первый многочлен на множители разложить
нельзя, т.к. у него нет общих множителей, а
группировка ничего не даст из-за того, что у него
три отрицательных коэффициента.

Второй многочлен на множители разложить
нельзя, т.к. показатель последнего члена слишком
велик.

Можно ли разложить на множители третий
многочлен сразу не видно. Пропустим его.

Четвертый многочлен разложить на множители
нельзя, т.к. группировка последнего члена с любым
из других ничего не дает.

Вывод: на множители можно разложить только
третий многочлен.

Приемы занимательности, связанные с
организацией и процессом решения задания.

Тестовые вопросы. Целесообразно
использовать этот прием при закреплении учебных
навыков. Приведем несколько примеров.

Пример 10.

5 класс. “На доске записано число 36. ученику
необходимо быстро ответить на вопросы учителя.

1) Назовите число:

а) большее 36;

б) меньшее 36.

2) представьте число 36 в виде суммы:

а) двух равных слагаемых;

б) двух неравных слагаемых;

в) трех неравных слагаемых;

г) трех равных слагаемых.

3) назовите дополнение числа 36:

а) до 100;

б) до 1000.

4) представьте число 36 в виде произведения:

а) двух равных множителей;

б) двух неравных множителей.”

6 класс. “ Дана дробь 7/20. ученик отвечает на
следующие вопросы:

1) дополнение до 1?

2) больше или меньше ??

3) обрати в десятичную дробь.

4) обратное?

5) представь в виде суммы (знаменатели
одинаковы).

6) представь в виде суммы ( знаменатели
различны).

7) представь в виде разности (знаменатели
одинаковы).

8) представь в идее разности ( знаменатели
различны).

9) представь в виде произведения.

10) представь в виде частного.”

7 класс. Алгебра. “На доске записаны
одночлены 10m? и 2m?. Учитель задает вопросы
в краткой форме, ученик быстро на них отвечает.

1) сумма?

2) разность?

3) разность?

4) произведение?

5) частное (m?0)?

6) частное?

7) квадрат?

8) квадрат?

9) квадрат суммы?

10) квадрат разности?”

8 класс. Геометрия. “В параллелограмме ABCD
AM – биссектриса угла A, MN || AB. Известно, что AB
= 10 м, AD = 15 м. Учитель называет отрезок, а
ученик быстро говорит, чему равна длина
названного отрезка:

1) MN; 2) BM; 3) AN; 4) BC; 5) AN;
6) ND; 7) MC.”

После любого ответа учитель может спросить:
почему? Ученик должен обосновать свой ответ.
Например, BM = 10 м. Так как AM – биссектриса,
то угол BAM равен углу MAN; так как AD || BC
и AM – секущая, то угол MAN равен углу AMB,
значит угол BAM равен углу AMB,
следовательно, треугольник AMB равнобедренный
и BM = 10м.

С одного взгляда. Ценность этого приема
замечена давно. Сама постановка вопроса
наталкивает учащихся на поиск нешаблонных
решений. Это умение сродни творческому подходу, к
тому же такое решение почти всегда бывает
красивым, что само по себе очень важно.

Так приобретается у учащихся вкус к
исследовательской работе.

Пример11. “Назовите дробь со знаменателем 371,
которая меньше 1/2.

Если, размышляя над этой задачей, ученик
задумывается об особенности дроби 1/2, он сможет
догадаться до довольно неочевидного факта: дробь
меньше 1/2, если ее числитель меньше половины
знаменателя. Тогда уже легко назвать несколько
искомых дробей”.

Подобные задания помогают вырабатывать у
учащихся приемы решения задач. Ученик приходит к
мысли, что задачу легче решить, если ее
переформулировать. Никакие призывы учителя к
использованию каких-либо эвристических приемов
мышления ни к чему не приведут, если у ученика не
будет сформирована готовность к этому. Решение
заданий с помощью приема “С одного взгляда”
очень хорошо формируют эту готовность. Эти
задания составляются таким образом, чтобы своим
решением подчеркивают суть того или иного
приема. Задания строятся на неочевидных
моментах, связанных с существом математики или
эвристическими приемами.

Пример 12. “Что больше: площадь одного
правильного треугольника со стороной 10 см или
сумма площадей десяти правильных треугольников
со стороной 1 см?

S₁ = 1/2 · 10² · sin 60° = 50 · sin 60°

S₂ = 1/2 · 1² · sin 60° = 1/2 · sin 60°.

Значит площадь треугольника со стороной 10 см
больше.

К этой задаче полезно вернуться при изучении
“Площади подобных фигур”. Тогда она решается
устно: сторона треугольника больше в 10 раз,
значит, его площадь больше в 100 раз”.

Пример 13. “Даны два треугольника, вырезанные
из бумаги. Требуется доказать, что эти
треугольники равновеликие, используя линейку
без делений.

Треугольники вырезаны так, что основания их
равны и высоты, проведенные к этим основаниям,
равны. Тогда, приложив эти треугольники дважды,
как показано на рисунке 2, ученик делает вывод,
что треугольники равновелики. Линейка нужна для
того, чтобы убедиться, что высоты треугольников
равны.

Учебные задания занимательного характера
ценны тем, что они наряду с привитием школьникам
интереса к учению способствуют также
определенному накоплению учебных умений и
навыков.

КРАСИВЫЕ ЗАДАЧИ В МАТЕМАТИКЕ

Паспорт проектной работы.

Тема проекта:

« Красивые задачи в математике »

СОДЕРЖАНИЕ

ВВЕДЕНИЕ………………………………………………………….

ЦЕЛЬ И ЗАДАЧИ ПРОЕКТА……………………………………..

ОСНОВНАЯ ЧАСТЬ……………………………………………..

2.1. КРАСОТА В МАТЕМАТИКЕ……………………………….

2.2. ПОНЯТИЕ О КРАСИВОЙ ЗАДАЧЕ

В РАЗЛИЧНЫХ ЛИТЕРАТУРНЫХ ИСТОЧНИКАХ…………

ПРАКТИЧЕСКАЯ ЧАСТЬ…………………………………………

3.1. ОТБОР КРАСИВЫХ ЗАДАЧ……………………………….

3.2. МОИ ЗАДАЧИ……………………………………………….

3.3. СОЗДАНИЕ СБОРНИКА КРАСИВЫХ ЗАДАЧ

И РЕКОМЕНДАЦИИ ПО ЕГО ПРИМЕНЕНИЮ……………

ЗАКЛЮЧЕНИЕ……………………………………………………

ГЛОССАРИЙ………………………………………………………

СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ……………..

ПРИЛОЖЕНИЕ…………………………………………………..

КРАТКАЯ ПОЯСНИТЕЛЬНАЯ ЗАПИСКА…………….

ОТЗЫВ РУКОВОДИТЕЛЯ О ПРОЕКТЕ………………..

ВВЕДЕНИЕ

Несколько раз во время подготовки к олимпиаде я сталкивался с «Красивыми» задачами. Мне стало интересно что же на самом деле они из себя представляют? В учебниках по математике четких формулировок что такое «Красивая» задача не оказалось, поэтому я попытался найти ответ на вопрос в дополнительной литературе и заметил, что даже у ученых мнения не сходятся. Каждый видит красоту задачи по — своему.

Вот я и решил провести анализ по данной проблеме и подготовить исследовательскую работу на конференцию по теме «Красивые» задачи в математике.

При разборе нестандартных задач я понял, что необходимо сначала провести поиск плана решения задачи, определить теоретический материал, который дает ключ к решению задачи. Решать «Красивые» задачи интересно и увлекательно.

Итак, гипотеза моего исследования – существуют задачи, отличающиеся нестандартной формулировкой, неожиданным решением, которые можно использовать и на уроках.

1. ЦЕЛЬ И ЗАДАЧИ ПРОЕКТА.

Цель моего исследования: изучение понятия красивая задача в математике и создание сборника таких задач.

Для достижения поставленной цели я решил:

Изучить научную литературу, научные публикации по данной теме и провести о

прос среди учащихся нашего училища понимание значения

словосочетания

“красивая задача”, проанализировать полученную информацию.

Определить понятие красивая задача в математике

Отобрать красивые задачи

Составить красивые задачи

С

пособ

ствовать рассмотрению

кр

асивых задач на уроках математики.

2. ОСНОВНАЯ ЧАСТЬ.

2.1 «Красота» в математике

Человек немыслим без такого качества, как восприятие мира в его красоте и гармонии.

Многие из учащихся считают математику строгой наукой, при изучении которой нет места эмоциям, хотя очень многие заинтересованы этим предметом.

Еще Д. фон Нейман отмечал, что математика “движима почти исключительно эстетическими мотивами”. Попытки раскрыть содержание понятий “чувство красоты”, “красивая задача” предпринимаются многими математиками.

2.2 Понятие о красивой задаче в различных литературных источниках

«Мне доставляет удовольствие решать красивую задачу, ведь это прекрасно – сидеть, мучиться и, наконец, добиться своего», – так отзывается о задачах Александров А. Д.- математик, физик, философ, альпинист. Все согласятся, наверное, что «красивые задачи могут доставлять удовольствие не только слуху и взору, но и разуму», «красивые задачи – путь к пониманию к изяществу математики», « красивая задача = неожиданность + удивительная простота + фантазия + удивление +труд +…».

Я люблю задачи, в которых бывает неожиданно простое решение.

Это вызывает у меня интерес и побуждает к поиску более коротких и простых путей решения.

Изучив множество литературы, я пришёл к такому выводу, что «красивая» математическая задача должна отвечать определенным требованиям:

Условие задачи должно быть интересно; если задача геометрическая, то чертеж к ней красивый.

Задача должна содержать

нестандартный элемент,

отличающий ее от большинства задач по данной теме, предлагаемых в учебниках. При этом нестандартность может проявляться как в самом условии, так и в методах решения. Особый интерес в этом смысле представляют задачи, имеющие несколько различных методов решения, и многовариантные задачи,

имеющие несколько ответов (причем желательно, чтобы факт наличия нескольких ответов не был явно указан в формулировке условия).

Задача может устанавливать интересный факт, порой неожиданный.

3адача должна быть доступна как по формулировке условия, так и по сложности и объему используемого в решении материала.

Наконец, основное: в решении задачи обязательно нужно спрятать «изюминку», чтобы оно было наглядно и удивительно просто.

Г

отовясь к математическим олимпиадам, я

прорешал

множество задач среди которых были такие, которые отвечали данным требованиям и я понял, что их можно классифицировать на несколько групп:

«Красивые» задачи по решению;

«Красивые» задачи по чертежу;

«Красивые» задачи по содержанию;

«Красивые» олимпиадные задачи;

3. ПРАКТИЧЕСКАЯ ЧАСТЬ

3.1 Отбор красивых задач

Занимательные задачи часто используются на уроках математики,

Существует ряд стандартных средств, которые используются при решении занимательных задач. Например, при решении некоторых используется принцип Дирихле, свойства делимости, идея обратного хода и т. д. Однако остаются без внимания логические методы решения задач, в частности метод рассуждения приведением к нелепости.

Метод рассуждения приведением к нелепости применяется в тех случаях, когда требуется опровергнуть предложение А, т. е. доказать предложение вида не — А. Суть этого метода заключается в следующем. Для того чтобы доказать предложение не — А, достаточно из предположения, что имеет место А, вывести противоречие (нелепость), т. е. Два предложения В и не — В для какого – нибудь предложения В. Рассмотрим примеры использования данного метода рассуждения при решении занимательных задач.

Задача 1. На каждой кочке в маленьком болоте сидит не меньше чем 3 лягушки, а всего лягушек 145. Докажите, что число кочек на этом болотце не может равняться 55.

Ответ Допустим, что число кочек на болотце равно 55. Поскольку лягушек на каждой кочке не меньше 3, то число лягушек на 55 кочках не меньше 165 (3х55=165). По условию число лягушек на болотце равно 145, т. е. Меньше 165. Получили противоречие. Следовательно, допущение неверно, а значит. На болотце не может быть 55 кочек.

Задача 2. Можно ли соединить 13 городов так, чтобы из каждого города выходило ровно 5 дорог?

Ответ Допустим, что можно соединить 13 городов дорогами так, чтобы из каждого города выходило ровно 5 дорог. Заметим что найдя произведение 13х5, мы каждую дорогу посчитаем дважды, а значит, это произведение должно быть четным числом. Однако 13х5=65 — число нечетное. Получили противоречие. Следовательно, допущение неверно, а значит, нельзя соединить 13 городов так, чтобы из каждого города выходило ровно 5 дорог.

Задача 3 Саша пригласил Петю в гости, сказав, что живет в 10 подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому Саши, Петя заметил, что дом девятиэтажный. Выясните. На какой этаж ему следует подняться.

Ответ. Рассмотрим случаи, когда на каждом этаже: 1) не более 3 квартир

2) 4 квартиры 3) Не менее 5 квартир. Допустим, что на каждом этаже не более 3 квартиры. Тогда в 10 подъездах всего квартир 1093=270. Таким образом, в 10 подъезде не может быть квартиры с номером 333, что противоречит условию. Следовательно, случай, когда на каждом этаже не более трех квартир, невозможен.

Допустим, что на каждом этаже не менее 5 квартир. Тогда в 9 подъездах их более 1095=450, т. е. В 10 подъезде не может быть квартиры № 333. Этот случай, когда на каждом этаже не менее 5 квартир, невозможен. Таким образом, Саша живет в доме, в котором на каждом этаже расположено по 4 квартиры. В девяти подъездах всего квартир 994=324. В десятом подъезде первая квартира имеет № 325. Получаем, что квартира № 333 находится на 3 этаже.

Задача 4. Пришел покупатель на базар и купил шапку за 10 рублей, дал продавцу 25-рублевую купюру, а у того не было сдачи. Пошел продавец к меняле, разменял эти 25 рублей и отдал покупателю сдачу 15 рублей. Вскоре прибежал меняла, бросил продавцу его 25-рублевую купюру и заявил: «Эта купюра фальшивая – верни мне деньги!» Продавец отдал меняле настоящие 25 рублей, сел и задумался, сколько же всего денег он потерял? (Считаем, что шапка — это 10 рублей)

Задачу может решить первоклассник, но может и не решить профессор!

Ответ: Рассмотрим отдельно «приход» и «расход» продавца. Он получил от менялы 25 рублей и больше ничего, а отдал шапку за 10 рублей, сдачу 15 рублей и вернул меняле 25 рублей. В итоге, он потерял 25 рублей. Задача 5. Можно ли расставить 9 чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9 по кругу так, чтобы сумма любых трех чисел, стоящих подряд, делилась на 3 и

а) Была больше 9? б) Была больше 12?

Ответ. а) Можно. Например 1, 9, 2, 7, 3, 5, 4, 6, 8.

б) Нельзя. Пусть сумма в каждой тройке соседних чисел больше 12. Так как сумма чисел в тройке кратна 3, то она должна быть не меньше 15. Так как сумма всех девяти чисел от 1 до 9 равна 45, то сумма в каждой тройке равна 15. Но тогда числа, стоящие через каждые два места, должны быть равны, что невозможно. Возможно решение, основанное на следующей идее: сумму 15 требует набрать 8 разными способами из предложенных чисел. Однако это сделать невозможно.

Задача 6. Один из двух мальчиков на любой вопрос либо отвечает «да», либо молчит, а другой либо отвечает «нет», либо молчит. При этом один из них правдивец, т. е. произносит свой ответ в точности тогда, этот ответ истинен, а другой — лжец, т. е. произносит свой ответ в точности тогда , когда этот ответ ложен. Можно ли задать им такой вопрос, чтобы по их реакции можно было определить, кто какой ответ произносит, а также кто из них правдивец и кто лжец?

Ответ: Можно задать, например, вопрос « Можешь ли ты сказать “да”?». На него обязательно ответит правдивец и промолчит лжец.

3.2 Мои задачи

Задача 1. На лугу растёт трава. Пустили на луг 9 коров, они опустошили луг за 4 дня. Если бы на луг пустили 8 коров, то они съели бы всю траву за 6 дней. Сколько коров могут кормиться на лугу всё время, пока растёт трава? Данная задача интересна тем, что нужно учитывать ежедневный прирост травы. И с помощью одного уравнения ее не решить. Поэтому я ввел две переменные и составил уравнение. Итак:

Решение :

Пусть x – доля травы, поедаемая 1 коровой за день.
у – прирост травы за день.

6у – 48х = 4у – 36х

6у – 4у = 48х – 36х

2у = 12х => y=6x т.е 6 коров поедают прирост травы и поэтому могут кормиться на лугу все время.

Ответ: 6 коров

Задача 2. Поезд проходит мост длиной в 450 м за 45 сек. и 15 секунд идёт мимо телеграфного столба. Вычислить скорость и длину поезда.

Решение: 15 секунд поезд движется мимо столба, значит, 15 секунд поезд «съезжает» с моста, т.е. паровоз пройдёт путь, равный длине поезда.

С момента, когда паровоз начал съезжать с него прошло 30 секунд. ( 45-15).Итак, за 30 секунд: паровоз проехал 450 м, откуда скорость паровоза: 900 метров в минуту,

Переводим в часы.

900 м = 900 = 900 = 900 =9000,06 = 54 км/час.

За 15 секунд ( или 14 минуты) паровоз пройдёт путь, равный длине поезда, значит, длина поезда равна 225м. Ответ: 54 км/ч и 225 м.

Задача 3. Женя похудел за весну на 20%,а потом за лето поправился на 30%,за осень опять похудел на 20 %,а за зиму поправился на 10 %.Поправился или похудел Женя за год?

Решение. Пусть х кг – масса Жени,

После весны вес Жени составил 80% от прежней массы. Переводим в дробь. Это 0,8х.

После лета его вес составил : 0,8∙ 1,3х.

После осени его вес составил : 0,8∙ 1,3∙0,8х.

После зимы его вес составил: 0,8∙ 1,3∙0,8∙1,1х = 0,9152х (кг) стала масса Жени. Значит, Женя похудел.

3.3 Создание сборника красивых задач и рекомендации по его

применению

Чтобы не потерять интерес к математике необходимо дополнительно прорешивать интересные задачи. Я решил создать сборник задач, которые заинтересовали меня( приложение 1).

В сборнике я собрал красивые задачи занимательного характера, которые помогут в проведение, например, увлекательных пятиминуток в начале урока. Увлекательные задачи буду подбирать и предлагать для решения сам.

Сам же я занимаюсь решением типовых олимпиадных задач.

Я думаю, что моим сборником могут пользоваться как учителя, так и учащиеся. Ребята, увлекающиеся математикой, не останутся равнодушными к нестандартным задачкам, а возможно и захотят сами придумывать похожие задачи. Некоторые разделы моего сборника могут заинтересовать преподавателя. Они смогут разнообразить пятиминутки интересными логическими задачками.

4. ЗАКЛЮЧЕНИЕ

За время работы над проектом я узнал для себя много полезной информации которая может пригодиться при решении задач. А именно:

1. Потраченные 2-3 минуты на тщательный анализ условия задачи окупается сторицей! Если за эти минуты ты используешь всю силу своего геометрического воображения, то даже и при сложном условии задачи сможешь обнаружить рациональное (краткое и изящное) решение. Приняв сразу бездумное шаблонное решение, ты увеличишь объем вычислительной работы и шансы появления ошибок.

2. Если задача сложная – найди «логику» решения задачи, напиши план решения задачи. В запутанной и особо «неподдающейся» задаче план решения обязателен.

3. Не волнуйся!

4. Дай полную волю своей интуиции! Интуиция поможет тебе наметить кратчайший путь к решению задачи.

5. Мысль способна незаметно «уйти в сторону» – следи за ней ( а, точнее, за собой) !

6. Удачное вспомогательное построение подчас сразу же раскрывает «секреты « условия задачи. Если проведенная вспомогательная линия все же окажется ненужной, то сразу же сотри ее – все лишнее мешает мыслительному процессу.

5. ГЛОССАРИЙ

Фон Нейман – (1903 – 1953) венгеро – американский математик, сделавший важный вклад в квантовую логику, функциональный анализ, теорию множеств и т.д..

Дирихле Петер Густав Лежен ( 1805– 1859) – немецкий математик. Принцип Дирихле утверждает, что если множество из N элементов разбито на n непересекающихся частей, не имеющих общих элементов , где N > n ,то по крайней мере в одной части будет более одного элемента.

6. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

«Математика в школе» выпуск № 6 за 2008 год.

Научно-теоретический и методический журнал «Математика в школе» выпуск №5 за 2009 год.

Издательский дом «Первое сентября» Выпуск за 20 октября 2007 год.

«Математика в школе» выпуск №3 за 2008 год.

Сборник олимпиадных задач

Интернет – информация.

8. КРАТКАЯ ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К ПРОЕКТУ.

Мною было рассмотрено много трактовок “Красивой задачи”, на основании которых можно сделать следующий вывод: к какому бы типу красивых задач не относилась данная, главное, что она вовлекает нас в творчество, заставляет мыслить нестандартно, искать новые подходы к решению, совершать всякий раз для себя небольшое открытие.

Результатом изучения научной литературы и интернет источников явилось создание сборника “Красивых задач”. Мне и самому понравилось составлять красивые задачи, думаю кому то они пригодятся для развития смекалки, мышления, воображения.

В работе я использовал следующие методы исследования:

использование интернет – ресурса при изучении вопроса;

обобщение собранного материала.

В основу моего проекта были положены поиски математических задач занимательного, творческого характера, а так же их классификация по типу интереса.

9. ОТЗЫВ

на индивидуальный проект

учащегося 8 класса ГБПОУ «Казанское училище олимпийского резерва)

Монастырева Сергея.

по теме: « Красивые задачи в математике »

Итоговый индивидуальный проект Монастырева Сергея представляет собой исследование и обобщение определенного типа задач именуемых

« красивыми». Содержание работы соответствует заявленной теме. Выводы и заключения сделаны грамотно, а так же сделана попытка собрания задач в сборник.

Оформлен проект в виде исследовательской работы по выбранной теме, в котором продемонстрировано умения работать с различными источниками информации, сформулирована собственная точка зрения по рассматриваемой проблеме и предложен сборник задач занимательного характера.

Данный проект является актуальным, поскольку он попробовал систематизировать задачи , решить их, а так же предложил составить из них сборник, для применения в классе.

В ходе выполнения индивидуального проекта Сергей продемонстрировал способность самостоятельно приобретать новые знания, пополнять и переносить их в индивидуальный проект.

Учащийся показал хороший уровень регулятивных умений планировать и осуществлять свою деятельность, отслеживать результаты ее выполнения. Проект был спланирован под руководством преподавателя и своевременно доведен обучающимся до конца.

В целом работа свидетельствует о способности обучающегося под руководством педагога ставить проблему и находить пути её решения, умение самостоятельно мыслить.

В работе Сергей умело пользуется ИКТ. В ходе выполнения проекта он своевременно выполнял задания, получаемые на консультациях, исправлял недоработки.

Работа включает в себя введение, основную часть, заключение, список используемых источников и литературы а так же сборник задач для применения в классе по развитию логического мышления учащихся. Во введении указывается актуальность исследования, ставятся цель и задачи, определяется проблема, предмет и методы исследования.

Достоинства работы. Сергей попробовал систематизировать, интересные на его взгляд, задачи , решить их, а так же предложил составить из них сборник, для применения в классе.

Практическая значимость. В проекте описывается исследование, а результаты оформлены в виде сборника. Завершается работа выводами, в которых излагаются результаты исследования и возможность применения задач в классе.

Рекомендации: индивидуальный проект Монастырева Сергея по теме

« Красивые задачи в математике » отвечает требованиям, предъявляемым к проекту, и рекомендуется к защите.

Заслуживает отметку « хорошо».

Руководитель Исанбаева В.А.

«25» апреля 2020г.



Совместимы ли творчество и математика? Если под словом «творчество» понимать не музыку и рисование, а «деятельность, порождающую нечто качественно новое, никогда ранее не бывшее» [1], то в математике, как и в любой деятельности, человек может проявить свои творческие способности.

Большинство методов и форм обучения математике способствует накоплению учеником суммы знаний, и в массовой школьной практике большинство математических задач рассматривается как средство отработки и закрепления школьного материала. К сожалению, имеет место и «разучивание» основных типов задач в целях успешной сдачи итоговой аттестации учащимися.

Можно ли обучить творчеству? Именно на этот вопрос и отвечает ТРИЗ-педагогика, в основу которой была положена теория решения изобретательских задач (ТРИЗ) школы Г. С. Альтшуллера.

Основным ее инструментом является «открытая задача». В отличие от «закрытых» задач, в которых есть четкое условие, известный алгоритм решения и единственный ответ, «открытые» задачи имеют «размытое» условие, различные пути решения и неоднозначные ответы. [2]

Закрытые задачи бывают двух видов: на вычисления какой-либо величины или на доказательство. Такие задачи можно даже назвать упражнениями по отработке некоторых учебных навыков при изучении нового материала.

Открытые задачи — это проблемные ситуации, встречающиеся в реальной жизни. Для решения их необходимо самостоятельно осмыслить, сформулировать условие, вопрос задачи, иногда найти сведения, необходимые для ее решения.

Открытые задачи можно разделить на «изобретательские» и «исследовательские». Можно также классифицировать их по разной степени открытости.

Как же составить открытую задачу? С чего начинать?

Сначала перечислим три основных требования к условию учебной (изобретательской или исследовательской) задачи:

− Достаточность условия

− Корректность вопроса

− Наличие противоречия. [3]

При этом не забываем, что условие задачи должно быть связано с жизненной ситуацией.

О чем необходимо помнить при составлении открытой задачи? Она должна быть интересной, понятной по тексту и принципиально решаемой. Некоторые из текстовых задач, предложенных в школьных учебниках математики, можно превратить в открытые исследовательские задачи. Рассмотрим одну из типовых школьных задач.

Задача: Из двух городов, расстояние между которыми 420 км, навстречу друг другу выехали два автомобиля. Скорость одного из них 68 км/ч, а скорость второго — 72 км/ч. Какое расстояние будет между ними через 2 часа?

Данная задача имеет единственный верный ответ и алгоритм решения. Уберем из текста задачи фразу «навстречу друг другу», и задача уже имеет неоднозначное решение. При ее решении ученики разбирают не только движение «навстречу друг другу», но и движение в «противоположном направлении» или в «одну сторону». Конечно, в каждой из этих ситуаций учащиеся придут к различным ответам. Измененное условие задачи хотя и делает из «закрытой» задачи «открытую», но при этом условие ее остается таким же скучным для школьника. Изменим текст задачи, сделаем ее более современной.

Задача: Между городами Саратов и Волгоград 380 км. Из Саратова выехал автомобиль «Тойота Камри», а из Волгограда — автомобиль «Шкода Октавия». Какое расстояние будет между ними через 30 минут, если каждая машина будет ехать с максимальной скорость?

Для справки: автомобиль «Тойота Камри» развивает скорость 210 км/ч, а автомобиль «Шкода Октавия» — 240 км/ч.

Рассмотрим еще одну школьную задачу

Задача: Покупка стоит 475 рублей. Сколько сдачи получит покупатель из кассы с пяти купюр по 100 рублей каждая?

Если в условии задачи, заменить число 475 переменной А, то получим простейшую задачу с параметром, которая также приводит к неоднозначному ответу.

Как изменить условие задачи, чтобы помимо открытости, она содержала и реальные жизненные ситуации? Здесь на помощь приходят факты и информация из различных школьных дисциплин. Также все ученики любят решать задачи, в которых главными героями являются они сами, задачи «о себе любимых».

Задачи: Кирилл и Никита одноклассники. Никита живет в 2 км от школы (по прямой), а Кирилл — в 3 км. На каком расстоянии друг от друга живут Никита и Кирилл?

К этой задаче прилагаем фрагмент карты города (выполненный в масштабе) со школой и прилежащими к ней улицами.

В реальной жизни мы получаем не только числа, необходимые нам для решения проблемы, но и избыточные данные. При решении таких заданий нужно определить, какие именно из предложенных величин нужны для поиска ответа на вопрос.

Для составления задач с избыточными данными можно взять любой научно-популярный текст из школьного учебника или одной из детских энциклопедий, предложить ученикам самостоятельно найти числовые величины для этого отрывка. Придумав вопросы, которые можно задать к этому фрагменты, ученик превращает его в условие задачи. Например, рассмотрим следующий текст:

Африканский страус

Африканский страус — самая крупная из современных птиц. Страус имеет плотное телосложение, длинную шею и небольшую уплощённую голову. Клюв прямой, плоский, с роговым «когтем» на надклювье, довольно мягкий. Страусы — нелетающие птицы. Крылья у страусов недоразвитые. Задние конечности длинные и сильные, всего с двумя пальцами. Один из пальцев заканчивается подобием рогового копыта — на него птица опирается при беге. Благодаря своему росту и прекрасному зрению, страусы первые замечают опасность. В случае опасности они бросаются в бегство.

Добавим в этот фрагмент числовые величины.

Задача: Африканский страус

Африканский страус — самая крупная из современных птиц: высотой до 270 см и массой до 156 кг [Википедия]. Страус имеет плотное телосложение, длинную шею и небольшую уплощённую голову. Клюв прямой, плоский, с роговым «когтем» на надклювье, довольно мягкий. Страусы — нелетающие птицы. Крылья у страусов недоразвитые. Задние конечности длинные и сильные, всего с двумя пальцами. Один из пальцев заканчивается подобием рогового копыта — на него птица опирается при беге. Благодаря своему росту и прекрасному зрению, страусы первые замечают опасность. В случае опасности они бросаются в бегство, развивая скорость до 70 км/ч и делая шаги до 4 м длиной, и при необходимости круто меняют направление бега, не снижая скорости. Страусята вылупляются зрячие, покрытые пухом и способные к передвижению. Только что вылупившийся страусёнок весит около 1,2 кг, а к четырём месяцам достигает 18–19 кг. Молодые страусы уже в месячном возрасте могут бегать со скоростью до 50 км/ч. [4] Придумайте вопросы, превращающие данный текст в условие задачи.

Учащиеся придумывают вопросы и самостоятельно проверяют, достаточно ли данных для решения задачи. Возможные вопросы к данной задаче:

− Во сколько раз вес вылупившегося страусенка меньше веса взрослого страуса?

− Сколько составляет среднесуточный привес страусенка в первые четыре месяца жизни?

− На какое расстояние переместится страус при бегстве, если через каждые три шага, будет менять направление движения под прямым углом к траектории, если он поменяет направление два раза? три раза?

Приобретая опыт составления и решения таких задач, школьники составляют свои собственные задачники по темам: «Растения», «Животные», «Древняя Греция».

Превратить школьные задачи в открытые изобретательские задачи лучше всего получается в геометрии. Для этого нужно только ввести в задачу ограничения (по инструментам, по материалам). Рассмотрим пример.

Задача: Наша школьная спортивная площадка будет ремонтироваться. Для расчета материалов нам нужно посчитать ее площадь. Как это сделать, если размеры площадки неизвестны и у вас только линейка 30 см, и небольшая (меньше метра) ленточка?

Лучше всего решать эту задачу практически, с выходом на местность. В этом случае можно предложить выполнить измерения различными способами и сравнить результаты.

Как показывает практика, ученики измеряют длину и ширину площадки шагами, иногда, связывая ноги ленточкой для фиксации длины шага. Измеряют ленточкой, пользуясь ею как эталоном длины и переводя результат в метрическую систему. Были и те, кто измерял длиной ступни, обходя площадку мелкими шажками.

Задача: «В русских усадьбах 19 века рядом с домом находилась парадная часть парка. Ее украшал цветник в виде клумбы овальной или округлой формы, в центре которой возвышалась ваза, скульптура или фонтан. Почти в каждой богатой усадьбе многие теплолюбивые деревья и кустарники выращивали в кадках и в летнее время выносили на открытый воздух» [5]. Пользуясь веревкой (4–5 м) и несколькими колышками, разбейте круглую клумбу и вдоль края клумбы на одинаковом расстоянии поставьте шесть кадок с цветами.

Эта задача подходит для любой командной игры на свежем воздухе. Для решения ее требуются знания геометрии 8–9 классов.

При решении этой задачи только небольшой процент учащихся начал вспоминать материал школьного курса геометрии. Большинство, проведя окружность с помощью веревки и двух колышков, расставляло кадки «на глазок», что не всегда приводило к верному результату.

Почти все задачи на доказательство школьного курса геометрии можно сделать открытыми задачами. Изучив весь курс планиметрии 7–9 классов, нужно вернуться к пройденным задачам и предложить ученикам найти другие доказательства.

Таким образом, решение и составление открытых задач позволяет ученикам выйти за пределы предмета «математика», овладеть общеучебными навыками, научиться решать практические задачи, связанные с различными жизненными ситуациями. Это позволяет реализовать требования ФГОС. Но нельзя построить весь процесс обучения только на открытых задачах. Нужно эффективно сочетать оба типа задач — открытые и закрытые.

Как показала практика, использование открытых задач повысило мотивацию школьников в изучении предмета «математика».

Литература:

1. Значение слова ТВОРЧЕСТВО в Большой советской энциклопедии, БСЭ // slovar.cc. URL: https://slovar.cc/enc/bse/2047434.html (дата обращения: 23.01.2020).
2. Гин А., Кавтрев А. Креатив-бой. — 3-е изд. — М.: Вита-Пресс, 2015. — 32 с.
3. Гин А. Приемы педагогической техники. — 6-е изд. — М.: Вита-Пресс, 2005. — 112 с.
4. Страус // Википедия. URL: https://ru.wikipedia.org/wiki/ %D0 %A1 %D1 %82 %D1 %80 %D0 %B0 %D1 %83 %D1 %81 (дата обращения: 23.01.2020).
5. Русские усадьбы // Greeninfo.ru. URL: https://www.greeninfo.ru/landscape/russian_estate.html (дата обращения: 23.01.2020).

             Составление текстовых задач учащимися.

В качестве одного из средств формирования математической культуры младших школьников можно рассматривать текстовые задачи. Большое обучающее и воспитательное значение имеет наличие в них познавательного материала, связанного с конкретными жизненными ситуациями. Это поможет показать младшим школьникам роль математики в познании окружающей действительности и развивать их умения применять математические знания на практике.

 Использование метода проектов формирует у учащихся навыки поиска и систематизации материала по заданной теме. Когда предлагается самостоятельно придумать задачи для своих одноклассников, у ребят загораются глаза. Они стараются придумать такие задачи, чтобы их друзья заинтересовались, удивились, узнали что-то новое. При составлении задач разрешаю пользоваться словарями, справочниками, энциклопедиями.

Детей очень увлекают задачи с биологическим сюжетом. Приведу примеры задач, которые придумали сами ребята:

     1.Стрекоза съедает за 2 часа 40 мух. Сколько мух она уничтожит за 7        

        часов?

     2.Ворона летит со скоростью 50км/час, а стриж в два раза быстрее.

        С какой скоростью летает стриж?

     3.Сова съедает 13 мышей. Сколько мышей она съест за неделю?

     4. Осёл живёт50 лет, а корова в два раза меньше.

        Сколько лет она может прожить?

Дети могут оформить такую задачу на альбомном листе, нарисовать рисунок.

Решают такие задачи с огромным интересом, ведь дети здесь сами выступают в роли авторов и художников. Такой вид творческой работы учащимся нравится.

Очень часто урок математики пересекается с литературой. Меры величины изучаются в начальных классах, но это современные, общепринятые меры. В сказках же и детской литературе наши школьники встречают много непонятных мер величины. На уроках математики можно решать задачи связанные с переводом « сказочных» величин в понятные им. Здесь часто приходится прибегать к работе с толковыми словарями.

                 1 «Волга проходит через всю

                    Россию на три тысячи

                    Сто шестьдесят верст»  (Л.Н.Толстой)    

 Слово верста обозначает старинную единицу длины, которая равна1,0668км  

                  2. « Она была нежная, маленькая

                       Всего дюйм ростом» (Х.К. Андерсен)

Слово дюйм обозначает единицу длины( британская система мер), которая равна 2,54см.

                   3. «Не было гроша- да вдруг алтын.» поговорка

Алтын монета (три копейки). При изучении денежных единиц можно рассказать детям о том, что на полушку (четверть копейки) можно было купить калач, а на алтын- обед в трактире.

А как активизируется деятельность учащихся, если на уроке присутствуют сказочные герои. Вот несколько задач ,придуманных моими ребятами. Очень интересно придумывать задачи для своих друзей.

1.От царства Кощея выехали в противоположных направлениях Баба-Яга в избушке и Емеля на печи. Баба-Яга ехала со скоростью 7км в час, а Емеля 8 км в час. На каком расстоянии друг от друга они будут

через 4 часа?

2.Однажды Гена принёс в детский сад к Чебурашке 42 игрушки. Чебурашка расставил их на несколько полок по 7 игрушек на каждую. Сколько полок занято этими игрушками?

3.Винни-Пух и Пятачок искали Кролика. Они вышли одновременно а противоположных направлениях. Через два часа расстояние между ними было 18 км. Винни-Пух шёл со скоростью 4 км в час, С какой скоростью шёл Пятачок?

Поиск решения задач позволяет развивать интеллект учеников, а привлекательные сюжеты способствуют развитию интереса к урокам математики. Дети не хуже взрослых умеют придумывать задачи, где главные герои- сказочные персонажи, наиболее любимые ими.

Немаловажную роль играет связь математики с историей. На таких уроках веду работу по сохранению историко-культурного наследия, работаю над расширением кругозора учащихся, воспитываю чувство гордости за наш народ.

1.Город Саратов был основан в 1590 году. Сколько лет исполнилось  Саратову в этом году?

2.Наша школа была открыта в 1981 году. Сколько лет нашей школе?

На уроках мы знакомимся с мерами длины. Обязательно знакомлю детей с первыми измерительными приборами, которыми были части тела: пальцы рук, ладонь, ступня, локоть. Дети с интересом измеряют длину парты в ладонях, ширину класса в ступнях. Они приходят к выводу, что современные приборы намного удобнее.

На уроках с интересом принимаются старинные задачи. Их решение требует от учащихся не только математические знания, но и сообразительности и умения логически мыслить, искать нетрадиционные пути решения. Эти задачи составлены давно, но их до сих пор решают. О тех ,кто составил задачи, помнят и гордятся ими. Это задачи ,найденные в рукописях Л.Магнитского.

Работа над текстовой задачей необходима на каждом уроке. Она помогает нам воспитать всесторонне  развитого человека. В процессе преподавания математики применение знаний, полученных при изучении других учебных дисциплин, положительно воздействует на познавательную деятельность учащихся, в результате чего приобретённые знания становятся более глубокими и прочными.