Как составить интерполяционный многочлен лагранжа - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 25 ноября 2021 года; проверки требуют 8 правок.

Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий заданные значения в заданном наборе точек, то есть решающий задачу интерполяции.

Определение[править | править код]

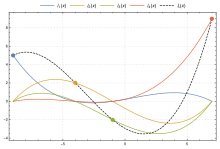
Интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9), а также полиномы ${displaystyle y_{i}l_{i}(x)}$ , каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных.

Пусть задана n+1 пара чисел ${displaystyle (x_{0},y_{0}),(x_{1},y_{1}),ldots ,(x_{n},y_{n}),}$ где все $x_{j}$ различны. Требуется построить многочлен L(x) степени не более , для которого ${displaystyle L(x_{j})=y_{j}}$ .

Общий случай[править | править код]

Ж. Л. Лагранж предложил следующий способ вычисления таких многочленов:

${displaystyle L(x)=sum _{i=0}^{n}y_{i}l_{i}(x),}$

где базисные полиномы $l_{i}$ определяются по формуле

${displaystyle l_{i}(x)=prod _{j=0,jneq i}^{n}{frac {x-x_{j}}{x_{i}-x_{j}}}={frac {x-x_{0}}{x_{i}-x_{0}}}cdots {frac {x-x_{i-1}}{x_{i}-x_{i-1}}}cdot {frac {x-x_{i+1}}{x_{i}-x_{i+1}}}cdots {frac {x-x_{n}}{x_{i}-x_{n}}}}$

Для любого многочлен $l_{i}$ имеет степень и

${displaystyle l_{i}(x_{j})=left{{begin{array}{rl}0,&jneq i,\1,&j=i.end{array}}right.}$

Отсюда следует, что L(x) , являющийся линейной комбинацией многочленов ${displaystyle l_{i}(x)}$ , имеет степень не больше и ${displaystyle L(x_{i})=y_{i}}$ .

Случай равноотстоящих узлов интерполяции[править | править код]

Пусть узлы интерполяции $x_{j}$ являются равноотстоящими, то есть выражаются через начальную точку $x_{0}$ и некоторую фиксированную положительную величину следующим образом:

${displaystyle x_{j}=x_{0}+jh.}$

Отсюда следует, что

${displaystyle x_{j}-x_{i}=(j-i)h.}$

Подставляя эти выражения в формулу для базисного полинома и вынося за знаки произведения в числителе и знаменателе, получим

${displaystyle l_{j}(x)={prod _{i=0,,ineq j}^{n}{(x-x_{i}) over (x_{j}-x_{i})}}={prod limits _{i=0,,ineq j}^{n}(x-x_{0}-ih) over h^{n}prod limits _{i=0,,ineq j}^{n}(j-i)}}$

Теперь можно ввести замену переменной

${displaystyle y={{x-x_{0}} over h}}$

и получить выражение для базисных полиномов через , которое строится с использованием только целочисленной арифметики:

${displaystyle l_{j}(x)=l_{j}(x_{0}+yh)=(-1)^{n-j}C_{n}^{j}{dfrac {y(y-1)ldots (y-n)}{(y-i)n!}}.}$

Данные величины называются коэффициентами Лагранжа. Они не зависят ни от ${displaystyle y_{0},ldots ,y_{n}}$ , ни от и потому могут быть вычислены заранее и записаны в виде таблиц. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования длинной арифметики.

Остаточный член[править | править код]

Если считать числа ${displaystyle y_{0},ldots ,y_{n}}$ значениями некоторой функции в узлах ${displaystyle x_{0},ldots ,x_{n}}$ , то ошибка интерполирования функции многочленом равна

${displaystyle f(x)-L(x)={dfrac {f^{(n+1)}(xi )}{(n+1)!}}(x-x_{0})ldots (x-x_{n}),}$

где – некоторая средняя точка между наименьшим и наибольшим из чисел ${displaystyle x_{0},ldots ,x_{n}}$ . Полагая ${displaystyle M_{n+1}=sup _{xin [x_{0},x_{n}]}|f^{(n+1)}(x)|}$ , можно записать

${displaystyle |f(x)-L(x)|leqslant {dfrac {M_{n+1}}{(n+1)!}}|(x-x_{0})ldots (x-x_{n})|.}$

Единственность[править | править код]

Существует единственный многочлен степени не превосходящей , принимающий заданные значения в n+1 заданной точке.

Это утверждение является обобщением того факта, что через любые две точки проходит единственная прямая.

С точки зрения линейной алгебры[править | править код]

На единственность интерполяционного многочлена можно также взглянуть с точки зрения СЛАУ. Рассмотрим систему уравнений ${displaystyle P(x_{0})=y_{0},P(x_{1})=y_{1},dots ,P(x_{n})=y_{n}}$ . В явном виде она записывается как

${displaystyle {begin{cases}a_{0}+a_{1}x_{0}+a_{2}x_{0}^{2}+dots +a_{n}x_{0}^{n}=y_{0},\a_{0}+a_{1}x_{1}+a_{2}x_{1}^{2}+dots +a_{n}x_{1}^{n}=y_{1},\dots dots dots dots dots dots dots dots dots dots dots dots ,\a_{0}+a_{1}x_{n}+a_{2}x_{n}^{2}+dots +a_{n}x_{n}^{n}=y_{n}\end{cases}}}$

Её можно переписать в виде системы уравнений с неизвестным вектором ${displaystyle a=(a_{0},a_{1},dots ,a_{n})}$ :

${displaystyle {begin{bmatrix}1&x_{0}&x_{0}^{2}&dots &x_{0}^{n}\1&x_{1}&x_{1}^{2}&dots &x_{1}^{n}\vdots &vdots &vdots &ddots &vdots \1&x_{n}&x_{n}^{2}&dots &x_{n}^{n}\end{bmatrix}}{begin{bmatrix}a_{0}\a_{1}\vdots \a_{n}end{bmatrix}}={begin{bmatrix}y_{0}\y_{1}\vdots \y_{n}end{bmatrix}}}$

Матрица в такой системе является матрицей Вандермонда и её определитель равен ${displaystyle prod limits _{i<j}(x_{i}-x_{j})}$ . Соответственно, если все точки ${displaystyle x_{0},x_{1},dots ,x_{n}}$ различны, то матрица невырождена и система обладает единственным решением.

С точки зрения китайской теоремы об остатках[править | править код]

По теореме Безу остаток от деления P(x) на (x-a) равен P(a) . Таким образом, всю систему можно воспринимать в виде системы сравнений:

${displaystyle {begin{cases}P(x)equiv y_{0}{pmod {x-x_{0}}},\P(x)equiv y_{1}{pmod {x-x_{1}}},\dots ,\P(x)equiv y_{n}{pmod {x-x_{n}}},\end{cases}}}$

По китайской теореме об остатках у такой системы есть единственное решение по модулю ${displaystyle (x-x_{0})(x-x_{1})dots (x-x_{n})}$ , то есть, заданная система однозначно определяет многочлен степени не выше . Такое представление многочлена в виде наборов остатков по модулям мономов аналогично представлению числа в виде остатков от деления на простые модули в системе остаточных классов. При этом явная формула для многочлена Лагранжа также может быть получена в соответствии с формулами китайской теоремы:
${textstyle P(x)=sum limits _{i=0}^{n}y_{i}M_{i}M_{i}^{-1}}$ , где ${displaystyle M_{i}=prod limits _{jneq i}(x-x_{j})}$ и ${displaystyle M_{i}^{-1}=prod limits _{jneq i}(x-x_{j})^{-1}{pmod {x-x_{i}}}=prod limits _{jneq i}(x_{i}-x_{j})^{-1}}$ .

Пример[править | править код]

Приближение функции (синяя линия) многочленом ${displaystyle L(x)=4,834848x^{3}-1,477474x}$ (зелёная линия).

Найдем формулу интерполяции для имеющей следующие значения:

${displaystyle {begin{aligned}x_{0}&=-1.5&&&&&f(x_{0})&=-14,1014\x_{1}&=-0.75&&&&&f(x_{1})&=-0,931596\x_{2}&=0&&&&&f(x_{2})&=0\x_{3}&=0.75&&&&&f(x_{3})&=0,931596\x_{4}&=1.5&&&&&f(x_{4})&=14,1014.end{aligned}}}$

${displaystyle l_{0}(x)={x-x_{1} over x_{0}-x_{1}}cdot {x-x_{2} over x_{0}-x_{2}}cdot {x-x_{3} over x_{0}-x_{3}}cdot {x-x_{4} over x_{0}-x_{4}}={1 over 243}x(2x-3)(4x-3)(4x+3)}$

${displaystyle l_{1}(x)={x-x_{0} over x_{1}-x_{0}}cdot {x-x_{2} over x_{1}-x_{2}}cdot {x-x_{3} over x_{1}-x_{3}}cdot {x-x_{4} over x_{1}-x_{4}}={}-{8 over 243}x(2x-3)(2x+3)(4x-3)}$

${displaystyle l_{2}(x)={x-x_{0} over x_{2}-x_{0}}cdot {x-x_{1} over x_{2}-x_{1}}cdot {x-x_{3} over x_{2}-x_{3}}cdot {x-x_{4} over x_{2}-x_{4}}={3 over 243}(2x+3)(4x+3)(4x-3)(2x-3)}$

${displaystyle l_{3}(x)={x-x_{0} over x_{3}-x_{0}}cdot {x-x_{1} over x_{3}-x_{1}}cdot {x-x_{2} over x_{3}-x_{2}}cdot {x-x_{4} over x_{3}-x_{4}}=-{8 over 243}x(2x-3)(2x+3)(4x+3)}$

${displaystyle l_{4}(x)={x-x_{0} over x_{4}-x_{0}}cdot {x-x_{1} over x_{4}-x_{1}}cdot {x-x_{2} over x_{4}-x_{2}}cdot {x-x_{3} over x_{4}-x_{3}}={1 over 243}x(2x+3)(4x-3)(4x+3).}$

Получим

${displaystyle {begin{aligned}L(x)&={1 over 243}{Big (}f(x_{0})x(2x-3)(4x-3)(4x+3)\&{}qquad {}-8f(x_{1})x(2x-3)(2x+3)(4x-3)\&{}qquad {}+3f(x_{2})(2x+3)(4x+3)(4x-3)(2x-3)\&{}qquad {}-8f(x_{3})x(2x-3)(2x+3)(4x+3)\&{}qquad {}+f(x_{4})x(2x+3)(4x-3)(4x+3){Big )}\&=4,834848x^{3}-1,477474x.end{aligned}}}$

Реализация общего случая на языке программирования Python (не оптимальный вариант)[править | править код]

import numpy as np

# данные для примера
xi = np.array([-1.5, -0.75, 0, 0.75, 1.5])
yi = np.array([-14.1014, -0.931596, 0, 0.931596, 14.1014])


def get_coefficients(_pl: np.ndarray, _xi: np.ndarray):
    '''
    Определение коэффициентов для множителей базисных полиномов l_i
    :param _pl: массив базисных полиномов
    :param _xi: массив значений x
    :return:
    '''
    n = int(_xi.shape[0])
    coefficients = np.empty((n, 2), dtype=float)
    for i in range(n):
        if i == _pl:
            coefficients[i][0] = float('inf')
            coefficients[i][1] = float('inf')
        else:
            coefficients[i][0] = 1 / (_xi[_pl] - _xi[i])
            coefficients[i][1] = -_xi[i] / (_xi[_pl] - _xi[i])
    filtered_coefficients = np.empty((n - 1, 2), dtype=float)
    j = 0
    for i in range(n):
        if coefficients[i][0] != float('inf'):
            # изменение последовательности, степень увеличивается
            filtered_coefficients[j][0] = coefficients[i][1]
            filtered_coefficients[j][1] = coefficients[i][0]
            j += 1
    return filtered_coefficients


def get_polynomial_l(_xi: np.ndarray):
    '''
    Определение базисных полиномов
    :param _xi: массив значений x
    :return:
    '''
    n = int(_xi.shape[0])
    pli = np.zeros((n, n), dtype=float)
    for pl in range(n):
        coefficients = get_coefficients(pl, _xi)
        for i in range(n - 1):  # проходим по массиву coefficients
            if i == 0:
                continue
            elif i == 1:  # на второй итерации занимаются 0-2 степени
                pli[pl][0] = coefficients[i - 1][0] * coefficients[i][0]
                pli[pl][1] = coefficients[i - 1][1] * coefficients[i][0] + coefficients[i][1] * coefficients[i - 1][0]
                pli[pl][2] = coefficients[i - 1][1] * coefficients[i][1]
            else:
                clone_pli = np.zeros(n, dtype=float)
                for val in range(n):
                    clone_pli[val] = pli[pl][val]
                zeros_pli = np.zeros(n, dtype=float)
                for j in range(n-1):  # проходим по строке pl массива pli
                    product_1 = clone_pli[j] * coefficients[i][0]
                    product_2 = clone_pli[j] * coefficients[i][1]
                    zeros_pli[j] += product_1
                    zeros_pli[j+1] += product_2
                for val in range(n):
                    pli[pl][val] = zeros_pli[val]
    return pli

def get_polynomial(_xi: np.ndarray, _yi: np.ndarray):
    '''
    Определение интерполяционного многочлена Лагранжа
    :param _xi: массив значений x
    :param _yi: массив значений y
    :return:
    '''
    n = int(_xi.shape[0])
    polynomial_l = get_polynomial_l(_xi)
    for i in range(n):
        for j in range(n):
            polynomial_l[i][j] *= yi[i]
    L = np.zeros(n, dtype=float)
    for i in range(n):
        for j in range(n):
            L[i] += polynomial_l[j][i]
    return L

# результат в виде массива коэффициентов многочлена при x в порядке увеличения степени
# [ 0.         -1.47747378  0.          4.8348476   0.        ]
# т.е. результирующий многочлен имеет вид: y(x) = -1.47747378*x + 4.8348476*x^3

Применения[править | править код]

Многочлены Лагранжа степеней от нулевой до пятой для функции

Численное интегрирование[править | править код]

Пусть для функции f(x) известны значения $y_{i}=f(x_{i})$ в некоторых точках. Тогда можно интерполировать эту функцию методом Лагранжа:

${displaystyle f(x)approx sum _{i=0}^{n}f(x_{i})l_{i}(x).}$

Полученное выражение можно использовать для приближённого вычисления определённого интеграла от функции :

$int limits _{a}^{b}f(x)dxapprox sum _{{i=0}}^{n}f(x_{i})int limits _{a}^{b}l_{i}(x)dx$

Значения интегралов от $l_{i}$ не зависят от f(x) и их можно вычислить заранее с использованием последовательности $x_{j}$ .

Литература[править | править код]

Березин, И. С., Жидков Н. П. Методы вычислений. Том I. — 2-е изд., стереотипное – М.: Физматлит. 1962.

Ссылки[править | править код]

М. А. Тынкевич. Глава 7.6.1. Интерполяционный многочлен Лагранжа // Численные методы анализа. — Кемерово, 2002. — ISBN 5-89070-042-1. (недоступная ссылка)
А. Г. Хованский. Полиномы Лагранжа и их применения. Видео-лекция. VI Летняя школа «Современная математика», Дубна, 2006.

См. также[править | править код]

Схема Эйткена
Интерполяционные формулы Ньютона
Интерполяция с кратными узлами
Схема разделения секрета Шамира
Комбинаторная теорема о нулях
Интерполяция алгебраическими многочленами

Источник

Интерполяционный
многочлен в форме Лагранжа (обозначим
)
есть иная форма записи алгебраического
многочлена
:

Из
определения интерполяционного многочлена
следует, что функции

должны обладать следующими свойствами:

1.
,

2.

при
,

т.
е. в узлах интерполяции интерполяционный
многочлен

совпадает с заданными значениями
.

Таким
образом,

есть многочлен степени
,
для которого все узлы

являются корнями. Тогда

(2.6)

Подставим
в (2.6) любой узел кроме

и убедимся, что

для любого
.
Коэффициент

выберем из следующих соображений:

или

Тогда

Интерполяционный
многочлен в форме Лагранжа:

(2.7)

Числитель
формулы (2.7)
представляет собой произведение
разностей между переменной x
и всеми узлами, кроме i-го,
а знаменатель – произведение разностей
между i-м
узлом и всеми остальными.

Пример.

Для
прежних исходных данных многочлен
Лагранжа (2.7) будет иметь вид:

(2.8)

Если
подставить исходные данные в (2.8), раскрыть
скобки и привести подобные члены в
полученном выражении, то получим тот
же многочлен в канонической форме:

Найдем
,
подставив x₄,
x₅
в (2.8):

1.3. Построение интерполяционного многочлена в форме Ньютона.

Интерполяционный
многочлен в форме Ньютона имеет вид:

(9)

где

– произвольная сетка узлов интерполяции;

– неизвестные пока коэффициенты.

Для
определения

воспользуемся критерием интерполяции:

{0,1,…,n}.

(10)

Условия
(2.10) приводят к системе уравнений:

(11)

Уравнения
(11)
представляют собой СЛАУ с нижней
треугольной матрицей, которая легко
решается прямой подстановкой: из первого
уравнения системы (11)
определяется
,
затем
подставляется
во второе уравнение для нахождения

и т.д.

Для
вычисления значения многочлена
используется модифицированная схема
Горнера:

(12)

Пример.

Используя
данные примера, получаем:

Используя
формулу (9), построим многочлен Ньютона:

Найдем

при тех же значениях x₄,
x₅,
используя модифицированную схему
Горнера (12):

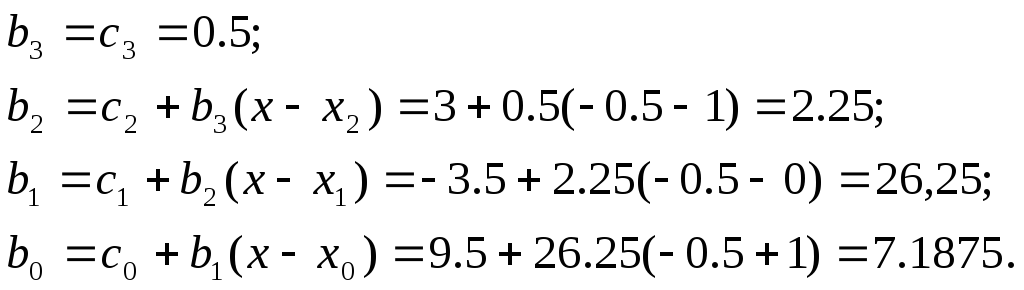
Интерполяционные
многочлены

– это разные формы записи одного и того
же алгебраического многочлена.

1.4. Задание на практику.

Исходные
данные представляют собой набор точек:

,
где
-значение
некоторой функции f(x)
в узлах
.

Построить
интерполяционный алгебраический
многочлен P_n(x),
значения которого в узлах x_i
совпадают со значениями функции y_i.
Используя
схему Горнера, найти значения P_n(x)
в точках x₄,
x₅.
Построить
интерполяционный многочлен в форме
Лагранжа L_n(x).
Построить
интерполяционный многочлен в форме
Ньютона N_n(x).
Используя
схему Горнера для формулы Ньютона,
рассчитать значения многочлена в точках
x₄,
x₅_.
Построить
график функции P_n(x),
используя значения функции в точках
x_i,
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Интерполяцио́нный многочле́н Лагра́нжа — многочлен минимальной степени, принимающий данные значения в данном наборе точек. Для пар чисел ${displaystyle (x_{0},y_{0}),(x_{1},y_{1})dots (x_{n},y_{n})}$ , где все ${displaystyle x_{i}}$ различны, существует единственный многочлен степени не более , для которого ${displaystyle L(x_{i})=y_{i}}$ .

В простейшем случае это линейный многочлен, график которого — прямая, проходящая через две заданные точки.

Определение

Файл:Lagrangepolys.png

Этот пример показывает интерполяционный многочлен Лагранжа для четырёх точек (-9,5), (-4,2), (-1,-2) и (7,9), а также полиномы y_j l_j(x), каждый из которых проходит через одну из выделенных точек, и принимает нулевое значение в остальных x_i

Лагранж предложил способ вычисления таких многочленов:

${displaystyle L(x)=sum _{j=0}^{n}y_{j}l_{j}(x)}$

где базисные полиномы определяются по формуле:

${displaystyle l_{j}(x)=prod _{i=0,jneq i}^{n}{frac {x-x_{i}}{x_{j}-x_{i}}}={frac {x-x_{0}}{x_{j}-x_{0}}}cdots {frac {x-x_{j-1}}{x_{j}-x_{j-1}}}{frac {x-x_{j+1}}{x_{j}-x_{j+1}}}cdots {frac {x-x_{n}}{x_{j}-x_{n}}},!}$

Легко видеть что ${displaystyle l_{j}(x)}$ обладают такими свойствами:

Отсюда следует, что , как линейная комбинация ${displaystyle l_{j}(x)}$ , может иметь степень не больше , и ${displaystyle L(x_{j})=y_{j}}$ , Q.E.D.

Применения

Полиномы Лагранжа используются для интерполяции, а также для
численного интегрирования.

Пусть для функции известны значения ${displaystyle y_{j}=f(x_{j})}$ в некоторых точках. Тогда мы можем интерполировать эту функцию как

${displaystyle f(x)approx sum _{j=0}^{n}f(x_{j})l_{j}(x)}$

В частности,

${displaystyle int limits _{a}^{b}f(x)dxapprox sum _{j=0}^{n}f(x_{j})int limits _{a}^{b}l_{j}(x)dx}$

Значения интегралов от ${displaystyle l_{j}}$ не зависят от , и их можно вычислить заранее, зная последовательность ${displaystyle x_{i}}$ .

Для случая равномерного распределения по отрезку узлов интерполяции

В указанном случае можно выразить ${displaystyle x_{i}}$ через расстояние между узлами интерполяции h и начальную точку ${displaystyle x_{0}}$ :

${displaystyle x_{j}equiv {x_{0}+jh}}$

и, следовательно,

${displaystyle {x_{i}-x_{j}}equiv (i-j)h}$

Подставив эти выражения в формулу полинома и вынеся h за знаки перемножения в числителе и знаменателе, получим

${displaystyle l_{i}(x)={prod _{j=0,,ineq j}^{n}{(x-x_{j}) over (x_{i}-x_{j})}}={prod limits _{j=0,,ineq j}^{n}(x-x_{0}-jh) over h^{n-1}prod limits _{j=0,,ineq j}^{n}(i-j)}}$

Теперь можно ввести замену переменной

${displaystyle y={{x-x_{0}} over h},!}$

и получить полином от XY, который строится с использованием только целочисленной арифметики. Недостатком данного подхода является факториальная сложность числителя и знаменателя, что требует использования алгоритмов с многобайтным представлением чисел.

cs:Lagrangeova interpolace
nl:Lagrange-polynoom
sr:Лагранжов полином
uk:Многочлен Лагранжа

Источник

Этот калькулятор может пригодиться при решении задач на интерполяцию полиномом Лагранжа. В таких задачах обычно требуется интерполировать значение неизвестной функции, соответствующее некоторому значению x, использую формулу интерполяционного многочлена Лагранжа, полученную из известного набора точек со значениями неизвестной функции (x, f(x)).

Калькулятор ниже обладает следующими функциями:

Он находит формулу полинома Лагранжа для заданного набора точек.
Он отображает пошаговый вывод формулы.
Он вычисляет значения интерполяционного многочлена Лагранжа для заданных точек (интерполирует функцию полиномом Лагранжа в заданных точках интерполяции)
Он отображает набор точек, значения в точках интерполяции, полином Лагранжа и все базисные полиномы на графике.

Как пользоваться

Сначала вводите набор точек – одна точка на строку в форме x f(x), значения разделены пробелом. Если вы хотите получить интерполяцию, вводите значения точек интерполяции в следующее поле в виде значений x, разделенных пробелом.

По умолчанию, калькулятор отображает формулу многочлена и его значения в точках интерполяции. Если нужно пошаговое решение, включите опцию “Показать пошаговое решение”. Также можно отключить отображение базисных полиномов.

Теория и формулы, как обычно, описаны под калькулятором.

Интерполяционный многочлен Лагранжа (полином Лагранжа)

Набор точек, одна точка на строку, значения разделяются пробелом

Точность вычисления

Знаков после запятой: 2

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Показать решение по шагам

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Показать базисные полиномы

Полином Лагранжа

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Интерполяционный многочлен Лагранжа

Предположим, что у нас есть набор значений, соответствующих неизвестной функции, при этом все x различны:

$(x_{0},y_{0}),ldots ,(x_{j},y_{j}),ldots ,(x_{k},y_{k})$

Сконструируем следующий многочлен (называемые многочленом Лагранжа):

$L(x):=sum _{j=0}^{k}y_{j}ell _{j}(x)$

где $ell _{j}(x)$ – базисный полином Лагранда

$ell _{j}(x):=prod _{begin{smallmatrix}0leq mleq k\mneq jend{smallmatrix}}{frac {x-x_{m}}{x_{j}-x_{m}}}={frac {(x-x_{0})}{(x_{j}-x_{0})}}cdots {frac {(x-x_{j-1})}{(x_{j}-x_{j-1})}}{frac {(x-x_{j+1})}{(x_{j}-x_{j+1})}}cdots {frac {(x-x_{k})}{(x_{j}-x_{k})}}$

Если посмотреть на формулу базисного полинома для любого j, то видно что для всех точек i не равных j, значение этого полинома обращается в ноль, а в самой точке j значение этого полинома j равно единице. Таким образом,

$y_{j}ell _{j}(x_{j})=y_{j} cdot 1=y_{j}$

$L(x_{j})=y_{j}+0+0+dots +0=y_{j}$

что означает, что полином Лагранжа точно интерполирует значение функции в заданных точках.

Стоит заметить, что формула интерполяционного многочлена Лагранжа подвержена воздействию так называемого феномена Рунге. Феномен Рунге связан к увеличением колебаний полинома на краях интервала при использовании полиномов высоких степеней на равноудаленных друг от друга точках. Таким образом, наличие большого количества точек далеко не всегда приводит к улучшению точности интерполяции.

Однако также стоит заметить, что в отличие от некоторых других формул интерполяции, формула Лагранжа не требует того, чтобы точки в наборе были равноудалены друг от друга. Это используется в некоторых способах борьбы с феноменом Рунге, например, при использовании в качестве точек интерполяции узлов Чебышева.

Источник

Определение[править | править код]

Общий случай[править | править код]

Случай равноотстоящих узлов интерполяции[править | править код]

Остаточный член[править | править код]

Единственность[править | править код]

С точки зрения линейной алгебры[править | править код]

С точки зрения китайской теоремы об остатках[править | править код]

Пример[править | править код]

Реализация общего случая на языке программирования Python (не оптимальный вариант)[править | править код]

Применения[править | править код]

Численное интегрирование[править | править код]

Литература[править | править код]

Ссылки[править | править код]

См. также[править | править код]

1.3. Построение интерполяционного многочлена в форме Ньютона.

1.4. Задание на практику.

Определение

Применения

Для случая равномерного распределения по отрезку узлов интерполяции

Как пользоваться

Интерполяционный многочлен Лагранжа (полином Лагранжа)

Интерполяционный многочлен Лагранжа

Вам также может понравиться

Как приготовить рис найти

Как найти точки дифференцируемости функции

Как найти добавленную стоимость пример

Добавить комментарий Отменить ответ