Как составить интервальную таблицу частот с шагом 20 - Сайт, где вы сможете решить свои вопросы

Варианты для выполнения работы

I. Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.

Почти все встречающиеся в жизни величины (урожайность сельскохозяйственных растений, продуктивности скота, производительность труда и заработная плата рабочих, объем производства продукции и т.д.) принимают неодинаковые значения у различных членов совокупности. Поэтому возникает необходимость в изучении их изменяемости. Это изучение начинается с проведения соответствующих наблюдений, обследований.

В результате наблюдений получают сведения о численной величине изучаемого признака у каждого члена данной совокупности.

Пример. Имеются данные о размере прибыли 100 коммерческих банков. Прибыль, млн. рублей.

30,2	51,9	43,1	58,9	34,1	55,2	47,9	43,7	53,2	34,9
47,8	65,7	37,8	68,6	48,4	67,5	27,3	66,1	52,0	55,6
54,1	26,9	53,6	42,5	59,3	44,8	52,8	42,3	55,9	48,1
44,5	69,8	47,3	35,6	70,1	39,5	70,3	33,7	51,8	56,1
28,4	48,7	41,9	58,1	20,4	56,3	46,5	41,8	59,5	38,1
41,4	70,4	31,4	52,5	45,2	52,3	40,2	60,4	27,6	57,4
29,3	53,8	46,3	40,1	50,3	48,9	35,8	61,7	49,2	45,8
45,3	71,5	35,1	57,8	28,1	57,6	49,6	45,5	36,2	63,2
61,9	25,1	65,1	49,7	62,1	46,1	39,9	62,4	50,1	33,1
33,3	49,8	39,8	45,9	37,3	78,0	64,9	28,8	62,5	58,7

Из данной таблицы видно, что интересующий нас признак (прибыль банков) меняется от одного члена совокупности к другому, варьирует. Варьирование есть изменяемость признака у отдельных членов совокупности.

Вариационным рядом называется последовательность вариант, записанных в возрастающем порядке и соответствующих им частот.

Число, показывающее, сколько раз повторяется в данной совокупности каждое значение признака, называется частотой.

Составим ранжированный вариационный ряд (выпишем варианты в порядке возрастания):

20,4	25,1	26,9	27,3	27,6	28,1	28,4	28,8	29,3	30,2
31,4	33,1	33,3	33,7	34,1	34,9	35,1	35,6	35,8	36,2
37,3	37,8	38,1	39,5	39,8	39,9	40,1	40,2	41,4	41,8
41,9	42,3	42,5	43,1	43,7	44,5	44,8	45,2	45,3	45,5
45,8	45,9	46,1	46,3	46,5	47,3	47,8	47,9	48,1	48,4
48,7	48,9	49,2	49,6	49,7	49,8	50,1	50,3	51,8	51,9
52,0	52,3	52,5	52,8	53,2	53,6	53,8	54,1	55,2	55,6
55,9	56,1	56,3	57,4	57,6	57,8	58,1	58,7	58,9	59,3
59,5	60,4	61,7	61,9	62,1	62,4	62,5	63,2	64,9	65,1
65,7	66,1	67,5	68,6	69,8	70,1	70,3	70,4	71,5	78,0

В нашем случае каждое значение признака (варианта вариационного ряда) повторилось только один раз, т.е. значение частоты для всех вариант равно единице. Перейдем к интервальному вариационному ряду, так как интересующий нас признак принимает дробные, практически не повторяющиеся значения.

Для этого необходимо определить число интервалов (классов) и длину интервала (классного промежутка), после чего произвести разноску, т.е. подсчитать для каждого интервала число вариант, попавших в него.

Количество классов устанавливают в зависимости от степени точности, с которой ведется обработка, и количества объектов в выборке. Считается удобным при объеме выборки (n) в пределах от 30 до 60 вариант распределять их на 6-7 классов, при n от 60 до 100 вариант — на 7-8 классов, при n от 100 и более вариант — на 9-17 классов.

Нужное количество групп также может быть ориентировочно вычислено по формуле Стерджесса:

где — число групп (классов, интервалов) ряда распределения; n — объем выборки.

Можно также использовать выражение:

При они дают примерно одинаковые результаты.

В рассматриваемом примере о размере прибыли коммерческих банков, n=100. Применяя формулу Стерджесса, получим:

Однако Таким образом, число интервалов может быть равно 8, 9, 10 и т.д.

Нахождение нужного количества групп и их размеров часто бывает взаимообусловлено. Для того, чтобы как-то определиться с числом интервалов, найдем размах вариации — разность между наибольшей и наименьшей вариантой:

$[R=x_{max}-x_{min}]$

где — размах вариации,

$x_{max}$ — наибольшее значение варьирующего признака,

$x_{min}$ — наименьшее значение варьирующего признака.

Найдем размах вариации для рассматриваемой задачи:

Для того, чтобы найти длину интервала (величину классового промежутка) необходимо разделить размах вариации на число классов и полученную величину округлить таким образом, чтобы было удобно производить сначала разноску, а затем и различные вычисления. Рекомендую округлять до единиц, до которых округлены варианты в исходной таблице, в нашем случае до десятых.

$[happrox frac{R}{k}]$

Согласно формуле получаем

$[happrox frac{57,6}{8}=7,2]$

Теперь необходимо определиться с началом первого интервала. Для этого можно использовать формулу:

$[x_1approx x_{min}-frac{h}{2}]$

$[x_1approx 20,4-frac{7,2}{2}=16,8.]$

Замечание. За начало первого интервала можно принять некоторое значение, несколько меньшее $x_{min}$ или само значение $x_{min}$ . Далее в табличном виде я покажу оба варианта.

Прибавив к началу первого интервала (нижней границе) шаг, получим верхнюю границу первого интервала и одновременно нижнюю границу второго интервала. Выполняя последовательно указанные действия, будем находить границы последующих интервалов до тех пор, пока не будет получено или перекрыто $x_{max}$ .

Таким образом, верхняя граница одного интервала одновременно является нижней границей другого интервала. Чтобы не возникало сомнений, в какой интервал отнести варианту, попавшую на границу, условимся относить ее к верхнему интервалу.

Составим теперь рабочую таблицу для построения интервального вариационного ряда и произведем подсчет частот вариант, попавших в тот или иной интервал.

Как и обещал покажу две таблицы построения ряда:

1. Отсчет ведем от $x_{min}$ , т.е. нижняя граница первого интервала совпадает с $x_{min}$ .

Группы банков по размеру прибыли (границы интервалов)	Количество банков, принадлежащих данной группе (частоты, )	Накопленные частоты,
20,4 — 27,6	4	4
27,6 — 34,8	11	15
34,8 — 42	16	31
42 — 49,2	21	52
49,2 — 56,4	21	73
56,4 — 63,6	15	88
63,6 — 70,8	10	98
70,8 — 78	2	100

2. Начало первого интервала определяем с помощью формулы: $x_1approx x_{min}-frac{h}{2}$ .

Группы банков по размеру прибыли (границы интервалов)	Количество банков, принадлежащих данной группе (частоты, )	Накопленные частоты,
16,8 — 24	1	1
24 — 31,2	9	10
31,2 — 38,4	13	23
38,4 — 45,6	17	40
45,6 — 52,8	23	63
52,8 — 60	18	81
60 — 67,2	11	92
67,2 — 74,4	7	99
74,4 — 81,6	1	100

Как мы видим в 1-м случае у нас получилось восемь интервалов, что полностью совпадает с результатом, который нам дала формула Стерджесса. Во втором случае у нас получилось девять интервалов, так как при поиске начала первого интервала пользовались специальной формулой.

Для дальнейшего исследования я буду пользоваться результатами второй таблицы, так как там ярко выражен модальный интервал (одна мода) и медиана практически точно попадает на середину вариационного ряда.

Мы получили интервальный вариационный ряд — упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами попаданий в каждый из них значений величины.

II. Графическая интерпретация вариационных рядов.

№ п/п	Границы интервалов, $[x_{i}; x_{i+1})$	Середины интервалов, $x_{i}^{*}=frac{x_i+x_{i+1}}{2}$	Частоты интервалов,	Относительные частоты $W_i=frac{n_i}{n}$	Плотность относит. частоты $frac{W_i}{h}$	Плотность частоты $frac{n_i}{h}$
1	16,8 — 24	20,4	1	0,01	0,001	0,139
2	24 — 31,2	27,6	9	0,09	0,013	1,250
3	31,2 — 38,4	34,8	13	0,13	0,018	1,806
4	38,4 — 45,6	42	17	0,17	0,024	2,361
5	45,6 — 52,8	49,2	23	0,23	0,032	3,194
6	52,8 — 60	56,4	18	0,18	0,025	2,500
7	60 — 67,2	63,6	11	0,11	0,015	1,528
8	67,2 — 74,4	70,8	7	0,07	0,010	0,972
9	74,4 — 81,6	78	1	0,01	0,001	0,139

Строим графики:

Далее найдем моду вариационного ряда:

$[M_o(X)=x_{M_o}+hfrac{(n_2-n_1)}{(n_2-n_1)+(n_2-n_3)}]$

где

$x_{M_o}$ — начало модального интервала;

— длина частичного интервала (шаг);

n_1 — частота предмодального интервала;

n_2 — частота модального интервала;

— частота послемодального интервала.

Определим модальный интервал — интервал, имеющий наибольшую частоту. Из таблицы видно, что модальным является интервал (45,6 — 52,8).

$[M_o(X)=45,6+7,2frac{(23-17)}{(23-17)+(23-18)}=]$

$[=45,6+7,2cdot frac{6}{6+5}=45,6+3,93=49,5]$

Медиана

Для интервального ряда медиана находится по формуле:

$[M_e(X)=x_{M_e}+hfrac{0,5n-S_{M_{e}-1}}{n_{M_e}}]$

где

$x_{M_e}$ — начало медианного интервала;

— длина частичного интервала (шаг);

— объем совокупности;

$S_{M_{e}-1}$ — накопленная частота интервала, предшествующая медианному;

$n_{M_e}$ — частота медианного интервала.

Определим медианный интервал — интервал, в котором впервые накопленная частота превышает половину объема выборки.Так как объем выборки n=100, то n/2=50. По таблице найдем интервал, где впервые накопленные частоты превысят это значение. Таким является интервал (45,6 — 52,8).

Получаем,

$[M_e(X)=45,6+7,2frac{0,5cdot 100-40}{23}approx 48,7.]$

III. Расчет сводных характеристик выборки.

Для определения $x_B, D_{B}, sigma_{B}$ составим расчетную таблицу. Для начала определимся с ложным нулем С. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).

Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. В нашем случае С=49,2.

Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.

Условными называют варианты, определяемые равенством:

$[U_i=frac{(x_i-C)}{h}]$

Произведем расчет условных вариант согласно формуле:

$[U_1=frac{20,4-49,2}{7,2}=-4]$

$[U_2=frac{27,6-49,2}{7,2}=-3]$

$[U_3=frac{34,8-49,2}{7,2}=-2]$

$[U_4=frac{42-49,2}{7,2}=-1]$

$[U_5=frac{49,2-49,2}{7,2}=0]$

$[U_6=frac{56,4-49,2}{7,2}=1]$

$[U_7=frac{63,6-49,2}{7,2}=2]$

$[U_8=frac{70,8-49,2}{7,2}=3]$

$[U_9=frac{78-49,2}{7,2}=4]$

N п/п	Середины интервалов, $x_{i}^{*}$	Частоты интервалов,	Условные варианты,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,	Произведения частот и условных вариант,
1	20,4	1	-4	-4	16	-64	256	9	81
2	27,6	9	-3	-27	81	-243	729	36	144
3	34,8	13	-2	-26	52	-104	208	13	13
4	42	17	-1	-17	17	-17	17	0	0
5	49,2	23	0	0	0	0	0	23	23
6	56,4	18	1	18	18	18	18	72	288
7	63,6	11	2	22	44	88	176	99	891
8	70,8	7	3	21	63	189	567	112	1792
9	78	1	4	4	16	64	256	25	625

Контроль:

$[sum n_i U_i^2 + 2sum n_iU_i+n=sum n_i{(U_i+1)}^2]$

$[sum n_i{(U_i+1)}^2=389]$

Контроль:

$[sum n_i U_i^4 + 4sum n_iU_i^3+6sum n_iU_i^2+4sum n_iU_i+n=sum n_i{(U_i+1)}^4]$

$[sum n_i{(U_i+1)}^4=3857]$

Равенство выполнено, следовательно вычисления произведены верно.

Вычислим условные моменты 1-го, 2-го, 3-го и 4-го порядков:

$[M_1^{*}=frac{sum n_iU_i}{n}=frac{-9}{100}=-0,09;]$

$[M_2^{*}=frac{sum n_iU_i^2}{n}=frac{307}{100}=3,07;]$

$[M_3^{*}=frac{sum n_iU_i^3}{n}=frac{-69}{100}=-0,69;]$

$[M_4^{*}=frac{sum n_iU_i^4}{n}=frac{2227}{100}=22,27.]$

Найдем выборочные среднюю, дисперсию и среднее квадратическое отклонение :

$[x_{B}=M_1^{*}cdot h+C=-0,09cdot 7,2+49,2=48,552;]$

$[D_{B}=(M_2^{*}-{(M_1^{*})}^2)h^2=(3,07-{(-0,09)}^2){7,2}^2approx 158,73.]$

$[sigma_{B}=sqrt{D_B}=sqrt{158,73}=12,6.]$

Также для оценки отклонения эмпирического распределения от нормального используют такие характеристики, как асимметрия и эксцесс.

Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:

$[a_s=frac{m_3}{sigma_B^3}]$

Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева — отрицательна.

Эксцесс эмпирического распределения определяется равенством:

$[e_k=frac{m_4}{sigma_B^4}-3]$

где — центральный эмпирический момент четвертого порядка.

Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.

Вычисляем центральные эмпирические моменты третьего и четвертого порядков:

$[m_3=(M_3^*-3M_1^*M_2^*+2{(M_1^*)}^3)cdot h^3=51,3;]$

$[m_4=(M_4^*-4M_3^*M_1^*+6M_2^*{(M_1^*)}^2-3{(M_1^*)}^4)cdot h^4=59580,97;]$

Найдем асимметрию и эксцесс:

$[a_s=frac{51,3}{{12,6}^3}=0,026]$

$[e_k=frac{59580,97}{{12,6}^4}-3=-0,635]$

IV. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.

Проверим генеральную совокупность значений размера прибыли банков по критерию Пирсона

Правило. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу : генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:

$[chi^2_{nabl}=sum frac{ {(n_i-n_i^{'})}^2}{n_i^{'}}]$

и по таблице критических точек распределения , по заданному уровню значимости и числу степеней свободы найти критическую точку $chi^2_{kp}(alpha;k)$ , где s — количество интервалов.

Если $chi^2_{nabl}<chi^2_{kp}$ — нет оснований отвергнуть нулевую гипотезу.

Если $chi^2_{nabl}>chi^2_{kp}$ — нулевую гипотезу отвергают.

Найдем теоретические частоты , для этого составим следующую таблицу.

Середины интервалов, $x_{i}^{*}$	Частоты интервалов,	Произведем расчет, $x_{i}^{*}-x_B$	Произведем расчет, $V_i=frac{(x_{i}^{*}-x_B)}{sigma_B}$	Значения функции Гаусса,	Произведем расчет, $frac{nh}{sigma_B}$	Теоретические частоты, $n_i^{'}=57 cdotvarphi(V_i)$
20,4	1	-28,152	-2,23	0,0332	57	2
27,6	9	-20,952	-1,66	0,1006	57	6
34,8	13	-13,752	-1,09	0,2203	57	13
42	17	-6,552	-0,52	0,3485	57	20
49,2	23	0,648	0,05	0,3984	57	23
56,4	18	7,848	0,62	0,3292	57	19
63,6	11	15,048	1,19	0,1965	57	11
70,8	7	22,248	1,77	0,0833	57	5
78	1	29,448	2,34	0,0258	57	1
						$sum n_i^{'}=100$

Вычислим $chi^2_{nabl}$ , для чего составим расчетную таблицу.

		$n_i^{'}$	$n_i-n_i^{'}$	${(n_i-n_i^{'})}^2$	$frac{{(n_i-n_i^{'})}^2}{n_i^'}$		$frac{n_i^2}{n_i^{'}}$
1	1	2	-1	1	0,5	1	0,5
2	9	6	3	9	1,5	81	13,5
3	13	13	0	0	0	169	13
4	17	20	-3	9	0,45	289	14,45
5	23	23	0	0	0	529	23
6	18	19	-1	1	0,05	324	17,05
7	11	11	0	0	0	121	11
8	7	5	2	4	0,8	49	9,8
9	1	1	0	0	0	1	1
	100	100			Наблюдаемое значение критерия, $chi^2_{nabl}=3,30$		103,30

Контроль:

$[sumfrac{n_i^2}{n_i^{'}}-n=sum frac{{(n_i-n_i^{'})}^2}{n_i^'}]$

$[sumfrac{n_i^2}{n_i'}-n=103,3-100=3,3]$

$[sum frac{{(n_i-n_i')}^2}{n_i'}=3,3]$

Вычисления произведены правильно.

Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) s=9;

По таблице критических точек распределения по уровню значимости и числу степеней свободы k=6 находим $chi^2_{kp}(0,025;6)=14,4.$

Так как $chi^2_{nabl}<chi^2_{kp}$ — нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.

На рисунке построены нормальная (теоретическая) кривая по теоретическим частотам (зеленый график) и полигон наблюдаемых частот (коричневый график). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.

V. Интервальные оценки.

Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.

Интервальной оценкой (с надежностью ) математического ожидания (а) нормально распределенного количественного признака Х по выборочной средней при известном среднем квадратическом отклонении sigma генеральной совокупности служит доверительный интервал

$[x_B-frac{tsigma}{sqrt{n}}<a<x_B+frac{tsigma}{sqrt{n}},]$

где $frac{tsigma}{sqrt{n}}=delta$ — точность оценки, n — объем выборки, t — значение аргумента функции Лапласа (см. приложение 2), при котором $phi(t)=frac{gamma}{2}$ ;

при неизвестном среднем квадратическом отклонении sigma (и объеме выборки n<30)

$[x_B-frac{t_{gamma}cdot S}{sqrt{n}}<a<x_B+frac{t_{gamma}cdot S}{sqrt{n}},]$

$[S=sqrt{frac{n}{n-1}D_B}]$

где S — исправленное выборочное среднее квадратическое отклонение, $t_{gamma}$ находят по таблице приложения по заданным n и .

В нашем примере среднее квадратическое отклонение известно, . А также , , . Поэтому для поиска доверительного интервала используем первую формулу:

$[x_B-frac{tsigma}{sqrt{n}}<a<x_B+frac{tsigma}{sqrt{n}}]$

Все величины, кроме t, известны. Найдем t из соотношения $phi(t)=frac{0,95}{2}=0,475.$ По таблице приложения находим t=1,96. Подставив t=1,96, , , в формулу, окончательно получим искомый доверительный интервал:

$[48,55-frac{1,96cdot 12,6}{10}<a<48,55+frac{1,96cdot 12,6}{10}]$

Интервальной оценкой (с надежностью ) среднего квадратического отклонения нормально распределенного количественного признака Х по «исправленному» выборочному среднему квадратическому отклонению S служит доверительный интервал

(при q<1), (*)

(при q>1),

где q — находят по таблице приложения по заданным n и .

По данным и n=100 по таблице приложения 4 найдем q=0,143. Так как q<1, то, подставив $S=sqrt{frac{n}{n-1}D_B}=sqrt{frac{100}{99}cdot 158,73}approx 12,66, quad quad q=0,143$ в соотношение (*), получим доверительный интервал:

Источник

Комментарий
1.4: При
построении интервального вариационного
ряда в качестве частот используют как
числа значений варианты n_i,
так и относительные ча-

стоты
ν_i
= n_i/n,
причём относительные величины обычно
употребляются при больших объёмах
выборок n.
В данном случае n
= 100 – выборка
достаточно большого объёма; будем
пользоваться относительными частотами.

Порядок построения
интервального вариационного ряда таков:

1.
Определим размах
вариаций значения признака

R
= x_max
– x_min
= 14,51 – 12,01 ≈
14,6 – 12,0 = 2,6 –

Комментарий
1.5: Граничнае
значения признака обычно округляют и
подправляют так, чтобы все выборочные
значения лежали внутри интервала R.

2.
Определим число
частичных интервалов:
если обозначить k
– число этих
интервалов, то, при объёме выборки n,
хорошее приближение для числа k
можно найти
по формуле

k
= [2 ln(n)],

где
[…] означает целую часть числа. В данном
случае получаем k
= 9

Комментарий
1.6: Ширина
h_i
i–го
частичного интервала выбирается
достаточно произвольно. Обычно это
определяется структурой вариационного
ряда. Во многих случаях эта структура
не проявляется и у нас нет никаких других
априорных данных. В таком случае
естественным является выбор одинаковой
ширины всех интервалов (поправки в
дальнейшем – возмржны).

Поправим,
в соответствии с комментарием 4, границы
интервала R,
чтобы было
удобно делить его на
9 одинаковых
интервала:

R
=14,7 – 12,0 =
2,7; 
i
h_i
= R/k
= 0,3.

3.
Определим границы
частичных интервалов: [12,0;12,3); [12,3;12,6);
[12,6;12,9); [12.9;13,2); [13,2;13,5); [13,5;13,8); [13,8;14,1);
[14,1;14,4); [14,4;14,7].

4.
Составим таблицу 3 для интервального
вариационногоряда.

Интервал	12,0-12,3	12,3-12,6	12,6-12,9	12,9-13,2	13,2-13,5	13,5-13,8	13.8-14,1	14,1-144	14,4-14,7
Середина интервала x_i	12,15	12,45	12,75	13,05	13,35	13,65	13,95	14,25	14,55
Частота n_i	2	6	8	10	35	21	9	7	2
Относитель ноя частота ν_i	0,02	0,06	0,08	0,1	0,35	0,21	0,09	0,07	0,02
Накоплен- ные частоты	0,02	0,08	0,16	0,26	0,61	0,82	0,91	0,98	1

Замечание:
как обычно
– начало интервала включается,
а конец – не включается в интервал
(исключая последний)

3. Эмпирическая функция распределения и графическое преставление распеделения частот

Эмпирической
(статистической)
функцией
распределения
назывыется функция F
^*(x),
равная относительной частоте события
X
< x:

где
n_x
– число вариант, меньших x;
n
– объём выборки.

Для нахождения
эмпирической функции распределения
воспользуемся формулой

Значениями
эмпирической функции распределения
являются, таким образом, накопленные
частоты, поэтому используем четвёртую
строку таблицы 3:

Изобразим
функцию F^*(x)
графически (рис. 1): вдоль оси абсцисс x
откладываем значения середин частичных
интервалов; вдоль оси ординат – накопленные
частоты.

На
этом же рисунке построим кумулянту
– график
накопленных частот; в данном случае это
ломанная линия, состоящая из отрезков
прямых, соединяющих точки с координатами
(x_i,
Σν_i).
Кумулянта является довольно хорошим
приближением графика функции распределения
непрерывной случайной величины X.

Комментарий
1.7: График
кумулянты точно совпадает с графиком
функции

распределения,
если все значения варианты в каждом
интервале, как и вся генральная
совокупность, распределены равномерно.

F^*(x)

1,0

0,98

0,92

0,82

0,61

0,26

0,16

0,08

0,02

12,15 12,45 12,75 13,05 13,35 13,65 13,95 14,25 14,55x

Рис.
1

Существует
два общих метода графического представления
частот: гистограмма
и
полигон распределения.

Полигон
распределеня
строят из отрезков, соединяющих точки,
координатами которых являюься значения
признака x_i
(середины частичных интервалов) и
соответствующие им частоты n_i
или относительные частоты n_i/n.

Гистограмма
– это последовательность столбцов,
каждый из которых опирается на один
частичный интервал, а высота его равна
частоте (или относительной частоте) в
этом интервале.

Оба
графика являются выборочным аналогом
плотности распределения непрерывной
случайной величины и обычно изображают
лишь один из них. Но здесь, в порядке
исключения, изобразим оба: рис.2 и рис.
3.

Комментарий
1.7: Следует
обратить внимание на то, что
суммарная площадь под гистограммой
всегда равна единице

ν_i
= n_i/n

0,35

0,21

0,10

0,09

0,08

0,07

0,06

0,02

12,15 12,45 12,75 13,05 13,35 13,65 13,95 14,25 14,55

Рис. 2 Полигон распределения

ν_i
= n_i/n

0,35

0,21

0,10

0,09

0,08

0,07

0,06

0,02

12,0 12,3 12,6 12,9 13,2 13,5 13,8 14,1 14,4 14,7 x

Рис. 3. Гистограмма

Источник

Методические
рекомендации к проведению урока

Тема
урока:
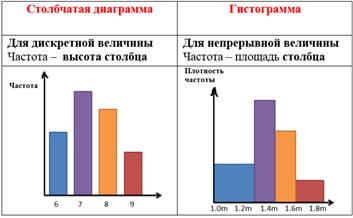
Интервальная таблица
частот. Гистограмма

Тип
урока: урок
закрепления знаний

Цели
обучения:

8.3.3.2

представлять
данные интервальной таблицы частот в виде гистограммы частот;

Цели
урока:

Учащиеся по данным
интервальной таблицы строят гистограмму, и наоборот, по гистограмме заполняют
интервальную таблицу частот.

Структура урока

1. Организационный
момент. Целеполагание.

2.
Повторение.

3.
Построение таблицы по гистограмме.

4.
Закрепление изученного материала.

5.
Подведение итогов урока. Рефлексия.

Теоретический
материал к уроку, определения к понятиям и др.

Частота
есть площадь столбца (прямоугольника), ось абсцисс – плотность частоты. Так как
площадь прямоугольника равна произведению его ширины и длины, то получим
формулу:

Частота=
длина интервала ´ плотность частоты.

Далее учитель совместно с учащимися подводит итоги о
гистограмме.

Гистограмма
применяется для изображения данных, представленных в виде интервального ряда.
Для построения гистограммы с одинаковыми интервалами на оси абсцисс отмечается
значение переменной, а на оси ординат можно взять абсолютную или относительную
частоту, а при построении гистограммы с различными интервалами на оси ординат
берется плотность частоты, а частота будет площадью столбца.

Учащимся демонстрируются отличия столбчатая диаграммы
и гистограммы.

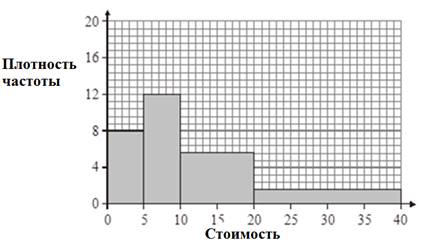
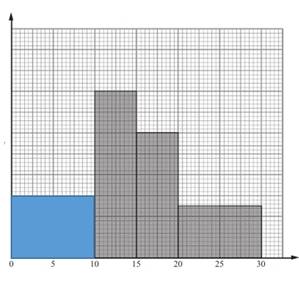
Пример 1. На гистограмме показана информация о количестве проданных
книг в определенном магазине в субботний день:

Заполните таблицу, используя гистограмму:

Стоимость (в тысячах тенге)	Частота
0 < P 5
5 < P 10
10 < P 20
20 < P 40

Решение: Частота – площадь прямоугольника, поэтому для ее нахождения
необходимо перемножить его ширину и высоту, например, площадь 1-го столбца
(частота) равна 8*5=40.

Стоимость (в тысячах тенге)	Частота
0 < P £ 5	40
5 < P £ 10	60
10 < P £ 20	56
20 < P £ 40	32

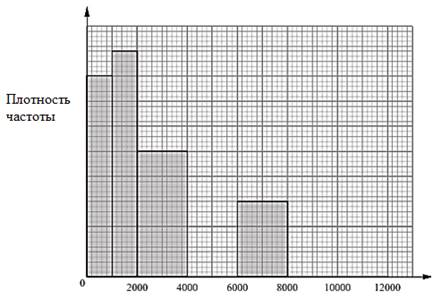
Пример
2.

Частично
заполненная таблица и частично построенная гистограмма показывают вес различных
машин.

а) Используя информацию, данную на
гистограмме, дополните таблицу.

вес (w) кг	частота
	16


	14

	4

b) Используя информацию в таблице, достройте
гистограмму.

При выполнении
таких заданий, необходимо обращать внимание прежде всего на интервалы.
Например, в указанном примере для интервала имеется
информация и в таблице, и в гистограмме. Частота – 16, длина интервала – 1000,
тогда плотность частоты равна 16/1000=0,016. После нахождения высоты столбца
(0,016), можно определить масштаб оси плотности частоты. Значение 0,016 равно
40 клеткам по вертикали, то есть одна клетка по вертикали – это 0,0004. Тогда
если высота столбца равна 50 клеткам, то
соответствующая плотность частоты равна 0,0004*50=0,02. А частота 0,02*1000=20
и т.д.

Инструкции
к демонстрациям и технике безопасности.

Демонстрация материала осуществляется с
помощью презентации PowerPoint. Слайды презентации содержат
анимации, которые позволяют поэтапно вывести на экран решения и ответы к
предложенным заданиям. Поэтому при показе презентации следует делать паузы
после демонстрации заданий и постановки вопросов, давая учащимся время на их выполнение
и обдумывание ответов.

Дополнительные
методические рекомендации по организации урока.

Структура и организация урока нацелены на
продуктивную деятельность учащихся, не допуская пассивного восприятия материала.
В связи с этим учителю необходимо задавать учащимся вопросы высокого порядка,
наталкивая их на «открытие» и освоение нового материала, при этом выдерживая
паузы, необходимые для обдумывания.

Дополнительные
разноуровневые (на дифференциацию) задания.

Базовый уровень

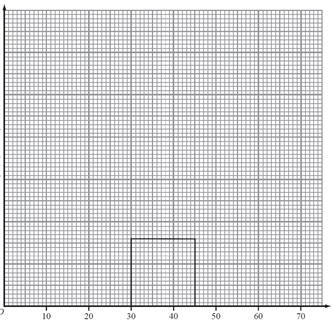
№1. В
соревнованиях по футболу между различными командами было забито 185 голов. В
таблице показана информация о временных интервалах забитых голов.

Временной интервал (в минутах)	Кол-во забитых голов
	9
	21
	46
	75
	34

а)
Гистограмма должна отображать заданную информацию. Известно, что для интервала его плотность частоты равна 3,0. Дополните
гистограмму.

Плотность

частоты

b) Найдите количество
голов, забитых в первые 20 минут игры.

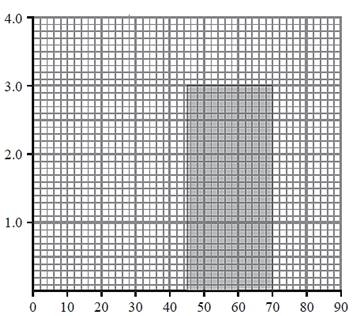
Продвинутый уровень

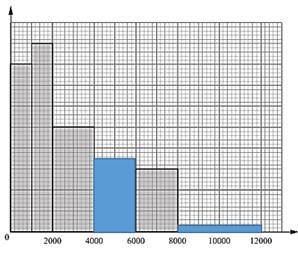
№2.
На определенном участке дороги на скорость автомобиля установлено ограничение
45 км/ч. В ходе наблюдения на данном участке дороги фиксировалась скорость 100 автомобилей.
Информация об этих скоростях представлена в таблице.

Зафиксированная скорость

(х, км/ч)

Кол-во автомобилей

а) дополните гистограмму.

Плотность

частоты

Скорость (х, км/ч)

b) Найдите количество автомобилей,
которые превысили установленное ограничение скорости.

Рекомендации
по формативному оцениванию.

Формативное оценивание производится
на каждом этапе урока (самооценивание, оценивание учителем по критериям). Оценка
путем наблюдения за вовлечением учеников в работу при выполнении заданий и за участием
в диалогах. Прогресс, ответную реакцию на задания в парах, в группах необходимо
отслеживать для того, чтобы оценить вклад каждого ученика и выявить наличие
ошибок для их дальнейшей коррекции.

Ответы,
критерии к заданиям, дополнительные материалы к уроку.

Ответы к заданиям будут полезны для
организации самооценивания или взаимооценивания учащихся.

Ответы к приложению 1.

1-ошибка:
между столбцами не должно быть зазоров;

2-ошибка:
не верно определены границы интервалов, верно вот так: [4,5; 9,5), [9,5;12,5),
[12,5;15,5), [15,5;18,5), [18,5;28,5), так как высота берез – непрерывная
величина. Если интервал 5-9 м взят с округлением, то на самом деле он равен
[4,5;9,5).

3-ошибка: Так как эти
интервалы различны по длине, то по оси ортинат должны рассматриваться не
частоты, а плотности частот.

Ответы к приложению 2.

№1.

Стоимость (в тысячах тенге)	Частота
0 < P £ 5	40
5 < P £ 10	60
10 < P £ 20	56
20 < P £ 40	32

№2.

Вес (w) кг	Частота
	16
	20
	20
	14
	12
	4

Ответы к приложению 3.

№1. Частота=8; длина интервала
= 5

Плотность частоты = 8:5=1,6

Масштаб оси плотности частоты = 1,6:40=0,04 (1 единица)

Частота интервала равна 6. Плотность
частоты = 6:10=0,6

0,6:0,04=15 единиц.

№2.

№3. 46,075

№4. a) – частота 19; – частота 24. b) 0,42

№5. b)

Критерии оценивания к каждому блоку заданий
прописаны в приложениях к уроку, а также указаны в краткосрочном плане.

Список полезных ссылок и литературы.

Мордкович А.Г., Семенов В.П. События,
Вероятности. Статическая обработка данных. Дополнительные параграфы к курсу
алгебры 7–9 классов общеобразовательных учреждений. – М.: Мнемозима, 2009.

Ткачева М.Ф., Федорова Н.Е. Элементы статистики и
вероятность. Учебное пособие для 7–9 классов общеобразовательных учреждений. –
М.: Просвещение, 2007.

Бродский Я.С. Статистика. Вероятность.
Комбинаторика. – М.: ООО «Издательство Оникс»; ООО «Издательство «Мир и
Образование», 2008.

Макарычев Ю. Н.Алгебра : элементы
статистики и теории вероятностей : учеб. пособие для учащихся 7—9 кл.
общеоб–разоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк; под ред. С. А.
Теляковского.— 3–е изд.— М. : Просвещение, 2005.

http://5klass.net/algebra–9–klass/Osnovy–statistiki/020–Poligon–raspredelenija–dannykh.html

http://x–uni.com/matematika/7klass/uchebniki/sobitiya–veroyatnosti–statisticheskaya–obrabotka–dannih–aalgebra–7–9–klass–mordkovich–a–g–semenov–p–v–2008

http://videouroki.net/filecom.php?fileid=98704116

Скачано с www.znanio.ru

Источник

3. Эмпирическая функция распределения и графическое преставление распеделения частот

Вам также может понравиться

Как составить резюме на работу образец бланк фото

Как найти xor двух чисел

Как исправить вмятины на кроссовках

Добавить комментарий Отменить ответ