Точечный прогноз
заключается в получении прогнозного
значения уp,
которое определяется путем подстановки
в уравнение регрессии соответствующего
(прогнозного) значения xp:
уp = a + b* xp
Интервальный
прогноз
заключается в построении доверительного
интервала прогноза, т. е. нижней и верхней
границ уpmin,
уpmax интервала,
содержащего точную величину для
прогнозного значения yp
(ypmin < yp <
ypmin) с заданной
вероятностью.
При построении
доверительного интервала прогноза
используется стандартная
ошибка прогноза:
 ,
,
где
![]()
Строится доверительный
интервал прогноза:
![]()
Множественный регрессионный анализ
(слайд
1)
Множественная регрессия применяется
в ситуациях, когда из множества факторов,
влияющих на результативный признак,
нельзя выделить один доминирующий
фактор и необходимо учитывать влияние
нескольких факторов. Например, объем
выпуска продукции определяется величиной
основных и оборотных средств, численностью
персонала, уровнем менеджмента и т. д.,
уровень спроса зависит не только от
цены, но и от имеющихся у населения
денежных средств.
Основная цель
множественной регрессии – построить
модель с несколькими факторами и
определить при этом влияние каждого
фактора в отдельности, а также их
совместное воздействие на изучаемый
показатель.
Таким образом,
множественная регрессия – это уравнение
связи с несколькими независимыми
переменными:
![]()
(слайд
2)
Построение уравнения множественной
регрессии
1. Постановка задачи
По имеющимся данным
n наблюдений
(табл. 3.1) за совместным изменением p+1
параметра y
и xj и
((yi,xj,i);
j=1,
2, …, p;
i=1,
2, …, n)
необходимо определить аналитическую
зависимость ŷ
= f(x1,x2,…,xp),
наилучшим образом описывающую данные
наблюдений.
Таблица 3.1
Данные наблюдений
|
y |
х1 |
х2 |
… |
хр |
|
|
1 |
y1 |
x11 |
х21 |
… |
xp1 |
|
2 |
y2 |
х12 |
х22 |
… |
xp2 |
|
… |
… |
… |
… |
… |
… |
|
n |
yn |
х1n |
x2n |
… |
xpn |
Каждая строка
таблицы представляет собой результат
одного наблюдения. Наблюдения различаются
условиями их проведения.
Вопрос о том, какую
зависимость следует считать наилучшей,
решается на основе какого-либо критерия.
В качестве такого критерия обычно
используется минимум суммы квадратов
отклонений расчетных значений
результативного показателя ŷi
от наблюдаемых
значений yi:
![]()
2. Спецификация модели
(слайд
3)
Спецификация модели включает в себя
решение двух задач:
– отбор факторов,
подлежащих включению в модель;
– выбор формы
уравнения регрессии.
2.1. Отбор факторов при построении множественной регрессии
Включение в
уравнение множественной регрессии того
или иного набора факторов связано прежде
всего с представлениями исследователя
о природе взаимосвязи моделируемого
показателя с другими экономическими
явлениями.
К факторам,
включаемым в модель, предъявляются
следующие требования:
1. Факторы должны
быть количественно измеримы.
Включение фактора в модель должно
приводить к существенному увеличению
доли объясненной части в общей вариации
зависимой переменной. Поскольку данная
величина характеризуется коэффициентом
детерминации,
включение нового фактора в модель должно
приводить к заметному изменению
коэффициента. Если этого не происходит,
то включаемый в анализ фактор не улучшает
модель и является лишним.
Например, если для
регрессии, включающей 5 факторов,
коэффициент детерминации составил
0,85, и включение шестого фактора дало
коэффициент детерминации 0,86, то вряд
ли целесообразно дополнять модель этим
фактором.
Если необходимо
включить в модель качественный фактор,
не имеющий количественной оценки, то
нужно придать ему количественную
определенность. В этом случае в модель
включается соответствующая ему
«фиктивная»
переменная,
имеющая конечное количество формально
численных значений, соответствующих
градациям качественного фактора (балл,
ранг).
Например, если
нужно учесть влияние уровня образования
(на размер заработной платы), то в
уравнение регрессии можно включить
переменную, принимающую значения: 0 –
при начальном образовании, 1 – при
среднем, 2 – при высшем.
Несмотря на то,
что теоретически регрессионная модель
позволяет учесть любое количество
факторов, на практике в этом нет
необходимости, т.к. неоправданное их
увеличение приводит к затруднениям в
интерпретации модели и снижению
достоверности результатов.
2. Факторы не
должны быть взаимно коррелированы
и, тем более, находиться в точной
функциональной связи. Наличие высокой
степени коррелированности между
факторами может привести к неустойчивости
и ненадежности оценок коэффициентов
регрессии, а также к невозможности
выделить изолированное влияние факторов
на результативный показатель. В результате
параметры регрессии оказываются
неинтерпретируемыми.
Пример.
Рассмотрим регрессию себестоимости
единицы продукции (у)
от заработной платы работника (х)
и производительности труда в час (z).
![]()
Коэффициент
регрессии при переменной z
показывает, что с ростом производительности
труда на 1 ед-цу в час себестоимость
единицы продукции снижается в среднем
на 10 руб. при постоянном уровне оплаты
труда.
А параметр при х
нельзя интерпретировать как снижение
себестоимости единицы продукции за
счет роста заработной платы. Отрицательное
значение коэффициента регрессии в
данном случае обусловлено высокой
корреляцией между х
и z
(0,95).
(слайд
4)
Считается, что две переменные явно
коллинеарны,
т.е. находятся между собой в линейной
зависимости, если коэффициент
интеркорреляции
(корреляции между двумя объясняющими
переменными) ≥ 0,7. Если факторы явно
коллинеарны, то они дублируют друг друга
и один из них рекомендуется исключить
из уравнения. Предпочтение при этом
отдается не тому фактору, который более
тесно связан с результатом, а тому,
который при достаточно тесной связи с
результатом имеет наименьшую тесноту
связи с другими факторами.
В этом требовании
проявляется специфика множественной
регрессии как метода исследования
комплексного воздействия факторов в
условиях их независимости друг от друга.
Наряду с парной
коллинеарностью может иметь место
линейная зависимость между более чем
двумя переменными – мультиколлинеарность,
т.е. совокупное воздействие факторов
друг на друга.
Наличие
мультиколлинеарности факторов может
означать, что некоторые факторы всегда
будут действовать в унисон. В результате
вариация в исходных данных перестанет
быть полностью независимой, что не
позволит оценить воздействие каждого
фактора в отдельности. Чем сильнее
мультиколлинеарность факторов, тем
менее надежна оценка распределения
суммы объясненной вариации по отдельным
факторам с помощью МНК.
(слайд
5) Включение
в модель мультиколлинеарных факторов
нежелательно по следующим причинам:
-
затрудняется
интерпретация параметров множественной
регрессии; параметры линейной регрессии
теряют экономический смысл; -
оценки параметров
не надежны, имеют большие стандартные
ошибки и меняются с изменением количества
наблюдений (не только по величине, но
и по знаку), что делает модель непригодной
для анализа и прогнозирования.
(слайд
6) Для
оценки мультиколлинеарности используется
определитель
матрицы парных коэффициентов
интеркорреляции:
(!)
Если факторы не коррелируют между собой,
то матрица коэффициентов интеркорреляции
является единичной, поскольку в этом
случае все недиагональные элементы
равны 0. Например, для уравнения с тремя
переменными
![]() матрица коэффициентов интеркорреляции
матрица коэффициентов интеркорреляции
имела бы определитель, равный 1, поскольку![]() и
и![]() .
.

(слайд
7)
(!)
Если между факторами существует полная
линейная зависимость
и все коэффициенты корреляции равны 1,
то определитель такой матрицы равен 0
(Если
две строки матрицы совпадают, то её
определитель равен нулю).

Чем ближе к 0
определитель матрицы коэффициентов
интеркорреляции, тем сильнее
мультиколлинеарность и ненадежнее
результаты множественной регрессии.
Чем ближе к 1
определитель
матрицы коэффициентов интеркорреляции,
тем меньше мультиколлинеарность
факторов.
(слайд
8)
Способы
преодоления мультиколлинеарности
факторов:
1)
исключение из модели одного или нескольких
факторов;
2)
переход к совмещенным уравнениям
регрессии, т.е. к уравнениям, которые
отражают не только влияние факторов,
но и их взаимодействие. Например, если
![]() ,
,
то можно построить следующее совмещенное
уравнение:![]() ;
;
3)
переход к уравнениям приведенной формы
(в уравнение регрессии подставляется
рассматриваемый фактор, выраженный из
другого уравнения).
(слайд
9)
2.2. Выбор формы уравнения регрессии
Различают следующие
виды уравнений
множественной регрессии:
-
линейные,
-
нелинейные,
сводящиеся к линейным, -
нелинейные, не
сводящиеся к линейным (внутренне
нелинейные).
В первых двух
случаях для оценки параметров модели
применяются методы классического
линейного регрессионного анализа. В
случае внутренне нелинейных уравнений
для оценки параметров применяются
методы нелинейной оптимизации.
Основное требование,
предъявляемое к уравнениям регрессии,
заключается в наличии наглядной
экономической интерпретации модели и
ее параметров. Исходя из этих соображений,
наиболее часто используются линейная
и степенная зависимости.
Линейная
множественная регрессия имеет вид:
![]()
Параметры bi
при факторах хi
называются коэффициентами
«чистой» регрессии.
Они показывают, на сколько единиц в
среднем изменится результативный
признак за счет изменения соответствующего
фактора на единицу при неизмененном
значении других факторов, закрепленных
на среднем уровне.
(слайд
10)
Например, зависимость спроса на товар
(Qd) от цены (P) и дохода (I) характеризуется
следующим уравнением:
Qd = 2,5 – 0,12P + 0,23 I.
Коэффициенты
данного уравнения говорят о том, что
при увеличении цены на единицу, спрос
уменьшится в среднем на 0,12 единиц, а при
увеличении дохода на единицу, спрос
возрастет в среднем 0,23 единицы.
Параметр а
не всегда может быть содержательно
проинтерпретирован.
Степенная
множественная регрессия имеет вид:
![]()
Параметры bj
(степени факторов хi)
являются коэффициентами эластичности.
Они показывают, на сколько % в среднем
изменится результативный признак за
счет изменения соответствующего фактора
на 1% при неизмененном значении остальных
факторов.
Наиболее широкое
применение этот вид уравнения регрессии
получил в производственных функциях,
а также при исследовании спроса и
потребления.
Например, зависимость
выпуска продукции Y от затрат капитала
K и труда L:
![]() говорит
говорит
о том, что увеличение затрат капитала
K на 1% при неизменных затратах труда
вызывает увеличение выпуска продукции
Y на 0,23%. Увеличение затрат труда L на 1%
при неизменных затратах капитала K
вызывает увеличение выпуска продукции
Y на 0,81 %.
Возможны и другие
линеаризуемые функции для построения
уравнения множественной регрессии:
-
экспонента
 ;
; -
гипербола
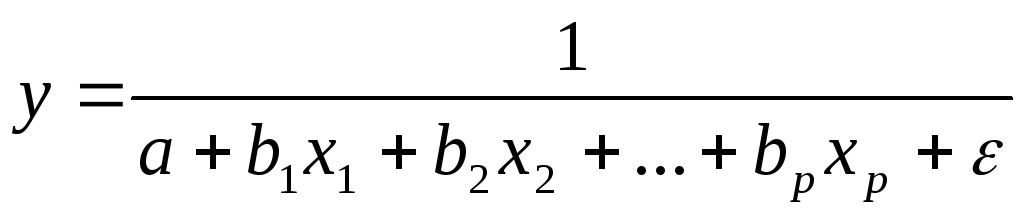 .
.
Чем сложнее функция,
тем менее интерпретируемы ее параметры.
Кроме того, необходимо помнить о
соотношении между количеством наблюдений
и количеством факторов в модели. Так,
для анализа трехфакторной модели должно
быть проведено не менее 21 наблюдения.
(слайд
11) 3.
Оценка параметров модели
Параметры уравнения
множественной регрессии оцениваются,
как и в парной регрессии, методом
наименьших квадратов,
согласно которому следует выбирать
такие значения
параметров а
и bi,
при которых сумма квадратов отклонений
фактических значений результативного
признака yi
от теоретических
значений ŷ
минимальна,
т. е.:
![]()
Если
![]() ,
,
тогдаS
является функцией неизвестных параметров
a,
bi:
![]()
Чтобы найти минимум
функции, нужно найти частные производные
по каждому из параметров и приравнять
их к 0:

Отсюда получаем
систему уравнений:

(слайд
12) Ее
решение может быть осуществлено методом
определителей:
![]() ,
,
где ∆
– определитель системы;
∆a,
∆b1,
∆bp
– частные определители (∆j).
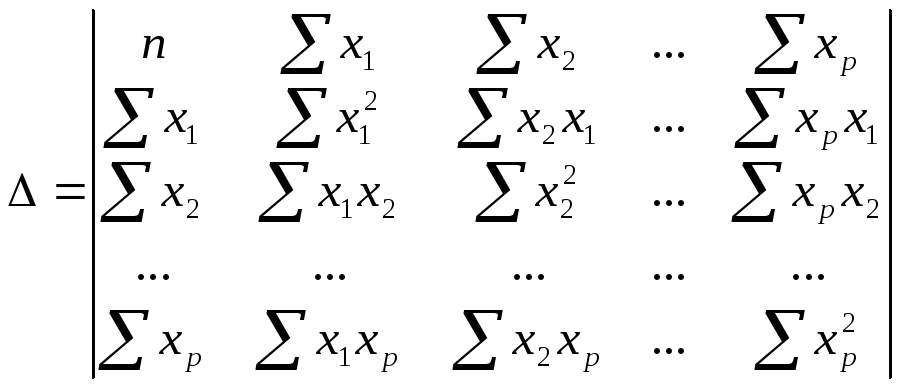 –определитель
–определитель
системы,
∆j
– частные
определители, которые получаются из
основного определителя путем замены
j-го столбца на столбец свободных членов
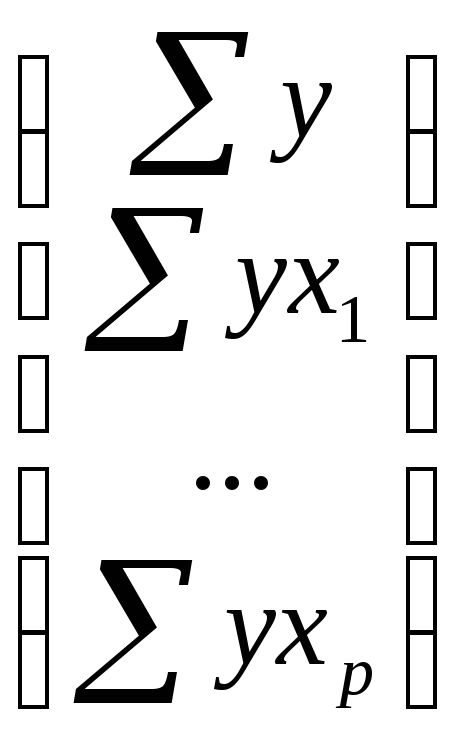 .
.
При использовании
данного метода возможно возникновение
следующих ситуаций:
1) если основной
определитель системы Δ равен
нулю и все определители Δj
также равны
нулю, то данная система имеет бесконечное
множество решений;
2) если основной
определитель системы Δ равен
нулю и хотя бы один из определителей Δj
также равен
нулю, то система решений не имеет.
(слайд
13) Помимо
классического МНК для определения
неизвестных параметров линейной модели
множественной регрессии используется
метод оценки параметров через
β-коэффициенты
– стандартизованные коэффициенты
регрессии.
Построение
модели множественной регрессии в
стандартизированном, или нормированном,
масштабе
означает, что все переменные, включенные
в модель регрессии, стандартизируются
с помощью специальных формул.
Уравнение
регрессии
в стандартизованном масштабе:
![]() ,
,
где
 ,
, – стандартизованные переменные;
– стандартизованные переменные;
![]() – стандартизованные
– стандартизованные
коэффициенты регрессии.
Т.е. посредством
процесса стандартизации точкой отсчета
для каждой нормированной переменной
устанавливается ее среднее значение
по выборочной совокупности. При этом в
качестве единицы измерения
стандартизированной переменной
принимается ее среднеквадратическое
отклонение σ.
β-коэффициенты
показывают,
на сколько сигм (средних квадратических
отклонений) изменится в среднем результат
за счет изменения соответствующего
фактора xi
на одну сигму при неизменном среднем
уровне других факторов.
Стандартизованные
коэффициенты регрессии βi
сравнимы
между собой, что позволяет ранжировать
факторы по силе их воздействия на
результат. Большее относительное влияние
на изменение результативной переменной
y оказывает
тот фактор, которому соответствует
большее по модулю значение коэффициента
βi.
В этом основное
достоинство стандартизованных
коэффициентов регрессии,
в отличие от коэффициентов «чистой»
регрессии, которые не сравнимы между
собой.
(слайд
14)
Связь коэффициентов «чистой» регрессии
bi
с коэффициентами βi
описывается соотношением:
 ,
,
или
![]()
Параметр a
определяется как
![]() .
.
Коэффициенты
β определяются при помощи
МНК
из следующей системы уравнений
методом определителей:

Для оценки параметров
нелинейных
уравнений множественной регрессии
предварительно осуществляется
преобразование последних в линейную
форму (с помощью замены переменных) и
МНК применяется для нахождения параметров
линейного уравнения множественной
регрессии в преобразованных переменных.
В случае внутренне
нелинейных
зависимостей для оценки параметров
приходится применять методы нелинейной
оптимизации.
(слайд
1) 4.
Проверка качества уравнения регрессии
Практическая
значимость уравнения множественной
регрессии оценивается с помощью
показателя множественной корреляции
и его квадрата – коэффициента детерминации.
Показатель
множественной корреляции
характеризует тесноту связи рассматриваемого
набора факторов с исследуемым признаком,
т.е. оценивает тесноту совместного
влияния факторов на результат.
Независимо от
формы связи показатель
множественной корреляции
рассчитывается по формуле:

Коэффициент
множественной корреляции принимает
значения в диапазоне 0 ≤ R
≤ 1. Чем ближе
он к 1, тем теснее связь результативного
признака со всем набором исследуемых
факторов.
При линейной
зависимости признаков формулу индекса
множественной корреляции можно записать
в виде:
![]() ,
,
где
![]() –
–
стандартизованные коэффициенты
регрессии,
![]() –
–
парные коэффициенты корреляции результата
с каждым фактором.
Данная формула
получила название линейного
коэффициента множественной корреляции,
или совокупного
коэффициента корреляции.
Индекс детерминации
для нелинейных по оцениваемым параметрам
функций принято называть «квази-![]() ».Для его
».Для его
определения по функциям, использующим
логарифмические преобразования
(степенная, экспонента), необходимо
сначала найти теоретические значения
ln
y,
затем трансформировать их через
антилогарифмы (антилогарифм ln
y
= y)
и далее определить индекс детерминации
как «квази-![]() »
»
по формуле:
![]() .
.
Величина «квази-![]() »
»
не будет совпадать с совокупным
коэффициентом корреляции, который может
быть рассчитан для линейного в логарифмах
уравнения множественной регрессии,
потому что в последнем раскладывается
на факторную и остаточную суммы квадратов
не![]() ,
,
а![]() .
.
(слайд
2)
Использование коэффициента множественной
детерминации
![]()
для оценки качества модели обладает
тем недостатком, что включение в модель
нового фактора (даже несущественного)
автоматически увеличивает величину![]() .
.
Поэтому при большом количестве факторов
предпочтительней использовать так
называемый скорректированный
(улучшенный) коэффициент множественной
детерминации
![]() ,
,
определяемый соотношением:
![]() ,
,
где n
– число наблюдений,
m
– число параметров при переменных х
(чем больше величина m,
тем сильнее различия между к-том множ.
детерминации
![]()
и скорректированным к-том
![]() ).
).
При заданном объеме
наблюдений и при прочих равных условиях
с увеличением числа независимых
переменных (параметров) скорректированный
к-т множ. детерминации убывает. Его
величина может стать и отрицательной
при слабых связях результата с факторами.
При небольшом числе наблюдений
нескорректированная величина к-та
имеет
тенденцию переоценивать долю вариации
результативного признака, связанную с
влиянием факторов, включенных в
регрессионную модель. Чем
больше объем совокупности, по которой
исчислена регрессия, тем меньше
различаются
![]() и
и
![]() .
.
Отметим, что низкое
значение коэффициента множественной
корреляции и коэффициента множественной
детерминации может быть обусловлено
следующими причинами:
– в регрессионную
модель не включены существенные факторы;
– неверно выбрана
форма аналитической зависимости, не
отражающая реальные соотношения между
переменными, включенными в модель.
(слайд
3)
Значимость уравнения множественной
регрессии в целом оценивается с помощью
F–
критерия Фишера:
![]()
Выдвигаемая
«нулевая» гипотеза H0 о статистической
незначимости уравнения регрессии
отвергается при выполнении условия F
> Fкрит,
где Fкрит
определяется по таблицам F-критерия
Фишера по двум степеням свободы k1
= m,
k2=
n-m–1
и заданному уровню значимости α.
Значимость одного
и того же фактора может быть различной
в зависимости от последовательности
введения его в модель.
(слайд
4) Мерой
для оценки включения фактора в модель
служит частный
F-критерий
(оценивает статистическую значимость
присутствия каждого из факторов в
уравнении):
 ,
,
где
![]() –
–
коэффициент множ. детерминации для
модели с полным
набором
факторов;
![]() –
–
тот же показатель, но без включения в
модель фактора х1;
n
– число наблюдений;
m
– число параметров при переменных х.
Если фактическое
значение F
превышает табличное, то дополнительное
включение в модель фактора xi
статистически оправдано и коэффициент
чистой регрессии bi
при факторе xi
статистически значим.
Если же фактическое
значение F
меньше табличного, то нецелесообразно
включать в модель дополнительный фактор,
поскольку он не увеличивает существенно
долю объясненной вариации результата,
а коэффициент регрессии при данном
факторе статистически не значим.
(слайд
5) Частный
F-критерий
оценивает значимость коэффициентов
чистой регрессии. Зная величину
![]() ,
,
можно определить и t-критерий
Стьюдента:
![]()
или
![]()
где mbi
– средняя квадратическая ошибка
коэффициента регрессии bi,
она может быть определена по формуле:
 .
.
Величина
стандартной ошибки совместно с
t-распределением Стьюдента при n-m-1
степенях свободы применяется для
проверки значимости коэффициента
регрессии и для расчета его доверительного
интервала.
Соседние файлы в папке Эконометрика
- #
- #
- #
- #
- #
- #
- #
- #
Точечный и интервальный прогнозы для модели парной регрессии
Построение прогноза по модели парной линейной регрессии начинается с нахождения прогнозного значения объясняемой переменной у для заданного значения объясняемой переменной х0:
Прогноз возможен для математического ожидания М(у х = х0) зависимой переменной у или для индивидуального (конкретного значения) у* Во втором случае нас интересует доверительный интервал для точного, наперед заданного значения объясняющей переменной х0.
Доверительный интервал для среднего значения (математического ожидания) зависимой переменной нри данном значении переменной х0 определяется по формуле
где
Дисперсия интервального прогноза для среднего значения у определяется по формуле
где X 2 — выборочная дисперсия:
Доверительный интервал для индивидуальных значений зависимой переменной у*Х() при данном значении переменной х0 определяется но формуле
где
Дисперсия интервального прогноза для индивидуального значения г/* равна
Выводы по доверительным областям для зависимой переменной.
- 1. Прогноз значений зависимой переменной Y по уравнению линейной регрессии оправдан, если значение х0 объясняющей переменной X не выходит за диапазон ее значений по выборке. Причем чем ближе х0 к х, тем точнее прогноз, уже доверительный интервал (3.38) и (3.40).
- 2. Использование уравнения линейной регрессии вне изученного диапазона значений объясняющей переменной X, даже если оно экономически оправдано исходя из смысла решаемой задачи, может привести к значительным погрешностям.
Построим доверительные интервалы для среднего и индивидуального значений зависимой переменной для уравнения регрессии, полученного но данным примера 3.1. Решение. Ранее получено уравнениерегрессии у< = 3,295 + 2,283.г,.
Выборочная дисперсия
Среднее значение объясняющей переменной х = 13,8; Qv = 135,6.
Пусть доверительная вероятность у = 0,95.
Критическая точка ?кр = t0 05; 8 = 2,306.
Прогнозное значение зависимой переменной
Дисперсия интервального прогноза для среднего значения у (формула (3.39)):
Доверительный интервал для среднего значения у (формула (3.38)):
Дисперсия интервального прогноза для индивидуального значения у<) (формула (3.41)):
Доверительный интервал для индивидуального значения уо (формула (3.40)):
Средняя ошибка аппроксимации. Фактические значения результативного признака отличаются от теоретических. Чем меньше это отличие, тем ближе теоретические значения подходят к эмпирическим данным, это лучшее качество модели. Величина отклонений фактических и расчетных значений результативного признака по каждому наблюдению представляет собой ошибку аппроксимации. Для сравнения используются величины отклонений, выраженные в процентах к фактическим значениям.
Средняя ошибка аппроксимации рассчитывается по формуле
Прогноз по модели парной регрессии
Точечный прогноз по уравнению регрессии
Если известно значение независимой переменной х, то прогноз зависимой переменной осуществляется подстановкой этого значения в оценку детерминированной составляющей:
Вследствие несмещенности оценок параметров регрессии этот прогноз также является несмещенным
Показателем точности прогноза служит его дисперсия (чем она меньше, тем точнее прогноз):
Из формулы (1.2.3) видно, что чем больше объем выборки, тем точнее прогноз. При фиксированном объеме выборки прогноз тем точнее, чем больше «разнесены» выборочные данные и чем ближе значение независимой переменной к среднему выборочному значению.
Интервальный прогноз по уравнению регрессии
Поскольку согласно (1.2.3) у(х)
N^y(x), а дисперсия а 2
в (1.2.3) заменяется ее несмещенной оценкой по формуле (1.1.15), то за середину доверительного интервала для детерминированной составляющей выбирается точечный прогноз зависимой переменной, а ширина доверительного интервала — пропорциональной стандартному отклонению точечного прогноза:
где ta — двусторонняя критическая граница распределения Стью- дента с (п — 2) степенями свободы.
О Пример 1.1. Зависимость розничного товарооборота от числа занятых
Исследуем зависимость розничного товарооборота (млн руб.) магазинов от среднесписочного числа работников. Товарооборот как результирующий признак обозначим через у, а среднесписочное число работников как независимую переменную (фактор) — через х.
На объем товарооборота влияют также такие факторы, как объем основных фондов, их структура, площадь торговых залов и подсобных помещений, расположение магазинов по отношению к потокам покупателей и т. п. Предположим, что в исследуемой группе магазинов значения этих других факторов примерно одинаковы, поэтому различие их значений на изменении объема товарооборота сказывается незначительно.
В табл. 1.1 в столбцах 2 и 3 приведены значения соответственно среднесписочного числа работников и объема розничного товарооборота, а в следующих столбцах — значения расчетных величин, необходимых для определения оценок коэффициентов регрессии и дисперсии случайной составляющей (Zj=Xj-x, Ayj=yj-y,
Фактические и выравненные значения товарооборота (млн руб.) в зависимости от числа занятых
Найдя по итогам столбцов 2 и 3 средние х = 904/8 = 113, у = 9,6/8 = 1,2, последовательно заполняем столбцы 4—8 и подводим итоги по этим столбцам. Теперь можно определять эмпирические коэффициенты регрессии. По формулам (1.1.6) находим следующие точечные оценки коэффициентов регрессии:
Значение нулевого коэффициента &° представляет собой ординату эмпирической линии регрессии в точке х = х = 113, а коэффициент регрессии dj = 0,01924 — угловой коэффициент этой прямой линии.
На рис. 1.2 изображены система соединенных штриховой линией точек наблюдений и прямая эмпирической регрессии.
Если не учитывать, что мы имеем не теоретическую, а эмпирическую линию регрессии (которая действительно является приближением теоретической линии регрессии), то коэффициент
а, = 0,01924 показывает, что увеличение среднесписочной численности на одного человека приводит к увеличению товарооборота в среднем на 19,24 тыс. руб. Это своего рода эмпирический норматив приростной эффективности использования работников для данной группы магазинов. Если увеличение численности на одного работника приводит к меньшему росту товарооборота, то прием его на работу необоснован.
Теперь можно вычислить выравненные значения (значения ординат эмпирической линии регрессии):
и использовать столбцы 9—11 табл. 1.1. Итог столбца 11, в свою очередь, позволяет получить оценку дисперсии случайной составляющей:
Зная дисперсию случайной составляющей, можно проверить статистические гипотезы о параметрах регрессии и уравнении
Рис. 1.2. Фактические (штриховая ломаная линия) и выравненные (сплошная прямая линия) значения товарооборота
в целом, а также построить интервальные оценки параметров регрессии и прогнозного значения детерминированной составляющей.
Для проверки гипотезы о том, значимо ли отличается от нуля выборочный коэффициент ос,, находим согласно равенству (1.1.18) его эмпирическую значимость
которую теперь надо сравнить с теоретическим значением ta(n — 2), найденным по таблице распределения Стьюдента (см. табл. П.5.2).
Выбираем уровень значимости ос равным 5% (т. е. с вероятностью 0,05 мы допускаем, что гипотеза Н0: ос, = 0 будет отвергнута в том случае, когда она на самом деле верна). По табл. П.5.2 находим /005(6) = 2,45. Эмпирическая значимость (14,198) существенно
больше теоретической (2,45), поэтому d1 значимо отличается от нуля, т. е. принимаем гипотезу Н <.ос, *0.
Этот вывод подтверждается и высоким значением коэффициента детерминации:
который показывает, что в исследуемой ситуации 97,1% общей вариабельности розничного товарооборота объясняется изменением числа работников, в то время как на все остальные факторы приходится лишь 2,9% вариабельности.
Этот статистический вывод не абсолютен. Допустим, что в магазинах исследуемой группы стало больше работников, при этом предельная эффективность работника падает и на первый план выходит влияние других факторов. По-видимому, это прежде всего доля дефицитных товаров в ассортименте, комплекс факторов, характеризующих культуру обслуживания, и расположение магазинов.
Построим интервальные оценки параметров регрессии а 0 , а,
в форме d° ± /а(Ьо, 6с, ± /„6^. Здесь середины интервалов являются точечными оценками коэффициентов регрессии, которые уже рассчитаны: &°=у = 1,2; а, =0,01924. При выборе уровня значимости 5% получаем /0,05(6) = 2,45. Остается только найти стандартные ошибки коэффициентов регрессии. Согласно формулам (1.1.8), (1.1.7)
заменяя а на 6, получаем
Отсюда окончательно получаем, что с вероятностью 0,95 истинные значения параметров лежат в следующих пределах:
Найденные отклонения фактических значений от выравненных (столбец 10) позволяют провести сравнительный анализ работы различных магазинов рассматриваемой группы. Прежде всего необходимо обратить внимание на магазины с отрицательным отклонением (3, 4 и 6-й). Особенно велико отклонение у 4-го магазина. В реальной ситуации необходимо внимательно обследовать эти магазины и установить причины отклонения фактического значения товарооборота от выравненного («нормативного») значения. Это может быть расположение магазина в стороне от основных потоков покупателей, плохое снабжение товарами повышенного спроса, устаревшее оборудование, неудовлетворительный кадровый состав и т. п. При статистическом анализе с учетом сделанных ранее предположений и на основе имеющихся данных приходим к выводу, что в этих магазинах, по-видимому, имеются резервы в организации труда работников. Напротив, в 1, 2, 5, 7 и 8-м магазинах эффективность использования работников выше статистического норматива, но может оказаться, что эти магазины объективно находятся в лучших условиях.
Полученное уравнение регрессии может быть использовано для прогноза. В частности, пусть намечается открытие магазина такого же типа с численностью работников х = 140, тогда достаточно обоснованный объем товарооборота следует установить по уравнению регрессии
С точки зрения принятой теоретической схемы полученный прогноз у(х) является лишь точечной оценкой истинной детерминированной составляющей у (х), а сама составляющая лежит внутри доверительного интервала у (x) ± , в котором согласно формуле (1.2.4)
В результате получаем следующий доверительный интервал для теоретического значения прогноза:
или
Вопросы и задачи
1. Предскажите время реакции полуторамесячного ребенка по следующим данным:
Построение интервального прогноза по модели парной линейной регрессии
Если построенное уравнение регрессии и показатели тесноты связи признаны статистически значимыми, то такую модель можно использовать для построения прогноза.
Точечный прогноз упрог„. определяется, если в уравнение регрессии подставить значение факторной переменной хпрогнпри котором нас интересует значение прогнозируемой эндогенной переменной.
Однако вероятность осуществления точечного прогноза невелика, поэтому прибегают к интервальному прогнозу, вероятность которого составляет 95 %. Расчеты, необходимые для интервального прогноза:
где Snp0ZH‘ — стандартная ошибка прогноза; S — стандартная ошибка уравнения регрессии (корень из остаточной дисперсии на одну степень свободы); п — объем выборки; х„рогн — значение факторной переменной, при которой прогнозируется эндогенная переменная; х, — индивидуальные значения независимой переменой; х — среднее арифметическое значений факторного признака.
Стандартная ошибка уравнения регрессии рассчитывается по формуле:
Доверительный интервал прогноза:
где t — табличное значение t-критерия Стьюдента при уровне значимости 0,05 и числе степеней свободы п-2.
АНАЛИЗ ОСТАТКОВ ПО МОДЕЛИ РЕГРЕССИИ
1. Требования к остаткам для качественной модели регрессии.
Понятие гомоскедастичности и гетероскедастичности остатков модели. Методы проверки ряда остатков модели на гетероскедастичносгь
Методика проведения теста Голдфелда — Квандта на гетероскедастичность остатков
Понятие автокорреляции в остатках. Методика проверки ряда остатков на наличие автокорреляции с помощью критерия Дарбина — Уотсона
Требования к остаткам для качественной модели регрессии
Для того чтобы построенная регрессионная модель адекватно описывала моделируемое явление или процесс и имела высокую прогностическую силу, ряд остатков по модели должен удовлетворять следующим требованиям:
- 1. Дисперсия остатков должна быть одинакова для различных наблюдений.
- 2. Остатки не должны зависеть друг от друга, т. е. не должно быть автокорреляции в остатках.
- 3. Остатки должны быть распределены по нормальному закону распределения.
После построения модели регрессии, расчета коэффициента корреляции, коэффициента детерминации, средней относительной ошибки аппроксимации, оценки статистической значимости параметров уравнения регрессии с помощью t-критерия Стьюдента и оценки статистической значимости уравнения регрессии в целом с помощью F-критерия Фишера необходимо проверить ряд остатков модели на постоянство их дисперсии и на автокорреляцию. [1]
После построения модели проверяют ряд ее остатков, и, если выявлено свойство гетероскедастичности остатков, модель не используют для прогноза и анализа явления, а строят новую модель, остатки которой гомоскедастичны.
Возможные причины гетероскедастичности остатков:
- 1) неучет в модели важных факторов, влияющих на моделируемый признак;
- 2) неверная форма модели.
Проверка выполнения требования гомоскедастичности остатков может быть произведена:
- 1) графическим методом, с помощью построения точечного графика зависимости остатков от теоретических значений результативного признака, а также графика зависимости остатков от значений факторного признака; в случае гомоскедастичности облако остатков находится в области, параллельной оси абсцисс; все прочие случаи указывают на гетероскедастичность остатков;
- 2) с помощью специальных тестов, среди которых:
- а) тест Голдфелда — Квандта;
- б) тест ранговой корреляции Спирмена;
- в) тест Уайта;
- г) тест Парка;
- д) тест Глейзера и др.
Примеры выявления гетероскедастичности в остатках визуально, графическим методом представлены на рис. 7.1-7.3.
Графики зависимости остатков от значений факторного признака выводятся автоматически при использовании надстройки «Анализ данных», инструмент анализа «Регрессия», если поставить галочку в диалоговом окне напротив опции «График остатков».
Рис. 7.1. Гетероскедастичные остатки
Рис. 7.2. Гетероскедастичные остатки 2
Рис. 7.3. Гетероскедастичные остатки 3 Пример графика гомоскедастичных остатков приведен на рис. 7.4.
Рис. 7.4. Гомоскедастичные остатки
Очень часто визуально сложно определить гомоскедастичны остатки или гетероскедастичны, поэтому используются более однозначные и точные количественные критерии.
3. МЕТОДИКА ПРОВЕДЕНИЯ ТЕСТА ГОЛ ДФЕ Л ДА — КВАНДТА НА ГЕТЕРОСКЕДАСТИЧНОСТЬ ОСТАТКОВ
Наиболее популярным критерием является критерий, предложенный С. Голдфелдом и Р. Квандтом в 1965 г. Процедура проверки остатков на го- москедастичность по тесту Голдфелда — Квандта следующая:
- 1) все наблюдения упорядочиваются по возрастанию фактора х;
- 2) упорядоченную совокупность делят на три группы, причем первая и третья должны быть равного объема; при малом числе наблюдений упорядоченную по признаку х совокупность можно разделить на две равные части; при большом числе наблюдений упорядоченную по признаку х совокупность делят на три равные части; авторы метода рекомендуют, чтобы объемы первой и третьей части удовлетворяли условию п7 = п3 = 3/8*и; из дальнейшего анализа исключается средняя часть наблюдений упорядоченной совокупности;
- 3) по первой и третьей группе наблюдений отдельно строят уравнения регрессии и определяют остаточные суммы квадратов по каждому уравнению SS и SSy,
- 4) находят отношение:
В числителе должна быть большая из сумм квадратов;
- 5) определяют табличное значение F-критерия Фишера при уровне значимости 0,05 и числе степеней свободы П]-т, где т — число оцениваемых параметров;
- 6) сравнивают расчетное значение F-критерия с табличным, если ^Расч>^табл, то остатки гетероскедастичны, т. е. чем больше найденное отношение Грасч, тем сильнее вероятность гетероскедастичности остатков; чем больше Граем превышает Гтабл, тем более нарушена предпосылка о равенстве остаточных дисперсий. [2]
Статистика DW принимает значения от 0 до 4. Если полученное значение DW не слишком отличается от 2, то можно сделать вывод об отсутствии автокорреляции в остатках.
Использование критерия Дарбина — Уотсона показано графически на схеме (рис. 7.5).
Рис. 7.5. Схема применения критерия Дарбина — Уотсона
Нижняя и верхняя границы критерия DWt и DW,, берутся из статистических таблиц с учетом уровня значимости 0,05, объема статистической совокупности (числа наблюдений) и количества параметров при факторном признаке в уравнении регрессии (для парной линейной регрессии такой параметр один — Ь).
[spoiler title=”источники:”]
http://studref.com/468914/ekonomika/prognoz_modeli_parnoy_regressii
http://bstudy.net/830446/ekonomika/postroenie_intervalnogo_prognoza_modeli_parnoy_lineynoy_regressii
[/spoiler]
Продолжение цикла публикаций статей про прогнозирование временных рядов. На повестке – перевод статьи How to Develop Multi-Step LSTM Time Series Forecasting Models for Power Usage.
Данную работу можно отнести к сильным в плане объёма предоставляемой информации. К тому же, как предупреждает её автор, она рассчитана на исследователя данных, имеющего багаж определённых знаний о временных рядах и прогнозировании в целом. Однако для облегчения понимания тех или иных деталей в статье будут представлены ссылки на связанные публикации. Со своей стороны я бы порекомендовал прочесть книгу Ф. Шолле «Глубокое обучение на Python», фрагментами из которой я сопроводил некоторые моменты переводимой статьи в виде примечания переводчика. В качестве беглого введения в прогнозирование временных желательно ознакомиться с публикацией «Прогнозирование временных рядов с помощью рекуррентных нейронных сетей», чтобы иметь представление о так называемых одномерных и многомерных моделях, а также о точечном и интервальном прогнозировании и их выполнении.
Опираясь на эти работы можно смело переделать некоторые вещи из переводимой статьи, – а вернее, адаптировать, как говорится, под себя – и расщёлкать ту или иную проблему, связанную с временными рядами.
Перевод сопровождается моими комментариями, которые нацелены помочь в быстром усвоении некоторых деталей.

Интервальное прогнозирование временных рядов с помощью рекуррентных нейронных сетей с долгой краткосрочной памятью: прогноз потребления электроэнергии
Обновлено 05.08.2019
С ростом использования интеллектуальных счётчиков электроэнергии и широкого внедрения различных технологий её производства, таких как солнечные батареи и др., появляется множество данных о потреблении электроэнергии.
Эти данные могут быть представлены как многомерный временной ряд и использоваться не только для моделирования, но и прогнозирования будущего потребления электроэнергии.
В отличие от других алгоритмов машинного обучения, рекуррентные нейронные сети с долгой кратковременной памятью (в англоязычной терминологии LSTM. – Прим. пер.) способны автоматически выявлять признаки из временных последовательностей, обрабатывать многомерные данные, а также выводить последовательности переменной длины, благодаря чему их можно использовать для интервального прогнозирования.
В этом руководстве вы узнаете, как подготовить рекуррентные нейронные сети с долгой кратковременной памятью (далее по тексту статьи будет использоваться сокращение – ДКП. – Прим. пер.), чтобы выполнить интервальное прогнозирование временных рядов домового потребления электроэнергии.
После завершения данного руководства вы узнаете:
- Как подготовить и оценить ДКП типа «кодировщик-декодировщик» для интервального прогнозирования временных рядов на основе как одномерных, так и многомерных входных данных.
- Как подготовить и оценить ДКП типа «кодировщик-декодировщик» с добавлением свёрточного слоя в качестве кодировщика для интервального прогнозирования временных рядов.
- Как подготовить и оценить свёрточную ДКП типа «кодировщик-декодировщик» для интервального прогнозирования временных рядов.
Узнайте как подготовить модели на основе многомерных входных данных для выполнения интервального прогнозирования временных рядов с помощью ДКП, а также многое другое в моей новой книге с 25-ю пошаговыми руководствами и полным исходным кодом.
Поехали!
Примечание. В целом это руководство ориентировано на продвинутого пользователя, и если вы только начинаете знакомится с прогнозированием временных рядов на Python, то сначала загляните сюда. Если вы только начинаете своё знакомство с методами глубокого обучения с использованием временных рядов, то начните с этой страницы. Если вы действительно нацелены начать работу с ДКП с временными рядами, начните отсюда.
- Обновление (июнь, 2019): исправлена ошибка в функции to_supervised(), которая отбрасывала данные за последнюю неделю набора данных (спасибо Маркусу).
Обзор руководства
Руководство состоит из девяти частей:
- Описание проблемы.
- Загрузка и подготовка набора данных.
- Оценка модели.
- ДКП для интервального прогнозирования временных рядов.
- ДКП на основе одномерных входных данных и выходного вектора.
- ДКП типа «кодировщик-декодировщик» на основе одномерных входных данных.
- ДКП типа «кодировщик-декодировщик» на основе многомерных входных данных.
- ДКП типа «кодировщик-декодировщик» с добавлением свёрточного слоя в качестве кодировщика на основе одномерных входных данных.
- Свёрточная ДКП типа «кодировщик-декодировщик» на основе одномерных входных данных.
Параметры среды Python
Для выполнения примеров руководства предполагается, что у вас установлены следующие Python-библиотеки: SciPy с версией Python 3, нейросетевая библиотека Keras (версия 2.2 или выше) с низкоуровневой библиотекой TensorFlow или Theano, а также Scikit-Learn, Pandas, NumPy и Matplotlib.
Если вам нужна помощь в настройке среды Python, то ознакомьтесь со следующей публикацией:
- Как настроить параметры среды Python для машинного и глубокого обучения
Для выполнения примеров руководства графическая карта не требуется. Тем не менее, за невысокую цену вы можете получить доступ к графическим процессорам на Amazon Web Services. В следующей публикации рассказано как это сделать:
- Как настроить графические процессоры Amazon AWS EC2 для обучения модели глубокого обучения Keras
Итак, переходим к погружению.
Описание проблемы
Набор данных «Домовое потребление электроэнергии» представляет собой многомерный временной ряд, отображающий потребление электроэнергии одной семьи в течение четырех лет.
Более полная информация об этом наборе данных представлена в следующей публикации:
- Как загрузить и исследовать данные об использовании электроэнергии в домашних условиях
Эти данные были собраны в период с декабря 2006 года по ноябрь 2010; замеры потребления электроэнергии выполнялись каждую минуту.
Помимо даты и времени набор данных состоит из семи переменных:
- global_active_power: общая активная мощность, потребляемая жилым домом (измеряется в киловаттах).
- global_reactive_power: общая реактивная мощность, потребляемая жилым домом (измеряется в киловаттах).
- voltage: среднее напряжение (измеряется в вольтах).
- global_intensity: среднее значение силы тока (измеряется в амперах).
- sub_metering_1: активная энергия потребления кухонной комнаты (измеряется в ватт-часах активной энергии).
- sub_metering_2: активная энергия потребления прачечной (измеряется в ватт-часах активной энергии).
- sub_metering_3: активная энергия потребления систем климат-контроля (измеряется в ватт-часах активной энергии).
Активная и реактивная энергия относятся к техническим деталям переменного тока (активная мощность это и есть потребляемая мощность, за которую мы, собственно, платим по счётчику. – Прим. пер.).
Переменная sub_metering может быть создана путём вычитания суммы трёх определённых sub_metering-переменных от общей потребляемой энергии следующим образом:
sub_metering_remainder = (global_active_power * 1000 / 60) - (sub_metering_1 + sub_metering_2 + sub_metering_3)
Загрузка и подготовка набора данных
Набор данных можно загрузить из архива UCI Machine Learning в виде сжатого файла формата .zip, размер которого составляет 20 мегабайт:
- household_power_consumption.zip
Загрузите набор данных и разархивируйте его в свой текущий рабочий каталог. После этого у вас появится файл «household_power_consumption.txt» в исходном виде, размер которого составляет примерно 127 мегабайт.
С помощью функции read_csv() мы можем загрузить данные и объединить первые два столбца в один столбец, объединяющий дату и время, — и использовать его в качестве индекса.
# load all data
dataset = read_csv('household_power_consumption.txt', sep=';', header=0, low_memory=False, infer_datetime_format=True, parse_dates={'datetime':[0,1]}, index_col=['datetime'])Далее мы можем заменить все пропущенные значения, обозначенные символом “?”, на значение NaN, являющимся числом с плавающей точкой.
Это позволит нам работать с данными как с одним сплошным массивом значений с плавающей запятой, а не с различными смешанными типами (что было бы не так эффективно).
# mark all missing values
dataset.replace('?', nan, inplace=True)
# make dataset numeric
dataset = dataset.astype('float32')Далее нужно заполнить пропущенные значения NaN.
Простое решение состоит в том, чтобы скопировать наблюдение с того же времени, но днём ранее. Мы можем реализовать это с помощью функции fill_missing(), принимающей массив данных NumPy и возвращающей скопированные значения ровно 24 часа назад.
# fill missing values with a value at the same time one day ago
def fill_missing(values):
one_day = 60 * 24
for row in range(values.shape[0]):
for col in range(values.shape[1]):
if isnan(values[row, col]):
values[row, col] = values[row - one_day, col]Мы можем применить эту функцию непосредственно к данным внутри DataFrame.
# fill missing
fill_missing(dataset.values)Теперь с помощью расчётов из предыдущего раздела создадим новый столбец, содержащий остаток sub-metering.
# add a column for for the remainder of sub metering
values = dataset.values
dataset['sub_metering_4'] = (values[:,0] * 1000 / 60) - (values[:,4] + values[:,5] + values[:,6])Далее сохраним подготовленную версию набора данных в отдельный файл: для этого мы просто изменим расширение файла на .csv и сохраним его как «household_power_consumption.csv».
# save updated dataset
dataset.to_csv('household_power_consumption.csv')Полный код загрузки, обработки и сохранения набора данных приведён ниже.
# load and clean-up data
from numpy import nan
from numpy import isnan
from pandas import read_csv
from pandas import to_numeric
# fill missing values with a value at the same time one day ago
def fill_missing(values):
one_day = 60 * 24
for row in range(values.shape[0]):
for col in range(values.shape[1]):
if isnan(values[row, col]):
values[row, col] = values[row - one_day, col]
# load all data
dataset = read_csv('household_power_consumption.txt', sep=';', header=0, low_memory=False, infer_datetime_format=True, parse_dates={'datetime':[0,1]}, index_col=['datetime'])
# mark all missing values
dataset.replace('?', nan, inplace=True)
# make dataset numeric
dataset = dataset.astype('float32')
# fill missing
fill_missing(dataset.values)
# add a column for for the remainder of sub metering
values = dataset.values
dataset['sub_metering_4'] = (values[:,0] * 1000 / 60) - (values[:,4] + values[:,5] + values[:,6])
# save updated dataset
dataset.to_csv('household_power_consumption.csv')При выполнении кода создаётся новый файл «household_power_consumption.csv», который мы будем использовать в качестве отправной точки для нашего проекта моделирования.
Оценка модели
В данном разделе мы рассмотрим, как подготовить и оценить модели, прогнозирующие домовое потребление электроэнергии.
Раздел состоит из четырёх частей:
- Постановка проблемы
- Метрика оценки
- Разделение набора данных на тренировочную и тестовую части
- Валидация с нарастающим размером блока
Постановка проблемы
Рассматриваемый в руководстве набор данных можно использовать для разных целей. В нашем случае мы будем использовать его для ответа на конкретный вопрос, а именно:
Учитывая текущий уровень потребления, какой расход электроэнергии будет на неделю вперед?
Чтобы ответить на этот вопрос, необходимо обучить модель прогнозировать ежедневную общую потребляемую мощность на следующие семь дней вперёд.
Примечание:
Общая потребляемая мощность (признак под индексом 0) будет использоваться для формирования целевых данных (y) применительно ко всем примерам данного руководства.
Технически, поставленная задача относится к задаче интервального прогнозирования временных рядов. При этом модель, на вход которой подаётся более одного признака, называется моделью на основе многомерных входных данных (или многомерная модель); она может использоваться для выполнения интервального прогнозирования.
Модель данного типа может быть полезна при планировании расходов домового потребления электроэнергии. Также модель может быть практичной с точки зрения оптимизации спроса на электроэнергию для конкретного дома/семьи.
Предполагается, что с учётом поставленной задачи было бы полезным уменьшить выборку с поминутных замеров потребления электроэнергии до ежедневных значений. Это не относится к обязательным шагам, однако, учитывая, что нас интересует дневная потребляемая мощность, в этом есть смысл.
Мы можем выполнить это с помощью pandas-функции resample(), применяемой к DataFrame. Применение этой функции с аргументом «D» позволяет группировать по дням загруженные данные, проиндексированные по дате и времени. Затем для каждой из восьми переменных мы можем рассчитать сумму всех наблюдений за каждый день и создать новый набор данных с ежедневным потреблением энергии.
Полный код обработки данных приведён ниже.
# resample minute data to total for each day
from pandas import read_csv
# load the new file
dataset = read_csv('household_power_consumption.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# resample data to daily
daily_groups = dataset.resample('D')
daily_data = daily_groups.sum()
# summarize
print(daily_data.shape)
print(daily_data.head())
# save
daily_data.to_csv('household_power_consumption_days.csv')При его выполнении создается новый набор данных с ежедневным потреблением электроэнергии, который затем сохраняется в отдельном файле «household_power_consumption_days.csv».
Созданный набор данных мы будем использовать для выполнения поставленной задачи с подбором и оценкой прогностических моделей.
Метрика оценки
Прогноз будет состоять из семи значений — по одному на каждый день предстоящей недели.
Как правило, при выполнении интервального прогнозирования каждый прогнозируемый временной шаг оценивается отдельно. Это полезно по нескольким причинам:
- Чтобы отметить уровень каждого временного шага (например, день «+1» против дня «+3»).
- Для сравнения качества моделей с разным временным шагом (например, модели с высокой оценкой прогноза на «день +1» и модели с высокой оценкой прогноза на «день +5»).
Так как единицами общей мощности являются киловатты, было бы полезным иметь метрику погрешности в тех же единицах (в том же масштабе). При этом и квадратный корень из среднеквадратической ошибки (RMSE), и средняя абсолютная ошибка (MAE) соответствуют этому масштабу, однако в руководстве будет использоваться именно квадратный корень из среднеквадратичной ошибки, поскольку эта метрика используется чаще. К тому же, в отличие от средней абсолютной ошибки, она больше штрафует модель за ошибки прогноза. Таким образом, метрикой для рассматриваемой проблемы в данном руководстве будет RMSE, рассчитываемая для каждого прогнозного временного шага (с 1-го по 7-мой день).
Эта же метрика будет использоваться в качестве результирующей оценки по всем прогнозируемым дням, учитывающей итоги работы модели. Это поможет в выборе лучшей модели.
Функция evaluate_forecasts(), представленная ниже, реализует вышеописанное решение.
# evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
scores = list()
# calculate an RMSE score for each day
for i in range(actual.shape[1]):
# calculate mse
mse = mean_squared_error(actual[:, i], predicted[:, i])
# calculate rmse
rmse = sqrt(mse)
# store
scores.append(rmse)
# calculate overall RMSE
s = 0
for row in range(actual.shape[0]):
for col in range(actual.shape[1]):
s += (actual[row, col] - predicted[row, col])**2
score = sqrt(s / (actual.shape[0] * actual.shape[1]))
return score, scoresПри выполнении функции сначала возвращается общее значение RMSE по всему прогнозу, а затем массив из значений RMSE по каждому дню.
Разделение набора данных на тренировочную и тестовую части
Первые три года данных мы будем использовать для обучения моделей, последний год – для их валидации (проверки).
Данные будут разделены на стандартные недели, которые начинаются в воскресенье, а заканчиваются в субботу.
Примечание: В США, Англии и других странах неделя начинается с воскресенья.
Это реалистичный и полезный способ подготовки данных для рассматриваемой проблемы прогнозирования энергопотребления на неделю вперёд. Это также практично с точки зрения использования моделей для прогнозирования конкретного дня (например, среды) или всей последовательности.
При этом разделение будет выполнено в обратном направлении – от валидационной части набора данных.
В ней последним годом является 2010 год, первое воскресение в котором было 3-го января. Заканчиваются данные в середине ноября 2010 года, ближайшая последняя суббота была 20 ноября. С учётом этого на валидацию отводится 46 недель.
Для подтверждения ниже приведены первая и последняя строки суточных данных валидационной части набора данных.
2010-01-03,2083.4539999999984,191.61000000000055,350992.12000000034,8703.600000000033,3842.0,4920.0,10074.0,15888.233355799992
...
2010-11-20,2197.006000000004,153.76800000000028,346475.9999999998,9320.20000000002,4367.0,2947.0,11433.0,17869.76663959999Обучающая часть набора данных формируется согласно следующему. Замеры начинаются в конце 2006 года. Первое воскресенье было 17 декабря, что соответствует второй строке данных. С учётом этого организация данных в стандартные недели даёт 159 полных недель для обучения модели.
2006-12-17,3390.46,226.0059999999994,345725.32000000024,14398.59999999998,2033.0,4187.0,13341.0,36946.66673200004
...
2010-01-02,1309.2679999999998,199.54600000000016,352332.8399999997,5489.7999999999865,801.0,298.0,6425.0,14297.133406600002Представленная ниже функция split_dataset() разбивает суточные данные на обучающие и валидационные части и организует их в еженедельные данные с помощью NumPy-функции split().
# split a univariate dataset into train/test sets
def split_dataset(data):
# split into standard weeks
train, test = data[1:-328], data[-328:-6]
# restructure into windows of weekly data
train = array(split(train, len(train)/7))
test = array(split(test, len(test)/7))
return train, testПротестируйте вышеописанную функцию, загрузив суточный набор данных и распечатав первую и последнюю строки обучающих и валидационных данных, чтобы убедиться в соответствии расчётам.
Полный код разбиения данных приведён ниже.
# split into standard weeks
from numpy import split
from numpy import array
from pandas import read_csv
# split a univariate dataset into train/test sets
def split_dataset(data):
# split into standard weeks
train, test = data[1:-328], data[-328:-6]
# restructure into windows of weekly data
train = array(split(train, len(train)/7))
test = array(split(test, len(test)/7))
return train, test
# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
train, test = split_dataset(dataset.values)
# validate train data
print(train.shape)
print(train[0, 0, 0], train[-1, -1, 0])
# validate test
print(test.shape)
print(test[0, 0, 0], test[-1, -1, 0])Его выполнение показывает, что обучающая часть действительно содержит 159 недель данных, тогда как на валидационную отводится 46 недель. При этом и первая и последняя строки обеих частей соответствуют тем, которые мы определили в качестве границ с учётом стандартных недель.
(159, 7, 8)
3390.46 1309.2679999999998
(46, 7, 8)
2083.4539999999984 2197.006000000004Валидация с нарастающим размером блока
Модели будут оцениваться с использованием схемы называемой «валидацией с нарастающим размером блока» (Walk-Forward Validation).
С учётом того, что целью моделирования является прогноз потребления мощности на неделю вперёд, то подаваемые на вход модели фактические еженедельные данные можно использовать в качестве основы для прогнозирования будущих еженедельных значений. Данный подход находит широкое применение на практике.
Принцип вышеописанного подхода продемонстрирован ниже.
Вход Прогноз
[Неделя1] Неделя2
[Неделя1 + Неделя2] Неделя3
[Неделя1 + Неделя2 + Неделя3] Неделя4
...Примечание:
Небольшое дополнение к демонстрации подхода. Поскольку набор данных разбит на две части, то с учётом валидации с нарастающим размером блока фактическими данными для прогнозирования первой недели из валидационной части данных (160-я неделя) будут первые 159 недель, т.е. вся обучающая часть данных. В свою очередь, для прогнозирования второй недели валидационной части данных (161-я неделя) фактическими данными будут 159 обучающих недель плюс предыдущая неделя из валидационной части данных (160 неделя) и т.д.:

Код функции evaluate_model(), в которой реализован данный подход к оценке моделей на основе рассматриваемого набора данных, представлен ниже.
Аргументами функции являются обучающая и валидационная части набора данных в формате еженедельных данных, а также дополнительный аргумент n_input, определяющий количество предыдущих наблюдений, которые модель будет использовать в качестве входных данных (параметр n_input лучше всего представить как историю. – Прим. пер.) каждого временного интервала для прогнозирования.
Наряду с этим в данной функции вызываются две новые подфункции: build_model(), используемая для конструирования и обучения модели на обучающих данных, и forecast(), применяемая для выполнения прогнозов при поступлении новых еженедельных данных. Эти функции будут рассмотрены в следующих разделах.
В данном руководстве мы будем работать с искусственными нейронными сетями. Сами по себе они обычно долго обучаются, однако быстро выдают оценку. В связи с этим предпочтительное использование моделей состоит в том, чтобы сконструировать и обучить их один раз на исторических данных, и далее использовать для прогнозирования каждого шага валидации с нарастающим размером блока. Модели являются статическими, то есть не обновляются во время их оценивания.
В этом заключается отличие от других моделей, которые быстрее обучаются, когда модель может быть переоснащена или обновлена на каждом шаге валидации с нарастающим размером блока при поступлении новых данных. Необходимо отметить, что при наличии достаточных ресурсов таким же образом можно использовать и искусственные нейронные сети, однако в этом руководстве это не будет рассматриваться.
Полный код функции evaluate_model() приведён ниже.
# evaluate a single model
def evaluate_model(train, test, n_input):
# fit model
model = build_model(train, n_input)
# history is a list of weekly data
history = [x for x in train]
# walk-forward validation over each week
predictions = list()
for i in range(len(test)):
# predict the week
yhat_sequence = forecast(model, history, n_input)
# store the predictions
predictions.append(yhat_sequence)
# get real observation and add to history for predicting the next week
history.append(test[i, :])
# evaluate predictions days for each week
predictions = array(predictions)
score, scores = evaluate_forecasts(test[:, :, 0], predictions)
return score, scoresПосле того как модель оценена, можно вывести итоги её выполнения.
Функция summarize_scores() отображает эффективность модели в виде строки со значениями для простого и наглядного сравнения с другими моделями.
# summarize scores
def summarize_scores(name, score, scores):
s_scores = ', '.join(['%.1f' % s for s in scores])
print('%s: [%.3f] %s' % (name, score, s_scores))Теперь у нас есть все элементы, чтобы начать выполнение оценки моделей на рассматриваемом наборе данных.
ДКП для интервального прогнозирования временных рядов
Рекуррентные нейронные сети (РНС) (в англоязычной терминологии Recurrent Neural Network, RNN. – Прим. пер.) предназначены для работы с данными в виде последовательностей.
Примечание:
Временные ряды или последовательности – трёхмерные тензоры с формой:
[образцы, метки времени, признаки]
Источник: Глубокое обучение на Python, Франсуа Шолле.
РНС – это разновидность искусственной нейронной сети, в которой выходные данные одного временного интервала предоставляются в качестве входных данных для следующего временного интервала. Данное обстоятельство позволяет РНС принимать решения об объекте прогноза, основываясь как на входных данных для текущего временного интервала, так и на выходных данных предыдущих шагов.
Возможно, наиболее успешным и оттого массово используемым типом (архитектурой) РНС является «Долгая краткосрочная память». Это объясняется тем, что данный тип преодолевает трудности, присущие обычной РНС*. В дополнении к особенности устанавливать связи между выходом предыдущего временного интервала и входом текущего, ДКП также имеет внутреннюю память, работающую как локальная переменная, что позволяет ДКП накапливать состояние поверх входной последовательности.
Примечание:
* Имеется в виду проблема затухания градиента, «напоминающего эффект, который наблюдается в нерекуррентных сетях (сетях прямого распространения) с большим количеством слоёв: по мере увеличения количества слоёв сеть в конечном итоге становится необучаемой… Слои LSTM и GRU создавались специально для решения этой проблемы».
Источник: Глубокое обучение на Python, Франсуа Шолле.
Для получения дополнительной информации о РНС смотрите следующую публикацию:
- Глубокое обучение с рекуррентными нейронными сетями: ускоренный курс
Для получения дополнительной информации о ДКП смотрите следующую публикацию:
- Введение в рекуррентные нейронные сети с долгой кратковременной памятью: круглый стол с экспертами
При интервальном прогнозировании временных рядов у ДКП есть ряд преимуществ перед другими методами:
- Встроенная поддержка последовательностей. ДКП – это тип РНС, предназначенный для работы с последовательностями в качестве входных данных, что отличает их от других моделей, в которых лагированные (взятые в предыдущий момент времени. – Прим. пер.) данные будут представлены как входные признаки.
- Многомерные входы. ДКП напрямую поддерживают множественные параллельные входные последовательности в виде многомерных входных данных, что отличает их от других моделей, в которых многомерные входные данные представляются в виде плоской (2Д) структуры.
- Векторный вывод. Как и другие искусственные нейронные сети, ДКП могут отображать входные последовательности напрямую в выходной вектор, который может предоставлять множественные выходные временные интервалы.
Кроме того, разработаны специализированные архитектуры РНС для интервального прогнозирования последовательностей, называемые прогнозированием «последовательность в последовательность» (в англоязычной терминологии sequence-to-sequence, или seq2seq для краткости. – Прим. пер.).
Примером данной архитектуры является ДКП типа «кодировщик-декодировщик».
ДКП типа «кодировщик-декодировщик» – это модель, состоящая из двух субмоделей – кодировщика, считывающего и сжимающего входные последовательности во внутреннее представление фиксированной длины, и декодировщика, интерпретирующего внутреннее представление для прогнозирования выходной последовательности.
Данный подход к прогнозированию последовательностей показывает себя гораздо эффективнее, чем прямой вывод вектора, что делает его предпочтительным подходом к прогнозированию данных в виде последовательностей.
В целом было обнаружено, что ДКП не так эффективны при проблемах типа авторегрессии, когда прогнозирования следующего временного интервала является функцией предыдущих временных интервалов.
Подробнее об этой проблеме смотрите в следующей публикации:
- О пригодности ДКП для прогнозирования временных рядов
Одномерные свёрточные нейронные сети (СНС) (в англоязычной терминологии Convolutional Neural Networks, CNN. – Прим. пер.) доказали свою эффективность в автоматическом изучении признаков из входных последовательностей.
Наиболее известный подход состоит в том, чтобы объединить СНС с ДКП в общую модель, в которой СНС выступает в качестве кодировщика для изучения признаков входных последовательных данных, передающихся ДКП как временные интервалы. Эта архитектура называется «СНС-ДКП» (в англоязычной терминологии CNN-LSTM. – Прим. пер.).
Для получения дополнительной информации об этой архитектуре смотрите следующую публикацию:
- Свёрточные нейронные сети с долгой краткосрочной памятью
Изменение уровня мощности в архитектуре «СНС-ДКП» представлено в свёрточной ДКП (в англоязычной терминологии Convolutional LSTM, или ConvLSTM для краткости. – Прим. пер.), которая использует свёрточное считывание входных последовательностей в ячейках ДКП. Этот подход оказался очень эффективным для классификации временных рядов и может быть адаптирован для выполнения их интервального прогнозирования.
В этом руководстве мы рассмотрим набор различных архитектур ДКП для выполнения интервального прогнозирования временных рядов. В частности, мы рассмотрим, как выполнить следующие модели:
- Модель ДКП на основе одномерных входных данных с векторным выходом
- Модель ДКП типа «кодировщик-декодировщик» на основе одномерных входных данных
- Модель ДКП типа «кодировщик-декодировщик» на основе многомерных входных данных
- Модель ДКП типа «кодировщик-декодировщик» с добавлением свёрточного слоя в качестве кодировщика на основе одномерных входных данных
- Свёрточная модель ДКП типа «кодировщик-декодировщик» на основе одномерных входных данных
Если вы новичок в использовании ДКП для прогнозирования временных рядов, то я настоятельно рекомендую следующую публикацию:
- Как разработать модели ДКП для прогнозирования временных рядов
Модели будут разработаны и продемонстрированы на примере решения проблемы прогнозирования домового энергопотребления. Модель будет считаться годной, если её оценка будет лучше, чем у наивной (упрощённой) модели, среднее значение оценки которой с учётом метрики RMSE составляет 465 киловатт (общая оценка за неделю).
Мы не будем фокусироваться на подборе оптимальных параметров моделей, чтобы улучшить их эффективность; вместо этого мы просто продемонстрируем модели, прогнозы которых лучше, чем наивный прогноз. Выбор представленных в примерах конфигураций и гиперпараметров ИНС объясняется методом проб и ошибок. Поэтому итоговые оценки следует рассматривать только в качестве примера, а не как исследование оптимальных параметров и конфигураций моделей для рассматриваемой проблемы.
Учитывая стохастический характер моделей, наиболее эффективно оценивать модель n-ое количество раз и затем вывести среднюю оценку эффективности. Однако вместо этого в целях сохранения простоты кода мы предоставим результаты одиночно оценённых моделей.
Мы не можем знать, какой подход будет наиболее эффективным для данной задачи интервального прогнозирования. Желательно изучить набор разных методов, чтобы выяснить, какие из них лучше всего работают на вашем наборе данных.
ДКП на основе одномерных входных данных и выходного вектора
Мы начнём с выполнения простой (или ванильной) модели ДКП, которая трансформирует общее еженедельное энергопотребление в дневные последовательности и выполняет прогноз энергопотребления на следующую неделю в виде выходного вектора.
Данное начало послужит основой для выполнения более сложных моделей, которые будут разработаны и описаны в последующих разделах.
Количество предыдущих дней, используемых в качестве входных данных, определяет одномерную последовательность данных, которая будет подаваться на вход ДКП для изучения и выделения признаков. Ниже представлены некоторые идеи об их возможном размере и характере.
- Все предыдущие дни за несколько лет.
- Предыдущие семь дней (одна неделя).
- Предыдущие две недели.
- Предыдущий месяц.
- Предыдущий год.
- Предыдущая неделя вместе с прошлогодней неделей.
Нет однозначного ответа на вопрос, какой размер использовать. Лучшим решением будет протестировать каждый из них вместе с другими подходами, а по результатам выполнения выбрать тот, который показал наилучшие результаты.
При этом выбор должен быть обусловлен следующими факторами:
- Каким образом должна быть подготовлена обучающая часть данных для обучения модели.
- Каким образом должна быть подготовлена валидационная часть данных для её оценки.
- Каким образом использовать законченную модель для выполнения прогнозов в будущем.
Хорошим началом будет использование семи предыдущих дней.
Модель ДКП ожидает, что входные данные будут иметь следующую (трёхмерную. – Прим. пер.) форму:
[образцы, временной интервал, признаки]С учётом семи дней ежедневной потребляемой мощности каждая выборка имеет временной интервал, длительность которого равна семи, и один признак.
Примечание:
Временной интервал это и есть «история» (параметр n_input), которая для нижеследующего примера принята за семь предыдущих дней.
Так как обучающая часть данных содержит 159 недель, то её форма будет иметь следующий вид:
[159, 7, 1]С этой формой данных модель будет использовать предыдущую неделю для прогнозирования следующей. Проблема в том, что 159 образцов – это очень маленькое количество данных для обучения модели.
Один из способов создания бóльшего количества данных состоит в том, чтобы изменить подход – выполнять прогнозирование потребления электроэнергии на следующие семь дней с учётом предыдущих несмотря на неделю (данное обстоятельство делает бессмысленным начальное преобразование обучающих и валидационных данных в еженедельную форму. – Прим. пер.).
Данное изменение относится только к обучающей части данных, предназначение валидационной части остаётся неизменным: с учётом данных предыдущей недели прогнозировать ежедневное энергопотребление на следующую неделю.
Для этого потребуется внести небольшие корректировки в подготовку обучающих данных.
Сначала обучающие данные на основе восьми признаков преобразовываются в недельные данные: в связи с этим их форма примет вид [159, 7, 8]. Следующим шагом является сглаживание данных. Делается это для того, чтобы получить восемь временных последовательностей (фактически выполняется обратное преобразование формы данных из 3Д в 2Д (см. примечание выше). – Прим. пер.).
# flatten data
data = train.reshape((train.shape[0]*train.shape[1], train.shape[2]))Затем выполняется разделение данных на так называемые перекрывающиеся окна с учётом установленного временного интервала.
К примеру:
Вход, Выход
[d01, d02, d03, d04, d05, d06, d07], [d08, d09, d10, d11, d12, d13, d14]
[d02, d03, d04, d05, d06, d07, d08], [d09, d10, d11, d12, d13, d14, d15]
...Это можно сделать путём отслеживания начальных и конечных индексов для входов и выходов при выполнении итераций по всей длине сглаженных данных с учётом установленного временного интервала.
При этом количество входов и выходов (n_input и n_out соответственно) будет выделено и представлено в качестве аргументов рассматриваемой далее функции. Это делается с той целью, чтобы вы могли поэкспериментировать с их различными значениями применительно к вашей собственной задаче.
Примечание:
Аргумент n_input – это, как уже было сказано, история, то есть на какой прошедший временной интервал «опереться» модели, чтобы выполнить прогноз (n_out), а n_out – это аргумент, определяющий насколько далеко в будущее модель должна научиться прогнозировать (устанавливает длительность прогнозируемого временного интервала).
Ниже приведена функция с именем to_supervised(), которая принимает обучающие данные, историю (количество предыдущих наблюдений, которые модель будет использовать в качестве входных данных) и длительность прогнозируемого временного интервала, а возвращает массивы в формате перекрывающихся скользящих окон.
# convert history into inputs and outputs
def to_supervised(train, n_input, n_out=7):
# flatten data
data = train.reshape((train.shape[0]*train.shape[1], train.shape[2]))
X, y = list(), list()
in_start = 0
# step over the entire history one time step at a time
for _ in range(len(data)):
# define the end of the input sequence
in_end = in_start + n_input
out_end = in_end + n_out
# ensure we have enough data for this instance
if out_end <= len(data):
x_input = data[in_start:in_end, 0]
x_input = x_input.reshape((len(x_input), 1))
X.append(x_input)
y.append(data[in_end:out_end, 0])
# move along one time step
in_start += 1
return array(X), array(y)При выполнении функции осуществляется преобразование 159 выборок в 1100; в связи с этим формы преобразованных данных примут следующий вид: X=[1100, 7, 1] и y=[1100, 7].
Далее определяется конфигурация модели и проводится её обучение.
По сути, данная проблема интервального прогнозирования временных рядов относится к авторегрессии. Это означает, что хороший результат может быть получен в том случае, когда следующие семь дней являются некоторой функцией наблюдений предыдущих. Данное обстоятельство наряду с относительно небольшим объёмом данных обуславливает применение «небольшой», простой по конфигурации, модели.
С учётом этого мы сконструируем модель с несколькими слоями. В роли первого скрытого слоя выступит слой ДКП с 200 нейронами (количество нейронов в скрытом слое не связано с длительностью временного интервала во входных последовательностях). За слоем ДКП следует полносвязный слой с 200 нейронами, назначение которого интерпретировать выявленные слоем ДКП признаки. Наконец, выходной слой будет напрямую выводить вектор с семью прогнозными элементами – по одному на каждый день в выходной последовательности.
За функцию потерь принята среднеквадратичная ошибка (MSE), поскольку она соответствует масштабу принятой ранее метрике (корень из среднеквадратической ошибки, RMSE). В качестве оптимизатора принят алгоритм Adam (вариант стохастического градиентного спуска), обучение модели будет длиться 70 эпох, размер пакета состоит из 16-ти образцов.
Небольшой размер пакета и стохастическая природа алгоритма означают, что одна и та же модель будет по-разному отображать входные и выходные данные при повторном обучении. Это приведёт к тому, что после выполнения оценки моделей, их результаты могу отличаться друг от друга. Вы можете попробовать выполнить обучение модели несколько раз и в подсчётах итоговых результатов использовать среднее значение.
Представленная ниже функция build_model() подготавливает обучающую часть данных, определяет конфигурацию модели, выполняет её обучение и возвращает обученную модель, которую затем можно использовать для выполнения прогнозов.
# train the model
def build_model(train, n_input):
# prepare data
train_x, train_y = to_supervised(train, n_input)
# define parameters
verbose, epochs, batch_size = 0, 70, 16
n_timesteps, n_features, n_outputs = train_x.shape[1], train_x.shape[2], train_y.shape[1]
# define model
model = Sequential()
model.add(LSTM(200, activation='relu', input_shape=(n_timesteps, n_features)))
model.add(Dense(100, activation='relu'))
model.add(Dense(n_outputs))
model.compile(loss='mse', optimizer='adam')
# fit network
model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)
return modelТеперь, когда модель обучена, мы можем проверить как она будет выполнять прогнозы.
Как правило, модель ожидает, что данные будут иметь одинаковую трёхмерную форму.
В нашем случае ожидаемая форма входного образца с учётом ежедневной потребляемой мощности следующая: «одна выборка – временной интервал длительностью 7 дней – один признак»:
[1, 7, 1]Данную форму должны иметь не только данные валидационной части набора данных, но и «новые», поступающие данные, которые будут использоваться обученной моделью для прогнозирования в будущем. При изменении параметра n-input на 14 дней длительность временного интервала будет также составлять 14 дней, поэтому форма обучающих данных и новых выборок для выполнения прогнозирования должны быть изменены соответствующим образом. При этом о длительности временного интервала необходимо позаботиться в самом начале.
В данном руководстве используется валидация с нарастающим размером блока, описанная в предыдущем разделе. В соответствии с принятыми решениями прогнозирование энергопотребления на предстоящую неделю выполняется на основе наблюдений предыдущей недели. Предыдущие недели собраны в массив, называемый history.
Чтобы предсказать следующую неделю, нужно возвратить последние дни наблюдений. Как и в случае с обучающими данными, сначала необходимо сгладить данные history, удалив недельную структуру, чтобы получить восемь параллельных временных последовательностей.
# flatten data
data = data.reshape((data.shape[0]*data.shape[1], data.shape[2]))Затем нужно получить ежедневные значения общей потребляемой мощности (признак под индексом 0) за последние семь дней.
Как и в случае с подготовкой обучающих данных, мы будем использовать для этого выделенный ранее параметр n_input, чтобы число предыдущих дней, используемых в качестве входных данных для модели, могло быть изменено в будущем.
# retrieve last observations for input data
input_x = data[-n_input:, 0]Затем изменим форму входных данных в ожидаемую моделью трёхмерную структуру.
# reshape into [1, n_input, 1]
input_x = input_x.reshape((1, len(input_x), 1))Далее на основе обученной модели и входных данных выполняется прогноз с извлечением выходного вектора, состоящего из семи дней.
# forecast the next week
yhat = model.predict(input_x, verbose=0)
# we only want the vector forecast
yhat = yhat[0]Представленная ниже функция forecast() реализует вышеописанные решения, принимая в качестве аргументов обученную модель, список данных предыдущих недель, наблюдаемых до настоящего времени (параметр history, сформированный по результатам валидации с нарастающим размером блока) и временной интервал.
# make a forecast
def forecast(model, history, n_input):
# flatten data
data = array(history)
data = data.reshape((data.shape[0]*data.shape[1], data.shape[2]))
# retrieve last observations for input data
input_x = data[-n_input:, 0]
# reshape into [1, n_input, 1]
input_x = input_x.reshape((1, len(input_x), 1))
# forecast the next week
yhat = model.predict(input_x, verbose=0)
# we only want the vector forecast
yhat = yhat[0]
return yhatВот и всё. Теперь у нас есть всё необходимое для выполнения интервального прогнозирования временных рядов с помощью модели ДКП на основе одномерных входных данных ежедневной общей потребляемой мощности.
Полный пример кода представлен ниже.
# univariate multi-step lstm
from math import sqrt
from numpy import split
from numpy import array
from pandas import read_csv
from sklearn.metrics import mean_squared_error
from matplotlib import pyplot
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import LSTM
# split a univariate dataset into train/test sets
def split_dataset(data):
# split into standard weeks
train, test = data[1:-328], data[-328:-6]
# restructure into windows of weekly data
train = array(split(train, len(train)/7))
test = array(split(test, len(test)/7))
return train, test
# evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
scores = list()
# calculate an RMSE score for each day
for i in range(actual.shape[1]):
# calculate mse
mse = mean_squared_error(actual[:, i], predicted[:, i])
# calculate rmse
rmse = sqrt(mse)
# store
scores.append(rmse)
# calculate overall RMSE
s = 0
for row in range(actual.shape[0]):
for col in range(actual.shape[1]):
s += (actual[row, col] - predicted[row, col])**2
score = sqrt(s / (actual.shape[0] * actual.shape[1]))
return score, scores
# summarize scores
def summarize_scores(name, score, scores):
s_scores = ', '.join(['%.1f' % s for s in scores])
print('%s: [%.3f] %s' % (name, score, s_scores))
# convert history into inputs and outputs
def to_supervised(train, n_input, n_out=7):
# flatten data
data = train.reshape((train.shape[0]*train.shape[1], train.shape[2]))
X, y = list(), list()
in_start = 0
# step over the entire history one time step at a time
for _ in range(len(data)):
# define the end of the input sequence
in_end = in_start + n_input
out_end = in_end + n_out
# ensure we have enough data for this instance
if out_end <= len(data):
x_input = data[in_start:in_end, 0]
x_input = x_input.reshape((len(x_input), 1))
X.append(x_input)
y.append(data[in_end:out_end, 0])
# move along one time step
in_start += 1
return array(X), array(y)
# train the model
def build_model(train, n_input):
# prepare data
train_x, train_y = to_supervised(train, n_input)
# define parameters
verbose, epochs, batch_size = 0, 70, 16
n_timesteps, n_features, n_outputs = train_x.shape[1], train_x.shape[2], train_y.shape[1]
# define model
model = Sequential()
model.add(LSTM(200, activation='relu', input_shape=(n_timesteps, n_features)))
model.add(Dense(100, activation='relu'))
model.add(Dense(n_outputs))
model.compile(loss='mse', optimizer='adam')
# fit network
model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)
return model
# make a forecast
def forecast(model, history, n_input):
# flatten data
data = array(history)
data = data.reshape((data.shape[0]*data.shape[1], data.shape[2]))
# retrieve last observations for input data
input_x = data[-n_input:, 0]
# reshape into [1, n_input, 1]
input_x = input_x.reshape((1, len(input_x), 1))
# forecast the next week
yhat = model.predict(input_x, verbose=0)
# we only want the vector forecast
yhat = yhat[0]
return yhat
# evaluate a single model
def evaluate_model(train, test, n_input):
# fit model
model = build_model(train, n_input)
# history is a list of weekly data
history = [x for x in train]
# walk-forward validation over each week
predictions = list()
for i in range(len(test)):
# predict the week
yhat_sequence = forecast(model, history, n_input)
# store the predictions
predictions.append(yhat_sequence)
# get real observation and add to history for predicting the next week
history.append(test[i, :])
# evaluate predictions days for each week
predictions = array(predictions)
score, scores = evaluate_forecasts(test[:, :, 0], predictions)
return score, scores
# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# split into train and test
train, test = split_dataset(dataset.values)
# evaluate model and get scores
n_input = 7
score, scores = evaluate_model(train, test, n_input)
# summarize scores
summarize_scores('lstm', score, scores)
# plot scores
days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']
pyplot.plot(days, scores, marker='o', label='lstm')
pyplot.show()Выполнение кода осуществляет обучение модели и её оценку в виде отображения строки с общим значением RMSE за всю неделю (по всему прогнозу) и значением RMSE по каждому дню прогнозируемой недели.
В виду стохастической природы алгоритма ваши результаты могут отличаться от представленных далее. Вы можете попробовать выполнить код несколько раз.
В данном случае по сравнению с наивным прогнозом модель справилась лучше: общее значение RMSE около 399 киловатт, что меньше значения 485 киловатт, достигнутого наивной моделью.
lstm: [399.456] 419.4, 422.1, 384.5, 395.1, 403.9, 317.7, 441.5График со значениями ошибки по каждому дню прогнозируемой недели представлен ниже.
Из графика видно, что вторники и пятницы являются более лёгкими для прогнозирования днями, чем остальные, а суббота является самым трудным днём для прогнозирования.
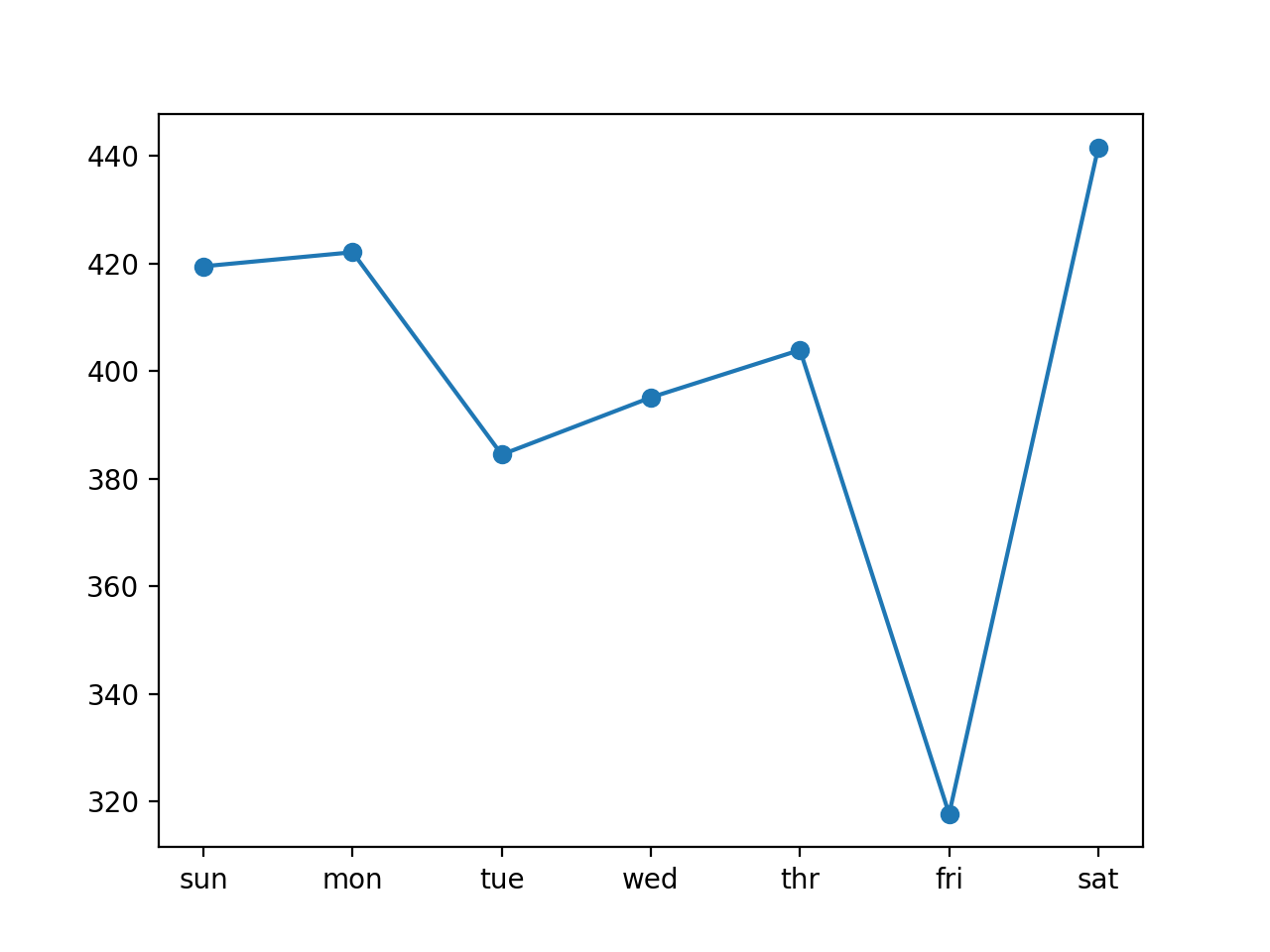
Примечание:
В примеры данного руководства было бы полезно включить графики, визуализирующие результаты выполнения прогнозирования. Графики можно выполнить по-разному. В виду того, что интервал прогноза энергопотребления составляет 7 дней в будущее (параметр n_out), что не так много и не вызывает затруднений в плане задействованных ресурсов и времени выполнения кода, то выведем отдельный график RMSE по каждому дню прогнозируемой недели. Для этого добавим новую функцию show_plot():
def show_plot(true, pred, title):
fig = pyplot.subplots()
pyplot.plot(true, label='Y_original')
pyplot.plot(pred, dashes=[4, 3], label='Y_predicted')
pyplot.xlabel('N_samples', fontsize=12)
pyplot.ylabel('Instance_value', fontsize=12)
pyplot.title(title, fontsize=12)
pyplot.grid(True)
pyplot.legend(loc='upper right')
pyplot.show()
Также дополним функцию evaluate_forecasts() следующими строками:
for j in range(predicted.shape[1]):
show_plot(actual[:, j], predicted[:, j], j + 1)
Наконец, построение графика со значениями ошибки по каждому дню прогнозируемой недели дополняется следующей строкой:
fig = pyplot.subplots()Полный код с учётом данных изменений находится здесь
# univariate multi-step lstm
from math import sqrt
from numpy import split
from numpy import array
from pandas import read_csv
from sklearn.metrics import mean_squared_error
from matplotlib import pyplot
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import LSTM
# split a univariate dataset into train/test sets
def split_dataset(data):
# split into standard weeks
train, test = data[1:-328], data[-328:-6]
# restructure into windows of weekly data
train = array(split(train, len(train)/7))
test = array(split(test, len(test)/7))
return train, test
def show_plot(true, pred, title):
fig = pyplot.subplots()
pyplot.plot(true, label='Y_original')
pyplot.plot(pred, dashes=[4, 3], label='Y_predicted')
pyplot.xlabel('N_samples', fontsize=12)
pyplot.ylabel('Instance_value', fontsize=12)
pyplot.title(title, fontsize=12)
pyplot.grid(True)
pyplot.legend(loc='upper right')
pyplot.show()
# # evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
scores = list()
# calculate an RMSE score for each day
for i in range(actual.shape[1]):
# calculate mse
mse = mean_squared_error(actual[:, i], predicted[:, i])
# calculate rmse
rmse = sqrt(mse)
# store
scores.append(rmse)
# calculate overall RMSE
s = 0
for row in range(actual.shape[0]):
for col in range(actual.shape[1]):
s += (actual[row, col] - predicted[row, col])**2
score = sqrt(s / (actual.shape[0] * actual.shape[1]))
# plot forecasts vs observations
for j in range(predicted.shape[1]):
show_plot(actual[:, j], predicted[:, j], j + 1)
return score, scores
# summarize scores
def summarize_scores(name, score, scores):
s_scores = ', '.join(['%.1f' % s for s in scores])
print('%s: [%.3f] %s' % (name, score, s_scores))
# convert history into inputs and outputs
def to_supervised(train, n_input, n_out=7):
# flatten data
data = train.reshape((train.shape[0]*train.shape[1], train.shape[2]))
X, y = list(), list()
in_start = 0
# step over the entire history one time step at a time
for _ in range(len(data)):
# define the end of the input sequence
in_end = in_start + n_input
out_end = in_end + n_out
# ensure we have enough data for this instance
if out_end <= len(data):
x_input = data[in_start:in_end, 0]
x_input = x_input.reshape((len(x_input), 1))
X.append(x_input)
y.append(data[in_end:out_end, 0])
# move along one time step
in_start += 1
return array(X), array(y)
# train the model
def build_model(train, n_input):
# prepare data
train_x, train_y = to_supervised(train, n_input)
# define parameters
verbose, epochs, batch_size = 0, 70, 16
n_timesteps, n_features, n_outputs = train_x.shape[1], train_x.shape[2], train_y.shape[1]
# define model
model = Sequential()
model.add(LSTM(200, activation='relu', input_shape=(n_timesteps, n_features)))
model.add(Dense(100, activation='relu'))
model.add(Dense(n_outputs))
model.compile(loss='mse', optimizer='adam')
# fit network
model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)
return model
# make a forecast
def forecast(model, history, n_input):
# flatten data
data = array(history)
data = data.reshape((data.shape[0]*data.shape[1], data.shape[2]))
# retrieve last observations for input data
input_x = data[-n_input:, 0]
# reshape into [1, n_input, 1]
input_x = input_x.reshape((1, len(input_x), 1))
# forecast the next week
yhat = model.predict(input_x, verbose=0)
# we only want the vector forecast
yhat = yhat[0]
return yhat
# evaluate a single model
def evaluate_model(train, test, n_input):
# fit model
model = build_model(train, n_input)
# history is a list of weekly data
history = [x for x in train]
# walk-forward validation over each week
predictions = list()
for i in range(len(test)):
# predict the week
yhat_sequence = forecast(model, history, n_input)
# store the predictions
predictions.append(yhat_sequence)
# get real observation and add to history for predicting the next week
history.append(test[i, :])
# evaluate predictions days for each week
predictions = array(predictions)
score, scores = evaluate_forecasts(test[:, :, 0], predictions)
return score, scores
# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0,
infer_datetime_format=True, parse_dates=['datetime'],
index_col=['datetime'])
# split into train and test
train, test = split_dataset(dataset.values)
# evaluate model and get scores
n_input = 7
score, scores = evaluate_model(train, test, n_input)
# summarize scores
summarize_scores('lstm', score, scores)
# plot scores
days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']
fig = pyplot.subplots()
pyplot.plot(days, scores, marker='o', label='lstm')
pyplot.show()
При его выполнении у меня отобразились следующие результаты
Давайте увеличим количество предыдущих дней, используемых в качестве входных данных, с 7 до 14 дней, изменив значение параметра n_input:
# evaluate model and get scores
n_input = 14Перезапуск примера с учётом выполненного изменения выведет сводную информацию о качестве модели.
Ваши результаты могут отличаться от представленных ниже. Попробуйте выполнить пример несколько раз.
По результатам видно, что значение общей ошибки RMSE снизилось до 370 киловатт. Поэтому можно предположить, что дальнейшая настройка размера n_input и, возможно, количества узлов модели может увеличить её эффективность.
lstm: [370.028] 387.4, 377.9, 334.0, 371.2, 367.1, 330.4, 415.1При сравнении значений RMSE по каждому дню друг с другом видно, что некоторые дни хуже, а другие лучше справляются с прогнозом по сравнению с использованием семидневных входных данных.
Можно предположить, что совместное использование двух входов с разными размерами – например, с помощью ансамбля, объединяющего два данных подхода, или единой модели («многоголовая» модель), считывающей обучающие данных разными способами, – способно принести пользу.
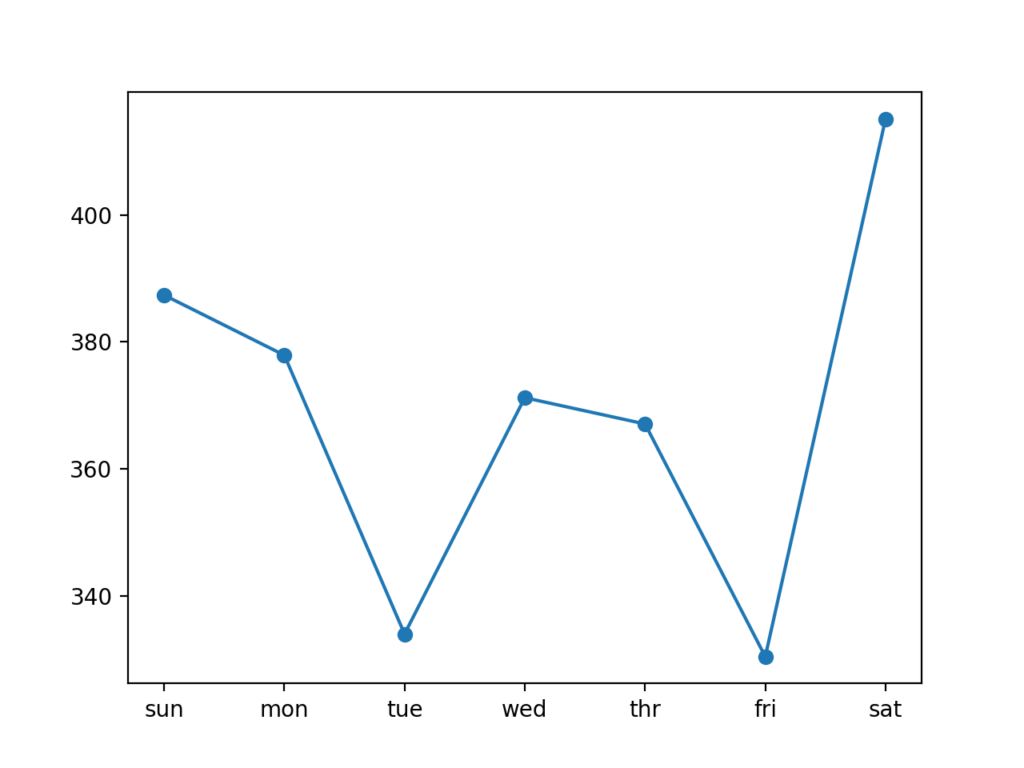
ДКП типа «кодировщик-декодировщик» на основе одномерных входных данных
В этом разделе рассказывается о том, как обновить ванильную модель до модели ДКП типа «кодировщик-декодировщик» (в англоязычной терминологии Encoder-Decoder LSTM. – Прим. пер.).
Модель не будет выводить векторную последовательность напрямую; она будет состоять из двух субмоделей – кодировщика, считывающего и кодирующего входную последовательность, и декодировщика, интерпретирующего кодированную входную последовательность и выполняющего точечное прогнозирование для каждого элемента в выходной последовательности.
Разница между моделями невелика: на практике они обе выводят прогноз в виде последовательности.
Особенность рассматриваемой в данном разделе модели в том, что ДКП используется в качестве декодировщика: слой с ДКП собирает информацию о выполнении прогнозирования в предыдущие дни в последовательности, а также накапливает внутреннее состояние при выводе каждой последовательности.
Рассмотрим подробнее, как определяется эта модель.
Как и прежде, определяется скрытый слой ДКП с 200 нейронами. Только этот слой будет выступать в роли декодировщика, который будет считывать входную последовательность и выводить вектор из 200 элементов (один выход на единицу) согласно выявленным из входной последовательности признакам. В качестве входных данных будут использованы 14 дней общего энергопотребления.
# define model
model = Sequential()
model.add(LSTM(200, activation='relu', input_shape=(n_timesteps, n_features)))В примере будет использована простая архитектура «кодировщик-декодировщик», которую легко реализовать с помощью Keras. Данная архитектура имеет много сходств с архитектурой ДКП типа «автокодировщик» (в англоязычной терминологии LSTM Autoencoder. – Прим. пер.).
Примечание:
ДКП типа «автокодировщик» – это одна из реализаций автокодировщика – разновидности ИНС, целью которой является кодирование входного малоразмерного скрытого пространства и последующего его декодирования – применительно к данным в виде последовательностей.
Сначала внутреннее представление входной последовательности повторяется несколько раз – по одному разу для каждого временного шага в выходной последовательности. Эта последовательность векторов будет представлена декодировщику ДКП.
model.add(RepeatVector(7))Затем определяется декодировщик в виде скрытого слоя ДКП с 200 нейронами.
Важно отметить, что декодировщик будет выводить всю последовательность, а не только вывод в конце последовательности, как было с кодировщиком. Это означает, что каждый из 200 нейронов будет связан с каждым днём прогнозируемой недели, что позволит определиться с тем, что именно нужно прогнозировать для каждого дня выходной последовательности.
model.add(LSTM(200, activation='relu', return_sequences=True))Далее следует полносвязный слой для интерпретации каждого временного шага в выходной последовательности перед окончательным выходным слоем. Важно отметить, что выходной слой прогнозирует один шаг в выходной последовательности, а не все семь дней сразу.
Это означает, что к каждому элементу в выходной последовательности будут применяться одинаковые слои: один и тот же полносвязный и выходной слои будут применены для обработки каждого временного шага, предоставляемого декодировщиком. Для этого слой интерпретации и выходной слой будут помещены в оболочку TimeDistributed, которая позволяет использовать обёрнутые слои для каждого временного шага.
model.add(TimeDistributed(Dense(100, activation='relu')))
model.add(TimeDistributed(Dense(1)))Это позволит ДКП-декодировщику установить связь между временными шагами в выходной последовательности и обёрнутыми полносвязными слоями, чтобы интерпретировать каждый из временных шагов по отдельности с использованием одних и тех же весовых коэффициентов. Альтернативным решением может быть сглаживание всей структуры, созданной декодировщиком, и прямой вывод вектора. Вы можете попробовать выполнить его в качестве расширения примера и посмотреть на результаты сравнения.
Таким образом, выход сети представляется в виде трёхмерного тензора с той же структурой, что и у входной последовательности: [образцы, временной интервал, признаки].
Имеется один признак – общая потребляемая мощность (в ежедневной форме) – и его семь лагированных наблюдений. Следовательно, один еженедельный прогноз будет иметь форму: [1, 7, 1].
Примечание:
Напоминание: в данном разделе рассматривается одномерная модель, то есть модель, в которой и набор входных признаков (X), и набор целевых данных (y) формируется на основе одного-единственного признака – общей потребляемой мощности.
Поэтому перед обучением модели необходимо преобразовать целевые данные (y) из двухмерной формы [образцы, признаки], использованной в предыдущем разделе, в трёхмерную форму.
# reshape output into [samples, timesteps, features]
train_y = train_y.reshape((train_y.shape[0], train_y.shape[1], 1))Обновлённая функция build_model() с учётом данных изменений представлена ниже.
# train the model
def build_model(train, n_input):
# prepare data
train_x, train_y = to_supervised(train, n_input)
# define parameters
verbose, epochs, batch_size = 0, 20, 16
n_timesteps, n_features, n_outputs = train_x.shape[1], train_x.shape[2], train_y.shape[1]
# reshape output into [samples, timesteps, features]
train_y = train_y.reshape((train_y.shape[0], train_y.shape[1], 1))
# define model
model = Sequential()
model.add(LSTM(200, activation='relu', input_shape=(n_timesteps, n_features)))
model.add(RepeatVector(n_outputs))
model.add(LSTM(200, activation='relu', return_sequences=True))
model.add(TimeDistributed(Dense(100, activation='relu')))
model.add(TimeDistributed(Dense(1)))
model.compile(loss='mse', optimizer='adam')
# fit network
model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)
return modelПолный пример кода одномерной модели ДКП типа «кодировщик-декодировщик» представлен ниже.
# univariate multi-step encoder-decoder lstm
from math import sqrt
from numpy import split
from numpy import array
from pandas import read_csv
from sklearn.metrics import mean_squared_error
from matplotlib import pyplot
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import LSTM
from keras.layers import RepeatVector
from keras.layers import TimeDistributed
# split a univariate dataset into train/test sets
def split_dataset(data):
# split into standard weeks
train, test = data[1:-328], data[-328:-6]
# restructure into windows of weekly data
train = array(split(train, len(train)/7))
test = array(split(test, len(test)/7))
return train, test
# evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
scores = list()
# calculate an RMSE score for each day
for i in range(actual.shape[1]):
# calculate mse
mse = mean_squared_error(actual[:, i], predicted[:, i])
# calculate rmse
rmse = sqrt(mse)
# store
scores.append(rmse)
# calculate overall RMSE
s = 0
for row in range(actual.shape[0]):
for col in range(actual.shape[1]):
s += (actual[row, col] - predicted[row, col])**2
score = sqrt(s / (actual.shape[0] * actual.shape[1]))
return score, scores
# summarize scores
def summarize_scores(name, score, scores):
s_scores = ', '.join(['%.1f' % s for s in scores])
print('%s: [%.3f] %s' % (name, score, s_scores))
# convert history into inputs and outputs
def to_supervised(train, n_input, n_out=7):
# flatten data
data = train.reshape((train.shape[0]*train.shape[1], train.shape[2]))
X, y = list(), list()
in_start = 0
# step over the entire history one time step at a time
for _ in range(len(data)):
# define the end of the input sequence
in_end = in_start + n_input
out_end = in_end + n_out
# ensure we have enough data for this instance
if out_end <= len(data):
x_input = data[in_start:in_end, 0]
x_input = x_input.reshape((len(x_input), 1))
X.append(x_input)
y.append(data[in_end:out_end, 0])
# move along one time step
in_start += 1
return array(X), array(y)
# train the model
def build_model(train, n_input):
# prepare data
train_x, train_y = to_supervised(train, n_input)
# define parameters
verbose, epochs, batch_size = 0, 20, 16
n_timesteps, n_features, n_outputs = train_x.shape[1], train_x.shape[2], train_y.shape[1]
# reshape output into [samples, timesteps, features]
train_y = train_y.reshape((train_y.shape[0], train_y.shape[1], 1))
# define model
model = Sequential()
model.add(LSTM(200, activation='relu', input_shape=(n_timesteps, n_features)))
model.add(RepeatVector(n_outputs))
model.add(LSTM(200, activation='relu', return_sequences=True))
model.add(TimeDistributed(Dense(100, activation='relu')))
model.add(TimeDistributed(Dense(1)))
model.compile(loss='mse', optimizer='adam')
# fit network
model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)
return model
# make a forecast
def forecast(model, history, n_input):
# flatten data
data = array(history)
data = data.reshape((data.shape[0]*data.shape[1], data.shape[2]))
# retrieve last observations for input data
input_x = data[-n_input:, 0]
# reshape into [1, n_input, 1]
input_x = input_x.reshape((1, len(input_x), 1))
# forecast the next week
yhat = model.predict(input_x, verbose=0)
# we only want the vector forecast
yhat = yhat[0]
return yhat
# evaluate a single model
def evaluate_model(train, test, n_input):
# fit model
model = build_model(train, n_input)
# history is a list of weekly data
history = [x for x in train]
# walk-forward validation over each week
predictions = list()
for i in range(len(test)):
# predict the week
yhat_sequence = forecast(model, history, n_input)
# store the predictions
predictions.append(yhat_sequence)
# get real observation and add to history for predicting the next week
history.append(test[i, :])
# evaluate predictions days for each week
predictions = array(predictions)
score, scores = evaluate_forecasts(test[:, :, 0], predictions)
return score, scores
# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# split into train and test
train, test = split_dataset(dataset.values)
# evaluate model and get scores
n_input = 14
score, scores = evaluate_model(train, test, n_input)
# summarize scores
summarize_scores('lstm', score, scores)
# plot scores
days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']
pyplot.plot(days, scores, marker='o', label='lstm')
pyplot.show()Выполнение кода осуществляет обучение модели и её оценку в виде отображения строки с общим значением RMSE за всю неделю и значением RMSE по каждому дню прогнозируемой недели на валидационной части набора данных.
В виду стохастической природы алгоритма ваши результаты могут отличаться от представленных далее. Вы можете попробовать выполнить код несколько раз.
В данном случае модель тоже справилась с прогнозом лучше, чем наивная модель: общее значение RMSE около 372 киловатт
lstm: [372.595] 379.5, 399.8, 339.6, 372.2, 370.9, 309.9, 424.8
График со значением ошибки RMSE по каждому дню прогнозируемой недели выполняется аналогично предыдущему разделу.
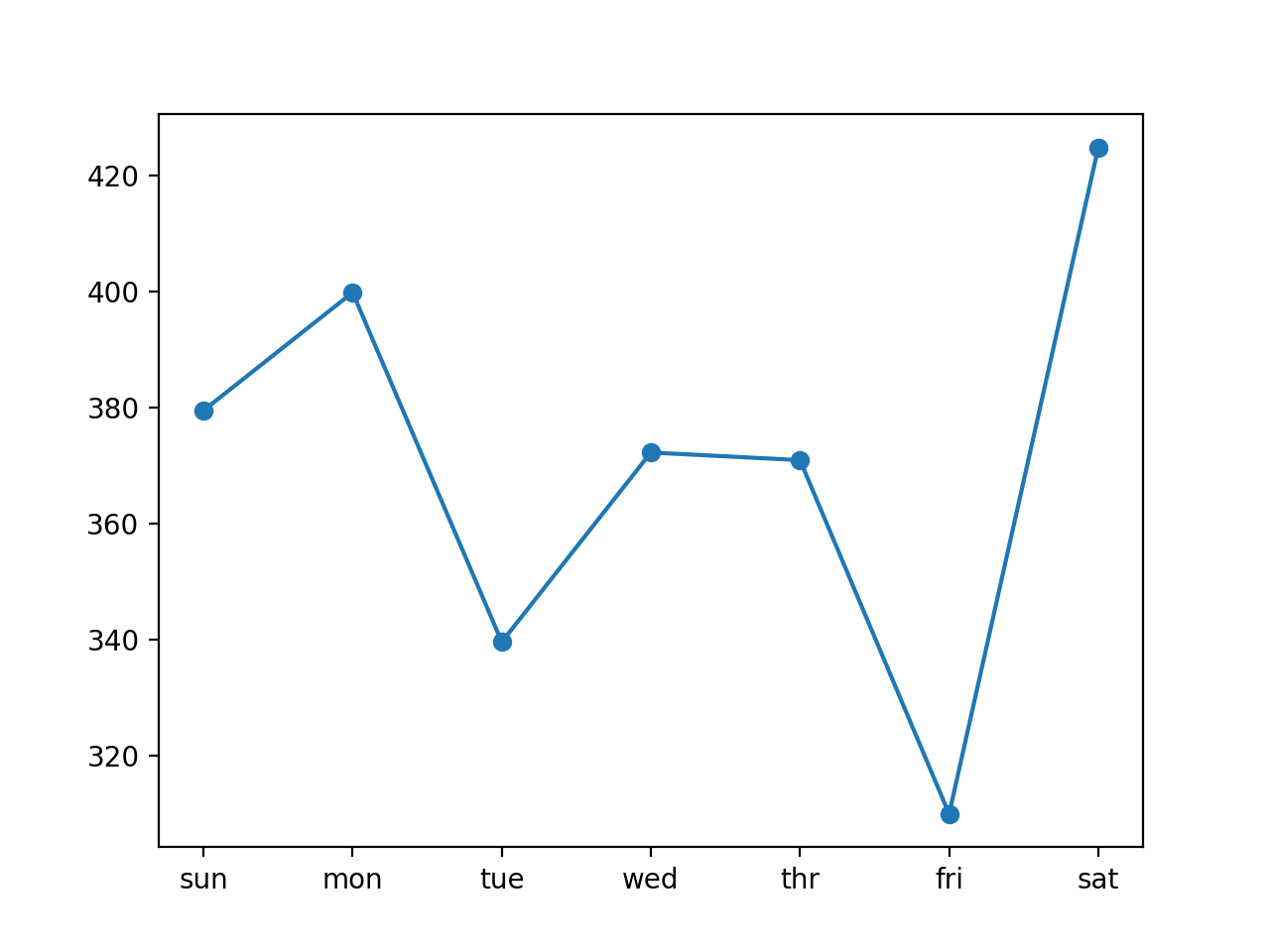
Примечание:
Для общего представления выведем совокупный график по всем временным интервалам
lstm: [369.602]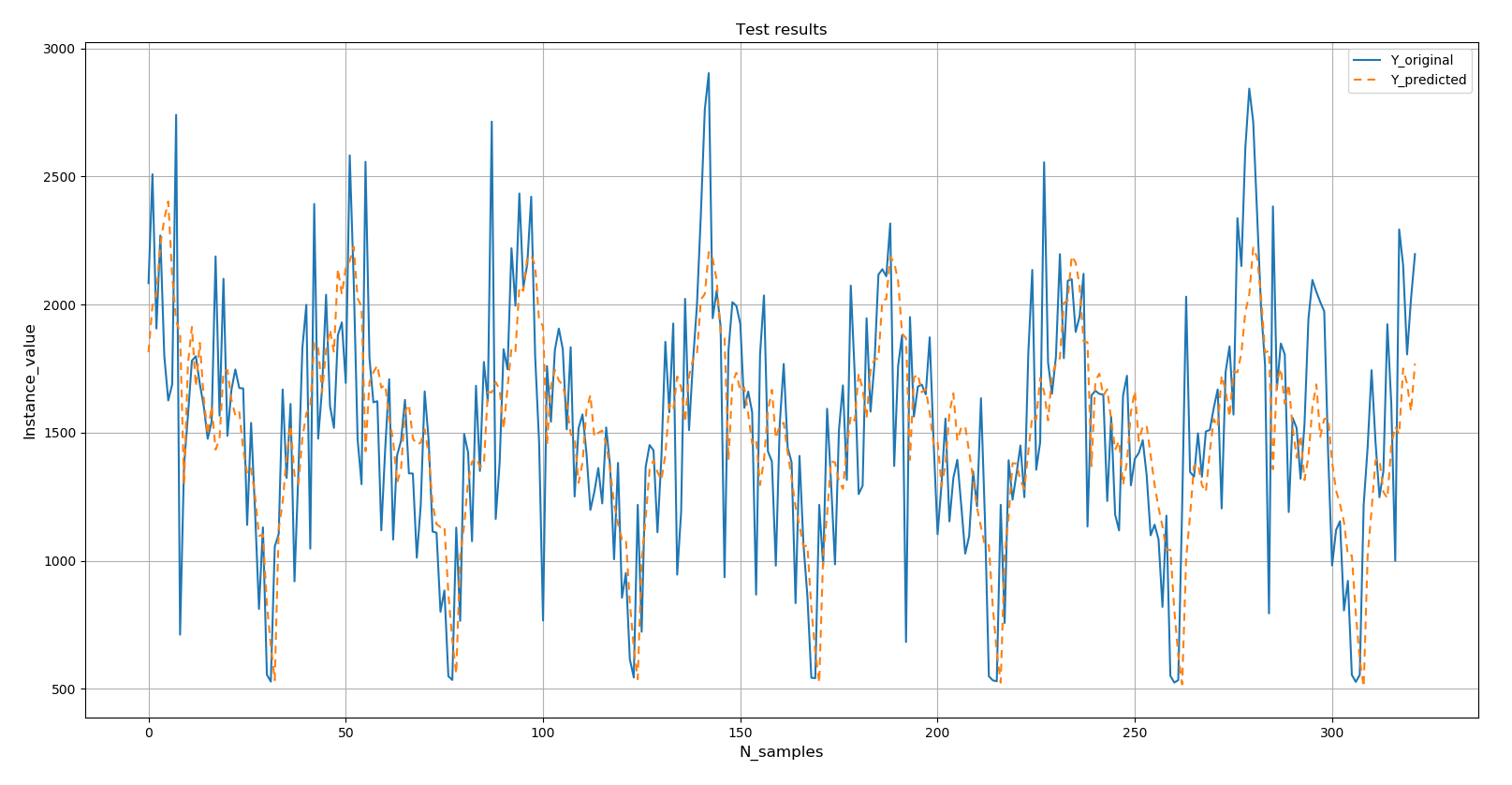
Видно, что волнообразная форма более-менее воспроизведена, однако большинство пик так и остались непокорёнными. Тут не то чтобы есть куда расти, а предстоит большая работа по дополнению кода. О некоторых техниках и методах, которые должны улучшить результаты моделирования, будет рассказано в конце статьи.
ДКП типа «кодировщик-декодировщик» на основе многомерных входных данных
В этом разделе будет рассмотрено обновление разработанной в предыдущем разделе модели ДКП типа «кодировщик-декодировщик», состоящее в том, чтобы для прогнозирования электроэнергии на следующую неделю использовать каждый из восьми признаков в виде одномерного временного ряда.
Для этого каждый из них будет представлен модели в виде отдельной входной последовательности.
В свою очередь ДКП создаст внутреннее представление для каждой входной последовательности, которые будут затем совместно использоваться для интерпретирования декодировщиком.
Использование многомерных входных данных полезно при решении проблем, когда выходная последовательность является некоторой функцией от наблюдений предыдущих временных интервалов множества различных признаков, а не только от прогнозируемого признака. Пока непонятно, подойдёт ли этот подход для решения проблемы прогнозирования потребления электроэнергии, поэтому необходимо исследовать этот вопрос.
Сначала выполним обновление подготовки обучающих данных, включив в неё все восемь признаков, а не только ежедневную общую потребляемую мощность, откорректировав одну строку:
X.append(data[in_start:in_end, :])Обновлённая функция to_supervised() с учётом данного изменения представлена ниже.
# convert history into inputs and outputs
def to_supervised(train, n_input, n_out=7):
# flatten data
data = train.reshape((train.shape[0]*train.shape[1], train.shape[2]))
X, y = list(), list()
in_start = 0
# step over the entire history one time step at a time
for _ in range(len(data)):
# define the end of the input sequence
in_end = in_start + n_input
out_end = in_end + n_out
# ensure we have enough data for this instance
if out_end <= len(data):
X.append(data[in_start:in_end, :])
y.append(data[in_end:out_end, 0])
# move along one time step
in_start += 1
return array(X), array(y)Также необходимо обновить функцию, используемую для выполнения прогнозов на основе обученной модели, чтобы использовать все восемь признаков на предыдущих временных интервалах.
Для этого внесём в неё небольшие изменения:
# retrieve last observations for input data
input_x = data[-n_input:, :]
# reshape into [1, n_input, n]
input_x = input_x.reshape((1, input_x.shape[0], input_x.shape[1]))Обновлённая функция forecast() с учётом данного изменения представлена ниже.
# make a forecast
def forecast(model, history, n_input):
# flatten data
data = array(history)
data = data.reshape((data.shape[0]*data.shape[1], data.shape[2]))
# retrieve last observations for input data
input_x = data[-n_input:, :]
# reshape into [1, n_input, n]
input_x = input_x.reshape((1, input_x.shape[0], input_x.shape[1]))
# forecast the next week
yhat = model.predict(input_x, verbose=0)
# we only want the vector forecast
yhat = yhat[0]
return yhatИспользуется та же архитектура и конфигурация модели, что и ранее, однако в виду восьмикратного увеличения количества входных данных количество тренировочных эпох увеличится с 20 до 50.
Полный пример кода многомерной модели ДКП типа «кодировщик-декодировщик» представлен ниже.
# multivariate multi-step encoder-decoder lstm
from math import sqrt
from numpy import split
from numpy import array
from pandas import read_csv
from sklearn.metrics import mean_squared_error
from matplotlib import pyplot
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import LSTM
from keras.layers import RepeatVector
from keras.layers import TimeDistributed
# split a univariate dataset into train/test sets
def split_dataset(data):
# split into standard weeks
train, test = data[1:-328], data[-328:-6]
# restructure into windows of weekly data
train = array(split(train, len(train)/7))
test = array(split(test, len(test)/7))
return train, test
# evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
scores = list()
# calculate an RMSE score for each day
for i in range(actual.shape[1]):
# calculate mse
mse = mean_squared_error(actual[:, i], predicted[:, i])
# calculate rmse
rmse = sqrt(mse)
# store
scores.append(rmse)
# calculate overall RMSE
s = 0
for row in range(actual.shape[0]):
for col in range(actual.shape[1]):
s += (actual[row, col] - predicted[row, col])**2
score = sqrt(s / (actual.shape[0] * actual.shape[1]))
return score, scores
# summarize scores
def summarize_scores(name, score, scores):
s_scores = ', '.join(['%.1f' % s for s in scores])
print('%s: [%.3f] %s' % (name, score, s_scores))
# convert history into inputs and outputs
def to_supervised(train, n_input, n_out=7):
# flatten data
data = train.reshape((train.shape[0]*train.shape[1], train.shape[2]))
X, y = list(), list()
in_start = 0
# step over the entire history one time step at a time
for _ in range(len(data)):
# define the end of the input sequence
in_end = in_start + n_input
out_end = in_end + n_out
# ensure we have enough data for this instance
if out_end <= len(data):
X.append(data[in_start:in_end, :])
y.append(data[in_end:out_end, 0])
# move along one time step
in_start += 1
return array(X), array(y)
# train the model
def build_model(train, n_input):
# prepare data
train_x, train_y = to_supervised(train, n_input)
# define parameters
verbose, epochs, batch_size = 0, 50, 16
n_timesteps, n_features, n_outputs = train_x.shape[1], train_x.shape[2], train_y.shape[1]
# reshape output into [samples, timesteps, features]
train_y = train_y.reshape((train_y.shape[0], train_y.shape[1], 1))
# define model
model = Sequential()
model.add(LSTM(200, activation='relu', input_shape=(n_timesteps, n_features)))
model.add(RepeatVector(n_outputs))
model.add(LSTM(200, activation='relu', return_sequences=True))
model.add(TimeDistributed(Dense(100, activation='relu')))
model.add(TimeDistributed(Dense(1)))
model.compile(loss='mse', optimizer='adam')
# fit network
model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)
return model
# make a forecast
def forecast(model, history, n_input):
# flatten data
data = array(history)
data = data.reshape((data.shape[0]*data.shape[1], data.shape[2]))
# retrieve last observations for input data
input_x = data[-n_input:, :]
# reshape into [1, n_input, n]
input_x = input_x.reshape((1, input_x.shape[0], input_x.shape[1]))
# forecast the next week
yhat = model.predict(input_x, verbose=0)
# we only want the vector forecast
yhat = yhat[0]
return yhat
# evaluate a single model
def evaluate_model(train, test, n_input):
# fit model
model = build_model(train, n_input)
# history is a list of weekly data
history = [x for x in train]
# walk-forward validation over each week
predictions = list()
for i in range(len(test)):
# predict the week
yhat_sequence = forecast(model, history, n_input)
# store the predictions
predictions.append(yhat_sequence)
# get real observation and add to history for predicting the next week
history.append(test[i, :])
# evaluate predictions days for each week
predictions = array(predictions)
score, scores = evaluate_forecasts(test[:, :, 0], predictions)
return score, scores
# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# split into train and test
train, test = split_dataset(dataset.values)
# evaluate model and get scores
n_input = 14
score, scores = evaluate_model(train, test, n_input)
# summarize scores
summarize_scores('lstm', score, scores)
# plot scores
days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']
pyplot.plot(days, scores, marker='o', label='lstm')
pyplot.show()Выполнение кода осуществляет обучение модели и её оценку в виде отображения строки с общим значением RMSE за всю неделю и значением RMSE по каждому дню прогноза на валидационной части набора данных.
Эксперимент показал, что модель ДКП типа «кодировщик-декодировщик» на основе многомерных входных данных выглядит менее стабильной, чем одномерная модель. Это может быть связано с различным масштабом данных входных признаков.
В виду стохастической природы алгоритма ваши результаты могут отличаться от представленных далее. Вы можете попробовать выполнить код несколько раз.
Видно, что и в этом случае модель справилась с прогнозом лучше, чем наивная модель: общее значение RMSE около 376 киловатт.
lstm: [376.273] 378.5, 381.5, 328.4, 388.3, 361.2, 308.0, 467.2
Ниже представлен график RMSE на каждый день прогнозируемой недели.
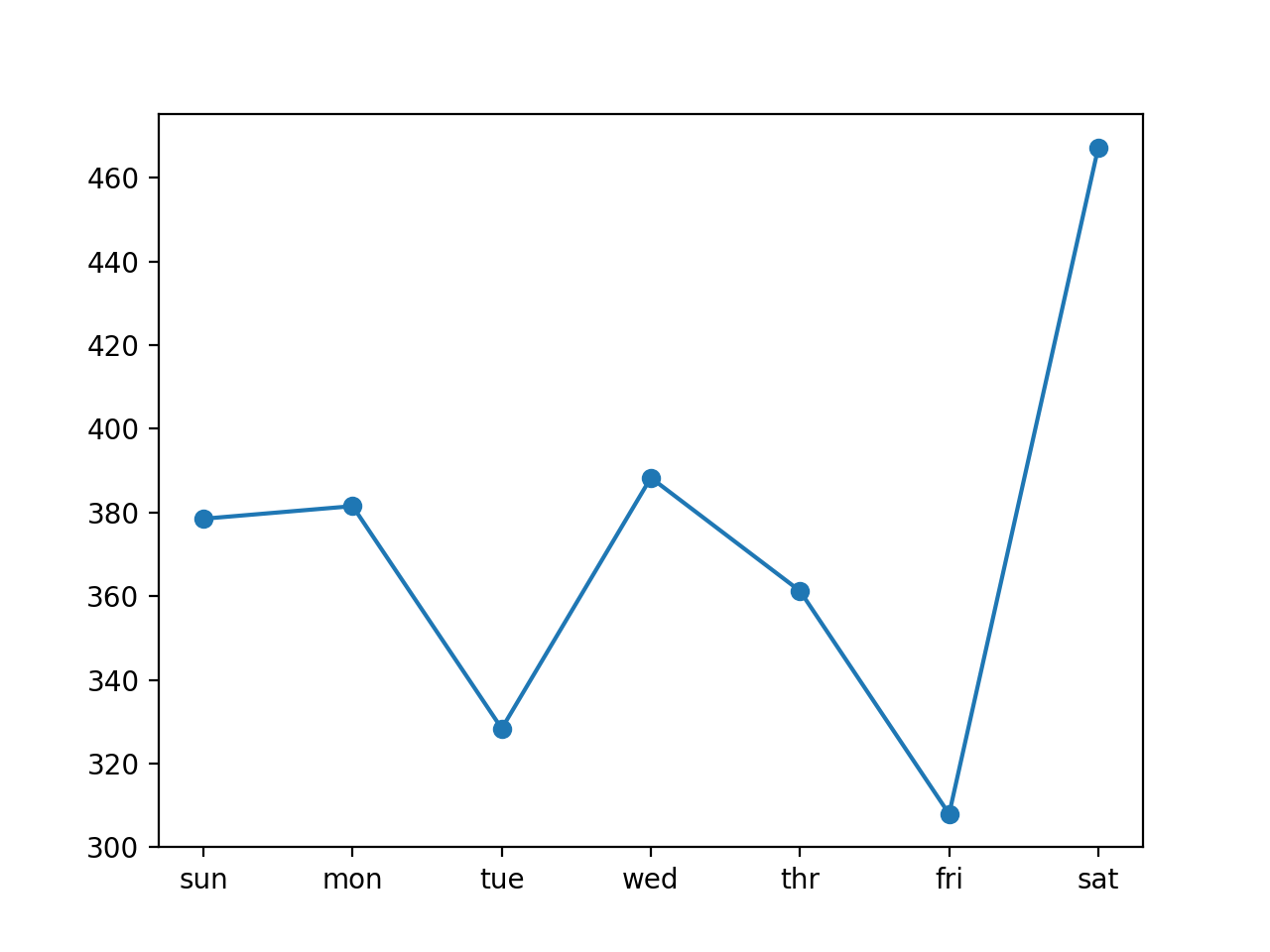
ДКП типа «кодировщик-декодировщик» с добавлением свёрточного слоя в качестве кодировщика на основе одномерных входных данных
Свёрточная нейронная сеть (СНС) может быть использована в качестве кодировщика в архитектуре ДКП типа «кодировщик-декодировщик».
При этом СНС не поддерживает ввод данных в виде последовательностей напрямую; вместо этого одномерная СНС способна последовательно считывать элементы входной последовательности и автоматически изучать характерные признаки (по сути свёртка работает методом перекрывающегося скользящего окна, которое перемещается не по тензору с изображением, а по входной последовательности. – Прим. пер.). Затем они могут быть интерпретированы декодировщиком ДКП как обычно. Совместное использование СНС и ДКП относится к гибридным моделям (СНС-ДКП).
Как и модель ДКП, СНС принимает на входе трёхмерные тензоры, только каждый из признаков считывается как отдельный канал, что в конечном итоге имеет тот же эффект.
Мы упростим пример, сосредоточившись на одномерной модели СНС-ДКП. Однако модель можно легко обновить, чтобы использовать все признаки (оставлено в качестве упражнения).
Примечание:
В Keras одномерные свёрточные сети создаются с помощью слоя Conv1D.
Окно свёртки — это одномерное окно на оси времени: оси с индексом 1 во входном тензоре.
Источник: Глубокое обучение на Python, Франсуа Шолле.
Как и прежде, в качестве входных данных будут использованы 14 дней общего энергопотребления.
Мы определим простую и в то же время эффективную архитектуру СНС в качестве кодировщика, состоящую из двух свёрточных уровней, за которым следует слой объединения по максимуму (MaxPooling1D), результаты которого далее сглаживаются.
Примечание:
Max-pooling – это операция выбора максимального значения из соседних. Её предназначение заключается «в агрессивном уменьшении разрешения карты признаков, во многом подобное свёртке с пробелами». Подробнее в книге Ф. Шолле.
Первый свёрточный слой последовательно считывает элементы входной последовательности и проецирует результаты на карты признаков. Второй свёрточный слой выполняет ту же операцию с той лишь разницей, что считывание выполняется уже на картах признаков, созданных первым слоем, пытаясь тем самым усилить любые существенные характеристики. Каждый свёрточный слой будет использовать 64 фильтра и считывать входные последовательности с размером ядра в три временных шага.
Слой объединения по максимуму выполняет упрощающие преобразования карты признаков, сохраняя ¼ значений с наибольшим (максимальным) сигналом. После слоя объединения по максимуму извлечённые карты признаков преобразуются в один длинный вектор, которым затем будет использован в качестве входных данных для процесса декодирования.
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(n_timesteps,n_features)))
model.add(Conv1D(filters=64, kernel_size=3, activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())Определение декодировщика аналогично предыдущему разделу.
Единственное дополнительное изменение – установить количество эпох обучения равным 20.
Обновлённая функция build_model() с учётом данных изменений представлена ниже.
# train the model
def build_model(train, n_input):
# prepare data
train_x, train_y = to_supervised(train, n_input)
# define parameters
verbose, epochs, batch_size = 0, 20, 16
n_timesteps, n_features, n_outputs = train_x.shape[1], train_x.shape[2], train_y.shape[1]
# reshape output into [samples, timesteps, features]
train_y = train_y.reshape((train_y.shape[0], train_y.shape[1], 1))
# define model
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(n_timesteps,n_features)))
model.add(Conv1D(filters=64, kernel_size=3, activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(RepeatVector(n_outputs))
model.add(LSTM(200, activation='relu', return_sequences=True))
model.add(TimeDistributed(Dense(100, activation='relu')))
model.add(TimeDistributed(Dense(1)))
model.compile(loss='mse', optimizer='adam')
# fit network
model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)
return modelТеперь всё готово, чтобы испытать архитектуру «кодировщик-декодировщик» со свёрточным слоем в качестве кодировщика.
Полный пример кода одномерной модели ДКП типа «кодировщик-декодировщик» с добавлением свёрточного слоя в качестве кодировщика представлен ниже.
# univariate multi-step encoder-decoder cnn-lstm
from math import sqrt
from numpy import split
from numpy import array
from pandas import read_csv
from sklearn.metrics import mean_squared_error
from matplotlib import pyplot
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import LSTM
from keras.layers import RepeatVector
from keras.layers import TimeDistributed
from keras.layers.convolutional import Conv1D
from keras.layers.convolutional import MaxPooling1D
# split a univariate dataset into train/test sets
def split_dataset(data):
# split into standard weeks
train, test = data[1:-328], data[-328:-6]
# restructure into windows of weekly data
train = array(split(train, len(train)/7))
test = array(split(test, len(test)/7))
return train, test
# evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
scores = list()
# calculate an RMSE score for each day
for i in range(actual.shape[1]):
# calculate mse
mse = mean_squared_error(actual[:, i], predicted[:, i])
# calculate rmse
rmse = sqrt(mse)
# store
scores.append(rmse)
# calculate overall RMSE
s = 0
for row in range(actual.shape[0]):
for col in range(actual.shape[1]):
s += (actual[row, col] - predicted[row, col])**2
score = sqrt(s / (actual.shape[0] * actual.shape[1]))
return score, scores
# summarize scores
def summarize_scores(name, score, scores):
s_scores = ', '.join(['%.1f' % s for s in scores])
print('%s: [%.3f] %s' % (name, score, s_scores))
# convert history into inputs and outputs
def to_supervised(train, n_input, n_out=7):
# flatten data
data = train.reshape((train.shape[0]*train.shape[1], train.shape[2]))
X, y = list(), list()
in_start = 0
# step over the entire history one time step at a time
for _ in range(len(data)):
# define the end of the input sequence
in_end = in_start + n_input
out_end = in_end + n_out
# ensure we have enough data for this instance
if out_end <= len(data):
x_input = data[in_start:in_end, 0]
x_input = x_input.reshape((len(x_input), 1))
X.append(x_input)
y.append(data[in_end:out_end, 0])
# move along one time step
in_start += 1
return array(X), array(y)
# train the model
def build_model(train, n_input):
# prepare data
train_x, train_y = to_supervised(train, n_input)
# define parameters
verbose, epochs, batch_size = 0, 20, 16
n_timesteps, n_features, n_outputs = train_x.shape[1], train_x.shape[2], train_y.shape[1]
# reshape output into [samples, timesteps, features]
train_y = train_y.reshape((train_y.shape[0], train_y.shape[1], 1))
# define model
model = Sequential()
model.add(Conv1D(filters=64, kernel_size=3, activation='relu', input_shape=(n_timesteps,n_features)))
model.add(Conv1D(filters=64, kernel_size=3, activation='relu'))
model.add(MaxPooling1D(pool_size=2))
model.add(Flatten())
model.add(RepeatVector(n_outputs))
model.add(LSTM(200, activation='relu', return_sequences=True))
model.add(TimeDistributed(Dense(100, activation='relu')))
model.add(TimeDistributed(Dense(1)))
model.compile(loss='mse', optimizer='adam')
# fit network
model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)
return model
# make a forecast
def forecast(model, history, n_input):
# flatten data
data = array(history)
data = data.reshape((data.shape[0]*data.shape[1], data.shape[2]))
# retrieve last observations for input data
input_x = data[-n_input:, 0]
# reshape into [1, n_input, 1]
input_x = input_x.reshape((1, len(input_x), 1))
# forecast the next week
yhat = model.predict(input_x, verbose=0)
# we only want the vector forecast
yhat = yhat[0]
return yhat
# evaluate a single model
def evaluate_model(train, test, n_input):
# fit model
model = build_model(train, n_input)
# history is a list of weekly data
history = [x for x in train]
# walk-forward validation over each week
predictions = list()
for i in range(len(test)):
# predict the week
yhat_sequence = forecast(model, history, n_input)
# store the predictions
predictions.append(yhat_sequence)
# get real observation and add to history for predicting the next week
history.append(test[i, :])
# evaluate predictions days for each week
predictions = array(predictions)
score, scores = evaluate_forecasts(test[:, :, 0], predictions)
return score, scores
# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# split into train and test
train, test = split_dataset(dataset.values)
# evaluate model and get scores
n_input = 14
score, scores = evaluate_model(train, test, n_input)
# summarize scores
summarize_scores('lstm', score, scores)
# plot scores
days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']
pyplot.plot(days, scores, marker='o', label='lstm')
pyplot.show()Выполнение кода осуществляет обучение модели и её оценку в виде отображения строки с общим значением RMSE за всю неделю и значением RMSE по каждому дню прогноза на валидационной части набора данных.
Небольшой эксперимент показал, что использование двух свёрточных слоёв делает модель более стабильной, чем при использовании только одного слоя.
В виду стохастической природы алгоритма ваши результаты могут отличаться от представленных далее. Вы можете попробовать выполнить код несколько раз.
Видно, что и в этом случае модель справилась с прогнозом лучше, чем наивная модель: общее значение RMSE около 372 киловатт.
lstm: [372.055] 383.8, 381.6, 339.1, 371.8, 371.8, 319.6, 427.2
Ниже представлен график RMSE на каждый день прогнозируемой недели.
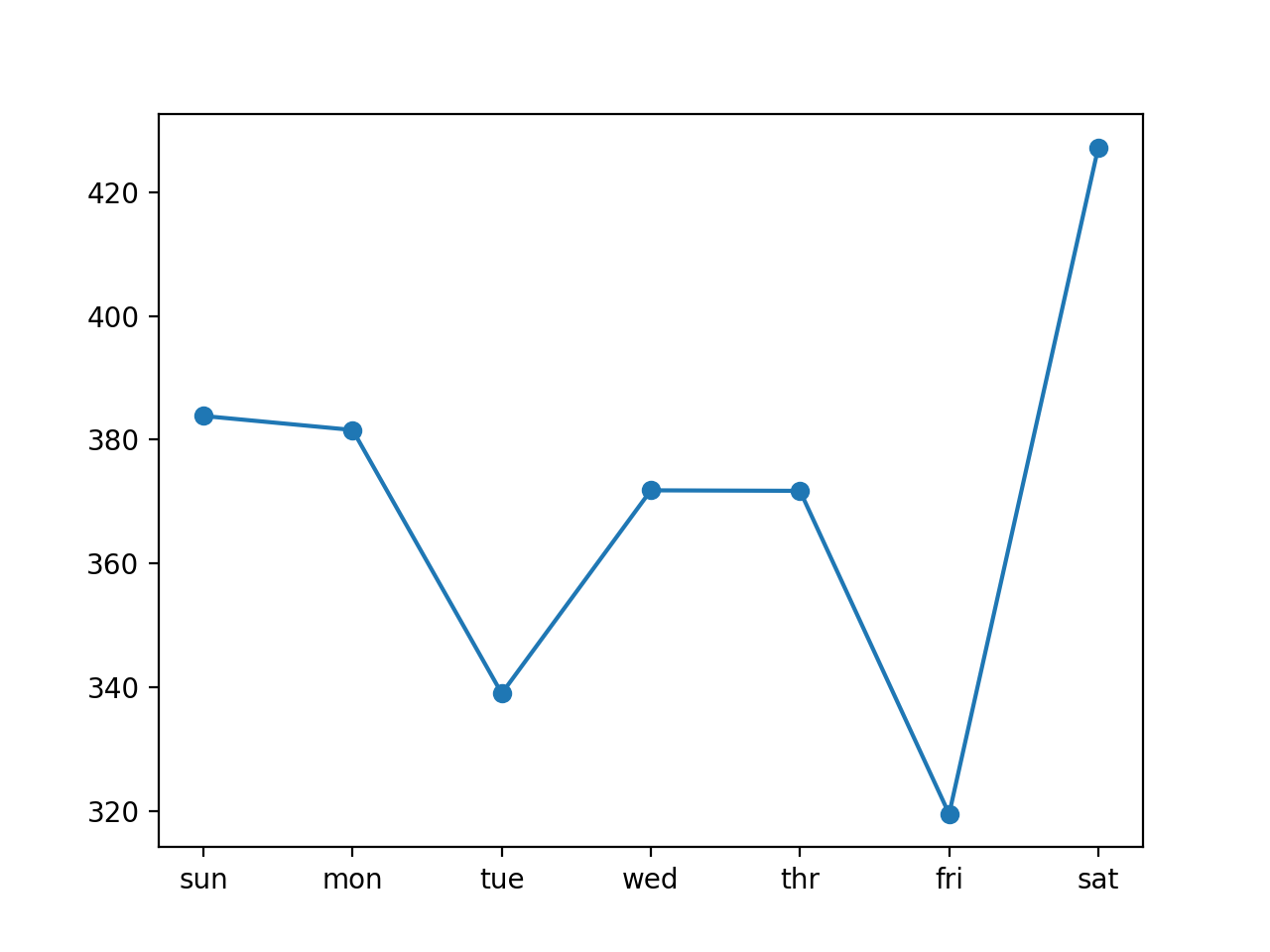
Свёрточная ДКП типа «кодировщик-декодировщик» на основе одномерных входных данных
Расширением подхода СНС-ДКП является выполнение свёрток СНС (например, как СНС считывает данные входной последовательности) как часть ДКП для каждого временного интервала.
Эта комбинация называется «свёрточная ДКП» (в англоязычной терминологии Convolutional LSTM, или ConvLSTM для краткости. – Прим. пер.). Как и СНС-ДКП она также используется для пространственно-временных данных.
В отличие от модели ДКП, считывающей данные напрямую для вычисления внутреннего состояния и переходов состояний, и модели СНС-ДКП, интерпретирующей выходные данные моделей СНС, свёрточная ДКП использует свёртки непосредственно как часть чтения входных данных в ячейках LSTM (имеется в виду, что не только входные, но и рекуррентные преобразования подвергаются свёртке; другими словами, внутренние матрицы заменяются операциями свёртки, в результате чего данные, проходящие через ячейки свёрточной ДКП сохраняют входное измерение вместо того, чтобы быть просто одномерным вектором. – Прим. пер.).
Более полная информация о том, как выводятся уравнения для свёрточной ДКП, представлена в следующей статье:
- Свёрточная сеть ДКП: новый подход на основе машинного обучения для прогнозирования текущей погоды, 2015.
Библиотека Keras предоставляет класс под названием ConvLSTM2D для работы со свёрточной ДКП на основе двухмерных данных (имеются в виду двухмерные изображения (ширина и высота). – Прим. пер.). Он также может быть настроен для выполнения прогнозирования одномерных временных рядов (1Д).
По умолчанию класс ConvLSTM2D ожидает, что входные данные будут иметь следующую (пятимерную. – Прим. пер.) форму:
[выборки, временной интервал, строки, столбцы, каналы]Где каждый из временных интервалов определяется как изображение (строки * столбцы) в виде точек (пикселей).
Предположим, что в качестве входных данных мы используем ежедневные данные за предыдущие две недели. В виду того, что мы работает с одномерной последовательностью общего потребления электроэнергии, то её можно интерпретировать как одну строку с 14 столбцами.
В этом случае свёрточная ДКП выполнит однократное чтение: ДКП будет считывать один временной интервал продолжительностью 14 дней и выполнять на них свёрточную операцию.
Это не идеально.
Вместо этого мы может разделить последовательность продолжительностью 14 дней на две подпоследовательности продолжительностью по 7 дней каждая. Затем свёрточная ДКП будет последовательно считывать элементы двух временных интервалов протяжённостью 7 дней с выполнением операции свёртки на каждом из них.
Таким образом, с учётом поставленной задачи вход для слоя ConvLSTM2D будет:
[n, 2, 1, 7, 1]Или:
- Образцы: n, количество примеров в обучающей части набора данных.
- Время: 2, для двух подпоследовательностей, на которые мы разбили последовательность в 14 дней.
- Строки: 1, для одномерной формы каждой подпоследовательности.
- Столбцы: 7, по семь дней в каждой подпоследовательности.
- Каналы: 1, для единственного признака, который используется в качестве входных данных.
Вы можете исследовать и другие возможные конфигурации: например, передачу на вход модели данных за 21 день в виде 3-х подпоследовательностей по 7 дней каждая и/или предоставление данных 8-ми признаков (каналов).
Теперь подготовим данные для модели ConvLSTM2D.
Сначала мы должны изменить форму обучающей части набора данных в ожидаемую моделью пятимерную структуру [выборки, временной интервал, строки, столбцы, каналы].
# reshape into subsequences [samples, time steps, rows, cols, channels]
train_x = train_x.reshape((train_x.shape[0], n_steps, 1, n_length, n_features))Затем определим в качестве кодировщика свёрточную ДКП (первый скрытый слой), за которым следует слой сглаживания данных для их подготовки к декодированию.
model.add(ConvLSTM2D(filters=64, kernel_size=(1,3), activation='relu', input_shape=(n_steps, 1, n_length, n_features)))
model.add(Flatten())При этом количество подпоследовательностей (n_steps) и длина каждой подпоследовательности (n_length) будут выделены и представлены в качестве аргументов функции.
В остальном конфигурация модели и её обучение аналогичны предыдущему разделу. Функция build_model() с учётом данных изменений представлена ниже.
# train the model
def build_model(train, n_steps, n_length, n_input):
# prepare data
train_x, train_y = to_supervised(train, n_input)
# define parameters
verbose, epochs, batch_size = 0, 20, 16
n_timesteps, n_features, n_outputs = train_x.shape[1], train_x.shape[2], train_y.shape[1]
# reshape into subsequences [samples, time steps, rows, cols, channels]
train_x = train_x.reshape((train_x.shape[0], n_steps, 1, n_length, n_features))
# reshape output into [samples, timesteps, features]
train_y = train_y.reshape((train_y.shape[0], train_y.shape[1], 1))
# define model
model = Sequential()
model.add(ConvLSTM2D(filters=64, kernel_size=(1,3), activation='relu', input_shape=(n_steps, 1, n_length, n_features)))
model.add(Flatten())
model.add(RepeatVector(n_outputs))
model.add(LSTM(200, activation='relu', return_sequences=True))
model.add(TimeDistributed(Dense(100, activation='relu')))
model.add(TimeDistributed(Dense(1)))
model.compile(loss='mse', optimizer='adam')
# fit network
model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)
return modelЭта модель ожидает пятимерные данные в качестве входных данных. Поэтому также необходимо обновить подготовку образцов в функции forecast() для последующего выполнения прогнозирования.
# reshape into [samples, time steps, rows, cols, channels]
input_x = input_x.reshape((1, n_steps, 1, n_length, 1))Обновлённая функция forecast() с учётом данного изменения и выделения параметров n_steps и n_length в качестве её аргументов представлена ниже.
# make a forecast
def forecast(model, history, n_steps, n_length, n_input):
# flatten data
data = array(history)
data = data.reshape((data.shape[0]*data.shape[1], data.shape[2]))
# retrieve last observations for input data
input_x = data[-n_input:, 0]
# reshape into [samples, time steps, rows, cols, channels]
input_x = input_x.reshape((1, n_steps, 1, n_length, 1))
# forecast the next week
yhat = model.predict(input_x, verbose=0)
# we only want the vector forecast
yhat = yhat[0]
return yhatТеперь у нас есть все элементы, чтобы начать выполнение оценки архитектуры «кодировщик-декодировщик» для интервального прогнозирования временных рядов, в которой в роли кодировщика используется свёрточная ДКП.
Полный пример кода одномерной свёрточной модели ДКП типа «кодировщик-декодировщик» представлен ниже.
# univariate multi-step encoder-decoder convlstm
from math import sqrt
from numpy import split
from numpy import array
from pandas import read_csv
from sklearn.metrics import mean_squared_error
from matplotlib import pyplot
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import Flatten
from keras.layers import LSTM
from keras.layers import RepeatVector
from keras.layers import TimeDistributed
from keras.layers import ConvLSTM2D
# split a univariate dataset into train/test sets
def split_dataset(data):
# split into standard weeks
train, test = data[1:-328], data[-328:-6]
# restructure into windows of weekly data
train = array(split(train, len(train)/7))
test = array(split(test, len(test)/7))
return train, test
# evaluate one or more weekly forecasts against expected values
def evaluate_forecasts(actual, predicted):
scores = list()
# calculate an RMSE score for each day
for i in range(actual.shape[1]):
# calculate mse
mse = mean_squared_error(actual[:, i], predicted[:, i])
# calculate rmse
rmse = sqrt(mse)
# store
scores.append(rmse)
# calculate overall RMSE
s = 0
for row in range(actual.shape[0]):
for col in range(actual.shape[1]):
s += (actual[row, col] - predicted[row, col])**2
score = sqrt(s / (actual.shape[0] * actual.shape[1]))
return score, scores
# summarize scores
def summarize_scores(name, score, scores):
s_scores = ', '.join(['%.1f' % s for s in scores])
print('%s: [%.3f] %s' % (name, score, s_scores))
# convert history into inputs and outputs
def to_supervised(train, n_input, n_out=7):
# flatten data
data = train.reshape((train.shape[0]*train.shape[1], train.shape[2]))
X, y = list(), list()
in_start = 0
# step over the entire history one time step at a time
for _ in range(len(data)):
# define the end of the input sequence
in_end = in_start + n_input
out_end = in_end + n_out
# ensure we have enough data for this instance
if out_end <= len(data):
x_input = data[in_start:in_end, 0]
x_input = x_input.reshape((len(x_input), 1))
X.append(x_input)
y.append(data[in_end:out_end, 0])
# move along one time step
in_start += 1
return array(X), array(y)
# train the model
def build_model(train, n_steps, n_length, n_input):
# prepare data
train_x, train_y = to_supervised(train, n_input)
# define parameters
verbose, epochs, batch_size = 0, 20, 16
n_timesteps, n_features, n_outputs = train_x.shape[1], train_x.shape[2], train_y.shape[1]
# reshape into subsequences [samples, time steps, rows, cols, channels]
train_x = train_x.reshape((train_x.shape[0], n_steps, 1, n_length, n_features))
# reshape output into [samples, timesteps, features]
train_y = train_y.reshape((train_y.shape[0], train_y.shape[1], 1))
# define model
model = Sequential()
model.add(ConvLSTM2D(filters=64, kernel_size=(1,3), activation='relu', input_shape=(n_steps, 1, n_length, n_features)))
model.add(Flatten())
model.add(RepeatVector(n_outputs))
model.add(LSTM(200, activation='relu', return_sequences=True))
model.add(TimeDistributed(Dense(100, activation='relu')))
model.add(TimeDistributed(Dense(1)))
model.compile(loss='mse', optimizer='adam')
# fit network
model.fit(train_x, train_y, epochs=epochs, batch_size=batch_size, verbose=verbose)
return model
# make a forecast
def forecast(model, history, n_steps, n_length, n_input):
# flatten data
data = array(history)
data = data.reshape((data.shape[0]*data.shape[1], data.shape[2]))
# retrieve last observations for input data
input_x = data[-n_input:, 0]
# reshape into [samples, time steps, rows, cols, channels]
input_x = input_x.reshape((1, n_steps, 1, n_length, 1))
# forecast the next week
yhat = model.predict(input_x, verbose=0)
# we only want the vector forecast
yhat = yhat[0]
return yhat
# evaluate a single model
def evaluate_model(train, test, n_steps, n_length, n_input):
# fit model
model = build_model(train, n_steps, n_length, n_input)
# history is a list of weekly data
history = [x for x in train]
# walk-forward validation over each week
predictions = list()
for i in range(len(test)):
# predict the week
yhat_sequence = forecast(model, history, n_steps, n_length, n_input)
# store the predictions
predictions.append(yhat_sequence)
# get real observation and add to history for predicting the next week
history.append(test[i, :])
# evaluate predictions days for each week
predictions = array(predictions)
score, scores = evaluate_forecasts(test[:, :, 0], predictions)
return score, scores
# load the new file
dataset = read_csv('household_power_consumption_days.csv', header=0, infer_datetime_format=True, parse_dates=['datetime'], index_col=['datetime'])
# split into train and test
train, test = split_dataset(dataset.values)
# define the number of subsequences and the length of subsequences
n_steps, n_length = 2, 7
# define the total days to use as input
n_input = n_length * n_steps
score, scores = evaluate_model(train, test, n_steps, n_length, n_input)
# summarize scores
summarize_scores('lstm', score, scores)
# plot scores
days = ['sun', 'mon', 'tue', 'wed', 'thr', 'fri', 'sat']
pyplot.plot(days, scores, marker='o', label='lstm')
pyplot.show()Выполнение кода осуществляет обучение модели и её оценку в виде отображения строки с общим значением RMSE за всю неделю и значением RMSE по каждому дню прогноза на валидационной части набора данных.
Небольшой эксперимент показал, что использование двух свёрточных слоёв делает модель более стабильной, чем при использовании только одного слоя.
Видно, что и в этом случае модель справилась с прогнозом лучше: общее значение RMSE около 367 киловатт.
lstm: [367.929] 416.3, 379.7, 334.7, 362.3, 374.7, 284.8, 406.7
Ниже представлен график RMSE на каждый день прогнозируемой недели.
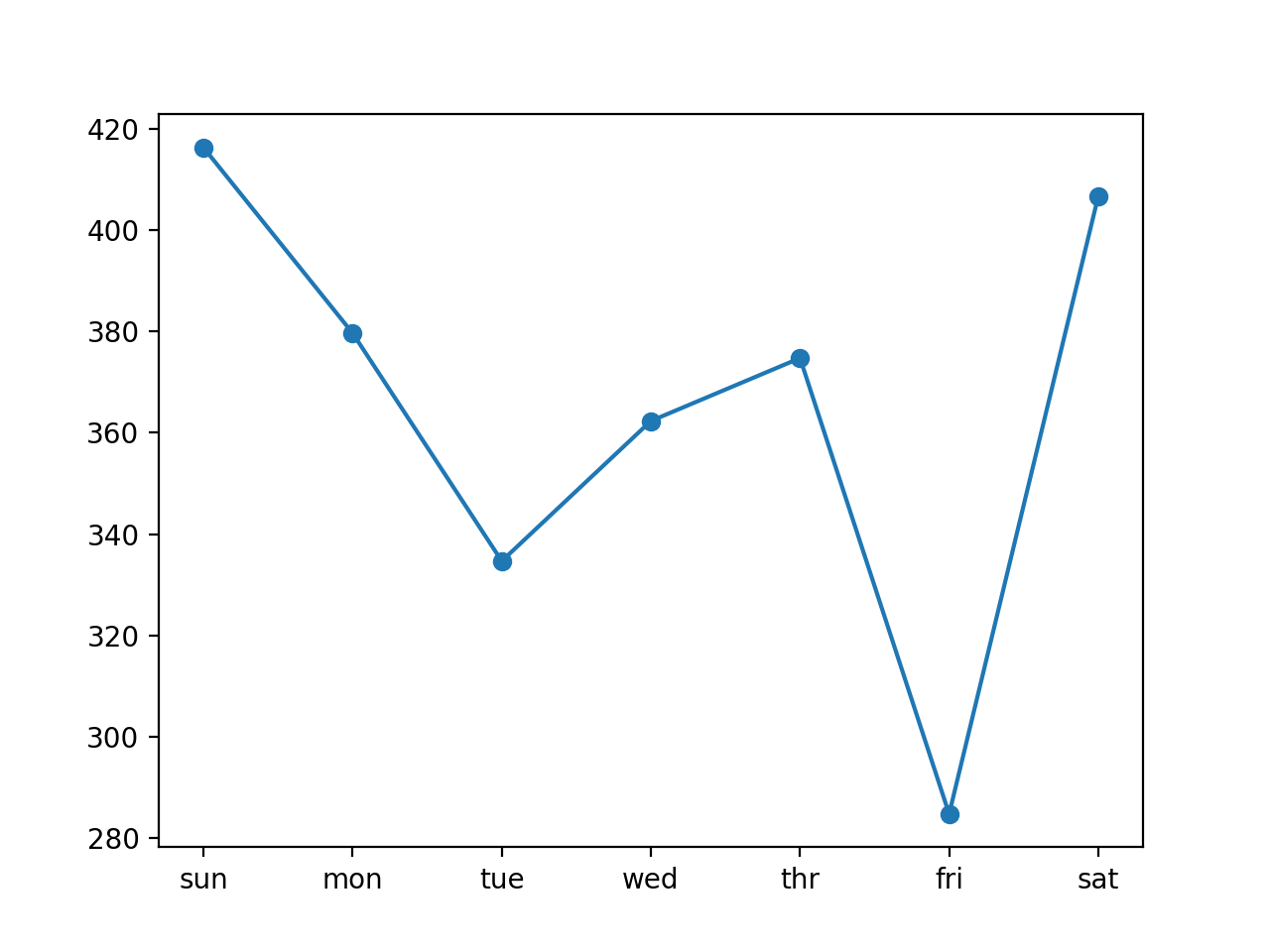
Дополнительные задания
В этом разделе перечислено несколько проектов, выходящих за рамки данного руководства, которые наверняка вас заинтересуют.
- Величина входа. Экспериментируйте с большим или меньшим количество дней в качестве входных данных для модели – например: 3 дня, 21 день, 30 дней и более.
- Отладка модели. Настройте структуру и гиперпараметры модели, чтобы повысить качество прогнозов модели в среднем.
- Масштабирование данных. Посмотрите как масштабирование данных, например, стандартизация или нормализация, коррелирует с улучшением качества прогнозов любой из представленных моделей ДКП.
- Мониторинг в процессе обучения и проверки. Контролируйте качество работы модели с помощью кривых обучения на этапах обучения и проверки, а также среднеквадратичной ошибки, чтобы настроить оптимальную структуру и гиперпараметры модели ДКП.
Если вы всё-таки дойдёте до этих заданий, дайте мне знать (видимо, автор в курсе, что редкая птица долетит до середины Днепра :). – Прим. пер.).
Рекомендуемая литература
Для тех, кто хочет узнать больше по этой теме. Здесь указаны важные источники.
Публикации
- 4 стратегии выполнения интервального прогнозирования временных рядов
- Глубокое обучение с рекуррентными нейронными сетями: ускоренный курс
- Введение в рекуррентные нейронные сети с долгой кратковременной памятью: круглый стол с экспертами
- О пригодности ДКП для прогнозирования временных рядов
- Свёрточные нейронные сети с долгой краткосрочной памятью
- Как с помощью Keras подготовить модель типа «кодировщик-декодировщик» для выполнения прогнозирования «последовательность в последовательность»
API
- pandas.read_csv API
- pandas.DataFrame.resample API
- Resample Offset Aliases
- sklearn.metrics.mean_squared_error API
- numpy.split API
Статьи
- Набор данных «Домовое потребление электроэнергии», архив UCI Machine Learning
- Питание переменного тока, Wikipedia
- Свёрточная сеть ДКП: новый подход на основе машинного обучения для прогнозирования текущей погоды, 2015
Заключение
Итак, теперь вы знаете как подготовить рекуррентные нейронные сети с долгой кратковременной памятью, чтобы выполнить интервальное прогнозирование временных рядов домового потребления электроэнергии.
В частности:
- Как подготовить и оценить ДКП типа «кодировщик-декодировщик» для интервального прогнозирования временных рядов на основе как одномерных, так и многомерных входных данных.
- Как подготовить и оценить ДКП типа «кодировщик-декодировщик» с добавлением свёрточного слоя в качестве кодировщика для интервального прогнозирования временных рядов.
- Как подготовить и оценить свёрточную ДКП типа «кодировщик-декодировщик» для интервального прогнозирования временных рядов.
Есть вопросы?
Задавайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить (это не примечание. – Прим. пер.).
Заметьте, что это была часть главы из моей книги «Глубокое обучение: прогнозирование временных рядов», в которой вы найдёте ещё больше пошаговых руководств для изучения методов глубокого обучения применительно к прогнозированию временных рядов.
17 авг. 2022 г.
читать 2 мин
В статистике простая линейная регрессия — это метод, который мы можем использовать для количественной оценки взаимосвязи между переменной-предиктором x и переменной отклика y.
Когда мы проводим простую линейную регрессию, мы получаем «линию наилучшего соответствия», которая описывает взаимосвязь между x и y, которую можно записать как:
ŷ = б 0 + б 1 х
куда:
- ŷ – прогнозируемое значение переменной отклика
- b 0 – точка пересечения с осью y
- b 1 – коэффициент регрессии
- x – значение переменной-предиктора
Иногда мы заинтересованы в использовании этой линии наилучшего соответствия для построения интервала предсказания для заданного значения x 0 , который является интервалом вокруг предсказанного значения ŷ 0 таким образом, что существует 95% вероятность того, что реальное значение y в население, соответствующее x 0 , находится внутри этого интервала.
Формула для расчета интервала прогнозирования для заданного значения x 0 записывается как:
ŷ 0 +/- t α/2,df=n-2 * se
куда:
se = S yx √(1 + 1/n + (x 0 – x ) 2 /SS x )
Формула может показаться немного пугающей, но на самом деле ее легко вычислить в Excel. Далее мы рассмотрим пример использования этой формулы для расчета интервала прогнозирования для заданного значения в Excel.
Пример: как построить интервал прогнозирования в Excel
Следующий набор данных показывает количество часов обучения вместе с экзаменационными баллами, полученными 15 разными студентами:
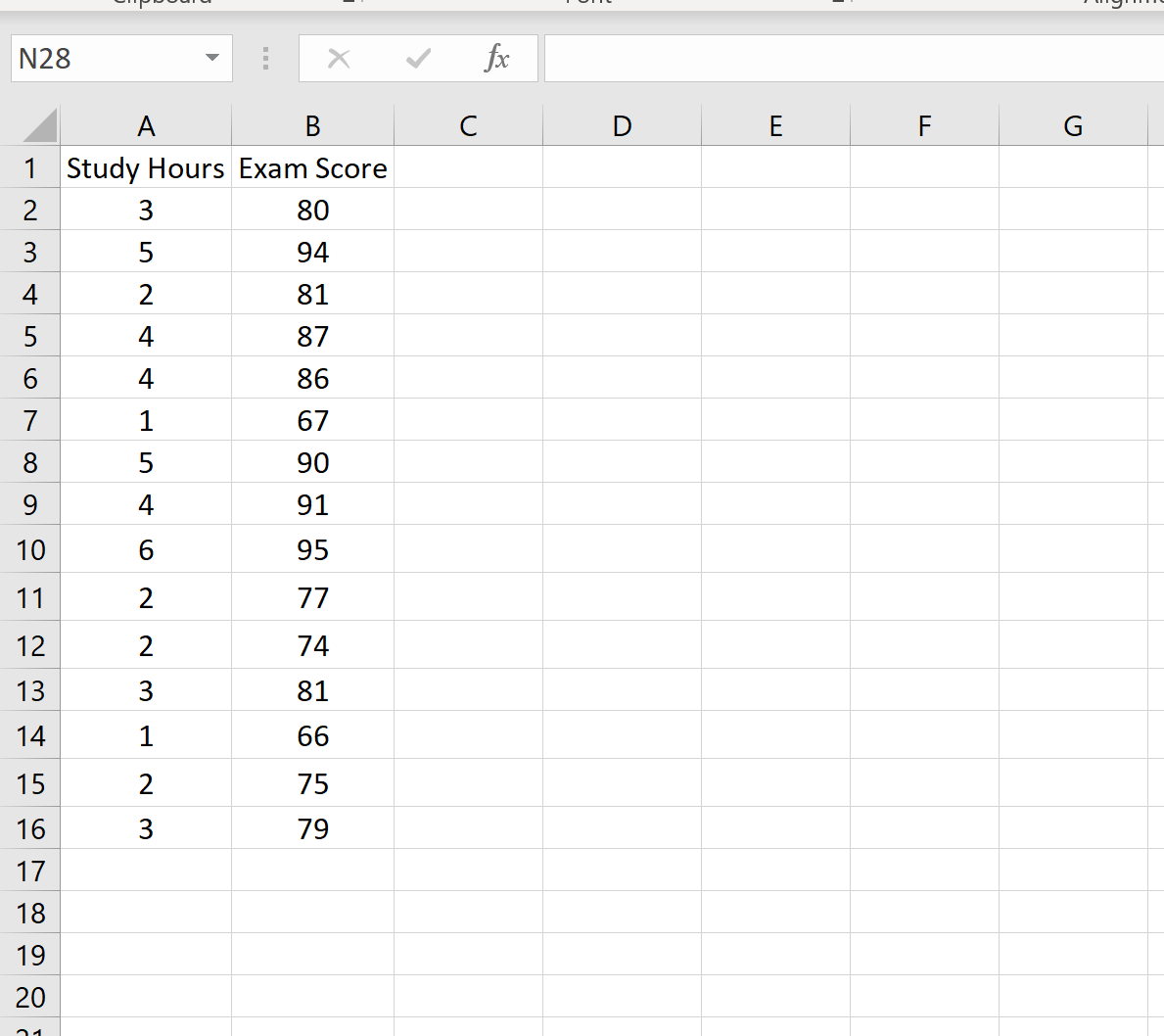
Предположим, мы хотим создать 95-процентный интервал предсказания для значения x 0 = 3. То есть мы хотим создать такой интервал, при котором существует 95-процентная вероятность того, что результат экзамена находится в пределах этого интервала для студента, который учится на 3 часа.
На следующем снимке экрана показано, как рассчитать все необходимые значения для получения этого интервала прогнозирования.
Примечание.Формулы в столбце F показывают, как были рассчитаны значения в столбце E.
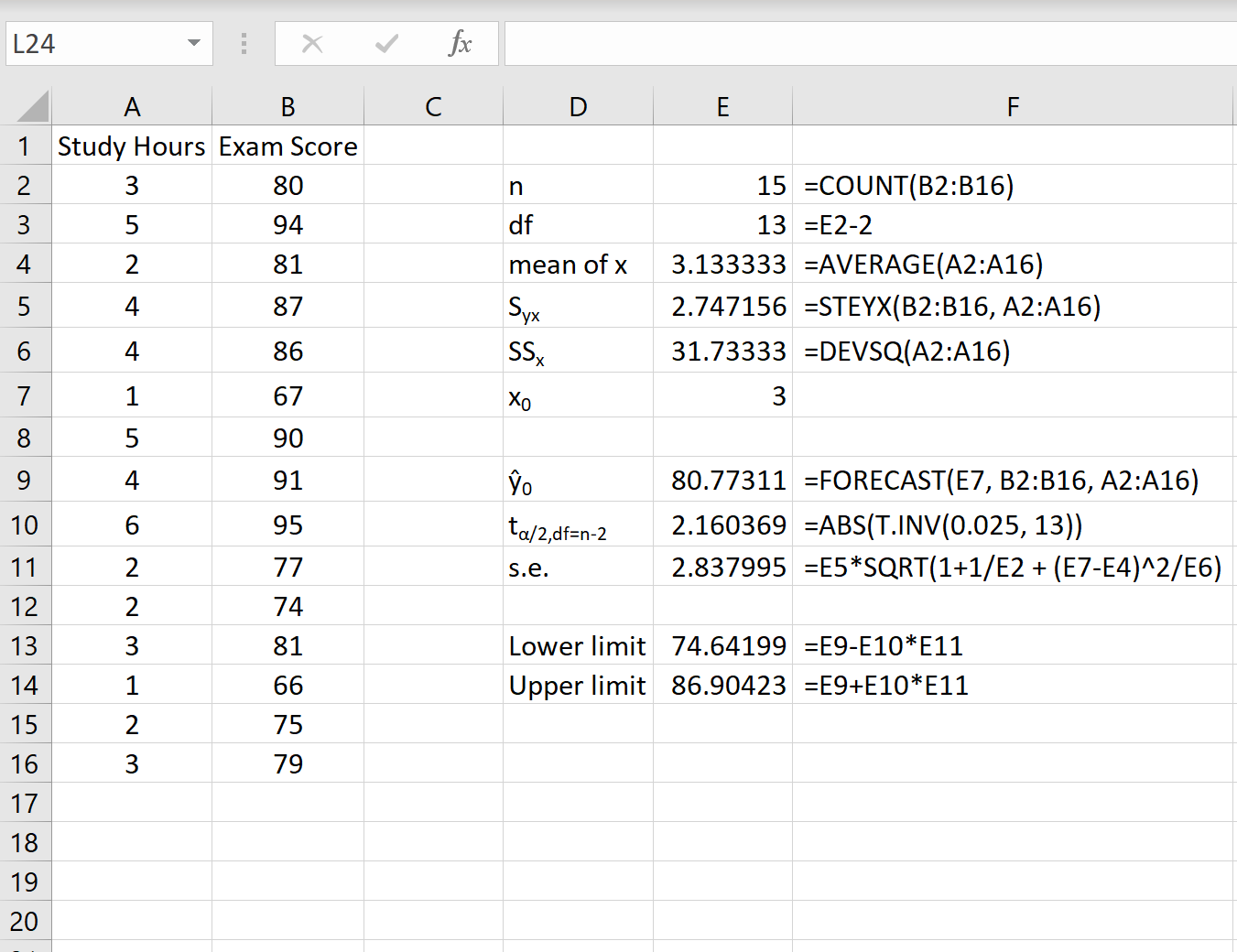
Интервал предсказания 95% для значения x 0 = 3 равен (74,64, 86,90).То есть мы прогнозируем с вероятностью 95%, что студент, который занимается 3 часа, получит от 74,64 до 86,90 баллов.
Несколько замечаний по используемым расчетам:
- Чтобы вычислить t-критическое значение t α/2,df=n-2 , мы использовали α/2 = 0,05/2 = 0,25, поскольку нам нужен интервал прогнозирования 95%. Обратите внимание, что более высокие интервалы прогнозирования (например, интервал прогнозирования 99%) приведут к более широким интервалам. И наоборот, более низкий интервал прогнозирования (например, интервал прогнозирования 90%) приведет к более узкому интервалу.
- Мы использовали формулу =ПРОГНОЗ() , чтобы получить предсказанное значение для ŷ 0 , но формула =ПРОГНОЗ.ЛИНЕЙНАЯ() вернет точно такое же значение.

