|
5,56 |
5,43 |
5,47 |
5,47 |
5,33 |
5,37 |
5,43 |
5,54 |
5,61 |
|
5,33 |
5,43 |
5,61 |
5,11 |
5,43 |
5,33 |
5,54 |
5,33 |
5,11 |
|
5,54 |
5,43 |
5,33 |
5,54 |
5,43 |
5,43 |
5,43 |
5,33 |
5,11 |
|
5,43 |
5,43 |
5,43 |
5,33 |
5,4 |
5,43 |
5,47 |
5,68 |
5,47 |
|
5,43 |
5,68 |
5,21 |
5,33 |
5,58 |
5,47 |
5,47 |
5,21 |
5,54 |
|
5,64 |
5,47 |
5,27 |
5,27 |
5,37 |
5,33 |
5,47 |
5,47 |
5,54 |
|
5,4 |
5,58 |
5,47 |
5,27 |
5,05 |
5,79 |
5,79 |
5,64 |
5,64 |
|
5,71 |
5,85 |
5,47 |
5,47 |
5,43 |
5,47 |
5,54 |
5,64 |
5,64 |
|
5,79 |
5,03 |
5,33 |
5,68 |
5,43 |
5,61 |
5,54 |
5,64 |
5,54 |
|
5,39 |
5,33 |
5,21 |
5,68 |
5,54 |
5,33 |
5,21 |
5,21 |
5,81 |
|
5,27 |
5,64 |
5,27 |
5,27 |
5,33 |
5,37 |
5,27 |
5,54 |
5,54 |
|
5,47 |
Таблица.
.1
Пример. По
результатам выборочного исследования
100 однотипных предприятий получены
данные объема основных фондов
Построение
интервального вариационного ряда
распределения включает следующие этапы.
1. Определение
среди имеющихся наблюдений минимального
и максимального
значения признака. В данном примере это
будут=5,03
и=5,85.
2. Определение
размаха варьирования признака
R=–
=5,85-5,03=0,82
3.Определение длины
интервала по формуле
объем
выборки. В данном примере
4. Определение
граничных значений интервалов
.
Так каки
являются случайными величинами,
рекомендуется отступить влево от нижнего
предела варьирования ().
За нижнюю границу
первого интервала предлагается принимать
величину, равную
.
Если окажется, что,
хотя по смыслу величина не отрицательная,
то можно принять.
Верхняя граница
первого интервала
.
Тогда, если–верхняя
границаi-го
интервала (причём
),
то,
и т.д. Построение интервалов продолжается
до тех пор, пока начало следующего по
порядку интервала не будет равным или
больше.
В примере граничные
значения составят:
,
,
,
и т.д.Границы последовательных интервалов
записывают в графе 1 таблицы 1.2.
5. Группировка
результатов наблюдений.
П
статистические данные в том порядке, в
каком они записаны в таблице 1.1, и значения
признака разносим по соответствующим
интервалам, обозначая их так
(по одному штриху для каждого
наблюдения). Так как граничные значения
признака могут совпадать с границами
интервалов, то условимся включать
варианты, большие, чем нижняя граница
интервала (),
и меньшие или равные верхней границе
().
Общее количество штрихов, отмеченных
в интервале (табл. 1.2, графа 2) дает его
частоту (табл. 1.2, графа 3). В результате
получим статистический ряд распределения
частот (табл. 1.2, графа 1 и 3).
Примечание. Число
интервалов обычно берут равным от 7 до
11 в зависимости от числа наблюдений и
точности измерений с таким расчетом,
чтобы интервалы были достаточно наполнены
частотами. Если получают интервалы с
нулевыми частотами, то нужно увеличить
ширину интервала (особенно в середине
интервального ряда).
|
Интервалы |
Подсчет |
Частота |
Накопленная |
|
4,97-5,08 5,08-5,19 5,19-5,30 5,30-5,41 5,41-5,52 5,52-5,63 5,63-5,74 5,74-5,85 |
|
2 3 12 19 29 18 13 4 |
2 5 17 36 65 83 96 100 |
|
100 |
Таблица 1.2.
Интервальный ряд распределения объемов
основных фондов 100 предприятий
2. Вычисление выборочных характеристик распределения (непосредственно)
Для вычисления
средней арифметической, дисперсии,
коэффициентов ассиметрии и эксцесса
рекомендуется следующий порядок
вычислений.
Заменяем интервальный
ряд дискретным, для чего все значения
признака в пределах интервала приравниваем
к его серединному значению, и считаем,
что частота относится к середине
интервала. Значения середин интервалов
равны
.
Для удобства
вычислений целесообразно составить
вспомогательную таблицу 1.3. Заменяя
середины интервалов заносят в графу 1,
соответствующие частоты в графу и т.д.
|
Интервалы |
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
4,97-5,08 5,08-5,19 5,19-5,30 5,30-5,41 5,41-5,52 5,52-5,63 5,63-5,74 5,74-5,85 |
5,03 5,14 5,25 5,36 5,47 5,58 5,69 5,80 |
2 3 12 19 29 18 13 4 |
2 5 17 36 65 83 96 100 |
10,06 15,42 63,00 101,84 158,63 100,44 73,97 23,20 |
50,60 79,26 330,75 545,86 867,71 560,46 420,89 134,56 |
-0,4356 -0,3256 -0,2156 -0,1056 0,0044 0,1144 0,2244 0,3344 |
|
100 |
546,56 |
2990,09 |
Таблица 1.3
Вспомогательная таблица для вычисления
выборочных характеристик
|
|
|
|
|
|
8 |
9 |
10 |
11 |
|
-0,8712 -0,9768 -2,5872 -2,0064 0,1276 2,0592 2,9172 1,3376 |
0,37949 0,31805 0,55780 0,21188 0,00056 0,23557 0,65462 0,44729 |
-0,1653 -0,10356 -0,12026 -0,02237 0,00000 0,02695 0,14690 0,14957 |
0,07201 0,03372 0,025928 0,00236 0,00000 0,00308 0,03296 0,05002 |
|
0 |
2,80526 |
0,08808 |
0,22008 |
В таблице
.
Пользуясь таблицей
1.3, вычислим среднюю арифметическую: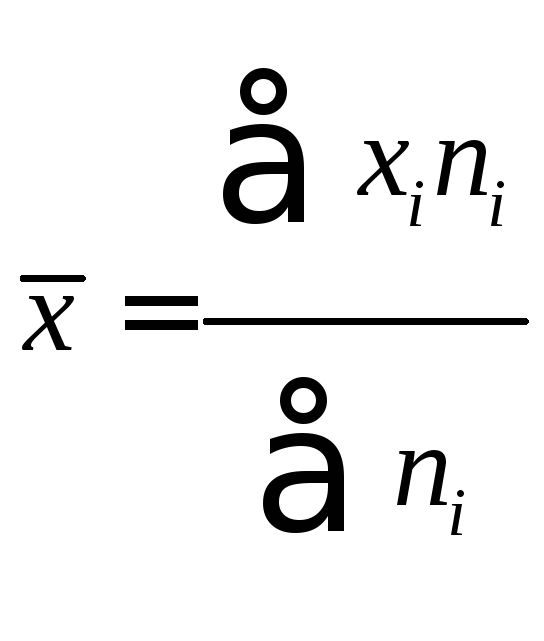
В нашем примеремлн.
руб. и характеризует среднее положение
наблюдаемых значений. Выборочный
центральный момент к-го порядка равен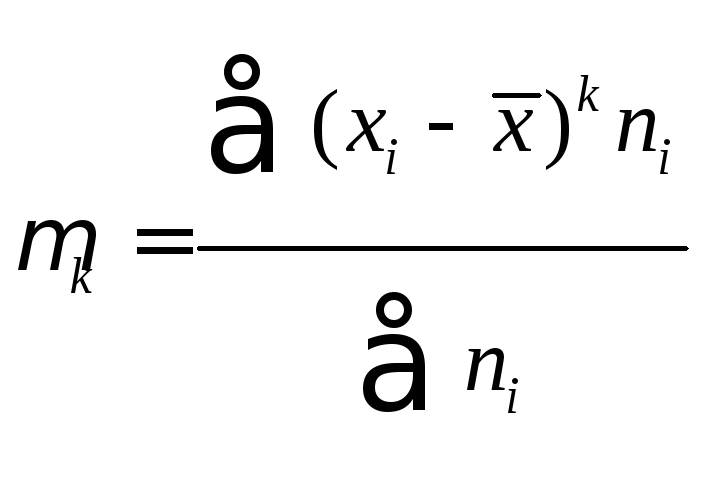
Для проверки правильности вычисленияи ввода в микрокалькулятор значений
,
рассчитывают:
В нашем примере
тождество выполняется. В итоговой строке
столбца 4 табл. 1.3. имеем 0.
В данном примере
.
Выборочная дисперсия
равна
центральному моменту второго порядка:
=
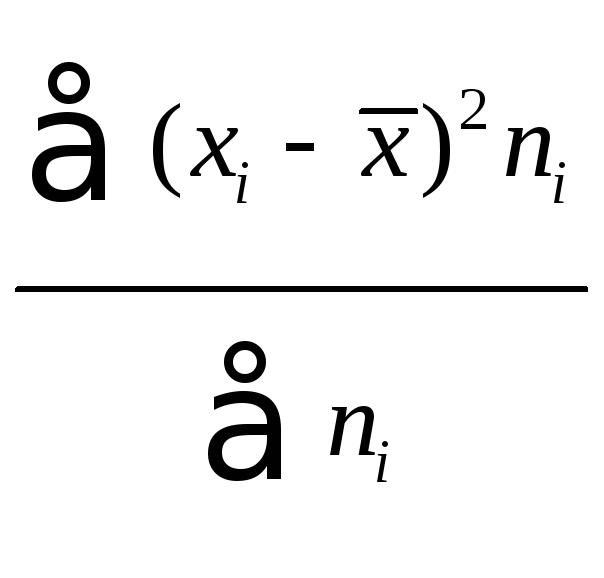
.
В нашем примере
=0,028,
а выборочное среднее квадратичное
отклонениемлн.руб.
Дисперсию можно
подсчитать и по-другому
В нашем примере
Выборочные
коэффициенты асимметрии
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Интервальный вариационный ряд и его характеристики
- Построение интервального вариационного ряда по данным эксперимента
- Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
- Выборочная средняя, мода и медиана. Симметрия ряда
- Выборочная дисперсия и СКО
- Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
- Алгоритм исследования интервального вариационного ряда
- Примеры
п.1. Построение интервального вариационного ряда по данным эксперимента
Интервальный вариационный ряд – это ряд распределения, в котором однородные группы составлены по признаку, меняющемуся непрерывно или принимающему слишком много значений.
Общий вид интервального вариационного ряда
| Интервалы, (left.left[a_{i-1},a_iright.right)) | (left.left[a_{0},a_1right.right)) | (left.left[a_{1},a_2right.right)) | … | (left.left[a_{k-1},a_kright.right)) |
| Частоты, (f_i) | (f_1) | (f_2) | … | (f_k) |
Здесь k – число интервалов, на которые разбивается ряд.
Размах вариации – это длина интервала, в пределах которой изменяется исследуемый признак: $$ F=x_{max}-x_{min} $$
Правило Стерджеса
Эмпирическое правило определения оптимального количества интервалов k, на которые следует разбить ряд из N чисел: $$ k=1+lfloorlog_2 Nrfloor $$ или, через десятичный логарифм: $$ k=1+lfloor 3,322cdotlg Nrfloor $$
Скобка (lfloor rfloor) означает целую часть (округление вниз до целого числа).
Шаг интервального ряда – это отношение размаха вариации к количеству интервалов, округленное вверх до определенной точности: $$ h=leftlceilfrac Rkrightrceil $$
Скобка (lceil rceil) означает округление вверх, в данном случае не обязательно до целого числа.
Алгоритм построения интервального ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Найти размах вариации (R=x_{max}-x_{min})
Шаг 2. Найти оптимальное количество интервалов (k=1+lfloorlog_2 Nrfloor)
Шаг 3. Найти шаг интервального ряда (h=leftlceilfrac{R}{k}rightrceil)
Шаг 4. Найти узлы ряда: $$ a_0=x_{min}, a_i=1_0+ih, i=overline{1,k} $$ Шаг 5. Найти частоты (f_i) – число попаданий значений признака в каждый из интервалов (left.left[a_{i-1},a_iright.right)).
На выходе: интервальный ряд с интервалами (left.left[a_{i-1},a_iright.right)) и частотами (f_i, i=overline{1,k})
Заметим, что поскольку шаг h находится с округлением вверх, последний узел (a_kgeq x_{max}).
Например:
Проведено 100 измерений роста учеников старших классов.
Минимальный рост составляет 142 см, максимальный – 197 см.
Найдем узлы для построения соответствующего интервального ряда.
По условию: (N=100, x_{min}=142 см, x_{max}=197 см).
Размах вариации: (R=197-142=55) (см)
Оптимальное число интервалов: (k=1+lfloor 3,322cdotlg 100rfloor=1+lfloor 6,644rfloor=1+6=7)
Шаг интервального ряда: (h=lceilfrac{55}{5}rceil=lceil 7,85rceil=8) (см)
Получаем узлы ряда: $$ a_0=x_{min}=142, a_i=142+icdot 8, i=overline{1,7} $$
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
п.2. Гистограмма и полигон относительных частот, кумулята и эмпирическая функция распределения
Относительная частота интервала (left.left[a_{i-1},a_iright.right)) – это отношение частоты (f_i) к общему количеству исходов: $$ w_i=frac{f_i}{N}, i=overline{1,k} $$
Гистограмма относительных частот интервального ряда – это фигура, состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – относительным частотам каждого из интервалов.
Площадь гистограммы равна 1 (с точностью до округлений), и она является эмпирическим законом распределения исследуемого признака.
Полигон относительных частот интервального ряда – это ломаная, соединяющая точки ((x_i,w_i)), где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Накопленные относительные частоты – это суммы: $$ S_1=w_1, S_i=S_{i-1}+w_i, i=overline{2,k} $$ Ступенчатая кривая (F(x)), состоящая из прямоугольников, ширина которых равна шагу ряда, а высота – накопленным относительным частотам, является эмпирической функцией распределения исследуемого признака.
Кумулята – это ломаная, которая соединяет точки ((x_i,S_i)), где (x_i) – середины интервалов.
Например:
Продолжим анализ распределения учеников по росту.
Выше мы уже нашли узлы интервалов. Пусть, после распределения всех 100 измерений по этим интервалам, мы получили следующий интервальный ряд:
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| (left.left[a_{i-1},a_iright.right)) cм | (left.left[142;150right.right)) | (left.left[150;158right.right)) | (left.left[158;166right.right)) | (left.left[166;174right.right)) | (left.left[174;182right.right)) | (left.left[182;190right.right)) | (left[190;198right]) |
| (f_i) | 4 | 7 | 11 | 34 | 33 | 8 | 3 |
Найдем середины интервалов, относительные частоты и накопленные относительные частоты:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 |
| (S_i) | 0,04 | 0,11 | 0,22 | 0,56 | 0,89 | 0,97 | 1 |
Построим гистограмму и полигон:
Построим кумуляту и эмпирическую функцию распределения:
Эмпирическая функция распределения (относительно середин интервалов): $$ F(x)= begin{cases} 0, xleq 146\ 0,04, 146lt xleq 154\ 0,11, 154lt xleq 162\ 0,22, 162lt xleq 170\ 0,56, 170lt xleq 178\ 0,89, 178lt xleq 186\ 0,97, 186lt xleq 194\ 1, xgt 194 end{cases} $$
п.3. Выборочная средняя, мода и медиана. Симметрия ряда
Выборочная средняя интервального вариационного ряда определяется как средняя взвешенная по частотам: $$ X_{cp}=frac{x_1f_1+x_2f_2+…+x_kf_k}{N}=frac1Nsum_{i=1}^k x_if_i $$ где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ X_{cp}=sum_{i=1}^k x_iw_i $$
Модальным интервалом называют интервал с максимальной частотой: $$ f_m=max f_i $$ Мода интервального вариационного ряда определяется по формуле: $$ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница модального интервала;
(f_m,f_{m-1},f_{m+1}) – соответственно, частоты модального интервала, интервала слева от модального и интервала справа.
Медианным интервалом называют первый интервал слева, на котором кумулята превысила значение 0,5. Медиана интервального вариационного ряда определяется по формуле: $$ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h $$ где
(h) – шаг интервального ряда;
(x_o) – нижняя граница медианного интервала;
(S_{me-1}) накопленная относительная частота для интервала слева от медианного;
(w_{me}) относительная частота медианного интервала.
Расположение выборочной средней, моды и медианы в зависимости от симметрии ряда аналогично их расположению в дискретном ряду (см. §65 данного справочника).
Например:
Для распределения учеников по росту получаем:
| (x_i) | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
$$ X_{cp}=sum_{i=1}^k x_iw_i=171,68approx 171,7 text{(см)} $$ На гистограмме (или полигоне) относительных частот максимальная частота приходится на 4й интервал [166;174). Это модальный интервал.
Данные для расчета моды: begin{gather*} x_o=166, f_m=34, f_{m-1}=11, f_{m+1}=33, h=8\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =166+frac{34-11}{(34-11)+(34-33)}cdot 8approx 173,7 text{(см)} end{gather*} На кумуляте значение 0,5 пересекается на 4м интервале. Это – медианный интервал.
Данные для расчета медианы: begin{gather*} x_o=166, w_m=0,34, S_{me-1}=0,22, h=8\ \ M_e=x_o+frac{0,5-S_{me-1}}{w_me}h=166+frac{0,5-0,22}{0,34}cdot 8approx 172,6 text{(см)} end{gather*} begin{gather*} \ X_{cp}=171,7; M_o=173,7; M_e=172,6\ X_{cp}lt M_elt M_o end{gather*} Ряд асимметричный с левосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|}=frac{2,0}{0,9}approx 2,2lt 3), т.е. распределение умеренно асимметрично.
п.4. Выборочная дисперсия и СКО
Выборочная дисперсия интервального вариационного ряда определяется как средняя взвешенная для квадрата отклонения от средней: begin{gather*} D=frac1Nsum_{i=1}^k(x_i-X_{cp})^2 f_i=frac1Nsum_{i=1}^k x_i^2 f_i-X_{cp}^2 end{gather*} где (x_i) – середины интервалов: (x_i=frac{a_{i-1}+a_i}{2}, i=overline{1,k}).
Или, через относительные частоты: $$ D=sum_{i=1}^k(x_i-X_{cp})^2 w_i=sum_{i=1}^k x_i^2 w_i-X_{cp}^2 $$
Выборочное среднее квадратичное отклонение (СКО) определяется как корень квадратный из выборочной дисперсии: $$ sigma=sqrt{D} $$
Например:
Для распределения учеников по росту получаем:
| $x_i$ | 146 | 154 | 162 | 170 | 178 | 186 | 194 | ∑ |
| (w_i) | 0,04 | 0,07 | 0,11 | 0,34 | 0,33 | 0,08 | 0,03 | 1 |
| (x_iw_i) | 5,84 | 10,78 | 17,82 | 57,80 | 58,74 | 14,88 | 5,82 | 171,68 |
| (x_i^2w_i) – результат | 852,64 | 1660,12 | 2886,84 | 9826 | 10455,72 | 2767,68 | 1129,08 | 29578,08 |
$$ D=sum_{i=1}^k x_i^2 w_i-X_{cp}^2=29578,08-171,7^2approx 104,1 $$ $$ sigma=sqrt{D}approx 10,2 $$
п.5. Исправленная выборочная дисперсия, стандартное отклонение выборки и коэффициент вариации
Исправленная выборочная дисперсия интервального вариационного ряда определяется как: begin{gather*} S^2=frac{N}{N-1}D end{gather*}
Стандартное отклонение выборки определяется как корень квадратный из исправленной выборочной дисперсии: $$ s=sqrt{S^2} $$
Коэффициент вариации это отношение стандартного отклонения выборки к выборочной средней, выраженное в процентах: $$ V=frac{s}{X_{cp}}cdot 100text{%} $$
Подробней о том, почему и когда нужно «исправлять» дисперсию, и для чего использовать коэффициент вариации – см. §65 данного справочника.
Например:
Для распределения учеников по росту получаем: begin{gather*} S^2=frac{100}{99}cdot 104,1approx 105,1\ sapprox 10,3 end{gather*} Коэффициент вариации: $$ V=frac{10,3}{171,7}cdot 100text{%}approx 6,0text{%}lt 33text{%} $$ Выборка однородна. Найденное значение среднего роста (X_{cp})=171,7 см можно распространить на всю генеральную совокупность (старшеклассников из других школ).
п.6. Алгоритм исследования интервального вариационного ряда
На входе: все значения признака (left{x_jright}, j=overline{1,N})
Шаг 1. Построить интервальный ряд с интервалами (left.right[a_{i-1}, a_ileft.right)) и частотами (f_i, i=overline{1,k}) (см. алгоритм выше).
Шаг 2. Составить расчетную таблицу. Найти (x_i,w_i,S_i,x_iw_i,x_i^2w_i)
Шаг 3. Построить гистограмму (и/или полигон) относительных частот, эмпирическую функцию распределения (и/или кумуляту). Записать эмпирическую функцию распределения.
Шаг 4. Найти выборочную среднюю, моду и медиану. Проанализировать симметрию распределения.
Шаг 5. Найти выборочную дисперсию и СКО.
Шаг 6. Найти исправленную выборочную дисперсию, стандартное отклонение и коэффициент вариации. Сделать вывод об однородности выборки.
п.7. Примеры
Пример 1. При изучении возраста пользователей коворкинга выбрали 30 человек.
Получили следующий набор данных:
18,38,28,29,26,38,34,22,28,30,22,23,35,33,27,24,30,32,28,25,29,26,31,24,29,27,32,24,29,29
Постройте интервальный ряд и исследуйте его.
1) Построим интервальный ряд. В наборе данных: $$ x_{min}=18, x_{max}=38, N=30 $$ Размах вариации: (R=38-18=20)
Оптимальное число интервалов: (k=1+lfloorlog_2 30rfloor=1+4=5)
Шаг интервального ряда: (h=lceilfrac{20}{5}rceil=4)
Получаем узлы ряда: $$ a_0=x_{min}=18, a_i=18+icdot 4, i=overline{1,5} $$
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
Считаем частоты для каждого интервала. Получаем интервальный ряд:
| (left.left[a_{i-1},a_iright.right)) лет | (left.left[18;22right.right)) | (left.left[22;26right.right)) | (left.left[26;30right.right)) | (left.left[30;34right.right)) | (left.left[34;38right.right)) |
| (f_i) | 1 | 7 | 12 | 6 | 4 |
2) Составляем расчетную таблицу:
| (x_i) | 20 | 24 | 28 | 32 | 36 | ∑ |
| (f_i) | 1 | 7 | 12 | 6 | 4 | 30 |
| (w_i) | 0,033 | 0,233 | 0,4 | 0,2 | 0,133 | 1 |
| (S_i) | 0,033 | 0,267 | 0,667 | 0,867 | 1 | – |
| (x_iw_i) | 0,667 | 5,6 | 11,2 | 6,4 | 4,8 | 28,67 |
| (x_i^2w_i) | 13,333 | 134,4 | 313,6 | 204,8 | 172,8 | 838,93 |
3) Строим полигон и кумуляту
Эмпирическая функция распределения: $$ F(x)= begin{cases} 0, xleq 20\ 0,033, 20lt xleq 24\ 0,267, 24lt xleq 28\ 0,667, 28lt xleq 32\ 0,867, 32lt xleq 36\ 1, xgt 36 end{cases} $$ 4) Находим выборочную среднюю, моду и медиану $$ X_{cp}=sum_{i=1}^k x_iw_iapprox 28,7 text{(лет)} $$ На полигоне модальным является 3й интервал (самая высокая точка).
Данные для расчета моды: begin{gather*} x_0=26, f_m=12, f_{m-1}=7, f_{m+1}=6, h=4\ M_o=x_o+frac{f_m-f_{m-1}}{(f_m-f_{m-1})+(f_m+f_{m+1})}h=\ =26+frac{12-7}{(12-7)+(12-6)}cdot 4approx 27,8 text{(лет)} end{gather*}
На кумуляте медианным является 3й интервал (преодолевает уровень 0,5).
Данные для расчета медианы: begin{gather*} x_0=26, w_m=0,4, S_{me-1}=0,267, h=4\ M_e=x_o+frac{0,5-S_{me-1}}{w_{me}}h=26+frac{0,5-0,4}{0,267}cdot 4approx 28,3 text{(лет)} end{gather*} Получаем: begin{gather*} X_{cp}=28,7; M_o=27,8; M_e=28,6\ X_{cp}gt M_egt M_0 end{gather*} Ряд асимметричный с правосторонней асимметрией.
При этом (frac{|M_o-X_{cp}|}{|M_e-X_{cp}|} =frac{0,9}{0,1}=9gt 3), т.е. распределение сильно асимметрично.
5) Находим выборочную дисперсию и СКО: begin{gather*} D=sum_{i=1}^k x_i^2w_i-X_{cp}^2=838,93-28,7^2approx 17,2\ sigma=sqrt{D}approx 4,1 end{gather*}
6) Исправленная выборочная дисперсия: $$ S^2=frac{N}{N-1}D=frac{30}{29}cdot 17,2approx 17,7 $$ Стандартное отклонение (s=sqrt{S^2}approx 4,2)
Коэффициент вариации: (V=frac{4,2}{28,7}cdot 100text{%}approx 14,7text{%}lt 33text{%})
Выборка однородна. Найденное значение среднего возраста (X_{cp}=28,7) лет можно распространить на всю генеральную совокупность (пользователей коворкинга).
Что такое группировка статистических данных, и как она связана с рядами распределения, было рассмотрено в первой части этой лекции, там же можно узнать, о том что такое дискретный и вариационный ряд распределения.
Ряды распределения одна из разновидностей статистических рядов (кроме них в статистике используются ряды динамики), используются для анализа данных о явлениях общественной жизни. Построение вариационных рядов вполне посильная задача для каждого. Однако есть правила, которые необходимо помнить.
Как построить дискретный вариационный ряд распределения
Пример 1. Имеются данные о количестве детей в 20 обследованных семьях. Построить дискретный вариационный ряд распределения семей по числу детей.
0 1 2 3 1
2 1 2 1 0
4 3 2 1 1
1 0 1 0 2
Решение:
- Начнем с макета таблицы, в которую затем мы внесем данные. Так как ряды распределения имеют два элемента, то таблица состоять будет из двух колонок. Первая колонка это всегда варианта – то, что мы изучаем – ее название берем из задания (конец предложения с заданием в условиях) — по числу детей – значит наша варианта это число детей.
Вторая колонка это частота – как часто встречается наша варианта в исследуемом явление – название колонки так же берем из задания — распределения семей – значит наша частота это число семей с соответствующим количеством детей.
В итоге макет нашей таблицы будет выглядеть так:
| Варианта Число детей в семье — (х) |
Частота Количество семей (f) |
- Теперь из исходных данных выберем те значения, которые встречаются хотя бы один раз. В нашем случае это
0 2 4 1 и 3.
И расставим эти данные в первой колонке нашей таблицы в логическом порядке, в данном случае возрастающем от 0 до 4. Получаем
| Число детей в семье — (х) | Количество семей (f) |
| 0 1 2 3 4 |
И в заключение подсчитаем, сколько же раз встречается каждое значение варианты.
0 1 2 3 1
2 1 2 1 0
4 3 2 1 1
1 0 1 0 2
В результате получаем законченную табличку или требуемый ряд распределения семей по количеству детей.
| Число детей в семье — (х) | Количество семей (f) |
| 0 1 2 3 4 |
4 8 5 2 1 |
| Итого | 20 |
Задание. Имеются данные о тарифных разрядах 30 рабочих предприятия. Построить дискретный вариационный ряд распределения рабочих по тарифному разряду. 2 3 2 4 4 5 5 4 6 3
1 4 4 5 5 6 4 3 2 3
4 5 4 5 5 6 6 3 3 4
Как построить интервальный вариационный ряд распределения
Построим интервальный ряд распределения, и посмотрим чем же его построение отличается от дискретного ряда.
Пример 2. Имеются данные о величине полученной прибыли 16 предприятий, млн. руб. — 23 48 57 12 118 9 16 22 27 48 56 87 45 98 88 63. Построить интервальный вариационный ряд распределения предприятий по объему прибыли, выделив 3 группы с равными интервалами.
Общий принцип построения ряда, конечно же, сохраниться, те же две колонки, те же варианта и частота, но в здесь варианта будет располагаться в интервале и подсчет частот будет вестись иначе.
Решение:
- Начнем аналогично предыдущей задачи с построения макета таблицы, в которую затем мы внесем данные. Так как ряды распределения имеют два элемента, то таблица состоять будет из двух колонок. Первая колонка это всегда варианта – то, что мы изучаем – ее название берем из задания (конец предложения с заданием в условиях) — по объему прибыли – значит, наша варианта это объем полученной прибыли.
Вторая колонка это частота – как часто встречается наша варианта в исследуемом явление – название колонки так же берем из задания — распределения предприятий – значит наша частота это число предприятий с соответствующей прибылью, в данном случае попадающие в интервал.
В итоге макет нашей таблицы будет выглядеть так:
| Варианта Объем полученной прибыли, млн. руб. — (х) | Частота Число предприятий (f) |
- Построим интервалы. Следует сказать, что есть несколько способов построения интервала: визуальный способ без дополнительных расчетов на основе логического анализа данных, расчет по формуле, если по условию требуется построить равные интервалы. Для упрощения расчетов величины интервала чаще всего эта формула имеет следующий вид:
где i – величина или длинна интервала,
Хmax и Xmin – максимальное и минимальное значение признака,
n – требуемое число групп по условию задачи.
Рассчитаем величину интервала для нашего примера. Для этого среди исходных данных найдем самое большое и самое маленькое
23 48 57 12 118 9 16 22 27 48 56 87 45 98 88 63 – максимальное значение 118 млн. руб., и минимальное 9 млн. руб. Проведем расчет по формуле.
В расчете получили число 36,(3) три в периоде, в таких ситуациях величину интервала нужно округлить до большего, чтобы после подсчетов не потерялось максимальное данное, именно поэтому в расчете величина интервала 36,4 млн. руб.
- Теперь построим интервалы – наши варианты в данной задаче. Первый интервал начинают строить от минимального значения к нему добавляется величина интервала и получается верхняя граница первого интервала. Затем верхняя граница первого интервала становится нижней границей второго интервала, к ней добавляется величина интервала и получается второй интервал. И так далее столько раз сколько требуется построить интервалов по условию.
| Объем полученной прибыли, млн. руб. — (х) | Число предприятий (f) |
| 9,0 + 36,4 = 45,4 45,4 + 36,4 = 81,8 81,8 + 36,4 = 118,2 |
Обратим внимание если бы мы не округлили величину интервала до 36,4, а оставили бы ее 36,3, то последнее значение у нас бы получилось 117,9. Именно для того чтобы не было потери данных необходимо округлять величину интервала до большего значения.
- Проведем подсчет количества предприятий попавших в каждый конкретный интервал. При обработке данных необходимо помнить, что верхнее значение интервала в данном интервале не учитывается (не включается в этот интервал), а учитывается в следующем интервале (нижняя граница интервала включается в данный интервал, а верхняя не включается), за исключением последнего интервала.
При проведении обработки данных лучше всего отобранные данные обозначить условными значками или цветом, для упрощения обработки.
23 48 57 12 118 9 16 22
27 48 56 87 45 98 88 63
Первый интервал обозначим желтым цветом – и определим сколько данных попадает в интервал от 9 до 45,4, при этом данное 45,4 будет учитываться во втором интервале (при условии что оно есть в данных) – в итоге получаем 7 предприятий в первом интервале. И так дальше по всем интервалам.
| Объем полученной прибыли, млн. руб. — (х) | Число предприятий (f) |
| 9,0 — 45,4 45,4 — 81,8 81,8 — 118,2 |
7 5 4 |
| Итого | 16 |
- (дополнительное действие) Проведем подсчет общего объема прибыли полученного предприятиями по каждому интервалу и в целом. Для этого сложим данные отмеченные разными цветами и получим суммарное значение прибыли.
По первому интервалу — 23 + 12 + 9 + 16 + 22 + 27 + 45 = 154 млн. руб.
По второму интервалу — 48 + 57 + 48 + 56 + 63 = 272 млн. руб.
По третьему интервалу — 118 + 87 + 98 + 88 = 391 млн. руб.
| Объем полученной прибыли, млн. руб. — (х) | Число предприятий (f) | Общий объем прибыли, млн. руб. |
| 9,0 — 45,4 45,4 — 81,8 81,8 — 118,2 |
7 5 4 |
154 272 391 |
| Итого | 16 | 817 |
Задание. Имеются данные о величине вклада в банке 30 вкладчиков, тыс. руб. 150, 120, 300, 650, 1500, 900, 450, 500, 380, 440,
600, 80, 150, 180, 250, 350, 90, 470, 1100, 800,
500, 520, 480, 630, 650, 670, 220, 140, 680, 320
Построить интервальный вариационный ряд распределения вкладчиков, по размеру вклада выделив 4 группы с равными интервалами. По каждой группе подсчитать общий размер вкладов.
Может еще поучимся? Загляни сюда!
2.2. Интервальный вариационный ряд
Предпосылкой построения интервального вариационного ряда (ИВР) является тот факт, что исследуемая величина принимает слишком много различных значений
. Зачастую ИВР появляется в результате
изучения непрерывной характеристики объектов. Типично – это время, масса, размеры и другие физические величины.
Вспоминаем Константина, который замерял время на лабораторной работе и Фёдора, который взвешивал помидоры.
В таких ситуациях затруднительно либо невозможно применить тот же подход, что для дискретного ряда. Это связано с тем, что ВСЕ варианты различны (во многих случаях). И
даже если встречаются совпадающие значения, например, 50 грамм и 50 грамм, то связано это с округлением, а фактически значения
всё равно отличаются хоть какими-то микрограммами.
Поэтому здесь используется другой подход, а именно определяется интервал,
в пределах которого варьируются значения , затем этот интервал делится на частичные интервалы (обычно равной длины
) и по каждому частичному интервалу
подсчитываются частоты (либо
) – количество вариант, которые в него попали.
Если варианта попала на «стык» интервалов, то её относят к старшему интервалу.
Интервальный вариационный ряд (ИВР) статистической совокупности – это
упорядоченное множество смежных интервалов и соответствующие им частоты, в сумме равные
объёму совокупности. Дабы не плодить лишних букв и индексов, я никак не обозначил эти
интервалы. Придирчивый читатель, к слову, наверняка заметил, что через я обозначаю как исходные варианты, так и значения сгруппированного
ряда.
Следует отметить, что исследуемая характеристика не обязана быть непрерывной, и мы как раз начнём с такой задачи:
Пример 6
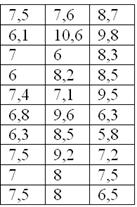
По результатам исследования цены некоторого товара в различных торговых точках города, получены следующие данные (в денежных
единицах):
Составить вариационный ряд, построить гистограмму частот, гистограмму и полигон относительных частот + бонус:
эмпирическую функцию распределения.
Решение: очевидно, что перед нами выборочная совокупность
объема , и вопрос номер
один: какой ряд составлять – дискретный или интервальный? Заметьте, что в
вопросе задачи ничего не сказано о характере ряда. Строго говоря, цены дискретны и среди них даже есть одинаковые. Однако они
могут быть округлены, да и разброс цен довольно велик. Поэтому здесь целесообразно провести интервальное разбиение.
Начнём с экстремальной ситуации, когда у вас под рукой нет Экселя или другого подходящего программного обеспечения. Только
ручка, карандаш, тетрадь и калькулятор.
Тактика действий похожа на работу с дискретным вариационным рядом. Сначала
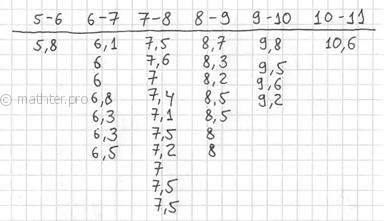
окидываем взглядом предложенные числа и определяем примерный интервал, в который вписываются эти значения. «Навскидку» все
значения заключены в пределах от 5 до 11. Далее делим этот интервал на удобные подынтервалы, в данном случае
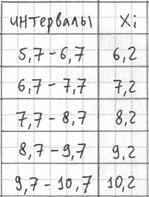
напрашиваются промежутки единичной длины. Записываем их на черновик:
Теперь начинаем вычёркивать числа из исходного списка и записываем их в соответствующие колонки нашей импровизированной
таблицы:
После этого находим самое маленькое число в левой колонке (минимальное значение) и самое большое число – в правой
(максимальное значение). Тут даже ничего искать не пришлось, честное слово, не нарочно получилось:)
ден. ед. – не забываем указывать
размерность!
Вычислим размах вариации:
ден. ед. – длина общего
интервала, в пределах которого варьируется цена.
Теперь его нужно разбить на частичные интервалы. Сколько интервалов рассмотреть? По умолчанию на этот счёт
существует формула Стерджеса:
, где
– десятичный логарифм* от объёма выборки и
– оптимальное количество
интервалов, при этом результат округляют до ближайшего левого целого значения.
* есть на любом более или менее приличном калькуляторе.
В нашем случае получаем: интервалов.
Следует отметить, что правило Стерджеса носит рекомендательный, но не обязательный характер. Нередко в условии
задачи прямо сказано, на какое количество интервалов следует проводить разбиение (на 4, 5, 6, 10 и т.д.), и тогда следует
придерживаться именно этого указания.
Длины частичных интервалов могут быть различны, но в большинстве случаев использует равноинтервальную
группировку:
– длина частичного интервала. В
принципе, здесь можно было не округлять и использовать длину 0,96, но удобнее, ясен день, 1.
И коль скоро мы прибавили 0,04, то по пяти частичным интервалам получается «перебор»: . Посему от самой малой варианты
отмеряем влево 0,1 влево (половину «перебора») и к
значению 5,7 начинаем прибавлять по ,
получая тем самым частичные интервалы. При этом сразу рассчитываем их середины (например,
) – они требуются почти во всех тематических задачах:
– убеждаемся в том, что самая большая варианта вписалась в последний частичный интервал и отстоит от его правого конца на
0,1.
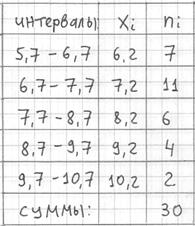
Далее подсчитываем частоты по каждому интервалу. Для этого в черновой таблице обводим значения, попавшие в тот или
иной интервал, подсчитываем их количество и вычёркиваем:
Так, значения из 1-го интервала я обвёл овалами (7 штук) и вычеркнул, значения из 2-го интервала – прямоугольниками (11
штук) и вычеркнул и так далее. Варианта попала на «стык» интервалов и, согласно озвученному выше правилу, её следует
отнести к последующему интервалу .
В результате получаем интервальный вариационный ряд:
при этом обязательно убеждаемся в том, что ничего не потеряно:
, ОК.
…Да, кстати, все ли представили свой любимый товар, чтобы было интереснее разбирать это длинное решение? J
Точно также как и в дискретном случае, интервальный вариационный ряд можно
(и нужно) изобразить графически. И здесь у нас весьма большое разнообразие. Но сначала добавим в таблицу дополнительные
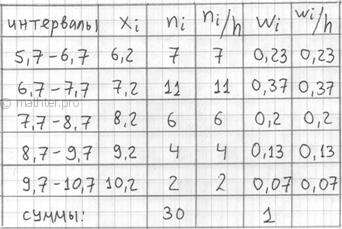
столбцы и продолжим расчёты:
По каждому интервалу рассчитываем (не тушуемся): плотность частот , относительные частоты
(округляем их до 2 знаков после запятой), а также плотность относительных
частот . Поскольку длина частичного
интервала , то вычисления заметно
упрощаются:
Если интервалы имеют разные длины , то
при нахождении плотностей каждую частоту нужно разделить на длину своего интервала: . Но у нас группировка равноинтервальная, да не
абы какая, а с единичным частичным интервалом. Дело за чертежами. Один за другим:


| Оглавление |
Варианты для выполнения работы
I. Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.
Почти все встречающиеся в жизни величины (урожайность сельскохозяйственных растений, продуктивности скота, производительность труда и заработная плата рабочих, объем производства продукции и т.д.) принимают неодинаковые значения у различных членов совокупности. Поэтому возникает необходимость в изучении их изменяемости. Это изучение начинается с проведения соответствующих наблюдений, обследований.
В результате наблюдений получают сведения о численной величине изучаемого признака у каждого члена данной совокупности.
Пример. Имеются данные о размере прибыли 100 коммерческих банков. Прибыль, млн. рублей.
| 30,2 | 51,9 | 43,1 | 58,9 | 34,1 | 55,2 | 47,9 | 43,7 | 53,2 | 34,9 |
| 47,8 | 65,7 | 37,8 | 68,6 | 48,4 | 67,5 | 27,3 | 66,1 | 52,0 | 55,6 |
| 54,1 | 26,9 | 53,6 | 42,5 | 59,3 | 44,8 | 52,8 | 42,3 | 55,9 | 48,1 |
| 44,5 | 69,8 | 47,3 | 35,6 | 70,1 | 39,5 | 70,3 | 33,7 | 51,8 | 56,1 |
| 28,4 | 48,7 | 41,9 | 58,1 | 20,4 | 56,3 | 46,5 | 41,8 | 59,5 | 38,1 |
| 41,4 | 70,4 | 31,4 | 52,5 | 45,2 | 52,3 | 40,2 | 60,4 | 27,6 | 57,4 |
| 29,3 | 53,8 | 46,3 | 40,1 | 50,3 | 48,9 | 35,8 | 61,7 | 49,2 | 45,8 |
| 45,3 | 71,5 | 35,1 | 57,8 | 28,1 | 57,6 | 49,6 | 45,5 | 36,2 | 63,2 |
| 61,9 | 25,1 | 65,1 | 49,7 | 62,1 | 46,1 | 39,9 | 62,4 | 50,1 | 33,1 |
| 33,3 | 49,8 | 39,8 | 45,9 | 37,3 | 78,0 | 64,9 | 28,8 | 62,5 | 58,7 |
Из данной таблицы видно, что интересующий нас признак (прибыль банков) меняется от одного члена совокупности к другому, варьирует. Варьирование есть изменяемость признака у отдельных членов совокупности.
Вариационным рядом называется последовательность вариант, записанных в возрастающем порядке и соответствующих им частот.
Число, показывающее, сколько раз повторяется в данной совокупности каждое значение признака, называется частотой.
Составим ранжированный вариационный ряд (выпишем варианты в порядке возрастания):
| 20,4 | 25,1 | 26,9 | 27,3 | 27,6 | 28,1 | 28,4 | 28,8 | 29,3 | 30,2 |
| 31,4 | 33,1 | 33,3 | 33,7 | 34,1 | 34,9 | 35,1 | 35,6 | 35,8 | 36,2 |
| 37,3 | 37,8 | 38,1 | 39,5 | 39,8 | 39,9 | 40,1 | 40,2 | 41,4 | 41,8 |
| 41,9 | 42,3 | 42,5 | 43,1 | 43,7 | 44,5 | 44,8 | 45,2 | 45,3 | 45,5 |
| 45,8 | 45,9 | 46,1 | 46,3 | 46,5 | 47,3 | 47,8 | 47,9 | 48,1 | 48,4 |
| 48,7 | 48,9 | 49,2 | 49,6 | 49,7 | 49,8 | 50,1 | 50,3 | 51,8 | 51,9 |
| 52,0 | 52,3 | 52,5 | 52,8 | 53,2 | 53,6 | 53,8 | 54,1 | 55,2 | 55,6 |
| 55,9 | 56,1 | 56,3 | 57,4 | 57,6 | 57,8 | 58,1 | 58,7 | 58,9 | 59,3 |
| 59,5 | 60,4 | 61,7 | 61,9 | 62,1 | 62,4 | 62,5 | 63,2 | 64,9 | 65,1 |
| 65,7 | 66,1 | 67,5 | 68,6 | 69,8 | 70,1 | 70,3 | 70,4 | 71,5 | 78,0 |
В нашем случае каждое значение признака (варианта вариационного ряда) повторилось только один раз, т.е. значение частоты для всех вариант равно единице. Перейдем к интервальному вариационному ряду, так как интересующий нас признак принимает дробные, практически не повторяющиеся значения.
Для этого необходимо определить число интервалов (классов) и длину интервала (классного промежутка), после чего произвести разноску, т.е. подсчитать для каждого интервала число вариант, попавших в него.
Количество классов устанавливают в зависимости от степени точности, с которой ведется обработка, и количества объектов в выборке. Считается удобным при объеме выборки (n) в пределах от 30 до 60 вариант распределять их на 6-7 классов, при n от 60 до 100 вариант — на 7-8 классов, при n от 100 и более вариант — на 9-17 классов.
Нужное количество групп также может быть ориентировочно вычислено по формуле Стерджесса:
где — число групп (классов, интервалов) ряда распределения; n — объем выборки.
Можно также использовать выражение:
При они дают примерно одинаковые результаты.
В рассматриваемом примере о размере прибыли коммерческих банков, n=100. Применяя формулу Стерджесса, получим:
Однако Таким образом, число интервалов может быть равно 8, 9, 10 и т.д.
Нахождение нужного количества групп и их размеров часто бывает взаимообусловлено. Для того, чтобы как-то определиться с числом интервалов, найдем размах вариации — разность между наибольшей и наименьшей вариантой:
где — размах вариации,
— наибольшее значение варьирующего признака,
— наименьшее значение варьирующего признака.
Найдем размах вариации для рассматриваемой задачи:
Для того, чтобы найти длину интервала (величину классового промежутка) необходимо разделить размах вариации на число классов и полученную величину округлить таким образом, чтобы было удобно производить сначала разноску, а затем и различные вычисления. Рекомендую округлять до единиц, до которых округлены варианты в исходной таблице, в нашем случае до десятых.
Согласно формуле получаем
Теперь необходимо определиться с началом первого интервала. Для этого можно использовать формулу:
Замечание. За начало первого интервала можно принять некоторое значение, несколько меньшее или само значение
. Далее в табличном виде я покажу оба варианта.
Прибавив к началу первого интервала (нижней границе) шаг, получим верхнюю границу первого интервала и одновременно нижнюю границу второго интервала. Выполняя последовательно указанные действия, будем находить границы последующих интервалов до тех пор, пока не будет получено или перекрыто .
Таким образом, верхняя граница одного интервала одновременно является нижней границей другого интервала. Чтобы не возникало сомнений, в какой интервал отнести варианту, попавшую на границу, условимся относить ее к верхнему интервалу.
Составим теперь рабочую таблицу для построения интервального вариационного ряда и произведем подсчет частот вариант, попавших в тот или иной интервал.
Как и обещал покажу две таблицы построения ряда:
1. Отсчет ведем от , т.е. нижняя граница первого интервала совпадает с
.
|
Группы банков по размеру прибыли (границы интервалов) |
Количество банков, принадлежащих данной группе (частоты, |
Накопленные частоты, |
| 20,4 — 27,6 | 4 | 4 |
| 27,6 — 34,8 | 11 | 15 |
| 34,8 — 42 | 16 | 31 |
| 42 — 49,2 | 21 | 52 |
| 49,2 — 56,4 | 21 | 73 |
| 56,4 — 63,6 | 15 | 88 |
| 63,6 — 70,8 | 10 | 98 |
| 70,8 — 78 | 2 | 100 |
2. Начало первого интервала определяем с помощью формулы: .
|
Группы банков по размеру прибыли (границы интервалов) |
Количество банков, принадлежащих данной группе (частоты, |
Накопленные частоты, |
| 16,8 — 24 | 1 | 1 |
| 24 — 31,2 | 9 | 10 |
| 31,2 — 38,4 | 13 | 23 |
| 38,4 — 45,6 | 17 | 40 |
| 45,6 — 52,8 | 23 | 63 |
| 52,8 — 60 | 18 | 81 |
| 60 — 67,2 | 11 | 92 |
| 67,2 — 74,4 | 7 | 99 |
| 74,4 — 81,6 | 1 | 100 |
Как мы видим в 1-м случае у нас получилось восемь интервалов, что полностью совпадает с результатом, который нам дала формула Стерджесса. Во втором случае у нас получилось девять интервалов, так как при поиске начала первого интервала пользовались специальной формулой.
Для дальнейшего исследования я буду пользоваться результатами второй таблицы, так как там ярко выражен модальный интервал (одна мода) и медиана практически точно попадает на середину вариационного ряда.
Мы получили интервальный вариационный ряд — упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами попаданий в каждый из них значений величины.
II. Графическая интерпретация вариационных рядов.
| № п/п |
Границы интервалов, |
Середины интервалов, |
Частоты интервалов, |
Относительные частоты |
Плотность относит. частоты |
Плотность частоты |
| 1 | 16,8 — 24 | 20,4 | 1 | 0,01 | 0,001 | 0,139 |
| 2 | 24 — 31,2 | 27,6 | 9 | 0,09 | 0,013 | 1,250 |
| 3 | 31,2 — 38,4 | 34,8 | 13 | 0,13 | 0,018 | 1,806 |
| 4 | 38,4 — 45,6 | 42 | 17 | 0,17 | 0,024 | 2,361 |
| 5 | 45,6 — 52,8 | 49,2 | 23 | 0,23 | 0,032 | 3,194 |
| 6 | 52,8 — 60 | 56,4 | 18 | 0,18 | 0,025 | 2,500 |
| 7 | 60 — 67,2 | 63,6 | 11 | 0,11 | 0,015 | 1,528 |
| 8 | 67,2 — 74,4 | 70,8 | 7 | 0,07 | 0,010 | 0,972 |
| 9 | 74,4 — 81,6 | 78 | 1 | 0,01 | 0,001 | 0,139 |
Строим графики:
Далее найдем моду вариационного ряда:
где
— начало модального интервала;
— длина частичного интервала (шаг);


— частота послемодального интервала.
Определим модальный интервал — интервал, имеющий наибольшую частоту. Из таблицы видно, что модальным является интервал (45,6 — 52,8).
Медиана
Для интервального ряда медиана находится по формуле:
где
— начало медианного интервала;
— длина частичного интервала (шаг);
— объем совокупности;
— накопленная частота интервала, предшествующая медианному;
— частота медианного интервала.
Определим медианный интервал — интервал, в котором впервые накопленная частота превышает половину объема выборки.Так как объем выборки n=100, то n/2=50. По таблице найдем интервал, где впервые накопленные частоты превысят это значение. Таким является интервал (45,6 — 52,8).
Получаем,
III. Расчет сводных характеристик выборки.
Для определения составим расчетную таблицу. Для начала определимся с ложным нулем С. В качестве ложного нуля можно принять любую варианту. Максимальная простота вычислений достигается, если выбрать в качестве ложного нуля варианту, которая расположена примерно в середине вариационного ряда (часто такая варианта имеет наибольшую частоту).
Варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю. В нашем случае С=49,2.
Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с разностью h.
Условными называют варианты, определяемые равенством:
Произведем расчет условных вариант согласно формуле:
| N п/п |
Середины интервалов, |
Частоты интервалов, |
Условные варианты, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
Произведения частот и условных вариант, |
| 1 | 20,4 | 1 | -4 | -4 | 16 | -64 | 256 | 9 | 81 |
| 2 | 27,6 | 9 | -3 | -27 | 81 | -243 | 729 | 36 | 144 |
| 3 | 34,8 | 13 | -2 | -26 | 52 | -104 | 208 | 13 | 13 |
| 4 | 42 | 17 | -1 | -17 | 17 | -17 | 17 | 0 | 0 |
| 5 | 49,2 | 23 | 0 | 0 | 0 | 0 | 0 | 23 | 23 |
| 6 | 56,4 | 18 | 1 | 18 | 18 | 18 | 18 | 72 | 288 |
| 7 | 63,6 | 11 | 2 | 22 | 44 | 88 | 176 | 99 | 891 |
| 8 | 70,8 | 7 | 3 | 21 | 63 | 189 | 567 | 112 | 1792 |
| 9 | 78 | 1 | 4 | 4 | 16 | 64 | 256 | 25 | 625 |
Контроль:
Контроль:
Равенство выполнено, следовательно вычисления произведены верно.
Вычислим условные моменты 1-го, 2-го, 3-го и 4-го порядков:
Найдем выборочные среднюю, дисперсию и среднее квадратическое отклонение :
Также для оценки отклонения эмпирического распределения от нормального используют такие характеристики, как асимметрия и эксцесс.
Асимметрией теоретического распределения называют отношение центрального момента третьего порядка к кубу среднего квадратического отклонения:
Асимметрия положительна, если «длинная часть» кривой распределения расположена справа от математического ожидания; асимметрия отрицательна, если «длинная часть» кривой расположена слева от математического ожидания. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции): если «длинная часть» кривой расположена правее моды, то асимметрия положительна, если слева — отрицательна.
Эксцесс эмпирического распределения определяется равенством:
где — центральный эмпирический момент четвертого порядка.
Для нормального распределения эксцесс равен нулю. Поэтому если эксцесс некоторого распределения отличен от нуля, то кривая этого распределения отличается от нормальной кривой: если эксцесс положительный, то кривая имеет более высокую и «острую» вершину, чем нормальная кривая; если эксцесс отрицательный, то сравниваемая кривая имеет более низкую и «плоскую» вершину, чем нормальная кривая. При этом предполагается, что нормальное и теоретическое распределения имеют одинаковые математические ожидания и дисперсии.
Вычисляем центральные эмпирические моменты третьего и четвертого порядков:
Найдем асимметрию и эксцесс:
IV. Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий согласия Пирсона.
Проверим генеральную совокупность значений размера прибыли банков по критерию Пирсона
Правило. Для того, чтобы при заданном уровне значимости проверить нулевую гипотезу : генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия:
и по таблице критических точек распределения , по заданному уровню значимости
и числу степеней свободы
найти критическую точку
, где s — количество интервалов.
Если — нет оснований отвергнуть нулевую гипотезу.
Если — нулевую гипотезу отвергают.
Найдем теоретические частоты , для этого составим следующую таблицу.
|
Середины интервалов, |
Частоты интервалов, |
Произведем расчет, |
Произведем расчет, |
Значения функции Гаусса, |
Произведем расчет, |
Теоретические частоты, |
| 20,4 | 1 | -28,152 | -2,23 | 0,0332 | 57 | 2 |
| 27,6 | 9 | -20,952 | -1,66 | 0,1006 | 57 | 6 |
| 34,8 | 13 | -13,752 | -1,09 | 0,2203 | 57 | 13 |
| 42 | 17 | -6,552 | -0,52 | 0,3485 | 57 | 20 |
| 49,2 | 23 | 0,648 | 0,05 | 0,3984 | 57 | 23 |
| 56,4 | 18 | 7,848 | 0,62 | 0,3292 | 57 | 19 |
| 63,6 | 11 | 15,048 | 1,19 | 0,1965 | 57 | 11 |
| 70,8 | 7 | 22,248 | 1,77 | 0,0833 | 57 | 5 |
| 78 | 1 | 29,448 | 2,34 | 0,0258 | 57 | 1 |
Вычислим , для чего составим расчетную таблицу.
| 1 | 1 | 2 | -1 | 1 | 0,5 | 1 | 0,5 |
| 2 | 9 | 6 | 3 | 9 | 1,5 | 81 | 13,5 |
| 3 | 13 | 13 | 0 | 0 | 0 | 169 | 13 |
| 4 | 17 | 20 | -3 | 9 | 0,45 | 289 | 14,45 |
| 5 | 23 | 23 | 0 | 0 | 0 | 529 | 23 |
| 6 | 18 | 19 | -1 | 1 | 0,05 | 324 | 17,05 |
| 7 | 11 | 11 | 0 | 0 | 0 | 121 | 11 |
| 8 | 7 | 5 | 2 | 4 | 0,8 | 49 | 9,8 |
| 9 | 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 100 | 100 |
Наблюдаемое значение критерия, |
103,30 |
Контроль:
Вычисления произведены правильно.
Найдем число степеней свободы, учитывая, что число групп выборки (число различных вариант) s=9;
По таблице критических точек распределения по уровню значимости
и числу степеней свободы k=6 находим
Так как — нет оснований отвергнуть нулевую гипотезу. Другими словами, расхождение эмпирических и теоретических частот незначительное. Следовательно, данные наблюдений согласуются с гипотезой о нормальном распределении генеральной совокупности.
На рисунке построены нормальная (теоретическая) кривая по теоретическим частотам (зеленый график) и полигон наблюдаемых частот (коричневый график). Сравнение графиков наглядно показывает, что построенная теоретическая кривая удовлетворительно отражает данные наблюдений.
V. Интервальные оценки.
Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.
Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.
Интервальной оценкой (с надежностью ) математического ожидания (а) нормально распределенного количественного признака Х по выборочной средней
при известном среднем квадратическом отклонении

где — точность оценки, n — объем выборки, t — значение аргумента функции Лапласа
(см. приложение 2), при котором
;
при неизвестном среднем квадратическом отклонении 
где S — исправленное выборочное среднее квадратическое отклонение, находят по таблице приложения по заданным n и
.
В нашем примере среднее квадратическое отклонение известно, . А также
,
,
. Поэтому для поиска доверительного интервала используем первую формулу:
Все величины, кроме t, известны. Найдем t из соотношения По таблице приложения находим t=1,96. Подставив t=1,96,
,
,
в формулу, окончательно получим искомый доверительный интервал:
Интервальной оценкой (с надежностью ) среднего квадратического отклонения

(при q<1), (*)
(при q>1),
где q — находят по таблице приложения по заданным n и .
По данным и n=100 по таблице приложения 4 найдем q=0,143. Так как q<1, то, подставив
в соотношение (*), получим доверительный интервал:
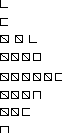
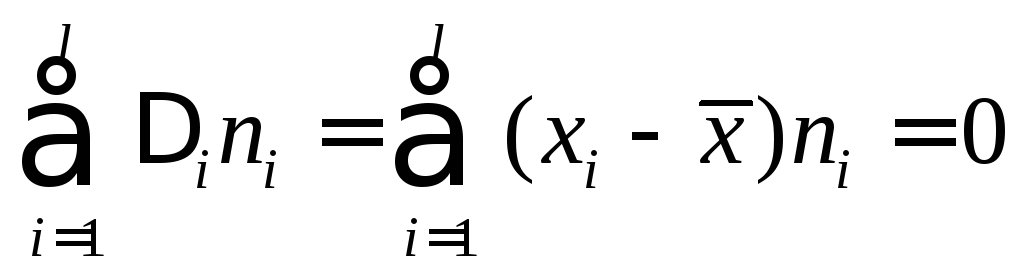
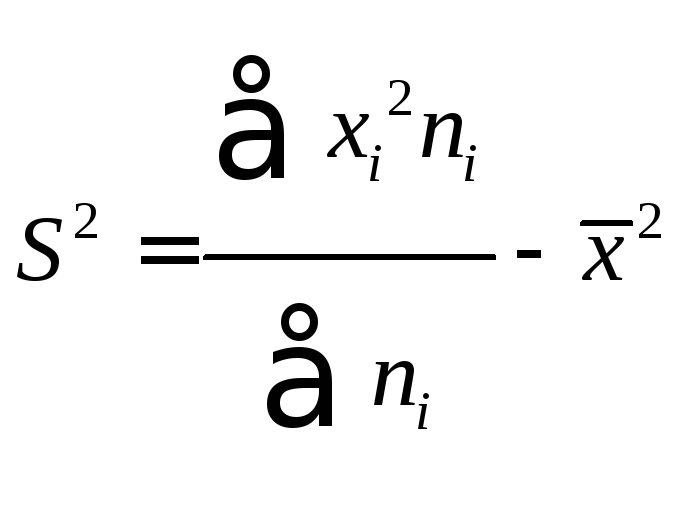














![Rendered by QuickLaTeX.com [chi^2_{nabl}=sum frac{ {(n_i-n_i^{'})}^2}{n_i^{'}}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-43685ed67e69272b6c950828a97acd89_l3.png)
![Rendered by QuickLaTeX.com [sumfrac{n_i^2}{n_i^{'}}-n=sum frac{{(n_i-n_i^{'})}^2}{n_i^'}]](https://ischanow.com/wp-content/ql-cache/quicklatex.com-6c32fcc2a5c6b3b4b603ae3d99533b4a_l3.png)

