Турнир по круговой системе является одной из популярных схем организации соревнований как в настольных логических играх, так и во многих других подвижных видах спорта.
Чтобы определить очередность игры и цвета фигур соперников (в логических играх) используют специальные таблицы очередности игры, которые также иногда называются таблицами Бергера.
Предварительно участники турнира получают определенный номер. Затем, по соответствующей таблице, определяется участники с какими номерами встречаются друг с другом в каждом туре.
Участник, номер которого указан в таблице очередности игры первым, начинает партию. Если в турнире принимает участие нечетное количество участников, то цифра, стоящая в первом столбике вне скобок, показывает, что участник под данным номером свободен от игры в данном туре.
Турнир по круговой системе. 3 или 4 участника
| Тур | Пары участников | |
|---|---|---|
| 1 | 1 — (4) | 2 — 3 |
| 2 | (4) — 3 | 1 — 2 |
| 3 | 2 — (4) | 3 — 1 |
Турнир по круговой системе. 5 или 6 участников
| Тур | Пары участников | ||
|---|---|---|---|
| 1 | 1 — (6) | 2 — 5 | 3 — 4 |
| 2 | (6) — 4 | 5 — 3 | 1 — 2 |
| 3 | 2 — (6) | 3 — 1 | 4 — 5 |
| 4 | (6) — 5 | 1 — 4 | 2 — 3 |
| 5 | 3 — (6) | 4 — 2 | 5 — 1 |
Турнир по круговой системе. 7 или 8 участников
| Тур | Пары участников | |||
| 1 | 1 — (8) | 2 — 7 | 3 — 6 | 4 — 5 |
| 2 | (8) — 5 | 6 — 4 | 7 — 3 | 1 — 2 |
| 3 | 2 — (8) | 3 — 1 | 4 — 7 | 5 — 6 |
| 4 | (8) — 6 | 7 — 5 | 1 — 4 | 2 — 3 |
| 5 | 3 — (8) | 4 — 2 | 5 — 1 | 6 — 7 |
| 6 | (8) — 7 | 1 — 6 | 2 — 5 | 3 — 4 |
| 7 | 4 — (8) | 5 — 3 | 6 — 2 | 7 — 1 |
Турнир по круговой системе. 9 или 10 участников
| Тур | Пары участников | ||||
| 1 | 1 — (10) | 2 — 9 | 3 — 8 | 4 — 7 | 5 — 6 |
| 2 | (10) — 6 | 7 — 5 | 8 — 4 | 9 — 3 | 1 — 2 |
| 3 | 2 — (10) | 3 — 1 | 4 — 9 | 5 — 8 | 6 — 7 |
| 4 | (10) — 7 | 8 — 6 | 9 — 5 | 1 — 4 | 2 — 3 |
| 5 | 3 — (10) | 4 — 2 | 5 — 1 | 6 — 9 | 7 — 8 |
| 6 | (10) — 8 | 9 — 7 | 1 — 6 | 2 — 5 | 3 — 4 |
| 7 | 4 — (10) | 5 — 3 | 6 — 2 | 7 — 1 | 8 — 9 |
| 8 | (10) — 9 | 1 — 8 | 2 — 7 | 3 — 6 | 4 — 5 |
| 9 | 5 — (10) | 6 — 4 | 7 — 3 | 8 — 2 | 9 — 1 |
Турнир по круговой системе. 11 или 12 участников
| Тур | Пары участников | |||||
| 1 | 1 — (12) | 2 — 11 | 3 — 10 | 4 — 9 | 5 — 8 | 6 — 7 |
| 2 | (12) — 7 | 8 — 6 | 9 — 5 | 10 — 4 | 11 — 3 | 1 — 2 |
| 3 | 2 — (12) | 3 — 1 | 4 — 11 | 5 — 10 | 6 — 9 | 7 — 8 |
| 4 | (12) — 8 | 9 — 7 | 10 — 6 | 11 — 5 | 1 — 4 | 2 — 3 |
| 5 | 3 — (12) | 4 — 2 | 5 — 1 | 6 — 11 | 7 — 10 | 8 — 9 |
| 6 | (12)- 9 | 10 — 8 | 11 — 7 | 1 — 6 | 2 — 5 | 3 — 4 |
| 7 | 4 — (12) | 5 — 3 | 6 — 2 | 7 — 1 | 8 — 11 | 9 — 10 |
| 8 | (12) — 10 | 11 — 9 | 1 — 8 | 2 — 7 | 3 — 6 | 4 -5 |
| 9 | 5 — (12) | 6 — 4 | 7 — 3 | 8 — 2 | 9 — 1 | 10 — 11 |
| 10 | (12) — 11 | 1 — 10 | 2 — 9 | 3 — 8 | 4 — 7 | 5 — 6 |
| 11 | 6 — (12) | 7 — 5 | 8 — 4 | 9 — 3 | 10 — 2 | 11 — 1 |
Турнир по круговой системе. 13 или 14 участников
| Тур | Пары участников | ||||||
| 1 | 1 — (14) | 2 — 13 | 3 — 12 | 4 — 11 | 5 — 10 | 6 — 9 | 7 — 8 |
| 2 | (14) — 8 | 9 — 7 | 10 — 6 | 11 — 5 | 12 — 4 | 13 — 3 | 1 — 2 |
| 3 | 2 — (14) | 3 — 1 | 4 — 13 | 5 — 12 | 6 — 11 | 7 — 10 | 8 — 9 |
| 4 | (14) — 9 | 10 — 8 | 11 — 7 | 12 — 6 | 13 — 5 | 1 — 4 | 2 — 3 |
| 5 | 3 — (14) | 4 — 2 | 5 — 1 | 6 — 13 | 7 — 12 | 8 — 11 | 9 — 10 |
| 6 | (14) — 10 | 11 — 9 | 12 — 8 | 13 — 7 | 1 — 6 | 2 — 5 | 3 — 4 |
| 7 | 4 — (14) | 5 — 3 | 6 — 2 | 7 — 1 | 8 — 13 | 9 — 12 | 10 — 11 |
| 8 | (14) — 11 | 12 — 10 | 13 — 9 | 1 — 8 | 2 — 7 | 3 — 6 | 4 — 5 |
| 9 | 5 — (14) | 6 — 4 | 7 — 3 | 8 — 2 | 9 — 1 | 10 — 13 | 11 — 12 |
| 10 | (14) — 12 | 13 — 11 | 1 — 10 | 2 — 9 | 3 — 8 | 4 — 7 | 5 — 6 |
| 11 | 6 — (14) | 7 — 5 | 8 — 4 | 9 — 3 | 10 — 2 | 11 — 1 | 12 — 13 |
| 12 | (14) — 13 | 1 — 12 | 2 — 11 | 3 — 10 | 4 — 9 | 5 — 8 | 6 — 7 |
| 13 | 7 — (14) | 8 — 6 | 9 — 5 | 10 — 4 | 11 — 3 | 12 — 2 | 13 — 1 |
Турнир по круговой системе. 15 или 16 участников
| Тур | Пары участников | |||||||
| 1 | 1 — (16) | 2 — 15 | 3 — 14 | 4 — 13 | 5 — 12 | 6 — 11 | 7 — 10 | 8 — 9 |
| 2 | (16) — 9 | 10 — 8 | 11 — 7 | 12 — 6 | 13 — 5 | 14 — 4 | 15 — 3 | 1 — 2 |
| 3 | 2 — (16) | 3 — 1 | 4 — 15 | 5 — 14 | 6 — 13 | 7 — 12 | 8 — 11 | 9 — 10 |
| 4 | (16) — 10 | 11 — 9 | 12 — 8 | 13 — 7 | 14 — 6 | 15 — 5 | 1 — 4 | 2 — 3 |
| 5 | 3 — (16) | 4 — 2 | 5 — 1 | 6 — 15 | 7 — 14 | 8 — 13 | 9 — 12 | 10 — 11 |
| 6 | (16) — 11 | 12 — 10 | 13 — 9 | 14 — 8 | 15 — 7 | 1 — 6 | 2 — 5 | 3 — 4 |
| 7 | 4 — (16) | 5 — 3 | 6 — 2 | 7 — 1 | 8 — 15 | 9 — 14 | 10 — 13 | 11 — 12 |
| 8 | (16) — 12 | 13 — 11 | 14 — 10 | 15 — 9 | 1 — 8 | 2 — 7 | 3 — 6 | 4 — 5 |
| 9 | 5 — (16) | 6 — 4 | 7 — 3 | 8 — 2 | 9 — 1 | 10 — 15 | 11 — 14 | 12 — 13 |
| 10 | (16) — 13 | 14 — 12 | 15 — 11 | 1 — 10 | 2 — 9 | 3 — 8 | 4 — 7 | 5 — 6 |
| 11 | 6 — (16) | 7 — 5 | 8 — 4 | 9 — 3 | 10 — 2 | 11 — 1 | 12 — 15 | 13 — 14 |
| 12 | (16) — 14 | 15 — 13 | 1 — 12 | 2 — 11 | 3 — 10 | 4 — 9 | 5 — 8 | 6 — 7 |
| 13 | 7 — (16) | 8 — 6 | 9 — 5 | 10 — 4 | 11 — 3 | 12 — 2 | 13 — 1 | 14 — 15 |
| 14 | (16) — 15 | 1 — 14 | 2 — 13 | 3 — 12 | 4 — 11 | 5 — 10 | 6 — 9 | 7 — 8 |
| 15 | 8 — (16) | 9 — 7 | 10 — 6 | 11 — 5 | 12 — 4 | 13 — 3 | 14 — 2 | 15 — 1 |
Тема: Системы розыгрыша: круговая с чередованием полей и без чередования, с выбыванием, смешанная.
Цель: Научить составлять графики игр по перечисленным системам розыгрыша.
I. Круговая система розыгрыша без чередования полей и с чередованием полей.
В практике проведения соревнований по видам спорта применяются две основные системы розыгрыша: круговая и с выбыванием. Иногда прибегают к применению смешанной системы, в которой соединены последовательно первая и вторая. В практике чаще встречается проведение соревнований на первом этапе с выбыванием, а на заключительном этапе – по круговой системе. При выборе той или иной системы учитываются задачи, которые стоят перед соревнованием, уровень подготовленности участников и команд, сроки проведения, наличие спортивных баз, материальное обеспечение участников.
Круговая система.
При круговой системе все участники и команды встречаются друг с другом. В зависимости от условий положения и от количества команд могут проводиться в два или несколько кругов с таким расчётом, чтобы каждая команда провела одинаковое количество встреч на своём поле и на поле противника. Победительницей является та команда, которая набирает большее количество очков (имеет большее количество выигранных встреч). По этому же принципу определяются и последующие места, занятые командами.
Круговая система позволяет точно определить силы команд, исключает элемент случайных проигрышей, позволяет определить место каждой команды. Недостатком этой системы является длительное время проведения соревнований, большие материальные затраты, связанные с проживанием участников. Эта система не позволяет охватить большое количество команд.
Календарь игр по круговой системе составляется следующим образом. При проведении жеребьёвки каждой команде (участнику) присваивается определённый номер. После этого составляются пары соперников на каждый день соревнований. Вначале определяется количество дней соревнования и общее количество встреч для того, чтобы составить расписание встреч.
Количество встреч определяется по формуле: 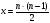
где  – количество встреч;
– количество встреч;  – количество участвующих команд.
– количество участвующих команд.
При нечётном количестве команд количество календарных дней будет равно количеству команд, при чётном – на один меньше. Очерёдность встреч при круговой системе определяется по специальной таблице, которую можно составить двумя способами: с чередованием полей и без чередования полей.
Первый способ (с чередованием полей). В этом способе команда, которая стоит в паре первой, играет на своём поле. Для составления таблицы всегда берётся нечётное количество участников и чертится соответственное количество вертикальных линий. Внизу под первой линией ставится первый номер, а остальные вписываются по порядку змейкой. В результате справа и слева от вертикальной линии будут располагаться участники одного дня соревнований.
Примерный календарь соревнований для пяти команд:
4 5
4 3 5 4 1 5
5 2 1 3 2 4
1 2 3
Команды, номера которых вписаны снизу и сверху вертикали, будут в этот день свободны от игры. Если количество команд будет чётным, то к команде, не играющей в этот день, подставляется очередная цифра, равная последней, и в строчку записываются пары.
В нашем примере для пяти команд календарь игр будет выглядеть так:
1-й день 1-0 5-2 4-3
2-й день 0-4 2-1 3-5
3-й день 2-0 1-3 5-4
4-й день 0-5 3-2 4-1
5-й день 3-0 2-4 1-5
Для шести команд календарь проведения встреч будет таким:
1-й день 1-6 2-5 3-4
2-й день 6-4 5-3 1-2
3-й день 2-6 3-1 4-5
4-й день 6-5 1-4 2-3
5-й день 3-6 4-2 5-1
Второй способ (без чередования полей) используется в тех случаях, когда смена полей не имеет значения или когда игры проводятся на одной площадке. Таблица составляется для чётного количества участников: если количество участников нечётное, то вместо следующего чётного номера ставят ноль.
Принцип составления таблицы следующий. Все участвующие команды делят пополам, и номера команд записывают вертикальным столбцом в два ряда. Первая половина номеров, начиная с первого, записываются сверху вниз, а последующая – снизу вверх. Номера, попавшие рядом, составляют пары первого дня соревнований. Для определения второго дня и последующих дней соревнований в таблице первый номер оставляют остальные передвигают на одно место по кругу против часовой стрелки.
Календарь встреч для семи команд:
1-й день 2-й день 3-й день 4-й день 5-й день 6-й день 7-й день
1-0 1-7 1-6 1-5 1-4 1-3 1-2
2-7 0-6 7-5 6-4 5-3 4-2 3-0
3-6 2-5 0-4 7-3 6-2 5-0 4-7
4-5 3-4 2-3 0-2 7-0 6-7 5-6
При участии большего количества команд и возникновении необходимости проведения соревнований в ограниченные сроки календарь встреч составляют с разбивкой команд на предварительные подгруппы. В этом случае часто прибегают к рассеиванию команд. В каждую подгруппу включают победителей предыдущего розыгрыша. Остальные участники определяются жребием. В каждой подгруппе встречи проводят по круговой системе и определяют место каждого участника. Занявшие первые места в подгруппах играют между собой и т.д.
Иногда применяют и другой вариант. Участники, занявшие 1 и 2 места, образуют первую финальную группу, где разыгрывают места по круговой системе; 3 и 4 места образуют вторую финальную группу и т.д.
II. Система розыгрыша с выбыванием. Смешанная система розыгрыша.
Эта система позволяет привлечь к участию в соревнованиях неограниченное количество команд, и провести розыгрыш в короткие сроки. Принцип этой системы: проигравший выбывает из соревнований, и в финале встречаются только две команды, которые разыгрывают между собой первое и второе место.
Недостатком системы с выбыванием является то, что половина всех участвующих выбывают из розыгрыша после первого поражения. Система не исключает элемента случайности (выход в финал не самых сильных команд). Жребий может свести между собой самых сильных участников в начальной стадии розыгрыша, и некоторым из них придётся выбыть из соревнований. Эта система не позволяет определить занятое место каждого участника или команды (кроме 1 и 2 места), принявшей участие в соревнованиях.
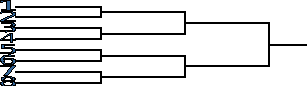
Составляя расписание игр и таблицы соревнований, порядковый номер команды в таблице определяют жеребьевкой. Если число участвующих команд удваивается (4,8,16,32 и т. д.), то название команд располагают в таблице сверху вниз в порядке, определенным жребием. Первая команда играет со второй, третья – с четвертой и т.д. В игру вступают все команды-участницы. Победители первого этапа играют между собой (также попарно) в порядке сверху вниз.
Если число участвующих команд не представляет степени числа 2, то часть команд, в зависимости от полученных ими по жеребьевке номеров, вступает в игру со второго тура, что определяется по формуле: (А — 2n)*2 = х, где А — количество участвующих команд, п — степень 2, дающая число, максимально приближенное к числу участвующих команд. Например: в соревнованиях участвуют 11 команд, приближенное число 2 в степени п будет 23, т. е. 8. Раскроем формулу: (А — 23)*2 = (11— 23)*2 = (11 — 8)*2 = 6. Следовательно, в первом туре должны играть 6-команд, а 5 команд начнут соревнования со второго тура.
Если число команд четное, то сверху и снизу играет во втором туре равное количество команд, а если нечетное — то снизу играет на одну команду больше, чем сверху.
Схема встреч для 8 команд.
1-й этап 2-й этап 3-й этап
(четвертьфинал) (полуфинал) (финал)
Расчёт числа команд по способу с выбыванием.
|
Общее число команд – участниц |
Число команд вступающих в борьбу в первом этапе |
Число команд, вступающих в борьбу со второго этапа |
||
|
всего |
«сверху» |
«снизу» |
||
|
4 |
4 |
– |
– |
– |
|
5 |
2 |
3 |
1 |
2 |
|
6 |
4 |
2 |
1 |
1 |
|
7 |
6 |
1 |
– |
– |
|
8 |
8 |
– |
– |
– |
|
9 |
2 |
7 |
3 |
4 |
|
10 |
4 |
6 |
3 |
3 |
|
11 |
6 |
5 |
2 |
3 |
|
12 |
8 |
4 |
2 |
2 |
|
13 |
10 |
3 |
1 |
2 |
|
14 |
12 |
2 |
1 |
1 |
|
15 |
14 |
1 |
– |
1 |
|
16 |
16 |
– |
– |
– |
|
17 |
2 |
15 |
7 |
8 |
|
18 |
4 |
14 |
7 |
7 |
|
19 |
6 |
13 |
6 |
7 |
|
20 |
8 |
12 |
6 |
6 |
|
21 |
10 |
11 |
5 |
6 |
|
22 |
12 |
10 |
5 |
5 |
|
23 |
14 |
9 |
4 |
5 |
|
24 |
16 |
8 |
4 |
4 |
Смешанная система. Смешанная система предполагает проведение встреч в определённой последовательности. Часто в начальной стадии соревнования проводятся по системе с выбыванием, а на заключительной – по круговой. Но встречается и обратный вариант.
|
|
Группа: Друзья Ранг: Старожил Сообщений: 2428
Замечаний: |
В детстве я увлекался шахматами. Причем как самой игрой, так и организацией всевозможных турниров (чемпионатов класса, школы, лагеря, факультета), старостой и главным судьей которых, как правило, я сам же и выступал.
На организаторском поприще особенно мне нравилось составлять расписания круговых (“каждый с каждым”) турниров. В этом мне помогала старенькая брошюра с гордым названием “Шахматный кодекс”, в конце которой имелись специальные таблицы для подготовки расписания встреч в турнирах с числом участников от 3 до 20, с равномерным чередованием цвета фигур у различных участников от тура к туру.
Как-то я задумался о том, что вот поеду я, например, в колхоз (студенческий) и захотят там устроить шахматный турнир, а Кодекса у меня с собой не будет и как же быть? И решил я на досуге попробовать разгадать алгоритм этих волшебных таблиц, чтобы при необходимости воспроизводить их с помощью лишь карандаша и бумаги (ну, и головы, конечно). О том, что эти таблицы называются таблицами Бергера, я узнал совсем недавно, прошерстив Интернет перед этой публикацией.
Получилось у меня следующее. Расписание всегда составляется для четного числа участников. При нечетном числе участник, которому в очередном туре выпадает встреча с последним (несуществующим) участником, отдыхает. Для первого тура пары образуются очень просто: первый номер играет с последним, второй – с предпоследним и т.д. Например, для 12 участников первый тур будет выглядеть следующим образом: 1-12, 2-11, 3-10, 4-9, 5-8, 6-7. А дальше с периодичностью в два тура повторяются операции перестановки, которые лучше всего изобразить графически (см. на листе “Алгоритм” в прилагаемом файле).
Номера участников следует определять жребием. Не следует связывать их с каким-либо рангом, рейтингом, например, по результатам прошлых заслуг в соревнованиях. Если же задать номера в соответствии с рангом, то следует иметь в виду, что по таблицам встреча номеров 1 и 2 происходит уже во втором туре, что ослабляет интригу турнира по сравнению с тем, если бы эта встреча состоялась в самом последнем туре. И всё же, при непреодолимом желании обеспечения хорошей интриги и нумерации участников в соответствии с рангом – туры, сформированные по таблицам Бергера, следует каким-либо способом перетасовать (подобная творческая перетасовка выходит за рамки данного сообщения).
В прилагаемом файле – 4 листа: “Бергер”, играющий основную вычислительную роль в демонстрируемом функционале, а также “Календарь”, “Участники”, “Алгоритм”.
На первом листе “Бергер” в ячейку A1 следует ввести количество участников – целое положительное число не более 50, после чего ниже на этом листе автоматически сформируется расписание турнира. На большее, чем 50, кол-во не настроены формулы, да и трудно представить круговой турнир с таким большим числом участников. Обычно при таких количествах уже используются другие системы соревнований – олимпийская, швейцарская и др. Но при большом желании или теоретическом интересе формулы могут быть легко добавлены и для числа больше 50 – пока не упремся по ширине таблицы в технические ограничения Excel. Наименования колонок “Б” и “Ч” означают белый и черный цвет фигур для шахмат, шашек и иных интеллектуальных игр. Сопутствующие наименования в скобках “(х)” и “(г)” означают “хозяина” и “гостя” – для футбола, баскетбола и т.д.
На втором листе “Календарь” встречи, сгенерированные на листе “Бергер” с горизонтальным расположением туров, развернуты в более привычную хронологическую последовательность туров (и встреч внутри туров) сверху вниз. Для удобства практического использования файла без дополнительного “формулизма” на этот же лист подтягиваются имена участников, соответствующие номерам (задаются на третьем листе).
На третьем листе “Участники” как раз и происходит расшифровка безликих числовых номеров. В качестве примера я выбрал список команд российской премьер-лиги по футболу сезона 2012-2013. Для какого-либо своего турнира пропишите на этот лист своих участников (Иванов, Петров, Сидоров и т.п.), после чего возьмите расписание встреч с листа “Календарь” и играйте на здоровье.
И, наконец, на четвертом листе “Алгоритм” – наглядная схема разгаданного мной когда-то принципа таблиц Бергера. Согласно этому принципу первый тур расписывается так, как я уже упоминал выше: первый – с последним, второй с – предпоследним и т.д. Белый цвет – у “левых” участников пар. После компоновки первого тура на нём рисуются стрелочки, представляющие собой встречи второго тура. В соответствии с этими стрелочками (выходят из будущих “левых”) записываются встречи второго тура. Первой (самой верхней) в любом следующем туре всегда записывается встреча с участием последнего номера (всегда четного), а далее сверху вниз – остальные встречи, начиная с самой нижней (и далее вверх) стрелки, нарисованной в предыдущем туре. После записи всех встреч второго тура на них рисуется свой (несколько иной) набор стрелок, в соответствии с которым далее расписывается третий тур и т.д. Как можно увидеть, наборы стрелок двух соседних туров отличаются друг от друга и далее так и повторяются – через тур. На самом последнем туре, разумеется, уже никакие стрелки не рисуются – за ненадобностью.
В качестве “Списка литературы” – несколько ссылок по таблицам Бергера, которые я отметил для себя:
http://otvet.mail.ru/question/35011020
http://www.tournamentdirector.co.uk/berger_pairings.html
http://www.fide.com/component/handbook/?id=20&view=category (см. раздел “Annex 1: Berger Tables for Round-Robin Tournaments”)
http://www.devenezia.com/round-robin/forum/YaBB.pl?num=1152214269
По третьей ссылке мне встретилось любопытное замечание, о котором я раньше не задумывался: “Для двухкругового турнира рекомендуется поменять местами два последних тура первого круга. Это позволит избежать трех последовательных игр с тем же самым цветом.” Например, номер 1 играет два первых тура белыми в первом круге и, следовательно, будет играть два первых тура черными во втором круге. Но он играет черными и в последнем туре первого круга, поэтому на рубеже первого и второго круга, если не последовать упомянутому замечанию, у номера 1 получится три партии подряд чёрными.
МОИ: Ник, Tip box: 41001663842605

