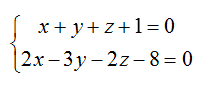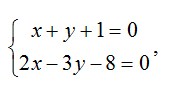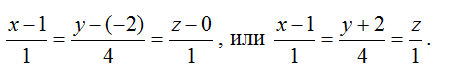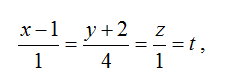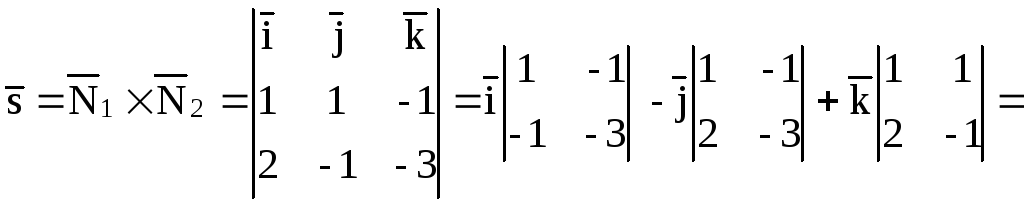Канонические уравнения линий второго порядка
Рассмотрим задачу приведения уравнения линии второго порядка к наиболее простому (каноническому) виду.
Напомним, что алгебраической линией второго порядка называется геометрическое место точек плоскости, которое в какой-либо аффинной системе координат может быть задано уравнением вида
где
— многочлен второй степени двух переменных
. Требуется найти прямоугольную систему координат, в которой уравнение линии приняло бы наиболее простой вид.
Результатом решения поставленной задачи является следующая основная теорема (3.3)
Классификация алгебраических линий второго порядка (теорема 3.3)
Для любой алгебраической линии второго порядка существует прямоугольная система координат , в которой уравнение этой линии принимает один из следующих девяти канонических видов:
Теорема 3.3 дает аналитические определения линий второго порядка. Согласно пункту 2 замечаний 3.1, линии (1), (4), (5), (6), (7), (9) называются вещественными (действительными), а линии (2), (3), (8) — мнимыми.
Приведем доказательство теоремы, поскольку оно фактически содержит алгоритм решения поставленной задачи.
Без ограничения общности можно предполагать, что уравнение линии второго порядка задано в прямоугольной системе координат . В противном случае можно перейти от непрямоугольной системы координат
к прямоугольной
, при этом уравнение линии будет иметь тот же вид и ту же степень согласно теореме 3.1 об инвариантности порядка алгебраической линии.
Пусть в прямоугольной системе координат алгебраическая линия второго порядка задана уравнением
(3.34)
в котором хотя бы один из старших коэффициентов отличен от нуля, т.е. левая часть (3.34) — многочлен двух переменных
второй степени. Коэффициенты при первых степенях переменных
и
, а также при их произведении
взяты удвоенными просто для удобства дальнейших преобразований.
Для приведения уравнения (3.34) к каноническому виду используются следующие преобразования прямоугольных координат:
– поворот на угол
(3.35)
– параллельный перенос
(3.36)
– изменение направлений координатных осей (отражения в координатных осях):
оси ординат оси абсцисс
обеих осей
– переименование координатных осей (отражение в прямой )
(3.38)
где и
— координаты произвольной точки в старой
и новой
системах координат соответственно.
Кроме преобразования координат обе части уравнения можно умножать на отличное от нуля число.
Рассмотрим сначала частные случаи, когда уравнение (3.34) имеет вид:
Эти уравнения (также многочлены в левых частях) называются приведенными. Покажем, что приведенные уравнения (I), (II), (III) сводятся к каноническим (1)–(9).
Уравнение (I). Если в уравнении (I) свободный член равен нулю , то, разделив обе части уравнения
на старший коэффициент
, получим
— уравнение двух совпадающих прямых (9), содержащих ось абсцисс
. Если же свободный член отличен от нуля
, то разделим обе части уравнения (I) на старший коэффициент
. Если величина
отрицательная, то, обозначив ее через
, где
, получаем
— уравнение пары параллельных прямых (7):
или
. Если же величина
положительная, то, обозначив ее через
, где
, получаем
— уравнение пары мнимых параллельных прямых (8). Это уравнение не имеет действительных решений, поэтому на координатной плоскости нет точек, отвечающих этому уравнению. Однако в области комплексных чисел уравнение
имеет два сопряженных решения
, которые иллюстрируются штриховыми линиями (см. пункт 8 теоремы 3.3).
Уравнение (II). Разделим уравнение на старший коэффициент и перенесем линейный член в правую часть:
. Если величина
отрицательная, то, обозначая
, получаем
— уравнение параболы (6). Если величина
положительная, то, изменяя направление оси абсцисс, т.е. выполняя второе преобразование в (3.37), получаем уравнение
или
, где
. Это уравнение параболы в новой системе координат
.
Уравнение (III). Возможны два случая: либо старшие коэффициенты одного знака (эллиптический случай), либо противоположных знаков (гиперболический случай).
В эллиптическом случае при
переносим свободный член в правую часть и делим обе части на
:
Если знак старших коэффициентов противоположен знаку
, то, обозначая положительные величины
и
через
и
, получаем
— уравнение эллипса (1).
Если знак старших коэффициентов совпадает со знаком
, то, обозначая положительные величины
и
через
и
, получаем
— уравнение мнимого эллипса (2). Это уравнение не имеет действительных решений. Однако оно имеет решения в области комплексных чисел, которые иллюстрируются штриховой линией (см. пункт 2 теоремы 3.3).
Можно считать, что в уравнениях эллипса (действительного или мнимого) коэффициенты удовлетворяют неравенству , в противном случае этого можно добиться, переименовывая координатные оси, т.е. делая преобразование (3.38) системы координат.
Если свободный член уравнения (III) равен нулю , то, обозначая положительные величины
и
через
и
, получаем
— уравнение пары мнимых пересекающихся прямых (3). Этому уравнению удовлетворяет только точка с координатами
и
, т.е. точка
— начало координат. Однако в области комплексных чисел левую часть уравнения можно разложить на множители
, поэтому уравнение имеет сопряженные решения
, которые иллюстрируются штриховыми линиями, пересекающимися в начале координат (см. пункт 3 теоремы 3.3).
В гиперболическом случае при
переносим свободный член в правую часть и делим обе части на
:
Величины и
имеют противоположные знаки. Без ограничения общности считаем, что знак
совпадает со знаком свободного члена
, т.е.
. В противном случае нужно переименовать координатные оси, т.е. сделать преобразование (3.38) системы координат. Обозначая положительные величины
и
через
и
, получаем
— уравнение гиперболы (4).
Пусть в уравнении (III) свободный член равен нулю . Тогда можно считать, что
, а
(в противном случае обе части уравнения умножим на –1) . Обозначая положительные величины
и
через
и
, получаем
— уравнение пары пересекающихся прямых (5). Уравнения прямых находятся в результате разложения на множители левой части уравнения
, то есть
Таким образом, приведенные уравнения (I),(II),(III) алгебраической линии второго порядка сводятся к одному из канонических видов (1)–(9), перечисленных в теореме 3.3.
Осталось показать, что общее уравнение (3.34) можно свести к приведенным при помощи преобразований прямоугольной системы координат.
Упрощение общего уравнения (3.34) производится в два этапа. На первом этапе при помощи поворота системы координат “уничтожается” член с произведением неизвестных. Если произведения неизвестных нет , то поворот делать не надо (в этом случае переходим сразу ко второму этапу). На втором этапе при помощи параллельного переноса “уничтожаются” один или оба члена первой степени. В результате получаются приведенные уравнения (I),(II),(III).
Первый этап: преобразование уравнения линии второго порядка при повороте прямоугольной системы координат.
Если коэффициент , выполним поворот системы координат на угол
. Подставляя выражения (3.35) в уравнение (3.34), получаем:
Приводя подобные члены, приходим к уравнению вида (3.34):
(3.39)
где
Определим угол так, чтобы
. Преобразуем выражение для
, переходя к двойному углу:
Угол должен удовлетворять однородному тригонометрическому уравнению
, которое равносильно уравнению
(3.40)
поскольку . Это уравнение имеет бесконечное количество корней
Выберем любой из них, например, угол из интервала
. Тогда в уравнении (3.39) исчезнет член
, поскольку
.
Обозначив оставшиеся старшие коэффициенты через и
, получим уравнение
(3.41)
Согласно теореме 3.1, уравнение (3.41) является уравнением второй степени (при преобразовании (3.35) порядок линии сохраняется), т.е. хотя бы один из старших коэффициентов или
отличен от нуля. Далее будем считать, что именно коэффициент при
не равен нулю
. В противном случае (при
и
) следует сделать поворот системы координат на угол
, который также удовлетворяет условию (3.40). Тогда вместо координат
в (3.41) получим
соответственно, т.е. отличный от нуля коэффициент
будет при
.
Второй этап: преобразование уравнения линии второго порядка при параллельном переносе прямоугольной системы координат.
Уравнение (3.41) можно упростить, выделяя полные квадраты. Нужно рассмотреть два случая: или
(согласно предположению
), которые называются центральный (включающий эллиптический и гиперболический случаи) или параболический соответственно. Геометрический смысл этих названий раскрывается в дальнейшем.
Центральный случай: и
. Выделяя полные квадраты по переменным
, получаем
После замены переменных
(3.42)
получаем уравнение
(3.43)
где .
Параболический случай: и
. Выделяя полный квадрат по переменной
, получаем
(3.44)
Если , то последнее уравнение приводится к виду
Сделав замену переменных
(3.45)
получим, где
(3.46)
Если , то уравнение (3.44) приводится к виду, где
,
(3.47)
(3.48)
Замены переменных (3.42), (3.45), (3.48) соответствуют параллельному переносу системы координат (см. пункт 1″a” замечаний 2.3).
Таким образом, при помощи параллельного переноса системы координат получаем новую систему координат
, в которой уравнение линии второго порядка принимает вид (3.43), или (3.46), или (3.47). Эти уравнения являются приведенными (вида (III),(II) или (I) соответственно).
Основная теорема 3.3 о приведении уравнения алгебраической линии второго порядка к каноническому виду доказана.
Замечания 3.8
1. Система координат, в которой уравнение алгебраической линии второго порядка имеет канонический вид, называется канонической. Каноническая система координат определяется неоднозначно. Например, изменяя направление оси ординат на противоположное, снова получаем каноническую систему координат, так как замена переменной на
не изменяет уравнений (1)–(9). Поэтому ориентация канонической системы координат не имеет принципиального значения, ее всегда можно сделать правой, изменив при необходимости направление оси ординат.
2. Ранее показано, что преобразования прямоугольных систем координат на плоскости сводятся к одному из преобразований (2.9) или (2.10):
Поэтому задача приведения уравнения линии второго порядка к каноническому виду сводится к нахождению начала канонической системы координат
и угла
наклона ее оси абсцисс
к оси абсцисс
исходной системы координат
.
3. В случаях (3),(5),(7),(8),(9) линии называются распадающимися, поскольку соответствующие им многочлены второй степени разлагаются в произведение многочленов первой степени.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Канонические уравнения прямой в пространстве: теория, примеры, решение задач
Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.
В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через 2 заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.
Что такое каноническое уравнение прямой в пространстве
О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.
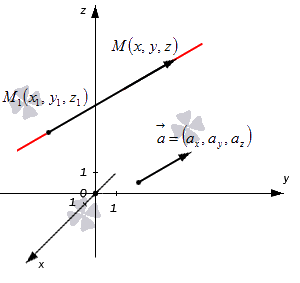
Допустим, у нас есть прямоугольная система координат O x y z , в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой a , а точку M , то можно записать, что M 1 ( x 1 , y 1 , z 1 ) лежит на прямой a и направляющим вектором этой прямой будет a → = ( a x , a y , a z ) . Чтобы множество точек M ( x , y , z ) определяло прямую a , векторы M 1 M → и a → должны быть коллинеарными,
Если мы знаем координаты векторов M 1 M → и a → , то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты a → . Для того чтобы получить координаты M 1 M → , нам необходимо вычислить разность между M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) . Запишем:
M 1 M → = x – x 1 , y – y 1 , z – z 1
После этого нужное нам условие мы можем сформулировать так: M 1 M → = x – x 1 , y – y 1 , z – z 1 и a → = ( a x , a y , a z ) : M 1 M → = λ · a → ⇔ x – x 1 = λ · a x y – y 1 = λ · a y z – z 1 = λ · a z
Здесь значением переменной λ может быть любое действительное число или ноль. Если λ = 0 , то M ( x , y , z ) и M 1 ( x 1 , y 1 , z 1 ) совпадут, что не противоречит нашим рассуждениям.
При значениях a x ≠ 0 , a y ≠ 0 , a z ≠ 0 мы можем разрешить относительно параметра λ все уравнения системы x – x 1 = λ · a x y – y 1 = λ · a y z – z 1 = λ · a z
Между правыми частями после этого можно будет поставить знак равенства:
x – x 1 = λ · a x y – y 1 = λ · a y z – z 1 = λ · a z ⇔ λ = x – x 1 a x λ = y – y 1 a y λ = z – z 1 a z ⇔ x – x 1 a x = y – y 1 a y = z – z 1 a z
В итоге у нас получились уравнения x – x 1 a x = y – y 1 a y = z – z 1 a z , с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.
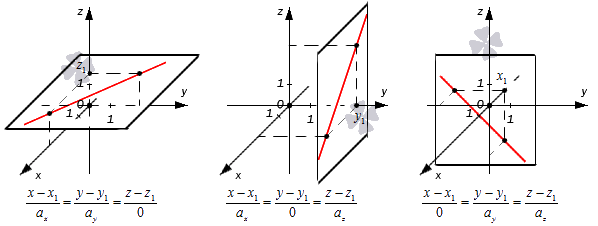
Такая запись используется даже при нулевых значениях одного или двух параметров a x , a y , a z , поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны 0 , поскольку направляющий вектор a → = ( a x , a y , a z ) нулевым не бывает.
Если один-два параметра a равны 0 , то уравнение x – x 1 a x = y – y 1 a y = z – z 1 a z носит условный характер. Его следует считать равным следующей записи:
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , λ ∈ R .
Частные случаи канонических уравнений мы разберем в третьем пункте статьи.
Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.
1) если исходная прямая будет проходить через две точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , то канонические уравнения примут следующий вид:
x – x 1 a x = y – y 1 a y = z – z 1 a z или x – x 2 a x = y – y 2 a y = z – z 2 a z .
2) поскольку a → = ( a x , a y , a z ) является направляющим вектором исходной прямой, то таковыми будут являться и все векторы μ · a → = μ · a x , μ · a y , μ · a z , μ ∈ R , μ ≠ 0 . Тогда прямая может быть определена с помощью уравнения x – x 1 a x = y – y 1 a y = z – z 1 a z или x – x 1 μ · a x = y – y 1 μ · a y = z – z 1 μ · a z .
Вот несколько примеров таких уравнений с заданными значениями:
x – 3 2 = y + 1 – 1 2 = z ln 7
Тут x 1 = 3 , y 1 = – 1 , z 1 = 0 , a x = 2 , a y = – 1 2 , a z = ln 7 .
x – 4 0 = y + 2 1 = z + 1 0
Тут M 1 ( 4 , – 2 , – 1 ) , a → = ( 0 , 1 , 0 ) .
Как составить каноническое уравнение прямой в пространстве
Мы выяснили, что канонические уравнения вида x – x 1 a x = y – y 1 a y = z – z 1 a z будут соответствовать прямой, проходящей через точку M 1 ( x 1 , y 1 , z 1 ) , а вектор a → = ( a x , a y , a z ) будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.
Разберем пару конкретных задач.
У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x + 1 4 = y 2 = z – 3 – 5 . Запишите координаты всех направляющих векторов для нее.
Решение
Чтобы получить координаты направляющего вектора, нам надо просто взять значения знаменателей из уравнения. Мы получим, что одним из направляющих векторов будет a → = ( 4 , 2 , – 5 ) , а множество всех подобных векторов можно сформулировать как μ · a → = 4 · μ , 2 · μ , – 5 · μ . Здесь параметр μ – любое действительное число (за исключением нуля).
Ответ: 4 · μ , 2 · μ , – 5 · μ , μ ∈ R , μ ≠ 0
Запишите канонические уравнения, если прямая в пространстве проходит через M 1 ( 0 , – 3 , 2 ) и имеет направляющий вектор с координатами – 1 , 0 , 5 .
Решение
У нас есть данные, что x 1 = 0 , y 1 = – 3 , z 1 = 2 , a x = – 1 , a y = 0 , a z = 5 . Этого вполне достаточно, чтобы сразу перейти к записи канонических уравнений.
x – x 1 a x = y – y 1 a y = z – z 1 a z ⇔ x – 0 – 1 = y – ( – 3 ) 0 = z – 2 5 ⇔ ⇔ x – 1 = y + 3 0 = z – 2 5
Ответ: x – 1 = y + 3 0 = z – 2 5
Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.
Канонические уравнения с одним или двумя a, равными нулю
Ранее мы уже говорили, что одно-два значения параметров a x , a y , a z в уравнениях могут иметь нулевые значения. При этом запись x – x 1 a x = y – y 1 a y = z – z 1 a z = λ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при λ ∈ R ):
x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ
Рассмотрим эти случаи подробнее. Допустим, что a x = 0 , a y ≠ 0 , a z ≠ 0 , a x ≠ 0 , a y = 0 , a z ≠ 0 , либо a x ≠ 0 , a y ≠ 0 , a z = 0 . В таком случае нужные уравнения мы можем записать так:
-
В первом случае:
x – x 1 0 = y – y 1 a y = z – z 1 a z = λ ⇔ x – x 1 = 0 y = y 1 + a y · λ z = z 1 + a z · λ ⇔ x – x 1 = 0 y – y 1 a y = z – z 1 a z = λ
Во втором случае:
x – x 1 a x = y – y 1 0 = z – z 1 a z = λ ⇔ x = x 1 + a x · λ y – y 1 = 0 z = z 1 + a z · λ ⇔ y – y 1 = 0 x – x 1 a x = z – z 1 a z = λ
В третьем случае:
x – x 1 a x = y – y 1 a y = z – z 1 0 = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z – z 1 = 0 ⇔ z – z 1 = 0 x – x 1 a x = y – y 1 a y = λ
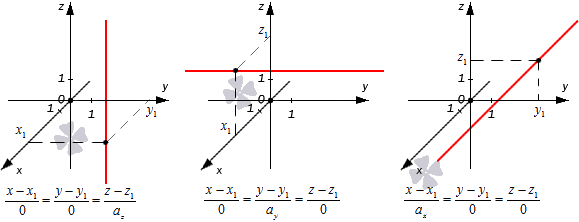
Получается, что при таком значении параметров нужные прямые находятся в плоскостях x – x 1 = 0 , y – y 1 = 0 или z – z 1 = 0 , которые располагаются параллельно координатным плоскостям (если x 1 = 0 , y 1 = 0 либо z 1 = 0 ). Примеры таких прямых показаны на иллюстрации.
Следовательно, мы сможем записать канонические уравнения немного иначе.
- В первом случае: x – x 1 0 = y – y 1 0 = z – z 1 a z = λ ⇔ x – x 1 = 0 y – y 1 = 0 z = z 1 + a z · λ , λ ∈ R
- Во втором: x – x 1 0 = y – y 1 a y = z – z 1 0 = λ ⇔ x – x 1 = 0 y = y 1 + a y · λ , λ ∈ R z – z 1 = 0
- В третьем: x – x 1 a x = y – y 1 0 = z – z 1 0 = λ ⇔ x = x 1 + a x · λ , λ ∈ R y = y 1 = 0 z – z 1 = 0
Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: x 1 = 0 y 1 = 0 , x 1 = 0 z 1 = 0 , y 1 = 0 z 1 = 0 . Их направляющие векторы имеют координаты 0 , 0 , a z , 0 , a y , 0 , a x , 0 , 0 . Если обозначить направляющие векторы координатных прямых как i → , j → , k → , то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:
Покажем на примерах, как применяются эти правила.
Найдите канонические уравнения, с помощью которых можно определить в пространстве координатные прямые O z , O x , O y .
Решение
Координатные векторы i → = ( 1 , 0 , 0 ) , j → = 0 , 1 , 0 , k → = ( 0 , 0 , 1 ) будут для исходных прямых направляющими. Также мы знаем, что наши прямые будут обязательно проходить через точку O ( 0 , 0 , 0 ) , поскольку она является началом координат. Теперь у нас есть все данные, чтобы записать нужные канонические уравнения.
Для прямой O x : x 1 = y 0 = z 0
Для прямой O y : x 0 = y 1 = z 0
Для прямой O z : x 0 = y 0 = z 1
Ответ: x 1 = y 0 = z 0 , x 0 = y 1 = z 0 , x 0 = y 0 = z 1 .
В пространстве задана прямая, которая проходит через точку M 1 ( 3 , – 1 , 12 ) . Также известно, что она расположена параллельно оси ординат. Запишите канонические уравнения этой прямой.
Решение
Учитывая условие параллельности, мы можем сказать, что вектор j → = 0 , 1 , 0 будет для нужной прямой направляющим. Следовательно, искомые уравнения будут иметь вид:
x – 3 0 = y – ( – 1 ) 1 = z – 12 0 ⇔ x – 3 0 = y + 1 1 = z – 12 0
Ответ: x – 3 0 = y + 1 1 = z – 12 0
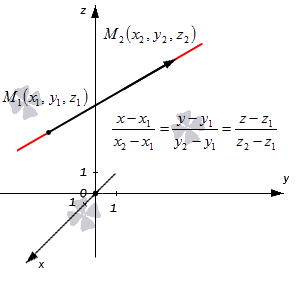
Как записать каноническое уравнение прямой, которая проходит через две заданные точки
Допустим, что у нас есть две несовпадающие точки M 1 ( x 1 , y 1 , z 1 ) и M 2 ( x 2 , y 2 , z 2 ) , через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?
Для начала примем вектор M 1 M 2 → (или M 2 M 1 → ) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:
M 1 M 2 → = x 2 – x 1 , y 2 – y 1 , z 2 – z 1
Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:
x – x 1 x 2 – x 1 = y – y 1 y 2 – y 1 = z – z 1 z 2 – z 1 x – x 2 x 2 – x 1 = y – y 2 y 2 – y 1 = z – z 2 z 2 – z 1
Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:
Приведем пример решения задачи.
в пространстве есть две точки с координатами M 1 ( – 2 , 4 , 1 ) и M 2 ( – 3 , 2 , – 5 ) , через которые проходит прямая. Запишите канонические уравнения для нее.
Решение
Согласно условиям, x 1 = – 2 , y 1 = – 4 , z 1 = 1 , x 2 = – 3 , y 2 = 2 , z 2 = – 5 . Нам требуется подставить эти значения в каноническое уравнение:
x – ( – 2 ) – 3 – ( – 2 ) = y – ( – 4 ) 2 – ( – 4 ) = z – 1 – 5 – 1 ⇔ x + 2 – 1 = y + 4 6 = z – 1 – 6
Если мы возьмем уравнения вида x – x 2 x 2 – x 1 = y – y 2 y 2 – y 1 = z – z 2 z 2 – z 1 , то у нас получится: x – ( – 3 ) – 3 – ( – 2 ) = y – 2 2 – ( – 4 ) = z – ( – 5 ) – 5 – 1 ⇔ x + 3 – 1 = y – 2 6 = z + 5 – 6
Ответ: x + 3 – 1 = y – 2 6 = z + 5 – 6 либо x + 3 – 1 = y – 2 6 = z + 5 – 6 .
Преобразование канонических уравнений прямой в пространстве в другие виды уравнений
Иногда пользоваться каноническими уравнениями вида x – x 1 a x = y – y 1 a y = z – z 1 a z не очень удобно. Для решения некоторых задач лучше использовать запись x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ . В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 . Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.
Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру λ и разрешим эти уравнения относительно других переменных. В итоге получим:
x – x 1 a x = y – y 1 a y = z – z 1 a z ⇔ x – x 1 a x = y – y 1 a y = z – z 1 a z ⇔ ⇔ x – x 1 a x = λ y – y 1 a y = λ z – z 1 a z = λ ⇔ x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ
Значение параметра λ может быть любым действительным числом, ведь и x , y , z могут принимать любые действительные значения.
В прямоугольной системе координат в трехмерном пространстве задана прямая, которая определена уравнением x – 2 3 = y – 2 = z + 7 0 . Запишите каноническое уравнение в параметрическом виде.
Решение
Сначала приравниваем каждую часть дроби к λ .
x – 2 3 = y – 2 = z + 7 0 ⇔ x – 2 3 = λ y – 2 = λ z + 7 0 = λ
Теперь разрешаем первую часть относительно x , вторую – относительно y , третью – относительно z . У нас получится:
x – 2 3 = λ y – 2 = λ z + 7 0 = λ ⇔ x = 2 + 3 · λ y = – 2 · λ z = – 7 + 0 · λ ⇔ x = 2 + 3 · λ y = – 2 · λ z = – 7
Ответ: x = 2 + 3 · λ y = – 2 · λ z = – 7
Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).
Равенство x – x 1 a x = y – y 1 a y = z – z 1 a z нужно для начала представить в виде системы уравнений:
x – x 1 a x = y – y 1 a y x – x 1 a x = z – z 1 a x y – y 1 a y = z – z 1 a z
Поскольку p q = r s мы понимаем как p · s = q · r , то можно записать:
x – x 1 a x = y – y 1 a y x – x 1 a x = z – z 1 a z y – y 1 a y = z – z 1 a z ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) a z · ( x – x 1 ) = a x · ( z – z 1 ) a z · ( y – y 1 ) = a y · ( z – z 1 ) ⇔ ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 = 0 a z · x – a x · z + a x · z 1 – a z · x 1 = 0 a z · y – a y · z + a y · z 1 – a z · y 1 = 0
В итоге у нас вышло, что:
x – x 1 a x = y – y 1 a y = z – z 1 a z ⇔ a y · x – a x · y + a x · y 1 – a y · x 1 = 0 a z · x – a x · z + a x · z 1 – a z · x 1 = 0 a z · y – a y · z + a y · z 1 – a z · y 1 = 0
Выше мы отмечали, что все три параметра a не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен 2 , поскольку a y – a x 0 a z 0 – a x 0 a z – a y = 0 и один из определителей второго порядка не равен 0 :
a y – a x a z 0 = a x · a z , a y 0 a z – a x = a x · a y , – a x 0 0 – a x = a x 2 a y – a x 0 a z = a y · a z , a y 0 0 – a y = – a y 2 , – a x 0 a z – a y = a x · a y a z 0 0 a z = a z 2 , a z – a x 0 – a y = – a y · a z , 0 – a x a z – a y = a x · a z
Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать 3 неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.
Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.
Прямая задана каноническим уравнением x – 1 2 = y 0 = z + 2 0 . Напишите для нее уравнение пересекающихся плоскостей.
Решение
Начнем с попарного приравнивания дробей.
x – 1 2 = y 0 = z + 2 0 ⇔ x – 1 2 = y 0 x – 1 2 = z + 2 0 y 0 = z + 2 0 ⇔ ⇔ 0 · ( x – 1 ) = 2 y 0 · ( x – 1 ) = 2 · ( z + 2 ) 0 · y = 0 · ( z + 2 ) ⇔ y = 0 z + 2 = 0 0 = 0
Теперь исключаем из расчетов последнее уравнение, потому что оно будет верным при любых x , y и z . В таком случае x – 1 2 = y 0 = z + 2 0 ⇔ y = 0 z + 2 = 0 .
Это и есть уравнения двух пересекающихся плоскостей, которые при пересечении образуют прямую, заданную с помощью уравнения x – 1 2 = y 0 = z + 2 0
Ответ: y = 0 z + 2 = 0
Прямая задана уравнениями x + 1 2 = y – 2 1 = z – 5 – 3 , найдите уравнение двух плоскостей, пересекающихся по данной прямой.
Решение
Приравниваем дроби попарно.
x + 1 2 = y – 2 1 = z – 5 – 3 ⇔ x + 1 2 = y – 2 1 x + 1 2 = z – 5 – 3 y – 2 1 = z – 5 – 3 ⇔ ⇔ 1 · ( x + 1 ) = 2 · ( y – 2 ) – 3 · ( x + 1 ) = 2 · ( z – 5 ) – 3 · ( y – 2 ) = 1 · ( z – 5 ) ⇔ x – 2 y + 5 = 0 3 x + 2 z – 7 = 0 3 y + 7 – 11 = 0
Получаем, что определитель основной матрицы полученной системы будет равен 0 :
1 – 2 0 3 0 2 0 3 1 = 1 · 0 · 1 + ( – 2 ) · 2 · 0 + 0 · 3 · 3 – 0 · 0 · 0 – 1 · 2 · 3 – ( – 2 ) · 3 · 1 = 0
Минор второго порядка нулевым при этом не будет: 1 – 2 3 0 = 1 · 0 – ( – 2 ) · 3 = 6 . Тогда мы можем принять его в качестве базисного минора.
В итоге мы можем вычислить ранг основной матрицы системы x – 2 y + 5 = 0 3 x + 2 z – 7 = 0 3 y + z – 11 = 0 . Это будет 2. Третье уравнение исключаем из расчета и получаем:
x – 2 y + 5 = 0 3 x + 2 z – 7 = 0 3 y + z – 11 = 0 ⇔ x – 2 y + 5 = 0 3 x + 2 z – 7 = 0
Ответ: x – 2 y + 5 = 0 3 x + 2 z – 7 = 0
Каноническое уравнение прямой в пространстве
Вы будете перенаправлены на Автор24
Существует несколько различных типов уравнений, описывающих кривую первого порядка, называемую прямой. Каждый из них оптимален для какой-то своей цели. Давайте познакомимся с ними поближе.
Каноническое уравнение прямой в пространстве
Канонический вид уравнения прямой в пространстве выглядит как следующее равенство:
где буквы $(x_0, y_0, z_0)$ используются для обозначения координат любой точки, возлежащей на данной прямой, а $(α, β, γ)$ — координаты направляющего эту прямую вектора, как несложно догадаться, они не могут быть нулевыми.
Не во всех случаях удобно и практично пользоваться каноническим уравнением, поэтому частенько возникает надобность использовать какое-то другое, например, можно прибегнуть к параметрическому.
Для каких прямых не представляется возможным или нельзя написать каноническое уравнение?
Глядя на это уравнение, видно, что его возможно использовать только в том случае, если координаты направляющих векторов исследуемых прямых не равны нулю, для таких прямых стоит воспользоваться параметрическими уравнениями.
Параметрический вид уравнений прямой в пространстве такой:
$begin x = x_1 + α cdot λ \ y = y_1 + β cdot λ \ z = z_1 + γ cdot λ \ end$,
где $x_1, y_1, z_1$ — координаты некоторой точки, находящейся на описываемой прямой, $α, β, γ$ — координаты параллельного или лежащего на данной прямой вектора, $λ$ — произвольное число-коэффициент, иногда для его обозначения используют слово “параметр”.
Параметрическое уравнение как раз удобно применять если одна из координат направляющего вектора равна нулю.
Чтобы произвести переход от параметрического вида уравнения к каноническому виду уравнения прямой в пространстве, осуществите вывод канонического уравнения прямой из параметрического.
Готовые работы на аналогичную тему
Для этого следует в к каждом уравнении перенести $λ$ в левую часть, а затем приравнять уравнения. Никакой магии, а только самая что ни на есть пресловутая арифметика:
Уравнение прямой, образуемой пересечением двух плоскостей
Рисунок 1. Связь канонического и общего уравнения прямой
Для того чтобы составить каноническое уравнение прямой в пространстве, заданной пересечением плоскостей, необходимо познакомиться поближе с 2 исследуемыми плоскостями.
Любую плоскость, находящуюся в пространстве, можно описать с помощью равенства:
$Ax + By + Cz + D = 0$,
где $A, B, C$ и $D$ – постоянные, причём $A, B, C$ не могут быть одновременно все нулевыми.
Соответственно, не нужно быть гением, чтобы понять, что если две плоскости пересечены между собой, то на их общей части будет возлежать некая прямая. Чтобы её найти, нужно получить общее решение следующей системы уравнений:
$begin A_1x + B_1y + C_1z + D_1 = 0 \ A_2x + B_2y + C_2z + D_2 = 0 \ end$
С помощью же частного решения этой системы уравнений можно узнать, принадлежит ли какая-либо точка трёхмерной системы координат описанным уравнениями плоскостям и, конечно же, нашей прямой. Для этого нужно просто подставить её икс, игрек и зет в систему.
Приведённая система уравнений является своеобразной “формулой”, служащей для нахождения общего уравнения прямой в пространстве.
Иногда в каких-либо практических задачах требуется получить из уравнения прямой в пространстве в общем виде параметрические или канонические уравнения, тогда в первую очередь вам стоит узнать координаты её направляющего вектора и какую-либо точку, находящуюся на изучаемой прямой.
Ну что ж, давайте решать нашу задачу. На первом этапе вычислим $x, y, z$ для направляющего вектора.
Найдём нормальные вектора для плоскостей. Если кто забыл, нормальный вектор — это такой вектор, который является перпендикулярным (ортогональным) к данной плоскости или прямой.
Для этого из нашего очаровательного примера системы уравнений необходимо взять коэффициенты из уравнений. В итоге для 1-ой плоскости вектор-нормаль будет выглядеть как $(A_1; B_1; C_1)$, а для второй как $(A_2; B_2; C_2)$.
Теперь необходимо перемножить оба вектора и получить их произведение, здесь $(i, j, k)$ – координаты единичного вектора.
$|overline cdot overline| = overline cdot (B_1 cdot C_2 – C_1 cdot B_2) – overline cdot (A_1 cdot C_2 – A_2 cdot C_1) + overline cdot (A_1 cdot B_2 – A_2 cdot B_1)$
Следующим этапом выполняем поиск координат точки, возлежащей на искомой прямой.
Для выполнения этого наиболее “сложного” пункта необходимо выбрать одну наиболее нравящуюся вам координату $x, y$ или $z$ и вместо неё подставить в систему уравнений, описывающую плоскости, нулевое значение.
Составьте каноническое уравнение прямой, получаемой из системы уравнений, описывающей пару пересечённых плоскостей:
$begin 2x – y + 3z + 4 = 0 \ x + 5y – 3z – 7 = 0 \ end$
Найдём направляющий вектор, для этого сначала запишем вектора нормалей плоскостей:
Ну а сейчас пора вычислить сам направляющий вектор:
Найдём точку, находящуюся на нашей прямой, тут всё просто, приравняем $y$ к нулю и внедрим в нашу систему уравнений:
$begin 2x + 3z + 4 = 0 \ x – 3z – 7 = 0 \ end$
Решение вышеприведённой системы уравнений будет: $x = 1, z = -2$, то есть координаты точки, возлежащей на нашей прямой, будут $(1; 0; -2)$.
Подставим все полученные нами цифры и получим следующее уравнение:
Составление канонического уравнения прямой по координатам двух точек
На практике это очень распространённая и любимая во многих вузах и других учебных заведениях задача — нужно найти уравнение прямой в пространстве, проходящей через 2 точки. Примем заранее, что эти две точки не обладают одинаковыми $x, y, z$.
Для того чтобы написать уравнение прямой в пространстве, проходящей через 2 точки, воспользуйтесь координатами ваших точек и внедрите их в следующее уравнение:
Это уравнение можно вывести из параметрического уравнения прямой.
Допустим, у нас есть две точки с координатами $(x_1; y_1; z_1)$, и для второй $(x_2; y_2; z_2)$.
Найти направляющий вектор для изучаемой прямой при наличии пары точек несложно, вектор с координатами $(x_2 – y_1; y_2 – y_2;z_2 – z_2)$ и будет желаемой частью результата.
Придумаем точку, находящуюся на нашей прямой, пусть она будет обладать координатами $(x_1;y_1;z_1)$.
Помещаем обнаруженные нами координаты вектора и точки в каноничное уравнение прямой в пространстве и получим уравнение прямой, проходящей через 2 точки.
Если же необходимо выразить именно параметрические уравнения из координат двух точек, через которые проведена некая одна прямая, то тут тоже всё довольно просто и без неожиданностей:
$begin x = x_1 + (x_2 – x_1) cdot λ \ y = y_1 + (y_2 – y_1)cdot λ \ z = z_1 + (z_2 – z_1) cdot λ \ end$
Уравнение прямой проходящей через две точки
Получить уравнение прямой, проходящей через две точки помогут созданные нами калькуляторы. Предлагаем найти каноническое и параметрическое уравнение прямой, а также уравнение прямой с угловым коэффициентом как на плоскости, так и в пространстве.
Прямая — это бесконечная линия, по которой проходит кратчайший путь между любыми двумя её точками.
Уравнения прямой, проходящей через две точки могут быть следующих видов:
- каноническое уравнение,
- параметрическое уравнение,
- общее уравнение прямой,
- уравнение прямой с угловым коэффициентом,
- уравнение прямой в полярных координатах и другие.
Для получения уравнений введите координаты двух точек прямой. Онлайн-калькулятор найдет уравнения и выдаст результат с подробным решением.
[spoiler title=”источники:”]
http://spravochnick.ru/matematika/parallelnost_pryamyh_i_ploskostey/kanonicheskoe_uravnenie_pryamoy_v_prostranstve/
http://mnogoformul.ru/uravnenie-pryamoj-po-dvum-tochkam
[/spoiler]
Прямую линию в прямоугольной системе координат можно задать с помощью канонического уравнения. В этой статье мы расскажем, что это такое, приведем примеры, рассмотрим связи канонических уравнений с другими типами уравнений для этой прямой. В последнем пункте мы разберем несколько задач на закрепление темы.
Понятие канонического уравнения прямой
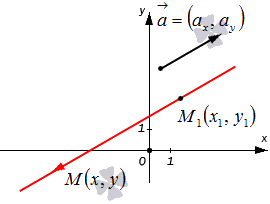
Допустим, что у нас есть декартова (прямоугольная) система координат, в которой задана прямая. Нам известны координаты произвольно взятой точки этой прямой M1(x1, y1), а также ее направляющего вектора a→=(ax, ay). Попробуем составить уравнение, которое описывало бы эту прямую.
Возьмем плавающую точку M(x, y). Тогда вектор M1M→ можно считать направляющим для исходной прямой. Его координаты будут равны x-x1, y-y1 (если нужно, повторите материал о том, как правильно вычислять координаты вектора с помощью координат отдельных его точек).
Множество произвольно взятых точек M(x, y) будут определять нужную нам прямую с направляющим вектором a→=(ax, ay) только в одном случае – если векторы M1M→ и a→=(ax, ay) будут коллинеарны по отношению друг к другу. Посмотрите на картинку:
Таким образом, мы можем сформулировать необходимое и достаточное коллинеарности этих двух векторов:
M1M→=λ·a→, λ∈R
Если преобразовать полученное равенство в координатную форму, то мы получим:
x-x1=λ·axy-y1=λ·ay
При условии, что ax≠0 и ay≠0, получим:
x-x1=λ·axy-y1=λ·ay⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay
Итог наших преобразований и будет каноническим уравнением прямой на плоскости. Запись вида x-x1ax=y-y1ay также называют уравнением прямой в каноническом виде.
Таким образом, с помощью уравнения x-x1ax=y-y1ay можно задать в прямоугольной системе координат на плоскости прямую, которая имеет направляющий вектор a→=(ax, ay) и проходит через точку M1(x1, y1).
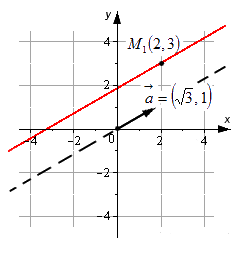
Примером уравнения подобного типа является, например, x-23=y-31. Прямая, которая задана с его помощью, проходит через M1(2, 3) и имеет направляющий вектор a→=3, 1. Ее можно увидеть на рисунке:
Из определения канонического уравнения нужно сделать несколько важных выводов. Вот они:
1. Если прямая, имеющая направляющий вектор a→=(ax, ay), проходит через две точки – M1(x1, y1) и M2(x2, y2), то уравнение для нее может быть записано как в виде x-x1ax=y-y1ay, так и x-x2ax=y-y2ay.
2. Если заданная прямая имеет направляющий вектор с координатами a→=(ax, ay), то множество всех ее векторов можно обозначить как μ·a→=(μ·ax, μ·ay), μ∈R, μ≠0. Таким образом, любое уравнение прямой в каноническом виде x-x1μ·ax=y-y1μ·ay будет соответствовать этой прямой.
Разберем важный пример задачи на нахождение канонического уравнения.
В прямоугольной системе координат на плоскости задана прямая, которая проходит через точку M1(2, -4) и имеет направляющий вектор с координатами a→=(1, -3). Запишите каноническое уравнение, описывающее данную прямую.
Решение
Для начала вспомним общий вид нужного нам канонического уравнения – x-x1ax=y-y1ay. Подставим в него имеющиеся значения x1=2, y1=-4, ax=1, ay=-3 и подсчитаем:
x-x1ax=y-y1ay⇔x-21=y-(-4)-3⇔x-21=y+4-3
Получившееся в итоге равенство и будет нужным ответом.
Ответ: x-21=y+4-3
Канонические уравнения прямой на плоскости с ax или ay, равными нулю
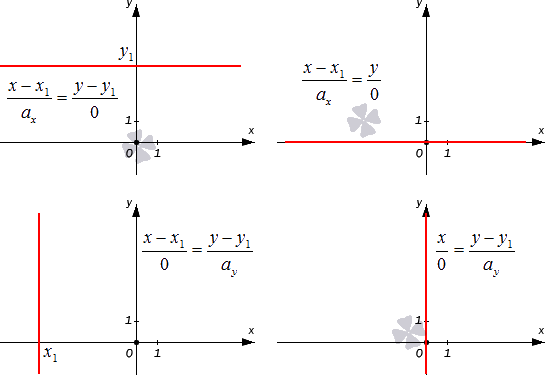
Если значение хотя бы одной переменной a является нулевым, то уравнение плоскости используют в первоначальном виде. Сразу две переменные нулевыми не могут быть по определению, поскольку нулевой вектор не бывает направляющим. В таком случае мы можем считать запись x-x1ax=y-y1ay условной и понимать ее как равенство ay(x-x1)=ax(y-y1).
Разберем случаи канонических уравнений на плоскости с одним нулевым a более подробно. Допустим, что x-x10=y-y1ay при ax=0, а исходная прямая будет проходить через M1(x1, y1). В таком случае она является параллельной оси ординат (если x1=0, то она будет с ней совпадать). Докажем это утверждение.
Для этой прямой вектор a→=(0, ay) будет считаться направляющим. Этот вектор является коллинеарным по отношению к координатному вектору j→=(0,1).
Если же нулевым является значение второго параметра, то есть ay=0, то мы получаем равенство вида x-x1ax=y-y10. Это уравнение описывает прямую, проходящую через M1(x1, y1), которая расположена параллельно оси абсцисс. Это утверждение верно, поскольку a→=(ax, 0) является для этой прямой направляющим вектором, а он в свою очередь является коллинеарным по отношению к координатному вектору i→=(1, 0).
Проиллюстрируем два частных случая канонического уравнения, описанные выше:
На плоскости задана прямая, параллельная оси Oy. Известно, что она проходит через точку M123, -17. Запишите каноническое уравнение для нее.
Решение
Если прямая по отношению оси ординат является параллельной, то мы можем взять координатный вектор j→=(0, 1) в качестве направляющего для нее. В таком случае искомое уравнение выглядит следующим образом:
x-230=y–171⇔x-230=y+171
Ответ: x-230=y+171
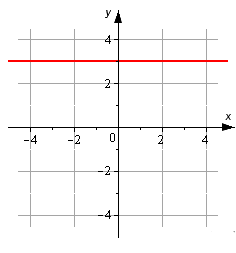
На рисунке изображена прямая. Запишите ее каноническое уравнение.
Решение
Мы видим, что исходная прямая проходит параллельно оси Ox через точку M1(0, 3). Мы берем координатный вектор i→=(1, 0) в качестве направляющего. Теперь у нас есть все данные, чтобы записать нужное уравнение.
x-01=y-30⇔x1=y-30
Ответ: x1=y-30
Преобразование канонического уравнения прямой в другие виды уравнений
Мы уже выяснили, что в прямоугольной системе координат на плоскости заданную прямую можно описать с помощью канонического уравнения. Оно удобно для решения многих задач, однако иногда лучше производить вычисления с помощью другого типа уравнений. Сейчас мы покажем, как преобразовать каноническое уравнение в другие виды, если это требуется по ходу решения.
Стандартной форме записи канонического уравнения x-x1ax=y-y1ay можно поставить в соответствие систему параметрических уравнений на плоскости x=x1+ax·λy=y1+ay·λ. Чтобы преобразовать один вид уравнения в другой, нам надо приравнять правую и левую часть исходного равенства к параметру λ. После этого надо выполнить разрешение получившихся равенств относительно переменных x и y:
x-x1ax=y-y1ay⇔x-x1ax=y-y1ay=λ⇔⇔x-x1ax=λy-y1ay=λ⇔x=x1+ax·λy=y1+ay·λ
Покажем на примере, как именно выполняется это действие с конкретными числами.
У нас есть прямая, заданная на плоскости с помощью канонического уравнения x+23=y-111. Запишите параметрические уравнения исходной прямой.
Решение
Сначала поставим знак равенства между отдельными частями уравнения и переменной λ и получим x+23=λy-111=λ.
Далее можно перейти к формулированию необходимых параметрических уравнений:
x+23=λy-111=λ⇔x+2=3·λy-1=11·λ⇔x=-2+3·λy=1+11·λ
Ответ: x=-2+3·λy=1+11·λ
Из канонического уравнения можно получить не только параметрические, но и общие уравнения прямой. Вспомним понятие пропорции: запись ab=cd можно представить в виде a·d=b·c с сохранением смысла. Значит, что x-x1ax=y-y1ay⇔ay(x-x1)=ax(y-y1)⇔ayx-axy-ayx1+axy1=0.
Это и есть общее уравнение прямой. Это станет более очевидно, если мы добавим в него значения параметров ay=A, -ax=B, -ayx1+axy1=C.
Прямая на плоскости описана с помощью канонического уравнения x-12=y+40. Вычислите общее уравнение этой прямой.
Решение
Делаем указанные выше действия по порядку.
x-12=y+40⇔0·(x-1)=2·(y+4)⇔y+4=0
Ответ: y+4=0 .
Также из канонического уравнения мы можем получить уравнение прямой в отрезках, прямой с угловым коэффициентом или нормальное уравнение прямой, но это действие выполняется в два шага: первым делом мы получаем общее уравнение прямой, а вторым – преобразуем его в уравнение указанного типа. Разберем пример такой задачи.
На плоскости задана прямая с помощью уравнения x+33=y-22. Запишите уравнение этой же прямой в отрезках.
Решение
Для начала преобразуем исходное каноническое уравнение в общее уравнение прямой.
x+33=y-22⇔2·(x+3)=3·(y-2)⇔2x-3y+6+23=0
Далее переходим к формулировке уравнения прямой в отрезках.
2x-3y+6+23=0⇔2x-3y=-6+23⇔⇔2-(6+23)x-3-(6+23)y=1⇔x-6+232+y6+233=1⇔x-3+3+y33+2=1
Ответ: x-3+3+y33+2=1
Достаточно легко решить и задачу, обратную этой, т.е. привести уравнение прямой на плоскости обратно к каноническому. Допустим, у нас есть общее уравнение прямой в стандартной формулировке – Ax+By+C=0. При условии A≠0 мы можем перенести By вправо с противоположным знаком. Получим Ax+C=-By. Теперь выносим A за скобки и преобразуем равенство так:
Ax+CA=-By
Получившееся уравнение мы записываем в виде пропорции: x+CA-B=yA.
У нас получилось нужное нам каноническое уравнение прямой на плоскости.
А как сделать преобразование, если B≠0? Переносим все слагаемые, кроме Ax, вправо с противоположными знаками. Получаем, что Ax=-By-C. Выносим -B за скобки:
Ax=-By+CB
Формируем пропорцию: x-B=y+CBA
Есть общее уравнение прямой x+3y-1=0. Перепишите его в каноническом виде.
Решение
Оставим с левой стороны только одну переменную x. Получим:
x=-3y+1
Теперь вынесем -3 за скобки: x=-3y-13. Преобразуем равенство в пропорцию и получим необходимый ответ:
x-3=y-131
Ответ: x-3=y-131
Таким же образом мы поступаем, если нам нужно привести к каноническому виду уравнение прямой в отрезках и уравнение прямой с угловым коэффициентом.
Наиболее простая задача – переход от параметрических уравнений к каноническим. Нужно просто выразить параметр λ в системе уравнений x=x1+ax·λy=y1+ay·λ и приравнять обе части равенств. Схема решения выглядит так:
x=x1+ax·λy=y1+ay·λ⇔λ=x-x1axλ=y-y1ay⇔x-x1ax=y-y1ay
Если значение одного из параметров a будет нулевым, мы поступаем точно таким же образом.
Прямая на плоскости описана с помощью системы параметрических уравнений x=3+0·λy=-2-4·λ. Запишите каноническое уравнение для этой прямой.
Решение
Для начала преобразуем исходные уравнения в систему x=3+0·λy=-2-4·λ. Следующим шагом будет выражение параметра в каждом уравнении:
x=3+0·λy=-2-4·λ⇔λ=x-30λ=y+2-4
Ставим знак равенства между получившимися частями и получаем нужное нам каноническое уравнение: x-30=y+2-4
Ответ: x-30=y+2-4
Как решать задачи на составление канонических уравнений
В первую очередь канонические уравнения используются для тех задач, где нужно выяснить, принадлежит ли некоторая точка заданной прямой или нет. Вспомним, что в случае, если точка лежит на прямой, ее координаты будут удовлетворять уравнению этой прямой.
На плоскости задана прямая, каноническое уравнение которой имеет вид x-12=y+12-3. Выясните, лежат ли на ней точки M13, -312 и M2(5, -4).
Решение
Для проверки принадлежности необходимо подставить координаты точки в исходное уравнение и проверить, получим ли мы в итоге верное равенство.
3-12=-312+12-2⇔1=1
Результат говорит нам, что точка M13, -312 принадлежит исходной прямой.
Точно так же поступим и с координатами второй точки:
5-12=-4+12-3⇔2=76
Получившееся в итоге равенство не является верным, значит, эта точка заданной прямой не принадлежит.
Ответ: первая точка лежит на заданной прямой, а вторая нет.
Есть две точки M1(2, 4) и M2(-1, 3). Будет ли прямая, которая задана в той же плоскости с помощью уравнения x-20=y-32, проходить через них?
Решение
Вспомним, что запись x-20=y-32 можно понимать как 2·(x-2)=0·(y-3)⇔x-2=0. Подставим координаты заданных точек в это равенство и проверим.
Начнем с первой точки M1(2, 4) : 2-2=0⇔0=0
Равенство верное, значит, эта точка расположена на заданной прямой.
Подставляем данные второй точки: -1-2=0⇔-3=0.
Равенство неверное, значит, точка M2(-1, 3) не лежит на исходной прямой.
Ответ: через точку M1(2, 4) прямая проходит, а через M2(-1, 3) нет.
Далее мы посмотрим, какие еще типичные задачи на нахождение канонического уравнения можно встретить. Возьмем примеры с разными условиями.
Наиболее простыми являются задачи на нахождение канонического уравнения прямой на плоскости, в которых уже заданы координаты некой точки, лежащей на прямой. В первой части материала мы уже приводили пример решения такой задачи.
Чуть сложнее будет найти нужное уравнение, если нам предварительно нужно будет вычислить координаты направляющего вектора исходной прямой. Чаще всего встречаются задачи, в которой нужная прямая проходит через две точки с известными координатами.
Прямая на плоскости проходит через точку M1(0, -3) и через точку M2(2, -2). Сформулируйте для этой прямой канонической уравнение.
Решение
Eсли у нас есть координаты двух точек, то мы можем вычислить по ним координаты вектора M1M2→=2, 1. По отношению к прямой, чье уравнение мы составляем, он будет направляющим вектором. После этого мы можем записать следующее:
x-02=y-(-3)1⇔x2=y+31
Также можно использовать координаты второй точки. Тогда мы получим: x-22=y-(-2)1⇔x-22=y+21
Ответ: x2=y+31
Посмотрим, как нужно составлять канонические уравнения прямой на плоскости в том случае, если направляющий вектор этой прямой нужно вычислять исходя из параллельных или перпендикулярных ей прямых.
Известно, что точка M1(1, 3) принадлежит некоторой прямой, которая параллельна второй прямой, заданной с помощью уравнения x2=y-5. Запишите каноническое уравнение первой прямой.
Решение
Для первой прямой можно определить направляющий вектор a→=2, -5. Его можно рассматривать и в качестве направляющего для второй прямой, что следует из самого определения направляющих векторов. Это позволяет нам получить всю информацию, нужную для записи искомого уравнения: x-12=y-3-5
Ответ: x-12=y-3-5
Через точку M1(-1, 6) проходит прямая, которая является перпендикулярной другой прямой, определенной на плоскости с помощью уравнения 2x-4y-7=0. Запишите каноническое уравнение первой прямой.
Решение
Из данного уравнения мы можем взять координаты нормального вектора второй прямой – 2, 4. Мы знаем, что этот вектор является направляющим по отношению к первой. Тогда мы можем записать искомое уравнение:
x-(-1)2=y-64⇔x+11=y-62
Ответ: x+11=y-62
Написать канонические и параметрические уравнения прямой, образованной пересечением плоскостей
Решение
1) Найдем координаты фиксированной точки. Из исходной системы уравнений
исключим z.
Положим z=0, тогда:
откуда находим: x=1, y= -2.
Таким образом, нашли координаты фиксированной точки M0(1,-2,0).
2) Направляющий вектор определяется как векторное произведение нормалей двух плоскостей, образующих прямую:
3) Запишем канонические уравнения:
4) Обозначив,
получаем параметрические уравнения:
x=t+1, y=4t-2, z=4
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
3.1. Канонические
уравнения прямой.
Пусть в системе
координат Oxyz
дана прямая, которая проходит через
точку

вектор, параллельный данной прямой.
Векторназываетсянаправляющим
вектором прямой.
Возьмем на прямой точку и рассмотрим вектор
Векторы
коллинеарны, следовательно, их
соответствующие координаты пропорциональны:
(3.3.1)
Эти уравнения
называются каноническими
уравнениями прямой.
уравнения прямой, проходящей через
точку M(1,
2, –1) параллельно вектору
Решение:
Вектор
является направляющим вектором искомой
прямой. Применяя формулы (3.1.1), получим:
Это канонические
уравнения прямой.
Замечание:
Обращение в нуль одного из знаменателей
означает обращение в нуль соответствующего
числителя, то есть y
– 2 = 0; y
= 2. Данная прямая лежит в плоскости y
= 2, параллельной плоскости Oxz.
3.2.
Параметрические
уравнения прямой.
Пусть прямая
задана каноническими уравнениями
Обозначим тогда
Величина t
называется параметром и может принимать
любые значения:
.
Выразим x,
y
и z
через t
:
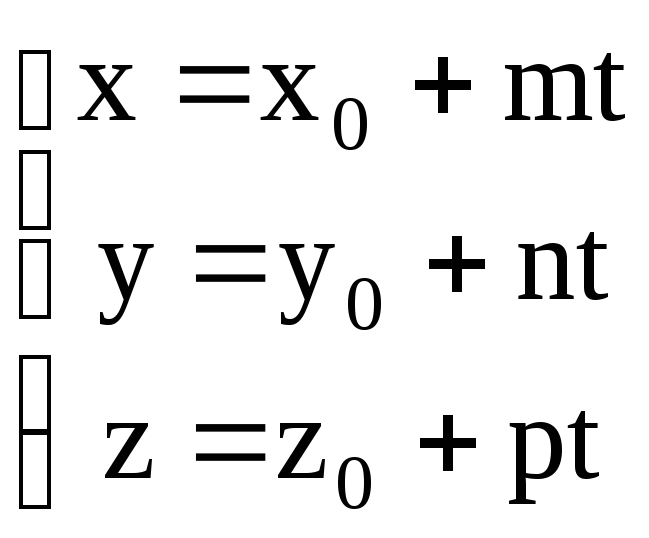
Полученные уравнения
называются параметрическими
уравнениями прямой.
Пример 1:
Составить
параметрические уравнения прямой,
проходящей через точку M
(1, 2, –1) параллельно вектору
Решение:
Канонические уравнения этой прямой
получены в примере пункта 3.1:
Для нахождения
параметрических уравнений прямой
применим вывод формул (3.2.1):
Итак,

прямой.
Ответ:
Пример 2.
Составить
параметрические уравнения прямой,
проходящей через точку M
(–1, 0, 1) параллельно вектору
гдеA
(2, 1, –1), B
(–1, 3, 2).
Решение:
Вектор является направляющим
вектором искомой прямой.
Найдем вектор .
= (–3; 2; 3). По формулам
(3.2.1) запишем уравнения прямой:

параметрические уравнения прямой.
3.3. Уравнения
прямой, проходящей через две заданные
точки.
Через две заданные
точки в пространстве проходит единственная
прямая (см. рис.20). Пусть даны точки
Вектор
можно принять за направляющий вектор
данной прямой. Тогда уравнения прямой
наход
по формулам (3.1.1):).
(3.3.1)
Пример 1.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
Решение:
Применяем
формулу (3.3.1)
Получили канонические
уравнения прямой. Для получения
параметрических уравнений применим
вывод формул (3.2.1). Получим

уравнения прямой.
Пример 2.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки
Решение:
По формулам
(3.3.1) получим:
Это канонические
уравнения.
Переходим к
параметрическим уравнениям:

уравнения.
Полученная прямая
параллельна оси oz
(см. рис.21).
3.4. Прямая как
линия пересечения двух плоскостей.
Пусть в
пространстве даны две плоскости
и
Если эти плоскости
не совпадают и не параллельны, то они
пересекаются по прямой:
Эта система двух
линейных уравнений задает прямую как
линию пересечения двух плоскостей. От
уравнений (3.4.1) можно перейти к каноническим
уравнениям (3.1.1) или параметрическим
уравнениям (3.2.1). Для этого необходимо
найти точку
лежащую на прямой, и направляющий вектор
Координаты точки
получим из системы (3.4.1), придав одной
из координат произвольное значение
(например,z
= 0). За направляющий вектор
можно взять векторное произведение
векторовто есть
Пример 1.
Составить
канонические уравнения прямой
Решение: Пусть
z
= 0. Решим систему
Сложив эти уравнения,
получим: 3x
+ 6 = 0
x
= –2. Подставим найденное значение x
= –2 в первое уравнение системы и получим:
–2 + y
+ 1 = 0
y
= 1.
Итак, точка
лежит на искомой прямой.
Для нахождения
направляющего вектора прямой запишем
нормальные векторы плоскостей:
и найдем их векторное произведение:
Уравнения прямой
находим по формулам (3.1.1):
Ответ: .
Другой способ:
Канонические и параметрические
уравнения прямой (3.4.1) легко получить,
найдя две различные точки на прямой из
системы (3.4.1), а затем применив формулы
(3.3.1) и вывод формул (3.2.1).
Пример 2.
Составить канонические и параметрические
уравнения прямой
Решение:
Пусть y
= 0. Тогда система примет вид:
Сложив уравнения,
получим: 2x
+ 4 = 0; x
= –2. Подставим x
= –2 во второе уравнение системы и
получим: –2 –z
+1 = 0
z
= –1. Итак, нашли точку
Для нахождения
второй точки положим x
= 0. Будем иметь:
То есть
Далее применяем
формулы (3.3.1):
Получили канонические
уравнения прямой.
Составим
параметрические уравнения прямой:
Ответ:
; 
3.5. Взаимное
расположение двух прямых в пространстве.
Пусть прямые
заданы уравнениями:
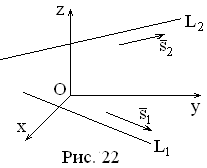
;
:
.
Под углом между
этими прямыми понимают угол между их
направляющими векторами
(см. рис.22). Этот угол
находим по формуле из векторной алгебры:
или
(3.5.1)
Если прямые перпендикулярны
(),то
Следовательно,
(3.5.2)
Это условие
перпендикулярности двух прямых в
пространстве.
Если прямые
параллельны (),то их направляющие
векторы коллинеарны (),
то есть
(3.5.3)
Это условие
параллельности двух прямых в пространстве.
Пример 1. Найти
угол между прямыми:
а).
и
б). и
Решение:
а). Запишем направляющий вектор прямой
Найдем направляющий вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему
Затем найдем их векторное произведение:
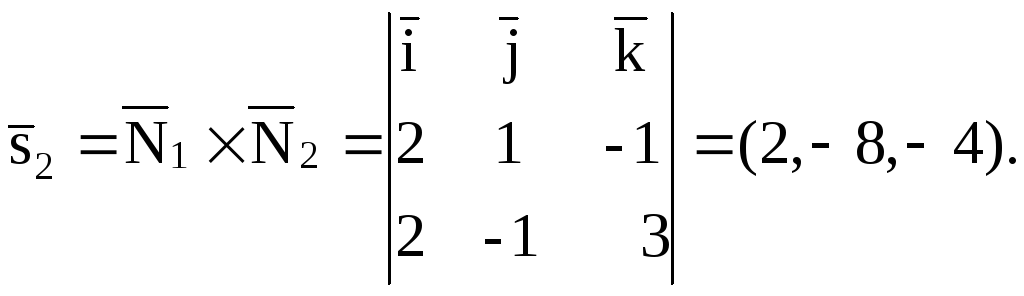
пункта 3.4).
По формуле (3.5.1)
получим:
Следовательно,
б). Запишем
направляющие векторы данных прямых:
Векторы
коллинеарны, так как их соответствующие
координаты пропорциональны:
Значит прямые
параллельны (
),
то есть
Ответ: а).
б).
Пример 2. Доказать
перпендикулярность прямых:
и
Решение:
Запишем направляющий вектор первой
прямой
Найдем направляющий
вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему:
Вычислим их векторное произведение:

Применим условие
перпендикулярности прямых (3.5.2):
Условие выполнено;
следовательно, прямые перпендикулярны
().
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #