Как составить канонические уравнения метода сил

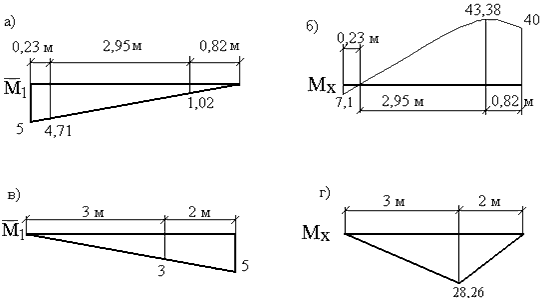
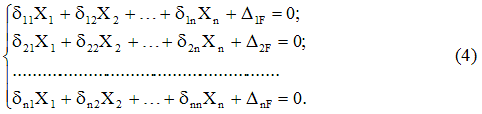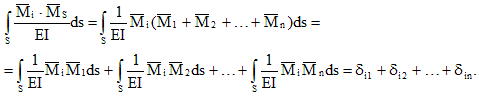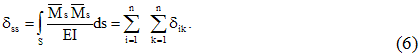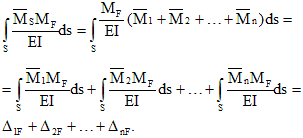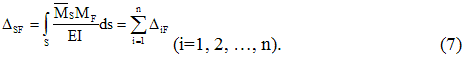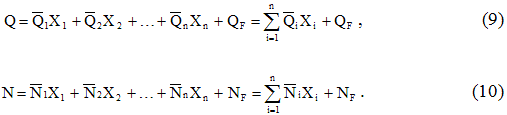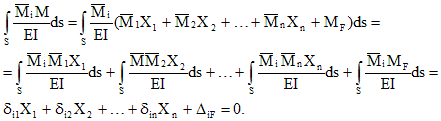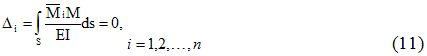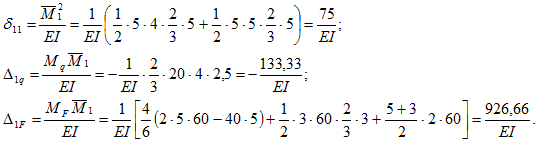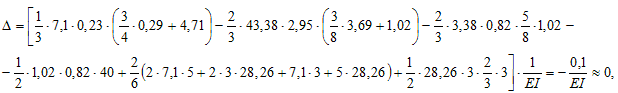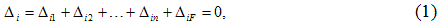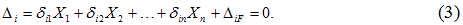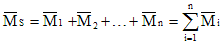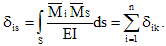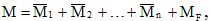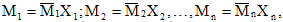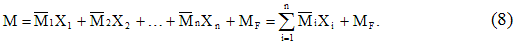Обратимся к
ранее рассмотренному примеру (рис. 7.5)

Рис. 7.5

В эквивалентной
системе, также как в заданной, перемещения
по направлению отброшенных связей
должны равняться нулю. На основании
принципа независимости действия сил
перемещения по
— тому направлению от всех сил можно
представить в виде:

(7.1)

Здесь первые
индексы означают направления перемещения
(и одновременно направление отбрасываемой
связи), а вторые — причину вызвавшую
эти перемещения. Таким образом
— означает перемещение по направлениюот— го силового фактора. Обозначим черезреакцию связи,
тогда поскольку перемещение пропорционально
соответствующей силе, то

,
(7.2)

где
— единичное перемещение по—
тому направлению от силы.
Подставляя (7.2) в (7.1), получим

.
(7.3)

Таким образом,
условие эквивалентности основной и
заданной
статически неопределимой системы
сводится к системелинейных алгебраических уравнений.

(7.4)

Уравнения (7.4)
являются каноническими уравнениями
метода сил. Они позволяют раскрыть
статические нагрузки системы. Первое
из (7.4) означает, что перемещения по
первому направлению от всех сил равно
нулю и т.д. Число уравнений системы равно
степени статической неопределимости.

Единичный
коэффициент
определяется с помощью интегралов Мора,
причем на основании теоремы взаимности
перемещений.

(7.5)

Грузовой коэффициент

(7.6)

Если с.н.с. состоит
из прямолинейных участков, то интегралы
Мора (4.2), (4.3) можно вычислять по правилу
Верещагина.

Вернемся теперь
к математическим свойствам системы
(4.1). Коэффициенты
называются главными, они всегда
положительные. Побочные коэффициенты
—,
могут быть положительными и отрицательными.— свободные члены уравнений или грузовые
коэффициенты. Могут быть положительными
и отрицательными.

Напомним еще раз,
что в балках и рамах в подавляющем
большинстве случаев перемещения от
изгиба и кручения намного больше
перемещений от растяжения и сдвига.
Поэтому в (7.5) и (7.6) последними тремя
интегралами, как правило, можно пренебречь.

7.5. Использование свойств симметрии при раскрытии статической неопределенности

Пусть имеется
симметричная в геометрическом смысле
рама (рис. 7.6), т.е. левая часть является
зеркальным отображением правой части
относительно оси симметрии. При расчете
таких систем решение канонических
уравнений можно упростить.

Рис. 7.6

Рассмотрим два
случая загружения рамы: симметричной
(рис. 7.6, б) и кососимметричной (рис. 7.6,
в) нагрузкой. Аналогично будем
классифицировать и внутренние силовые
факторы. Рассекая стержень в общем
случае нагружения, будем иметь шесть
составляющих внутренних усилий.

Докажем
следующее положение: у симметричной
рамы при симметричной нагрузке обращаются
в нуль, кососимметричные неизвестные,
а при кососимметричной нагрузке —
симметричные неизвестны.

Рис. 7.7

Рассмотрим
раму, изображенную на рис. 7.6. Основная
система при использовании свойств
симметрии должна быть обязательно
симметричной. Она будет общей как при
симметричном, так и кососимметричном
загружении. На рисунке 7.8 показаны
основная и эквивалентные системы.

Рис. 7.8

Обозначая
через
и— кососимметричные силовые факторы, и
черезисимметричные, выпишем систему канонических
уравнений. В данном случае их будет
шесть:

Заменим теперь,
что в этих уравнениях многие из
коэффициентов обращаются в нуль. Это
будут все коэффициенты, у которых один
индекс принадлежит симметричному, а
другой — кососимметричному фактору.
Например, обращается в нуль коэффициент
.
Индекс 1 принадлежит кососимметричному
фактору, а индекс 3 — симметричному
фактору. Обращаются также в нульи т.д. Сказанное становится более
очевидным, если учесть, что в рассматриваемой
системе эпюра изгибающих моментов от
кососимметричных факторов будет
кососимметричной, а от симметричных
факторов — симметричной. При перемножении
таких эпюр, естественно получим нуль,
в то время как перемножение кососимметричной
эпюры на кососимметричную и симметричной
на симметричную дает результат, отличный
от нуля.

Вычеркивая
из системы уравнений коэффициенты,
обращающиеся в нуль, получим:

Как видим,
система уравнений распалась на две
независимые.

Теперь
положим, что внешняя нагрузка является
симметричной. Из сказанных выше
соображений следует, что
.
Первая система уравнений становится
однородной. Тогда.
Следовательно, при симметричной нагрузке
кососимметричные силовые факторы
обращаются в нуль.

При
кососимметричной нагрузке
.
Тогда.
В этом случае в плоскости симметрии
обращаются в нуль симметричные силовые
факторы.

Таким образом,
при симметричной нагрузке кососимметричные
неизвестные равны нулю, а при
кососимметричной нагрузке —симметричные
раны нулю. Если внешняя нагрузка не
обладает свойствами симметрии, то ее
всегда можно разложить на симметричную
и кососимметричную, как показано на
рис. 7.9.

Рис. 7.9

При этом
задача распадается на две, которые
решаются отдельно. Окончательные эпюры
получаются сложением эпюр от симметричной
и кососимметричной нагрузки.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Метод сил – расчет статически неопределимых рам

Заказать решение           Способ оплаты

При решении задач сопромата, статически неопределимой называется такая система, которая не может быть рассчитана при помощи одних только уравнений статики, так как имеет лишние связи. Для расчета таких систем составляются дополнительные уравнения, учитывающие деформации системы.

Оговоримся, что здесь и далее понятие “расчет” подразумевает только построение эпюр внутренних силовых факторов, возникающих в элементах системы, а не расчет на прочность, жесткость и т.д.

Статически неопределимые системы обладают рядом характерных особенностей:

1. Статически неопределимые конструкции являются более жесткими, чем соответствующие статически определимые, так как имеют дополнительные связи.
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках.
3. Нарушение лишних связей в статически неопределимой системе не всегда приводит к разрушению, в то время как потеря связи в статически определимой системе делает ее геометрически изменяемой.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Основными методами расчетастатически неопределимых систем являются:

1. Метод сил. Здесь в качестве неизвестных рассматриваются усилия – силы и моменты.
2.Метод перемещений. Неизвестными являются деформационные факторы – углы поворотов и линейные смещения.
3.Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения.
4. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитичеких методов при расчете особо сложных систем используются различные численные методы.

Канонические уравнения метода сил

Для получения дополнительных уравнений, о которых говорилось в предыдущем параграфе, нужно прежде всего превратить заданную, n раз статически неопределимую систему, в статически определимую, удалив из нее лишние связи. Полученная статически определимая система называется основной. Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой, однако изложение этого вопроса выходит за рамки этого пособия. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными.

В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения.

Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:

где первый индекс означает направление перемещения и номер отброшенной связи, а второй указывает на причину, вызвавшую перемещение, т.е. – это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи; – перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.

В методе сил реакцию k-ой связи принято обозначать через Xk. С учетом этого обозначения и в силу справедливости закона Гука перемещения можно представить в виде:

где – единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией т.е. реакцией, совпадающей по направлению с Xk, но равной единице.

Подставляя (2) в (1), получим:

Физический смысл уравнения (3): перемещение в основной системе по направлению i-ой отброшенной связи равно нулю.

Записывая выражения, аналогичные (3), для всей совокупности отброшенных связей, получим систему канонических уравнений метода сил:

Вид уравнения (4), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей.

Коэффициенты системы канонических уравнений (4) определяются методом Мора-Верещагина путем перемножения соответствующих эпюр. Все эти коэффициенты, как указывалось выше, представляют собой перемещения; коэффициенты, стоящие при неизвестных – единичные перемещения, а свободные члены – грузовые. Единичные перемещения делятся на главные, расположенные по главной диагонали и имеющие одинаковые индексы и побочные (). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е. .

Алгоритм расчета методом сил

Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил:

1. Определить степень статической неопределимости.
2. Выбрать основную систему.
3. Сформировать эквивалентную систему.
4. Записать систему канонических уравнений.
5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.
6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.
7. Построить суммарную единичную эпюру.
8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов.
9. Решить систему (4), т.е. определить реакции лишних связей.
10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры).
11. Выполнить статическую и кинематическую проверки.
Отметим, что пункты 7, 8, 11 приведенного алгоритма не являются безусловно необходимыми, хотя и позволяют контролировать правильность выполнения расчета. А для систем с одной лишней связью пункты 7 и 8 просто лишены смысла, так как в этом случае суммарная единичная эпюра совпадает с единичной.
Остановимся подробнее на некоторых из вышеперечисленных этапов расчета.

Выбор основной системы

Это важнейший этап расчета, так как рациональный выбор основной системы существенно упрощает вычислительную работу. Рассмотрим возможные способы удаления лишних связей, что и определяет вид основной системы.

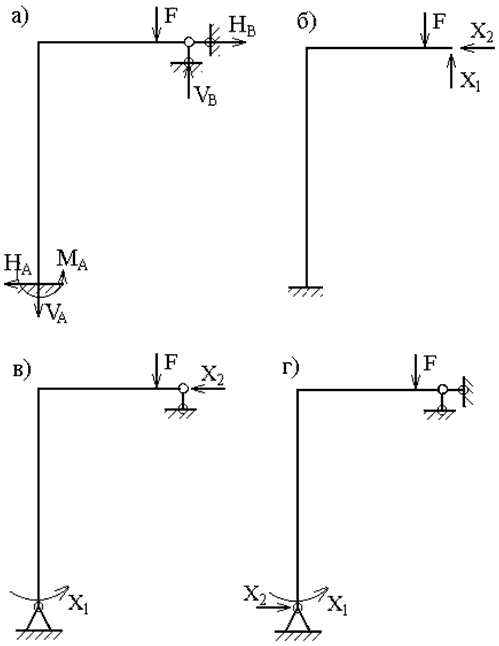
1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в направлениях отброшенных связей, являются лишними неизвестными. На рис.1,б, в, г показаны различные варианты эквивалентной системы, полученные этим способом для рамы (рис.1,а).

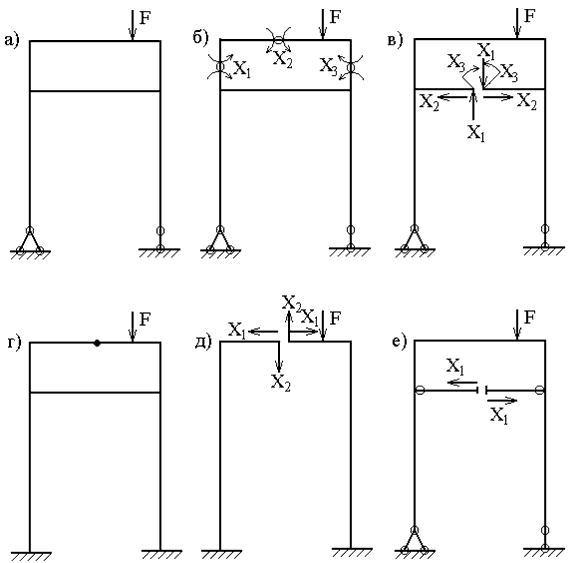
2.Постановка шарниров в промежуточных сечениях стержней позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту. Эти моменты являются лишними неизвестными. Для рамы, имеющей степень статической неопределимости n=3 (рис.2,а), при выборе основной системы необходимо поставить три шарнира. Положение этих шарниров может быть произвольным, но удовлетворяющим требованию геометрической неизменяемости системы (рис.2,б).

3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.2,в). В частных случаях (рис.2,г) рассечение стержня по шарниру освобождает две связи (рис.2,д), а рассечение прямолинейного стержня с шарнирами по концам – одну связь (рис.2,е).

рис. 1

Среди связей статически неопределимой системы различают абсолютно необходимые и условно необходимые. К абсолютно необходимым относятся связи, при удалении которых система становится геометрически изменяемой. Для абсолютно необходимой связи характерна статическая определимость усилия в ней, т.е. реакция такой связи может быть вычислена из условия равновесия. При выборе основной системы абсолютно необходимые связи отбрасывать нельзя.

рис. 2

Связи, при удалении которых система продолжает оставаться геометрически неизменяемой, называются условно необходимыми. Система, у которой удалили такую связь, может являться основной системой метода сил.

Вычисление коэффициентов и свободных членов канонических уравнений

Этому этапу расчета предшествует построение единичных и грузовых эпюр внутренних силовых факторов (для балок и рам – эпюр изгибающих моментов). Единичные эпюры строятся от действия безразмерной единичной силы или безразмерного единичного момента, совпадающих по направлению с направлением соответствующей лишней неизвестной в эквивалентной системе, и обозначаются через , а единичная эпюра – через .

Грузовая эпюра строится от внешней нагрузки, приложенной к основной системе. При этом можно строить одну эпюру от одновременного действия всех внешних нагрузок или несколько эпюр, отдельно от каждой из приложенных нагрузок. Такое разбиение одной грузовой эпюры на несколько  более простых, как правило, целесообразно только тогда, когда среди действующих нагрузок есть равномерно распределенная, и эпюра моментов на соответствующем участке под ней является знакопеременной. При этом в каждом каноническом уравнении число свободных членов будет равно числу построенных грузовых эпюр.

Единичные и грузовые перемещения (коэффициенты и свободные члены канонических уравнений) в общем случае можно вычислить методом Мора. Для балок и рам это можно сделать при помощи правила Верещагина.

Универсальная проверка коэффициентов и свободных членов канонических уравнений

Для выполнения универсальной проверки необходимо построить суммарную единичную эпюру – эпюру моментов от одновременного действия всех единичных сил, приложенных к основной системе:

Перемножим суммарную единичную эпюру с эпюрой :

Таким образом результат перемножения суммарной и i-ой единичной эпюр – это перемещение по направлению i-ой связи от совместного действия единичных лишних неизвестных. Это перемещение равно сумме коэффициентов i-го канонического уравнения:

Такая проверка называется построчной и выполняется для каждого канонического уравнения.
Вместо n построчных проверок чаще всего выполняется одна – универсальная поверка, которая состоит в перемножении суммарной единичной эпюры самой на себя и проверке условия:

Если универсальная проверка выполняется, значит единичные перемещения вычислены правильно; если нет – необходимо выполнить построчные проверки, что позволит уточнить перемещение, при вычислении которого допущена ошибка.

Для выполнения проверки грузовых перемещений необходимо перемножить суммарную единичную и грузовую эпюры изгибающих моментов:

Таким образом, проверка свободных членов системы канонических уравнений (4) состоит в выполнении условия:

Построение окончательных эпюр внутренних силовых факторов

Окончательные эпюры можно построить двумя способами.

Так как при найденных значениях лишних неизвестных Xi выполняются условия совместности деформаций, то из расчета основной системы можно получить все искомые внутренние усилия заданной системы. На основании принципа независимости действия сил для изгибающих моментов получим:

или, учитывая, что

приходим к выражению:

Аналогично определяется продольные и поперечные силы:

Второй способ основан на том, что в результате вычисления реакций лишних связей Xi исходная статически неопределимая система приведена к статически определимой системе, загруженной внешними нагрузками и реакциями лишних связей. Поэтому окончательные эпюры внутренних силовых факторов можно построить для эквивалентной системы, вычислив предварительно (и то не всегда) из условий равновесия опорные реакции последней.

Недостатком первого способа является то обстоятельство, что для его реализации необходимо дополнительно построить эпюры Qi, Ni (i=1, 2, …,n), Qf, Nf, которые не используются в расчете методом сил и поэтому не были построены ранее.

В связи с этим для построения окончательных эпюр более рациональным представляется второй способ, а условие (8) можно использовать в качестве дополнительной проверки.

Проверка окончательной эпюры изгибающих моментов

Эта проверка выполняется в двух вариантах: статическая и кинематическая.

При статической проверке, выполняемой обычно для рам, вырезаются узлы и записываются условия их равновесия под действием узловых сосредоточенных моментов и изгибающих моментов на концах стержней. Эта проверка является вспомогательной и выполняется автоматически при правильных эпюрах изгибающих моментов в основной системе и при выполнении кинематической проверки.

Статическая проверка эпюр Q и N состоит в том, что для любой отсеченной части рамы сумма проекций на две оси всех действующих сил – внешних нагрузок и  внутренних усилий – должна быть равна нулю.

Основной проверкой окончательной эпюры моментов в методе сил является кинематическая проверка, которая может быть построчной или универсальной.<br /> При построчной проверке каждая единичная эпюра моментов перемножается с окончательной эпюрой моментов М:

Таким образом, в результате перемножения каждой единичной эпюры с окончательной эпюрой моментов получим ноль:

Вариантом построчной проверки является проверка по замкнутомуконтуру, состоящая в том, что сумма приведенных (т.е. деленных на жесткость соответствующего стержня или его участка) площадь эпюры М, находящихся внутри каждого замкнутого бесшарнирного контура, должна быть равна сумме приведенных площадей, находящихся снаружи этого контура.

Суммируя выражения типа (11) для всех n, получим выражение, служащее для универсальной кинематической проверки окончательной эпюры изгибающих моментов:

Формулу (12) можно интерпретировать следующим образом: условное перемещение эквивалентной, или, что то же самое, заданной системы по направлению всех неизвестных от действия всех неизвестных и внешних нагрузок, равно нулю.

Определение перемещений в статически неопределимых системах

Для определения перемещения в статически неопределимой системе используется тождественность заданной и эквивалентной систем в том смысле, что если условия совместности деформаций выполняются, т.е. справедливы уравнения (4), то перемещения в эквивалентной системе соответствуют перемещениям заданной системы. Тогда, построив для основной системы эпюру изгибающих моментов от единичной силы (или единичного момента) приложенной в направлении искомого перемещения, величину перемещения находим по формуле:

где М – эпюра изгибающих моментов от внешней нагрузки, построенная для статически неопределимой системы.

Отметим, что при вычислении перемещения можно поступить и наоборот: единичную эпюру моментов построить в статически неопределимой заданной системе, а эпюру моментов от внешних нагрузок М – в основной (статически определимой) системе.

Пример расчета

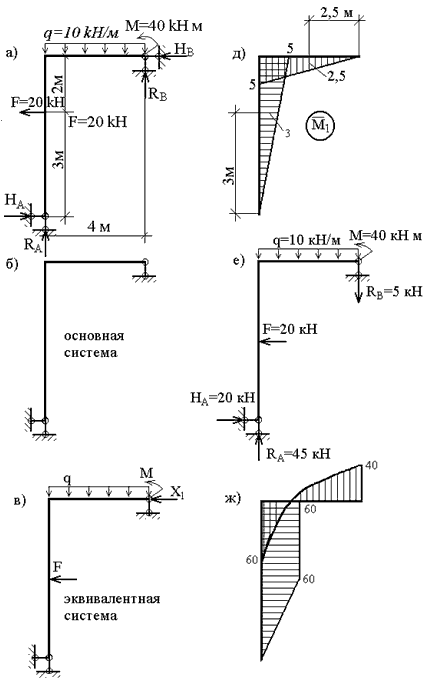
Построить эпюры продольных, поперечных сил и изгибающих моментов для плоской рамы (рис.3,а).

Степень статической неопределимости рамы:

n = r – s = 4 – 3 = 1

Выбираем основную систему, отбрасывая на правой опоре горизонтальный стержень (рис.3,б),  т.е. заменяем шарнирно-неподвижною опору на шарнирно-подвижную. На базе основной системы формируем эквивалентную систему (рис.3,в).

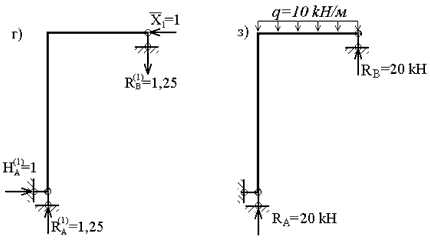
Заменяя реакцию лишней связи соответствующей единичной силой, (рис. 3,г) строим эпюру моментов M1 (рис.3,д).

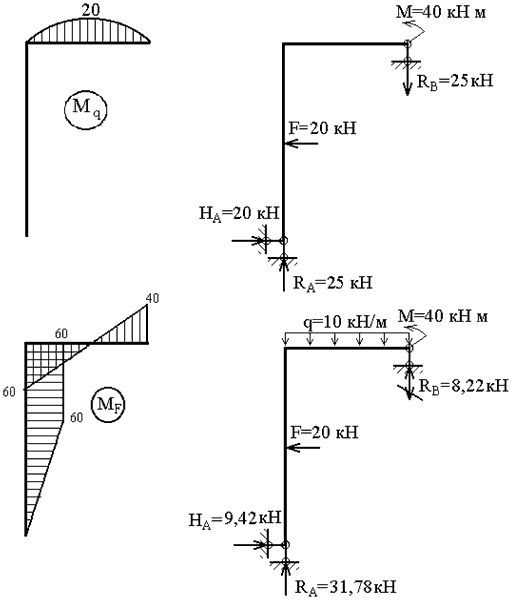
Грузовая эпюра моментов (рис.3,ж), построенная от одновременного действия всех внешних нагрузок (рис.3,е), является знакопеременной на участке, где действует нагрузка q. Это создает определенные трудности (хотя и не непреодолимые!) при ее перемножении с единичной эпюрой M1. В связи с этим целесообразно построить две грузовых эпюры – отдельно от нагрузки q (эпюра Mq) и от совместного действия F и M (эпюра MF). Эти варианты нагружения и эпюры представлены на рис.3,з и рис.3,а,б,в.

При таком разбиении внешней нагрузки каноническое уравнение метода сил содержит два грузовых перемещения и имеет вид:

Вычислим коэффициенты канонического уравнения:

Реакция лишних связи:

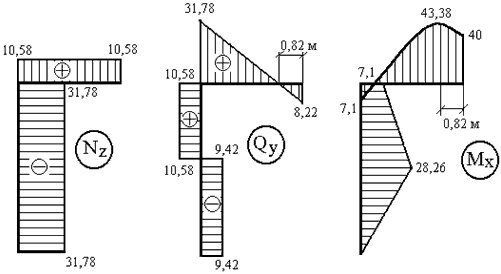
Эпюры Nz, Qy, Mx для заданной системы, загруженной нагрузками F, M, q и X1 (рис.3,г) представлены на рис.3,д,е,ж.

Как уже говорилось, при построении эпюр Nz и Q в рамах ординаты можно откладывать в любую сторону, но обязательно указывать знаки; а при построении эпюр Mx знаки можно не указывать, но обязательно откладывать ординаты со стороны сжатых волокон соответствующих элементов.

В рассмотренном примере универсальная проверка правильности вычисления коэффициентов канонического уравнения и свободных членов не выполнялась, так как рама имеет степень статической неопределимости n = 1, а, значит, суммарная единичная эпюра (если ее построить) совпадет с единичной эпюрой M1. В этом случае можно (и желательно!) проверить правильность выполнения расчета при помощи универсальной кинематической проверки окончательной эпюры моментов Mx.

Выполним эту проверку для рамы, рассмотренной в последнем примере (рис.3,а). Должно выполняться условие:

Покажем отдельно фрагменты перемножаемых эпюр (рис.3,д и рис.4,ж) для ригеля (рис.5,а,б) и стойки (рис.5,в,г) с указанением всех характерных размеров и соответствующих им ординат. Причем стойка (на рис.5,в,г) показана в горизонтальном положении.

Точка пересечения кривой на ригеле эпюры  Mx с осью (рис.5,б) определяется следующим образом. Обозначим координату произвольного сечения, отсчитываемую от правого конца ригеля, через z, тогда момент Mx определяется в виде:

откуда z = 3,77 м (второй корень этого уравнения лишен физического смысла).

рис. 3

рис. 4

следовательно, расчет выполнен правильно.

 

Заказать решение

Метод сил – расчет статически неопределимых рам

При решении задач сопромата, статически неопределимой называется такая система, которая не может быть рассчитана при помощи одних только уравнений статики, так как имеет лишние связи. Для расчета таких систем составляются дополнительные уравнения, учитывающие деформации системы.

Оговоримся, что здесь и далее понятие “расчет” подразумевает только построение эпюр внутренних силовых факторов, возникающих в элементах системы, а не расчет на прочность, жесткость и т.д.

Статически неопределимые системы обладают рядом характерных особенностей:

1. Статически неопределимые конструкции являются более жесткими, чем соответствующие статически определимые, так как имеют дополнительные связи.
2. В статически неопределимых системах возникают меньшие внутренние усилия, что определяет их экономичность по сравнению со статически определимыми системами при одинаковых внешних нагрузках.
3. Нарушение лишних связей в статически неопределимой системе не всегда приводит к разрушению, в то время как потеря связи в статически определимой системе делает ее геометрически изменяемой.
4. Для расчета статически неопределимых систем необходимо предварительно задаваться геометрическими характеристиками поперечных сечений элементов, т.е. фактически их формой и размерами, так как их изменение приводит к изменению усилий в связях и новому распределению усилий во всех элементах системы.
5. При расчете статически неопределимых систем необходимо заранее выбрать материал конструкции, так как необходимо знать его модули упругости.
6. В статически неопределимых системах температурное воздействие, осадка опор, неточности изготовления и монтажа вызывают появление дополнительных усилий.

Основными методами расчетастатически неопределимых систем являются:

1. Метод сил. Здесь в качестве неизвестных рассматриваются усилия – силы и моменты.
2.Метод перемещений. Неизвестными являются деформационные факторы – углы поворотов и линейные смещения.
3.Смешанный метод. Здесь часть неизвестных представляет собой усилия, а другая часть – перемещения.
4. Комбинированный метод. Используется при расчете симметричных систем на несимметричные нагрузки. Оказывается, что на симметричную составляющую заданной нагрузки систему целесообразно рассчитывать методом перемещений, а на обратносимметричную составляющую – методом сил.
Помимо указанных аналитичеких методов при расчете особо сложных систем используются различные численные методы.

Канонические уравнения метода сил

Для получения дополнительных уравнений, о которых говорилось в предыдущем параграфе, нужно прежде всего превратить заданную, n раз статически неопределимую систему, в статически определимую, удалив из нее лишние связи. Полученная статически определимая система называется основной. Отметим, что преобразование заданной системы в статически определимую не является обязательным. Иногда используется модификация метода сил, в которой основная система может быть статически неопределимой, однако изложение этого вопроса выходит за рамки этого пособия. Устранение каких-либо связей не изменяет внутренние усилия и деформации системы, если к ней приложить дополнительные силы и моменты, представляющие собой реакции отброшенных связей. Значит, если к основной системе приложить заданную нагрузку и реакции удаленных связей, то основная и заданная системы станут эквивалентными.

В заданной системе по направлениям имеющихся жестких связей, в том числе и тех связей, которые отброшены при переходе к основной системе, перемещений быть не может, поэтому и в основной системе перемещения по направлениям отброшенных связей должны равняться нулю. А для этого реакции отброшенных связей должны иметь строго определенные значения.

Условие равенства нулю перемещения по направлению любой i-ой связи из n отброшенных на основании принципа независимости действия сил имеет вид:

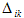
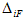
где первый индекс означает направление перемещения и номер отброшенной связи, а второй указывает на причину, вызвавшую перемещение, т.е. – это перемещение по направлению i-ой связи, вызванное реакцией k-ой связи; – перемещение по направлению i-ой связи, вызванное одновременным действием всей внешней нагрузки.

В методе сил реакцию k-ой связи принято обозначать через Xk. С учетом этого обозначения и в силу справедливости закона Гука перемещения 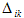можно представить в виде:

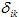
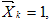
где – единичное (или удельное) перемещение по направлению i-ой связи, вызванное реакцией т.е. реакцией, совпадающей по направлению с Xk, но равной единице.

Подставляя (2) в (1), получим:

Физический смысл уравнения (3): перемещение в основной системе по направлению i-ой отброшенной связи равно нулю.

Записывая выражения, аналогичные (3), для всей совокупности отброшенных связей, получим систему канонических уравнений метода сил:

Вид уравнения (4), т.е. количество слагаемых в каждом из них и их общее число, определяется только степенью статической неопределимости системы и не зависит от ее конкретных особенностей.

Коэффициенты системы канонических уравнений (4) определяются методом Мора-Верещагина путем перемножения соответствующих эпюр. Все эти коэффициенты, как указывалось выше, представляют собой перемещения; коэффициенты, стоящие при неизвестных – единичные перемещения, а свободные члены – грузовые. 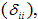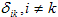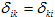Единичные перемещения делятся на главные, расположенные по главной диагонали и имеющие одинаковые индексы и побочные (). Главные перемещения всегда положительные, в отличие от побочных. Симметрично расположенные перемещения в соответствии с теоремой о взаимности перемещений равны друг другу, т.е. .

Алгоритм расчета методом сил

Независимо от особенностей рассматриваемой конструкции, можно выделить следующую последовательность расчета статически неопределимых систем методом сил:

1. Определить степень статической неопределимости.
2. Выбрать основную систему.
3. Сформировать эквивалентную систему.
4. Записать систему канонических уравнений.
5. Построить единичные и грузовые эпюры внутренних силовых факторов, возникающих в элементах рассматриваемой конструкции.
6. Вычислить коэффициенты при неизвестных и свободные члены системы канонических уравнений.
7. Построить суммарную единичную эпюру.
8. Выполнить универсальную проверку коэффициентов при неизвестных и свободных членов.
9. Решить систему (4), т.е. определить реакции лишних связей.
10. Построить эпюры возникающих внутренних силовых факторов для заданной системы (иначе говоря, окончательные эпюры).
11. Выполнить статическую и кинематическую проверки.
Отметим, что пункты 7, 8, 11 приведенного алгоритма не являются безусловно необходимыми, хотя и позволяют контролировать правильность выполнения расчета. А для систем с одной лишней связью пункты 7 и 8 просто лишены смысла, так как в этом случае суммарная единичная эпюра совпадает с единичной.
Остановимся подробнее на некоторых из вышеперечисленных этапов расчета.

Выбор основной системы

Это важнейший этап расчета, так как рациональный выбор основной системы существенно упрощает вычислительную работу. Рассмотрим возможные способы удаления лишних связей, что и определяет вид основной системы.

1. Отбрасывание лишних связей осуществляется полным удалением некоторых опор или их заменой опорами с меньшим числом связей. Реакции, действующие в направлениях отброшенных связей, являются лишними неизвестными. На рис.1,б, в, г показаны различные варианты эквивалентной системы, полученные этим способом для рамы (рис.1,а).

2.Постановка шарниров в промежуточных сечениях стержней позволяет в каждом таком сечении установить связь, соответствующую изгибающему моменту. Эти моменты являются лишними неизвестными. Для рамы, имеющей степень статической неопределимости n=3 (рис.2,а), при выборе основной системы необходимо поставить три шарнира. Положение этих шарниров может быть произвольным, но удовлетворяющим требованию геометрической неизменяемости системы (рис.2,б).

3. Рассечение стержня устраняет три связи, соответствующие внутренним усилиям M, Q, N (рис.2,в). В частных случаях (рис.2,г) рассечение стержня по шарниру освобождает две связи (рис.2,д), а рассечение прямолинейного стержня с шарнирами по концам – одну связь (рис.2,е).

Среди связей статически неопределимой системы различают абсолютно необходимые и условно необходимые. К абсолютно необходимым относятся связи, при удалении которых система становится геометрически изменяемой. Для абсолютно необходимой связи характерна статическая определимость усилия в ней, т.е. реакция такой связи может быть вычислена из условия равновесия. При выборе основной системы абсолютно необходимые связи отбрасывать нельзя.

Связи, при удалении которых система продолжает оставаться геометрически неизменяемой, называются условно необходимыми. Система, у которой удалили такую связь, может являться основной системой метода сил.

Вычисление коэффициентов и свободных членов канонических уравнений

Этому этапу расчета предшествует построение единичных и грузовых эпюр внутренних силовых факторов (для балок и рам – эпюр изгибающих моментов). Единичные эпюры строятся от действия безразмерной единичной силы или безразмерного единичного момента, совпадающих по направлению с направлением соответствующей лишней неизвестной в эквивалентной системе, и обозначаются через 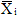, а единичная эпюра – через .

Грузовая эпюра строится от внешней нагрузки, приложенной к основной системе. При этом можно строить одну эпюру от одновременного действия всех внешних нагрузок или несколько эпюр, отдельно от каждой из приложенных нагрузок. Такое разбиение одной грузовой эпюры на несколько более простых, как правило, целесообразно только тогда, когда среди действующих нагрузок есть равномерно распределенная, и эпюра моментов на соответствующем участке под ней является знакопеременной. При этом в каждом каноническом уравнении число свободных членов будет равно числу построенных грузовых эпюр.

Единичные и грузовые перемещения (коэффициенты и свободные члены канонических уравнений) в общем случае можно вычислить методом Мора. Для балок и рам это можно сделать при помощи правила Верещагина.

Универсальная проверка коэффициентов и свободных членов канонических уравнений

Для выполнения универсальной проверки необходимо построить суммарную единичную эпюру – эпюру моментов от одновременного действия всех единичных сил, приложенных к основной системе:

Перемножим суммарную единичную эпюру с эпюрой :

Таким образом результат перемножения суммарной и i-ой единичной эпюр – это перемещение по направлению i-ой связи от совместного действия единичных лишних неизвестных. Это перемещение равно сумме коэффициентов i-го канонического уравнения:

Такая проверка называется построчной и выполняется для каждого канонического уравнения.
Вместо n построчных проверок чаще всего выполняется одна – универсальная поверка, которая состоит в перемножении суммарной единичной эпюры самой на себя и проверке условия:

Если универсальная проверка выполняется, значит единичные перемещения вычислены правильно; если нет – необходимо выполнить построчные проверки, что позволит уточнить перемещение, при вычислении которого допущена ошибка.

Для выполнения проверки грузовых перемещений необходимо перемножить суммарную единичную и грузовую эпюры изгибающих моментов:

Таким образом, проверка свободных членов системы канонических уравнений (4) состоит в выполнении условия:

Построение окончательных эпюр внутренних силовых факторов

Окончательные эпюры можно построить двумя способами.

Так как при найденных значениях лишних неизвестных Xi выполняются условия совместности деформаций, то из расчета основной системы можно получить все искомые внутренние усилия заданной системы. На основании принципа независимости действия сил для изгибающих моментов получим:

или, учитывая, что

приходим к выражению:

Аналогично определяется продольные и поперечные силы:

Второй способ основан на том, что в результате вычисления реакций лишних связей Xi исходная статически неопределимая система приведена к статически определимой системе, загруженной внешними нагрузками и реакциями лишних связей. Поэтому окончательные эпюры внутренних силовых факторов можно построить для эквивалентной системы, вычислив предварительно (и то не всегда) из условий равновесия опорные реакции последней.

Недостатком первого способа является то обстоятельство, что для его реализации необходимо дополнительно построить эпюры Qi, Ni (i=1, 2, …,n), Qf, Nf, которые не используются в расчете методом сил и поэтому не были построены ранее.

В связи с этим для построения окончательных эпюр более рациональным представляется второй способ, а условие (8) можно использовать в качестве дополнительной проверки.

Проверка окончательной эпюры изгибающих моментов

Эта проверка выполняется в двух вариантах: статическая и кинематическая.

При статической проверке, выполняемой обычно для рам, вырезаются узлы и записываются условия их равновесия под действием узловых сосредоточенных моментов и изгибающих моментов на концах стержней. Эта проверка является вспомогательной и выполняется автоматически при правильных эпюрах изгибающих моментов в основной системе и при выполнении кинематической проверки.

Статическая проверка эпюр Q и N состоит в том, что для любой отсеченной части рамы сумма проекций на две оси всех действующих сил – внешних нагрузок и внутренних усилий – должна быть равна нулю.

Основной проверкой окончательной эпюры моментов в методе сил является кинематическая проверка, которая может быть построчной или универсальной.
При построчной проверке каждая единичная эпюра моментов перемножается с окончательной эпюрой моментов М:

Таким образом, в результате перемножения каждой единичной эпюры с окончательной эпюрой моментов получим ноль:

Вариантом построчной проверки является проверка по замкнутомуконтуру, состоящая в том, что сумма приведенных (т.е. деленных на жесткость соответствующего стержня или его участка) площадь эпюры М, находящихся внутри каждого замкнутого бесшарнирного контура, должна быть равна сумме приведенных площадей, находящихся снаружи этого контура.

Суммируя выражения типа (11) для всех n, получим выражение, служащее для универсальной кинематической проверки окончательной эпюры изгибающих моментов:

Формулу (12) можно интерпретировать следующим образом: условное перемещение эквивалентной, или, что то же самое, заданной системы по направлению всех неизвестных от действия всех неизвестных и внешних нагрузок, равно нулю.

Определение перемещений в статически неопределимых системах

Для определения перемещения в статически неопределимой системе используется тождественность заданной и эквивалентной систем в том смысле, что если условия совместности деформаций выполняются, т.е. справедливы уравнения (4), то перемещения в эквивалентной системе соответствуют перемещениям заданной системы. Тогда, построив для основной системы эпюру изгибающих моментов от единичной силы (или единичного момента) приложенной в направлении искомого перемещения, величину перемещения находим по формуле:

где М – эпюра изгибающих моментов от внешней нагрузки, построенная для статически неопределимой системы.

Отметим, что при вычислении перемещения можно поступить и наоборот: единичную эпюру моментов построить в статически неопределимой заданной системе, а эпюру моментов от внешних нагрузок М – в основной (статически определимой) системе.

Пример расчета

Построить эпюры продольных, поперечных сил и изгибающих моментов для плоской рамы (рис.3,а).

Степень статической неопределимости рамы:

n = r – s = 4 – 3 = 1

Выбираем основную систему, отбрасывая на правой опоре горизонтальный стержень (рис.3,б), т.е. заменяем шарнирно-неподвижною опору на шарнирно-подвижную. На базе основной системы формируем эквивалентную систему (рис.3,в).

Заменяя реакцию лишней связи соответствующей единичной силой, (рис. 3,г) строим эпюру моментов M1 (рис.3,д).

Грузовая эпюра моментов (рис.3,ж), построенная от одновременного действия всех внешних нагрузок (рис.3,е), является знакопеременной на участке, где действует нагрузка q. Это создает определенные трудности (хотя и не непреодолимые!) при ее перемножении с единичной эпюрой M1. В связи с этим целесообразно построить две грузовых эпюры – отдельно от нагрузки q (эпюра Mq) и от совместного действия F и M (эпюра MF). Эти варианты нагружения и эпюры представлены на рис.3,з и рис.3,а,б,в.

При таком разбиении внешней нагрузки каноническое уравнение метода сил содержит два грузовых перемещения и имеет вид:

Вычислим коэффициенты канонического уравнения:

Реакция лишних связи:

Эпюры Nz, Qy, Mx для заданной системы, загруженной нагрузками F, M, q и X1 (рис.3,г) представлены на рис.3,д,е,ж.

Как уже говорилось, при построении эпюр Nz и Q в рамах ординаты можно откладывать в любую сторону, но обязательно указывать знаки; а при построении эпюр Mx знаки можно не указывать, но обязательно откладывать ординаты со стороны сжатых волокон соответствующих элементов.

В рассмотренном примере универсальная проверка правильности вычисления коэффициентов канонического уравнения и свободных членов не выполнялась, так как рама имеет степень статической неопределимости n = 1, а, значит, суммарная единичная эпюра (если ее построить) совпадет с единичной эпюрой M1. В этом случае можно (и желательно!) проверить правильность выполнения расчета при помощи универсальной кинематической проверки окончательной эпюры моментов Mx.

Выполним эту проверку для рамы, рассмотренной в последнем примере (рис.3,а). Должно выполняться условие:

Покажем отдельно фрагменты перемножаемых эпюр (рис.3,д и рис.4,ж) для ригеля (рис.5,а,б) и стойки (рис.5,в,г) с указанением всех характерных размеров и соответствующих им ординат. Причем стойка (на рис.5,в,г) показана в горизонтальном положении.

Точка пересечения кривой на ригеле эпюры Mx с осью (рис.5,б) определяется следующим образом. Обозначим координату произвольного сечения, отсчитываемую от правого конца ригеля, через z, тогда момент Mx определяется в виде:

откуда z = 3,77 м (второй корень этого уравнения лишен физического смысла).

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Архив рубрики: Задачи на метод сил

Расчет статически неопределимой рамы по методу сил

Задача. Для статически неопределимой рамы построить эпюры М, Q, N методом сил и выполнить проверки.Задано соотношение I₂=2I₁

Заданная система. Жесткость у стержней рамы разная. Примем I₁ =I, тогда I₂=2I.

1.Определим степень статической неопределимости заданной системы по формуле:

Система 2 раза статически неопределима, и для её решения потребуется два дополнительных уравнения.

Это канонические уравнения метода сил:

2.Освободим заданную систему от «лишних» связей и получим основную систему. За «лишние» связи в данной задаче примем опору А и опору С.

Теперь основную систему следует преобразовать в систему, эквивалентную (равнозначную) заданной.

Для этого загрузим основную систему заданной нагрузкой, действия «лишних» связей заменим их неизвестными реакциями Х₁ и Х₂ и вместе с системой канонических уравнений (1) данная система будет эквивалентна заданной.

3.По направлению предполагаемой реакции отброшенных опор к основной системе поочередно прикладываем единичные силы Х₁=1 и Х₂=1 и строим эпюры .

Теперь основную систему загрузим заданной нагрузкой и построим грузовую эпюру М_F.

М₂= –q·4·2 = -16кНм (сжатые волокна внизу)

М₃= –q·8·4 = -64кНм (сжатые волокна внизу)

М₄= –q·8·4 = -64кНм (сжатые волокна справа)

4.Определяем коэффициенты и свободные члены канонического уравнения по формуле Симпсона перемножением эпюр (обращаем внимание на разные жесткости участков).

Подставляем в каноническое уравнение, сокращаем на ЕI.

Поделим первое и второе уравнения на сомножители при Х₁, а затем из одного уравнения вычтем второе. Найдем неизвестные.

1. Строим окончательную эпюру моментов по формуле:

Сначала строим эпюры :

Тогда эпюра М_ок

Проверки окончательной эпюры моментов (М_ок).

1.Статическая проверка – методом вырезания жестких узлов рамы – они должны находиться в равновесии.

Узел находится в равновесии.

2. Деформационная проверка.

где М_S – суммарная эпюра единичных моментов, для её построения одновременно к основной системе прикладываем Х₁=1 и Х₂=1.

Физический смысл деформационной проверки – перемещения по направлению всех отброшенных связей от действия неизвестных реакций и всей внешней нагрузки должны быть равны 0.

Выполняем деформационную проверку по ступеням:

1. Построение Эп Q поЭп М_ок.

Эп Q строим по формуле:

Если на участке нет равномерно-распределенной нагрузки, то применяем формулу:

где М_пр – момент правый,

М_лев – момент левый,

ℓ — длина участка.

Разобьем Эп М_ок на участки:

IV участок (с равномерно-распределенной нагрузкой).

Зарисуем IV участок отдельно как балку и нанесем моменты.

z меняется от 0 до ℓ

Строим ЭпQ:

Вырезаем узлы рамы, показываем поперечные силы с эпюры Q и уравновешиваем узлы продольными силами.

Строим Эп N.

1. Общая статическая проверка рамы. На заданной схеме рамы показываем значения опорных реакций с построенных эпюр и проверяем по уравнениям статики.

Все проверки сошлись. Задача решена.

Расчет плоской статически неопределимой рамы методом сил

Для статически неопределимой рамы требуется построить эпюры изгибающих моментов, поперечных и продольных сил, проверить правильность построения эпюр. Дано: L=8 м, F=4кН, q=2 кН/м, h=8 м, соотношение жесткостей I₁=2I, I₂=I

1. Определяем степень статической неопределимости: n = R — Ш – 3 = 5 – 0 – 3 = 2, где R – число всех неизвестных реакций, Ш – число простых соединительных шарниров, в данной схеме их нет. Рама получилась дважды статически неопределима.

2. Выбираем основную систему путем отбрасывания лишних связей Основная система

3. Зарисовываем эквивалентную систему: к основной системе прикладываем всю внешнюю нагрузку и вместо отброшенных связей их неизвестные реакции Х₁, Х₂

Эквивалентная система

4. Составляем канонические уравнения:

5. Строим единичные эпюры: к основной системе прикладываем сначала Х₁=1, затем Х₂=1. Эпюры моментов построим на растянутых волокнах.

а) Построение эпюры М₁

б) Построение эпюры М₂

6. Строим грузовую эпюру моментов. К основной системе прикладываем всю заданную внешнюю нагрузку

7. Определяем коэффициенты канонических уравнений по формуле Симпсона:

8. Проверяем коэффициенты канонических уравнений.

Для этого строим суммарную единичную эпюру : к основной системе прикладываем одновременно Х₁=1 и Х₂=1. Эпюра M_s = M₁ + M₂

а) Первая проверка заключается в равенстве: M_s ∙ M_s = ∑δ_ij

При умножении суммарной единичной эпюры саму на себя мы должны получить сумму единичных коэффициентов канонических уравнений

верно

б) Вторая проверка заключается в равенстве: M_s ∙ M_F = ∑Δ_iF

Умножая суммарную единичную эпюру на грузовую, мы должны получить сумму грузовых коэффициентов

верно

Все проверки выполняются, значит, коэффициенты определены верно.

9. Решаем систему канонических уравнений:

10. Строим окончательную эпюру моментов М_ок по формуле:

11. Проверки окончательной эпюры моментов М­_ОК:

а) Статическая проверка: заключается в проверке равновесия вырезанных узлов. Вырезается узел, пунктирной линией показываются растянутые волокна, прикладываются узловые моменты со стороны растянутых волокон и проверяется равновесие вырезанного узла

Выполним статическую проверку вырезанием узлов

Узды находятся в равновесии

б) Деформационная проверка: заключается в определении перемещений по направлению отброшенных связей. Эти перемещения должны быть равны нулю. Ошибка может составлять не более 5%. Для выполнения этой проверки умножим окончательную эпюру моментов на суммарную эпюру единичных моментов.

Ошибка составляет:

12. По эпюре М_ОК строим эпюру поперечных сил Q с использованием формулы: , где М пр и М лев – моменты с эпюры М_ок, соответственно с правой и с левой стороны участка . Моменты берутся со своими знаками, l— длина участка, q — распределенная нагрузка на участке. Если нагрузки на участке нет, и эпюра моментов представляет собой прямую линию, то в формуле полагаем q=0.

13. По эпюре Q строим эпюру продольных сил N : вырезаем узел, к узлу прикладываем неизвестные продольные силы в положительном направлении (от узла — растяжение), затем известные поперечные силы с эпюры Q со своим знаком (+ по часовой стрелке) и рассматриваем равновесие данного узла.

Вырезаем узел 1

Вырезаем узел 2

14. Общая статическая проверка: зарисовывается исходная рама, в опорах показываются все реакции (их числовые значения необходимо брать с построенных эпюр M, Q, N с учетом знаков), заданная нагрузка и проверяется равновесие рамы в целом

Составляем уравнения равновесия:

Все проверки выполняются.

Расчет статически неопределимой рамы (метод сил) с подбором сечения

Построить эпюры внутренних усилий М, Q, N и подобрать размеры поперечного сечения в виде двутавра из условия прочности по нормальным напряжениям для рамы, если дано F=80 кН, М=30кНм, q=60кН/м, h=2м, а=1,6м, EI_x=const, σ_adm=160МПа.

Итак, заданная система:

Найдем степень статической неопределимости системы:

n = R — Ш – 3 = 5 – 0 – 3 = 2, где R – число всех неизвестных реакций, Ш – число простых соединительных шарниров, в данной схеме их нет; 3 — количество уравнений статики. Рама получилась дважды статически неопределима ( две «лишние» связи и требуется два дополнительных канонических уравнений метода сил).

Выбираем основную систему путем отбрасывания лишних связей:

Зарисовываем эквивалентную систему: к основной системе прикладываем всю внешнюю нагрузку и вместо отброшенных связей неизвестные реакции Х₁, Х₂ .

Запишем систему канонических уравнений для выбранной эквивалентной системы:

Построим эпюру изгибающих моментов M_F для основной системы от действия заданных нагрузок, предварительно определив реакции и значения внутренних усилий в характерных сечениях. Определяем опорные реакции:

Так как Н_К и V_K получились со знаком минус, меняем их направление действия на схеме.

Определяем значения изгибающих моментов в характерных сечениях силовых участков.

Построим эпюру изгибающих моментов M_{F .} Строим эпюру на сжатых волокнах.

Проверка равновесия узлов:

Построим единичные эпюры изгибающих моментов для основной системы от действия соответственно

При действии :

Сначала определим опорные реакции:

Определим изгибающие моменты на силовых участках:

Строим эпюру.

При действии :

Опорные реакции:

Определим изгибающие моменты на силовых участках:

Строим эпюру.

Строим суммарную эпюру изгибающих моментов от действия единичных усилий:

Определим коэффициенты канонических уравнений метода сил перемножением эпюр по формуле Симпсона

:

Итак, приступим к расчету:

Выполним проверку правильности вычисления единичных коэффициентов:

Проверка верна.

Определим грузовые коэффициенты:

Выполним проверку правильности вычисления грузовых коэффициентов:

Проверка верна.

Решаем систему канонических уравнений:

Построим эпюры изгибающих моментов для основной системы от действия неизвестных усилий, для этого умножим единичные эпюры моментов на найденные значения X:

Построим окончательную эпюру изгибающих моментов для заданной системы путём сложения составляющих

Выполним деформационную проверку правильности построения эпюры М – произведение окончательной и суммарной единичной эпюр должно быть равно нулю (разница не более 5%).

Проверка верна.

Построим эпюры поперечных и продольных сил, используя зависимость , где , и рассматривая уравнения равновесия для вырезанных узлов.

Поперечная сила на силовых участках:

Строим эпюру Q

Определяем продольную силу. Из рассмотрения равновесия узлов D и С следует:

Строим эпюру N

Подбираем размеры поперечного сечения из условия прочности:

Согласно сортаменту прокатной стали выбираем двутавр №27, у которого W_x= 371см 3 .

Перенапряжение составляет

Перенапряжение меньше 5% ,что допустимо.

Расчет статически неопределимой рамы по методу сил

Рассчитать статически неопределимую раму методом сил. Для рамы построить эпюры M_ок,Q, N со всеми проверками.

Зададимся соотношением моментов инерции. Пусть первый I₁=I , тогда второй I₂=2 I

1) определим степень статической неопределимости системы:

λ=Соп-3=5-3=2

где Соп – число опорных реакций

3 – число уравнений статики

то есть, система дважды статически неопределима. т.е. для ее решения требуются два дополнительных уравнения. Это будут канонические уравнения метода сил.

Тогда система канонических уравнений будет:

2) построим основную систему, отбросив некоторое число опор, суммарное количество реакций которых должно соответствовать значению статической неопределимости (т.е. в нашем случае – 2 реакции). Отбросим опоры В и С. Действие опор заменим двумя неизвестными силами — X_{1 ,} X_2.

2) загружаем основную систему заданной нагрузкой, определяем реакции опор и строим эпюру изгибающих моментов — грузовую эпюру.

Построим грузовую эпюру моментов (все значения откладываются на сжатых волокнах):

Посчитаем так же момент в середине действия распределённой нагрузки

3) По направлению предполагаемых реакций отброшенных опор к основной системе поочерёдно прикладываем единичные силы х₁=1 и х₂=1, строим единичные эпюры М₁ и М₂

Построим эпюру M₁ от действия x₁=1.

Сначала определим опорные реакции

Проверка ∑Y=0 R_A— R_D= 0 верно

Теперь определим моменты в характерных точках

M_F лев =R_A2=22=4 (сжатые волокна сверху). Строим эпюру M₁

Построим эпюру M₂ от действия x₂=1.

Сначала определим опорные реакции

Проверка ∑Y=0 R_A— R_D= 0 верно

Моменты в характерных точках

M_F лев =R_A2=12=2 (сжатые волокна сверху)

4) определяем коэффициенты канонических уравнений перемножением эпюр по формуле Симпсона. Следует помнить о соотношении жесткостей стержней.

Знак минус перед слагаемыми в грузовых коэффициентах ставим потому, что эпюры на грузовой и единичной эпюрах расположены по разные стороны стержней.

5) подставляем значения перемещений в канонические уравнения, сокращаем на EI, находим значения x₁ и x₂ :

17,33X₁ +12X₂ -333 ,32 =0

Поделим первое и второе уравнения на сомножители при X₂ (первое делим на 17,33, второе на 12). Получим:

Вычтем из первого уравнения второе. Тогда получим:

6) Умножаем единичные эпюры на найденные значения X_{1 ,} X_2.

При построении эпюры M₂x₂ следует обратить внимание на то, что значение x₂ — отрицательное.

7) строим окончательную эпюру моментов, складывая эпюры:

M_F л = 93,6 — 12,8 -100 = — 19,2 кНм (сжатые волокна внизу)

M_F пр = -40 кНм (сжатые волокна внизу)

M_F низ = 93,6 -12,80 – 60 = 20, 8 кНм (сжатые волокна справа)

M_E= 46,8 – 12,8 – 40 = -6 кНм (сжатые волокна слева)

Посчитаем так же момент в середине действия распределённой нагрузки

M_ср= 70,2 – 12,8 – 55 = 2,4 кНм (сжатые волокна справа)

8) Произведем проверки окончательной эпюры М

Статическая проверка (методом вырезания узлов рамы — они должны находиться в равновесии):

верно

Деформационная проверка: заключается в определении перемещений по направлению отброшенных связей. Эти перемещения должны быть равны нулю. Ошибка может составлять не более 5%.

Эпюра M_s = M₁ + M₂ Это суммарная единичная эпюра: к основной системе прикладываем одновременно Х ₁ =1 и Х ₂ =1.

Сначала проверим коэффициенты канонических уравнений.

1 проверка.

Первая проверка заключается в равенстве: M_s ∙ M_s = ∑δ_ij

Произведение суммарной эпюры саму на себя должно равняться сумме единичных коэффициентов.

верно

Вторая проверка заключается в равенстве: M_s ∙ M_F = ∑Δ_iF

Произведение суммарной эпюры на грузовую эпюру должно равняться сумме грузовых коэффициентов.

Все проверки выполняются, значит, коэффициенты определены верно.

И наконец, третья, деформационная проверка.

Ошибка составляет: , что допустимо.

9) построим эпюру поперечной силы Q по М_ок:

где М пр и М лев – моменты с эпюры М_ок, соответственно с правой и с левой стороны участка. Моменты берутся со своими знаками, l— длина участка, q — распределенная нагрузка на участке. Если нагрузки на участке нет, и эпюра моментов представляет собой прямую линию, то в формуле полагаем q=0.

Q_AF=(-19,2 — 0)/2= -9,6 кН

Q_FB=(0 – (-40))/2=20 кН

На участке EF приложена распределённая нагрузка. Рассмотрим этот участок отдельно.

М_прав = -20,8 , М_лев = 6

Значение поперечной силы в точке E:

Значение в точке F найдём:

Строим эпюру Q

10) Построение эпюры N по Q методом вырезания узлов

Вырезаем узел, к узлу прикладываем известные поперечные силы с эпюры Q с соответствующим знаком (+ по часовой стрелке), неизвестные продольные силы, и рассматриваем равновесие данного узла. Знаки у продольных сил — от узла — растяжение.

Рассмотрим узел Е

∑х = 0, — 3 -3,4 + N = 0 N = 6,4 (растяжение)

Рассмотрим узел F

∑х = 0, — N₁ + 23,4 = 0

N₁ = 23,4 кН (сжатие –к узлу)

∑у = 0 , N₂ – 9,6 – 20= 0

N 2 = 29,6 кН (сжатие –к узлу)

Строим эпюру N

11) Общая статическая проверка: зарисовывается исходная рама, в опорах показываются все реакции (их числовые значения необходимо брать с построенных эпюр M, Q, N с учетом знаков), и проверяется равновесие рамы в целом

Все проверки выполняются.

Задачи на расчет статически неопределимых балок и рам. Метод сил

Задача 1. Расчет неразрезной балки. Неразрезная балка загружена нагрузкой. Построить эпюру моментов.

1. Степень статической неопределимости балки:

1. Основную систему выбираем удалением одной внутренней моментной связи из сечения над промежуточной опорой. Следовательно, в качестве «лишней» неизвестной в таком случае принимаем величину изгибающего момента (Х₁) в этой удаленной связи.
2. К основной системе, состоящей из двух простых балок, прикладываем в качестве внешних сил: всю заданную нагрузку (M и q), а так же и лишнюю неизвестную силу Х₁. Получается эквивалентная система.
3. Строим в основной системе:- эпюру от действия только Х₁=1,— эпюру М_F от действия только заданной нагрузки (M и q).
4. Вычисляем коэффициенты канонического уравнения
5. Решая каноническое уравнение, находим значение Х₁:
6. Умножаем ординаты эпюры на Х₁.
7. Суммируем эпюры и М_Fи получаем окончательную эпюру моментов.

Задача 2 Расчет статически неопределимой рамы

1) Степень статической неопределимости n = R — Ш – 3 = 6-1-3=2.

2) Выбор основной системы и эквивалентной системы.

Возможное количество ее вариантов бесконечно. Покажем только два из них. В первом варианте в качестве двух лишних неизвестных выберем внутренние усилия (Q и N) в среднем сечении ригеля. Удалив внутренний шарнир, то есть то место, где и возникают эти усилия, получаем основную систему:

Соответствующая эквивалентная система показана рядом. Здесь введены стандартные обозначения неизвестных: Х₁вместо Q в шарнире и Х₂ вместо N в шарнире.

Во втором варианте основной системы в качестве лишних неизвестных примем по одной реакции (реактивному моменту) в каждой из двух опор. Удалив соответствующие моментные связи из жестких заделок, имеем:

3) Составляем систему канонических уравнений при n=2:

4) Строим в основной системе три эпюры моментов:

Все эпюры показаны на растянутых волокнах.

5) Вычисляем коэффициенты уравнений:

6) Решаем уравнения:

7) Строим окончательную эпюру суммированием эпюр

Расчет канонических уравнений метода сил

Наиболее широко применяемым в машиностроении общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Отсюда и название «метод сил». Такой прием не является единственно возможным. В строительной механике широко применяются и другие методы, например метод деформаций, в котором за неизвестные принимаются не силовые факторы, а перемещения в элементах стержневой системы.

Итак, раскрытие статической неопределимости любой рамы методом сил начинается с отбрасывания дополнительных связей. Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы.

а-д) модификации основной системы
Рис.1. пример стержневой рамы:

Для каждой статически неопределимой стержневой системы можно подобрать, как правило, сколько угодно основных систем. Например, для рамы, показанной на рис. 1, можно предложить основные системы, а), б). которые получены путем отбрасывания семи дополнительных связей в различных комбинациях. Вместе с тем нужно помнить, что не всякая система с семью отброшенными связями может быть принята как основная. На рис. 2 показано три примера для той же рамы, в которой также отброшено семь связей, однако сделано это неправильно, так как оставшиеся связи не обеспечивают кинематической неизменяемости системы, с одной стороны, и статической определимости во всех узлах,— с другой.

Рис.2.Некорректные преобразования заданной системы в основные по причине кинематической изменяемости- а) б), или статической определимости во всех узлах — в)

После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо, как уже говорилось, ввести вместо связей неизвестные силовые факторы. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы будем обозначать X_i-, где i — номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы X_i, — являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.

а)-д) по отношению к заданной системе
Рис.3. Пять разновидностей основных систем

Основная система, к которой приложены все внешние заданные силы и неизвестные силовые факторы, носит название эквивалентной системы. На рис. 3 показано пять эквивалентных систем, которые соответствуют приведенным выше основным системам (рис. 1). Принцип приложения неизвестных силовых факторов становится ясным без дальнейших пояснений.

Теперь остается составить уравнения для определения неизвестных.

Обратимся к некоторому конкретному примеру. Рассмотрим, например, первую эквивалентную систему из числа представленных на рис. 3,4. Тем, что рассматривается конкретно взятая семь раз статически неопределимая система, общность рассуждений не будет нарушена.

Перейдем теперь к составлению уравнений для определения неизвестных силовых факторов. Условимся через обозначать взаимное смещение точек системы.

Рис.4. Пример расчета рамы а)по выбранной основной системе- б)

Первый индекс при соответствует направлению перемещения, а второй — силе, вызвавшей это перемещение.

В рассматриваемой раме в точке А отброшена неподвижная опора. Следовательно, горизонтальное перемещение здесь равно нулю и можно записать:

Индекс 1 означает, что речь идет о перемещении по направлению силы Х₁, а индекс [Х₁, Х₂. Р] показывает, что перемещение определяется суммой всех сил, как заданных, так и неизвестных.

Аналогично можно записать:

Так как под величиной понимается взаимное смещение точек, то обозначает вертикальное смещение точки В относительно С, — горизонтальное взаимное смещение тех же точек, есть взаимное угловое смещение сечений В и С. Угловым смещением будет также в рассматриваемой системе величина .

В точках A и D смещения являются абсолютными. Но абсолютные смещения можно рассматривать как смещения, взаимные с неподвижными отброшенными опорами. Поэтому принятые обозначения приемлемы для всех сечений системы.

Пользуясь принципом независимости действия сил, раскроем выражения для перемещений

Аналогичным образом запишем и остальные пять уравнений: каждое из слагаемых , входящих в уравнение, обозначает перемещение в направлении силы с первым индексом под действием силы, стоящей во втором индексе. Поскольку каждое перемещение пропорционально соответствующей силе, величину можно записать в следующем виде:

Что касается перемещений , и т. д., то под индексом Р будем понимать не просто внешнюю силу Р, а вообще систему внешних сил, которая может быть произвольной Поэтому величины , . в уравнениях оставим неизменными.

Теперь уравнения примут вид:

Эти уравнения являются окончательными и носят название канонических уравнений метода сил. Число их равно степени статической неопределимости системы. В некоторых случаях, как увидим далее, когда имеется возможность сразу указать значения некоторых неизвестных, число совместно решаемых уравнений снижается. Остается теперь выяснить, что представляют собой коэффициенты и как следует их определять. Для этого обратимся к выражению (6.1).

Если , то

Следовательно, коэффициент это есть перемещение по направлению i-го силового фактора под действием единичного фактора, заменяющего k-й фактор. Например, коэффициент уравнения представляет собой взаимное горизонтальное смещение точек B и С, которое возникло бы в раме, если бы к ней вместо всех сил была приложена только единичная сила в точке А (рис. 5 а). Если, например, вместо сил приложив единичные силы, а все прочие силы с эквивалентной системы снять (рис. 5 б), то угол поворота в сечении D под действием этих сил будет , горизонтальное перемещение в точке А будет и т. д.

а) , б) и
Рис.5. Интерпретация коэффициентов уравнений метода сил:

Весьма существенно отметить, что в проделанном выводе совершенно не обусловливается то, каким образом возникают перемещения . Хотя мы и рассматриваем раму, работающую на изгиб, все сказанное с равным успехом может быть отнесено, вообще, к любой системе, работающей на кручение, растяжение и изгиб или на то, другое и третье совместно.

Обратимся к интегралам Мора. Для того чтобы определить величину , следует вместо внешних сил рассматривать единичную силу, заменяющую k-й фактор. Поэтому внутренние моменты и силы , , , , и в интегралах Мора заменим на , , , , и , понимая под ними внутренние моменты и силы от единичного k-го фактора. В итоге получим:

где , — внутренние моменты и силы, возникающие под действием i-го единичного фактора. Таким образом, коэффициенты получаются как результат перемножения i-го и k-го внутренних единичных силовых факторов. Индексы i и k непосредственно указывают, какие факторы должны быть перемножены под знаком интегралов Мора. Если рама состоит из прямых участков и можно пользоваться правилом Верещагина, то представляет собой результат перемножения i-х единичных эпюр на k-е единичные эпюры.

Это следует, с одной стороны, непосредственно из выражений для , а с другой стороны, из теоремы о взаимности перемещений, поскольку перемещения и возникают под действием одной и той же силы, равной единице.

Величины , входящие в канонические уравнения, представляют собой перемещения в направлениях 1, 2. возникающие под действием заданных внешних сил в эквивалентной системе. Они определяются перемножением эпюры моментов заданных сил на соответствующие единичные эпюры.

Пример Раскрыть статическую неопределимость и построить эпюру изгибающих моментов для рамы, показанной на рис. 6.

Рис.6. Заданная расчетная схема

Рама три раза статически неопределима. Выбираем основную систему, отбрасывая левую заделку. Действие заделки заменяем двумя силами , и моментом и определяем эквивалентную систему (рис. 7).

Рис.7. Динамика решения: от эквивалентной системы и силовой эпюры Р, включая эпюры моментов от единичных сил: 1, 2, 3 в точках приложения неизвестных , ,

Канонические уравнения (6.2) принимают для рассматриваемой системы такой вид:

Основные перемещения в рассматриваемой раме определяются изгибом. Поэтому, пренебрегая сдвигом и сжатием стержней, строим эпюры изгибающих моментов от заданной силы P и от трех единичных силовых факторов (рис. 7).

Определяем коэффициенты уравнений, считая, что жесткость на изгиб всех участков рамы постоянна и равна EJ. Величина определяется перемножением первой единичной эпюры самой на себя. Для каждого участка берется, следовательно, площадь эпюры и умножается на ординату этой же эпюры, проходящую через ее центр тяжести:

Заметим, что величины при всегда положительны, поскольку площади эпюр и ординаты имеют общий знак.

Определяем, далее, и остальные коэффициенты уравнений, перемножая эпюры с соответствующими номерами:

, , , , , , , .

Подставляем найденные коэффициенты в канонические уравнения. После сокращений получаем:

, ,

Решая эти уравнения, находим:

, ,

Раскрытие статической неопределимости на этом заканчивается.

Рис.8. Суммарная эпюра изгибающих моментов.

Эпюра изгибающих моментов может быть получена наложением на эпюру моментов заданных сил трех единичных эпюр, увеличенных соответственно в , и раза Суммарная эпюра изгибающих моментов представлена на рис. 8. Там же пунктиром показана форма изогнутой оси рамы.

[spoiler title=”источники:”]

http://prosopromat.ru/zadachi/zadachi-na-metod-sil

http://toehelp.ru/theory/sopromat/38.html

[/spoiler]