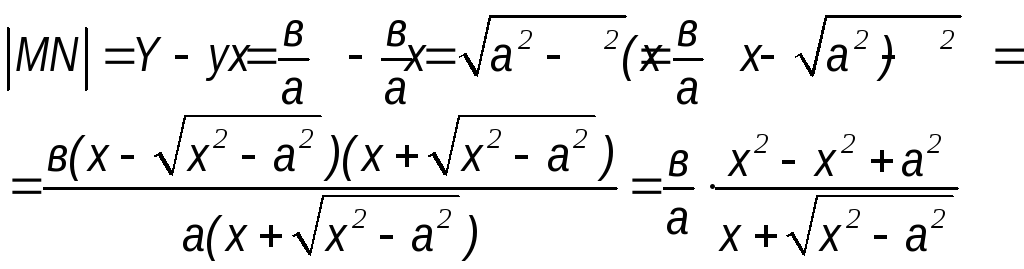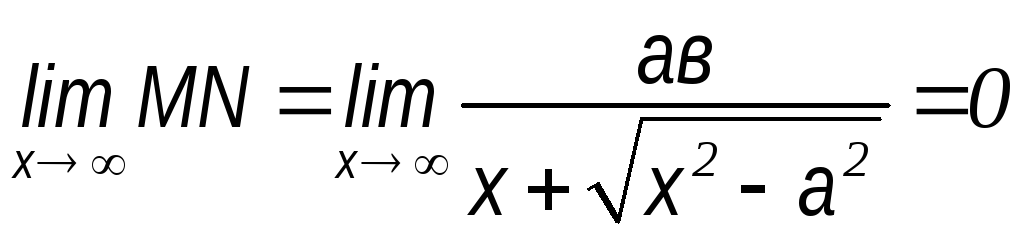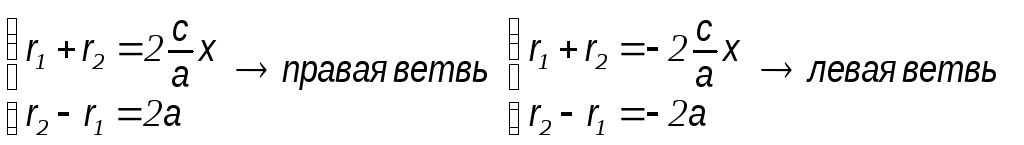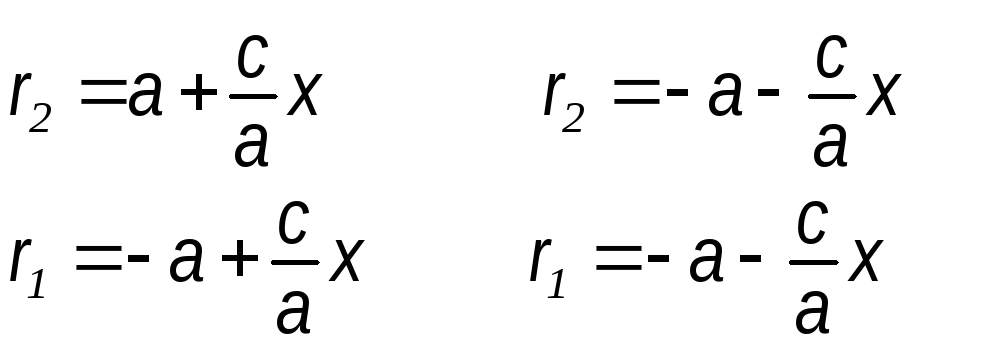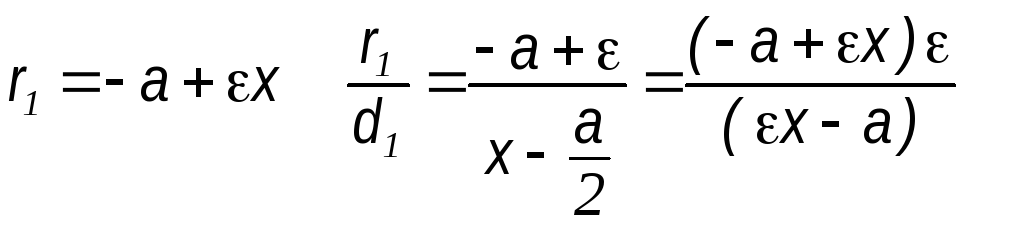Как составить каноническое уравнение гиперболы асимптот гиперболы

Была ли эта статья полезной?

Гипербола и ее каноническое уравнение

Определение.
Гиперболой называется геометрическое
место точек, разность от каждой из
которых до двух данных точек, называемых
фокусами есть величина постоянная

Возьмем
систему координат, так чтобы фокусы
лежали на оси абсцисс, а начало координат
делило отрезок F₁
F₂
пополам (рис. 30). Обозначим F₁
F₂
= 2c.
Тогда F₁
(с; 0); F₂
(-c;
0)

M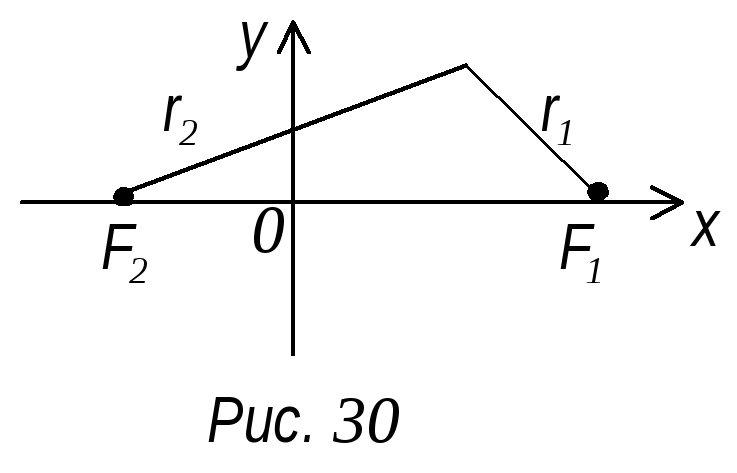F₂
= r₂,
MF₁
= r₁
– фокальные радиусы гиперболы.

Согласно
определения гиперболы r₁
– r₂
= const.

Обозначим
ее через 2а

Тогда
r₂–
r₁
= ±2a
итак:

=>
каноническое
уравнение гиперболы

Так
как уравнение гиперболы х и у в четных
степенях, то если точка М₀
(х₀;
у₀)
лежит на гиперболе, то на ней лежат также
точки М₁
(х₀;
-у₀)
М₂
(-х₀;
-у₀)
М₃
(-х₀;
-у₀).

Следовательно,
гипербола симметрична относительно
обеих координатных осей.

При
у = 0 х²
= а²
х = ± а. Вершинами гиперболы будут точки
А₁
(а; 0); А₂
(-а; 0).

.
В силу симметрии исследование ведем в
I
четверти

1)
при

у имеет мнимое значение, следовательно,
точек гиперболы с абсциссами

не существует

2)
при х = а; у = 0 А₁
(а; 0) принадлежит гиперболе

3)
при x
> a;
y
> 0. Причем при неограниченном возрастании
х ветвь гиперболы уходит в бесконечность.

Отсюда
следует, что гипербола представляет
собой кривую, состоящую из двух бесконечных
ветвей.

П 6. Асимптоты гиперболы

Рассмотрим
вместе с уравнением

уравнение прямой

Кривая
будет лежать ниже прямой (рис. 31).
Рассмотрим точкиN
(x,
Y)
и М (х, у) у которой абсциссы одинаковы,
а У – у = MN.
Рассмотрим
длину отрезка MN

Найдем

Итак,
если точка М, двигаясь по гиперболе в
первой четверти удаляется в бесконечность,
то ее расстояние от прямой

уменьшается и стремится к нулю.

В
силу симметрии таким же свойством
обладает прямая
.

Определение.
Прямые к которым при

кривая неограниченно приближается
называются асимптотами.

И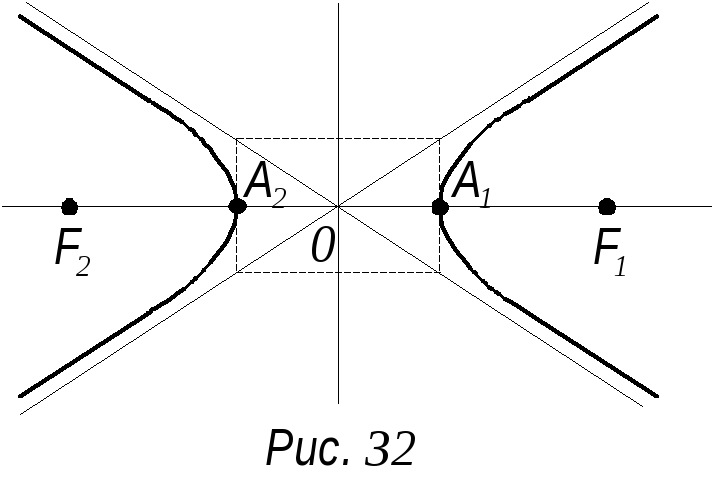так,
уравнение асимптот гиперболы
.

Асимптоты
гиперболы располагаются по диагоналям
прямоугольника, одна сторона которого
параллельна оси ох и равна 2а, а другая
параллельна оси оу и равна 2в, а центр
лежит в начале координат (рис. 32).

П 7. Эксцентриситет и директрисы гиперболы

r₂
– r₁
= ± 2a
знак + относится к правой ветви
гиперболы

знак
– относится к левой ветви гиперболы

Определение.
Эксцентриситетом
гиперболы называется отношение расстояния
между фокусами этой гиперболы к расстоянию
между ее вершинами.

.
Так как c
> a,
ε
> 1

Выразим
фокальные радиусы гиперболы через
эксцентриситет:

Определение.
Назовем прямые
,
перпендикулярные фокальной оси гиперболы
и расположенными на расстоянии

от ее центра директрисами гиперболы,
соответствующие правому и левому
фокусам.

Т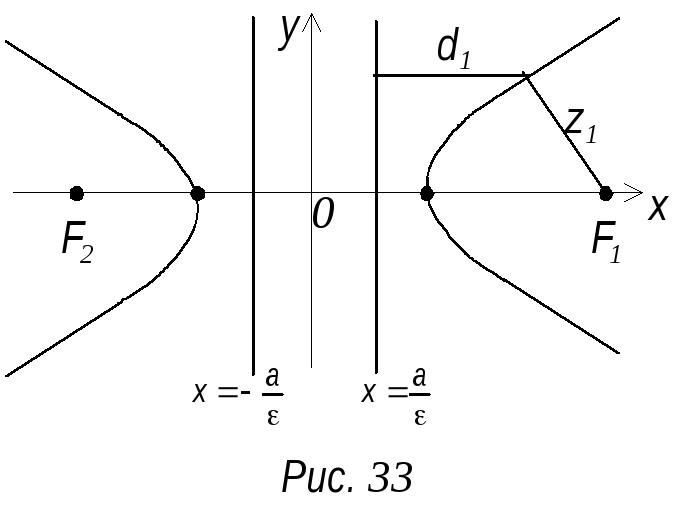ак
как для гиперболы

следовательно, директрисы гиперболы,
располагаются между ее вершинами (рис.
33). Покажем, что отношение расстояний
любой точки гиперболы до фокуса и
соответствующей директрисы есть величина
постоянная и равная ε.

П. 8 Парабола и ее уравнение

О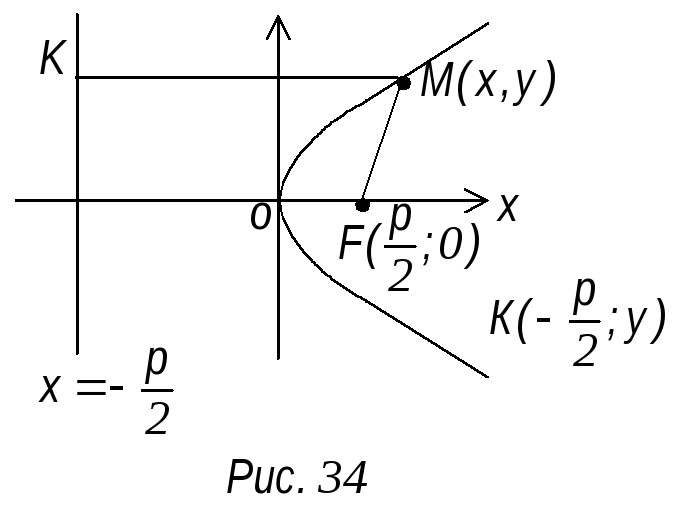пределение.Парабола
есть геометрическое место точек
равностоящих от данной точки, называемой
фокусом и от данной прямой называемой
директрисой.

Чтобы
составить уравнение параболы примем
за ось х прямую, проходящую через фокус
F₁
перпендикулярную к директрисе и будем
считать ось х направленной от директрисы
к фокусу. За начало координат возьмем
середину О отрезка от точки F
до данной прямой, длину которого обозначим
через р (рис. 34). Величину р назовем
параметром параболы. Точка координат
фокуса
.

Пусть
М (х, у) – произвольная точка параболы.

Согласно
определению

у²
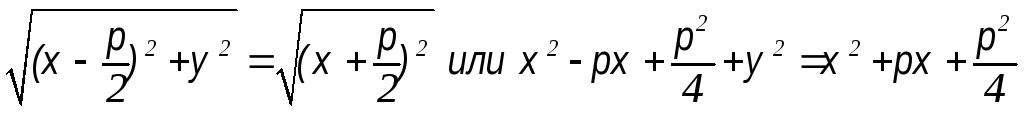
= 2рх – каноническое уравнение параболы

Для
определения вида параболы преобразуем
ее уравнение

отсюда следует
.
Следовательно, вершина параболы находится
в начале координат и осью симметрии
параболы является ох. Уравнение у²
= -2рх при положительном р сводится к
уравнению у²
= 2рх путем замены х на –х и ее график
имеет вид (рис. 35).

У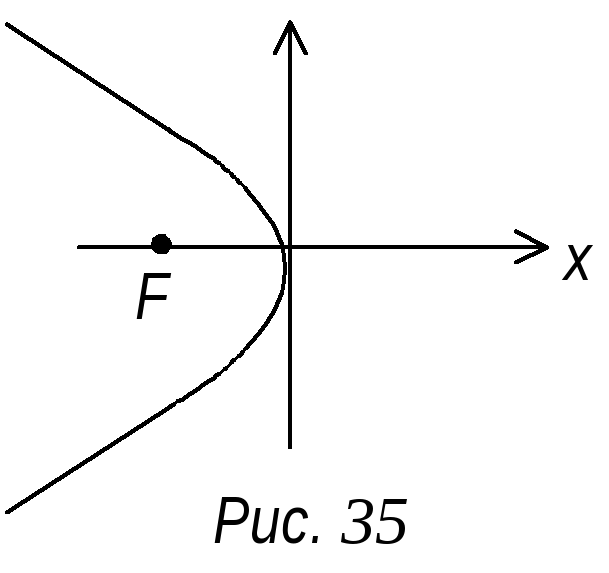равнение
х²
= 2ру является уравнением параболы с
вершиной в точке О (0; 0) ветви которой
направлены вверх.

х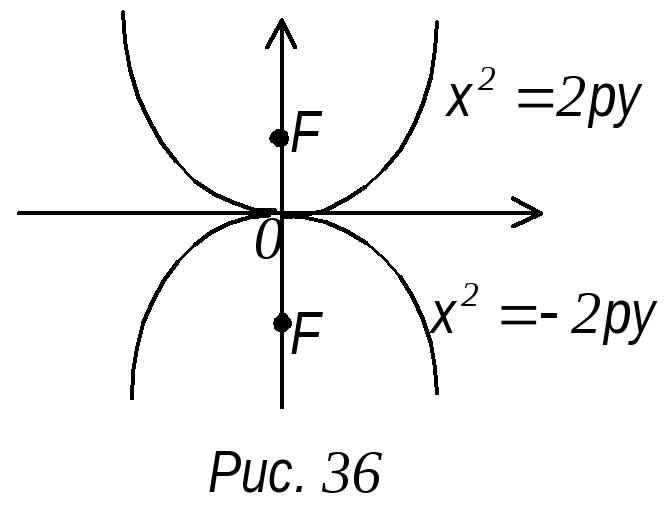²
= -2ру – уравнение параболы с центром в
начале координат симметричная относительно
оси у, ветви которой направлены вниз
(рис. 36).

У
параболы одна ось симметрии.

Если
х в первой степени, а у во второй, то ось
симметрии есть х.

Если
х во второй степени, а у в первой, то ось
симметрии есть ось оу.

Замечание
1.
Уравнение
директрисы параболы имеет вид
.

Замечание
2.Так
как для параболы
,
то ε
параболы равен 1. ε
= 1.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Гипербола: определение, свойства, построение

Гиперболой называется геометрическое место точек плоскости, модуль разности расстояний от каждой из которых до двух заданных точек и есть величина постоянная , меньшая расстояния между этими заданными точками (рис.3.40,а). Это геометрическое определение выражает фокальное свойство гиперболы.

Фокальное свойство гиперболы

Точки и называются фокусами гиперболы, расстояние между ними — фокусным расстоянием, середина отрезка — центром гиперболы, число — длиной действительной оси гиперболы (соответственно, — действительной полуосью гиперболы). Отрезки и , соединяющие произвольную точку гиперболы с ее фокусами, называются фокальными радиусами точки . Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение , где , называется эксцентриситетом гиперболы. Из определения следует, что .

Геометрическое определение гиперболы, выражающее ее фокальное свойство, эквивалентно ее аналитическому определению — линии, задаваемой каноническим уравнением гиперболы:

Действительно, введем прямоугольную систему координат (рис.3.40,б). Центр гиперболы примем за начало системы координат; прямую, проходящую через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки к точке ); прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат оказалась правой).

Составим уравнение гиперболы, используя геометрическое определение, выражающее фокальное свойство. В выбранной системе координат определяем координаты фокусов и . Для произвольной точки , принадлежащей гиперболе, имеем:

Записывая это уравнение в координатной форме, получаем:

Выполняя преобразования, аналогичные преобразованиям, используемым при выводе уравнения эллипса (т.е. избавляясь от иррациональности), приходим к каноническому уравнению гиперболы:

где , т.е. выбранная система координат является канонической.

Проводя рассуждения в обратном порядке, можно показать, что все точки, координаты которых удовлетворяют уравнению (3.50), и только они, принадлежат геометрическому месту точек, называемому гиперболой. Таким образом, аналитическое определение гиперболы эквивалентно его геометрическому определению.

---

Директориальное свойство гиперболы

Директрисами гиперболы называются две прямые, проходящие параллельно оси ординат канонической системы координат на одинаковом расстоянии от нее (рис.3.41,а). При , когда гипербола вырождается в пару пересекающихся прямых, директрисы совпадают.

Гиперболу с эксцентриситетом можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки (фокуса) к расстоянию до заданной прямой (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету (директориальное свойство гиперболы). Здесь и — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

В самом деле, например, для фокуса и директрисы (рис.3.41,а) условие можно записать в координатной форме:

Избавляясь от иррациональности и заменяя , приходим к каноническому уравнению гиперболы (3.50). Аналогичные рассуждения можно провести для фокуса и директрисы :

---

Уравнение гиперболы в полярной системе координат

Уравнение правой ветви гиперболы в полярной системе координат (рис.3.41,б) имеет вид

, где — фокальный параметр гиперболы.

В самом деле, выберем в качестве полюса полярной системы координат правый фокус гиперболы, а в качестве полярной оси — луч с началом в точке , принадлежащий прямой , но не содержащий точки (рис.3.41,б). Тогда для произвольной точки , принадлежащей правой ветви гиперболы, согласно геометрическому определению (фокальному свойству) гиперболы, имеем . Выражаем расстояние между точками и (см. пункт 2 замечаний 2.8):

Следовательно, в координатной форме уравнение гиперболы имеет вид

Уединяем радикал, возводим обе части уравнения в квадрат, делим на 4 и приводим подобные члены:

Выражаем полярный радиус и делаем замены :

что и требовалось доказать. Заметим, что в полярных координатах уравнения гиперболы и эллипса совпадают, но описывают разные линии, поскольку отличаются эксцентриситетами ( для гиперболы, для эллипса).

---

Геометрический смысл коэффициентов в уравнении гиперболы

Найдем точки пересечения гиперболы (рис.3.42,а) с осью абсцисс (вершины гиперболы). Подставляя в уравнение , находим абсциссы точек пересечения: . Следовательно, вершины имеют координаты . Длина отрезка, соединяющего вершины, равна . Этот отрезок называется действительной осью гиперболы, а число — действительной полуосью гиперболы. Подставляя , получаем . Длина отрезка оси ординат, соединяющего точки , равна . Этот отрезок называется мнимой осью гиперболы, а число — мнимой полуосью гиперболы. Гипербола пересекает прямую, содержащую действительную ось, и не пересекает прямую, содержащую мнимую ось.

Замечания 3.10.

1. Прямые ограничивают на координатной плоскости основной прямоугольник, вне которого находится гипербола (рис.3.42,а).

2. Прямые , содержащие диагонали основного прямоугольника, называются асимптотами гиперболы (рис.3.42,а).

Для равносторонней гиперболы, описываемой уравнением (т.е. при ), основной прямоугольник является квадратом, диагонали которого перпендикулярны. Поэтому асимптоты равносторонней гиперболы также перпендикулярны, и их можно взять в качестве координатных осей прямоугольной системы координат (рис.3.42,б). В этой системе координат уравнение гиперболы имеет вид (гипербола совпадает с графиком элементарной функции, выражающей обратно-пропорциональную зависимость).

В самом деле, повернем каноническую систему координат на угол (рис.3.42,б). При этом координаты точки в старой и новой системах координат связаны равенствами

Подставляя эти выражения в уравнение равносторонней гиперболы и приводя подобные члены, получаем

3. Координатные оси (канонической системы координат) являются осями симметрии гиперболы (называются главными осями гиперболы), а ее центр — центром симметрии.

Действительно, если точка принадлежит гиперболе . то и точки и , симметричные точке относительно координатных осей, также принадлежат той же гиперболе.

Ось симметрии, на которой располагаются фокусы гиперболы, является фокальной осью.

4. Из уравнения гиперболы в полярных координатах (см. рис.3.41,б) выясняется геометрический смысл фокального параметра — это половина длины хорды гиперболы, проходящей через ее фокус перпендикулярно фокальной оси ( при ).

5. Эксцентриситет характеризует форму гиперболы. Чем больше , тем шире ветви гиперболы, а чем ближе к единице, тем ветви гиперболы уже (рис.3.43,а).

Действительно, величина угла между асимптотами гиперболы, содержащего ее ветвь, определяется отношением сторон основного прямоугольника: . Учитывая, что и , получаем

Чем больше , тем больше угол . Для равносторонней гиперболы имеем и . Для угол тупой, а для угол острый (рис.3.43,а).

6. Две гиперболы, определяемые в одной и той же системе координат уравнениями и называются сопряженными друг с другом. Сопряженные гиперболы имеют одни и те же асимптоты (рис.3.43,б). Уравнение сопряженной гиперболы приводится к каноническому при помощи переименования координатных осей (3.38).

7. Уравнение определяет гиперболу с центром в точке , оси которой параллельны координатным осям (рис.3.43,в). Это уравнение сводится к каноническому при помощи параллельного переноса (3.36). Уравнение определяет сопряженную гиперболу с центром в точке .

---

Параметрическое уравнение гиперболы

Параметрическое уравнение гиперболы в канонической системе координат имеет вид

где — гиперболический косинус, a гиперболический синус.

Действительно, подставляя выражения координат в уравнение (3.50), приходим к основному гиперболическому тождеству .

---

Пример 3.21. Изобразить гиперболу в канонической системе координат . Найти полуоси, фокусное расстояние, эксцентриситет, фокальный параметр, уравнения асимптот и директрис.

Решение. Сравнивая заданное уравнение с каноническим, определяем полуоси: — действительная полуось, — мнимая полуось гиперболы. Строим основной прямоугольник со сторонами с центром в начале координат (рис.3.44). Проводим асимптоты, продлевая диагонали основного прямоугольника. Строим гиперболу, учитывая ее симметричность относительно координатных осей. При необходимости определяем координаты некоторых точек гиперболы. Например, подставляя в уравнение гиперболы, получаем

Следовательно, точки с координатами и принадлежат гиперболе. Вычисляем фокусное расстояние

эксцентриситет ; фокальныи параметр . Составляем уравнения асимптот , то есть , и уравнения директрис: .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Каноническое уравнение гиперболы имеет следующий вид:
$frac{x^2}{a^2} – frac{y^2}{b^2} = 1$, где $a, b$ – положительные действительные числа.

Для того чтобы составить каноническое уравнение гиперболы, нужно привести квадратное уравнение к каноническому виду.

Вывод канонического уравнения гиперболы

Рассмотрим гиперболу с фокусами $F_1$ и $F_2$, находящимися на оси $OX$, причём точка $O$ лежит в центе между фокусами.

Следовательно координаты $F_1(-c; 0)$, а $F_2(c; 0)$, где $c$ – расстояние до фокуса гиперболы.

Рассмотрим произвольную точку $M$, принадлежащую гиперболе.

Отрезки $r_1 =|F_1M|$ и $r_2 =|F_2M|$ называются фокальными радиусами точки $M$ гиперболы.

Из определения гиперболы следует, что $|r_1 -r_2| =2a$, следовательно $r_1 – r_2=±2a$, причём $r_1 = sqrt{(x + c)^2 + y^2}$, а $r_2 = sqrt{(x – c)^2 + y^2}$.

Соответственно, уравнение $r_1 – r_2=±2a$ иначе можно записать как $sqrt{(x + c)^2 + y^2} – sqrt{(x – c)^2 + y^2} = ±2a$ (1).

Умножим выражение (1) на $frac{$sqrt{(x + c)^2 + y^2} + sqrt{(x – c)^2 + y^2}}{±2a}$, получается:, получается:

$frac{(x + c)^2 + y^2 – (x – c)^2 – y^2}{±2a} = sqrt{(x + c)^2 + y^2} + sqrt{(x – c)^2 + y^2}$

Упростим: $frac{2cx}{±a} = sqrt{(x + c)^2 + y^2} + sqrt{(x – c)^2 + y^2}$ (2)

Сложим уравнения (1) и (2), получим:

$±(frac{cx}{a}) + a = sqrt{(x + c)^2 + y^2}$ (3)

Возведём (3) в квадрат:

$frac{c^2 x^2}{a^2} + 2xc + a^2 = (x^2 +2x c + c^2 + y^2)$

$frac{c^2 – a^2}{a^2} cdot x^2 – y^2 = c^2 – a^2$

Пусть $b^2 = c^2 – a^2$, так как $c > 0$ и, следовательно $frac{b^2}{a^2}x^2 – y^2 = b^2$

«Каноническое уравнение гиперболы» 👇

Получаем уравнение:
$frac{x^2}{a^2} – frac{y^2}{b^2} = 1$ (4), являющееся каноническим уравнением гиперболы с центром в начале координат.

Каноническое уравнение параболы и гиперболы немного похожи между собой.

Уравнение параболы выглядит следующим образом:

$y^2 = px$, где число $p$ должно быть больше нуля; это число называется фокальным параметром.

Каноническое уравнение гиперболы примеры решения

Построение гиперболы по каноническому уравнению

Теперь давайте рассмотрим, как построить гиперболу по каноническому уравнению.

1. Для начала необходимо построить асимптоты для данной гиперболы, их формулы определяются из уравнения $y = ±frac{bcdot x}{a}$.
   Для нашего канонического уравнения гиперболы они будут выглядеть так: $y = ±frac{sqrt{5}} {2}cdot x$

2. Теперь найдём вершины гиперболы, они расположены на оси абсисс в точках $(0; a)$ и $(0; -a)$, назовём их точками $A_1, A_2$.
   Вершины нашей гиперболы находятся в точках $(2; 0)$ и $(-2; 0)$.

Далее необходимо найти две-три точки, принадлежащие любой из двух ветвей гиперболы, если гипербола без смещения – точки на второй ветви будут симметричны им относительно осей гиперболы.
Выразим $y$ из канонического уравнения нашей гиперболы:

$y = ±frac{1}{2} sqrt{5 x^2 – 4}$

Найдём точки для положительной части гиперболы:

при $x = 3, y =2.5$,
а при $x = 3, y ≈3,87$.

Теперь можно отложить все эти точки и построить график гиперболы.

1. Гипербола и её форма.

   Начать изучение
   

2. Фокусы, эксцентриситет и директрисы гиперболы.

   Начать изучение
   

3. Точки гиперболы и их свойства.

   Начать изучение
   

4. Уравнение касательной к гиперболе.

   Начать изучение
   

Гипербола и её форма.

Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac{x^{2}}{a^{2}}-frac{y^{2}}{b^{2}}=1.label{ref9}
$$

Из этого уравнения видно, что для всех точек гиперболы (|x| geq a), то есть все точки гиперболы лежат вне вертикальной полосы ширины (2a) (рис. 8.6). Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами ((a, 0)) и ((-a, 0)), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа (a) и (b) называются соответственно вещественной и мнимой полуосями гиперболы.

Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде (y=kx), поскольку мы уже знаем, что прямая (x=0) не пересекает гиперболу. Абсциссы точек перечения находятся из уравнения
$$
frac{x^{2}}{a^{2}}-frac{k^{2}x^{2}}{b^{2}}=1.
$$
Поэтому, если (b^{2}-a^{2}k^{2} > 0), то
$$
x=pm frac{ab}{sqrt{b^{2}-a^{2}k^{2}}}.
$$
Это позволяет указать координаты точек пересечения ((ab/v, abk/v)) и ((-ab/v, -abk/v)), где обозначено (v=(b^{2}-a^{2}k^{2})^{1/2}). В силу симметрии достаточно проследить за движением первой из точек при изменении (k) (рис. 8.7).

Числитель дроби (ab/v) постоянен, а знаменатель принимает наибольшее значение при (k=0). Следовательно, наименьшую абсциссу имеет вершина ((a, 0)). С ростом (k) знаменатель убывает, и (x) растет, стремясь к бесконечности, когда (k) приближается к числу (b/a). Прямая (y=bx/a) с угловым коэффициентом (b/a) не пересекает гиперболу, и прямые с большими угловыми коэффициентами ее тем более не пересекают. Любая прямая с меньшим положительным угловым коэффициентом пересекает гиперболу.

Если мы будем поворачивать прямую от горизонтального положения по часовой стрелке, то (k) будет убывать, (k^{2}) расти, и прямая будет пересекать гиперболу во все удаляющихся точках, пока не займет положения с угловым коэффициентом (-b/a).

К прямой (y=-bx/a) относится все, что было сказано о (y=bx/a): она не пересекает гиперболу и отделяет прямые, пересекающие ее, от не пересекающих. Из приведенных рассуждений вытекает, что гипербола имеет вид, изображенный на рис. 8.7.

Запишем уравнения асимптот в виде (bx-ay=0) и (bx+ay=0). Расстояния от точки (M(x, y)) до асимптот равны соответственно
$$
h_{1}=frac{|bx-ay|}{sqrt{a^{2}+b^{2}}}, h_{2}=frac{|bx+ay|}{sqrt{a^{2}+b^{2}}}.nonumber
$$
Если точка (M) находится на гиперболе, то (b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2}), и
$$
h_{1}h_{2}=frac{|b^{2}x^{2}-a^{2}y^{2}|}{a^{2}+b^{2}}=frac{a^{2}b^{2}}{a^{2}+b^{2}}.nonumber
$$

Отсюда следует важное свойство асимптот.

---

Фокусы, эксцентриситет и директрисы гиперболы.

Отношение (varepsilon=c/a), как и для эллипса, называется эксцентриситетом. У гиперболы (varepsilon > 1).

Заметим, что равенства eqref{ref11} можно подробнее записать так:

• для правой ветви гиперболы ((x geq a))
  $$
  r_{1}=varepsilon x-a, r_{2}=varepsilon x+a;nonumber
  $$
• для левой ветви гиперболы ((x leq -a))
  $$
  r_{1}= a-varepsilon x, r_{2}=-varepsilon x-a;nonumber
  $$

Итак, для правой ветви (r_{2}-r_{1}=2a), а для левой ветви (r_{1}-r_{2}=2a). В обоих случаях
$$
|r_{2}-r_{1}|=2a.label{ref12}
$$

Директрисами гиперболы называются прямые, задаваемые в канонической системе координат уравнениями
$$
x=frac{a}{varepsilon}, x=-frac{a}{varepsilon}.label{ref13}
$$

Директрисы лежат ближе к центру, чем вершины, и, следовательно, не пересекают гиперболу. Директриса и фокус, лежащие по одну сторону от центра, считаются соответствующими друг другу.

---

Точки гиперболы и их свойства.

---

Уравнение касательной к гиперболе.

Уравнение касательной к гиперболе в точке (M_{0}(x_{0}, y_{0})), лежащей на ней, выводится так же, как соответствующее уравнение касательной для эллипса. Оно имеет вид
$$
frac{xx_{0}}{a^{2}}-frac{yy_{0}}{b^{2}}=1.label{ref14}
$$