Как составить каноническое уравнение по трем точкам

Уравнение плоскости онлайн

С помощю этого онлайн калькулятора можно построить уравнение плоскости, проходящей через три точки, и уравнение плоскости, проходящей через одну точку и имеющий заданный нормаль плоскости. Дается подробное решение с пояснениями. Для построения уравнения плоскости выберите вариант задания исходных данных, введите координаты точек в ячейки и нажимайте на кнопку “Решить”.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Уравнение плоскости, проходящей через три точки

Рассмотрим цель − вывести уравнение плоскости, проходящей через три различные точки M₁(x₁, y₁, z₁), M₂(x₂, y₂, z₂), M₃(x₃, y₃, z₃), не лежащие на одной прямой. Так как эти точки не лежат на одной прямой, векторы и 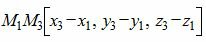не коллинеарны. Следовательно точка M(x, y, z) лежит в одной плоскости с точками M₁, M₂, M₃ тогда и тольно тогда, когда векторы M₁M₂, M₁M₃ и компланарны. Но векторы M₁M₂, M₁M₃, M₁M компланарны тогда и только тогда, когда их смешанное произведение равно нулю. Используя смешанное произведение векторов M₁M₂, M₁M₃, M₁M в координатах, получим необходимое и достаточное условие принадлежности точки M(x, y, z) к указанной плоскости:

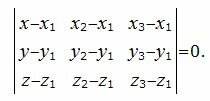
Разложив определитель в левой части выражения, например, по первому столбцу и упростив, получим уравнение плоскости в общей форме, проходящий по точкам M₁, M₂, M₃:

Пример 1. Построить уравнение плоскости, проходящую через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2).

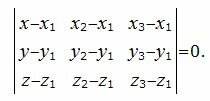(1)

Подставляя координаты точек A, B, C в (1), получим:

Разложим определитель по первому столбцу:

Уравнение плоскости, проходящей через точки A(1, 2, 1), B(4, 5, -4), С(2, 1, 2) имеет вид:

Уравнение плоскости, проходящей через одну точку и имеющий нормаль n

Пример 2. Построить плоскость, проходящую через точку M₀(-1, 2, 1) и имеюший нормаль n(1, 4/5, 1).

(2)

Подставляя координаты векторов M₀ и n в (2), получим:

Уравнение плоскости, которая проходит через три заданные точки, не лежащие на одной прямой

В рамках этого материала мы разберем, как найти уравнение плоскости, если мы знаем координаты трех различных ее точек, которые не лежат на одной прямой. Для этого нам понадобится вспомнить, что такое прямоугольная система координат в трехмерном пространстве. Для начала мы введем основной принцип данного уравнения и покажем, как именно использовать его при решении конкретных задач.

Как найти уравнение плоскости, которая проходит через 3 заданные точки

Для начала нам необходимо вспомнить одну аксиому, которая звучит следующим образом:

Если три точки не совпадают друг с другом и не лежат на одной прямой, то в трехмерном пространстве через них проходит только одна плоскость.

Иными словами, если у нас есть три разных точки, координаты которых не совпадают и которые нельзя соединить прямой, то мы можем определить плоскость, проходящую через нее.

Допустим, у нас имеется прямоугольная система координат. Обозначим ее O x y z . В ней лежат три точки M с координатами M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) , которые нельзя соединить прямой линией. Исходя из этих условий, мы можем записать уравнение необходимой нам плоскости. Есть два подхода к решению этой задачи.

1. Первый подход использует общее уравнение плоскости. В буквенном виде оно записывается как A ( x – x 1 ) + B ( y – y 1 ) + C ( z – z 1 ) = 0 . С его помощью можно задать в прямоугольной системе координат некую плоскость альфа, которая проходит через первую заданную точку M 1 ( x 1 , y 1 , z 1 ) . У нас получается, что нормальный вектор плоскости α будет иметь координаты A , B , C .

Зная координаты нормального вектора и координаты точки, через которую проходит плоскость, мы можем записать общее уравнение этой плоскости.

Из этого мы и будем исходить в дальнейшем.

Таким образом, согласно условиям задачи, мы имеем координаты искомой точки (даже трех), через которую проходит плоскость. Чтобы найти уравнение, нужно вычислить координаты ее нормального вектора. Обозначим его n → .

Вспомним правило: любой не равный нулю вектор данной плоскости является перпендикулярным нормальному вектору этой же плоскости. Тогда мы имеем, что n → будет перпендикулярным по отношению к векторам, составленным из исходных точек M 1 M 2 → и M 1 M 3 → . Тогда мы можем обозначить n → как векторное произведение вида M 1 M 2 → · M 1 M 3 → .

Поскольку M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) а M 1 M 3 → = x 3 – x 1 , y 3 – y 1 , z 3 – z 1 (доказательства этих равенств приведены в статье, посвященной вычислению координат вектора по координатам точек), тогда получается, что:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1

Если мы вычислим определитель, то получим необходимые нам координаты нормального вектора n → . Теперь мы можем записать нужное нам уравнение плоскости, проходящей через три заданные точки.

2. Второй подход нахождения уравнения, проходящей через M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) , основан на таком понятии, как компланарность векторов.

Если у нас есть множество точек M ( x , y , z ) , то в прямоугольной системе координат они определяют плоскость для заданных точек M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) только в том случае, когда векторы M 1 M → = ( x – x 1 , y – y 1 , z – z 1 ) , M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) и M 1 M 3 → = ( x 3 – x 1 , y 3 – y 1 , z 3 – z 1 ) будут компланарными.

На схеме это будет выглядеть так:

Это будет означать, что смешанное произведение векторов M 1 M → , M 1 M 2 → , M 1 M 3 → будет равно нулю: M 1 M → · M 1 M 2 → · M 1 M 3 → = 0 , поскольку это является основным условием компланарности: M 1 M → = ( x – x 1 , y – y 1 , z – z 1 ) , M 1 M 2 → = ( x 2 – x 1 , y 2 – y 1 , z 2 – z 1 ) и M 1 M 3 → = ( x 3 – x 1 , y 3 – y 1 , z 3 – z 1 ) .

Запишем полученное уравнение в координатной форме:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

После того, как мы вычислим определитель, мы сможем получить нужное нам уравнение плоскости для трех не лежащих на одной прямой точек M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) .

От полученного в результате уравнения можно перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости, если этого требуют условия задачи.

В следующем пункте мы приведем примеры того, как указанные нами подходы реализуются на практике.

Примеры задач на составление уравнения плоскости, проходящих через 3 точки

Ранее мы выделили два подхода, с помощью которых можно найти искомое уравнение. Давайте посмотрим, как они применяются в решениях задач и когда следует выбирать каждый из них.

Есть три точки, не лежащие на одной прямой, с координатами M 1 ( – 3 , 2 , – 1 ) , M 2 ( – 1 , 2 , 4 ) , M 3 ( 3 , 3 , – 1 ) . Составьте уравнение плоскости, проходящей через них.

Решение

Используем поочередно оба способа.

1. Найдем координаты двух нужных нам векторов M 1 M 2 → , M 1 M 3 → :

M 1 M 2 → = – 1 – – 3 , 2 – 2 , 4 – – 1 ⇔ M 1 M 2 → = ( 2 , 0 , 5 ) M 1 M 3 → = 3 – – 3 , 3 – 2 , – 1 – – 1 ⇔ M 1 M 3 → = 6 , 1 , 0

Теперь вычислим их векторное произведение. Вычисления определителя расписывать при этом не будем:

n → = M 1 M 2 → × M 1 M 3 → = i → j → k → 2 0 5 6 1 0 = – 5 · i → + 30 · j → + 2 · k →

У нас получился нормальный вектор плоскости, которая проходит через три искомые точки: n → = ( – 5 , 30 , 2 ) . Далее нам нужно взять одну из точек, например, M 1 ( – 3 , 2 , – 1 ) , и записать уравнение для плоскости с вектором n → = ( – 5 , 30 , 2 ) . Мы получим, что: – 5 · ( x – ( – 3 ) ) + 30 · ( y – 2 ) + 2 · ( z – ( – 1 ) ) = 0 ⇔ – 5 x + 30 y + 2 z – 73 = 0

Это и есть нужное нам уравнение плоскости, которая проходит через три точки.

2. Используем другой подход. Запишем уравнение для плоскости с тремя точками M 1 ( x 1 , y 1 , z 1 ) , M 2 ( x 2 , y 2 , z 2 ) , M 3 ( x 3 , y 3 , z 3 ) в следующем виде:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0

Сюда можно подставить данные из условия задачи. Поскольку x 1 = – 3 , y 1 = 2 , z 1 = – 1 , x 2 = – 1 , y 2 = 2 , z 2 = 4 , x 3 = 3 , y 3 = 3 , z 3 = – 1 , в итоге мы получим:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = x – ( – 3 ) y – 2 z – ( – 1 ) – 1 – ( – 3 ) 2 – 2 4 – ( – 1 ) 3 – ( – 3 ) 3 – 2 – 1 – ( – 1 ) = = x + 3 y – 2 z + 1 2 0 5 6 1 0 = – 5 x + 30 y + 2 z – 73

Мы получили нужное нам уравнение.

Ответ: – 5 x + 30 y + 2 z – 73 .

А как быть, если заданные точки все же лежат на одной прямой и нам нужно составить уравнение плоскости для них? Здесь сразу надо сказать, что это условие будет не совсем корректным. Через такие точки может проходить бесконечно много плоскостей, поэтому вычислить один-единственный ответ невозможно. Рассмотрим такую задачу, чтобы доказать некорректность подобной постановки вопроса.

У нас есть прямоугольная система координат в трехмерном пространстве, в которой размещены три точки с координатами M 1 ( 5 , – 8 , – 2 ) , M 2 ( 1 , – 2 , 0 ) , M 3 ( – 1 , 1 , 1 ) . Необходимо составить уравнение плоскости, проходящей через нее.

Решение

Используем первый способ и начнем с вычисления координат двух векторов M 1 M 2 → и M 1 M 3 → . Подсчитаем их координаты: M 1 M 2 → = ( – 4 , 6 , 2 ) , M 1 M 3 → = – 6 , 9 , 3 .

Векторное произведение будет равно:

M 1 M 2 → × M 1 M 3 → = i → j → k → – 4 6 2 – 6 9 3 = 0 · i ⇀ + 0 · j → + 0 · k → = 0 →

Поскольку M 1 M 2 → × M 1 M 3 → = 0 → , то наши векторы будут коллинеарными (перечитайте статью о них, если забыли определение этого понятия). Таким образом, исходные точки M 1 ( 5 , – 8 , – 2 ) , M 2 ( 1 , – 2 , 0 ) , M 3 ( – 1 , 1 , 1 ) находятся на одной прямой, и наша задача имеет бесконечно много вариантов ответа.

Если мы используем второй способ, у нас получится:

x – x 1 y – y 1 z – z 1 x 2 – x 1 y 2 – y 1 z 2 – z 1 x 3 – x 1 y 3 – y 1 z 3 – z 1 = 0 ⇔ x – 5 y – ( – 8 ) z – ( – 2 ) 1 – 5 – 2 – ( – 8 ) 0 – ( – 2 ) – 1 – 5 1 – ( – 8 ) 1 – ( – 2 ) = 0 ⇔ ⇔ x – 5 y + 8 z + 2 – 4 6 2 – 6 9 3 = 0 ⇔ 0 ≡ 0

Из получившегося равенства также следует, что заданные точки M 1 ( 5 , – 8 , – 2 ) , M 2 ( 1 , – 2 , 0 ) , M 3 ( – 1 , 1 , 1 ) находятся на одной прямой.

Если вы хотите найти хоть один ответ этой задачи из бесконечного множества ее вариантов, то нужно выполнить следующие шаги:

1. Записать уравнение прямой М 1 М 2 , М 1 М 3 или М 2 М 3 (при необходимости посмотрите материал об этом действии).

2. Взять точку M 4 ( x 4 , y 4 , z 4 ) , которая не лежит на прямой М 1 М 2 .

3. Записать уравнение плоскости, которая проходит через три различных точки М 1 , М 2 и M 4 , не лежащих на одной прямой.

Уравнение плоскости через 3 точки

Вы будете перенаправлены на Автор24

Для начала стоит напомнить, как выглядит общее уравнение плоскости:

$Ax cdot + By + Cz + D = 0left(1right)$,

при этом: $$ — координаты нормального вектора данной плоскости, а $D$ — свободный член.

В общем уравнении коэффициенты $A, B, C$ не могут быть одновременно равны нулю, если же один из коэффициентов нулевой — уравнение называется неполным. При $D=0$ плоскость проходит через центр осей координат.

Также в дальнейшем нам пригодится уравнение плоскости, заданной точкой, лежащей в данной плоскости и нормальным вектором:

здесь $(x_0; y_0; z_0)$ — координаты точки плоскости.

Теперь непосредственно к делу.

Уравнение плоскости через три точки можно выразить несколькими способами: с помощью смешанного произведения векторов и выразив сначала нормальный вектор плоскости и используя одну точку.

Уравнение плоскости, проходящей через 3 точки, через смешанное произведение векторов

Рассмотрим три точки $M_1, M_2, M_3$, не находящиеся на одной прямой. Соответственно аксиоме стереометрии о том, что три точки задают плоскость, и притом только одну, все эти точки лежат в одной плоскости $α$.

Рисунок 1. Плоскость через 3 точки. Автор24 — интернет-биржа студенческих работ

Рассмотрим точку $M$, лежащую в плоскости $α$. Если описать плоскость $α$ как множество точек $M$, вектора $vec$, $vec$ и $vec$ должны быть компланарны между собой. А как известно, вектора компланарны между собой если их смешанное произведение равно нулю.

Соответственно, для того чтобы вычислить это смешанное произведение, необходимо вычислить определитель третьего порядка, каждая строка которого является координатами вышеперечисленных векторов.

Готовые работы на аналогичную тему

Пусть координаты точек $M, M_1, M_2, M_3$ — $(x; y; z), (x_1;y_1; z_1), (x_2;y_2; z_2), (x_3;y_3;z_3)$ соответственно. Тогда координаты каждого из вышеперечисленных векторов составят:

Составим определитель, описывающий смешанное произведение векторов:

$begin <|ccc|>x-x_1 && y-y_1 && z-z_1 \ x_2-x_1 && y_2-y_1 && z_2-z_1 \ x_3-x_1 && y_3-y_1 &&z_3-z_1 \ end=0$ — уравнение плоскости через 3 точки.

При вычислении этого определителя получается общее уравнение плоскости, проходящей через три точки. Это можно увидеть, раскрыв определитель по первой строке:

$begin <|cc|>y_2-y_1 && z_2-z_1 \ y_3-y_1 &&z_3-z_1 \ end cdot ( x-x_1) + begin <|cc|>x_2-x_1 && z_2-z_1 \ x_3-x_1 &&z_3-z_1 \ end cdot (y-y_1) + begin <|cc|>x_2-x_1 && y_2-y_1 \ x_3-x_1 && y_3-y_1 \ end cdot (z-z_1) = 0left(3right)$.

Коэффициенты из уравнения $(3)$ также совпадают с координатами векторного произведения $vec×vec$ и, так как два этих вектора неколлинеарны и параллельны рассматриваемой плоскости $α$, данное векторное произведение представляет собой нормальный вектор к плоскости, для которой составляется уравнение.

Уравнение плоскости, заданной 3 точками, через нормальный вектор и точку

Другим альтернативным методом задания плоскости является использование нормального вектора плоскости и точки, принадлежащей данной плоскости.

Для того чтобы воспользоваться данным методом, найдём векторное произведение векторов $vec$ и $vec$:

$[vec × vec]= begin <|ccc|>vec &&vec &&vec \ x_2-x_1 &&y_2-y_1 &&z_2-z_1 \ x_3-x_1 &&y_3-y_1 &&z_3-z_1 \ end=0$.

Данное произведение является нормальным вектором плоскости, для которой составляется уравнение. Полученные координаты нормального вектора можно использовать непосредственно для составления уравнения плоскости.

Зная точку, принадлежащую этой плоскости, можно подставить координаты нормального вектора и координаты точки в уравнение $(2)$ и получить уравнение плоскости:

В этом уравнении $n_x; n_y; n_z$ — координаты нормального вектора, определённого из векторного произведения векторов $vec$ и $vec$, а $(x_3; y_3; z_3)$ — некая точка, принадлежащая данной плоскости.

По сути, два вышеприведённых метода представляют одно и то же, так как в обоих необходимо найти координаты нормального вектора и затем, используя их и координаты третьей неиспользованной точки, получить уравнение самой плоскости.

К данной задаче можно также свести задачу с нахождением уравнения плоскости по уравнениям лежащих в ней параллельных и пересекающихся прямых.

Cоставить уравнение плоскости, проходящей через 3 точки $M_1,M_2, M_3$ c координатами $(1;2;3), (1;2;4)$ и $(4;2;-1)$ соответственно.

Воспользуемся вторым способом и найдём координаты вектора через векторное произведение. Для этого сначала выразим координаты векторов:

Найдём их векторное произведение:

Подставим координаты нормального вектора в уравнение $(2)$:

$0cdot(x-4)+(-3) cdot (y-2)+0 cdot(z+1)=0$.

$-3y+6=0$ — искомое уравнение плоскости.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 14 03 2021

[spoiler title=”источники:”]

http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/uravnenie-ploskosti-kotoraja-prohodit-cherez-tri-z/

http://spravochnick.ru/matematika/uravnenie_ploskosti_cherez_3_tochki/

[/spoiler]

I Уравнение плоскости, проходящей через три точки

Выведем уравнение
плоскости, которая проходит через три
различные точки M₁(x₁,y₁,z₁),
M₂(x₂,y₂,z₂)
и M₃(x₃,y₃,z₃),
не лежащие на одной прямой. Так как
указанные точки не лежат на одной прямой,
векторы
инеколлинеарны, а потому произвольная
точкаM(x,y,z)
лежит в одной
плоскости с точками M₁,
M₂,
M₃
тогда и только
тогда, когда векторы
,икомпланарны. Но компланарность равносильна
равенству нулю смешанного произведения
векторов. Записав смешанное произведение
через проекции векторов, получим:

. (1)

Это и есть уравнение
плоскости проходящей через данные три
точки.

II Уравнение плоскости “в отрезках”

Рассмотрим
плоскость, которая пересекает все
координатные оси и не проходит через
начало координат. Введем обозначения
для точек пересечения с осями: M₁(a;0;0),
M₂(0;b;0)
и M₃(0;0;c).
Составим уравнение плоскости, используя
формулу (1):

.

Вычислив
определитель, получим:

(x–a)bc+yac+zab=0.

Разделим
обе части уравнения на abc:

.

И
окончательно

. (2)

Это и есть уравнение
плоскости “в отрезках”.

§7. Прямая в пространстве

I Общие уравнения прямой

Как уже говорилось
ранее, в аналитической геометрии линию
в пространстве понимают как пересечение
двух поверхностей. В частности, прямую
линию мы будем рассматривать как
пересечение двух плоскостей. Поэтому,
если в пространстве задананекоторая
ДПСК,то
уравнениями прямойслужит
система двух уравнений первой степени:

(1)

Будем называть
эти уравнения общими уравнениями прямой
(конечно, предполагается, что прямые
пересекаются).

Очевидно, существует
бесчисленное множество пар плоскостей,
пересекающихся по данной прямой, и
соответственно этому существует
бесчисленное множество общих уравнений
(1) для данной прямой.

Общие уравнения
удобны при решении задачи о пересечении
прямой и плоскости или двух прямых,
задачи о проектировании прямой на
плоскость. В других задачах более
удобными оказываются иные формы уравнений
прямой.

II Канонические уравнения прямой

Определение.
Всякий ненулевой вектор, лежащий на
данной прямой или параллельный ей,
называется ее направляющим вектором.
Обозначение:
.

Составим уравнение
прямой, проходящей через точку
M₀(x₀,y₀,z₀)
в направлении вектора
.
Возьмем текущую точку прямойM(x,y,z)
и рассмотрим вектор
.
Он лежит на данной прямой и поэтому
коллинеарен ее направляющему вектору.
Осталось написать условие коллинеарности,
т.е. пропорциональность проекций:

. (2)

Это и есть
канонические уравнения прямой, проходящей
через точку M₀(x₀,y₀,z₀)
и имеющей направляющий вектор
.

Пример.
Найти канонические уравнения прямой

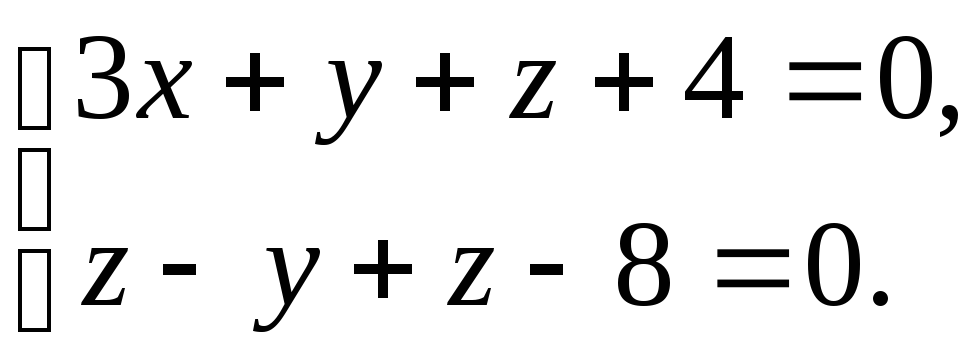(3)

Решение.
Чтобы составить канонические уравнения
прямой, нужно: 1) найти какую-либо точку
прямой; 2) найти направляющий вектор
прямой.

1) Найти какую-нибудь
точку прямой (3) – это означает найти
какое-нибудь решение этой системы двух
уравнений с тремя неизвестными. Положим,
например, x=0.
Система (3) превратится в

Отсюда нетрудно
найти: z=2,
y=
–6. Итак, точка
M₀(0;–6;
2) принадлежит
прямой (3).

2) Прямая определена
как пересечения двух плоскостей, значит
она лежит в каждой из них и поэтому
перпендикулярна их нормальным векторам

и.
В качестве направляющего вектора можно
взять любой вектор перпендикулярный к
векторами,
например, их векторное произведение

,

или вектор,
коллинеарный ему
.
Итак, искомые канонические уравнения
имеют вид

Пример.
Составить уравнения прямой, проходящей
через точки M₁(x₁,y₁,z₁)
и M₂(x₂,y₂,z₂).

Решение.
Для того, чтобы использовать канонические
уравнения (2), положим M₀=M₁,
.
Получим:

. (4)

Имея эти уравнения,
предыдущей пример можно решить, не
находя направляющий вектор прямой. Надо
только найти не одну точку, лежащую на
прямой, а две.

Соседние файлы в папке Конспект

• #
• #
• #
• #
• #
• #
• #

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Вводить можно числа или дроби (-2.4, 5/7, …). Более подробно читайте в правилах ввода чисел.

Уравнения прямых в пространстве

Уравнение прямой как линии пересечения двух плоскостей

Пусть в координатном пространстве (в прямоугольной системе координат) две плоскости заданы общими уравнениями

в которых коэффициенты при неизвестных непропорциональны, т.е. . Это условие означает, что плоскости и пересекаются (см. условие (4.25)), поскольку их нормали и неколлинеарны (рис.4.25). Тогда линия пересечения плоскостей описывается системой уравнений

Система (4.31) называется общим уравнением прямой в пространстве.

---

Пример 4.13. В координатном пространстве (в прямоугольной системе координат) заданы вершины треугольника (рис.4.26). Требуется составить уравнение прямой, содержащей высоту треугольника.

Решение. Прямая является линией пересечения двух плоскостей: плоскости , треугольника и плоскости , проходящей через точку перпендикулярно вектору (рис.4.26). По формуле (4.21) составим уравнение плоскости проходящей через три точки

По формуле (4.14) составим уравнение плоскости , проходящей через точку перпендикулярно вектору

Следовательно, общее уравнение (4.31) прямой имеет вид

---

Параметрическое уравнение прямой в пространстве

Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.

Пусть в координатном пространстве заданы точка и ненулевой вектор (рис.4.27). Требуется составить уравнение прямой, коллинеарной вектору и проходящей через точку .

Выберем на прямой произвольную точку . Обозначим — радиус-векторы точек и (рис.4.28).

Точка принадлежит заданной прямой тогда и только тогда, когда векторы и коллинеарны. Запишем условие коллинеарности: , где — некоторое действительное число (параметр). Учитывая, что , получим векторное параметрическое уравнение прямой в пространстве:

где — направляющий вектор прямой, а — радиус-вектор заданной точки принадлежащей прямой.

Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве

где — координаты направляющего вектора прямой. Параметр в уравнениях (4.32),(4.33) имеет следующий геометрический смысл: величина пропорциональна расстоянию от заданной точки до точки . Физический смысл параметра в параметрических уравнениях (4.32),(4.33) — это время при равномерном и Прямолинейном движении точки по прямой. При точка совпадает с заданной точкой . При возрастании параметра движение происходит в направлении направляющего вектора.

---

Каноническое уравнение прямой в пространстве

Выразим параметр из каждого уравнения системы (4.33): , а затем исключим этот параметр:

Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты не равны нулю одновременно, так как это координаты направляющего вектора прямой.

---

Замечания 4.6.

1. Если один или два из трех знаменателей дробей в (4.34) равны нулю, то считается, что соответствующий числитель дроби равен нулю. Например:

а) каноническое уравнение — это уравнение прямой, параллельной оси аппликат (рис.4.29,а);

б) каноническое уравнение — это уравнение прямой, параллельной координатной плоскости (рис.4.29,б).

2. Направляющий вектор прямой определяется неоднозначно. Например, любой ненулевой вектор , где , также является направляющим вектором для той же прямой.

Переход от общего уравнение к каноническому

3. Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:

1) найти любое решение системы определяя тем самым координаты точки , принадлежащей прямой;

2) найти направляющий вектор прямой как векторное произведение нормалей заданных плоскостей:

3) записать каноническое уравнение (4.34) с учетом пунктов 1 и 2.

4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы

и привести подобные члены.

5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):

6. Если в каноническом уравнении (4.34) прямой фиксировать координаты точки , а коэффициентам придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке , т.е. совокупность всех прямых, проходящих через точку .

7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.

---

Пример 4.14. В координатном пространстве (в прямоугольной системе координат) заданы вершины треугольника (рис. 4.30). Требуется:

а) составить каноническое уравнение прямой, содержащей высоту треугольника;

б) составить общее уравнение прямой, содержащей биссектрису треугольника.

Решение. а) Общее уравнение прямой получено в примере 4.13: Перейдем от общего уравнения к каноническому.

1) Найдем любое решение системы, например, (это координаты точки ).

2) Найдем направляющий вектор прямой как векторное произведение нормалей заданных плоскостей

3) Запишем каноническое уравнение (4.34): .

б) Сначала составим каноническое уравнение прямой . Для этого нужно найти направляющий вектор этой прямой. Учитывая, что диагональ ромба является биссектрисой, , где и — единичные векторы, одинаково направленные с векторами и соответственно. Находим

Составляем каноническое уравнение прямой .

Записывая двойное равенство в виде системы, получаем общее уравнение прямой

---

Расстояние от точки до прямой в пространстве

Найдем расстояние от точки до прямой , заданной каноническим уравнением (рис.4.31)):

Искомое расстояние равно высоте параллелограмма, построенного на векторах

и , то есть.

---

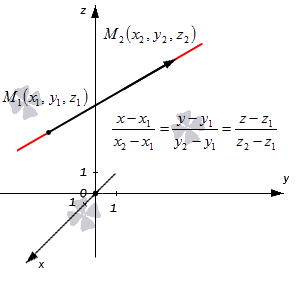
Уравнение прямой, проходящей через две заданные точки

Пусть в координатном пространстве заданы две точки и . Требуется составить уравнение прямой, проходящей через заданные точки.

Как показано в разд., точка принадлежит прямой тогда и только тогда, когда ее радиус-вектор удовлетворяет условию (рис.4.32): , где — некоторое действительное число (параметр). Это уравнение, а также его координатную форму

будем называть аффинным уравнением прямой, проходящей через две точки и .

Выражая параметр из каждого уравнения системы (4.36), получаем: . Исключая параметр , приходим к уравнению прямой, проходящей через две точки и :

Уравнение (4.37) можно получить из канонического уравнения (4.34), выбирая в качестве направляющего вектора вектор т.е. подставляя

---

Пример 4.15. В координатном пространстве (в прямоугольной системе координат) заданы вершины треугольника (рис.4.33). Требуется:

а) составить уравнение прямой ;

б) составить уравнение прямой, содержащей медиану треугольника;

в) найти высоту треугольника, опущенную на сторону .

Решение. а) Записываем уравнение (4.37) прямой, проходящей через точки

б) Находим координаты середины стороны . Составляем уравнение (4.37) прямой

в) Искомую высоту находим по формуле (4.35), полагая и

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.

В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через 2 заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.

Что такое каноническое уравнение прямой в пространстве

О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.

Допустим, у нас есть прямоугольная система координат Oxyz, в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой a, а точку M, то можно записать, что M1(x1, y1, z1) лежит на прямой a и направляющим вектором этой прямой будет a→=(ax, ay, az). Чтобы множество точек M(x, y, z) определяло прямую a, векторы M1M→ и a→ должны быть коллинеарными,

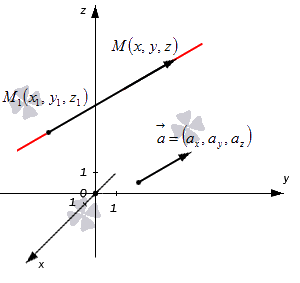
Если мы знаем координаты векторов M1M→ и a→, то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты a→. Для того чтобы получить координаты M1M→, нам необходимо вычислить разность между M(x, y, z) и M1(x1, y1, z1). Запишем:

M1M→=x-x1, y-y1, z-z1

После этого нужное нам условие мы можем сформулировать так: M1M→=x-x1, y-y1, z-z1 и a→=(ax, ay, az): M1M→=λ·a→⇔x-x1=λ·axy-y1=λ·ayz-z1=λ·az

Здесь значением переменной λ может быть любое действительное число или ноль. Если λ=0, то M(x, y, z) и M1(x1, y1, z1)совпадут, что не противоречит нашим рассуждениям.

При значениях ax≠0, ay≠0, az≠0 мы можем разрешить относительно параметра λ все уравнения системы x-x1=λ·axy-y1=λ·ayz-z1=λ·az

Между правыми частями после этого можно будет поставить знак равенства:

x-x1=λ·axy-y1=λ·ayz-z1=λ·az⇔λ=x-x1axλ=y-y1ayλ=z-z1az⇔x-x1ax=y-y1ay=z-z1az

В итоге у нас получились уравнения x-x1ax=y-y1ay=z-z1az, с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.

Такая запись используется даже при нулевых значениях одного или двух параметров ax, ay, az, поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны 0, поскольку направляющий вектор a→=(ax, ay, az) нулевым не бывает.

Если один-два параметра a равны 0, то уравнение x-x1ax=y-y1ay=z-z1az носит условный характер. Его следует считать равным следующей записи:

x=x1+ax·λy=y1+ay·λz=z1+az·λ, λ∈R.

Частные случаи канонических уравнений мы разберем в третьем пункте статьи.

Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.

1) если исходная прямая будет проходить через две точки  M1(x1, y1, z1) и M2(x2, y2, z2), то канонические уравнения примут следующий вид:

x-x1ax=y-y1ay=z-z1az или x-x2ax=y-y2ay=z-z2az.

2) поскольку a→=(ax, ay, az) является направляющим вектором исходной прямой, то таковыми будут являться и все векторы μ·a→=μ·ax, μ·ay, μ·az, μ∈R, μ≠0. Тогда прямая может быть определена с помощью уравнения x-x1ax=y-y1ay=z-z1az или x-x1μ·ax=y-y1μ·ay=z-z1μ·az.

Вот несколько примеров таких уравнений с заданными значениями:

Как составить каноническое уравнение прямой в пространстве

Мы выяснили, что канонические уравнения вида x-x1ax=y-y1ay=z-z1az будут соответствовать прямой, проходящей через точку M1(x1, y1, z1), а вектор a→=(ax, ay, az) будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.

Разберем пару конкретных задач.

Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.

Канонические уравнения с одним или двумя a, равными нулю

Ранее мы уже говорили, что одно-два значения параметров ax, ay, az в уравнениях могут иметь нулевые значения. При этом запись x-x1ax=y-y1ay=z-z1az=λ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при λ∈R):

x=x1+ax·λy=y1+ay·λz=z1+az·λ

Рассмотрим эти случаи подробнее. Допустим, что ax=0, ay≠0, az≠0, ax≠0, ay=0, az≠0, либо ax≠0, ay≠0, az=0. В таком случае нужные уравнения мы можем записать так:

1.  В первом случае: 
   x-x10=y-y1ay=z-z1az=λ⇔x-x1=0y=y1+ay·λz=z1+az·λ⇔x-x1=0y-y1ay=z-z1az=λ

2.  Во втором случае:
   x-x1ax=y-y10=z-z1az=λ⇔x=x1+ax·λy-y1=0z=z1+az·λ⇔y-y1=0x-x1ax=z-z1az=λ

3.  В третьем случае:
   x-x1ax=y-y1ay=z-z10=λ⇔x=x1+ax·λy=y1+ay·λz-z1=0⇔z-z1=0x-x1ax=y-y1ay=λ

Получается, что при таком значении параметров нужные прямые находятся в плоскостях x-x1=0, y-y1=0 или z-z1=0, которые располагаются параллельно координатным плоскостям (если x1=0, y1=0 либо z1=0). Примеры таких прямых показаны на иллюстрации.

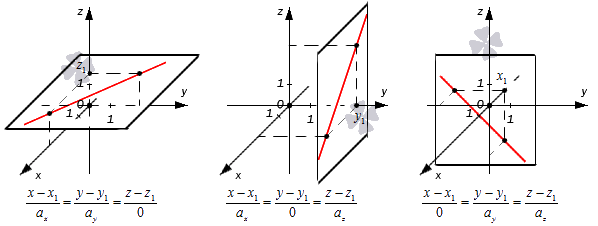
Следовательно, мы сможем записать канонические уравнения немного иначе.

1. В первом случае: x-x10=y-y10=z-z1az=λ⇔x-x1=0y-y1=0z=z1+az·λ, λ∈R
2. Во втором: x-x10=y-y1ay=z-z10=λ⇔x-x1=0y=y1+ay·λ, λ∈Rz-z1=0
3. В третьем: x-x1ax=y-y10=z-z10=λ⇔x=x1+ax·λ, λ∈Ry=y1=0z-z1=0

Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: x1=0y1=0, x1=0z1=0, y1=0z1=0. Их направляющие векторы имеют координаты  0, 0, az, 0, ay, 0, ax, 0, 0. Если обозначить направляющие векторы координатных прямых как i→, j→, k→, то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:

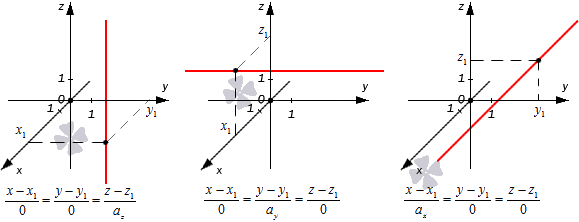
Покажем на примерах, как применяются эти правила.

Как записать каноническое уравнение прямой, которая проходит через две заданные точки

Допустим, что у нас есть две несовпадающие точки M1(x1, y1, z1) и M2(x2, y2, z2), через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?

Для начала примем вектор M1M2→ (или M2M1→) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:

M1M2→=x2-x1, y2-y1, z2-z1

Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:

x-x1x2-x1=y-y1y2-y1=z-z1z2-z1x-x2x2-x1=y-y2y2-y1=z-z2z2-z1

Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:

Приведем пример решения задачи.

Преобразование канонических уравнений прямой в пространстве в другие виды уравнений

Иногда пользоваться каноническими уравнениями вида x-x1ax=y-y1ay=z-z1az не очень удобно. Для решения некоторых задач лучше использовать запись x=x1+ax·λy=y1+ay·λz=z1+az·λ. В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0. Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.

Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру λ и разрешим эти уравнения относительно других переменных. В итоге получим:

x-x1ax=y-y1ay=z-z1az⇔x-x1ax=y-y1ay=z-z1az⇔⇔x-x1ax=λy-y1ay=λz-z1az=λ⇔x=x1+ax·λy=y1+ay·λz=z1+az·λ

Значение параметра λ может быть любым действительным числом, ведь и x, y, z могут принимать любые действительные значения.

Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).

Равенство x-x1ax=y-y1ay=z-z1az нужно для начала представить в виде системы уравнений:

x-x1ax=y-y1ayx-x1ax=z-z1axy-y1ay=z-z1az

Поскольку pq=rs мы понимаем как p·s=q·r, то можно записать:

x-x1ax=y-y1ayx-x1ax=z-z1azy-y1ay=z-z1az⇔ay·(x-x1)=ax·(y-y1)az·(x-x1)=ax·(z-z1)az·(y-y1)=ay·(z-z1)⇔⇔ay·x-ax·y+ax·y1-ay·x1=0az·x-ax·z+ax·z1-az·x1=0az·y-ay·z+ay·z1-az·y1=0

В итоге у нас вышло, что:

x-x1ax=y-y1ay=z-z1az⇔ay·x-ax·y+ax·y1-ay·x1=0az·x-ax·z+ax·z1-az·x1=0az·y-ay·z+ay·z1-az·y1=0

Выше мы отмечали, что все три параметра a не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен 2, поскольку ay-ax0az0-ax0az-ay=0 и один из определителей второго порядка не равен 0:

ay-axaz0=ax·az, ay0az-ax=ax·ay,  -ax00-ax=ax2ay-ax0az=ay·az, ay00-ay=-ay2, -ax0az-ay=ax·ayaz00az=az2, az-ax0-ay=-ay·az, 0-axaz-ay=ax·az

Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать 3 неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.

Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.