Написать канонические и параметрические уравнения прямой, образованной пересечением плоскостей
Решение
1) Найдем координаты фиксированной точки. Из исходной системы уравнений
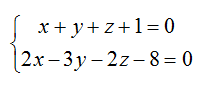
исключим z.
Положим z=0, тогда:
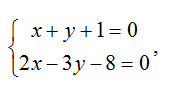
откуда находим: x=1, y= -2.
Таким образом, нашли координаты фиксированной точки M0(1,-2,0).
2) Направляющий вектор определяется как векторное произведение нормалей двух плоскостей, образующих прямую:
3) Запишем канонические уравнения:
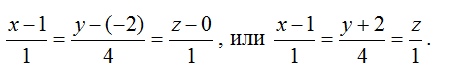
4) Обозначив,
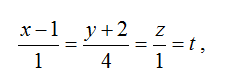
получаем параметрические уравнения:
x=t+1, y=4t-2, z=4
Больше уроков и заданий по всем школьным предметам в онлайн-школе “Альфа”. Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
5.4.4. Прямая, заданная пересечением двух плоскостей
Если плоскости 
пересекаются, то система линейных уравнений 
задаёт прямую в пространстве.
То есть прямая задана уравнениями двух плоскостей. Типовая и
распространенная задача состоит в том, чтобы переписать уравнения прямой в каноническом виде:
Задача 151
Записать канонические уравнения прямой 
Решение: чтобы составить канонические уравнения прямой, нужно знать точку и направляющий вектор. А у нас даны уравнения двух
плоскостей….
1) Сначала найдём какую-либо точку, принадлежащую данной прямой. Как это сделать? Методом подбора. В системе уравнений обнулим
какую-нибудь координату, например, 
. Тогда получается система двух линейных
уравнений с двумя неизвестными: 
. Почленно складываем уравнения и находим
решение системы:
Таким образом, точка 
принадлежит данной прямой. Но принадлежит ли?
Выполним проверку – подставим её координаты в исходную систему уравнений:
Получены верные равенства, значит, действительно 
.
В процессе подбора обратите внимание на следующий технический момент: желательно найти точку с целыми координатами. Если бы в
системе мы обнулили «икс» или «зет», то не факт, что получилась бы «хорошая» точка без дробных координат. Такой анализ и подбор точки следует
проводить мысленно или на черновике.
2) Как найти направляющий вектор прямой? Существует готовая формула: если прямая задана пересечением двух
плоскостей 
, то вектор 
является направляющим вектором данной прямой.
В нашей задаче:
Однако всех формул не упомнишь и поэтому очень важно понимать, откуда они взялись. Направляющий вектор нашей прямой ортогонален нормальным векторам плоскостей: 
и 
, поэтому вектор «пэ» можно найти как векторное произведение векторов нормали: 
.
Из уравнений плоскостей 
«снимаем» их векторы нормали:
и находим направляющий вектор прямой:
Проверим результат с помощью скалярного произведения:
, ч.т.п.
И, наконец, завершающий этап:
3) Составим канонические уравнения прямой по точке 
и
направляющему вектору 
:
Ответ: 
Аналогичная задача для самостоятельного решения:
Задача 152
Записать канонические уравнения прямой 
Будьте внимательны! Ваш ответ может отличаться от моего ответа (смотря, какую точку подберёте). Если отличие есть, то для проверки возьмите точку из вашего уравнения
и подставьте в моё уравнение (или наоборот).
Полное решение и ответ в конце книги.
И сейчас самое время перейти к простейшим задачам с пространственной прямой:
5.5.1. Взаимное расположение прямых
5.4.3. Параметрические уравнения прямой
| Оглавление |
Автор: Aлeксaндр Eмeлин
Прямую
линию в пространстве можно определить
как линию пересечения двух непараллельных
плоскостей.
. (7.1)
Часто
удобнее канонический вид уравнения
прямой.
Определение
7.1. Любой ненулевой вектор
,
параллельный данной прямой будем
называть направляющим вектором прямой.
Задача
7.1. Составить уравнение прямой
,
проходящей через точку
параллельно вектору
.
Решение.
Рассмотрим
вектор
,
начало которого совпадает с точкой
,
а конец − в произвольной точке
.
Чтобы
точка
лежала на прямой
,
вектор
должен быть параллелен вектору
.
Условие параллельности векторов состоит
в пропорциональности сходственных
координат, из чего следует
(7.2)
Это
уравнение называется каноническим
уравнением прямой
в пространстве.
Приравняв
выражение (7.2) параметру
,
получим параметрические
уравнения прямой.
(7.3)
Эти
уравнения имеют наглядное физическое
истолкование. Если принять что,
−время,
а
вектор скорости, то уравнения (7.3) − это
три проекции уравнения движения точки
на координатные оси.
Уравнение
прямой, проходящей через две заданные
точки
и
получим из уравнения (7.2), приняв, что
направляющий вектор
(7.4)
и
подставив выражение (7.4) в (7.2):
(7.5)
Чтобы
привести к каноническому
виду уравнение
прямой, заданной как линия пересечения
двух плоскостей, нужно найти направляющий
вектор прямой и точку, лежащую на прямой.
Длина вектора − произвольная, точка,
лежащая на прямой − любая.
Пусть
прямая есть линия пересечения плоскостей
(7.6)
. (7.6)
Направляющий
вектор прямой
ортогонален каждому из нармальных
векторов плоскостей
и
.
Поэтому
определим вектор
,
как векторное произведение нормальных
векторов
(7.7)
Компоненты
вектора
будут иметь вид
(7.8)
Для
определения координат точки, лежащей
на прямой, добавим в систему уравнений
(7.6) уравнение третьей плоскости. Удобно
добавить одну из координатных плоскостей
или
.
Чтобы
получающаяся система уравнений второго
порядка имела единственное решение, её
главный определитель не должен обращаться
в нуль. Это накладывает ограничения на
выбор координатной плоскости.
Пусть
.
Пусть в полученной системе уравнений
. (7.9)
главный
определитель
.
Тогда
координаты искомой точки определяются
по формулам Крамера
. (7.10)
Искомое
каноническое уравнение запишем в
следующем виде
(7.11)
-
Уравнение прямой, проходящей через 2 заданные точки в пространстве. Параметрическое уравнение прямой. Нахождение точки пересечения прямой и плоскости.
Чтобы
точка M
лежала на прямой L,
вектор M1M
должен быть параллелен вектору q.
Условие параллельности векторов состоит
в пропорциональности сходственных
координат, из чего следует
(1)
Уравнение
прямой, проходящей через две заданные
точки
M1(x1,y1,z1)
и M2(x2,y2,z2)
получим из уравнения (1), приняв, что
направляющий вектор
(2)
и
подставив выражение (2) в (1):
(3)
Приравняв
выражение (1) параметру t,
получим параметрические
уравнения прямой.
(4)
Эти
уравнения имеют наглядное физическое
истолкование. Если принять что, t
−время, а
вектор скорости, то уравнения (4) − это
три проекции уравнения движения точки
на координатные оси.
Найти
точку пересечения прямой:
(1)
и
плоскости:
(2)
Решение.
Приравняем
выражение (1) к параметру t
и выразим через него x,
y
и z
(3)
(4)
Подставим
x,
y
и z
из (4) в уравнение плоскости.
(5)
Координаты
точки пересечения прямой и плоскости
получим, подставив значение t0,
найденное из (5) в уравнения (4).
(6)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
