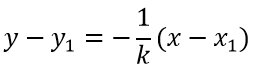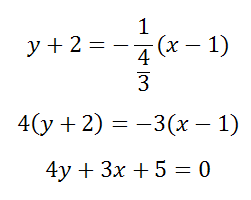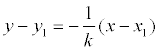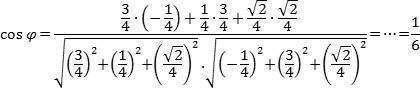Как составить каноническое уравнение прямой проходящее через точку перпендикулярно к прямым

В данной статье научимся составлять уравнения прямой, проходящей через заданную точку на плоскости перпендикулярно заданной прямой. Изучим теоретические сведения, приведем наглядные примеры, где необходимо записать такое уравнение.

Принцип составления уравнения прямой, проходящей через заданную точку плоскости перпендикулярно заданной прямой

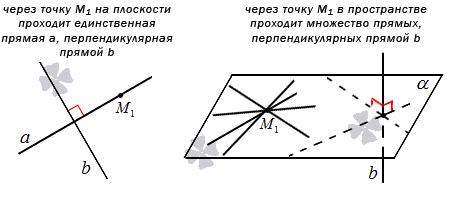
Перед нахождением уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой. Теорема рассматривается в средней школе. Через заданную точку, лежащую на плоскости, можно провести единственную прямую, перпендикулярную данной. Если имеется трехмерное пространство, то количество таких прямых увеличится до бесконечности.

Если плоскость α проходит через заданную точку М1 перпендикулярно к заданной прямой b, то прямые, лежащие  в этой плоскости, в том числе и проходящая через М1 являются перпендикулярными заданной прямой b.

Отсюда можно прийти к выводу, что составление уравнения прямой, проходящей через заданную точку перпендикулярно заданной прямой применимо только для случая на плоскости.

Задачи с трехмерным пространством подразумевают поиск уравнения плоскости, проходящей через заданную точку перпендикулярно к заданной прямой.

Если на плоскости с системой координат Охуz имеем прямую b, то ей соответствует уравнение прямой на плоскости, задается точка с координатами M1(x1, y1), а необходимо составить уравнение прямой a, которая проходит через точку М1 , причем перпендикулярно прямой b.

По условию имеем координаты точки М1. Для написания уравнения прямой необходимо иметь координаты направляющего вектора прямой a, или координаты нормального вектора прямой a, или угловой коэффициент прямой a.

Необходимо получить данные из заданного уравнения прямой b. По условию прямые a и b перпендикулярные, значит, направляющий вектор прямой b считается нормальным вектором прямой a. Отсюда получим, что угловые коэффициенты обозначаются как kb и ka. Они связаны при помощи соотношения kb·ka=-1.

Получили, что направляющий вектор  прямой b имеет вид b→=(bx, by), отсюда нормальный вектор – na→=(A2, B2), где значения A2=bx, B2=by. Тогда запишем общее уравнение прямой, проходящее через точку с координатами M1(x1, y1), имеющее нормальный вектор na→=(A2, B2), имеющее вид A2·(x-x1)+B2·(y-y1)=0.

Нормальный вектор прямой b определен и имеет вид nb→=(A1, B1), тогда направляющий вектор прямой a является вектором a→=(ax, ay), где значения ax=A1, ay=B1. Значит осталось составить каноническое или параметрическое уравнение прямой a, проходящее через точку с координатами M1(x1, y1) с направляющим вектором a→=(ax, ay), имеющее вид x-x1ax=y-y1ay или x=x1+ax·λy=y1+ay·λ соответственно.

После нахождения углового коэффициента kb прямой b можно высчитать угловой коэффициент прямой a. Он будет равен -1kb. Отсюда следует, что можно записать уравнение прямой a, проходящей через M1(x1, y1) с угловым коэффициентом -1kb в виде y-y1=-1kb·(x-x1).

Полученное уравнение прямой, проходящее через заданную точку плоскости перпендикулярно заданной. Если того требуют обстоятельства, можно переходить к другому виду данного уравнения.

Решение примеров

Рассмотрим составление уравнения прямой, проходящей через заданную точку плоскости и перпендикулярно заданной прямой.

Skip to content

1.Пусть прямая, проходит через точку T₁(x₁;y₁) и перпендикулярно прямой y=kx+b, тогда её можно представить уравнением (уравнение прямой перпендикулярной данной прямой):

Это и есть уравнение прямой, проходящей через точку перпендикулярно к прямой.
2.  Если прямая проходит через ту же точку T₁(x₁;y₁) и перпендикулярно прямой, но только записанной в виде Ax+By+C = 0, то уравнение можно представить как:

A (y − y₁) − B (x − x₁ ) = 0

---

Пример 1
Составить уравнение прямой, проходящей через точку L(1;-2) и перпендикулярно прямой

4x-3y-1 =  0 (на рисунке прямая, обозначенная красным цветом)

Решение
Данную прямую можно представить уравнением y = 4/3x-1/3 (здесь a = 4/3). Уравнение искомой прямой есть

---

Пример 2
Составить уравнение прямой, проходящей через точку M(-1;-2) и перпендикулярной к прямой 3y+2=0

Решение
Здесь A=0, B=3, получаем 3(x+1)=0, т.е. x+1=0. В этом случае формула неприменима.

23131

Условие

Все решения

Написать комментарий

Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой

Определение. Прямая,
проходящая через точку М₁ (х₁ ,
у₁ )
и перпендикулярная к прямой у = kx + b
представляется уравнением:

Расстояние от точки до прямой

Теорема. Если
задана точка М(х₀ ,
у₀ ),
то расстояние до прямой Ах + Ву + С =0
определяется как

.

Доказательство. Пусть
точка М ₁(х ₁,
у ₁)
– основание перпендикуляра, опущенного
из точки М на заданную прямую. Тогда
расстояние между точками М и М₁ :

Второе
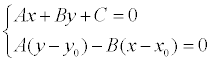
уравнение системы – это уравнение
прямой, проходящей через заданную точку
М ₀ перпендикулярно
заданной прямой. Если преобразовать
первое уравнение системы к виду:

A(x
– x ₀ )
+ B(y – y₀ )
+ Ax₀ +
By₀ +
C = 0,

то,
решая, получим:
Подставляя эти выражения в уравнение
(1), находим:

Угол между двумя прямыми.

.
Угол между двумя прямыми равен углу
между их направляющими векторами. Таким
образом, если вам удастся найти координаты
направляющих векторов a = (x₁;
y₁;
z₁)
и b = (x₂;
y₂;
z₂),
то сможете найти угол. Точнее, косинус
угла по формуле:

Посмотрим,
как эта формула работает на конкретных
примерах:

Угол между двумя прямыми

30
мая 2011

Буду
кратким. Угол между двумя прямыми равен
углу между их направляющими векторами.
Таким образом, если вам удастся найти
координаты направляющих векторов a =
(x₁;
y₁;
z₁)
и b = (x₂;
y₂;
z₂),
то сможете найти угол. Точнее, косинус
угла по формуле:

Посмотрим,
как эта формула работает на конкретных
примерах:

Задача.
В кубе ABCDA₁B₁C₁D₁ отмечены
точки E и F — середины ребер A₁B₁ и
B₁C₁ соответственно.
Найдите угол между прямыми AE и BF.

Поскольку
ребро куба не указано, положим AB = 1.
Введем стандартную систему координат:
начало в точке A, оси x, y, z направим вдоль
AB, AD и AA₁ соответственно.
Единичный отрезок равен AB = 1. Теперь
найдем координаты направляющих векторов
для наших прямых.

Найдем
координаты вектора AE. Для этого нам
потребуются точки A = (0; 0; 0) и E = (0,5; 0; 1).
Поскольку точка E — середина отрезка
A₁B₁,
ее координаты равны среднему арифметическому
координат концов. Заметим, что начало
вектора AE совпадает с началом координат,
поэтому AE = (0,5; 0; 1).

Теперь
разберемся с вектором BF. Аналогично,
разбираем точки B = (1; 0; 0) и F = (1; 0,5; 1), т.к.
F — середина отрезка B₁C₁.
Имеем:
BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1).

Итак,
направляющие векторы готовы. Косинус
угла между прямыми — это косинус угла
между направляющими векторами, поэтому
имеем:

Задача.
В правильной трехгранной призме
ABCA₁B₁C₁,
все ребра которой равны 1, отмечены точки
D и E — середины ребер A₁B₁ и
B₁C₁соответственно.
Найдите угол между прямыми AD и BE.Введем
стандартную систему координат: начало
координат в точке A, ось x направим вдоль
AB, z — вдоль AA₁.
Ось y направим так, чтобы плоскость OXY
совпадала с плоскостью ABC. Единичный
отрезок равен AB = 1. Найдем координаты
направляющих векторов для искомых
прямых.

Для
начала найдем координаты вектора AD.
Рассмотрим точки: A = (0; 0; 0) и D = (0,5; 0; 1),
т.к. D — середина отрезка A₁B₁.
Поскольку начало вектора AD совпадает
с началом координат, получаем AD = (0,5; 0;
1).

Теперь
найдем координаты вектора BE. Точка B =
(1; 0; 0) считается легко. С точкой E —
серединой отрезка C₁B₁ —
чуть сложнее. Имеем:Осталось
найти косинус угла:Задача.
В правильной шестигранной призме
ABCDEFA₁B₁C₁D₁E₁F₁,
все ребра которой равны 1, отмечены точки
K и L — середины ребер A₁B₁ и
B₁C₁ соответственно.
Найдите угол между прямыми AK и BL.Введем
стандартную для призмы систему координат:
начало координат поместим в центр
нижнего основания, ось x направим вдоль
FC, ось y — через середины отрезков AB и
DE, а ось z — вертикально вверх. Единичный
отрезок снова равен AB = 1. Выпишем
координаты интересующих нас точек:Точки
K и L — середины отрезков A₁B₁ и
B₁C₁ соответственно,
поэтому их координаты находятся через
среднее арифметическое. Зная точки,
найдем координаты направляющих векторов
AK и BL:

Теперь
найдем косинус угла:Задача.
В правильной четырехугольной пирамиде
SABCD, все ребра которой равны 1, отмечены
точки E и F — середины сторон SB и SC
соответственно. Найдите угол между
прямыми AE и BF.Введем
стандартную систему координат: начало
в точке A, оси x и y направим вдоль AB и AD
соответственно, а ось z направим
вертикально вверх. Единичный отрезок
равен AB = 1.

Точки
E и F — середины отрезков SB и SC соответственно,
поэтому их координаты находятся как
среднее арифметическое концов. Выпишем
координаты интересующих нас точек:
A
= (0; 0; 0); B = (1; 0; 0)

Координаты
вектора AE совпадают с координатами
точки E, поскольку точка A — начало
координат. Осталось найти косинус угла:

Условия
параллельности и перпендикулярности
прямых

Определение
1.Уравнением
линии на плоскости Oxy называется
уравнение F(x,y)=0,
которому удовлетворяют координаты x и y каждой
точки линии и только они.

Если
из этого уравнения выразить переменную y,
то получится уравнение y=f(x).

Если
линии заданы уравнениями, то точкой
пересечения двух линий называется
любая точка, координаты x и y которой
удовлетворяют уравнениям, т.е. являются
решением системы двух уравнений.

Основные
виды уравнений прямой на плоскости:

1) у=0
– уравнение оси Ох; y=b –
уравнение прямой, параллельной оси Ох;

2) х=0
– уравнение оси Оу; х=а –
уравнение прямой, параллельной оси Оу;

3) y=kх –
уравнение прямой, проходящей через
начало координат, с угловым
коэффициентом k=tga,
где a- угол наклона прямой к оси Oх;

4) y=kх+b – уравнение
прямой с угловым коэффициентом k=tga,
где a- угол наклона прямой с положительным
направлением оси Oх.

y–y₀=k(x–x₀)
– уравнение
прямой, проходящей через точку (x₀,y₀)
и имеющей
угловой коэффициент k.

уравнение
прямой, проходящей через две данные
точки (x₁,y₁)
и (x₂,y₂)
, если x₁¹x₂ и y₁¹y₂.

Определение
1.Уравнение
с двумя переменными Ax + By + C =
0, где A и B не
равны 0 одновременно, называется общим
уравнением прямой на плоскости.

Теорема
1.Любая
прямая на плоскости может быть задана
общим уравнением.

Если
В¹0, то 

т.е. y=кх+b .
При этом:
а)
если А=0, то y=b;

б)
если А=0 и С=0, то y=0;

в)
если С=0, то y=кх .

Если
В=0 и А¹0, то ,
т.е.х=а –
если С¹0 и х=0
– если С=0.

Теорема
доказана.

Точка
пересечения двух прямых A₁x + B₁y + C₁ =
0и A₂x + B₂y + C₂ =
0есть решение системы линейных уравнений

Пусть
две прямые заданы уравнениями с угловыми
коэффициентами y=к₁х+b₁ и y=к₂х+b₂,
т.е. k₁=tga₁ и k₂=tga₂ ,
где a₁ и
a₂ –
углы наклона прямых к оси Ох.

Рассмотрим
угол j=a₂-a₁ –
угол между данными прямыми. Тогда, по
формуле тангенса разности, ,
т.е..

Если
прямые параллельны, то j = 0 , tgj = 0.

Итак, условием
параллельности двух прямых является
равенство их угловых коэффициентов,
т.е. k₁= k₂ .

Если
прямые перпендикулярны, то j = p/2 , ctgj = 0.

Итак, условием
перпендикулярности двух прямых является
равенство k₁× k₂ =-1.

Замечание.Можно
показать, что если две прямые заданы
общими уравнениями A₁x + B₁y + C₁ =
0и A₂x + B₂y + C₂ =
0, то:

условие
параллельности прямых: ;

условие
перпендикулярности прямых: A₁A₂ + B₁B₂ =
0.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #