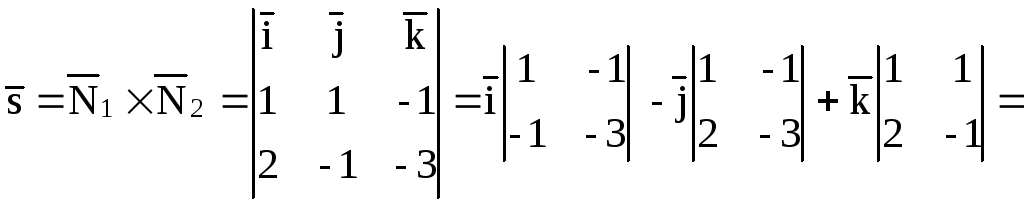Как составить каноническое уравнение прямой в пространстве

Одним из видов уравнений прямой в пространстве является каноническое уравнение. Мы рассмотрим это понятие во всех подробностях, поскольку знать его необходимо для решения многих практических задач.

В первом пункте мы сформулируем основные уравнения прямой, расположенной в трехмерном пространстве, и приведем несколько примеров. Далее покажем способы вычисления координат направляющего вектора при заданных канонических уравнениях и решение обратной задачи. В третьей части мы расскажем, как составляется уравнение прямой, проходящей через 2 заданные точки в трехмерном пространстве, а в последнем пункте укажем на связи канонических уравнений с другими. Все рассуждения будут проиллюстрированы примерами решения задач.

Что такое каноническое уравнение прямой в пространстве

О том, что вообще из себя представляют канонические уравнения прямой, мы уже говорили в статье, посвященной уравнениям прямой на плоскости. Случай с трехмерным пространством мы разберем по аналогии.

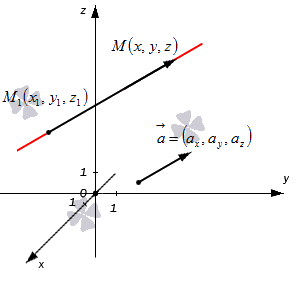
Допустим, у нас есть прямоугольная система координат Oxyz, в которой задана прямая. Как мы помним, задать прямую можно разными способами. Используем самый простой из них – зададим точку, через которую будет проходить прямая, и укажем направляющий вектор. Если обозначить прямую буквой a, а точку M, то можно записать, что M1(x1, y1, z1) лежит на прямой a и направляющим вектором этой прямой будет a→=(ax, ay, az). Чтобы множество точек M(x, y, z) определяло прямую a, векторы M1M→ и a→ должны быть коллинеарными,

Если мы знаем координаты векторов M1M→ и a→, то можем записать в координатной форме необходимое и достаточное условие их коллинеарности. Из первоначальных условий нам уже известны координаты a→. Для того чтобы получить координаты M1M→, нам необходимо вычислить разность между M(x, y, z) и M1(x1, y1, z1). Запишем:

M1M→=x-x1, y-y1, z-z1

После этого нужное нам условие мы можем сформулировать так: M1M→=x-x1, y-y1, z-z1 и a→=(ax, ay, az): M1M→=λ·a→⇔x-x1=λ·axy-y1=λ·ayz-z1=λ·az

Здесь значением переменной λ может быть любое действительное число или ноль. Если λ=0, то M(x, y, z) и M1(x1, y1, z1)совпадут, что не противоречит нашим рассуждениям.

При значениях ax≠0, ay≠0, az≠0 мы можем разрешить относительно параметра λ все уравнения системы x-x1=λ·axy-y1=λ·ayz-z1=λ·az

Между правыми частями после этого можно будет поставить знак равенства:

x-x1=λ·axy-y1=λ·ayz-z1=λ·az⇔λ=x-x1axλ=y-y1ayλ=z-z1az⇔x-x1ax=y-y1ay=z-z1az

В итоге у нас получились уравнения x-x1ax=y-y1ay=z-z1az, с помощью которых можно определить искомую прямую в трехмерном пространстве. Это и есть нужные нам канонические уравнения.

Такая запись используется даже при нулевых значениях одного или двух параметров ax, ay, az, поскольку она в этих случаях она также будет верна. Все три параметра не могут быть равны 0, поскольку направляющий вектор a→=(ax, ay, az) нулевым не бывает.

Если один-два параметра a равны 0, то уравнение x-x1ax=y-y1ay=z-z1az носит условный характер. Его следует считать равным следующей записи:

x=x1+ax·λy=y1+ay·λz=z1+az·λ, λ∈R.

Частные случаи канонических уравнений мы разберем в третьем пункте статьи.

Из определения канонического уравнения прямой в пространстве можно сделать несколько важных выводов. Рассмотрим их.

1) если исходная прямая будет проходить через две точки M1(x1, y1, z1) и M2(x2, y2, z2), то канонические уравнения примут следующий вид:

x-x1ax=y-y1ay=z-z1az или x-x2ax=y-y2ay=z-z2az.

2) поскольку a→=(ax, ay, az) является направляющим вектором исходной прямой, то таковыми будут являться и все векторы μ·a→=μ·ax, μ·ay, μ·az, μ∈R, μ≠0. Тогда прямая может быть определена с помощью уравнения x-x1ax=y-y1ay=z-z1az или x-x1μ·ax=y-y1μ·ay=z-z1μ·az.

Вот несколько примеров таких уравнений с заданными значениями:

Пример 1

x-32=y+1-12=zln 7

Тут x1=3, y1=-1, z1=0, ax=2, ay=-12, az=ln 7.

Пример 2

x-40=y+21=z+10

Тут M1(4, -2, -1), a→=(0, 1, 0).

Мы выяснили, что канонические уравнения вида x-x1ax=y-y1ay=z-z1az будут соответствовать прямой, проходящей через точку M1(x1, y1, z1), а вектор a→=(ax, ay, az) будет для нее направляющим. Значит, если мы знаем уравнение прямой, то можем вычислить координаты ее направляющего вектора, а при условии заданных координат вектора и некоторой точки, расположенной на прямой, мы можем записать ее канонические уравнения.

Разберем пару конкретных задач.

Пример 3

У нас есть прямая, заданная в трехмерном пространстве с помощью уравнения x+14=y2=z-3-5. Запишите координаты всех направляющих векторов для нее.

Решение

Чтобы получить координаты направляющего вектора, нам надо просто взять значения знаменателей из уравнения. Мы получим, что одним из направляющих векторов будет a→=(4, 2, -5), а множество всех подобных векторов можно сформулировать как μ·a→=4·μ, 2·μ, -5·μ. Здесь параметр μ – любое действительное число (за исключением нуля).

Ответ: 4·μ, 2·μ, -5·μ, μ∈R, μ≠0

Пример 4

Запишите канонические уравнения, если прямая в пространстве проходит через M1(0, -3, 2) и имеет направляющий вектор с координатами -1, 0, 5.

Решение

У нас есть данные, что x1=0, y1=-3, z1=2, ax=-1, ay=0, az=5. Этого вполне достаточно, чтобы сразу перейти к записи канонических уравнений.

Сделаем это:

x-x1ax=y-y1ay=z-z1az⇔x-0-1=y-(-3)0=z-25⇔⇔x-1=y+30=z-25

Ответ: x-1=y+30=z-25

Эти задачи – самые простые, потому что в них есть все или почти все исходные данные для записи уравнения или координат вектора. На практике чаще можно встретить те, в которых сначала нужно находить нужные координаты, а потом записывать канонические уравнения. Примеры таких задач мы разбирали в статьях, посвященных нахождению уравнений прямой, проходящей через точку пространства параллельно заданной, а также прямой, проходящей через некоторую точку пространства перпендикулярно плоскости.

Канонические уравнения с одним или двумя a, равными нулю

Ранее мы уже говорили, что одно-два значения параметров ax, ay, az в уравнениях могут иметь нулевые значения. При этом запись x-x1ax=y-y1ay=z-z1az=λ приобретает формальный характер, поскольку мы получаем одну или две дроби с нулевыми знаменателями. Ее можно переписать в следующем виде (при λ∈R):

x=x1+ax·λy=y1+ay·λz=z1+az·λ

Рассмотрим эти случаи подробнее. Допустим, что ax=0, ay≠0, az≠0, ax≠0, ay=0, az≠0, либо ax≠0, ay≠0, az=0. В таком случае нужные уравнения мы можем записать так:

В первом случае:
x-x10=y-y1ay=z-z1az=λ⇔x-x1=0y=y1+ay·λz=z1+az·λ⇔x-x1=0y-y1ay=z-z1az=λ
Во втором случае:
x-x1ax=y-y10=z-z1az=λ⇔x=x1+ax·λy-y1=0z=z1+az·λ⇔y-y1=0x-x1ax=z-z1az=λ
В третьем случае:
x-x1ax=y-y1ay=z-z10=λ⇔x=x1+ax·λy=y1+ay·λz-z1=0⇔z-z1=0x-x1ax=y-y1ay=λ

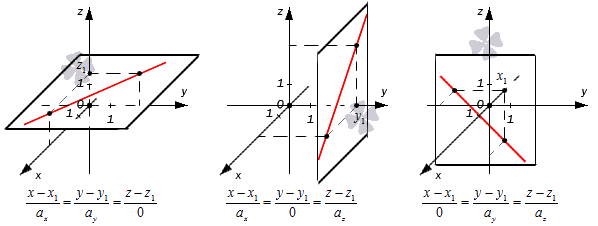
Получается, что при таком значении параметров нужные прямые находятся в плоскостях x-x1=0, y-y1=0 или z-z1=0, которые располагаются параллельно координатным плоскостям (если x1=0, y1=0 либо z1=0). Примеры таких прямых показаны на иллюстрации.

Следовательно, мы сможем записать канонические уравнения немного иначе.

В первом случае: x-x10=y-y10=z-z1az=λ⇔x-x1=0y-y1=0z=z1+az·λ, λ∈R
Во втором: x-x10=y-y1ay=z-z10=λ⇔x-x1=0y=y1+ay·λ, λ∈Rz-z1=0
В третьем: x-x1ax=y-y10=z-z10=λ⇔x=x1+ax·λ, λ∈Ry=y1=0z-z1=0

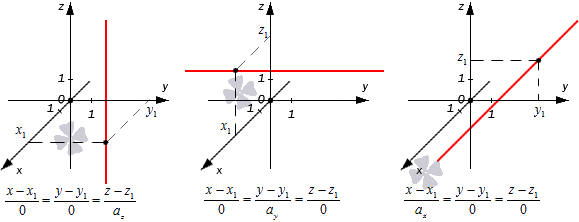
Во всех трех случаях исходные прямые будут совпадать с координатными осями или окажутся параллельными им: x1=0y1=0, x1=0z1=0, y1=0z1=0. Их направляющие векторы имеют координаты 0, 0, az, 0, ay, 0, ax, 0, 0. Если обозначить направляющие векторы координатных прямых как i→, j→, k→, то направляющие векторы заданных прямых будут коллинеарными по отношению к ним. На рисунке показаны эти случаи:

Покажем на примерах, как применяются эти правила.

Пример 5

Найдите канонические уравнения, с помощью которых можно определить в пространстве координатные прямые Oz, Ox, Oy.

Решение

Координатные векторы i→=(1, 0, 0), j→=0, 1, 0, k→=(0, 0, 1) будут для исходных прямых направляющими. Также мы знаем, что наши прямые будут обязательно проходить через точку O(0, 0, 0), поскольку она является началом координат. Теперь у нас есть все данные, чтобы записать нужные канонические уравнения.

Для прямой Ox: x1=y0=z0

Для прямой Oy: x0=y1=z0

Для прямой Oz: x0=y0=z1

Ответ: x1=y0=z0, x0=y1=z0, x0=y0=z1.

Пример 6

В пространстве задана прямая, которая проходит через точку M1(3, -1, 12). Также известно, что она расположена параллельно оси ординат. Запишите канонические уравнения этой прямой.

Решение

Учитывая условие параллельности, мы можем сказать, что вектор j→=0, 1, 0 будет для нужной прямой направляющим. Следовательно, искомые уравнения будут иметь вид:

x-30=y-(-1)1=z-120⇔x-30=y+11=z-120

Ответ: x-30=y+11=z-120

Как записать каноническое уравнение прямой, которая проходит через две заданные точки

Допустим, что у нас есть две несовпадающие точки M1(x1, y1, z1) и M2(x2, y2, z2), через которые проходит прямая. Как в таком случае мы можем сформулировать для нее каноническое уравнение?

Для начала примем вектор M1M2→ (или M2M1→) за направляющий вектор данной прямой. Поскольку у нас есть координаты нужных точек, сразу вычисляем координаты вектора:

M1M2→=x2-x1, y2-y1, z2-z1

Далее переходим непосредственно к записи канонического уравнения, ведь все нужные данные у нас уже есть. Исходная прямая будет определяться записями следующего вида:

x-x1x2-x1=y-y1y2-y1=z-z1z2-z1x-x2x2-x1=y-y2y2-y1=z-z2z2-z1

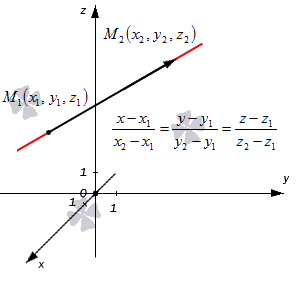
Получившиеся равенства – это и есть канонические уравнения прямой, проходящей через две заданные точки. Взгляните на иллюстрацию:

Приведем пример решения задачи.

Пример 7

в пространстве есть две точки с координатами M1(-2, 4, 1) и M2(-3, 2, -5), через которые проходит прямая. Запишите канонические уравнения для нее.

Решение

Согласно условиям, x1=-2, y1=-4, z1=1, x2=-3, y2=2, z2=-5. Нам требуется подставить эти значения в каноническое уравнение:

x-(-2)-3-(-2)=y-(-4)2-(-4)=z-1-5-1⇔x+2-1=y+46=z-1-6

Если мы возьмем уравнения вида x-x2x2-x1=y-y2y2-y1=z-z2z2-z1, то у нас получится: x-(-3)-3-(-2)=y-22-(-4)=z-(-5)-5-1⇔x+3-1=y-26=z+5-6

Ответ: x+3-1=y-26=z+5-6 либо x+3-1=y-26=z+5-6.

Преобразование канонических уравнений прямой в пространстве в другие виды уравнений

Иногда пользоваться каноническими уравнениями вида x-x1ax=y-y1ay=z-z1az не очень удобно. Для решения некоторых задач лучше использовать запись x=x1+ax·λy=y1+ay·λz=z1+az·λ. В некоторых случаях более предпочтительно определить нужную прямую с помощью уравнений двух пересекающихся плоскостей A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0. Поэтому в данном пункте мы разберем, как можно перейти от канонических уравнений к другим видам, если это требуется нам по условиям задачи.

Понять правила перехода к параметрическим уравнениям несложно. Сначала приравняем каждую часть уравнения к параметру λ и разрешим эти уравнения относительно других переменных. В итоге получим:

x-x1ax=y-y1ay=z-z1az⇔x-x1ax=y-y1ay=z-z1az⇔⇔x-x1ax=λy-y1ay=λz-z1az=λ⇔x=x1+ax·λy=y1+ay·λz=z1+az·λ

Значение параметра λ может быть любым действительным числом, ведь и x, y, z могут принимать любые действительные значения.

Пример 8

В прямоугольной системе координат в трехмерном пространстве задана прямая, которая определена уравнением x-23=y-2=z+70. Запишите каноническое уравнение в параметрическом виде.

Решение

Сначала приравниваем каждую часть дроби к λ.

x-23=y-2=z+70⇔x-23=λy-2=λz+70=λ

Теперь разрешаем первую часть относительно x, вторую – относительно y, третью – относительно z. У нас получится:

x-23=λy-2=λz+70=λ⇔x=2+3·λy=-2·λz=-7+0·λ⇔x=2+3·λy=-2·λz=-7

Ответ: x=2+3·λy=-2·λz=-7

Следующим нашим шагом будет преобразование канонических уравнений в уравнение двух пересекающихся плоскостей (для одной и той же прямой).

Равенство x-x1ax=y-y1ay=z-z1az нужно для начала представить в виде системы уравнений:

x-x1ax=y-y1ayx-x1ax=z-z1axy-y1ay=z-z1az

Поскольку pq=rs мы понимаем как p·s=q·r, то можно записать:

x-x1ax=y-y1ayx-x1ax=z-z1azy-y1ay=z-z1az⇔ay·(x-x1)=ax·(y-y1)az·(x-x1)=ax·(z-z1)az·(y-y1)=ay·(z-z1)⇔⇔ay·x-ax·y+ax·y1-ay·x1=0az·x-ax·z+ax·z1-az·x1=0az·y-ay·z+ay·z1-az·y1=0

В итоге у нас вышло, что:

x-x1ax=y-y1ay=z-z1az⇔ay·x-ax·y+ax·y1-ay·x1=0az·x-ax·z+ax·z1-az·x1=0az·y-ay·z+ay·z1-az·y1=0

Выше мы отмечали, что все три параметра a не могут одновременно быть нулевыми. Значит, ранг основной матрицы системы будет равен 2, поскольку ay-ax0az0-ax0az-ay=0 и один из определителей второго порядка не равен 0:

ay-axaz0=ax·az, ay0az-ax=ax·ay, -ax00-ax=ax2ay-ax0az=ay·az, ay00-ay=-ay2, -ax0az-ay=ax·ayaz00az=az2, az-ax0-ay=-ay·az, 0-axaz-ay=ax·az

Это дает нам возможность исключить одно уравнение из наших расчетов. Таким образом, канонические уравнения прямой можно преобразовать в систему из двух линейных уравнений, которые будут содержать 3 неизвестных. Они и будут нужными нам уравнениями двух пересекающихся плоскостей.

Рассуждение выглядит довольно сложным, однако на практике все делается довольно быстро. Продемонстрируем это на примере.

Пример 9

Прямая задана каноническим уравнением x-12=y0=z+20. Напишите для нее уравнение пересекающихся плоскостей.

Решение

Начнем с попарного приравнивания дробей.

x-12=y0=z+20⇔x-12=y0x-12=z+20y0=z+20⇔⇔0·(x-1)=2y0·(x-1)=2·(z+2)0·y=0·(z+2)⇔y=0z+2=00=0

Теперь исключаем из расчетов последнее уравнение, потому что оно будет верным при любых x, y и z. В таком случае x-12=y0=z+20⇔y=0z+2=0.

Это и есть уравнения двух пересекающихся плоскостей, которые при пересечении образуют прямую, заданную с помощью уравнения x-12=y0=z+20

Ответ: y=0z+2=0

Пример 10

Прямая задана уравнениями x+12=y-21=z-5-3, найдите уравнение двух плоскостей, пересекающихся по данной прямой.

Решение

Приравниваем дроби попарно.

x+12=y-21=z-5-3⇔x+12=y-21x+12=z-5-3y-21=z-5-3⇔⇔1·(x+1)=2·(y-2)-3·(x+1)=2·(z-5)-3·(y-2)=1·(z-5)⇔x-2y+5=03x+2z-7=03y+7-11=0

Получаем, что определитель основной матрицы полученной системы будет равен 0:

1-20302031=1·0·1+(-2)·2·0+0·3·3-0·0·0-1·2·3-(-2)·3·1=0

Минор второго порядка нулевым при этом не будет: 1-230=1·0-(-2)·3=6. Тогда мы можем принять его в качестве базисного минора.

В итоге мы можем вычислить ранг основной матрицы системы x-2y+5=03x+2z-7=03y+z-11=0. Это будет 2. Третье уравнение исключаем из расчета и получаем:

x-2y+5=03x+2z-7=03y+z-11=0⇔x-2y+5=03x+2z-7=0

Ответ: x-2y+5=03x+2z-7=0

Источник

3.1. Канонические
уравнения прямой.

Пусть в системе
координат Oxyz
дана прямая, которая проходит через
точку

(см. рис.18).Обозначим через
вектор, параллельный данной прямой.
Векторназываетсянаправляющим
вектором прямой.
Возьмем на прямой точку и рассмотрим вектор
Векторыколлинеарны, следовательно, их
соответствующие координаты пропорциональны:

(3.3.1)

Эти уравнения
называются каноническими
уравнениями прямой.

Пример: Написать
уравнения прямой, проходящей через
точку M(1,
2, –1) параллельно вектору

Решение:
Вектор
является направляющим вектором искомой
прямой. Применяя формулы (3.1.1), получим:

Это канонические
уравнения прямой.

Замечание:
Обращение в нуль одного из знаменателей
означает обращение в нуль соответствующего
числителя, то есть y
– 2 = 0; y
= 2. Данная прямая лежит в плоскости y
= 2, параллельной плоскости Oxz.

3.2.
Параметрические
уравнения прямой.

Пусть прямая
задана каноническими уравнениями

Обозначим тогдаВеличина t
называется параметром и может принимать
любые значения:
.

Выразим x,
y
и z
через t
:

(3.2.1)

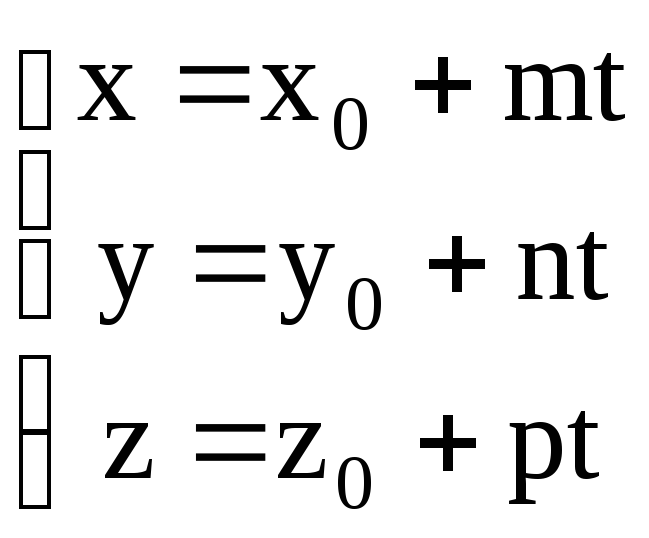
Полученные уравнения
называются параметрическими
уравнениями прямой.

Пример 1:
Составить
параметрические уравнения прямой,
проходящей через точку M
(1, 2, –1) параллельно вектору

Решение:
Канонические уравнения этой прямой
получены в примере пункта 3.1:

Для нахождения
параметрических уравнений прямой
применим вывод формул (3.2.1):

Итак,
– параметрические уравнения данной
прямой.

Ответ:

Пример 2.
Составить
параметрические уравнения прямой,
проходящей через точку M
(–1, 0, 1) параллельно вектору
гдеA
(2, 1, –1), B
(–1, 3, 2).

Решение:
Вектор является направляющим
вектором искомой прямой.

Найдем вектор .

= (–3; 2; 3). По формулам
(3.2.1) запишем уравнения прямой:

– это искомые
параметрические уравнения прямой.

3.3. Уравнения
прямой, проходящей через две заданные
точки.

Через две заданные
точки в пространстве проходит единственная
прямая (см. рис.20). Пусть даны точки
Векторможно принять за направляющий вектор
данной прямой. Тогда уравнения прямой
находим
по формулам (3.1.1):).

(3.3.1)

Пример 1.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки

Решение:

Применяем
формулу (3.3.1)

Получили канонические
уравнения прямой. Для получения
параметрических уравнений применим
вывод формул (3.2.1). Получим

– это параметрические
уравнения прямой.

Пример 2.
Составить канонические и параметрические
уравнения прямой, проходящей через
точки

Решение:

По формулам
(3.3.1) получим:

Это канонические
уравнения.

Переходим к
параметрическим уравнениям:

– параметрические
уравнения.

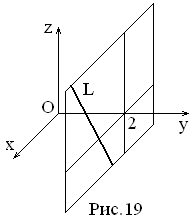
Полученная прямая
параллельна оси oz
(см. рис.21).

3.4. Прямая как
линия пересечения двух плоскостей.

Пусть в
пространстве даны две плоскости

Если эти плоскости
не совпадают и не параллельны, то они
пересекаются по прямой:

Эта система двух
линейных уравнений задает прямую как
линию пересечения двух плоскостей. От
уравнений (3.4.1) можно перейти к каноническим
уравнениям (3.1.1) или параметрическим
уравнениям (3.2.1). Для этого необходимо
найти точку
лежащую на прямой, и направляющий векторКоординаты точкиполучим из системы (3.4.1), придав одной
из координат произвольное значение
(например,z
= 0). За направляющий вектор
можно взять векторное произведение
векторовто есть

Пример 1.
Составить
канонические уравнения прямой

Решение: Пусть
z
= 0. Решим систему

Сложив эти уравнения,
получим: 3x
+ 6 = 0
x
= –2. Подставим найденное значение x
= –2 в первое уравнение системы и получим:
–2 + y
+ 1 = 0
y
= 1.

Итак, точка
лежит на искомой прямой.

Для нахождения
направляющего вектора прямой запишем
нормальные векторы плоскостей:
и найдем их векторное произведение:

Уравнения прямой
находим по формулам (3.1.1):

Ответ: .

Другой способ:
Канонические и параметрические
уравнения прямой (3.4.1) легко получить,
найдя две различные точки на прямой из
системы (3.4.1), а затем применив формулы
(3.3.1) и вывод формул (3.2.1).

Пример 2.
Составить канонические и параметрические
уравнения прямой

Решение:
Пусть y
= 0. Тогда система примет вид:

Сложив уравнения,
получим: 2x
+ 4 = 0; x
= –2. Подставим x
= –2 во второе уравнение системы и
получим: –2 –z
+1 = 0
z
= –1. Итак, нашли точку

Для нахождения
второй точки положим x
= 0. Будем иметь:

То есть

Далее применяем
формулы (3.3.1):

Получили канонические
уравнения прямой.

Составим
параметрические уравнения прямой:

Ответ:

; .

3.5. Взаимное
расположение двух прямых в пространстве.

Пусть прямые
заданы уравнениями:

;: .

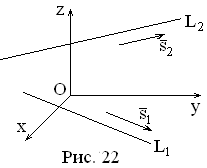
Под углом между
этими прямыми понимают угол между их
направляющими векторами
(см. рис.22). Этот уголнаходим по формуле из векторной алгебры:

или

(3.5.1)

Если прямые перпендикулярны
(),то
Следовательно,

(3.5.2)

Это условие
перпендикулярности двух прямых в
пространстве.

Если прямые
параллельны (),то их направляющие
векторы коллинеарны (),
то есть

(3.5.3)

Это условие
параллельности двух прямых в пространстве.

Пример 1. Найти
угол между прямыми:

а).
и

б). и

Решение:
а). Запишем направляющий вектор прямой
Найдем направляющий векторвторой прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему

Затем найдем их векторное произведение:

(см. пример 1
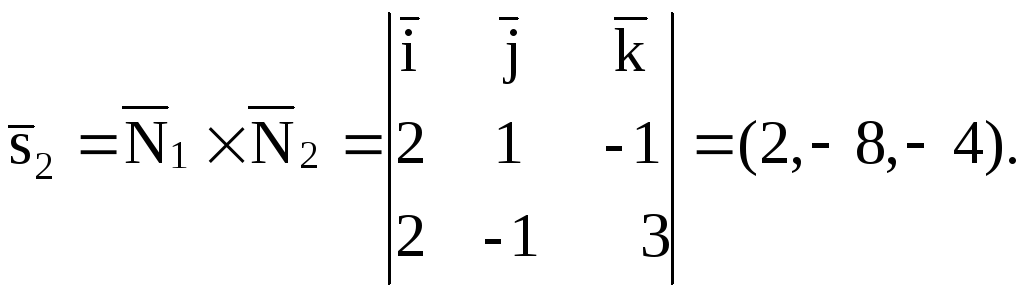
пункта 3.4).

По формуле (3.5.1)
получим:

Следовательно,

б). Запишем
направляющие векторы данных прямых:
Векторыколлинеарны, так как их соответствующие
координаты пропорциональны:

Значит прямые
параллельны (),
то есть

Ответ: а).
б).

Пример 2. Доказать
перпендикулярность прямых:

Решение:
Запишем направляющий вектор первой
прямой

Найдем направляющий
вектор
второй прямой. Для этого находим
нормальные векторыплоскостей, входящих в систему:

Вычислим их векторное произведение:

(См. пример 1пункта 3.4).

Применим условие
перпендикулярности прямых (3.5.2):

Условие выполнено;
следовательно, прямые перпендикулярны
().

Соседние файлы в предмете Математика

#
#
#
#
#
#
#
#
#
03.03.20154.96 Кб8Содержание OneNote.onetoc2
#

Источник

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Существует несколько различных типов уравнений, описывающих кривую первого порядка, называемую прямой. Каждый из них оптимален для какой-то своей цели. Давайте познакомимся с ними поближе.

Каноническое уравнение прямой в пространстве

Определение 1

Канонический вид уравнения прямой в пространстве выглядит как следующее равенство:

$frac{x – x_0}{α} = frac{y – y_0}{β} = frac{z – z_0}{γ}$,

где буквы $(x_0, y_0, z_0)$ используются для обозначения координат любой точки, возлежащей на данной прямой, а $(α, β, γ)$ — координаты направляющего эту прямую вектора, как несложно догадаться, они не могут быть нулевыми.

Не во всех случаях удобно и практично пользоваться каноническим уравнением, поэтому частенько возникает надобность использовать какое-то другое, например, можно прибегнуть к параметрическому.

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

Для каких прямых не представляется возможным или нельзя написать каноническое уравнение?

Глядя на это уравнение, видно, что его возможно использовать только в том случае, если координаты направляющих векторов исследуемых прямых не равны нулю, для таких прямых стоит воспользоваться параметрическими уравнениями.

Определение 2

Параметрический вид уравнений прямой в пространстве такой:

$begin{cases} x = x_1 + α cdot λ \ y = y_1 + β cdot λ \ z = z_1 + γ cdot λ \ end{cases}$,

где $x_1, y_1, z_1$ — координаты некоторой точки, находящейся на описываемой прямой, $α, β, γ$ — координаты параллельного или лежащего на данной прямой вектора, $λ$ — произвольное число-коэффициент, иногда для его обозначения используют слово “параметр”.

Параметрическое уравнение как раз удобно применять если одна из координат направляющего вектора равна нулю.

Чтобы произвести переход от параметрического вида уравнения к каноническому виду уравнения прямой в пространстве, осуществите вывод канонического уравнения прямой из параметрического.

«Каноническое уравнение прямой в пространстве» 👇

Для этого следует в к каждом уравнении перенести $λ$ в левую часть, а затем приравнять уравнения. Никакой магии, а только самая что ни на есть пресловутая арифметика:

$begin{cases} λ = frac{x – x_1}{ α} \ λ = frac{y – y_1}{β} \ λ = frac{z – z_1}{γ} \ end{cases}$

$frac{x – x_0}{α} = frac{y – y_0}{β} = frac{z – z_0}{γ}$

Уравнение прямой, образуемой пересечением двух плоскостей

Рисунок 1. Связь канонического и общего уравнения прямой

Для того чтобы составить каноническое уравнение прямой в пространстве, заданной пересечением плоскостей, необходимо познакомиться поближе с 2 исследуемыми плоскостями.

Любую плоскость, находящуюся в пространстве, можно описать с помощью равенства:

$Ax + By + Cz + D = 0$,

где $A, B, C$ и $D$ – постоянные, причём $A, B, C$ не могут быть одновременно все нулевыми.

Соответственно, не нужно быть гением, чтобы понять, что если две плоскости пересечены между собой, то на их общей части будет возлежать некая прямая. Чтобы её найти, нужно получить общее решение следующей системы уравнений:

$begin{cases} A_1x + B_1y + C_1z + D_1 = 0 \ A_2x + B_2y + C_2z + D_2 = 0 \ end{cases}$

С помощью же частного решения этой системы уравнений можно узнать, принадлежит ли какая-либо точка трёхмерной системы координат описанным уравнениями плоскостям и, конечно же, нашей прямой. Для этого нужно просто подставить её икс, игрек и зет в систему.

Приведённая система уравнений является своеобразной “формулой”, служащей для нахождения общего уравнения прямой в пространстве.

Иногда в каких-либо практических задачах требуется получить из уравнения прямой в пространстве в общем виде параметрические или канонические уравнения, тогда в первую очередь вам стоит узнать координаты её направляющего вектора и какую-либо точку, находящуюся на изучаемой прямой.

Ну что ж, давайте решать нашу задачу. На первом этапе вычислим $x, y, z$ для направляющего вектора.

Найдём нормальные вектора для плоскостей. Если кто забыл, нормальный вектор — это такой вектор, который является перпендикулярным (ортогональным) к данной плоскости или прямой.

Для этого из нашего очаровательного примера системы уравнений необходимо взять коэффициенты из уравнений. В итоге для 1-ой плоскости вектор-нормаль будет выглядеть как $(A_1; B_1; C_1)$, а для второй как $(A_2; B_2; C_2)$.

Теперь необходимо перемножить оба вектора и получить их произведение, здесь $(i, j, k)$ – координаты единичного вектора.

$overline{a} = [overline{n} cdot overline{n}] = left| begin{array}{ccc} overline{i} & overline{j} & overline{k} \ A_1 & B_1 & C_1 \ A_2 & B_2 & C_2 \ end{array} right| = overline{i} cdot left| begin{array}{cc}\B_1 & C_1 \ B_2 & C_2\ end{array} right| – overline{j} cdot left| begin{array}{cc}\ A_1 & C_1 \ A_2 & C_2 \ end{array} right| + overline{k} cdot left| begin{array}{cc} \ A_1 & B_1 \ A_2 & B_2 \ end{array} right| $

$|overline{n} cdot overline{n}| = overline{i} cdot (B_1 cdot C_2 – C_1 cdot B_2) – overline{j} cdot (A_1 cdot C_2 – A_2 cdot C_1) + overline{k} cdot (A_1 cdot B_2 – A_2 cdot B_1)$

Следующим этапом выполняем поиск координат точки, возлежащей на искомой прямой.

Для выполнения этого наиболее “сложного” пункта необходимо выбрать одну наиболее нравящуюся вам координату $x, y$ или $z$ и вместо неё подставить в систему уравнений, описывающую плоскости, нулевое значение.

Пример 1

Составьте каноническое уравнение прямой, получаемой из системы уравнений, описывающей пару пересечённых плоскостей:

$begin{cases} 2x – y + 3z + 4 = 0 \ x + 5y – 3z – 7 = 0 \ end{cases}$

Найдём направляющий вектор, для этого сначала запишем вектора нормалей плоскостей:

$overline{n_1}(2;-1;3), overline{n_2}(1;-5;-3)$

Ну а сейчас пора вычислить сам направляющий вектор:

$overline{a} = left| begin{array}{ccc} overline{i} & overline{j} & overline{k} \ 2 & -1 & 3 \ 1 & 5 & -3 \ end{array} right| = overline{i} cdot left| begin{array}{cc}\ -1 & 3 \ 5 & -3\ end{array} right| – overline{j} cdot left| begin{array}{cc}\ 2 & 3 \ 1 & -3 \ end{array} right| + overline{k} cdot left| begin{array}{cc} \ 2 & -1 \ 1 & 5 \ end{array} right| $

$overline{a} = (3 – 15) cdot overline{i} – (-6-3) cdot overline{j} + (10 +1) cdot overline{k} = -12 overline{i} + 9 overline{j} + 11 overline{k}$

Найдём точку, находящуюся на нашей прямой, тут всё просто, приравняем $y$ к нулю и внедрим в нашу систему уравнений:

$begin{cases} 2x + 3z + 4 = 0 \ x – 3z – 7 = 0 \ end{cases}$

Решение вышеприведённой системы уравнений будет: $x = 1, z = -2$, то есть координаты точки, возлежащей на нашей прямой, будут $(1; 0; -2)$.

Подставим все полученные нами цифры и получим следующее уравнение:

$frac{x-1}{-12} = frac{y}{9} = frac{z+2}{11}$

Составление канонического уравнения прямой по координатам двух точек

На практике это очень распространённая и любимая во многих вузах и других учебных заведениях задача — нужно найти уравнение прямой в пространстве, проходящей через 2 точки. Примем заранее, что эти две точки не обладают одинаковыми $x, y, z$.

Для того чтобы написать уравнение прямой в пространстве, проходящей через 2 точки, воспользуйтесь координатами ваших точек и внедрите их в следующее уравнение:

$frac{x – x_1}{x2 – x_1} = frac{y – y_1}{y_2 – y_1} = frac{z – z_1}{z_2 – z_1}$

Это уравнение можно вывести из параметрического уравнения прямой.

Допустим, у нас есть две точки с координатами $(x_1; y_1; z_1)$, и для второй $(x_2; y_2; z_2)$.

Найти направляющий вектор для изучаемой прямой при наличии пары точек несложно, вектор с координатами $(x_2 – y_1; y_2 – y_2;z_2 – z_2)$ и будет желаемой частью результата.

Придумаем точку, находящуюся на нашей прямой, пусть она будет обладать координатами $(x_1;y_1;z_1)$.

Помещаем обнаруженные нами координаты вектора и точки в каноничное уравнение прямой в пространстве и получим уравнение прямой, проходящей через 2 точки.

Если же необходимо выразить именно параметрические уравнения из координат двух точек, через которые проведена некая одна прямая, то тут тоже всё довольно просто и без неожиданностей:

$begin{cases} x = x_1 + (x_2 – x_1) cdot λ \ y = y_1 + (y_2 – y_1)cdot λ \ z = z_1 + (z_2 – z_1) cdot λ \ end{cases}$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Прямая в пространстве – это линия, которая проходит от одной точки к другой, а также за пределы этих точек в бесконечность. Есть несколько видов уравнения прямой в пространстве: каноническое, параметрическое, угол между двумя прямыми в пространстве и т. д. Про это расскажем в данной статье и для наглядности предоставим несколько примеров.

Параметрическое и каноническое уравнение прямой в пространстве
Уравнение прямой в пространстве, которая проходит через две заданные точки
Общее уравнение прямой – переход к каноническому уравнению
Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых
Примеры решения задач

Параметрическое и каноническое уравнение прямой в пространстве

Параметрическое и каноническое уравнение прямой рассматривается практически так, как и для прямой на плоскости. Значит, нужно составить уравнение прямой , которая проходит через данную точку $M_{1} (x_{1}, y_{1}, z_{1})$ параллельно направляющему вектору .

Пусть, – произвольная точка прямой, тогда векторы $overline{M_{1}M} = (x - x_{1}, y - y_{1}, z - z_{1})$ и коллинеарные, а это значит, что координаты их пропорциональны, поэтому получаем:

${x - x_{1}over{l}} = {y - y_{1}over{m}} = {z - z_{1}over{p}}$

(1)

это и есть канонические уравнения прямой.

Приравнивая каждую из дробей (1) к параметру , запишем параметрические уравнения прямой:

$left{ begin{aligned} x = lt + x_{0}\ y = mt + y_{0}\ z = pt + z_{0} end{aligned}$

(2)

Уравнение прямой в пространстве, которая проходит через две заданные точки

Уравнение прямой в пространстве – тема очень лёгкая, так как здесь самое важное – знать нужную формулу. Тогда легко можно решить любую задачу.

Итак, через две точки $M_{1}(x_{1}, y_{1}z_{1}$ и $M_{2}(x_{2}, y_{2}, z_{2})$ можно не только геометрично провести линию, но и сложить её уравнения.

За направляющий вектор возьмём $overline{S} = overline{M_{1}M} = (x_{2} - x_{1}, y_{2} - y_{1}, z_{2} - z_{1})$ , тогда по формуле (1) у нас получается:

${x - x_{1}over{x_{2} - x_{1}}} = {y - y_{1}over{y_{2} - y_{1}}} = {z - z_{1}over{z_{2} - z_{1}}}$

(3)

уравнение прямой в пространстве, которые проходят через две заданные точки.

Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Общее уравнение прямой – переход к каноническому уравнению

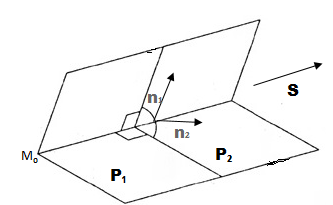
Объяснение про общее уравнение прямой начнём с прямой, которая задана двумя плоскостями, что пересекаются по этой прямой.

Пусть известны их уравнения:

$left{begin{aligned}A_{1}x + B_{1}y + C_{1}z + D_{1} = 0\A_{2}x + B_{2}y + C{2}z + D_{2} = 0 end{aligned}$

(4)

Тогда система (4) называется общим уравнением прямой.

Чтобы перейти к каноническим уравнениям вида (1), необходимо найти вектор и точку $M_{0}$ этой прямой.

Точку $M_{0}$ находим, как один из решений системы (4). Например, положив в (4) находим $x_{0}, y_{0}$ , тогда и точку $M_{0} (x_{0}, y_{0}, 0)$ . Направляющий вектор , который параллелен к каждой из плоскостей $P_{1}$ и $P_{2}$ и перпендикулярен к их нормальным векторам $overline{n_{1}} = (A_{1}, B_{1}, C_{1})$ и $overline{n_{2}} = (A_{2}, B_{2}, C_{2})$ , то есть $overline{S}perp{overline{n_{1}}}$ , $overline{S}perp{overline{n_{2}}}$ . (см. рис. 1). Поэтому вектор можно найти при помощи векторного произведения $overline{n_{1}}$ и $overline{n_{2}}$

= $overline{n}_{1}$ x $overline{n}_{2}$ = $begin{vmatrix} overline{i}&overline{j}&overline{k}\ A_{1}&B_{1}&C_{1}\ A_{2}&B_{2}&C_{2} end{vmatrix}$

Найдены координаты $M_{0}$ и подставим в каноническое уравнение (1).

Например, от общих уравнений прямой:

$left{begin{aligned} 2x + 7y - z - 4 = 0\ 4x - 9y - 2z - 8 = 0 end{aligned}$

Перейдём к каноническим, положив в системе (при нём относительно больше коэффициенты). найдём $x = 2, z = 0, M_{0} (2, 0, 0)$ . Нормальные векторы $overline{n_{1}} = (2, 7, -1)$ и $overline{n_{2}} = (4, -9, -2)$ . Тогда направляющий вектор

Рис. 1

$overline{S} = overline{n}_{1}$ x $overline{n}_{2}$ = $begin{vmatrix} overline{i}&overline{j}&overline{k}\ 2&7&-1\ 4&-9&-2 end{vmatrix} = -23overline{i} - 0overline{j} - 46overline{k}$ ,

и канонические уравнения станут:

Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых

Угол между двумя прямыми :

${x - x_{1}over{l_{1}}} = {y - y_{1}over{m_{1}}} = {z - z_{1}over{p_{1}}}$ и ${x - x_{2}over{l_{2}}} = {y - y_{2}over{m_{2}}} = {z - z_{2}over{p_{2}}}$

равен углу между их направляющими векторами $overline{S_{1}} = (l_{1}, m_{1}, p_{1})$ и $overline{S_{2}} = (l_{2}, m_{2}, p_{2})$ , поэтому

${cosvarphi = cos(overline{S}_{1}}, overline{S}_{2}})$ = ${l_{1}l_{2} + m_{1}m_{2} + p_{1}p_{2}}over{sqrt{l_{1}^2 + m_{1}^2 + p_{1}^2}} * {sqrt{l_{2}^2 + m_{2}^2 + p_{2}^2}}$

(5)

Условия параллельности и перпендикулярности прямых соответственно запишутся:

${l_{1}over{l_{2}}} = {m_{1}over{m_{2}}} = {p_{1}over{p_{2}}}$ и $l_{1}l_{2} + m_{1}m_{2} + p_{1}p_{2} = 0$ .

(6)

Примеры решения задач

Давайте рассмотрим первый пример, где можно двумя способами построить прямую:

Задача

При точке и направляющем векторе необходимо:

составить каноническое уравнение прямой;
построить эту прямую.

Решение

1) По формуле (1) запишем каноническое уравнение прямой :

= .

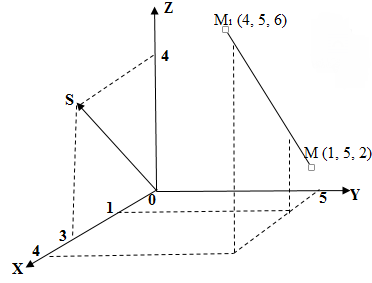
2) Рассмотрим два способа построения прямой .

Первый способ

В системе координат строим вектор и точку и проводим через точку прямую параллельную вектору .

Второй способ

По формуле (2) запишем каноническое уравнение прямой в параметрическом виде:

$left{begin{aligned} x = 3t + 1\ y = 0 * t + 5\ z = 4t + 2 end{aligned} right$

На рисунке видно, что при произвольных значениях из системы находим координаты соответствующих точек, которые принадлежат прямой . Так при находим координаты $M_{1}(4, 5, 6)$ . Через две точки и $M_{1}$ проводим прямую .

Очевидно, что найти острый угол между прямыми совершенно не сложно при знании темы и определённых формул. Давайте разберём такой пример:

Задача

Найти острый угол между прямыми:

(7)

Решение

По формуле (7) получаем:

= ${6 * (-2) + (-2)(-1) + 3 * (-2)}over{sqrt{6^2 + (-2)^2 + 3^2} * sqrt{(-2)^2 + (-1)^2 + (-2)^2}$ = =

Так как , тогда угол тупой, , а острый угол .

Ответ

Рассмотрим последний пример, где нужно составить уравнение. Здесь, как и в каждой задаче, важно знать и понимать, какой формулой нужно воспользоваться.

Задача

Составить уравнение прямой , которая проходит через точку и параллельна прямой .

Решение

От параметрического уравнения переходим к каноническому При условии параллельности прямых $overline{S}||overline{S_{1}}$ то есть направляющим вектором новой прямой может служить известный вектор и по формуле (1) у нас получается:

Ответ

Источник

Уравнения прямых в пространстве

Уравнение прямой как линии пересечения двух плоскостей

Пусть в координатном пространстве Oxyz (в прямоугольной системе координат) две плоскости заданы общими уравнениями

$begin{aligned}rho_{1}colon & ,A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0;\[2pt] rho_{2}colon & ,A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0,end{aligned}$

в которых коэффициенты при неизвестных непропорциональны, т.е. $operatorname{rang}!begin{pmatrix}A_{1}&B_{1}&C_{1}\A_{2}&B_{2}&C_{2}end{pmatrix}=2$ . Это условие означает, что плоскости $rho_{1}$ и $rho_{2}$ пересекаются (см. условие (4.25)), поскольку их нормали $vec{n}_{1}=A_{1}vec{i}+B_{1}vec{j}+C_{1}vec{k}$ и $vec{n}_{2}=A_{2}vec{i}+B_{2}vec{j}+C_{2}vec{k}$ неколлинеарны (рис.4.25). Тогда линия пересечения плоскостей описывается системой уравнений

$begin{cases} A_{1}cdot x+D_{1}cdot y+C_{1}cdot z+D_{1}=0,\ A_{2}cdot x+D_{2}cdot y+C_{2}cdot z+D_{2}=0. end{cases}$

(4.31)

Система (4.31) называется общим уравнением прямой в пространстве.

Общее уравнение прямой в пространстве как пересечение двух плоскостей

Пример 4.13. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1;2;3), B(3;0;2), C(7;4;6) треугольника (рис.4.26). Требуется составить уравнение прямой, содержащей высоту треугольника.

Решение. Прямая является линией пересечения двух плоскостей: плоскости $rho_{1}$ , треугольника ABC и плоскости $rho_{2}$ , проходящей через точку перпендикулярно вектору overrightarrow{BC} (рис.4.26). По формуле (4.21) составим уравнение плоскости $rho_{1},$ проходящей через три точки A,,B,,C:

$begin{vmatrix}x-1&y-2&z-3\3-1&0-2&2-3\7-1&4-2&6-3end{vmatrix}= begin{vmatrix} x-1&y-2&z-3\ 2&-2&-1\ 6&2&3 end{vmatrix}=0 quad Leftrightarrow quad x+3y-4z+5=0.$

По формуле (4.14) составим уравнение плоскости $rho_{2}$ , проходящей через точку перпендикулярно вектору overrightarrow{BC}=(7-3)vec{i}+(4-0)vec{j}+(6-2)vec{k}=4vec{i}+4vec{j}+4vec{k}:

4cdot(x-1)+4cdot(y-2)+4cdot(z-3)=0 quad Leftrightarrow quad x+y+z-6=0.

Следовательно, общее уравнение (4.31) прямой имеет вид $begin{cases}x+3y-4z+5=0,\x+y+z-6=0.end{cases}$

Параметрическое уравнение прямой в пространстве

Напомним, что направляющий вектором прямой называется ненулевой вектор, коллинеарный этой прямой, т.е. принадлежащий или параллельный ей.

Пусть в координатном пространстве Oxyz заданы точка $M_{0}(x_{0}, y_{0}, z_{0})$ и ненулевой вектор vec{p}= avec{i}+ bvec{j}+ cvec{k} (рис.4.27). Требуется составить уравнение прямой, коллинеарной вектору vec{p} и проходящей через точку $M_{0}(x_{0},y_{0},z_{0})$ .

Выберем на прямой произвольную точку $M_{0}(x,y,z)$ . Обозначим vec{r}=overrightarrow{OM}, $vec{r}_{0}=overrightarrow{OM_{0}}$ — радиус-векторы точек M(x,y,z) и $M_{0}(x_{0},y_{0},z_{0})$ (рис.4.28).

Параметрическое уравнение прямой в пространстве и направляющий вектор прямой

Точка принадлежит заданной прямой тогда и только тогда, когда векторы $overrightarrow{M_{0}M}$ и vec{p} коллинеарны. Запишем условие коллинеарности: $overrightarrow{M_{0}M}=tvec{p}$ , где — некоторое действительное число (параметр). Учитывая, что $overrightarrow{M_{0}M}=vec{r}-vec{r}_{0}$ , получим векторное параметрическое уравнение прямой в пространстве:

$vec{r}=vec{r}_{0}+tcdotvec{p}, quad tinmathbb{R},,$

(4.32)

где vec{p} — направляющий вектор прямой, а $vec{r}_{0}$ — радиус-вектор заданной точки $M_{0}(x_{0},y_{0},z_{0})$ принадлежащей прямой.

Координатная форма записи уравнения (4.32) называется параметрическим уравнением прямой в пространстве

$begin{cases}x=x_{0}+acdot t,\y=y_{0}+bcdot t,\z=z_{0}+ccdot t,end{cases}tinmathbb{R},,$

(4.33)

где a,b,c — координаты направляющего вектора vec{p} прямой. Параметр в уравнениях (4.32),(4.33) имеет следующий геометрический смысл: величина пропорциональна расстоянию от заданной точки $M_{0}(x_{0}, y_{0}, z_{0})$ до точки $M(x,y,z)equiv M(x_{0}+at,y_{0}+bt,z_{0}+ct)$ . Физический смысл параметра в параметрических уравнениях (4.32),(4.33) — это время при равномерном и Прямолинейном движении точки по прямой. При t=0 точка M(x,y,z) совпадает с заданной точкой $M_{0}$ . При возрастании параметра движение происходит в направлении направляющего вектора.

Каноническое уравнение прямой в пространстве

Выразим параметр из каждого уравнения системы (4.33): $t=frac{x-x_{0}}{a},, t=frac{y-y_{0}}{b},, t=frac{z-z_{0}}{c}$ , а затем исключим этот параметр:

$frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{c}, quad a^2+b^2+c^2ne0.$

(4.34)

Уравнение (4.34) называется каноническим уравнением прямой в пространстве. В этом уравнении коэффициенты a,b,c не равны нулю одновременно, так как это координаты направляющего вектора прямой.

Замечания 4.6.

1. Если один или два из трех знаменателей дробей в (4.34) равны нулю, то считается, что соответствующий числитель дроби равен нулю. Например:

а) каноническое уравнение $frac{x-x_{0}}{0}=frac{y-y_{0}}{0}=frac{z-z_{0}}{c}$ — это уравнение $begin{cases}x=x_{0},\y=y_{0}end{cases}$ прямой, параллельной оси аппликат (рис.4.29,а);

б) каноническое уравнение $frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{0}$ — это уравнение $begin{cases}z=z_{0},\dfrac{x-x_{0}}{a}=dfrac{y-y_{0}}{b}end{cases}$ прямой, параллельной координатной плоскости Oxy (рис.4.29,б).

Прямые в пространстве, параллельные координатным плоскостям

2. Направляющий вектор vec{p} прямой определяется неоднозначно. Например, любой ненулевой вектор lambdacdotvec{p} , где lambdainmathbb{R} , также является направляющим вектором для той же прямой.

Переход от общего уравнение к каноническому

3. Для перехода от общего уравнения прямой (4.31) к каноническому (4.34) нужно выполнить следующие действия:

1) найти любое решение $(x_{0},y_{0},z_{0})$ системы $begin{cases} A_{1}cdot x+B_{1}cdot y+C_{1}cdot z+D_{1}=0,\ A_{2}cdot x+B_{2}cdot y+C_{2}cdot z+D_{2}=0, end{cases}$ определяя тем самым координаты точки $M_{0}(x_{0},y_{0},z_{0})$ , принадлежащей прямой;

2) найти направляющий вектор vec{p} прямой как векторное произведение нормалей $vec{n}_{1}=A_{1}vec{i}+B_{1}vec{j}+C_{1}vec{k},$ $vec{n}_{2}= A_{2}vec{i}+ B_{2}vec{j}+ C_{2}vec{k},$ заданных плоскостей:

$vec{p}= begin{bmatrix}vec{n}_{1},vec{n}_{2}end{bmatrix}= acdotvec{i}+ bcdotvec{j}+ ccdotvec{k}= begin{vmatrix} vec{i}&vec{j}&vec{k}\ A_{1}&B_{1}&C_{1}\ A_{2}&B_{2}&C_{2} end{vmatrix}.$

3) записать каноническое уравнение (4.34) с учетом пунктов 1 и 2.

4. Чтобы перейти от канонического уравнения к общему, достаточно двойное равенство (4.34) записать в виде системы

$left{!begin{aligned}frac{x-x_{0}}{a}&=frac{y-y_{0}}{b},,\frac{y-y_{0}}{b}&=frac{z-z_{0}}{c},,end{aligned}right.$ и привести подобные члены.

5. Чтобы перейти от канонического уравнения к параметрическому, следует приравнять каждую дробь в уравнении (4.34) параметру t и записать полученные равенства в виде системы (4.33):

$frac{x-x_{0}}{a}=frac{y-y_{0}}{b}=frac{z-z_{0}}{c}=t quad Leftrightarrow quad begin{cases}x=x_{0}+acdot t,\y=y_{0}+bcdot t,\z=z_{0}+ccdot t,end{cases} tinmathbb{R},.$

6. Если в каноническом уравнении (4.34) прямой фиксировать координаты $x_{0},y_{0},z_{0}$ точки $M_{0}$ , а коэффициентам a,b,c придавать произвольные значения (не равные нулю одновременно), то получим уравнение связки прямых с центром в точке $M_{0}(x_{0},y_{0},z_{0})$ , т.е. совокупность всех прямых, проходящих через точку $M_{0}$ .

7. Параметрическое (4.33) и каноническое (4.34) уравнения прямой, полученные в прямоугольной системе координат, имеют тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнениях остается прежним.

Пример 4.14. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1;2;3), B(3;0;2), C(7;4;6) треугольника (рис. 4.30). Требуется:

В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1,2,3), B(3,0,2), C(7,4,6) треугольника

а) составить каноническое уравнение прямой, содержащей высоту треугольника;

б) составить общее уравнение прямой, содержащей биссектрису треугольника.

Решение. а) Общее уравнение прямой получено в примере 4.13: $begin{cases}x+3cdot y-4cdot z+5=0,\x+y+z-6=0.end{cases}$ Перейдем от общего уравнения к каноническому.

1) Найдем любое решение $(x_{0},y_{0},z_{0})$ системы, например, $x_{0}=1,$ $y_{0}=2,$ $z_{0}=3$ (это координаты точки A(1;2;3) ).

2) Найдем направляющий вектор vec{p} прямой как векторное произведение нормалей $vec{n}_{1}=vec{i}+3vec{j}-4vec{k},$ $vec{n}_{2}=vec{i}+vec{j}+vec{k}$ заданных плоскостей

$vec{p}= begin{bmatrix}vec{n}_{1},vec{n}_{2}end{bmatrix}= begin{vmatrix} vec{i}&vec{j}&vec{k}\ 1&3&-4\ 1&1&1 end{vmatrix}= 7cdotvec{i}-5cdotvec{j}-2cdotvec{k},.$

3) Запишем каноническое уравнение (4.34): $frac{x-1}{7}=frac{y-2}{-5}=frac{z-3}{-2}$ .

б) Сначала составим каноническое уравнение прямой . Для этого нужно найти направляющий вектор vec{l} этой прямой. Учитывая, что диагональ ромба является биссектрисой, vec{l}=vec{b}+vec{c} , где vec{b} и vec{c} — единичные векторы, одинаково направленные с векторами overrightarrow{AB} и overrightarrow{AC} соответственно. Находим

$begin{gathered}overrightarrow{AB}= 2cdotvec{i}-2cdotvec{j}-1cdotvec{k}, quad begin{vmatrix}overrightarrow{AB}end{vmatrix}=3, quad vec{b}= frac{overrightarrow{AB}}{begin{vmatrix} overrightarrow{AB}end{vmatrix}}= frac{2}{3}cdot vec{i}-frac{2}{3} cdotvec{j}-frac{1}{3}cdot vec{k},;\[3pt] overrightarrow{AC}= 6cdot vec{i}+ 2cdotvec{j}+3cdotvec{k}, quad begin{vmatrix} overrightarrow{AC} end{vmatrix}=7, quad vec{c}= frac{overrightarrow{AC}}{begin{vmatrix} overrightarrow{AC}end{vmatrix}}= frac{6}{7}cdotvec{i}+ frac{2}{7}cdotvec{j}+ frac{3}{7}cdotvec{k},;\[3pt] vec{l}=vec{a}+vec{c}= left(frac{2}{3}cdotvec{i}-frac{2}{3}cdotvec{j}-frac{1}{3}cdotvec{k}right)+ left(frac{6}{7}cdotvec{i}+frac{2}{7}cdotvec{j}+frac{3}{7}cdotvec{k}right)= frac{32}{21}cdotvec{i}-frac{8}{21}cdotvec{j}+frac{2}{21}cdotvec{k},. end{gathered}$

Составляем каноническое уравнение прямой $ALcolon,frac{x-1}{32/21}=frac{y-2}{-8/21}=frac{z-3}{2/21}$ .

Записывая двойное равенство в виде системы, получаем общее уравнение прямой AL:

$left{!begin{aligned}frac{x-1}{32/21}&=frac{y-2}{-8/21},\ frac{y-2}{-8/21}&=frac{z-3}{2/21},end{aligned}right. quad Leftrightarrow quad begin{cases}x+4cdot y-9=0,\ y+4cdot z-14=0.end{cases}$

Расстояние от точки до прямой, заданной каноническим уравнением

Расстояние от точки до прямой в пространстве

Найдем расстояние от точки $M_{1}(x_{1},y_{1},z_{1})$ до прямой , заданной каноническим уравнением (рис.4.31)):

$lcolon, frac{x-x_{0}}{a}= frac{y-y_{0}}{b}= frac{z-z_{0}}{c},.$

Искомое расстояние равно высоте параллелограмма, построенного на векторах

vec{p}=avec{i}+bvec{j}+cvec{k} и $vec{m}=overrightarrow{M_{0}M_{1}}=(x_{1}-x_{0})vec{i}+(y_{1}-y_{0})vec{j}+(z_{1}-z_{0})vec{k}$ , то есть.

$d=frac{begin{vmatrix}begin{bmatrix}vec{m},vec{p}end{bmatrix}end{vmatrix}}{begin{vmatrix}vec{p}end{vmatrix}}= frac{sqrt{begin{vmatrix}x_{1}-x_{0}&y_{1}-y_{0}\a&bend{vmatrix}^2+ begin{vmatrix}y_{1}-y_{0}&z_{1}-z_{0}\b&cend{vmatrix}^2+ begin{vmatrix}x_{1}-x_{0}&z_{1}-z_{0}\a&cend{vmatrix}^2}}{sqrt{a^2+b^2+c^2}},.$

(4.35)

Уравнение прямой, проходящей через две заданные точки

Уравнение прямой в пространстве, проходящей через две заданные точки

Пусть в координатном пространстве Oxyz заданы две точки $M_{0}(x_{0},y_{0},z_{0})$ и $M_{1}(x_{1},y_{1},z_{1})$ . Требуется составить уравнение прямой, проходящей через заданные точки.

Как показано в разд., точка M(x,y,z) принадлежит прямой $M_{0}M_{1}$ тогда и только тогда, когда ее радиус-вектор overrightarrow{OM} удовлетворяет условию (рис.4.32): $overrightarrow{OM}= (1-t)cdot overrightarrow{OM_{0}}+ tcdotoverrightarrow{OM_{1}}$ , где — некоторое действительное число (параметр). Это уравнение, а также его координатную форму

$begin{pmatrix}x\y\zend{pmatrix}= (1-t)cdot!begin{pmatrix}x_{0}\y_{0}\z_{0}end{pmatrix}+tcdot!begin{pmatrix}x_{1}\y_{1}\z_{1}end{pmatrix}! quad Leftrightarrow quad !begin{cases} x=(1-t)cdot x_{0}+tcdot x_{1},\ y=(1-t)cdot y_{0}+tcdot y_{1},\ z=(1-t)cdot z_{0}+tcdot z_{1}.end{cases} tinmathbb{R}$

(4.36)

будем называть аффинным уравнением прямой, проходящей через две точки $M_{0}(x_{0},y_{0},z_{0})$ и $M_{1}(x_{1},y_{1},z_{1})$ .

Выражая параметр из каждого уравнения системы (4.36), получаем: $frac{x-x_{0}}{x_{1}-x_{0}}=frac{y-y_{0}}{y_{1}-y_{0}}=frac{z-z_{0}}{z_{1}-z_{0}}=t$ . Исключая параметр , приходим к уравнению прямой, проходящей через две точки $M_{0}(x_{0},y_{0},z_{0})$ и $M_{1}(x_{1},y_{1},z_{1})$ :

$frac{x-x_{0}}{x_{1}-x_{0}}=frac{y-y_{0}}{y_{1}-y_{0}}=frac{z-z_{0}}{z_{1}-z_{0}},.$

(4.37)

Уравнение (4.37) можно получить из канонического уравнения (4.34), выбирая в качестве направляющего вектора vec{p}=avec{i}+bvec{j}+cvec{k} вектор $overrightarrow{M_{0}M_{1}}=(x_{1}-x_{0})vec{i}+(y_{1}-y_{0})vec{j}+(z_{1}-z_{0})vec{k},$ т.е. подставляя $a=x_{1}-x_{0},$ $b=y_{1}-y_{0},$ $c=z_{1}-z_{0}.$

Треугольник в пространстве по координатам вершин, его высота и медиана

Пример 4.15. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы вершины A(1;2;3), B(3;0;2), C(7;4;6) треугольника (рис.4.33). Требуется:

а) составить уравнение прямой ;

б) составить уравнение прямой, содержащей медиану треугольника;

в) найти высоту h=|AH| треугольника, опущенную на сторону .

Решение. а) Записываем уравнение (4.37) прямой, проходящей через точки B(3;0;2), C(7;4;6):

$frac{x-3}{7-3}=frac{y-0}{4-0}=frac{z-2}{6-2}~ Leftrightarrow~ frac{x-3}{1}=frac{y}{1}=frac{z-2}{1},.$

б) Находим координаты середины стороны BCcolon M(5;2;4) . Составляем уравнение (4.37) прямой AM:

$frac{x-1}{5-1}=frac{y-2}{2-2}=frac{z-3}{4-3}~ Leftrightarrow~ frac{x-1}{4}=frac{y-2}{0}=frac{z-3}{1},.$

в) Искомую высоту находим по формуле (4.35), полагая vec{m}=overrightarrow{BA}=-2vec{i}+2vec{j}+vec{k} и vec{p}=vec{i}+vec{j}+vec{k}:

$h=|AH|=frac{begin{vmatrix}begin{bmatrix}vec{m},vec{p}end{bmatrix}end{vmatrix}}{begin{vmatrix}vec{p}end{vmatrix}}= frac{sqrt{begin{vmatrix}-2&2\1&1end{vmatrix}^2+begin{vmatrix}2&1\1&1end{vmatrix}^2+begin{vmatrix}-2&1\1&1end{vmatrix}^2}}{sqrt{1^2+1^2+1^2}}=frac{sqrt{16+1+9}}{sqrt{3}}= sqrt{frac{26}{3}},.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Что такое каноническое уравнение прямой в пространстве