Метод диаграмм Вейча
Диаграмма
Вейча – это специального вида таблица,
используемая для задания логических
функций и позволяющая упростить процесс
поиска минимальных форм.
Для логических
функций, зависящих от n
переменных, диаграмма Вейча представляет
собой прямоугольник, разделенный на 2n
клеток. Каждой клетке диаграммы ставится
в соответствие двоичный n-мерный
набор. Взаимно однозначное соответствие
между двоичными наборами и клетками
диаграммы устанавливается разметкой
последней.
Для функций,
зависящих от трех переменных, один из
возможных вариантов разметки диаграммы
Вейча имеет вид, показанный на рис.1.
Четыре верхних
клетки диаграммы соответствуют двоичным
наборам, в которых переменная х1
принимает значение 0; четыре нижних
клетки соответствуют наборам, в которых
переменная х1
принимает значение 1.
Клетки, составляющие
левую половину диаграммы, соответствуют
наборам, в которых переменная х2
принимает значения 1, а в правой половине
находятся клетки, в которых переменная
х2
принимает значение 0.
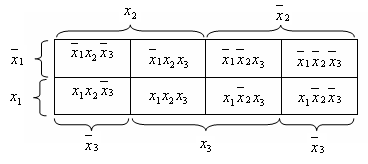
Рис. 1.
Четыре центральные
клетки соответствуют наборам, в которых
переменная х3
принимает значения 1, а в левом и правом
крайних столбцах находятся клетки, в
которых переменная х3
принимает значение 0.
На рис. 2 приведены
пример разметки диаграммы для логических
функций четырех переменных.
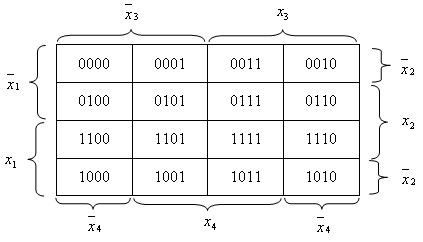
Рис. 2.
Диаграммы Вейча
для большего числа переменных могут
быть составлены из диаграмм меньшего
числа переменных. Например, диаграмму
Вейча для пяти переменных можно составить,
соединив две диаграммы для четырех
переменных. При этом удобно подсоединять
их друг к другу одноименными столбцами
(рис. 3). Тогда соседними клетками будут
также клетки столбцов, симметрично
расположенных относительно линии
присоединения диаграмм Вейча четырех
переменных для одноименных строк.
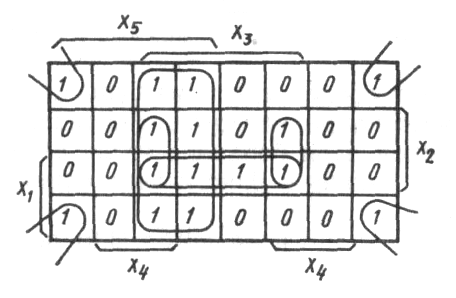
Рис. 3.
В клетки,
соответствующие конституентам единицы
минимизируемой булевой функции,
записываются единицы, а в остальные —
нули. Поэтому исходная минимизируемая
функция первоначально должна быть
представлена в СДНФ. Если функция задана
аналитически, то она приводится к СДНФ
с помощью операции развертывания,
заключающейся в умножении некоторых
членов на выражение вида
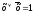 .
.
Минимизация булевых
функций с использованием диаграмм Вейча
основывается на отыскании склеивающихся
конституент единицы. Для диаграммы
Вейча склеивающиеся конституенты
единицы располагаются в соседних,
вертикально или горизонтально
расположенных клетках. Для диаграммы
трех переменных (рис. 1) соседними клетками
являются также клетки левого и правого
столбцов для одноименных строк. Наглядно
это можно представить, если наклеить
диаграмму на цилиндр так, чтобы левая
ее граница совпала с правой.
Для диаграммы
Вейча четырех переменных (рис. 2) соседними
клетками будут также клетки, расположенные
в верхних и нижних строках для одноименных
столбцов.
Процесс отыскания
минимальной ДНФ заключается в том, чтобы
всю совокупность единиц диаграммы Вейча
накрыть наименьшим числом наиболее
коротких произведений. Для этого соседние
клетки диаграммы, содержащие единицы,
объединяют в группы (склеиваются).
Каждой такой группе
будет соответствовать группа склеивающихся
конституент единицы. Причем количество
клеток, входящих в одну группу, равно
2k
(где k
= 1, 2, 3, …), а каждая клетка, входящая в
группу, должна иметь k
соседних клеток.
Для получения
минимальной ДНФ достаточно выполнить
следующие условия:
каждая единичная
клетка должна входить хотя бы в одну
группу (при этом одна и та же клетка
может входить в несколько групп);
в каждую группу
должно входить максимальное количество
клеток, т.е. ни одна группа, удовлетворяющая
обоим вышеприведенным правилам, не
должна быть частью другой группы,
удовлетворяющей этим же правилам;
количество групп
должно быть минимальным.
Рекомендации по
минимизации булевых функций с
использованием диаграмм Вейча:
1. Рассматриваются
поочередно клетки, содержащие единицы,
и анализируются всевозможные варианты
склеивания. При этом сначала склеивание
выполняется только для тех клеток
(единиц), для которых вариант склеивания
единственный. В результате будут выделены
обязательные (или существенные) простые
импликанты.
2. Оставшиеся
несклеенные клетки (единицы) необходимо
склеивать таким образом, чтобы образовать
минимальное число групп с максимальным
числом клеток в каждой группе.
3. Каждой группе
объединенных клеток в минимальной ДНФ
будет соответствовать простая импликанта,
определяемая как конъюнкция только тех
переменных, значения которых постоянны
для всех наборов, задающих клетки данной
группы.
Группе, состоящей
из 2k
клеток, соответствует конъюнкция из n
– k
букв, где n
— число переменных в исходной булевой
функции.
Пример 1.
Найти минимальную ДНФ для булевой
функции трех переменных, заданных
следующей таблицей истинности(табл.1):
Таблица 1
|
№ на |
х1 |
х2 |
х3 |
z |
|
0 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
1 |
|
5 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
1 |
СДНФ для этой
функции
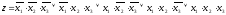 .
.
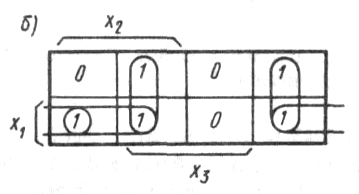
Составим диаграмму
Вейча (рис. 4)
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Метод минимизирующих карт (карты Карно, диаграммыВейча)
Карты Карно (их разновидностью являются диаграммы Вейча) являются графическим представлением таблиц истинности. Поэтому они строятся или по таблице истинности анализируемой функции, или же по ее СДНФ.
Диаграммы Вейча представляет собой прямоугольник, разбитый на ячейки, число которых равно общему числу наборов для данной функции n переменных, то есть оно равно 2n. Так, для функции 3-х переменных ячеек будет 8, для 4-х переменных – 16 и т.д.
Каждая ячейка соответствует определенному набору, или терму, причем наборы располагаются так, чтобы соседние наборы, или термы как по горизонтали, так и по вертикали, отличались бы только значением одной переменной: в одной ячейке она была бы в прямом виде, а в соседней – с инверсией. Причем надо учесть, что ячейки, расположенные на противоположных концах каждой строки или столбца, также являются соседними.
Функцию в СДНФ наносят на карту, отмечая, например, знаком “1” ячейки, соответствующие тем наборам, на которых ФАЛ равна единице, т.е. в СДНФ функции эта ячейка соответствует одному изееминтермов. Остальные ячейки отмечаются знаком “0”.
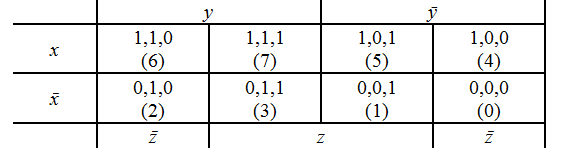
Диаграмма Вейча для функции 3-х переменных
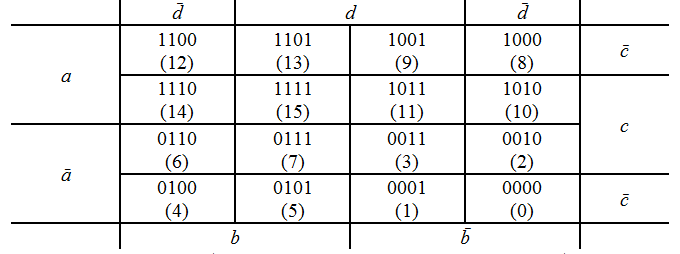
Диаграмма Вейча для функции 4-х переменных
Если данную таблицу рассматривать как цилиндр, образованный соединением первой и последней колонок, то тогда склеивающиеся между собой конституэнты единицы или нуля в диаграммах Вейча будут расположены в соседних клетках. При этом прямоугольники, покрывающие 2kсоседних клеток, описывают имликанту (имплиценту), имеющую ранг (n-k), где n – число переменных, от которых зависит функция.
Клетки, содержащие в диаграмме Вейча единицы, будем называть 1-клетками, а клетки, содержащие нули – 0-клетками.
Основное свойство диаграмм Вейча заключается в том, что любая первичная импликанта ранга (n-m) образует на ней прямоугольник и только прямоугольник 1-клеток площадью 2m, где n – количество переменных, от которых зависит функция. Такие прямоугольники называют m-кубами (m=0,1,…,n.; 0-кубу соответствует минтерм, а n-кубу – константа “единица”). Так любая пара единиц в соседних клетках диаграммы Вейча для логической функции трех переменных представляется импликантой второго ранга. Четыре единицы, образующие прямоугольник, выражаются одной переменной (с отрицанием или без него).
Чтобы записать первичную импликанту, представляющую собой некий m-куб на диаграмме Вейча, необходимо просто составить конъюнкцию тех переменных, которые в пределах данного m-куба сохраняют постоянные значения (только прямые или только инверсные).
Получение минимальной ДНФ с помощью диаграмм Вейча сводится к отысканию минимального числа m-кубов максимально-го размера, состоящих из 1-клеток, и составлению дизъюнкции импликант, соответствующих этим m-кубам (каждая 1-клетка должна войти хотя бы в один m-куб, любая 1-клетка может входить одновременно в несколько различных m-кубов).
При получении МДНФ с помощью диаграммы Вейча необходимо обратить внимание на следующее:
- m-кубу, покрывающему2m 1-клеток, соответствует первичная импликанта, не зависящая от m переменных, причем исключаются те m переменных, которые в прямоугольной области на диаграмме Вейча, состоящей из 1-клеток, имеют различное значение (прямое и инверсное);
- прямоугольные области на диаграмме Вейча, используемые при минимизации, могут состоять только из 2m соседних клеток, где m = 0,1,…,n;
- каждая клетка на диаграмме Вейча, вне зависимости от способа разметки этой диаграммы, имеет ровно n соседних клеток; в связи с этим диаграмма Вейча представляется нанесенной на поверхность соответствующего тела (цилиндра – для случая трех переменных, тора – для случая четырех переменных);
- поиск минимального покрытия 1-клеток следует начинать с выбора тех 1-клеток, которые могут войти в один и только один m-куб; если после этого на диаграмме остаются 1 клетки, не вошедшие ни в один из m-кубов, то следует рассмотреть несколько вариантов покрытий этих клеток; с целью минимизации результата оставшиеся 1-клетки покрываются, по возможности, m-кубами максимального размера.
Получение минимальной КНФ проводится аналогичным образом по отношению к 0 клеткам.
Схемотехника. Минимизация логических функций
Время на прочтение
5 мин
Количество просмотров 367K
Минимизация логических функций является одной из типовых задач в процессе обучения схемотехнике. Посему считаю, что такая статья имеет место быть, надеюсь Вам понравится.

Зачем это нужно?
Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы (цепи), пропорциональны числу логических операций и числу вхождений переменных или их отрицаний. В принципе любая логическая функция может быть упрощена непосредственно с помощью аксиом и теорем логики, но, как правило, такие преобразования требуют громоздких выкладок.
К тому же процесс упрощения булевых выражений не является алгоритмическим. Поэтому более целесообразно использовать специальные алгоритмические методы минимизации, позволяющие проводить упрощение функции более просто, быстро и безошибочно. К таким методам относятся, например, метод Квайна, метод карт Карно, метод испытания импликант, метод импликантных матриц, метод Квайна-Мак-Класки и др. Эти методы наиболее пригодны для обычной практики, особенно минимизация логической функции с использованием карт Карно. Метод карт Карно сохраняет наглядность при числе переменных не более шести. В тех случаях, когда число аргументов больше шести, обычно используют метод Квайна-Мак-Класки.
В процессе минимизации той или иной логической функции, обычно учитывается, в каком базисе эффективнее будет реализовать ее минимальную форму при помощи электронных схем.
Минимизация логических функций при помощи карт Карно
Карта Карно — графический способ минимизации переключательных (булевых) функций, обеспечивающий относительную простоту работы с большими выражениями и устранение потенциальных гонок. Представляет собой операции попарного неполного склеивания и элементарного поглощения. Карты Карно рассматриваются как перестроенная соответствующим образом таблица истинности функции. Карты Карно можно рассматривать как определенную плоскую развертку n-мерного булева куба.
Карты Карно были изобретены в 1952 Эдвардом В. Вейчем и усовершенствованы в 1953 Морисом Карно, физиком из «Bell Labs», и были призваны помочь упростить цифровые электронные схемы.
В карту Карно булевы переменные передаются из таблицы истинности и упорядочиваются с помощью кода Грея, в котором каждое следующее число отличается от предыдущего только одним разрядом.
Основным методом минимизации логических функций, представленных в виде СДНФ или СКНФ является операция попарного неполного склеивания и элементарного поглощения. Операция попарного склеивания осуществляется между двумя термами (членами), содержащими одинаковые переменные, вхождения которых (прямые и инверсные) совпадают для всех переменных, кроме одной. В этом случае все переменные, кроме одной, можно вынести за скобки, а оставшиеся в скобках прямое и инверсное вхождение одной переменной подвергнуть склейке. Например:

Возможность поглощения следует из очевидных равенств

Таким образом, главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением, что для больших форм может оказаться достаточно сложной задачей. Карты Карно предоставляют наглядный способ отыскания таких термов.
Как известно, булевы функции N переменных, представленные в виде СДНФ или СКНФ могут иметь в своём составе 2N различных термов. Все эти члены составляют некоторую структуру, топологически эквивалентную N–мерному кубу, причём любые два терма, соединённые ребром, пригодны для склейки и поглощения.
На рисунке изображена простая таблица истинности для функции из двух переменных, соответствующий этой таблице 2-мерный куб (квадрат), а также 2-мерный куб с обозначением членов СДНФ и эквивалентная таблица для группировки термов:
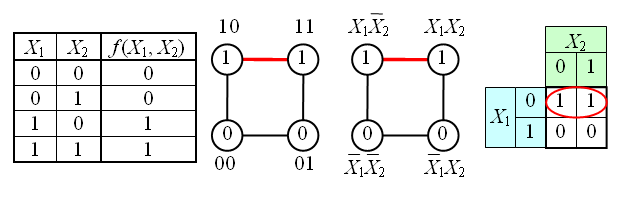
В случае функции трёх переменных приходится иметь дело с трёхмерным кубом. Это сложнее и менее наглядно, но технически возможно. На рисунке в качестве примера показана таблица истинности для булевой функции трёх переменных и соответствующий ей куб.
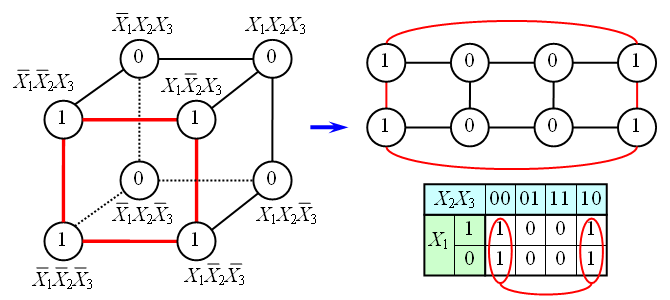
Как видно из рисунка, для трёхмерного случая возможны более сложные конфигурации термов. Например, четыре терма, принадлежащие одной грани куба, объединяются в один терм с поглощением двух переменных:

В общем случае можно сказать, что 2K термов, принадлежащие одной K–мерной грани гиперкуба, склеиваются в один терм, при этом поглощаются K переменных.
Для упрощения работы с булевыми функциями большого числа переменных был предложен следующий удобный приём. Куб, представляющий собой структуру термов, разворачивается на плоскость как показано на рисунке. Таким образом появляется возможность представлять булевы функции с числом переменных больше двух в виде плоской таблицы. При этом следует помнить, что порядок кодов термов в таблице (00 01 11 10) не соответствует порядку следования двоичных чисел, а клетки, находящиеся в крайних столбцах таблицы, соседствуют между собой.

Аналогичным образом можно работать с функциями четырёх, пяти и более переменных. Примеры таблиц для N=4 и N=5 приведены на рисунке. Для этих таблиц следует помнить, что соседними являются клетки, находящиеся в соответственных клетках крайних столбцов и соответственных клетках верхней и нижней строки. Для таблиц 5 и более переменных нужно учитывать также, что квадраты 4х4 виртуально находятся друг над другом в третьем измерении, поэтому соответственные клетки двух соседних квадратов 4х4 являются сосоедними, и соответствующие им термы можно склеивать.
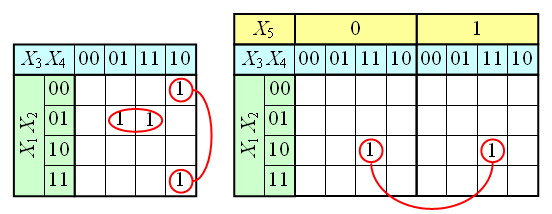
Карта Карно может быть составлена для любого количества переменных, однако удобно работать при количестве переменных не более пяти. По сути Карта Карно — это таблица истинности составленная в 2-х мерном виде. Благодаря использованию кода Грея в ней верхняя строка является соседней с нижней, а правый столбец соседний с левым, т.о. вся Карта Карно сворачивается в фигуру тор (бублик). На пересечении строки и столбца проставляется соответствующее значение из таблицы истинности. После того как Карта заполнена, можно приступать к минимизации.
Если необходимо получить минимальную ДНФ, то в Карте рассматриваем только те клетки которые содержат единицы, если нужна КНФ, то рассматриваем те клетки которые содержат нули. Сама минимизация производится по следующим правилам (на примере ДНФ):
- Объединяем смежные клетки содержащие единицы в область, так чтобы одна область содержала 2n (n целое число = 0…
 ) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули;
) клеток(помним про то что крайние строки и столбцы являются соседними между собой), в области не должно находиться клеток содержащих нули; - Область должна располагаться симметрично оси(ей) (оси располагаются через каждые четыре клетки);
- Не смежные области расположенные симметрично оси(ей) могут объединяться в одну;
- Область должна быть как можно больше, а кол-во областей как можно меньше;
- Области могут пересекаться;
- Возможно несколько вариантов накрытия.
Далее берём первую область и смотрим какие переменные не меняются в пределах этой области, выписываем конъюнкцию этих переменных, если неменяющаяся переменная нулевая, проставляем над ней инверсию. Берём следующую область, выполняем то же самое что и для первой, и т. д. для всех областей. Конъюнкции областей объединяем дизъюнкцией.
Например(для Карт на 2-ве переменные):
 |
 |
 |
 |
 |
 |
 |
 |
|||||||
 |
 |
 |
 |
 |
 |
 |
 |
|||||||
 |
 |
 |
 |
 |
 |
|||||||||
 |
 |
 |
 |
 |
 |
|||||||||
 |
 |
 |
 |
 |
 |
|||||||||
 |
 |
Для КНФ всё то же самое, только рассматриваем клетки с нулями, не меняющиеся переменные в пределах одной области объединяем в дизъюнкции (инверсии проставляем над единичными переменными), а дизъюнкции областей объединяем в конъюнкцию. На этом минимизация считается законченной. Так для Карты Карно на рис.1 выражение в формате ДНФ будет иметь вид:
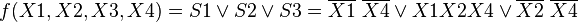
В формате КНФ:

Скачать материал

Скачать материал




- Сейчас обучается 270 человек из 64 регионов




Описание презентации по отдельным слайдам:
-

1 слайд
4 занятие
Геометрическое представление булевых функций. Карта Карно. Карта Вейча. -

2 слайд
Булевы функции названы в честь английского математика ХIХ века Дж. Буля, который впервые применил алгебраические методы для решения логических задач. Они образуют самый простой класс дискретных функций – их аргументы и значения могут принимать всего два значения ( 0 или 1). С другой стороны, этот класс достаточно богат и его функции имеют много интересных свойств. Булевы функции находят применение в логике, электротехнике, многих разделах информатики.
-

3 слайд
Булева функция. Булев куб.
-

4 слайд
Произвольная булева функция задается одним из трех способов: матричным (табличным), геометрическим и аналитическим.
-

5 слайд
При матричном способе булева функция f (х1, …,хn) задается таблицей истинности (табл. 1.1 и 1.2), в левой части которой представлены все возможные двоичные наборы длины n, а в правой указывается значение функции на этих наборах.
-

6 слайд
Под двоичным набором y = < y1, y2,…,yn> yi E {0, 1} понимается совокупность значений аргументов х1, х2, …, xn булевой функции f. Двоичный набор имеет длину n, если он представлен n цифрами из множества {0,1}. В табл. 1.1 передставлены все двоичные наборы длины 3.
Иногда двоичные наборы в таблице истинности булевой функции удобно представлять номерами наборов. Запишем аргументы х1, х2, …, xn в порядке возрастания их индексов. Тогда любой двоичный набор y = < y1, y2,…,yn> yi E {0, 1} можно рассматривать как целое двоичное число N:N=y1*2n-1+y2*2n-2+…+yn
называемое номером набора y. Например, двоичные наборы 101 и 111 имеют номера 5 и 7 соответственно. Очевидно, любая булева функция может быть задана таблицей истинности, в которой двоичные наборы заменены своими номерами (табл. 1.2). -

7 слайд
При геометрическом способе булева функция f (х1, …, хn) задается с помощью n-мерного куба. В геометрическом смысле каждый двоичный набор у = <y1, y2,…,yn> yi E {0,1} есть n-мерный вектор, определяющий точку n-мерпого пространства. Исходя из этого, все множество наборов, на которых определена функция n переменных, представляется вершинами n-мерного куба. Отмечая точками вершины куба, в которых функция принимает единичное (либо нулевое) значение, получим геометрическое представление функции. Например, булева функция, заданная табл. 1.1, геометрически представляется 3-мерным кубом.
-

8 слайд
При аналитическом способе булева функция задается формулами, т. е. аналитическими выражениями, построенными на основе операций булевой алгебры. Аналитический способ задания булевых функций занимает особое место в проектировании цифровых автоматов. Фактически, все преобразования над булевыми функциями, необходимые для построения цифровых автоматов, ведутся на аналитическом уровне.
-

9 слайд
Рассмотрим области определения булевых функций. Как уже отмечалось, между двоичными наборами и двоичными числами существует взаимно однозначное соответствие. Следовательно, существует 2n различных наборов двоичных переменных.
Таким образом, областью определения булевой функции n переменных при матричном способе задания является множество всех возможных двоичных наборов длины n, а при геометрическом способе задания – множество всех вершин n-мерного единичного куба.
Булеву функцию, определенную на всех своих наборах, называют полностью определенной. В табл. 1.1, 1.2 приведены примеры полностью определенных булевых функций.
Булеву функцию n переменных называют неполностью определенной или частичной, если она определена не на всех двоичных наборах длины n. Неполностью определенная булева функция не попадает под определение, данное в начале , но при произвольном доопределении (на всех наборах, на которых она не определена) это несоответствие снимается.
Легко убедиться, что если булева функция f не определена на m наборах аргументов, то путем ее доопределения можно получить 2m различных полностью определенных функций. В табл. 1.5 приведен пример неполностью определенной булевой функции трех переменных. -

-

11 слайд
Существует не более чем 22^n различных булевых функций n переменных. К этому выводу легко прийти, пользуясь простыми комбинаторными рассуждениями, и вспомнив, что на каждом из 2n наборов функции могут принимать два значения.
Функции двух переменных представлены в табл. 1.6.
Наиболее часто употребляются следующие: -

12 слайд
f0 (x1, x2) = 0 – тождественный ноль (константа 0);
f1 (x1, x2) = x1 * x2 – конъюнкция. Вместо знака “*” иногда употребляется знак & или /. Эту функцию часто называют логическим произведением или логическим умножением;
f3 (x1, х2) = x1 – повторение x1;
f5 (x1, x2) = x2 – повторение х2;
f6 (x1, x2) = х1 x2 – сложение по модулю 2 или сумма mod 2 (далее +);
f7 (х1, х2) = x1 V x2 – дизъюнкция (логическое ИЛИ);
f8 (x1, x2) = x1 | х2 – функция Вебба (стрелка Пирса);
f9 (х1, х2) = x1 ~ x2 – эквивалентность;
f13(x1, x2) = x1 —> x2 – импликация;
f14(x1, x2) = x1x2 – штрих Шеффера;
f15(x1, x2) = 1-тождественная единица (константа 1). -

13 слайд
Справедливы три аксиомы:
закон коммутативности – х v у = у V х, ху = ух;
закон ассоциативности – (х v у) v z = х v(y v z), (х y) z = х(у z);
закон дистрибутивности – х (у v x) = ху v хz, х v y * z = (х v y)(х v z). -

14 слайд
Теоремы де Моргана
-

15 слайд
Алгебра Жегалкина
В ряде случаев, преобразования над формулами булевых функций удобно призводить в алгебре Жегалкина.
Алгебра Жегалкина включает две двухместные операции: конъюнкцию и сложение по модулю 2 (*, (прим. далее + ) ), а также константу 1. Здесь имеют место те же законы:
х + y = y + х, х у = у х (закон коммутативности);
х + (у + z) = (х + у) + z, х(у z) = (х у)z (закон ассоциативности);
x (y + z) = x y + x z (закон дистрибутивности).
Для упрощения формул могут быть использованы следующие соотношения:
х + 0 = х;
х 1 = х;
х 0 = 0;
х + х = 0;
х х = х.
Из коммутативности и ассоциативности дизъюнкции следует, что дизъюнкция нескольких переменных может выполняться последовательно, причем порядок взятия дизъюнкции не влияет на результат.” -

-

-

-

-

-

-

-

23 слайд
Карта Карно
https://youtu.be/zhQtHTFaNzQ -

24 слайд
Метод диаграмм Вейча
Метод позволяет быстро получать минимальные ДНФ булевой функции f небольшого числа переменных. В основе метода лежит задание булевых функций диаграммами некоторого специального вида, получившими название диаграмм Вейча. Для булевой функции двух переменных диаграмма Вейча имеет вид -

25 слайд
Каждая клетка диаграммы соответствует набору переменных булевой функции в ее таблице истинности. В (табл. 4.4.1) это соответствие показано, В клетке диаграммы Вейча ставится единица, если булева функция принимает единичное значение на соответствующем наборе. Нулевые значения булевой функции в диаграмме Вейча не ставятся. Для булевой функции трех переменных диаграмма Вейча имеет следующий вид (табл. 4.4.2).
-

26 слайд
Добавление к ней еще такой же таблицы дает диаграмму для функции 4-х переменных (табл. 4.4.3).
-

27 слайд
Таким же образом, т. е. приписыванием еще одной диаграммы 3-х переменных к только что рассмотренной, можно получить диаграмму для функции 5-ти переменных и т. д., однако диаграммы для функций с числом переменных больше 4-х используются редко. Для приведенных диаграмм характерно следующее: каждой клетке диаграммы соответствует свой набор;
соседние наборы расположены рядом в строке либо в столбце. -

28 слайд
Соседними наборами называются наборы, отличающиеся одной компонентой. Напомним, что конституенты, соответствующие таким наборам, склеиваются (см. метод Квайна- Мак-Класки). Например, для функции, заданной табл. 9.22,
-

29 слайд
конституенты, соответствующие паре единиц в левой части таблицы, склеиваются и порождают элементарное произведение из 2-х букв:
-

30 слайд
О паре единиц в правой части диаграммы можно сказать то же самое:
/х1х2/х3 v /x1/x2/x 3 = /x1/x3
Отметим, что получающееся элементарное произведение легко определить сразу по диаграмме: это произведение переменных, принимающих одно и то же значение в обеих клетках.
Еще одно важное замечание: столбцы, расположенные по краям диаграммы, тоже считаются соседними. Для нашего примера это означает, что имеет место еще одно склеивание, в результате которого, следуя указанному правилу, получаем элементарное произведение x2/x3 Из рассмотренных ранее методов нам известно, что возможно дальнейшее склеивание получаемых элементарных произведений. На диаграммах Вейча они тоже располагаются рядом. Общее правило склеивания на диаграммах Вейча можно сформулировать следующим образом: склеиванию подлежат прямоугольные конфигурации, заполненные единицами и содержащие число клеток, являющееся степенью 2. Получающееся новое элементарное произведение определяется как произведение переменных, не меняющих своего значения на всех склеиваемых наборах. -

31 слайд
Число m оставшихся переменных в элементарном произведении определяется легко:
m = n – log2M
где n – число переменных функции, М – число склеиваемых наборов. Метод широко используется на практике, благодаря простоте и удобству. После небольшой тренировки достигается элементарный навык определения минимальной ДНФ по диаграмме “с первого взгляда”. Минимизация булевой функции заключается в нахождении минимального накрытия всех единиц диаграммы Вейча блоками из единиц (указанной конфигурации), расположенных в соседних клетках диаграммы. При этом всегда считается, что левый край диаграммы Bейча 4-х переменных примыкает к ее правому краю, а верхний oкрай диаграммы примыкает к нижнему ее краю. После получения минимального накрытия всех единиц диаграммы Вейча, минимальная ДНФ булевой функции записывается как дизъюнкция элементарных конъюнкций, соответствующих выделенным блокам единиц в диаграмме. Рассмотрим несколько примеров.
-

32 слайд
http://ptca.narod.ru/lec/lec4_4.html
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 252 396 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 17.09.2015
- 1022
- 2
- 17.09.2015
- 2948
- 48
- 17.09.2015
- 636
- 0
- 17.09.2015
- 838
- 0
- 17.09.2015
- 3280
- 20
- 17.09.2015
- 573
- 0
- 17.09.2015
- 769
- 0
Вам будут интересны эти курсы:
-
Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
-
Курс повышения квалификации «Основы туризма и гостеприимства»
-
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
-
Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»
-
Курс профессиональной переподготовки «Экскурсоведение: основы организации экскурсионной деятельности»
-
Курс повышения квалификации «Основы построения коммуникаций в организации»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС технических направлений подготовки»
-
Курс повышения квалификации «Управление финансами: как уйти от банкротства»
-
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
-
Курс повышения квалификации «Маркетинг в организации как средство привлечения новых клиентов»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС медицинских направлений подготовки»
-
Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
-
Курс профессиональной переподготовки «Стратегическое управление деятельностью по дистанционному информационно-справочному обслуживанию»
