Как составить кейс пример по математике - Сайт, где вы сможете решить свои вопросы

Скачать материал

без ожидания

Скачать материал

без ожидания

Сейчас обучается 957 человек из 80 регионов

Сейчас обучается 47 человек из 29 регионов

Сейчас обучается 41 человек из 28 регионов

Описание презентации по отдельным слайдам:

1 слайд

КЕЙС – МЕТОД на уроке математики

Асташова Елена Викторовна,
учитель начальных классов
МОБУ СОШ №117, Первомайский район
2 слайд

Кейс –это
реальный случай, который можно перевести из статуса «жизненной ситуации» в статус задачи, и затем решать с последующей рефлексией хода и ресурсов решения. Название метода происходит от англ.case – случай, ситуация и от понятия «кейс» – чемоданчик для хранения различных бумаг,
документов, журналов и пр.
3 слайд

История возникновения
Кейс-метод возник в начале XX в.в Школе бизнеса Гарвардского университета (США). Особый упор делался на самостоятельную работу студентов.
В 1920 г. профессор Копленд издал первый сборник кейсов.
В российских изданиях чаще всего говорится о методе анализа конкретных ситуаций (АКС), деловых ситуаций, кейс-методе, ситуационных задачах.
5 слайд

Кейс-метод, метод конкретных ситуаций означает:
набор практических ситуаций, которые должны изучаться, анализироваться учащимися.
Применение кейс–технологии в групповой работе, направленное на формирование универсальных учебных действий учащихся в рамках реализации ФГОС второго поколения
6 слайд

Работа ученика с кейсом

1 этап — знакомство с ситуацией, её особенностями;
2 этап — выделение основной проблемы (проблем),
3 этап — предложение концепций или тем для «мозгового штурма»;
4 этап — анализ последствий принятия того или иного решения;
5 этап — предложение одного или нескольких вариантов последовательности действий.
7 слайд

Действия учителя в кейс – технологии:

1)распределение учеников по малым группам (4-6 человек);
2) знакомство учащихся с ситуацией, системой оценивания
решений проблемы, сроками выполнения заданий
организация работы учащихся в малых группах, определение докладчиков;
3) организация презентации решений в малых группах;
4) организация общей дискуссии;
5) обобщающее выступление учителя, его анализ ситуации;
6) оценивание учащихся учителем
9 слайд

Реальные жизненные ситуации, детально и подробно отраженные. При этом их учебное назначение может сводиться к тренингу обучаемых, закреплению знаний, умений и навыков поведения (принятия решений) в данной ситуации. Кейсы должны быть максимально наглядными и детальными.
Практические кейсы
10 слайд

Отражают типовые ситуации, которые наиболее часты в жизни. Ситуация, проблема и сюжет здесь не реальные, а такие, какими они могут быть в жизни, не отражают жизнь «один к одному»
Обучающие кейсы
11 слайд

Они выступают моделями для получения нового знания о ситуации и поведения в ней. Обучающая функция сводится к исследовательским процедурам.
Научно-исследовательские кейсы
12 слайд

Что дает использование
кейс-технологии
Преподавателю
Ученику
Доступ к базе современных учебно-методических материалов
Организация гибкого учебного процесса
Возможность реализации некоторых элементов учебного процесса во внеурочное время

Работа с дополнительными материалами
Общение с другими учащимися в группе
Освоение современных информационных технологий
13 слайд

ПРАКТИЧЕСКАЯ ЧАСТЬ:
Математика
раздел «Куб и его изображение»
Тип кейса: исследовательский кейс
Содержание кейса
Задание: Мы с вами живем в мире, который неразрывно связан с геометрией. Нас окружает много предметов, которые подчиняются правилам геометрии :наш дом , любимые игрушки ,вещи , которыми мы пользуемся в повседневной жизни.
Задача – рассмотреть изображение куба, основные свойства куба и научиться изображать куб .
Проблема: к какому виду геометрических фигур можно отнести куб.
Для решения проблемы учащиеся должны :
-рассмотреть модель куба;
– выяснить, из каких геометрически фигур построен куб;
– как называются стороны куба( грани), отрезки( ребра,вершины
– свойства куба;
– научиться выполнять чертёж куба.
Цель:организовать исследование объекта, сбор и изучение информации о кубе.
14 слайд

Работа в группах. Затем организуется работа в подгруппах по поиску решения поставленной проблемы. Группам предлагается оформить карточку-задание.

Обсуждение. На следующем этапе организуется обсуждение вариантов решений в группах. Каждая из групп поочередно работает над заданием. Все выводы заносит в таблицу.

Вывод. Преподаватель совместно с учащимися делает выводы, опираясь на презентованные группами варианты решений, подводятся итоги занятия.

Практическая часть. Учащиеся выполняют индивидуально чертёж.

Рефлексия. В завершение проводится рефлексия.
15 слайд

РАБОТА С КЕЙСОМ:
Кейс предоставляется ученикам непосредственно на занятии.
Задание №1.Вопросы для обсуждения:
– Какие фигуры называются многоугольниками?
– На какие группы можно разделить многоугольниками?
-Назовите свойства прямоугольника, четырехугольника, квадрата?
– Что необходимо учитывать при выборе материалов?
– Посмотрите на чертёж. Что изображено на чертеже? (Фигуры)
– Какая фигура лишняя и почему? (Круг – он без углов, треугольник – у него 3 угла, ромб – нет прямых углов)
– Какие геометрические фигуры остались? (Прямоугольник и квадрат)
16 слайд

Задание №2

– Посмотрите на чертёж. Что изображено на чертеже? (Фигуры)
– Какая фигура лишняя и почему? (Круг – он без углов, треугольник – у него 3 угла, ромб – нет прямых углов)
– Какие геометрические фигуры остались? (Прямоугольник, квадрат и ??????)
22 слайд

Задание №4
Практическая часть
Учащиеся выполняют чертёж куба на бумаге.
23 слайд

Благодарю
Всех за внимание и желаю творческих учеников!

Краткое описание документа:

КЕЙС-МЕТОД на уроке математики

Кейс-технология – это общее название технологий обучения, представляющих собой методы анализа.

Итак, кейс-технология – это интерактивная технология для краткосрочного обучения на основе реальных или вымышленных ситуаций, направленная не столько на освоение знаний, сколько на формирование у слушателей новых качеств и умений.

Преимущества этой технологии: коллективный характер познавательной деятельности, творческий подход к познанию, сочетание теоретического знания и практических навыков столь привлекательны, что привлечение его к работе, даже при наличии трудностей в реализации методики в рамках школы имеет очень много плюсов.

История возникновения

Исторически Кейс-метод возник в начале XX в.в Школе бизнеса Гарвардского университета (США). Особый упор делался на самостоятельную работу студентов, в процессе которой просматривался и анализировался практический материал. В 1920 г. профессор Копленд издал первый сборник кейсов.

К середине прошлого столетия данная технология приобрела четкий технологический алгоритм, стала активно использоваться не только в американском, но и в западноевропейском образовании.

В последнее время в Российской школе широкое распространение получили активные методы обучения, которые направлены на развитие личности и формирование здоровья, среди них метод проектов, ИКТ, кейс – технологии.

Кейс (с английского case)

– Портфель, чемодан, сумка, папка (в нашем варианте – пакет документов для работы учащихся);

Особенностью кейс – технологии является создание проблемной ситуации на основе фактов из реальной жизни.

Данная технология имеет многоплановые цели:

научить обучающихся как индивидуально, так и в составе группы анализировать информацию;
сортировать информацию для решения выбранной задачи;
выявлять ключевые проблемы предложенной ситуации;
генерировать альтернативные пути решения и оценивать их;
выбирать оптимальное решение и формировать программы действий:Работа ученика с кейсом1 этап — знакомство с ситуацией, её особенностями;2 этап — выделение основной проблемы (проблем), 3 этап — предложение концепций или тем для «мозгового штурма»;4 этап — анализ последствий принятия того или иного решения;5 этап — решение кейса — предложение одного или нескольких вариантов последовательности действий. Действия учителя в кейс – технологии:1)создание кейса или использование уже имеющегося; 2) распределение учеников по малым группам (4-6 человек);3) знакомство учащихся с ситуацией, системой оценивания решений проблемы, сроками выполнения заданий организация работы учащихся в малых группах, определение докладчиков;4) организация презентации решений в малых группах; 5) организация общей дискуссии; 6) обобщающее выступление учителя, его анализ ситуации; 7) оценивание учащихся учителемВиды кейсов:

1.Практические кейсы. Реальные жизненные ситуации, детально и подробно отраженные. При этом их учебное назначение может сводиться к тренингу обучаемых, закреплению знаний, умений и навыков поведения (принятия решений) в данной ситуации. Кейсы должны быть максимально наглядными и детальными.

2.Научно-исследовательские кейсы. Они выступают моделями для получения нового знания о ситуации и поведения в ней. Обучающая функция сводится к исследовательским процедурам.

3.Обучающие кейсы. Отражают типовые ситуации, которые наиболее часты в жизни. Ситуация, проблема и сюжет здесь не реальные, а такие, какими они могут быть в жизни, не отражают жизнь «один к одному».

При применении кейс – технологии достигаются и социальные компетентности.

Обучаемые:

получают коммуникативные навыки;
развивают презентационные умения;
формируют интерактивные умения, позволяющие эффективно взаимодействовать и принимать коллективные решения;
приобретают экспертные умения и навыки;
учатся учиться, самостоятельно отыскивая необходимые знания для решения ситуационной проблемы.Примерная структура кейса: 1.Ситуация – случай, проблема, история из реальной жизни 2.Контекст ситуации – хронологический, исторический, контекст места, особенности действия или участников ситуации. 3.Комментарий ситуации, представленный автором4.Вопросы или задания для работы с кейсом5.Приложения Пример применения кейс-технологии на уроках математики при изучении раздела «Куб и его изображение»Вид кейса: обучающийТип кейса: исследовательский кейсСодержание кейса Задание:Мы с вами живем в мире, который неразрывно связан с геометрией. Нас окружает много предметов, которые подчиняются правилам геометрии :наш дом , любимые игрушки ,вещи , которыми мы пользуемся в повседневной жизни. Изучить куб.Задача – рассмотреть изображение куба, основные свойства куба и научиться изображать куб .Проблема:к какому виду геометрических фигур можно отнести куб.Для решения проблемы учащиеся должны :-рассмотреть модель куба;– выяснить, из каких геометрически фигур построен куб;– как называются стороны куба( грани), отрезки( ребра,вершины– свойства куба;– научиться выполнять чертёж куба.Цель: организовать исследованиеобъекта, сбор и изучениеинформации о кубе. Класс делится на 4 группы, каждая группа получает задачу.1 группа–рассмотреть стороны куба, просчитать ихи выяснить какой фигуройявляетсягрань куба( воспользоваться материалом учебника У с. 23№62)2 группа– рассмотреть вершины куба, просчитать ихи выяснитьсколько ребер выходит из вершины( воспользоваться материалом учебника У с. 23№62)3 группа– рассмотреть стороны куба, просчитать ихи выяснить какой фигуройявляетсягрань куба, определить все ли грани куба равны между собой( воспользоваться материалом учебника У с. 23№62)4 группа–– рассмотреть куб, выяснить ,что является ребром куба? просчитать ихи выяснитьсколько ребер выходит из вершины( воспользоваться материалом учебника У с. 23№62)Подготовительный этап
Группам выдаются песочные часы.( на каждый этап отводится время для обсуждения и вывода)
Назначается жюри(заполняют бланк «Критерии оценок работы групп»)
Назначаются старшие групп.
Задания выдаются из кейсастаршим групп в конверте.Работа в группах. Затем организуется работа в подгруппах по поиску решения поставленной проблемы. Группам предлагается оформить карточку-задание.

Задание 1.

– Посмотрите на чертёж. Что изображено на чертеже? (Фигуры)

– Какая фигура лишняя и почему? (Круг – он без углов, треугольник – у него 3 угла, ромб – нет прямых углов)

– Какие геометрические фигуры остались? (Прямоугольник, квадрат и ?????)

– Кто догадался, какая тема урока? Кто может назвать, сформулировать её?

Задание 2.

– Обведите замкнутой линией все прямоугольники на чертеже.

– Обведите замкнутой линией все квадраты на чертеже.

– Что вы заметили? (Что квадраты находятся внутри множества прямоугольников). Почему? (Это тоже прямоугольник)

– Четыре угла значит четырёхугольник, все углы прямые. Из этого следует, что квадрат прямоугольник. Но это особенный прямоугольник. У квадрата все стороны равны/

Задание 3.

№	Группа 1	ответы
	рассмотреть стороны куба, просчитать (воспользоваться материалом учебника У с. 23№62)
1	Сколько сторон у куба
2	Грань куба -это
3	Все ли грани куба равны
Вывод:
Отметить на рисункецветными карандашамиграни куба

№	Группа 2	ответы
	рассмотреть стороны куба( воспользоваться материалом учебника У с. 23№62)
1	Сколько рёбер у куба
2	Сколько ребер выходит из вершины
3	Что является ребром куба
	Вывод:
Вывод:
Отметить на рисункецветными карандашамирёбра куба

№	Группа 3	ответы
	рассмотреть стороны куба, просчитать ихи выяснить какой фигуройявляетсягрань куба, определить все ли грани куба равны между собой
1	Сколько сторон у куба
2	Грань куба-это
3	Все грани куба-
Вывод:
Отметить на рисункецветными карандашамистороны куба

№	Группа 4	ответы
	рассмотреть куб и выяснить, что является ребром куба? просчитать ихи выяснитьсколько ребер выходит из вершины
1	Сколько реберкуба
2	Реброкуба-это
3	Ребра кубамежду собой
Вывод:
Отметить на рисункецветными карандашамиребракуба

Критерии оценок работы групп.

Наименование критерия	балл	балл
Работа по карточке
Правильно дан ответ на вопрос №1	1
Правильно дан ответ на вопрос №2	1
Правильно дан ответ на вопрос №3	1

Активность работы всех членов группы	1
Четкость и грамотность математического языка	1
Правильно сделан вывод	1
Соблюдение регламента	1
Штрафные баллы (нарушение правил ведения дискуссии, некорректность поведения и т.д.)	-1
Итого

Обсуждение. На следующем этапе организуется обсуждение вариантов решенийв группах. Каждая из групп поочередно работает над заданием. Все выводы заносит в таблицу.

Вывод. Преподаватель совместно с учащимися делает выводы, опираясь на презентованные группами варианты решений, подводятся итоги занятия.

Практическая часть. Учащиеся выполняют индивидуально чертёж.

Рефлексия. В конце урока в качестве рефлексии учащимся и всем присутствующим даётся возможность осуществить самоанализ, дать качественную оценку своей деятельности и содержанию урока.

Выводы:

Кейс-технология не является обязательным на каждый день и составляется на основе поурочного плана и не отнимает много времени.

Поэтому, опираясь на индивидуальные особенности учащихся и их степень компетентности, этапы работы над определенными умениями и навыками, следует использовать «кейс» – технологию.

Задания разного уровня, анализ информации на установление соответствия и с выбором ответа дают хороший результат активности, личностного соревновательного духа и вдохновения, а также обеспечивает эффективный индивидуальный контроль системной деятельности учащихся на уроке для взаимодействия с родителями.

Информационные источники

Специальный сайт, посвященный методике ситуационного обучения с использованием кейсов.. http://www.casemethod.ru/
Реферативный обзор на тему «Метод case-study как современная технология профессионально-ориентированного обучения» подготовлен коллективом Отдела методического обеспечения учебного процесса под руководством Н.Н. Комиссаровой с использованием литературных источников (учебных пособий, сборников статей, материалов периодических изданий), опубликованных в открытой печати на русском языке, а также интеллектуальных ресурсов сети Интернет. http://volkov.mmm-tasty.ru/entries/31269
Доценко И.Г. Проектирование социально-педагогической деятельности классным руководителем//Воспитание школьников, 2010 №1.- С. 27-33
Иванова Н. В. Возможности и специфика применения проектного метода в начальной школе. //Начальная школа.-2004.-№ 2.-с. 96—101.
Крюкова Е.А. Теоретические основы проектирования и применения личностно-развивающих педагогических средств. Дис. … д-ра пед. наук. – Волгоград, 2000. – 251 с

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 256 057 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Другие материалы

11.02.2018
565
1

11.02.2018
387
2

Вам будут интересны эти курсы:

Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

Источник

тема: «Кейсовые технологии. Применение кейсовых технологий на уроке математики»

Выполнил:

Зеленцова Наталья Евгеньевна

г. Подольск

2019

СОДЕРЖАНИЕ

Введение	3
1. Кейс-технология: история создания, особенности, классификация, структура.	4
1.1 История создания	4
1.2 Технологические особенности метода CASE-STUDY	5
1.3 Классификация кейсов	7
1.4 Структура кейса	10
2. Применения кейс-метода на уроках математики	11
Пример №1	11
Пример №2	14
Пример №3	15
Пример №4	16
Пример №5	18
Пример №6	20
Выводы	29
Заключение	30
Список использованных источников	32

ВВЕДЕНИЕ

Проблема усвоения знаний давно не дает покоя учителям. Практически любое действие человека в жизни, не только учеба, связана с необходимостью усвоения и переработки тех или иных знаний, той или иной информации. Научить учиться, а именно усваивать и должным образом перерабатывать информацию – главный тезис деятельного подхода к обучению.

В соответствии с федеральным государственным образовательным стандартом второго поколения (ФГОС) основным результатом деятельности современной школы должна стать не сама по себе система знаний, умений, навыков учащихся, а комплекс компетентностей в различных областях деятельности. Необходимо учить ребенка так, чтобы выпускник школы мог самостоятельно решать возникающие жизненные проблемы. Для этого от учителя требуется организовать деятельность учеников в поисковом режиме.

Каждому педагогу необходимо ориентироваться в широком спектре современных инновационных технологий, идей школ, направлений, не тратить время на открытие уже известного. Сегодня быть педагогически грамотным специалистом нельзя без изучения всего обширного арсенала образовательных технологий. Тем более это нашло отражение в должностных инструкциях, в аттестационных материалах. Использование инновационных образовательных технологий является одним из критериев оценки профессиональной деятельности преподавателя.

Цель моей работы – знакомство с технологией кейс-метода, исследование применения учителями кейс-метода на уроках математики, для использования в образовательном процессе.

Кейс-технология является одной из современных образовательных технологий, способствующей развитию умения анализировать жизненные ситуации, оценивать альтернативы, выбирать оптимальный вариант и планировать его осуществление, или метод конкретных ситуаций. Внедрение учебных кейсов в практику российского образования в настоящее время является весьма актуальной задачей. Организационной основой кейс-методов является активное обучение, а содержательной основой – проблемное обучение. Главное предназначение кейс-технологий – развивать способность прорабатывать различные проблемы и находить их решение, другими словами научиться работать с информацией. При этом акцент делается не на получение готовых знаний, а на их выработку, на сотворчество учителя и ученика! Если такой подход в течение учебного цикла применяется многократно, то у обучающихся вырабатывается устойчивый навык решения практических задач. По сравнению с широко распространенными методами активного обучения школьников эта технология не столь известна. Еще менее опробована она в применении к математике в школе, поскольку в отличие от гуманитарных дисциплин она предполагает разрешение участниками учебных групп проблемы, по своей сути, не имеющей однозначного решения.

1. КЕЙС-ТЕХНОЛОГИЯ: ИСТОРИЯ СОЗДАНИЯ, ОСОБЕННОСТИ, КЛАССИФИКАЦИЯ, СТРУКТУРА.

1.1 История создания

Кейс-технология, или CASE-STUDY, (от англ. Case –случай, ситуация, рассмотрение конкретного случая») – это метод конкретных ситуаций, т.е. Техника обучения, использующая описание реальных экономических, социальных и других ситуаций. Ученики должны вникнуть в суть проблемы, подыскать возможные пути решения, провести анализ и выбрать наиболее оптимальное решение.

«Родиной» данного метода, являются Соединенные Штаты Америки. Метод кейсов впервые был применён в гарвардской школе бизнеса в 1924 году, а в России был опробован в 70-х годах хх века в МГУ имени Ломоносова. Слушателям давались описания определённой ситуации, в которой оказалась реальная организация в ходе своей деятельности, и они должны были – самостоятельно или коллективно – найти решение проблемы.

«культурологической основой появления и развития кейс-метода явился принцип «прецедента» или «случая».

Кейс – это описание реальной ситуации.

Кейс – это жизненная история, включающая в себя необходимую информацию: для принятия решения, разрешения конфликта или проблемы, которая может быть предложена для обсуждения в группе, и выявления позиций слушателей по существу вопроса.

Кейс – это события, реально произошедшие в той или иной сфере деятельности и описанные авторами для того, чтобы спровоцировать дискуссию в учебной аудитории, “сподвигнуть” учащихся к обсуждению и анализу ситуации, и принятию решения.

Кейс – не просто правдивое описание событий, а единый информационный комплекс, позволяющей понять ситуацию (по Смоляниновой О.Г.).

1.2 Технологические особенности метода CASE-STUDY:

Метод представляет собой специфическую разновидность исследовательской аналитической технологии, т.е. включает в себя операции исследовательского процесса, аналитические процедуры.
Метод CASE-STUDY выступает как технология коллективного

Обучения, важнейшими составляющими которой выступают работа в группе (или подгруппах) и взаимный обмен информацией.

Метод CASE-STUDY в обучении можно рассматривать

Как синергетическую технологию, суть которой заключается в подготовке процедур погружения группы в ситуацию, формирования эффектов умножения знания, инсайтного озарения, обмена открытиями и т.п.

метод CASE-STUDY интегрирует в себе технологии развивающего обучения, включая процедуры индивидуального, группового и коллективного развития, формирования многообразных личностных качеств обучаемых.
выступает как специфическая разновидность проектной технологии. В обычной обучающей проектной технологии идет процесс разрешения имеющейся проблемы посредством совместной деятельности учащихся, тогда как в методе CASE-STUDY идет формирование проблемы и путей ее решения на основании кейса, который выступает одновременно в виде технического задания и источника информации для осознания вариантов эффективных действий.
Концентрирует в себе значительные достижения

Технологии «создания успеха». В нем предусматривается деятельность по активизации обучающихся стимулирование их успеха, подчеркивание достижений обучаемых. Именно достижение успеха выступает одной из главных движущих сил метода, формирования устойчивой позитивной мотивации, наращивание познавательной активности.

Метод предполагает:

Подготовленный в письменном виде пример

Кейса из практики;

Самостоятельное изучение и обсуждение кейса

Учащимися;

Совместное обсуждение кейса в классе под

Руководством учителя;

Следование принципу “процесс обсуждения

Важнее самого решения”.

Форма активного проблемно-ситуативного учебного занятия. Непосредственная цель CASE-STUDY-совместными усилиями:

Сформулировать,

Проанализировать,

Дать оценку,

Выработать алгоритм практического решения проблемной ситуации, возникающей в контексте конкретного положения дел — случая.

Основная функция метода CASE-STUDY – учить решать сложные неструктурированные проблемы, которые невозможно решить аналитическим способом.

1.3 Классификация кейсов

По наличию сюжета

Сюжетные кейсы – обычно содержат рассказ о произошедших событиях, включают действия лиц и организаций;

Бессюжетные кейсы – как правило,

Прячут сюжет, потому что четкое изложение сюжета в значительной степени раскрывает решение. Внешне они представляют собой совокупность статистических материалов, расчетов, выкладок, которые должны помочь

Диагностике ситуации, восстановлению сюжета.

По временной последовательности

Материала:

Кейсы с естественной временной

Последовательностью событий (от прошлого к

Настоящему) позволяют хорошо выявлять причинно-

Следственные связи.

Кейсы-воспоминания характеризуются тем, что время в них прокручивается назад: герои что-то вспоминают, сами воспоминания отрывочны, часто несистемные, фрагментарны, что затрудняет восстановление временных цепочек. По сути дела, анализ кейса сводится к реконструкции ситуации, её осмыслению в аспекте той или иной познавательной парадигмы.
Прогностические кейсы, представляя описание событий недавнего прошлого и настоящего, ставят задачу выработать наилучший вариант (сценарии) развития ситуации. Точной классификации кейсов не существует. Виды и типы кейсов подразделяются:

По объему:

Мини-кейс

Кейс средних размеров

Макро-кейс

Обучающиеся изучают полученные материалы и анализируют ситуацию в группах. После чего в каждой группе генерируются различные идеи по поводу

Решения данной проблемы, затем принятые предложения оформляются для презентации всей аудитории; на следующем этапе работы проводится презентация, в ходе которой каждая группа предлагается всей аудитории решение данной проблемы с обоснованием своих аргументов; после презентации материалов всех групп

Проводится пресс-конференция, в ходе которой обучающиеся делятся своими выводами о ходе групповой работы и сути решенной (или решаемой) проблемы.

Методы кейс технологии:

Метод инцидентов
Метод разбора деловой корреспонденции
Игровое проектирование
Ситуационно-ролевая игра
Метод дискуссии
КЕЙС-СТАДИ

Метод инцидента

Род дискуссионных методов обучения, основанный на разборе случаев из реальной практики. Это анализ инцидентов – случай, происшествие, столкновение (обычно неприятного характера).

Цель — поиск информации для принятия решения самим слушателем. Как следствие – обучение его работе с необходимой информацией: ее сбору, систематизации и анализу.

Сообщение может быть письменным или устным

По типу: “случилось или произошло…для принятия обучающимися обоснованного решения им предлагается явно недостаточная информация, поэтому необходимо прежде всего:

* разобраться в обстановке;

* определить, есть ли проблема и в чем она состоит;

* подумать. Что надо делать;

* выяснить что надо знать для принятия того или иного решения.

Метод разбора деловой корреспонденции

Цель – получение навыков работы с документами и бумагами, относящимися к или иной организации, ситуации, проблеме.

Игровое проектирование

Цель данного метода – процесс создания совершенствования объектов. Игровое проектирование может включать в себя проекты разного типа:

•исследовательский

•поисковый

•творческий

•прогностический

•аналитический.

Метод проигрывания ролей (инсценировки)

Цель данного метода – в виде инсценировки создать

Перед аудиторией правдивую историческую, правовую,

Социально-психологическую ситуацию и затем дать возможность оценить поступки и поведение участников игры. Разновидности: «разыгрывание ситуаций в ролях»

Ролевые игры.

Групповая дискуссия

Дискуссия – обмен мнениями по какому-либо вопросу в

Соответствии с более или менее определенными правилами процедуры. К интенсивным технологиям обучения относятся групповые и межгрупповые дискуссии.

Порядок работы по методу “КЕЙС-СТАДИ”

Индивидуальная работа 30% времени

1. Ознакомление с ситуацией (по тексту или работа по рассказу).

2. Выявление проблем.

3. Обобщение информации.

4. Анализ информации.

Групповая работа 50% времени

1. Уточнение проблем и их иерархия.

2. Формирование альтернатив решения

3. Составление перечня преимуществ и недостатка каждого решения.

4. Оценка альтернатив.

Индивидуальная и групповая работа 20% времени

1 обоснование возможности применения альтернатив.

2 подготовка отчета и презентации результата

Роль учителя при использовании метода кейсов двояка: он может быть консультантом и искать пути решения вместе с учениками, а может играть роль эксперта. приведу конкретные примеры уроков с применением метода кейсов.

Классификация кейсов может производиться по различным признакам исходя из целей и задач процесса обучения.

Как написать хороший “кейс”?

1.4 Структура кейса:

Название (интригующее, проблемное);

Контекст (значимые данные об окружающих (внешних) факторах которые помогают понять и интерпретировать кейс);

Случай (это определенная вещь, которая нас интересует и как она связана с главным вопросом исследования);

Факты (объективная информация (статистика, отрывки из документов, результаты анкетирования, экспертные мнения, фото и пр.);

Решения (вариативная часть кейса которая может содержать рефлексию, комментарии, сценарий).

Как разработать “кейс”? Ряд типовых шагов для

Создания кейса:

1. Определение темы и вопроса исследования;
2. Выбор объекта исследования – «конкретной ситуации»;
3. Определение контекста;
4. Планирование кейс-исследования, проведение сбора материала и анализа материала;
5. Поиск решений, обсуждение возможных сценариев дальнейшего развития ситуации;
6. Описание и редактирование кейса;
7. Формулирование вопроса для дальнейшего обсуждения ситуации.

Что не является «кейсом»?

Хью Мак Лин выделяет три признака:

Не актуальный и не вызывающий интереса материал (отсутствие загадки, отсутствие вопроса, отсутствие противоречия).
Материал, в котором отсутствует изложения контекста.
Отсутствие в описании материала определенных живых элементов: истории, интервью, жизненных ситуаций.

2. ПРИМЕНЕНИЯ КЕЙС-МЕТОДА НА УРОКАХ МАТЕМАТИКИ

Пример № 1 – урок по теме “практическое применение средних величин”. Данный урок рекомендуется проводить в 8-11 классах

Учащиеся получают” кейсы”. В кейсах содержится необходимая информация: что представляет собою статистика, где, как и когда она оформилась как наука, какие виды средних величин существуют и используются в статистике – даются определения средних: среднего арифметического, среднего геометрического, среднего гармонического, среднего квадратичного, моды, медианы, размаха, дисперсии, приводятся примеры их вычисления. Это – содержание кейса. Ученики в течение определённого времени знакомятся с этим содержанием, а затем учитель оглашает сюжет: на место токаря претендуют двое рабочих, для которых был установлен испытательный срок. В течение этого срока они должны были изготовить по одинаковому количеству деталей.

Результаты этой работы представлены в таблице (таблицу можно показать на слайде):

День недели	Дневная выработка
1-й рабочий	2-й рабочий
Понедельник	52	61
Вторник	54	40
Среда	50	55
Четверг	48	50
Пятница	46	44

Учащимся предлагается выбрать лучшего претендента.

Вот тут и начинается процесс поиска решения: поначалу учащиеся считают среднее арифметическое количества деталей, производимое каждым рабочим в день, средняя производительность труда у обоих рабочих оказывается одинаковой (50 деталей в день). Понятно, что возникает предположение проверить данные по другим средним, оказывается, что и они не приводят к ответу. Так, например, мода, т.е. число, наиболее часто встречающееся в ряду данных, просто отсутствует. При испытании медианы (если ранжировать ряд данных, то медиана – это среднее число в ряду) получаем, что в обоих случаях медианы одинаковы. Здесь учитель может выступить в роли консультанта и посоветовать посчитать отклонения от среднего арифметического. Учащиеся при подсчёте убеждаются, что сумма этих отклонений и в первом, и во втором случае 0, тогда возникает идея о том, что если бы не было знаков «минус», то нуля бы не получилось. Возникает попытка посчитать квадраты отклонений, т.к. при возведении в квадрат минусы исчезают, и вот достигается результат: для первого рабочего это будет 40, а для второго 282, что означает, что второй рабочий имеет нестабильную производительность труда: в какие-то дни работает не в полную силу, а в какие-то дни навёрстывает упущенное, а это наверняка сказывается на качестве производимой продукции.

Если класс сильный и работает быстро, то на этом же уроке может быть “проиграна” более сложная ситуация: во время прохождения отбора на замещение вакантной должности рабочие работали с одинаковой производительностью труда, но разное количество дней. Окажется, что квадраты отклонений, сравнение которых в предыдущей ситуации привело к решению проблемы, здесь будет одинаковым, а к окончательному ответу на вопрос учащихся привет подсчет среднего арифметического квадратов отклонений, т.е. дисперсии. Например, «два токаря вытачивали одинаковые детали, причём первый работал полную неделю, а второй только 4 дня. Дневная выработка первого токаря – 53, 54, 49, 48, 46, а второго – 52, 46, 53, 49. Кто из них работает стабильнее?»

Cоставляется план решения задачи:

Найдём среднее арифметическое дневной выработки i рабочего (50).
Найдём среднее арифметическое дневной выработки ii рабочего (50)
Найдём ежедневные отклонения от среднего для каждого рабочего (3, 4, – 1, – 2, – 4 – для i рабочего; 2, – 4, 3, – 1 – для ii рабочего)
Найдём квадраты отклонений (9, 16, 1, 4,16 и 4, 16, 9, 1) – одинаковы, а в предыдущей задаче это сравнение приводило к ответу.
Найдём среднее арифметическое квадратов отклонений, т.е. дисперсию – 9,2 для первого рабочего и 7,5 для второго.
Ответ: второй токарь работает стабильнее первого.

Понятно, что в завершении урока нужно проанализировать деятельность учащихся, отметив наиболее яркие озарения, и, подводя итог, подчеркнуть, что теоретические знания о средних статистических величинах помогают решать насущные практические вопросы, например, вопрос отбора наиболее подходящих для данного вида деятельности работников. для более младших школьников (6-7 классов) другой урок.

Пример № 2 – практическое применение средних величин «определение стоимости жилья». Урок для школьников (6-7 классов). Ученики получают содержание кейса – от чего зависит стоимость жилья – в виде таблицы, где указана стоимость 1 кв.м, в условных единицах:

Номер зоны		Количество комнат
	1	2	3
1	875	906	931
2	628	647	659
3	639	659	668
4	596	624	635
5	574	604	622
6	611	631	664
7	605	624	648
8	616	635	652
9	713	728	743
10	721	742	769
11	622	639	658
12	669	684	679

Поправочные коэффициенты, влияющие на стоимость квартиры

Параметры	Примечания	%
Этаж	Первый	-3
	Последний	-1
	Не крайний	0
Лифт	Нет	-1
	Есть	+1
Балкон	Балкон или лоджия	+1
	Без балкона	-1
Мусоропровод	Нет	-1,5
	Есть	0
Окна	Двор	+2,5
	Двор, улица	0
	Улица	-2

Кроме этого, в «кейсе» напоминание о процентах – что это такое, где и как зародились, как решается главная задача – нахождение процента от числа.

Далее ученики, изучив содержание «кейса» разбиваются на группы, и каждая группа получает условную сумму, исходя из размеров которой должна подобрать оптимальный вариант жилья (например, двухкомнатной квартиры) – это сюжетная линия «кейса». Здесь учитель может варьировать «проблемы», например, потенциальному покупателю необходимо, чтобы окна квартиры выходили во двор и т.д. на данном уроке учитель выступает в роли эксперта.

Пример 3. Ситуационно-ролевая игра.

Сейчас я предлагаю вам принять участие в игре. Я предлагаю открыть вам три фирмы по реставрации и художественной отделке зданий. Итак, вам поступил заказ на реставрацию великой китайской стены. И вам необходимо составить смету расходов по выполнению реставрационных работ с внешней стороны стены. Условия таковы: длина стены – 8875,8м, высота в среднем – 4 метра. У первой фирмы «феникс» имеются мраморные плиты площадью – 1 квадратный метр и стоимостью – 1600 руб. У второй фирмы «альтернатива» плиты горных пород площадью 0,8 квадратных метров стоимостью 1300 руб. У третьей фирмы «гамма» облицовочный камень площадью 0,5 квадратных метров и стоимостью 1000 руб. Вам необходимо выполнить необходимые расчеты и выбрать самый недорогой вариант отделки.

Ответ:

1 ряд: 1) 8875,8*4=35503,2

2) 35503,2:1=35503,2 плит

3)35503,2*1600=56 805 120 (млн. Руб.) Стоимость работ.

2 ряд: 1) 8875,8*4=35503,2

2) 35503,2: 0,8= 44379

3) 44379*1300=57 692 700 (млн. Руб.) Стоимость работ.

3 ряд: 1) 8875,8*4=35503,2

2) 35503,2:0,5=71006,4

3) 71006,4*1000=71 006 400 (млн. Руб.) Стоимость работ.

Давайте сделаем вывод, у какой фирмы наиболее дешевый вариант отделки. Вывод: самый дорогой вариант отделки у фирмы «гамма», самый дешевый у фирмы «феникс».

На уроке рассмотрение конкретных ситуаций позволяет ученику «примерить на себя» ту или иную профессию, для того чтобы сделать наиболее осознанный выбор. Применение в профильном обучении кейс-технологии позволит сформировать у учащихся высокую мотивацию к учебе, развивать личностные качества, значимые для будущей профессиональной деятельности.

Пример 4. По теме «действительные числа»

В математике есть комплекс нестандартных заданий, которые могут способствовать не только возникновению интереса к данной теме у учащихся, но и повысить качество знаний школьников. К числу таких заданий относятся математические фокусы [1], основанные на каких-либо математических законах. Смысл их обычно состоит в отгадывании чисел или в проведении несложных операций над ними. Фокус заключается в том, что только фокусник знает секрет, под которым подразумеваются свойства чисел, на которых строится сам фокус. Мы предлагаем научно-исследовательские кейсы, в основе которых лежит исследование теоретической базы математических фокусов. На первом этапе работы с кейс-задачей ученики знакомятся ситуацией, представленной в фокусе, разбирают ее на конкретных примерах. На втором этапе начинается работа в группах: школьники изучают рекомендованную учителем обязательную и дополнительную литературу. В результате работы над вторым этапом школьники должны сформировать теоретические положения и факты, которые помогут им понять математический фокус, разгадать его смысл. На третьем этапе учащиеся в группах ищут возможные альтернативные решения. На заключительном этапе группы сравнивают свои решения. Кейс-задача 1. Задача: запишите трехзначное число, затем отнимите от него сумму цифр этого числа. Далее зачеркните одну цифру и сообщите сумму оставшихся. Учитель без труда называет вычеркнутую цифру, так как знает, что сумма цифр полученного числа всегда кратна 9. Например, ученик записал число 458, далее он вычитает 17, получает число 441. Если он вычеркнет 4, то сообщает, что сумма оставшихся чисел равна 5, вы называете цифру 4, если вычеркнет 1 и сообщит вам сумму, равную восьми, то вы называете цифру 1. На следующем этапе работы с кейс-задачей школьники обобщают изученный материал по теме «действительные числа», выписывают основные теоремы, определения, свойства чисел, которые помогут им «расшифровать» математический фокус. На третьем этапе учащиеся предлагают свои решения. Рассмотрим одно из них:

1. Как известно, трехзначное число можно записать в виде

a . 102 + b . 10 + c.

2. Выполним над данным числом последовательность действий, предлагаемых в фокусе:

a .102 + b . 10 + c – (a + b + c) = a . 102 + b . 10 + c – a – b – c =

a . (102 – 1) + b . (10 – 1) = 99 a + 9 b.

Замечаем, что 99 a ÷ 9 и 9 b ÷ 9, следовательно, (99 a + 9 b) ÷ 9.

Отметим, что учащимся необходимо резюмировать свой действия, то есть выделить основные используемые теоретические факты при разгадке фокуса, а именно: – запись числа в десятичной системе счисления; – теорема: если каждое слагаемое делится на некоторое число, то и сумма делится на это число.

Мы рассмотрели некоторые математические фокусы из огромного количества, которые можно использовать в качестве основы исследовательских кейсов, предлагаемых ученикам старшей школы. Применение их в практике на уроках математики может увеличить мотивацию к изучению математики, сделать интересным и полезным отвлечение от учебного материала, развить математические навыки, расширить представления о свойствах чисел.

Пример 5. Кейс «проценты в жизни» метод КЕЙС-СТАДИ.

Вид кейса: печатный.

Цели урока.

1. Развитие познавательного интереса к вычислению процентов, через решения жизненных задач;

2. Отработка практических навыков при решении задач на проценты;

3. Развитие интереса учащихся к математике. Расширение кругозора через решение задач связанными с жизненными ситуациями.

Задачи: образовательная: углубление и систематизация теоретических знаний, отработка умений и навыков при вычислении процентов на примерах решения задач; развивающая: развитие умения распознавать типы задач на проценты; воспитательная: воспитание активности, побуждение познавательного интереса, воспитание настойчивости в достижении цели.

Пример фрагмента содержания кейса.

Задание №1. Познакомиться с ситуацией, представленной в кейсе и с документами, связанными с взятием кредита.

Задание №2. Исследовать представленную историю и документы. Выяснить причины, почему могла произойти такая ситуация.

Задание №3. Выписать все неизвестные термины и узнать их значение.

Задание №4. Рассчитать долг по кредиту. Предложить свои варианты решений данной ситуации. Проанализировать последствия принятия того или иного решения. Сформулировать советы людям, которые собираются брать кредит.

Задание №5. Представить полученные результаты своей работы перед ребятами. Текст задания.

Это было почти три года назад. Я взял в кредит ноутбук за 30 тысяч рублей. Исправно платил по 2500 рублей в месяц, в течение двух лет и трех месяцев, а потом вдруг лишился работы. На этот случай у меня были отложены деньги (приличная сумма), но, увы, деньги незадолго до моего увольнения я потратил на новый телефон.

Как я выжил – отдельная тема. У родителей нет возможности помогать. Друзей, способных занять денег на оплату квартиры и кредит, у меня не было.

Я устроился на работу, но пока стажировался, пока устраивался, пока получил зарплату прошло около двух месяцев. Были подработки, но и кушать нужно было. Получил зарплату, ура! Думаю, ну ладно – два месяца я не платил кредит, буду платить с отсрочкой и ничего не будет. Вот наивный. Оказывается, мне начисляли штраф за каждый день просрочки. Долг рос с каждым днем….

Фрагмент документа.

Общий размер кредита – 30 000 тыс. рублей. Кредит предоставляется на оплату ноутбука.

Ссудозаемщик обязуется погасить кредит до “1” октября 2015г. При не поступлении средств в погашение кредита в указанный срок задолженность по ссуде, включая проценты, вносится на счет просроченных ссуд и списывается со счета n ____________________ в _________________________ банке.

За пользование кредитом ссудозаемщик вносит плату в размере 18 процентов годовых. Проценты начисляются и взыскиваются банком ежемесячно после 20 числа каждого месяца в бесспорном порядке инкассовым поручением с расчетного счета ссудозаемщик. Отсчет срока по начислению процентов начинается с даты выдачи средств со ссудного счета и заканчивается датой зачисления средств в погашение кредита на ссудный счет ссудозаемщика. В случае не поступления на счет банка средств в погашение причитающихся со ссудозаемщика процентов до 5 числа следующего месяца, причитающиеся со ссудозаемщика проценты по кредиту считаются как несвоевременно оплаченные. В случае нарушения срока погашения кредита и уплаты процентов банк взыскивает штраф в размере 5 процентов от непогашенной суммы задолженности кредита за каждый день просрочки.

пример 6. “Тяжкое бремя выбора”. При подготовке учащихся к сдаче выпускного экзамена.

Учащиеся 9-11 классов в составе 27 человек были случайным образом разбиты на 5 групп. Каждой группе в бумажном и электронном виде были предложены: текст мини-кейса, образцы задач, вызывавших затруднения, подсказки для аудитории, вспомогательные вопросы, а также ссылки на сайт Дениса Биге с советами как сделать хорошую презентацию.

Усилия всей семьи усердной ученицы 9 класса Алисы старательной направлены на внедрение её в число студенток любого, но очень престижного, экономического вуза (поближе к большим деньгам, которых в данное время в самой семье не наблюдается). Хотя девочка учится еще только в 9 классе, её многочисленные родные изучили всевозможные сайты учебных заведений, прочитали все положения о проведении ГИА. На семейном совете было принято стратегическое решение: создать условия для подготовки Алисы к итоговой аттестации, уделив особое внимание проблемным местам. Любая стратегическая цель достигается посредством решения многих тактических задач. В настоящий момент выявилась одна из жестких проблем: как показал обзор источников информации, зачастую вместо стандартно сформулированных математических задач на экзаменах появляются задания, отражающие “какие-то связи” с реальной жизнью. Ситуация усугубляется тем, что встреча с любыми величинами, напоминающими таковые в учебниках физики, приводит Алису в состояние стойкого оцепенения (ну не получается у неё полюбить физику). Успокаивающими поначалу казались слова учителя математики, что уже сейчас она может решить не менее 50% задач из итогового задания для выпускников 11 классов. Просмотрев задания первой части ЕГЭ для выпускников 11 класса, Алиса сразу узнала своего “противника” – задание В10. Алисе нельзя отказать в здравом смысле, но даже ей показалось сложным оценить величие и различие слов “доход”, “прибыль”, “выручка”, мелькающих в текстовых задачах. Но ведь встречаются в этих задачах и худшие монстры: брошенные камни, перегревающиеся приборы, законы излучения звезд. Просмотрев учебник математики, который с таким трудом удалось заказать на класс в этом году, Алиса поняла, что дела плохи. Она боится изотерм, а в учебнике обсуждаются изокванты (наверное, это их исследование уже на квантовом уровне), слава богу, в географии удалось пройти изобары. К счастью, Алиса – неисправимая оптимистка. И как у любого оптимиста у неё много друзей. И почему бы не сосредоточить их интеллектуальные ресурсы во времени и пространстве, на выработку поначалу подхода к этой мини ситуации: как одолеть задание В10? Может кто-то уже его победил? Может у кого-то есть верный способ, как обойти проблему? И как понять, нужно ли ей вообще волноваться по данному поводу?

Для успеха надо детально изучить будущего противника. Как выяснилось, не во всех вузах, которые присмотрели для будущего алисы родственники, ограничиваются сдачей ЕГЭ: на экономические специальности в них проводится дополнительный экзамен по математике. И кто знает, что будет в стране через три года введено для выпускников? Выбрали тогда родители заведение экономического профиля, рейтинг которого в нашей стране зашкаливает – ВШЭ, и чтобы оценить требования к подготовке отобрали три задачи из 30 заданий, которые предлагалось абитуриентам решить за 1,5 часа. Каждая из них была последней, самой трудной в наборе. К чести авторов, упомянем, что их интересовал только правильный ответ, без утомительных подробностей. Есть ли у этих вузовских заданий общие черты с заданиями ЕГЭ?

Итак – цель полезного использования нашего мини-кейса: разработать рекомендации к системе подготовки к решению подобных задач и убедить Алису в преимуществах выбранной методики. А, может быть, в процессе достижения данной цели удастся её переосмыслить и заменить другими, более значащими.

Хочу отметить, что предложение учащимся для изучения именно задания В10 было обусловлено несколькими причинами. Одной из них явился невысокий процент решивших задания этого типа на диагностических работах для 10 и 11 классов. Второй причиной стала принципиальная доступность заданий в10 уже для учащихся 9 классов. И, конечно же, интересным аспектом для изучения этого задания стали проблемы с интерпретацией физических формул учащимися и отказ по этой причине от решения подобных задач.

Подсказки для аудитории.

CASE – технологии – метод ситуационного обучения

Метод CASE STUDIES предполагает:

Подготовленный в письменном виде пример кейса;
Самостоятельное изучение и обсуждение кейса учащимися;
Совместное обсуждение кейса в аудитории под руководством преподавателя;
Следование принципу “процесс обсуждения важнее самого решения”.

Этапы	Цель этапа
Знакомство с конкретным случаем	Понимание проблемной ситуации и ситуации принятия решения
Поиск: оценка информации, полученной из материалов задания, и самостоятельно привлеченной	Научиться добывать информацию, необходимую для поиска решения и оценивать ее
Обсуждение: обсуждение возможностей альтернативных решений	Развитие альтернативного мышления
Резолюция: нахождение решения в группах	Сопоставление и оценка вариантов решения.
Диспут: отдельные группы защищают свое решение	Аргументированная защита решений
Сопоставление итогов: сравнение решений, принятых в группах	Оценить взаимосвязь интересов, в которых находятся отдельные решения

Предполагаемый временной сценарий.

На работу с данным кейсом отводится 3 занятия. 1 занятие посвящено знакомству с ситуацией и первичному анализу информации. В ходе этого занятия формируется несколько групп из числа учащихся. 2 занятие посвящено обсуждению ситуации в группах и принятию коллективного решения. Предполагается предварительная домашняя обработка информации. 3 занятие посвящается представлению предложений, одобренных в группах и сопоставлению результатов.

Во время проведения первого занятия все его участники имели возможность, ознакомившись с представленными материалами, провести их обсуждение внутри группы, задать вопросы преподавателю и разработать начальный вариант подхода к разрешению проблемы. Группы учащихся формировались случайным образом, что имело как свои плюсы, так и свои минусы. С одной стороны, внутри разновозрастных групп могут появиться многогранные решения, с другой стороны сложно организовать равноправное взаимодействие учащихся. Хочется отметить, что второе и третье занятия проходили в гораздо более раскрепощенной обстановке, так как совместное обсуждение и выработка общих подходов сблизили участников.

Проводя занятие, хотелось, чтобы учащиеся, заинтересовавшись, поближе познакомились с подтипами заданий В10 на примере открытого банка данных, online – тестирования, диагностических работ. Сразу отметим, что все предложенные задания были учащимися опознаны, даже с учетом имеющихся индивидуальных опечаток. Ниже приводятся варианты задач, “вызывавших” затруднения Алисы. В реальных вариантах у учащихся не были указаны источники текстов.

Образцы задач В10 из сборников, рекомендованных в 2011 году.

Типовые тестовые задания А.Л. Семенов, И.В. Ященко.

Тренировочная работа 1 задание В10.

Задача №1. Зависимость объема спроса q (тыс. руб.?) На продукцию предприятия-монополиста от цены p (тыс. руб.) Задается формулой q=160-10p. Выручка предприятия за месяц r(в тыс. руб.) Вычисляется по формуле r(p)=q*p. Определите наибольшую цену p, при которой месячная выручка r(p) составит не менее 280 тыс. руб. Ответ приведите в тыс. руб.

Математика подготовка к ЕГЭ – 2011 под редакцией Ф.Ф. Лысенко. Вариант 9 задание В10.

Задача №2. Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой h(t)= -5t2+39t, где h – высота в метрах, t – время в секундах, прошедшее с момента броска. Найдите, сколько секунд камень находился на высоте не менее 28 метров.

Математика подготовка к ЕГЭ – 2011 под редакцией Ф.Ф. Лысенко. Вариант 11 задание В10.

Задача №3. Зависимость температуры (в градусах кельвина) от времени (в минутах) для некоторого прибора была получена экспериментально и на исследуемом интервале температур задается выражением t(t) = t0 +a·t +b·t2, где t0 = 296 k, a = 5k/мин, b = -1/8 k/мин2. Известно, что при нагреве прибора свыше 338 градусов он может выйти из строя, поэтому его нужно отключать. Определите, через какое время в минутах после начала работы нужно отключать прибор?

А.А. Быков сборник задач по математике ГУ ВШЭ.

Часть 2. Варианты вступительных испытаний по математике.

Задача №4. Доход нефтяной компании (в у.е.) Равен численно произведению квадрата числа геологов на куб числа добытчиков. Наем одного геолога обходится в 4 у.е., одного добытчика – в 27 у.е. Найдите число t, равное отношению числа геологов x к числу добытчиков y, если доход заданной величины получен при наименьшем возможном расходе на наем.

Задача №5. Предприниматель должен израсходовать 1440 у.е. на наем грузчиков (2 у.е. на каждого) и менеджеров (15 у.е. на каждого), причем ожидаемый доход (в у.е.) равен численно произведению числа грузчиков на квадрат числа менеджеров. Сколько всего сотрудников нужно нанять, чтобы получить максимальный доход?

Задача №6. Расстояние от Парижа до марселя (по шоссе) равно 77 лье. В Париже квартирует 9000 мушкетеров, в марселе – 16000. На каком расстоянии (в лье) от Парижа следует расположить винокуренный завод для обслуживания мушкетеров, чтобы минимизировать транспортные издержки, если затраты на перевозку p тонн бургундского на расстояние l лье составляют p·l3 бурбонов?

Оговорюсь, что при презентации найденных подходов к решению задания не предполагалось обсуждения и сравнения решений самих задач, однако, при подготовке к занятиям, участники групп рассмотрели все задачи. В ходе работы возникало много вопросов, которые были заданы учителем при формулировке задания, прозвучали со стороны учащихся, причем, некоторые из них прогнозировались заранее, а другие были неожиданными. Их достаточно полный перечень приведен ниже. Он может быть полезен для оценки, как работы учащихся, так и проведения занятия.

Вспомогательные вопросы:

Попробуйте понять, для чего лично вам может пригодиться сегодняшнее занятие?
Есть ли особенности при подготовке к экзамену по математике? Следует ли уделять одинаковое внимание всем учебным предметам или сосредотачиваться на изучении только некоторых?
Какие у вас общие интересы, какие возможные выгоды от вашей совместной работы вы способны почерпнуть?
Вы сами сталкивались когда-либо с подобной проблемой?
Воспользовались бы вы сами подсказками и советами со стороны?
А можно ли определить склонность к будущей профессии в 9 классе?
Какая информация для нас является ценной, а полезной? Забываем ли мы с течением времени ценную или полезную информацию?
Что есть общего в представленных заданиях?
Что отличает эту группу заданий от других на выпускных экзаменах?
Есть ли такие задачи в наших учебниках?
Что хотят проверить составители подобных заданий? Какие наши умения и компетентности предполагается использовать?
Надо ли в ходе работы решить сами задания?
Можно ли задания так переформулировать, чтобы свести к известным вариантам?
Что такое ким? Что такое открытый сегмент ким? Где найти задания открытого сегмента ким?
Хватит ли времени решить предварительно все задачи открытого сегмента?
Стоит ли это делать?
Разве не является задачей школьного учителя подготовить нас к выпускным экзаменам?
Что означает находиться на высшей ступени рейтинга? Почему вшэ пользуется такой популярностью абитуриентов?
Непонимание физики подчеркивается в задании как фатальное условие?
Зачем нужна физика экономисту?
Какие возможные приемы подарит нам старшая школа для решения задач?
Чем отличаются задачи из вариантов ВШЭ от задач, предлагавшихся на ЕГЭ? Можно ли их перевести на стандартный язык школьной математики?
А существует ли стандартная школьная математика? Что под ней можно подразумевать?
Стоит ли при подготовке пользоваться компьютером как инструментом для получения, представления, обработки информации?
Где используется ситуативное обучение?
Являются ли задачи с практическим содержанием из практики ЕГЭ отражением реальных ситуаций?
В какой мере математическое моделирование отражает реальные ситуации?
Как распознать “бантики”, развлекающие публику, привлеченную к решению задач и суть самой задачи? Надо убирать “бантики” или они помогают в работе?
Можно ли, проанализировав задачу, подготовиться к решению целого набора заданий?
Верны ли цитаты преподавателей высшей школы, что в средней школе единственно, что умеют хорошо делать выпускники, так это решать квадратные уравнения?
Какая связь между объемом информации и набором умений действовать?
Бывают ли ошибки в условиях задач на экзаменах и как поступать в этих случаях?
Экстремальные задачи? Их следует решать через производные?
Надо ли понимать смысл задания В10, если собираешься – не собираешься стать физиком? Собираешься – не собираешься стать экономистом?
Стоит ли задумываться о смысле входящих в уравнения и неравенства величин, если компьютер проверяет лишь численный результат?
Могу ли я сам найти информацию в сети интернет, например, полезные ссылки на online тестирование? Все ли они помогут при подготовке к экзаменам?
Если это единый экзамен, зачем какая-то другая литература, кроме школьных учебников?
Живя в обществе, будучи просто потребителем, ты подходишь к оценке ситуации иначе, чем производители?
По предмету экономика нет ЕГЭ. Нужны ли уроки экономики в школе?
Для будущих экономистов: учитывают ли ваши предложения соотношения цена – качество?

К анализу условия задания 1.монополист?

что выгоднее реализовывать: малый объем по большой цене или большие объемы по малой цене?

Что такое эксклюзивный товар? Может ли в условиях монополии рядовой товар стать эксклюзивным?

Выручка, доход, прибыль?

В реальных обстоятельствах: должно ли предприятие ориентироваться на максимальный объем выручки?

Какими способами можно увеличивать цену товара? Обязательно ли падает спрос с увеличением цены? Примеры?

Насколько усложняется модель, если заменить линейную зависимость между входящими величинами?

Спор, дискуссия, аргументация? Когда они важны?

Анализируете ли вы причины, почему вам хочется соглашаться с той или иной точкой зрения?

Прибегали вы и считаете ли полезным обращение к психологу при подготовке к экзаменам?

Кто больше переживает по поводу результатов вашей учебы: вы или родители?

Используете ли вы возможности дистанционного обучения?

Знаете ли вы о возможностях поступления в вузы через перечень олимпиад и конкурсов, утвержденных советом ректоров вузов России?

Видите ли, вы и какие преимущества коллективного и индивидуального обучения?

Хочется отметить, что данная форма проведения занятий интересна и организатору, и учащимся, как исполнителям “главных ролей”. Самостоятельность и свободное изложение подходов участников к разрешению проблем проявились наиболее полно на третьем занятии, которое прошло в форме конкурса презентаций. К подобному формату защиты своих идей подталкивали участников групп полученные ими в электронной форме материалы, содержащие советы, рекомендации и примеры по подготовке удачных электронных презентаций.

ВЫВОДЫ

Может найти разнообразные сюжеты для “кейсов” и наполнить их необходимым содержанием – использование этого метода сразу принесёт ощутимые плоды: во-первых, на уроке, проводимом по такой технологии, не бывает равнодушных и практически невозможно “отсидеться” в стороне, во-вторых, каждый учащийся, ощутив недостаток знаний по теме ”кейса”, сделает для себя вывод, что эти знания не абстрактные, а необходимы для применения на практике, следовательно, нужно подойти к этому серьёзно, если не хочешь затем в жизни испытывать трудности, в-третьих, у учащихся перед глазами содержание “кейса”, следовательно, можно повторить теоретические основы, на которые затем опираться при решении практических вопросов.

Главное предназначение кейс-технологий – развивать способность прорабатывать различные проблемы и находить их решение, другими словами научиться работать с информацией.

Откуда брать ситуации? Самый лучший путь получения конкретных ситуаций— взять их из жизни, то что интересно старшеклассникам, то с чем они сталкиваются ежедневно или могут столкнуться в ближайшем будущем.

ЗАКЛЮЧЕНИЕ

Кейс-технология – это интерактивная технология для краткосрочного обучения на основе реальных или вымышленных ситуаций, направленная не столько на освоение знаний, сколько на формирование у слушателей новых качеств и умений.

Если говорить о кейс-методе как о педагогической технологии, то эта технология предполагает совокупность исследовательских, поисковых, проблемных методов, творческих по самой своей сути.

Кейс – технология заключается в создании и комплектации специально разработанных учебно-методических материалов в специальный набор «кейс» и их передаче (пересылке) обучающимся. Каждый кейс представляет собой полный комплект учебно-методических материалов, разработанных на основе производственных ситуаций.

Работа по кейс – технологии формирует у обучающихся УУД (универсальные учебные действия), такие как обретение первичного опыта работы с информацией самостоятельно; навыки самостоятельного конструирования алгоритмов; самоконтроль и промежуточная диагностика; рефлексия.

Результаты выполненных проектов должны быть, что называется, «осязаемыми», т.е., если это теоретическая проблема, то конкретное ее решение, если практическая – конкретный результат, готовый к использованию (на уроке, в реальной жизни).

Кейс-метод, в отличие от многих традиционных методов обучения, позволяет учащимся применить в практической ситуации имеющиеся теоретические знания и понять, что эти знания получены не зря, но при этом не забывать, что реальный мир далёк от мира теоретических моделей. Метод кейсов способствует активному усвоению знаний и накоплению практической информации, которая в жизни может оказаться более полезной, чем теоретические знания. Также в процессе работы по методу кейсов развиваются различные универсальные умения и навыки (аналитические, творческие, коммуникативные и т.п.), которые необходимы для жизни в современном мире.

Кейс дает возможность приблизиться к практике, встать на позицию человека, реально принимающего решения, учиться на ошибках других.

При обучении формируются: Аналитические навыки. Умения отличать данные от информации, классифицировать, выделять существенную и несущественную информацию и уметь восстанавливать их. Практические навыки. Использование на практике академических теории, методов и принципов. Творческие навыки. Одной логикой, как правило, кейс – ситуацию не решить. Очень важны творческие навыки в генерации альтернативных решений, которые нельзя найти логическим путём.

Достоинством кейс технологий является их гибкость, вариативность, что способствует развитию креативности у педагога и обучающихся.

Конечно, использование кейс-технологий в обучении не решит всех проблем и не должно стать самоцелью. Необходимо учитывать цели и задачи каждого занятия, характер материала, возможности обучающихся. Наибольшего эффекта можно достичь при разумном сочетании традиционных и интерактивных технологий обучения, когда они взаимосвязаны и дополняют друг друга.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Гарднер м. Математические чудеса и тайны. М.: Наука, 1978.  128 с.
Федеральный государственный образовательный стандарт среднего (полного) общего образования. [электронный ресурс]: официальный ресурс министерства образования и науки российской федерации
Вендина А.А., Михоненко О. Технологии при изучении темы «числа и их свойства», статья, г. Ставрополь
Смолянинова О.Г. Методические материалы по теме: «Технологии формирования образовательных компетенций учащихся на уроке» Кейс-стади метод, к.п.н., доцент, декан ппф кгу, статья
Хью МакЛин, И. Кузнецова, Т. Никулина, А.Поздняков, А.Зоткин. Кейс-стадивобразовании. Сборник материалов для создания кейсов с элеектронным сопровождением / Под ред. И. Кузнецовой.
Закуцкая М.В Использование кейс-технологии на уроках математики, статья, г. Санкт-Петербург
ГоголеваО.А Урок алгебры. Подготоовка к ЕГЭ. Кейс-технологии на уроках математики, публикация 2015 г.
Жаворонкова Т.В. CASE-технологии на уроках математики, статья, 2017 г.
Балакирева Г.В. Применение кейс-технологии на уроках математики, доклад. г. Нефтеюганск, 2015 г.
Кривкова И.В. Применение кейс-технологий на уроках математики. Презентация, 2016 г.

Источник

ОБЩАЯ ХАРАКТЕРИСТИКА ПРАКТИЧЕСКОГО КЕЙСА

Актуальность: процесс обучения направлен не только на достижение предметных результатов, но и на формирование личности детей и на овладение ими навыками, которые в дальнейшем будут им полезны. Решение данного кейса способствует формированию коммуникационных умений, умению находить, обрабатывать и использовать информацию, демонстрировать свой опыт и результаты личной работы.

Цель:

формирование у обучающихся умения решать практические кейсы;
совершенствование навыков решения практических задач по теме «Объёмы тел», привитие познавательного интереса через решение задач с практическим содержанием.

Задачи:

Обучающие

повторить формулы для вычисления объёмов тел;
проверить умение применять теорию по данной теме к решению задач;
убедить обучающихся в значимости математики для решения задач из реальной жизни; связи с другими областями науки.

Развивающие

развивать навыки создания и интерпретации математических моделей реальных явлений;
развивать умение обрабатывать и использовать информацию;
развивать логическое и критическое мышление, творческие способности.

Воспитательные

развитие навыка работы в малой группе (коммуникативная компетентность): организация работы, распределение заданий между участниками группы в соответствии с общей структурой задачи и возможностями участников, взаимодействие и взаимопомощь в ходе решения задачи, взаимоконтроль;
развивать личностные качества такие как независимость, ответственность, инициативность, толерантность.

Возраст обучающихся: 16-17 лет (10-11 класс).

Время выполнения кейса: 2 часа.

Форма работы: малыми группами.

Планируемые результаты обучения:

Личностные:

готовность и способность обучающихся к саморазвитию, целенаправленной познавательной деятельности;
способность ставить цели и строить жизненные планы;
формирование ответственного отношения к учению.

Метапредметные:

самостоятельность планирования и осуществления учебной деятельности и организации учебного сотрудничества с педагогами и сверстниками;
умение самостоятельно планировать пути достижения целей, в том числе альтернативные;
владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной деятельности.

Предметные:

формирование представлений о математике как о методе познания действительности, позволяющем описывать и изучать реальные процессы и явления;
развитие умения моделировать реальные ситуации на языке математики, исследовать построенные модели с использованием аппарата математики, интерпретировать полученный результат;
развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости дополнительных материалов, полученных из разных источников информации.

Текст практического кейса:

Введение (история, сюжет, время действия и др.)

В рамках реализации концепции развития городского парка им. Гагарина предусмотрена реконструкция существующего фонтана с установкой современной фонтанной системы.

Основная часть (главный массив информация, проблема)

Для срочных строительных работ требуется перевезти песок, брёвна, цемент и керамическую плитку. В 20 км данный материал складирован следующим образом:

– на участке, имеющим квадратную форму со стороной 4м, в виде прямой треугольной призмы уложены брёвна, высота укладки 1,3 м;

– куча песка имеет конусообразную форму, диаметр основания равен 3м, высота кучи – 2м;

– цемент в порошке упакован в мешки и уложен на поддон размерами 3,2м x 1,9м, высота укладки 0,5м;

– керамическая плитка уложена на поддоны 1,3м x 1,3м, высота укладки 1,3 м

Заключительная часть (ситуация, требующая решения)

В наличие у компании, осуществляющей перевозку груза, есть четыре автомобиля: ЗИЛ – 4333, ГАЗ – 3307, КАМАЗ – 53215, ЗИЛ – 5301. В виду срочности работ требуется одним рейсом перевезти заказанный груз.

Вопросы и задания к практическому кейсу

1. Возможно ли, используя эти четыре автомобиля, выполнить данный заказ?

2. Если перевозка возможна, то выполните заказ рациональным способом.

3. Используя информацию на сайтах, рекомендуйте транспортной компании машины для более рациональной перевозки груза.

https://jplife.ru/stati/klassifikatsiya-i-vidy-gruzovykh-avtomobiley/
https://studfile.net/preview/5051226/page:11/

Методические рекомендации

Приложение 1

Приложение 2

Источник

Обособленное структурное подразделение «Детский технопарк «Кванториум»

Государственного автономного учреждения дополнительного профессионального образования Липецкой области «Институт развития образования»

Кейс по математике «Микрорайон мечты»

Авторы:

Светлова Виктория Сергеевна, педагог дополнительного образования Марасанова Елена Вячеславовна, педагог дополнительного образования

Липецк, 2022

Базовый кейс 1. Микрорайон мечты

Описание проблемной ситуации или феномена

Активный и ответственный кванторианец Вася хочет успевать за день сделать много дел. После школы он приходит домой делает уроки и идет забирать сестру из садика, при этом заходит в магазин. Потом, погуляв с собакой, торопится на занятия в Кванториум, находящийся далеко от дома. В итоге, отсутствует время на просмотр мультфильмов.

Вася пытается решить эту проблему, но не очень разбирается в построении моделей микрорайонов. Как бы вы решили эту проблему? Возможно ли построить микрорайон, в котором все вышеописанные локации будут присутствовать?

Категория кейса (уровень сложности)

вводный

Место в структуре модуля

базовый, мотивационный кейс

Количество учебных часов/занятий, на которые рассчитан кейс (может варьироваться в зависимости от уровня подготовки, условий, и т.д.)

Кейс рассчитан на 16 ч/8 занятий

Перечень и содержание занятий

Занятие 1

Цель: Произвести постановку проблемной ситуации и осуществить поиск путей решения.

Что делаем: Представление проблемной ситуации в виде инженерного ограничения (социально-математического) (отклик на существующую потребность). Анализ проблемной ситуации, генерация и обсуждение методов ее решения и возможности достижения идеального конечного результата.

Компетенции: Умение генерировать идеи указанными методами, слушать и слышать собеседника, аргументировано отстаивать свою точку зрения, искать информацию в свободных источниках и структурировать ее. Умение комбинировать, видоизменять и улучшать идеи.

Занятие 2

Цель: Построить графическую информационную модель «микрорайона мечты» в виде связного графа.

Что делаем: Знакомство с теорией графов, их видами и областями применения. Создание карты микрорайона.

Компетенции: Командная работа. Применение знаний об основных понятиях теории графов для решения задач, возникающих в профессиональной сфере. Владение навыками практического использования современного математического инструментария для решения или анализа задач, предусматривающими знания оптимальных алгоритмов.

Занятие 3

Цель: Применить теорию о базовой геометрии для модели «микрорайона мечты».

Что делаем: Знакомство с основными понятиями базовой геометрии (геометрические фигуры, площадь, периметр). Оптимизация расположения объектов на карте с использованием полученных знаний. Доработать эскиз карты микрорайона.

Компетенции: Командная работа. Расчет площади и периметра при решении задач, возникающих в повседневной жизни. Исследование различных вариантов решения задач с использованием геометрических характеристик объектов, выбор наилучшего, принимая во внимание различные критерии.

Занятие 4

Цель: Применить теорию множеств для реализации модели «микрорайона мечты».

Что делаем: Знакомство с теорией множеств (операции над множествами, комбинаторика, математическая логика). Распределить наиболее выгодные коммуникации (например, любители собак располагаются рядом с питомником для собак и подальше от питомника для кошек) внутри микрорайона. Доработать эскиз карты микрорайона.

Компетенции: Командная работа. Умение абстрагироваться от реальных объектов и свести работу с объектами к работе с моделями. Умение разбивать сложную задачу на более простые и выстраивать работу с ними.

Занятие 5

Цель: Применить теорию вероятностей для оптимизации модели «микрорайона мечты».

Что делаем: Знакомство с теорией вероятностей (определение события, вероятности, ее характеристики). Сбор статистики и последующий анализ. На основе полученных данных произвести оптимизацию «микрорайона мечты». Доработать эскиз карты микрорайона.

Компетенции: Командная работа. Использование основных методов теоретико-вероятностных исследований в научном анализе реальных проблем.

Занятие 6

Цель: Построить карту «микрорайона мечты» с учетом полученных навыков и знаний.

Что делаем: Подвести итоги полученных знаний и навыков. Доработать эскиз карты микрорайона. Обзор программного обеспечения, необходимого для визуализации модели «микрорайона мечты». Оформление проекта.

Компетенции: Командная работа. Основы работы в программе для создания карты. Критическое мышление и умение объективно оценивать результаты своей работы.

Занятие 7

Цель: Выполнить подготовку к публичной демонстрации и защите результатов кейса.

Что делаем: Подготовка речи выступления и презентации по итогам работы над кейсом. Создание презентации.

Компетенции: Организаторские качества. Умение грамотно формулировать свои мысли как в устной, так и в письменной форме. Критическое мышление и умение объективно оценивать результаты своей работы.

Занятие 8

Цель: Выполнить подготовку к публичной демонстрации и защите результатов кейса.

Что делаем: Подготовка речи выступления и презентации по итогам работы над кейсом. Создание презентации. Рефлексия. Обсуждение результатов кейса.

Компетенции: Основы ораторского искусства. Опыт публичных выступлений. Основы работы в текстовом редакторе и программе для создания презентации.

Метод работы с кейсом (метод проектов, аналитический метод, … – выбор метода определяет содержание руководства для наставников)

Метод проектов

Минимально необходимый уровень входных компетенций:

Требования к минимальному уровню входных компетенций отсутствуют, за исключением знания персонального компьютера на уровне пользователя

Предполагаемые образовательные результаты учащихся (артефакты, решения), формируемые навыки (Soft и Hard Skills)

В результате прохождения данного образовательного модуля обучающийся должен знать следующие ключевые понятия: граф, вершина, ребро, степень вершины, путь, связность, фигура на плоскости, площадь, периметр, прямоугольник, трапеция, параллелограмм, окружность, множество, комбинаторик, факториал, вероятность, событие, испытание.

Прохождение данного образовательного модуля должно сформировать у обучающихся следующие компетенции. Все выработанные компетенции могут быть применены в ходе реализации последующих образовательных модулей:

умение генерировать идеи указанными методами;

умение слушать и слышать собеседника;

умение аргументировано отстаивать свою точку зрения;

умение искать информацию в свободных источниках и структурировать ее;

умение комбинировать, видоизменять и улучшать идеи;

навыки командной работы;

умение грамотно письменно формулировать свои мысли;

критическое мышление и умение объективно оценивать результаты своей работы;

основы ораторского искусства;

основы работы в текстовом редакторе и программе для создания презентаций;

использование графов для систематизации знаний и наглядного представления информации

поиск оптимального пути с помощью графов и логических рассуждений

расположение объектов с использованием фигур на плоскости

практическое использование формул для расчета площадей и периметров

умение абстрагироваться от реальных объектов и свести работу с объектами к работе с моделями.

умение разбивать сложную задачу на более простые и выстраивать работу с ними.

использование основных методов теоретико-вероятностных исследований в научном анализе реальных проблем.

Процедуры и формы выявления образовательного результата

Промежуточный контроль результата проектной деятельности осуществляется по итогам выполнения групповых и индивидуальных заданий, а также по итогам самостоятельной работы участников команды.

Итоговый контроль состоит в публичной демонстрации результатов проектной деятельность перед экспертной комиссией с ответами на вопросы по содержанию проекта, методам решения и полученным инженерно-техническим и изобретательским результатам.

Необходимые материалы и оборудование

Для успешного выполнения кейса потребуется следующее оборудование, материалы, программное обеспечение и условия. Количество единиц оборудования и материалов приведено из расчета количественного состава группы обучающихся (12 человек). Распределение комплектов оборудования и материалов – 1 комплект на 2-4 обучающихся:

работа над кейсом должна производиться в хорошо освещенном, просторном, проветриваемом помещении;

компьютер (ноутбук) с монитором, клавиатурой и мышкой, на который установлено следующие программное обеспечение: операционная система Windows (версия не ниже 7), Gimp, Blender, Graph Online, пакет офисных программ MS Office – 7 шт.;

компьютеры (ноутбуки) должны быть подключены к единой Wi-Fi-сети с доступом в Интернет;

презентационное оборудование (проектор с экраном/телевизор с большим экраном) с возможностью подключения к компьютеру (ноутбуку) – 1 комплект;

флипчарт с комплектом листов/маркерная доска, соответствующий набор письменных принадлежностей – 1 шт.;

каждый стол для работы над кейсом должен позволять разместить за одним компьютером (ноутбуком) двух обучающихся и предоставлять достаточно места для работы с компонентами создаваемого устройства;

распечатанный материал кейса 1 – 6 шт.;

листы бумаги А4 и А3;

ручки, карандаши;

набор для черчения.

В ходе работы предлагается следующее распределение участников в группе:

• участники работают все вместе в ходе обсуждения проблемной ситуации, рефлексии и подготовки к защите проекта;

• участники работают в подгруппах по 2-4 человек в ходе построения графической модели и выполнения самостоятельных заданий.

Источники

Ануфриенко С.А. Введение в теорию множеств и комбинаторику. 1998;

Березина Л. Ю. Графы и их применение: пособие для учителей. 1979;

Лютикас В.С. Школьнику о теории вероятностей. 1983;

Смирнов В.А. и др. Наглядная геометрия. 2013;

Третьяк И.В. Геометрия в схемах и таблицах. 2016.

Педагогический сценарий (руководство для наставника)

В ходе данного кейса вводятся математические модели, позволяющие рационально планировать расположение объектов социальной инфраструктуры с учётом самых разных факторов (размеры и форма зданий, назначение зданий и т.д.). Участники кейса построят «микрорайон мечты», расположив все социальные объекты наиболее оптимально.

Сценарий кейса включает в себя:

• введение в проблему посредством беседы с группой обучающихся (приведение конкретных жизненных примеров, в которых проблемная ситуация раскрывается; приведение неоспоримых фактов того, что решение проблемной ситуации не может быть отложено на неопределенный срок);

• изучение проблемы (групповое обсуждение; анализ материалов в свободном доступе, выявление существующих готовых технических решений для данной или похожих проблемных ситуаций; выявление достоинств и недостатков найденных решений);

• распределение ролей в проектной группе по результатам предыдущих шагов сценария с учетом предпочтений участников;

• поиск технического решения проблемы (в зависимости от возрастного состава участников группы и уровня их подготовки рекомендуется использовать: мозговой штурм; методы теории решения изобретательских задач и методы поиска технических решений; метод инженерных ограничений);

• составление минимального технического задания на разработку технического решения с указанием продолжительности выполнения каждого этапа технического задания;

• непосредственно выполнение этапов технического задания, создание модели микрорайона;

• тестирования для проверки работоспособности модели микрорайона (поиска и устранения недочетов в работе);

• итоговая доработка модели микрорайона;

• подготовка выступления и представление итогов работы над кейсом в виде презентации с демонстрацией графической модели микрорайона;

• подведение итогов, групповая рефлексия.

Теоретический материал и задания к занятию 2

Графы – замечательные математические объекты, с их помощью можно решать очень много различных, внешне не похожих друг на друга задач. В математике существует целый раздел – теория графов, который изучает графы, их свойства и применение. Мы же обсудим только самые основные понятия, свойства графов и некоторые способы решения задач.

Термин «граф» впервые появился в книге венгерского математика Д.Кенига в 1936 году, хотя важнейшие теоремы о графах восходят к Леонарду Эйлеру (1707 – 1783). Графом называется совокупность конечного числа точек, называемых вершинами графа, и попарно соединяющих некоторые из этих вершин линий, называемых ребрами или дугами графа.

Дугой называется ребро с указанным направлением. Дуга (ребро) может начинаться и заканчиваться в одной и той же вершине, в этом случае соответствующая дуга (ребро) называется петлей.

Вершины графа, которые не принадлежат ни одному ребру, называются изолированными.

Граф, в котором каждая пара вершин соединена ребром, называется полным.

Граф, который можно представить на плоскости в таком виде, когда его ребра пересекаются только в вершинах, называется плоским.

Количество ребер, выходящих из данной вершины, называется степенью (валентностью) этой вершины.

Путь – последовательность ребер, каждое следующее из которых начинается в конце предыдущего.

Висячей вершиной называется вершина, из которой выходит ровно одно ребро.

Циклом называется путь, в котором совпадают начальная и конечная точка.

Длиной пути, проложенного на цикле, называется число ребер этого пути.

Граф называется связным, если каждые две его вершины соединены путем; если же в графе найдется хотя бы одна пара несвязных вершин, то граф называется несвязным.

Деревом называется связный граф, не содержащий циклов. В дереве вершин всегда на одну больше, чем ребер.

Вершины, соединенные ребром или дугой, называются смежными. Ребра, имеющие одну и ту же вершину, также называют смежными.

Многоугольник плоского графа, не содержащий внутри себя никаких вершин или ребер, называется гранью.

Двудольный (четный) граф или биграф — это граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части.

Формула Эйлера. Для всякого связного плоского графа верно равенство: n–m+f=2, где n – число вершин, m – число ребер, f – число граней графа.

Лемма о рукопожатиях. Для любого связного графа верно утверждение: сумма степеней всех вершин равна удвоенному количеству ребер.

При решении многих олимпиадных задач используются следующие утверждения, относящиеся к обходу ребер графа:

если в графе больше двух нечетных вершин, то его правильный обход (т.е. обход, при котором каждое ребро проходится один раз) невозможен;

для всякого четного связного графа существует правильный обход, который можно начать с любой вершины и который обязательно кончается в той же вершине, с которой начался;

если в связном графе ровно две нечетные вершины, то существует правильный обход, причем в одной из них он начинается, а в другой кончается;

в любом графе количество нечетных вершин четно.

Задачи.

1. Разумные муравьи живут в колониях. Колонии состоят из ячеек, которые муравьи строят, которые соединяются в концах при помощи специального раствора. В одной ячейке живет один муравей. Колония состоит из 58 палочек, которые скрепили в 30 местах. Сколько муравьев живет в колонии?

Решение. Представим схему колоний как плоский граф. Граф имеет 30 вершин, 58 ребер. С помощью формулы Эйлера найдем число граней в нем f=2-n+m=2-30+58=30. Так как каждая грань графа, за исключением внешней, соответствует ячейке, то в колонии живут 29 муравьев.

2. В турнире принимает участие 15 шахматистов. Может ли быть, чтобы в некоторый момент каждый из них сыграл ровно 7 партий?

Решение. Нет, так как 15 нечетных вершин у графа быть не может.

3. В соревновании по круговой системе с двенадцатью участниками провели все встречи. Сколько встреч было сыграно?

Решение. Построим граф встреч игроков так. Поскольку каждая пара игроков встретилась между собой, то в графе каждая пара вершин будет соединена ребром. Данный граф будет являться полным. Найдем число ребер данного графа. В произведении каждое ребро учтено дважды, поэтому граф имеет ребер.

4. Может ли в государстве, в котором из каждого города выходит ровно три дороги, быть ровно 100 дорог между городами?

Решение. Построим граф, в котором вершины изображают города, а ребра – дороги. Из условий задачи следует, что степень каждой вершины равна трем. Пусть граф имеет n вершин. Из леммы о рукопожатиях вытекает, что . Последнее равенство при целых n невозможно.

5. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля – Меркурий, Плутон – Венера, Земля – Плутон, Плутон – Меркурий, Меркурий – Венера, Уран – Нептун, Нептун – Сатурн, Сатурн – Юпитер, Юпитер – Марс и Марс – Уран. Можно ли добраться (возможны пересадки) с Земли до Марса?

Решение. Нарисуем схему: планетам будут соответствовать точки, а соединяющим их маршрутам – непересекающиеся между собой линии.

Мы составили граф, соответствующий условию задачи. Видно, что все планеты Солнечной системы разделились на две не связанных между собой группы. Земля принадлежит одной группе, а Марс – в =торой. Долететь с Земли до Марса нельзя.

6. В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией тогда и только тогда, когда двузначное число, составленное из цифр-названий этих городов, делится на 3. Можно ли из города 1 добраться в город 9?

Решение. Покажем возможные маршруты, нарисовав граф. И в этой задаче 1 и 9 попали в две разных части графа. Ясно, что в правой части графа сгруппировались города-цифры нацело делящиеся на 3, а в левой части графа ребра соединяют две цифры: одну — делящуюся на 3 с остатком 1, а другую — делящуюся на 3 с остатком 2.

7. В государстве 100 городов. Из каждого города выходит 4 дороги. Сколько всего дорог в государстве.

Решение. Подсчитаем общее количество выходящих городов дорог – . Однако при таком подсчете каждая дорога посчитана 2 раза – она выходит из одного города и входит в другой. Значит всего дорог в два раза меньше, т.е. 200.

Теоретический материал и задания к занятию 3:

Геометрические задачи

Открывая учебник геометрии, вы даже не предполагали, что эта книга является упрощенной переработкой книги, созданной более 2000 лет назад. Название этой древней книги – «Начала». Создание ее обычно связывают с именем греческого математика Евклида, жившего в III в. до н.э. в Александрии – центре научной мысли греков. А зачатки геометрических знаний теряются в глубине тысячелетий. Древнейшие из памятников культуры – египетские папирусы и вавилонские глиняные таблички с клинописными записями говорят о том, что уже за 4000 – 5000 лет до нашего времени люди знали многое из того, что мы сейчас изучаем в школе. Сегодня, решая геометрические задачи, мы прикоснемся с вами к этой великой науке.

1. Можно ли в тетрадном листке вырезать такую дырку, через которую пролез бы человек?

Решение. Нужно сложить лист вдвое, вырезать вдоль линии сгиба узкое отверстие, а затем сделать много прямолинейных разрезов так, как показано на рисунке. Первый разрез делает «дырку», а остальные увеличивают длину «краёв» этой дырки.

2. а) Вспомните, как найти площадь прямоугольника, зная длины его сторон.

б) Как найти площадь прямоугольного треугольника, зная длины двух его сторон, прилегающих к прямому углу?

Решение: а) ab; б) ab⁄2. Приложим к гипотенузе такой же треугольник, чтобы получился прямоугольник со сторонами a и b. Тогда площадь треугольника равна половине площади прямоугольника, т.е. ab⁄2.

3. Найдите площади многоугольников, изображенных на рисунке (сторона клетки равна 1).

Решение: Чтобы найти эти площади нужно разбить фигуры на прямоугольные треугольники и квадратики. Площадь и тех и других мы умеем вычислять по первой задаче.

Ответ. 13; 12; 39,5.

4. (Квантик-2016) Барон Мюнxгаузен утверждает, что может нарисовать две пересекающиеся прямые и 15-угольник так, что каждая вершина 15-угольника будет лежать на одной из этих прямых. Не хвастает ли барон?
(Ответ обоснуйте: либо нарисуйте пример, либо докажите, что такого примера нет.) (Павел Кожевников)

Решение. Пример.

5. Как посадить 9 деревьев так, чтобы получилось 10 прямых рядов по три дерева в каждом?

6. Приведите пример карты, на которой четыре треугольные страны граничат каждая с каждой.

Р ешение.

Теоретический материал и задания к занятию 4

Множества. Операции над множествами

Множество – первичное понятие в математике и поэтому неопределяемое через другие. Математическое понятие множество постепенно выделилось из привычных интуитивных представлений о совокупности, наборе, собрании, коллекции, классе, семействе и т.д. Георг Кантор, создатель теории множеств, дает такое пояснительное определение множества, как «объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслей». В определении требуется, чтобы объекты были различны между собой. Элементами множества могут быть объекты различной природы: числа, буквы, точки, углы, предметы, люди и т.п. Множества, состоящие из конечного числа элементов, называются конечными, а множества, состоящие из бесконечного числа элементов, – бесконечными. Элементы, составляющие множество обычно обозначаются строчными латинскими буквами; сами множества – прописными латинскими. Множества задают либо перечислением его элементов, либо описанием характеристического свойства множества, которое четко определяет совокупность его элементов.

Отношения между множествами

1. Если каждый элемент множества A принадлежит множеству B, то множество A является подмножеством множества B (включено в B)( ).

2. Если и , то .

Множество, не содержащее ни одного элемента, называется пустым (Ø).

Множество, подмножествами которого являются все остальные множества из этой теории, называется универсальным (U).

Любое множество есть подмножество самого себя.

Операции над множествами.

1. Объединением двух множеств называется такое множество, которое содержит всевозможные элементы, входящие хотя бы в одно из данных множеств ( ).

2. Пересечением двух множеств называется такое множество, которое состоит из элементов, входящих в каждое из данных множеств ( ).

3. Дополнением множества до универсального называют множество всех тех элементов U , которые не принадлежат исходному множеству.

4. Разностью двух множеств называется такое множество, которое состоит из элементов, входящих в первое из данных множеств, и не входящих во второе из данных множеств ( ).

Диаграммы Эйлера – Венна.

В элементарной теории множеств для интерпретаций результатов операций над множествами используются диаграммы Эйлера – Венна. Диаграммой Эйлера называют фигуры, изображающие множества и наглядно демонстрирующие некоторые свойства булевых операций. Универсальное множество изображают в виде прямоугольника, а его подмножества изображают кругами.

Задачи.

1. Все мои друзья заботятся в своих квартирах о домашних животных. Шестеро из них разводят хомячков, а пятеро – рыбок. И только у двоих есть и хомячки, и рыбки. Сколько у меня друзей?

Решение. Обратимся к кругам Эйлера:

Изобразим два круга, так как у нас два вида питомцев. В одном будем фиксировать владельцев хомячков, в другом – рыбок. Поскольку у некоторых друзей есть и те, и другие животные, то круги нарисуем так, чтобы у них была общая часть. В этой общей части ставим цифру 2 так как хомячки и рыбки у двоих. В оставшейся части «хомячкового» круга ставим цифру 4 (6 − 2 = 4). В свободной части «рыбного» круга ставим цифру 3 (5 − 2 = 3). А теперь рисунок сам подсказывает, что всего у меня 4 + 2 + 3 = 9 друзей.

2. В футбольной команде «Спартак» 30 игроков, среди них 18 нападающих. 11 полузащитников, 17 защитников и вратари. Известно, что трое могут быть нападающими и защитниками, 10 защитниками и полузащитниками, 6 нападающими и защитниками, а 1 и нападающим, и защитником, и полузащитником. Вратари не заменимы. Сколько в команде «Спартак» вратарей?

Решение.

18+11+17-3-10-6+1=28 (игроков) на этой диаграмме. Но в команде всего 30 футболистов. Значит, вратарей будет 30-28=2.

3. Когда после зимних каникул одна из групп центра «Стратегия» вернулась к занятиям, преподаватель спросил, ходили ли они в это время в кино, в театр и в боулинг. Стало известно, что из 36 человек только двое не были ни в кино, ни в театре, ни в боулинге. В кино побывало 25 человек, в театре – 11, в боулинге – 17, в кино и в театре – 6, в кино и в боулинге – 10, а в театре и в боулинге – 4. Однако сколько человек посетили все три места осталось загадкой. Разгадайте ее.

Решение. Составим к задаче диаграмму Эйлера – Венна.

Имеем, 2 + (9 + x) + (1 + x) + (3 + x) + (6 – x) + (10 – x) + (4 – x) + x = 36, x = 1.

4. На полу площадью 12 м2 лежат три ковра. Площадь одного ковра 5 м2, другого – 4 м2, третьего – 3 м2. Каждые два ковра перекрываются на площади 1,5 м2. Все три ковра перекрываются на площади 0,5 м2.

а) Какова площадь пола, не покрытая коврами?

б) Какова площадь, покрытая только первым ковром?

Ответ: а) 12 – (5+4+3-1.5∙3+0.5) = 4; б) 5 – 1 – 1 – 0.5 = 2.5.

5. Среди математиков каждый седьмой – философ, а среди философов каждый девятый – математик. Кого больше: философов или математиков?

Ответ: философов больше.

Задача1.1.Дано: а)A,B⊆Z, A = {1;3;4;5;9}, B = {2;4;5;10}. б)A,B⊆R, A = [-3;3), B = (2;10].

Найти: A∩B, A∪B, AB, BA, B.

Решение.

a) A∩B = {4;5}, A∪B = {1;2;3;4;5;9;10}, A B = {1;3;9}, B A = {2;10}, B = Z B;

б) A∩B = (2;3), A∪B = [-3;10] , AB = [-3,2], BA = [3,10],B ZB = (-∞,2]∪(10,+∞).

Задача 1.3. На уроке литературы учитель решил узнать, кто из 40 учеников класса читал книги A, B, C. Результаты опроса оказались таковы: книгу A читали 25 учеников; книгу B читали 22 ученика; книгу C читали 22 ученика; книги A или B читали 33 ученика; книги A или C читали 32 ученика; книги B или C читали 31 ученик; все книги читали 10 учеников. Определите: 1) Сколько учеников прочли только книгу A?

2) Сколько учеников прочли только книгу B?

3) Сколько учеников прочли только книгу C?

4) Сколько учеников прочли только по одной книге?

5) Сколько учеников прочли хотя бы одну книгу?

6) Сколько учеников не прочитали ни одной книги?

Решение.

Пусть U – множество учеников в классе. Тогда

|U| = 40, |A| = 25, |B| = 22, |C| = 22, |A ∪ B| = 33, |A ∪ C| = 32, |B ∪ C| = 31, |A ∩ B ∩ C| = 10

Попробуем проиллюстрировать задачу.

Разобьём множество учеников, прочитавших хотя бы одну книгу, на семь подмножеств k1, k2, k3, k4, k5, k6, k7, где

k1 – множество учеников, прочитавших только книгу A;

k3 – множество учеников, прочитавших только книгу B;

k7 – множество учеников, прочитавших только книгу C;

k2 – множество учеников, прочитавших книги A и B и не читавших книгу C;

k4 – множество учеников, прочитавших книги A и C и не читавших книгу B;

k6 – множество учеников, прочитавших книги B и C и не читавших книгу A;

k5 – множество учеников, прочитавших книги A, B и C.

Вычислим мощность каждого из этих подмножеств.

|k2| = |A ∩ B|-|A ∩ B ∩ C|; |k4| = |A ∩ C|-|A ∩ B ∩ C|;

|k6| = |B ∩ C| – |A ∩ B ∩ C|; |k5| = |A ∩ B ∩ C|.

Тогда |k1| = |A| – |k2| – |k4| – |k5|, |k3| = |B| – |k2| – |k6| – |k5|, |k7| = |C| – |k6| – |k| – |k5|.

Найдём |A ∩ B|, |A ∩ C|, |B ∩ C|.

|A ∩ B| = | A| +| B| – |A ∩ B| = 25 + 22 – 33 = 14 ,

|A ∩ C| = |A| + |C| – |A ∩ C| = 25 + 22 – 32 = 15 ,

|B ∩ C| = |B| + |C| – |B ∩ C| = 22 + 22 – 31 = 13 .

Тогда k1 = 25-4-5-10 = 6; k3 = 22-4-3-10 = 5; k7 = 22-5-3-10 = 4;

|A ∪ B ∪ C| = |A ∪ B| + |C| – |(A ∪ B ) ∪ C| .

Из рисунка ясно, что |C| – |( A ∪ B ) ∪ C| = |k7| = 4, тогда |A ∪ B ∪ C| = 33+4 = 37 – число учеников, прочитавших хотя бы одну книгу.

Так как в классе 40 учеников, то 3 ученика не прочитали ни одной книги.

Ответ:

6 учеников прочли только книгу A.

5 учеников прочли только книгу B.

4 ученика прочли только книгу C.

15 учеников прочли только по одной книге.

37 учеников прочли хотя бы одну книгу из A, B, C.

3 ученика не прочитали ни одной книги.

Теоретический материал и задания к занятию 5

Классическое определение вероятности. Пусть производится некоторое испытание, которое может иметь ровно n различных исходов. Будем считать, что все эти исходы несовместны (не могут произойти одновременно) и равновероятны (данное понятие лежит за рамками математической теории и понимается в интуитивном смысле). Каждому событию A, являющемуся подмножеством пространства элементарных событий проводимого испытания, поставим в соответствие число

p(A)=m/n,

где m – число исходов испытания, благоприятствующих событию A. Число p(A) называют вероятностью события A при данном испытании.

Анализ и решение задач. Анализ и решение задач могут быть выполнены по следующей схеме:

Уясните, в чем состоит испытание, рассматриваемое в задаче.

Установите, являются ли исходы испытания несовместными и равновероятными.

Подсчитайте число n всех возможных исходов испытания.

Сформулируйте событие, вероятность наступления которого необходимо найти.

Подсчитайте число m исходов испытания, благоприятствующих рассматриваемому событию.

Вычислите по предложенной формуле вероятность появления рассматриваемого события.

Элементарные события опыта – простейшие события, которыми может окончиться случайный опыт.

Сумма вероятностей всех элементарных событий опыта равна 1.

Вероятность события A (обозначается P(A)) равна сумме вероятностей элементарных событий, благоприятствующих этому событию.

Объединение событий A∪B – событие, состоящее из элементарных исходов, благоприятствующих хотя бы одному из событий A или B.

Пересечение событий A∩B – событие, состоящее из элементарных исходов, благоприятствующих обоим событиям A и B.

Событие A¯, состоящее из тех и только тех элементарных исходов опыта, которые не входят в A, называется противоположным событию A.

События A и B называются независимыми, если P(A∩B)=P(A)⋅P(B).

Несовместными называются события, которые не наступают одновременно ни в одном опыте.

Например, противоположные события несовместны.

Условная вероятность P(B|A) – это вероятность наступления события B при условии, что событие A наступило.

Формула противоположного события:

P(A¯)=1−P(A).

Формула сложения вероятностей:

P(A∪B)=P(A)+P(B)−P(A∩B).

Формула сложения вероятностей для несовместных событий:

P(A∪B)=P(A)+P(B).

Формула умножения вероятностей:

P(A∩B)=P(A)⋅P(B|A).

1. Василий Петров выполняет задание по английскому языку. В этом задании есть 10 английских выражений и их переводы на русский в случайном порядке. Нужно установить верные соответствия между выражениями и их переводами. За каждое правильно установленное соответствие даётся 1 балл. Таким образом, можно получить от 0 до 10 баллов. Вася ничего не знает, поэтому выбирает варианты наугад. Найдите вероятность того, что он получит ровно 9 баллов.

Решение: если угадано девять верных ответов, то десятый ответ тоже будет верным. Значит, искомая вероятность равна нулю.

2. Тетрадь в клеточку показывает, как можно замостить плоскость равными квадратами. А как замостить плоскость:

а) равными шестиугольниками;

б) равными треугольниками, причём у каждого из них должна быть хотя бы одна точка, которая граничит ещё с хотя бы 10 треугольниками?

3. В строящемся доме в каждом подъезде одинаковое число квартир. В первом подъезде расположены 1/5 всех проданных квартир и 1/7 непроданных. Сколько подъездов у дома?

Источник

Применение кейс-метода на уроках математики

В современном обучении школьников все большую актуальность приобретают новые методы обучения. Кейс-метод основан на предоставлении учащимся информационных образовательных ресурсов в виде специальных наборов (кейсов) учебно-методических материалов, предназначенных для изучения. Методологически кейс-метод принципиально отличается от аналогичного содержания обучения, которое не использует кейс-метод.

Основными этапами кейс-метода на уроках математики являются:

Представление кейса учителем;
Индивидуальное изучение кейса каждым членом группы;
Разработка вариантов индивидуальных решений;
Обсуждение вариантов индивидуальных решений в каждой подгруппе;
Подготовка к обсуждению и дискуссия.

Для реализации данного метода будет лучше, если два урока математики стоят в расписании рядом.

Урок начинается с того, что каждый ученик получает кейс материал, первая страница которого представляет собой название темы, цели изучения темы, режим работы, правила работы с кейсом, указывается литература, которой может пользоваться учащийся (если не был дан список рекомендуемой литературы в начале учебного года). Учащимся сообщается, что на изучение данной темы отводится определенное количество учебных часов, по истечении которых будет проведена диагностика знаний по теме.

Обращается внимание учащихся на различные уровни сложности практических заданий:

сложность 0 – материал для устного счета,

сложность 1 – обязательный уровень подготовки, который может быть оценен только удовлетворительной оценкой,

сложность 2 – задания для хорошей и отличной оценки,

сложность 3 – творческие задания, требующие применения логического и нестандартного мышления.

Остальные страницы представляют собой теоретический и практический материал, оценочный лист для самооценки учащимися своих знаний и критерии оценки. Проводится обобщение изученной темы учителем, проводится консультация по вопросам, вызвавшим затруднения у учащихся. Консультировать не обязательно учителю – это может делать и любой из учеников, у которого предложенный вопрос не вызвал затруднений. Учащимся предлагается провести самодиагностику, проставив оценки за каждый этап изученной темы в оценочный лист.

Роль учителя при использовании кейс-метода существенно отличается от традиционной. Он как бы передает свои полномочия ученикам, его руководящая роль сводится к минимуму. Учитель должен удерживаться от соблазна предлагать свои варианты решения и оценивать правильность действий учеников в ходе работы над кейсом. Вмешательство учителя в работу учеников должно быть ограничено, оно сводится лишь к регулирующей функции, ему отводится роль наблюдателя. Учитель должен знать, как работают подгруппы, и с этой целью следует подходить к подгруппам, слушать ход обсуждения, иногда воодушевлять обучающихся.

В отведенный период времени каждая подгруппа должна подготовиться к общему обсуждению. Далее выбирается подгруппа, которая сообщает результаты своей работы. Лучше, если решение будет представлено на доске. После этого остальные подгруппы высказывают свою, обязательно аргументированную, точку зрения относительно предлагаемого решения и вносят соответствующие предложения. И лишь после общего обсуждения учитель возвращается к традиционной роли и подводит итоги занятия. Для этого сначала следует вернуться к теоретическому материалу и напомнить его ученикам, т.е. нужно указать название темы или раздела, которые были закреплены с помощью данного кейса.

Ниже приведен пример конспекта урока по алгебре на тему «Координатная плоскость» с использованием кейс-метода и кейсы по теме «Линейная функция»

Урок разработан согласно тематическому планированию главы «Линейная функция» по учебнику А.Г. Мордковича «Алгебра. 7 класс.

Конспект урока с применением кейс-метода «Координатная плоскость» для учащихся 7 класса

Тема урока: «Координатная плоскость».

Цель урока: систематизировать знания по теме «Координатная плоскость»

Задачи:

актуализировать знания по теме «Координатная плоскость»;
выработать умения в нахождении координат точек и построении точек по координатам;
проверить умения применять знания в стандартных и нестандартных ситуациях;
развивать навыки групповой самоорганизации;
воспитывать аккуратность и дисциплинированность.

Оборудование урока: компьютер с выходом в Интернет.

Ход урока:

I. Организационный момент.

II. Постановка задач урока. Выдать каждому ученику кейс.

Представление кейса.

Сегодня на уроке мы будем работать с так называемым «кейсом». Под кейсом понимаются задания с необходимым теоретическим материалом, который вам понадобится для выполнения заданий. Сейчас у каждого из вас есть кейс. В течение двух уроков мы будем работать с данным кейсом. Давайте разберем, из каких разделов он состоит и как с ним работать.

Кейс имеет собственное название, которое соответствует теме нашего урока. Озвучьте её.
Рассмотрим цели нашего урока.
Рассмотрим таблицу «Режим работы». Обратите внимание на то, что согласно распределению времени первые два этапа приходится на первый урок, с третьим этапом вы будете работать на двух уроках, а остальные этапы на второй.
Далее вам нужно прочитать правила работы с кейсом и приступать к теоретической части с заданиями.
После индивидуального выполнения всех заданий, вы будете в микрогруппах обсуждать выполненные задания. После этого правильность будем проверять всем классом.
Критерии самооценивания вы видите в последней таблице. В конце второго урока вы поставите согласно этой таблице в тетрадях баллы. Сумму этих баллов сообщите мне.

III. Актуализация знаний. (Фронтальный опрос)
Для того чтобы приступить к работе с кейсом, давайте вспомним некоторый материал из прошлого года обучения. На координатной прямой прописаны точки – жильцы, у каждой точки есть свой номер дома – ее координата. Если же точка берётся в плоскости, то для её прописки нужно указывать не только номер дома, но и номер квартиры. Припомним, как это делается.

Построить координатную плоскость (учитель выполняет задание на доске). Обозначить начало отсчета, единичный отрезок, назвать координатные оси, пронумеровать координатные углы.
Отметить в координатной плоскости точки: В(8; -3), М(-1; -4), С(5;0), Е(3; 6).

а) назвать абсциссы и ординаты точек;

б) в каком координатном углу находятся точки В, М, Е;

в) на какой координатной оси лежит точка С.

3. Назвать координаты точек:

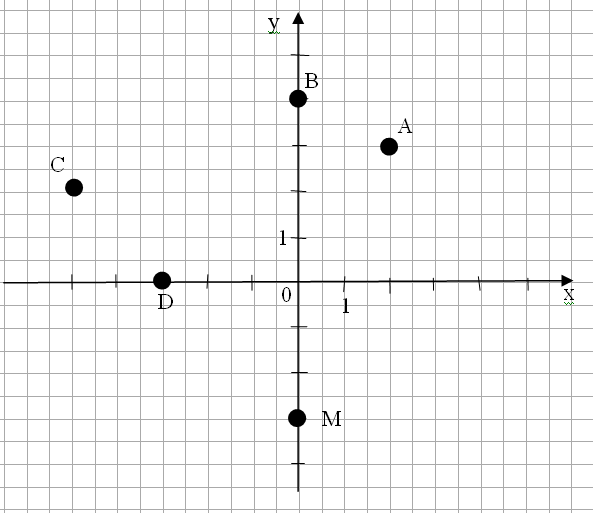
IV. Работа в парах.

Составить алгоритм построения точки; составить алгоритм нахождения координат точки.

V. Работа с кейсом.

Итак, мы вспомнили понятие координатной плоскости, повторили, как строить точку на координатной плоскости и как находить координату точки на координатной плоскости. Теперь перейдем к кейсу.

Индивидуальное изучение кейса каждым учеником.
Разработка вариантов индивидуальных решений.
VI. Усвоение нового материала
Обсуждение вариантов индивидуальных решений в каждой микрогруппе.
VII. Итоги урока

Каждый ученик записывает баллы в тетради по таблице самооценивания. Отметить степень участия или не участия каждого ученика. Возможно оценивание учеников по следующей шкале.
Наибольшее количество баллов 15.
14 – 15 – «5»,
11 –13 – «4»,

8 – 10 – «3».
VIII. Домашнее задание

Составить 5 вопросов по пройденной теме.
Выполнить задания в тетради: 6.2(в); 6.5(б, г); 6.7.(б); 6.15(в); 6.20, 6.24(а, г), 6.27(г), 6.30(а, б), 6.34, 6.39.

Кейсы по теме «Линейная функция»

Кейс «Координатная плоскость»

Глава – Линейная функция.

Цели занятия:

повторить понятие координатной плоскости
научиться строить точку на координатной плоскости и находить координаты точки на координатной плоскости;
учиться свободно ориентироваться на координатной плоскости, чётко и аккуратно выполнять геометрические построения.

1. Режим работы.

№

Этапы работы

Время на этап

Представление кейса.

Повторение изученного материала.

Индивидуальное изучение кейса каждым учеником. Разработка вариантов индивидуальных решений.

Обсуждение вариантов индивидуальных решений в каждой микрогруппе.

Вопросы для обсуждения

Подведение итогов

5 мин

12 мин

25 мин

18 мин

15 мин

7 мин

2. Правила работы над кейсом.

Все решения заданий следует записывать в тетради. Переписывать в тетрадь задания и чертежи не требуется, если это не предусмотрено самим заданием.

В данном кейсе нельзя писать решения. Внимательно читайте и выполняйте практические задания индивидуально по порядку. За консультацией можно обращаться только к учителю. Следи за временем, отведенным на каждый этап работы.

3. Теоретический материал и задания.

Если провести две взаимно перпендикулярные координатные прямые и считать началом отсчета на обеих прямых точку их пересечения – точку О, то говорят, что на плоскости задана прямоугольная система координат, которая превращает обычную плоскость в координатную.

Прямые углы, образуемые осями координат, называют координатными углами (квадрантами) и нумеруют так, как показано на рисунке. Горизонтальная ось системы координат (ось Ох) называется осью абсцисс; вертикальная ось (ось Оу) – осью ординат.

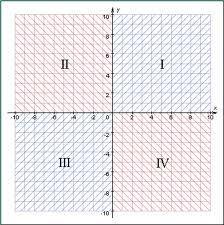
На числовой оси изображается любое число. В прямоугольной системе координат изображается любая пара чисел (х; у). Причем первое число обязательно х, второе – у.

Впервые прямоугольную систему координат на плоскости в 1637 году ввел французский математик Рене Декарт (1596 – 1650) в работе «Геометрия». Для решения геометрических задач алгебраическими методами и, обратно, для замены алгебраических моделей геометрическими. Прямоугольную систему координат часто называют декартовой системой координат.

Задание 1. Изобразите схематично на координатной плоскости точки:

-абсцисса которых равна 0

-ордината которых равна 0

-имеющие одну и ту же абсциссу, равную 4

-имеющие одну и ту же ординату, равную (-2).

Задание 2. Отметьте точки по их координатам в координатной плоскости, последовательно соединяя их отрезками. Если точки построены правильно, то в результате получится рисунок.

(4;-4), (4;-6), (8,5;-7,5), (9;-7), (9;-6), (9,5;-5), (9,5;-3,5), (10;-3), (9,5;-2,5), (4;5), (3;6), (2;6), (0;5),(-3;5), (-7;3), (-9;-1), (-8;-5), (-8;-7), (-4,5;-8), (-4,5;-7), (-5;-6,5), (-5;-6), (-4,5;-5), (-4;-5), (-4;-7), (-1;-7),(-1;-6), (-2;-6), (-1;-4), (1;-8), (3;-8), (3;-7), (2;-7), (2;-6), (3;-5), (3;-6), (5;-7), (7;-7), ухо (6;-4), (6;-3), (7;-2,5), (7,5;-3), глаз (8;-6).

Задание 3.

Построить прямые АВ и СD, если А(1; 3), В(-2; 6), С(-1; -1), D(-5; -3). Записать координаты точек пересечения: а) прямых АВ и СD; б) прямой АВ с осью ординат; в) прямой СD с осью абсцисс.
Написать координаты точек В и С, симметричных точке А(2; -3) относительно оси х и оси у соответственно.
Отметить на координатной плоскости все точки, у которых абсцисса и ордината – неположительные числа и их сумма равна (-5). Какую фигуру будут составлять эти точки?

Задание 4. В какой координатной четверти расположена точка:

Точка	(7;-2)	(-7;-5)	(-1;-2)	(-4;9)	(3;4)	(6;-4)	(3;-5)	(-6;-7)	(8;1)
Четверть

Задание 5.

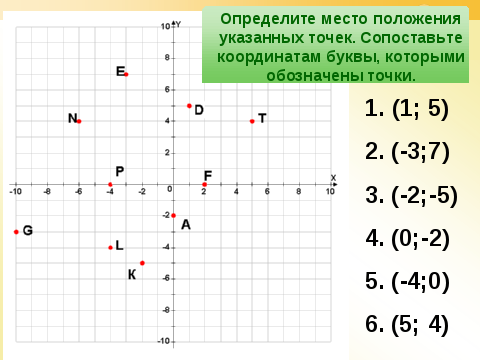
Задание 6. Подготовить сообщение о жизни Рене Декарта.

Задание 7.

Соедините последовательно точки, координаты которых узнаете,
решив все уравнения:

1. –2х + 19 = 5х – 16 (х; 1)

2. 8х – 25 = 3х + 20 (х; 0)

3. 6 – у = 3(3у – 8) (5; у)

4. 5(у + 1,2) = 7у + 4 (1; у)

5. 4(х – 3) – 16 = 5(х – 5) (х; 3)

6. 3х – 17 = 8х + 18 (х; 0)

7. 11 – 5у = 12 – 6у (–3; у)

8. 4у + (11,8 – у) = 3,8 – 5у (1; у)

9. 3х + 16 = 8х – 9 (х; 1)

4. Критерии самооценивания.

№

Наименование критерия

количество баллов

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Задание 7

Работа в микрогруппе.

Участие в обсуждении.

Штрафные баллы за нарушение дисциплины

-2

№ 1 – 6.

0 – не выполнено.

1 – выполнено не полностью либо выполнено с ошибкой.

2 – выполнено верно.

№ 7.

0 – не выполнено.

1 – верно отмечено менее 4 точек.

2 – верно отмечено более 4 точек.

3 – выполнено верно.

№ 8 – 9.

0 – не работал (а).

1 – работал (а).

Кейс «Линейное уравнение с двумя переменными и его график»

Глава – Линейная функция.

Цели занятия:

научиться по виду определять линейное уравнение и его коэффициенты;
учиться по заданному значению х находить соответствующее значение у, и наоборот;
научиться применять на практике алгоритм построения графика линейного уравнения;
учиться составлять линейное уравнение, как математическую модель ситуации.

1. Режим работы.

№

Этапы работы

Время на этап

Представление кейса.

Повторение изученного материала.

Индивидуальное изучение кейса каждым учеником. Разработка вариантов индивидуальных решений.

Обсуждение вариантов индивидуальных решений в каждой микрогруппе.

Вопросы для обсуждения

Подведение итогов

3 мин

7 мин

30 мин

18 мин

15 мин

7 мин

2. Правила работы над кейсом.

3. Теоретический материал и задания.

Математическую модель ах + by + с = 0, где а, b, с — числа (коэффициенты), причем а, называют линейным уравнением с двумя переменными х, у.
Решением уравнения ах + by + с = 0 называется пара значений переменных (х; у), при подстановке которых уравнение становится верным числовым равенством.

Задание № 1.

1. Определить из данных уравнений линейные уравнения с двумя переменными и указать для них значения коэффициентов а, b и с:
х – 7у – 6 = 0; 4х – 8 = 0; 7х + 13у + 1 = 0;

х² – 2у – 9 = 0; 6х + у – 3 = 0; ху = 67.

2. Для уравнения вида 2х – 5у = -9 определить решения из данных пар чисел: .

3. Для уравнения 2х – 5у + 3 = 0 предложить пару чисел, которая является его решением, и предложить пару чисел, не являющуюся решением уравнения.

Задание № 2.

1. Выразите переменную у через переменную х из уравнения:
а) б) в) .
2. Выразите переменную х через переменную у из уравнения:
а) б) в) .

х	0	1	2	3
у

Задание № 3

1. 2х – у + 5 = 0

х
у	0	1	2	3

2. х + 2у – 3 =0

Для каждого уравнения:

– вычислить недостающие значения и заполнить таблицу;

– отметить точки с координатами (х; у) на координатной плоскости;

– провести линию через полученные точки;

– ответить на вопрос: Как называется данная линия?

– сделать вывод.

Задание № 4. Построить график уравнения 4х + 3у – 12 = 0.
Действуйте по алгоритму.

1) если х = 0, то , отсюда у =…

2) если у = 0, то , отсюда х = …

3) Построим на координатной плоскости хОу две точки: (0; у) — она найдена на первом шаге алгоритма и (х; 0) — она найдена на втором шаге.

4) Проведем через точки (0; у) и (х; 0) прямую. Это и есть искомый график.

Задание № 5.

Известно, что (2; 1) – решение уравнения 3х + bу + 1 = 0. найти коэффициент b и еще одно решение этого уравнения.

Задание № 6.

Рассмотреть по учебнику на стр. 40 решение примера № 4.
Составить уравнение по условию задачи и найти несколько его решений: «18 туристов расположились на ночлег в двухместных и в трехместных палатках. Сколько палаток у туристов было двухместных и сколько трехместных?»

Решение: Пусть у туристов было х… и у… палаток.

Решить задачу с выделением трех этапов математического моделирования: «В классе есть небольшой театральный коллектив, который поставил два спектакля. В первом спектакле девочек участвует на одну больше, чем мальчиков. Во втором спектакле участвуют 12 человек, причем число девочек вдвое больше, чем в первом спектакле, а число мальчиков втрое больше, чем в первом спектакле. Сколько всего учеников занято в первом спектакле?»

4. Критерии самооценивания.

№

Наименование критерия

количество баллов

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Работа в микрогруппе.

Участие в обсуждении.

Штрафные баллы за нарушение дисциплины

-2

№ 1 – 5.

0 – не выполнено.

1 – выполнено не полностью либо выполнено с ошибкой.

2 – выполнено верно.

№ 6.

0 – не выполнено.

1 – верно составлено уравнение из п.2 и определены верные решения.

2 – верно составлены оба уравнения из п.3.

3 – выполнено верно.

№ 7 – 8.

0 – не работал (а).

1 – работал (а).

Кейс «Линейная функция и ее график»

Глава – Линейная функция.

Цели занятия:

научиться преобразовывать линейное уравнение с двумя переменными в линейную функцию;
научиться строить график линейной функции;
учиться строить график линейной функции на заданном промежутке и указывать наименьшее и наибольшее значения линейной функции.

1. Режим работы.

№

Этапы работы

Время на этап

Представление кейса.

Повторение изученного материала.

Индивидуальное изучение кейса каждым учеником. Разработка вариантов индивидуальных решений.

Обсуждение вариантов индивидуальных решений в каждой микрогруппе.

Вопросы для обсуждения

Подведение итогов

3 мин

8 мин

30 мин

18 мин

15 мин

7 мин

2. Правила работы над кейсом.

3. Теоретический материал и задания.

Рассмотрим преобразование линейного уравнения с двумя переменными, для этого выразим переменную у через переменную х:

ax + by + c = 0;

by = – ax – c;

y =;

y=.

Введем обозначения: получим y=kx + m.

Таким образом, любое линейное уравнение с двумя переменными можно преобразовать к виду y=kx + m, где k и m – числа (коэффициенты), причем k≠0 (Почему?).

Этот частный вид линейного уравнения с двумя переменными будем называть линейной функцией.

y=kx + m – линейная функция, где х – независимая переменная (аргумент), а у – зависимая переменная (значение функции).

Задание 1.

Установить, задает ли уравнение линейную функцию y=kx + m, если да, то чему равны коэффициенты k и m. Результат записать в тетрадь.

y=3x – 1;
у= – х³;
у=0,5 + х;
у=;
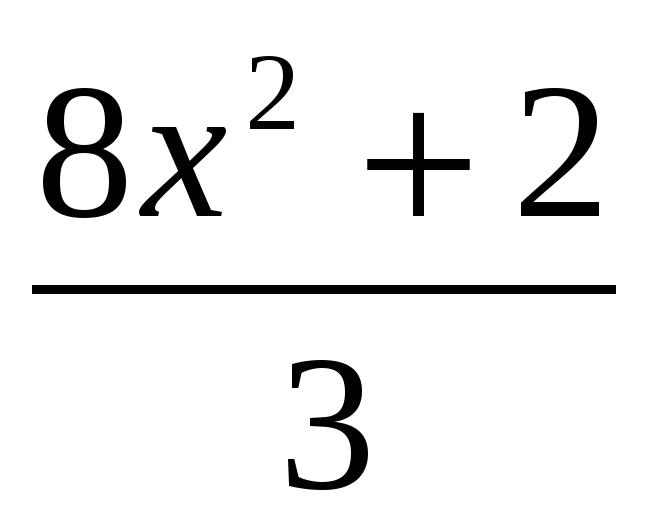у=;
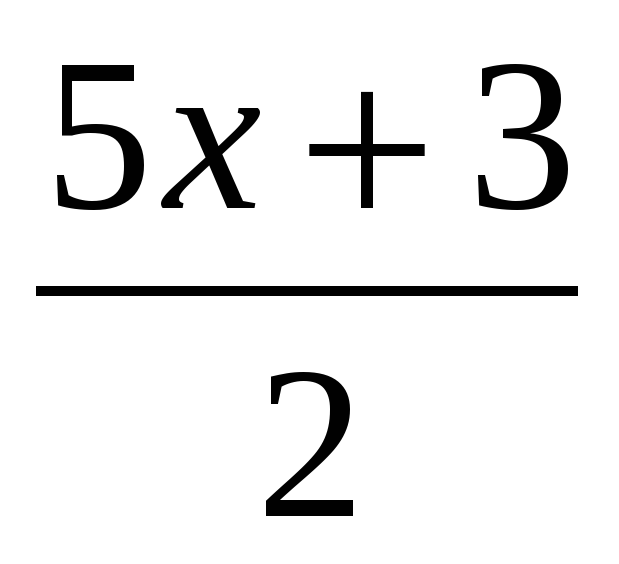у= – 3х.

Задание 2.

Преобразовать линейное уравнение с двумя переменными к виду y=kx + m. Результат записать в тетрадь.

– х + у – 5 = 0;
3х- у – 4 = 0;
5х + 2у – 4 = 0;
2х – 3у + 6 = 0.

С помощью уравнения линейной функции легко, указав конкретные значения х, вычислить соответствующие значения у.

Пусть, например, у = 3х – 1. Тогда:

если х = 0, то у = – 1 (у = 3·0 – 1);

если х = 1, то у = 2 (у = 3·1 – 1);

если х = 2, то у = 5 (у = 3·2 – 1);

если х = – 1, то у = – 4 (у = 3·(- 1) – 1).

Обычно эти результаты оформляют в виде таблицы:

х	0	1	2	– 1
у	– 1	2	5	– 4

Затем наносят получившиеся точки с координатами на координатную плоскость и соединяют.

Так как линейная функция – это частный вид линейного уравнения, то ее графиком также является прямая. Для построения прямой достаточно знать координаты двух точек.

Задание 3. Построить график линейной функции, заданной таблицей; заполнить пустые ячейки по построенному графику.

x	у
-1	-3
0	-1
1
7

б)

x	у
-2	5
0	3
-3
	1

в)

x	у
6	-1
-4	-1
-5
0

Задание 4.

В тетради построить графики линейных функций, которые получились после преобразования в задании № 2.

Если линейную функцию y=kx + m надо рассматривать не при всех значениях х, а лишь для значений х из некоторого промежутка Х, то пишут: y=kx + m, хХ.

Чтобы построить график линейной функции на отрезке, надо сначала построить график всей функции, затем выбрать значения функции, которые соответствуют данному отрезку. Если мы выделяем интервал, то его концами являются светлые кружочки.

Задание 5.

Выделить на чертежах задания № 4 соответствующие отрезки графиков функции.

[- 2, 0];
[2, 3];
[- 2, 2];
[- 3, 6].

Задание 6.

Найти наибольшее и наименьшее значения линейных функций на отрезках из задания № 5. Ответы записать в тетрадь.

Рассмотрим графики линейной функции, изображенные на рисунке 1. Если двигаться по этому графику слева направо, то ординаты точек все время увеличиваются, мы как бы «поднимаемся в горку». В таких случаях математики употребляют термин «возрастание» и говорят так: если k0, то линейная функция y=kx + m возрастает.

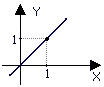
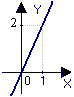
Рисунок 1

Рассмотрим графики линейной функции, изображенные на рисунке 2. Если двигаться по этому графику слева направо, то ординаты точек все время уменьшаются, мы как бы «спускаемся с горки». В таких случаях математики употребляют термин «убывание» и говорят так: если ky=kx + m убывает.

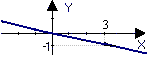
Рисунок 2

График линейной функции y=kx+b пересекает ось ординат в точке (0; m).

Задание 7.

Для каждой из записанных здесь формул указать коэффициенты k и m, найди соответствующий график на рисунке, определить, возрастает или убывает линейная функция:
1. у = – +2,
2. у = –5x,
3. у = –x –5,
4. у = 4,
5. у = 3x –5.

4. Критерии самооценивания.

№

Наименование критерия

количество баллов

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Задание 6

Задание 7

Работа в микрогруппе.

Участие в обсуждении.

Штрафные баллы за нарушение дисциплины

-2

№ 1 – 6.

0 – не выполнено.

1 – выполнено не полностью либо выполнено с ошибкой.

2 – выполнено верно.

№ 7.

0 – не выполнено.

1 – верно указаны коэффициенты.

2 – верно определено возрастание и убывание.

3 – выполнено верно.

№ 8 – 9.

0 – не работал (а).

1 – работал (а).

Кейс «Линейная функция y=kx»

Глава – Линейная функция.

Цели занятия:

научиться строить график линейной функции y=kx;
научиться вычислять угловой коэффициент;
учиться определять положение графика линейной функции y=kx в зависимости от значения k.

Режим работы.

№

Этапы работы

Время на этап

Представление кейса.

Повторение изученного материала.

Индивидуальное изучение кейса каждым учеником. Разработка вариантов индивидуальных решений.

Обсуждение вариантов индивидуальных решений в каждой микрогруппе.

Вопросы для обсуждения

Подведение итогов

2 мин

5 мин

18 мин

8 мин

10 мин

2 мин

2. Правила работы над кейсом.

3. Теоретический материал и задания.

При рассмотрении линейных функций у=kx+m особо выделяют случай, когда m=0; тогда линейная функция принимает вид y=kx.

y=kx – частный случай линейной функции, значит, ее графиком также является прямая. Если х = 0, то и у = 0. Значит, графиком линейной функции y=kx является прямая, проходящая через начало координат.

График линейной функции y=kx обычно строят так: берут точку (1; k) и проводят прямую через эту точку и начало координат. В случае необходимости точку (1; k) можно заменить другой точкой, более удобной (если k – дробное число).

Задание 1.

Постройте график линейной функции y=kx:

у = 2х;
у = – 3х;
у = 0,5х.

Задание 2.

Постройте график линейной функции y=kx, если известно, что ему принадлежит точка М(- 16; 32). Найдите наибольшее и наименьшее значения функции на отрезке [- 2, 2].

Задание 3.

Определить коэффициент k и записать уравнение линейной функции в тетрадь.

От коэффициента k зависит угол, который построенная прямая образует с положительным направлением оси х. Этот угол отсчитывается в направлении против часовой стрелки от оси х до прямой.

Если k0, то этот угол острый, если kтупой. Если k0, то чем больше k, тем больше угол. При увеличении k увеличивается и угол между прямой и положительным направлением оси абсцисс. Поэтому коэффициент k в записи y = kx называют угловым коэффициентом.

Задание 4.

Найти ошибку в построениях графиков линейных функций y = kx и показать схематично их правильное расположение на координатной плоскости в тетради.

Задание 5.

Найти координаты точки пересечения графиков линейных функций y = x и y= x+ 4.

4. Критерии самооценивания.

№

Наименование критерия

количество баллов

1

2

3

4

5

6

7

8

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Работа в микрогруппе.

Участие в обсуждении.

Штрафные баллы за нарушение дисциплины

2

2

2

2

2

1

1

-2

№ 1 – 5.

0 – не выполнено.

1 – выполнено не полностью либо выполнено с ошибкой.

2 – выполнено верно.

№ 6 – 7.

0 – не работал (а).

1 – работал (а).

Кейс «Взаимное расположение графиков линейных функций»

Глава – Линейная функция.

Цели занятия:

рассмотреть взаимное расположение графиков линейных функций;

научиться определять взаимное расположение графиков линейных функций без построения;

научиться подбирать значения коэффициентов k и т линейных функций y= kx+m для заданного взаимного расположения их графиков.

1. Режим работы.

№

Этапы работы

Время на этап

1

2

3

4

5

6

Представление кейса.

Повторение изученного материала.

Индивидуальное изучение кейса каждым учеником. Разработка вариантов индивидуальных решений.

Обсуждение вариантов индивидуальных решений в каждой микрогруппе.

Вопросы для обсуждения

Подведение итогов

2 мин

5 мин

18 мин

9 мин

8 мин

2 мин

2. Правила работы над кейсом.

Все решения заданий следует записывать в тетради. Переписывать в тетрадь задания и чертежи не требуется, если это не предусмотрено самим заданием.

В данном кейсе нельзя писать решения. Внимательно читайте и выполняйте практические задания индивидуально по порядку. За консультацией можно обращаться только к учителю. Следи за временем, отведенным на каждый этап работы.

3. Теоретический материал и задания.

Графиком линейной функции является прямая, значит, сегодня мы будем говорить о взаимном расположении прямых на координатной плоскости.

Задание 1.

Вставите пропущенные слова:

Две прямые, построенные в одной плоскости могут:

1) …

2) …

3) …

Задание 2.

Указать коэффициенты k и т линейных функций y= kx+m. Построить в одной координатной плоскости графики данных функций. Сделать вывод о взаимном расположении графиков.

у = х; у = х + 4.

у = х + 4; у = 2х + 4.

у = 2х + 4; у = х – 2.

Задание 3.

Используя выводы предыдущего задания, заполнить таблицу:

Линейные функции

Алгебраическое условие

Геометрический вывод

y= k₁х + т₁

y= k₂х+m₂

k₁ = k₂, т₁≠ т₂

k₁ = k₂, т₁= т₂

k₁ ≠ k₂

4) k₁ ≠ k₂, т₁= т₂

1)

2)

3)

4)

Задание 4.

Подставить вместо * такое число, чтобы:

графики заданных линейных функций пересекались:

а) у = 6х+ 1 и у = *х – 3;

б) у = *х + 12 и у = *х + 9;

в) у = 2х + * и у = х – *.

2) графики заданных линейных функций были параллельны:

а) у = *х + 6 и у = 12 – 7х;

б) у = *х + 5 и у = *х – 7;

в) у = – *х – 3 и у = *х + 1.

3) графики заданных линейных функций совпадали:

а) у = *х + 8 и у = 5х + 8;

б) у = 4,5х – * и у= 4,5х + *;

в) у = *х + 5 и у = х + 7.

Задание 5.

Задать формулой линейную функцию y= kx, график которой параллелен прямой: 2х + у – 3= 0.

4. Критерии самооценивания.

№

Наименование критерия

количество баллов

1

2

3

4

5

6

7

8

Задание 1

Задание 2

Задание 3

Задание 4

Задание 5

Работа в микрогруппе.

Участие в обсуждении.

Штрафные баллы за нарушение дисциплины

2

2

2

2

2

1

1

-2

№ 1 – 5.

0 – не выполнено.

1 – выполнено не полностью либо выполнено с ошибкой.

2 – выполнено верно.

№ 7 – 8.

0 – не работал (а).

1 – работал (а).

Источник

Описание презентации по отдельным слайдам:

Краткое описание документа:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Другие материалы

Вам будут интересны эти курсы:

ОБЩАЯ ХАРАКТЕРИСТИКА ПРАКТИЧЕСКОГО КЕЙСА

Текст практического кейса:

Основная часть (главный массив информация, проблема)

Заключительная часть (ситуация, требующая решения)

Вам также может понравиться

Как найти скорость течения реки через собственную

Как найти звездочку баттерфляй

Отслаивается нарощенный ноготь как исправить

Добавить комментарий Отменить ответ