Как составить код хемминга - Сайт, где вы сможете решить свои вопросы

Двоичный код Хэмминга
Код Хэмминга с
Назван в честь	Ричард Хэмминг
Тип	линейный блочный код
Длина блока	${displaystyle 2^{r}-1}$
Длина сообщения	${displaystyle 2^{r}-r-1}$
Доля	${displaystyle 1-{frac {2}{2^{r}-1}}}$
Расстояние	3
Размер алфавита	2
Обозначение	${displaystyle [2^{r}-1,2^{r}-r-1,3]_{2}}$
Медиафайлы на Викискладе

Код Хэ́мминга — самоконтролирующийся и самокорректирующийся код. Построен применительно к двоичной системе счисления.

Позволяет исправлять одиночную ошибку (ошибка в одном бите слова) и находить двойную^[1].

Назван в честь американского математика Хэмминга Ричарда Уэсли, предложившего код.

История[править | править код]

В середине 1940-х годов в лаборатории Белла была создана счётная машина Bell Model V. Это была электромеханическая машина, использующая релейные блоки, скорость которых была очень низка: одна операция за несколько секунд. Данные вводились в машину с помощью перфокарт с ненадёжными устройствами чтения, поэтому в процессе чтения часто происходили ошибки. В рабочие дни использовались специальные коды, чтобы обнаруживать и исправлять найденные ошибки, при этом оператор узнавал об ошибке по свечению лампочек, исправлял и снова запускал машину. В выходные дни, когда не было операторов, при возникновении ошибки машина автоматически выходила из программы и запускала другую.

Хэмминг часто работал в выходные дни и всё больше раздражался, так как должен был перезагружать свою программу из-за ненадёжности считывателя перфокарт. На протяжении нескольких лет он искал эффективный алгоритм исправления ошибок. В 1950 году он опубликовал способ кодирования, который известен как код Хэмминга.

Систематические коды[править | править код]

Систематические коды образуют большую группу из блочных, разделимых кодов (в которых все символы слова можно разделить на проверочные и информационные). Особенностью систематических кодов является то, что проверочные символы образуются в результате линейных логических операций над информационными символами. Кроме того, любая разрешенная кодовая комбинация может быть получена в результате линейных операций над набором линейно независимых кодовых комбинаций.

Самоконтролирующиеся коды[править | править код]

Коды Хэмминга являются самоконтролирующимися кодами, то есть кодами, позволяющими автоматически обнаруживать ошибки при передаче данных. Для их построения достаточно приписать к каждому слову один добавочный (контрольный) двоичный разряд и выбрать цифру этого разряда так, чтобы общее количество единиц в изображении любого числа было, например, нечётным. Одиночная ошибка в каком-либо разряде передаваемого слова (в том числе, может быть, и в контрольном разряде) изменит чётность общего количества единиц. Счётчики по модулю 2, подсчитывающие количество единиц, которые содержатся среди двоичных цифр числа, дают сигнал о наличии ошибок. При этом невозможно узнать, в какой именно позиции слова произошла ошибка, и, следовательно, нет возможности исправить её. Остаются незамеченными также ошибки, возникающие одновременно в двух, четырёх, и т. д. — в чётном количестве разрядов. Предполагается, что двойные, а тем более многократные ошибки маловероятны.

Самокорректирующиеся коды[править | править код]

Коды, в которых возможно автоматическое исправление ошибок, называются самокорректирующимися. Для построения самокорректирующегося кода, рассчитанного на исправление одиночных ошибок, одного контрольного разряда недостаточно. Как видно из дальнейшего, количество контрольных разрядов должно быть выбрано так, чтобы удовлетворялось неравенство или , где — количество информационных двоичных разрядов кодового слова. Минимальные значения k при заданных значениях m, найденные в соответствии с этим неравенством, приведены в таблице.

Диапазон m	k_min
1	2
2-4	3
5-11	4
12-26	5
27-57	6

Наибольший интерес представляют двоичные блочные корректирующие коды. При использовании таких кодов информация передаётся в виде блоков одинаковой длины, и каждый блок кодируется и декодируется независимо от другого. Почти во всех блочных кодах символы можно разделить на информационные и проверочные или контрольные. Таким образом, все слова разделяются на разрешённые (для которых соотношение информационных и проверочных символов возможно) и запрещённые.

Основные характеристики самокорректирующихся кодов:

Число разрешённых и запрещённых комбинаций. Если — число символов в блоке, — число проверочных символов в блоке, — число информационных символов, то $2^{n}$ — число возможных кодовых комбинаций, — число разрешённых кодовых комбинаций, ${displaystyle 2^{n}-2^{k}}$ — число запрещённых комбинаций.
Избыточность кода. Величину ${displaystyle {tfrac {r}{n}}}$ называют избыточностью корректирующего кода.
Минимальное кодовое расстояние. Минимальным кодовым расстоянием называется минимальное число искажённых символов, необходимое для перехода одной разрешённой комбинации в другую.
Число обнаруживаемых и исправляемых ошибок. Если — количество ошибок, которое код способен исправить, то необходимо и достаточно, чтобы
Корректирующие возможности кодов.

Граница Плоткина даёт верхнюю границу кодового расстояния:

${displaystyle dleqslant {tfrac {ncdot 2^{k-1}}{2^{k}-1}},}$

или:

${displaystyle rgeq 2cdot (d-1)-log _{2}d}$

при

Граница Хэмминга устанавливает максимально возможное число разрешённых кодовых комбинаций:

${displaystyle 2^{k}leq {2^{n}}/sum _{i=0}^{tfrac {d-1}{2}}C_{n}^{i},}$

где

— число сочетаний из

элементов по

элементам. Отсюда можно получить выражение для оценки числа проверочных символов:

${displaystyle rgeq log _{2}left(sum _{i=0}^{(d-1)/2}C_{n}^{i}right).}$

Для значений разница между границей Хэмминга и границей Плоткина невелика.

Граница Варшамова — Гилберта для больших n определяет нижнюю границу числа проверочных символов:

${displaystyle rgeq log _{2}left(sum _{i=0}^{d-2}C_{n-1}^{i}right).}$

Все вышеперечисленные оценки дают представление о верхней границе при фиксированных и или оценку снизу числа проверочных символов.

Код Хэмминга[править | править код]

Построение кодов Хэмминга основано на принципе проверки на чётность числа единичных символов: к последовательности добавляется такой элемент, чтобы число единичных символов в получившейся последовательности было чётным:

${displaystyle r_{1}=i_{1}oplus i_{2}oplus ...oplus i_{k}.}$

Знак oplus здесь означает сложение по модулю 2:

${displaystyle S=i_{1}oplus i_{2}oplus ...oplus i_{n}oplus r_{1}.}$

Если S=0 — то ошибки нет, если — то однократная ошибка.

Такой код называется или . Первое число — количество элементов последовательности, второе — количество информационных символов.

Для каждого числа проверочных символов существует классический код Хэмминга с маркировкой:

${displaystyle (n,k)=(2^{r}-1,2^{r}-1-r),}$

то есть —

При иных значениях получается так называемый усечённый код, например международный телеграфный код МТК-2, у которого k = 5 . Для него необходим код Хэмминга который является усечённым от классического

Для примера рассмотрим классический код Хемминга . Сгруппируем проверочные символы следующим образом:

${displaystyle r_{1}=i_{1}oplus i_{2}oplus i_{3},}$

${displaystyle r_{2}=i_{2}oplus i_{3}oplus i_{4},}$

${displaystyle r_{3}=i_{1}oplus i_{2}oplus i_{4}.}$

Получение кодового слова выглядит следующим образом:

$begin{pmatrix} i_1 & i_2 & i_3 & i_4 & \ end{pmatrix}$

$begin{pmatrix} 1 & 0 & 0 & 0 & 1 & 0 & 1 \ 0 & 1 & 0 & 0 & 1 & 1 & 1 \ 0 & 0 & 1 & 0 & 1 & 1 & 0 \ 0 & 0 & 0 & 1 & 0 & 1 & 1 \ end{pmatrix}$

= $begin{pmatrix} i_1 & i_2 & i_3 & i_4 & r_1 & r_2 & r_3 \ end{pmatrix}$

На вход декодера поступает кодовое слово
${displaystyle V=(i_{1}', i_{2}', i_{3}', i_{4}', r_{1}', r_{2}', r_{3}')}$ , где штрихом помечены символы, которые могут исказиться в результате действия помехи. В декодере в режиме исправления ошибок строится последовательность синдромов:

${displaystyle S_{1}=r_{1}oplus i_{1}oplus i_{2}oplus i_{3},}$

${displaystyle S_{2}=r_{2}oplus i_{2}oplus i_{3}oplus i_{4},}$

${displaystyle S_{3}=r_{3}oplus i_{1}oplus i_{2}oplus i_{4}.}$

${displaystyle S=(S_{1}, S_{2}, S_{3})}$ называется синдромом последовательности.

Получение синдрома выглядит следующим образом:

$begin{pmatrix} i_1 & i_2 & i_3 & i_4 & r_1 & r_2 & r_3 \ end{pmatrix}$

$begin{pmatrix} 1 & 0 & 1 \ 1 & 1 & 1 \ 1 & 1 & 0 \ 0 & 1 & 1 \ 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \ end{pmatrix}$

= ${displaystyle {begin{pmatrix}S_{1}&S_{2}&S_{3}\end{pmatrix}}}$

				$r_{1}$	$r_{2}$						$r_{1}$	$r_{2}$
0	0	0	0	0	0	0	1	0	0	0	1	0	1
0	0	0	1	0	1	1	1	0	0	1	1	1	0
0	0	1	0	1	1	0	1	0	1	0	0	1	1
0	0	1	1	1	0	1	1	0	1	1	0	0	0
0	1	0	0	1	1	1	1	1	0	0	0	1	0
0	1	0	1	1	0	0	1	1	0	1	0	0	1
0	1	1	0	0	0	1	1	1	1	0	1	0	0
0	1	1	1	0	1	0	1	1	1	1	1	1	1

Кодовые слова кода Хэмминга приведены в таблице.

Синдром указывает на то, что в последовательности нет искажений. Каждому ненулевому синдрому соответствует определённая конфигурация ошибок, которая исправляется на этапе декодирования.

Синдром	001	010	011	100	101	110	111
Конфигурация ошибок	0000001	0000010	0001000	0000100	1000000	0010000	0100000
Ошибка в символе		$r_{2}$		$r_{1}$

Для кода в таблице справа указаны ненулевые синдромы и соответствующие им конфигурации ошибок (для вида: i_1 i_2 i_3 i_4 $r_{1}$ $r_{2}$ r_3 ).

Алгоритм кодирования[править | править код]

Предположим, что нужно сгенерировать код Хэмминга для некоторого информационного кодового слова. В качестве примера возьмём 15-битовое кодовое слово ${displaystyle x_{1}dots x_{15},}$ хотя алгоритм пригоден для кодовых слов любой длины. В приведённой ниже таблице в первой строке даны номера позиций в кодовом слове, во второй — условное обозначение битов, в третьей — значения битов.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
x₁	x₂	x₃	x₄	x₅	x₆	x₇	x₈	x₉	x₁₀	x₁₁	x₁₂	x₁₃	x₁₄	x₁₅
1	0	0	1	0	0	1	0	1	1	1	0	0	0	1

Вставим в информационное слово контрольные биты ${displaystyle r_{0}dots r_{4}}$ таким образом, чтобы номера их позиций представляли собой целые степени двойки: 1, 2, 4, 8, 16… Получим 20-разрядное слово с 15 информационными и 5 контрольными битами. Первоначально контрольные биты устанавливаем равными нулю. На рисунке контрольные биты выделены розовым цветом.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
r₀	r₁	x₁	r₂	x₂	x₃	x₄	r₃	x₅	x₆	x₇	x₈	x₉	x₁₀	x₁₁	r₄	x₁₂	x₁₃	x₁₄	x₁₅
0	0	1	0	0	0	1	0	0	0	1	0	1	1	1	0	0	0	0	1

В общем случае количество контрольных бит в кодовом слове равно двоичному логарифму числа, на единицу большего, чем количество бит кодового слова (включая контрольные биты); логарифм округляется в большую сторону. Например, информационное слово длиной 1 бит требует двух контрольных разрядов, 2-, 3- или 4-битовое информационное слово — трёх, 5…11-битовое — четырёх, 12…26-битовое — пяти и т. д.

Добавим к таблице 5 строк (по количеству контрольных битов), в которые поместим матрицу преобразования. Каждая строка будет соответствовать одному контрольному биту (нулевой контрольный бит — верхняя строка, четвёртый — нижняя), каждый столбец — одному биту кодируемого слова. В каждом столбце матрицы преобразования поместим двоичный номер этого столбца, причём порядок следования битов будет обратный — младший бит расположим в верхней строке, старший — в нижней. Например, в третьем столбце матрицы будут стоять числа 11000, что соответствует двоичной записи числа три: 00011.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
r₀	r₁	x₁	r₂	x₂	x₃	x₄	r₃	x₅	x₆	x₇	x₈	x₉	x₁₀	x₁₁	r₄	x₁₂	x₁₃	x₁₄	x₁₅
0	0	1	0	0	0	1	0	0	0	1	0	1	1	1	0	0	0	0	1
1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	r₀
0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	r₁
0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	r₂
0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	r₃
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	r₄

В правой части таблицы оставили пустым один столбец, в который поместим результаты вычислений контрольных битов. Вычисление контрольных битов производим следующим образом: берём одну из строк матрицы преобразования (например, $r_{0}$ ) и находим её скалярное произведение с кодовым словом, то есть перемножаем соответствующие биты обеих строк и находим сумму произведений. Если сумма получилась больше единицы, находим остаток от его деления на 2. Иными словами, мы подсчитываем, сколько раз в кодовом слове и соответствующей строке матрицы в одинаковых позициях стоят единицы, и берём это число по модулю 2.

Если описывать этот процесс в терминах матричной алгебры, то операция представляет собой перемножение матрицы преобразования на матрицу-столбец кодового слова, в результате чего получается матрица-столбец контрольных разрядов, которые нужно взять по модулю 2.

Например, для строки $r_{0}$ :

$r_{0}$

= (1·0+0·0+1·1+0·0+1·0+0·0+1·1+0·0+1·0+0·0+1·1+0·0+1·1+0·1+1·1+0·0+1·0+0·0+1·0+0·1) mod 2 = 5 mod 2 = 1.

Полученные контрольные биты вставляем в кодовое слово вместо стоявших там ранее нулей. По аналогии находим проверочные биты в остальных строках. Кодирование по Хэммингу завершено. Полученное кодовое слово — 11110010001011110001.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
r₀	r₁	x₁	r₂	x₂	x₃	x₄	r₃	x₅	x₆	x₇	x₈	x₉	x₁₀	x₁₁	r₄	x₁₂	x₁₃	x₁₄	x₁₅
1	1	1	1	0	0	1	0	0	0	1	0	1	1	1	1	0	0	0	1
1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	r₀	1
0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	r₁	1
0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	r₂	1
0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	r₃	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	r₄	1

Алгоритм декодирования[править | править код]

Алгоритм декодирования по Хэммингу абсолютно идентичен алгоритму кодирования. Матрица преобразования соответствующей размерности умножается на матрицу-столбец кодового слова, и каждый элемент полученной матрицы-столбца берётся по модулю 2. Полученная матрица-столбец получила название «матрица синдромов». Легко проверить, что кодовое слово, сформированное в соответствии с алгоритмом, описанным в предыдущем разделе, всегда даёт нулевую матрицу синдромов.

Матрица синдромов становится ненулевой, если в результате ошибки (например, при передаче слова по линии связи с шумами) один из битов исходного слова изменил своё значение. Предположим для примера, что в кодовом слове, полученном в предыдущем разделе, шестой бит изменил своё значение с нуля на единицу (на рисунке обозначено красным цветом). Тогда получим следующую матрицу синдромов.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
r₀	r₁	x₁	r₂	x₂	x₃	x₄	r₃	x₅	x₆	x₇	x₈	x₉	x₁₀	x₁₁	r₄	x₁₂	x₁₃	x₁₄	x₁₅
1	1	1	1	0	1	1	0	0	0	1	0	1	1	1	1	0	0	0	1
1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	s₀	0
0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	s₁	1
0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	s₂	1
0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	s₃	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	s₄	0

Заметим, что при однократной ошибке матрица синдромов всегда представляет собой двоичную запись (младший разряд в верхней строке) номера позиции, в которой произошла ошибка. В приведённом примере матрица синдромов (01100) соответствует двоичному числу 00110 или десятичному 6, откуда следует, что ошибка произошла в шестом бите.

Применение[править | править код]

Код Хэмминга используется:

в некоторых прикладных программах в области хранения данных;
при построении дисковых массивов RAID 2;
в памяти типа ECC и позволяет «на лету» исправлять однократные и обнаруживать двукратные ошибки.

См. также[править | править код]

Бит чётности
Циклический код
Циклический избыточный код
Код Рида — Соломона

Примечания[править | править код]

↑ Коды Хемминга — “Все о Hi-Tech”. all-ht.ru. Дата обращения: 20 января 2016. Архивировано 15 января 2016 года.

Литература[править | править код]

Питерсон У., Уэлдон Э. Коды, исправляющие ошибки: Пер. с англ. М.: Мир, 1976, 594 c.
Пенин П. Е., Филиппов М.Р. Радиотехнические системы передачи информации. М.: Радио и Связь, 1984, 256 с.
Блейхут Р. Теория и практика кодов, контролирующих ошибки. Пер. с англ. М.: Мир, 1986, 576 с.

Источник

Код Хэмминга. Пример работы алгоритма

Время на прочтение
4 мин

Количество просмотров 511K

Вступление.

Прежде всего стоит сказать, что такое Код Хэмминга и для чего он, собственно, нужен. На Википедии даётся следующее определение:

Коды Хэмминга — наиболее известные и, вероятно, первые из самоконтролирующихся и самокорректирующихся кодов. Построены они применительно к двоичной системе счисления.

Другими словами, это алгоритм, который позволяет закодировать какое-либо информационное сообщение определённым образом и после передачи (например по сети) определить появилась ли какая-то ошибка в этом сообщении (к примеру из-за помех) и, при возможности, восстановить это сообщение. Сегодня, я опишу самый простой алгоритм Хемминга, который может исправлять лишь одну ошибку.

Также стоит отметить, что существуют более совершенные модификации данного алгоритма, которые позволяют обнаруживать (и если возможно исправлять) большее количество ошибок.

Сразу стоит сказать, что Код Хэмминга состоит из двух частей. Первая часть кодирует исходное сообщение, вставляя в него в определённых местах контрольные биты (вычисленные особым образом). Вторая часть получает входящее сообщение и заново вычисляет контрольные биты (по тому же алгоритму, что и первая часть). Если все вновь вычисленные контрольные биты совпадают с полученными, то сообщение получено без ошибок. В противном случае, выводится сообщение об ошибке и при возможности ошибка исправляется.

Как это работает.

Для того, чтобы понять работу данного алгоритма, рассмотрим пример.

Подготовка

Допустим, у нас есть сообщение «habr», которое необходимо передать без ошибок. Для этого сначала нужно наше сообщение закодировать при помощи Кода Хэмминга. Нам необходимо представить его в бинарном виде.

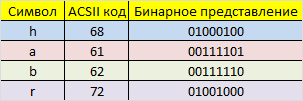
На этом этапе стоит определиться с, так называемой, длиной информационного слова, то есть длиной строки из нулей и единиц, которые мы будем кодировать. Допустим, у нас длина слова будет равна 16. Таким образом, нам необходимо разделить наше исходное сообщение («habr») на блоки по 16 бит, которые мы будем потом кодировать отдельно друг от друга. Так как один символ занимает в памяти 8 бит, то в одно кодируемое слово помещается ровно два ASCII символа. Итак, мы получили две бинарные строки по 16 бит:

После этого процесс кодирования распараллеливается, и две части сообщения («ha» и «br») кодируются независимо друг от друга. Рассмотрим, как это делается на примере первой части.
Прежде всего, необходимо вставить контрольные биты. Они вставляются в строго определённых местах — это позиции с номерами, равными степеням двойки. В нашем случае (при длине информационного слова в 16 бит) это будут позиции 1, 2, 4, 8, 16. Соответственно, у нас получилось 5 контрольных бит (выделены красным цветом):

Было:

Стало:

Таким образом, длина всего сообщения увеличилась на 5 бит. До вычисления самих контрольных бит, мы присвоили им значение «0».

Вычисление контрольных бит.

Теперь необходимо вычислить значение каждого контрольного бита. Значение каждого контрольного бита зависит от значений информационных бит (как неожиданно), но не от всех, а только от тех, которые этот контрольных бит контролирует. Для того, чтобы понять, за какие биты отвечает каждых контрольный бит необходимо понять очень простую закономерность: контрольный бит с номером N контролирует все последующие N бит через каждые N бит, начиная с позиции N. Не очень понятно, но по картинке, думаю, станет яснее:

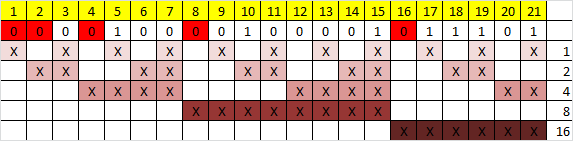
Здесь знаком «X» обозначены те биты, которые контролирует контрольный бит, номер которого справа. То есть, к примеру, бит номер 12 контролируется битами с номерами 4 и 8. Ясно, что чтобы узнать какими битами контролируется бит с номером N надо просто разложить N по степеням двойки.

Но как же вычислить значение каждого контрольного бита? Делается это очень просто: берём каждый контрольный бит и смотрим сколько среди контролируемых им битов единиц, получаем некоторое целое число и, если оно чётное, то ставим ноль, в противном случае ставим единицу. Вот и всё! Можно конечно и наоборот, если число чётное, то ставим единицу, в противном случае, ставим 0. Главное, чтобы в «кодирующей» и «декодирующей» частях алгоритм был одинаков. (Мы будем применять первый вариант).
Высчитав контрольные биты для нашего информационного слова получаем следующее:

и для второй части:

Вот и всё! Первая часть алгоритма завершена.

Декодирование и исправление ошибок.

Теперь, допустим, мы получили закодированное первой частью алгоритма сообщение, но оно пришло к нас с ошибкой. К примеру мы получили такое (11-ый бит передался неправильно):

Вся вторая часть алгоритма заключается в том, что необходимо заново вычислить все контрольные биты (так же как и в первой части) и сравнить их с контрольными битами, которые мы получили. Так, посчитав контрольные биты с неправильным 11-ым битом мы получим такую картину:

Как мы видим, контрольные биты под номерами: 1, 2, 8 не совпадают с такими же контрольными битами, которые мы получили. Теперь просто сложив номера позиций неправильных контрольных бит (1 + 2 + 8 = 11) мы получаем позицию ошибочного бита. Теперь просто инвертировав его и отбросив контрольные биты, мы получим исходное сообщение в первозданном виде! Абсолютно аналогично поступаем со второй частью сообщения.

Заключение.

В данном примере, я взял длину информационного сообщения именно 16 бит, так как мне кажется, что она наиболее оптимальная для рассмотрения примера (не слишком длинная и не слишком короткая), но конечно же длину можно взять любую. Только стоит учитывать, что в данной простой версии алгоритма на одно информационное слово можно исправить только одну ошибку.

Примечание.

На написание этого топика меня подвигло то, что в поиске я не нашёл на Хабре статей на эту тему (чему я был крайне удивлён). Поэтому я решил отчасти исправить эту ситуацию и максимально подробно показать как этот алгоритм работает. Я намеренно не приводил ни одной формулы, дабы попытаться своими словами донести процесс работы алгоритма на примере.

Источники.

1. Википедия
2. Calculating the Hamming Code

Источник

Binary Hamming codes
The Hamming(7,4) code (with r = 3)
Named after	Richard W. Hamming
Classification
Type	Linear block code
Block length	2^r − 1 where r ≥ 2
Message length	2^r − r − 1
Rate	1 − r/(2^r − 1)
Distance	3
Alphabet size	2
Notation	[2^r − 1, 2^r − r − 1, 3]₂-code
Properties
perfect code
v t e

In computer science and telecommunication, Hamming codes are a family of linear error-correcting codes. Hamming codes can detect one-bit and two-bit errors, or correct one-bit errors without detection of uncorrected errors. By contrast, the simple parity code cannot correct errors, and can detect only an odd number of bits in error. Hamming codes are perfect codes, that is, they achieve the highest possible rate for codes with their block length and minimum distance of three.^[1]
Richard W. Hamming invented Hamming codes in 1950 as a way of automatically correcting errors introduced by punched card readers. In his original paper, Hamming elaborated his general idea, but specifically focused on the Hamming(7,4) code which adds three parity bits to four bits of data.^[2]

In mathematical terms, Hamming codes are a class of binary linear code. For each integer r ≥ 2 there is a code-word with block length n = 2^r − 1 and message length k = 2^r − r − 1. Hence the rate of Hamming codes is R = k / n = 1 − r / (2^r − 1), which is the highest possible for codes with minimum distance of three (i.e., the minimal number of bit changes needed to go from any code word to any other code word is three) and block length 2^r − 1. The parity-check matrix of a Hamming code is constructed by listing all columns of length r that are non-zero, which means that the dual code of the Hamming code is the shortened Hadamard code, also known as a Simplex code. The parity-check matrix has the property that any two columns are pairwise linearly independent.

Due to the limited redundancy that Hamming codes add to the data, they can only detect and correct errors when the error rate is low. This is the case in computer memory (usually RAM), where bit errors are extremely rare and Hamming codes are widely used, and a RAM with this correction system is a ECC RAM (ECC memory). In this context, an extended Hamming code having one extra parity bit is often used. Extended Hamming codes achieve a Hamming distance of four, which allows the decoder to distinguish between when at most one one-bit error occurs and when any two-bit errors occur. In this sense, extended Hamming codes are single-error correcting and double-error detecting, abbreviated as SECDED.

History[edit]

Richard Hamming, the inventor of Hamming codes, worked at Bell Labs in the late 1940s on the Bell Model V computer, an electromechanical relay-based machine with cycle times in seconds. Input was fed in on punched paper tape, seven-eighths of an inch wide, which had up to six holes per row. During weekdays, when errors in the relays were detected, the machine would stop and flash lights so that the operators could correct the problem. During after-hours periods and on weekends, when there were no operators, the machine simply moved on to the next job.

Hamming worked on weekends, and grew increasingly frustrated with having to restart his programs from scratch due to detected errors. In a taped interview, Hamming said, “And so I said, ‘Damn it, if the machine can detect an error, why can’t it locate the position of the error and correct it?'”.^[3] Over the next few years, he worked on the problem of error-correction, developing an increasingly powerful array of algorithms. In 1950, he published what is now known as Hamming code, which remains in use today in applications such as ECC memory.

Codes predating Hamming[edit]

A number of simple error-detecting codes were used before Hamming codes, but none were as effective as Hamming codes in the same overhead of space.

Parity[edit]

Parity adds a single bit that indicates whether the number of ones (bit-positions with values of one) in the preceding data was even or odd. If an odd number of bits is changed in transmission, the message will change parity and the error can be detected at this point; however, the bit that changed may have been the parity bit itself. The most common convention is that a parity value of one indicates that there is an odd number of ones in the data, and a parity value of zero indicates that there is an even number of ones. If the number of bits changed is even, the check bit will be valid and the error will not be detected.

Moreover, parity does not indicate which bit contained the error, even when it can detect it. The data must be discarded entirely and re-transmitted from scratch. On a noisy transmission medium, a successful transmission could take a long time or may never occur. However, while the quality of parity checking is poor, since it uses only a single bit, this method results in the least overhead.

Two-out-of-five code[edit]

A two-out-of-five code is an encoding scheme which uses five bits consisting of exactly three 0s and two 1s. This provides ten possible combinations, enough to represent the digits 0–9. This scheme can detect all single bit-errors, all odd numbered bit-errors and some even numbered bit-errors (for example the flipping of both 1-bits). However it still cannot correct any of these errors.

Repetition[edit]

Another code in use at the time repeated every data bit multiple times in order to ensure that it was sent correctly. For instance, if the data bit to be sent is a 1, an n = 3 repetition code will send 111. If the three bits received are not identical, an error occurred during transmission. If the channel is clean enough, most of the time only one bit will change in each triple. Therefore, 001, 010, and 100 each correspond to a 0 bit, while 110, 101, and 011 correspond to a 1 bit, with the greater quantity of digits that are the same (‘0’ or a ‘1’) indicating what the data bit should be. A code with this ability to reconstruct the original message in the presence of errors is known as an error-correcting code. This triple repetition code is a Hamming code with m = 2, since there are two parity bits, and 2² − 2 − 1 = 1 data bit.

Such codes cannot correctly repair all errors, however. In our example, if the channel flips two bits and the receiver gets 001, the system will detect the error, but conclude that the original bit is 0, which is incorrect. If we increase the size of the bit string to four, we can detect all two-bit errors but cannot correct them (the quantity of parity bits is even); at five bits, we can both detect and correct all two-bit errors, but not all three-bit errors.

Moreover, increasing the size of the parity bit string is inefficient, reducing throughput by three times in our original case, and the efficiency drops drastically as we increase the number of times each bit is duplicated in order to detect and correct more errors.

Description[edit]

If more error-correcting bits are included with a message, and if those bits can be arranged such that different incorrect bits produce different error results, then bad bits could be identified. In a seven-bit message, there are seven possible single bit errors, so three error control bits could potentially specify not only that an error occurred but also which bit caused the error.

Hamming studied the existing coding schemes, including two-of-five, and generalized their concepts. To start with, he developed a nomenclature to describe the system, including the number of data bits and error-correction bits in a block. For instance, parity includes a single bit for any data word, so assuming ASCII words with seven bits, Hamming described this as an (8,7) code, with eight bits in total, of which seven are data. The repetition example would be (3,1), following the same logic. The code rate is the second number divided by the first, for our repetition example, 1/3.

Hamming also noticed the problems with flipping two or more bits, and described this as the “distance” (it is now called the Hamming distance, after him). Parity has a distance of 2, so one bit flip can be detected but not corrected, and any two bit flips will be invisible. The (3,1) repetition has a distance of 3, as three bits need to be flipped in the same triple to obtain another code word with no visible errors. It can correct one-bit errors or it can detect – but not correct – two-bit errors. A (4,1) repetition (each bit is repeated four times) has a distance of 4, so flipping three bits can be detected, but not corrected. When three bits flip in the same group there can be situations where attempting to correct will produce the wrong code word. In general, a code with distance k can detect but not correct k − 1 errors.

Hamming was interested in two problems at once: increasing the distance as much as possible, while at the same time increasing the code rate as much as possible. During the 1940s he developed several encoding schemes that were dramatic improvements on existing codes. The key to all of his systems was to have the parity bits overlap, such that they managed to check each other as well as the data.

General algorithm[edit]

The following general algorithm generates a single-error correcting (SEC) code for any number of bits. The main idea is to choose the error-correcting bits such that the index-XOR (the XOR of all the bit positions containing a 1) is 0. We use positions 1, 10, 100, etc. (in binary) as the error-correcting bits, which guarantees it is possible to set the error-correcting bits so that the index-XOR of the whole message is 0. If the receiver receives a string with index-XOR 0, they can conclude there were no corruptions, and otherwise, the index-XOR indicates the index of the corrupted bit.

An algorithm can be deduced from the following description:

Number the bits starting from 1: bit 1, 2, 3, 4, 5, 6, 7, etc.
Write the bit numbers in binary: 1, 10, 11, 100, 101, 110, 111, etc.
All bit positions that are powers of two (have a single 1 bit in the binary form of their position) are parity bits: 1, 2, 4, 8, etc. (1, 10, 100, 1000)
All other bit positions, with two or more 1 bits in the binary form of their position, are data bits.
Each data bit is included in a unique set of 2 or more parity bits, as determined by the binary form of its bit position.
1. Parity bit 1 covers all bit positions which have the least significant bit set: bit 1 (the parity bit itself), 3, 5, 7, 9, etc.
2. Parity bit 2 covers all bit positions which have the second least significant bit set: bits 2-3, 6-7, 10-11, etc.
3. Parity bit 4 covers all bit positions which have the third least significant bit set: bits 4–7, 12–15, 20–23, etc.
4. Parity bit 8 covers all bit positions which have the fourth least significant bit set: bits 8–15, 24–31, 40–47, etc.
5. In general each parity bit covers all bits where the bitwise AND of the parity position and the bit position is non-zero.

If a byte of data to be encoded is 10011010, then the data word (using _ to represent the parity bits) would be __1_001_1010, and the code word is 011100101010.

The choice of the parity, even or odd, is irrelevant but the same choice must be used for both encoding and decoding.

This general rule can be shown visually:

Encoded data bits	p1	p2	d1	p4	d2	d3	d4	p8	d5	d6	d7	d8	d9	d10	d11	p16	d12	d13	d14	d15
Bit position	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	…
Parity bit coverage	p1
p2
p4
p8
p16

Shown are only 20 encoded bits (5 parity, 15 data) but the pattern continues indefinitely. The key thing about Hamming Codes that can be seen from visual inspection is that any given bit is included in a unique set of parity bits. To check for errors, check all of the parity bits. The pattern of errors, called the error syndrome, identifies the bit in error. If all parity bits are correct, there is no error. Otherwise, the sum of the positions of the erroneous parity bits identifies the erroneous bit. For example, if the parity bits in positions 1, 2 and 8 indicate an error, then bit 1+2+8=11 is in error. If only one parity bit indicates an error, the parity bit itself is in error.

With m parity bits, bits from 1 up to $2^{m}-1$ can be covered. After discounting the parity bits, 2^m-m-1 bits remain for use as data. As m varies, we get all the possible Hamming codes:

Parity bits	Total bits	Data bits	Name	Rate
2	3	1	Hamming(3,1) (Triple repetition code)	1/3 ≈ 0.333
3	7	4	Hamming(7,4)	4/7 ≈ 0.571
4	15	11	Hamming(15,11)	11/15 ≈ 0.733
5	31	26	Hamming(31,26)	26/31 ≈ 0.839
6	63	57	Hamming(63,57)	57/63 ≈ 0.905
7	127	120	Hamming(127,120)	120/127 ≈ 0.945
8	255	247	Hamming(255,247)	247/255 ≈ 0.969
9	511	502	Hamming(511,502)	502/511 ≈ 0.982
…
m	${displaystyle n=2^{m}-1}$	${displaystyle k=2^{m}-m-1}$	Hamming

Hamming codes with additional parity (SECDED)[edit]

Hamming codes have a minimum distance of 3, which means that the decoder can detect and correct a single error, but it cannot distinguish a double bit error of some codeword from a single bit error of a different codeword. Thus, some double-bit errors will be incorrectly decoded as if they were single bit errors and therefore go undetected, unless no correction is attempted.

To remedy this shortcoming, Hamming codes can be extended by an extra parity bit. This way, it is possible to increase the minimum distance of the Hamming code to 4, which allows the decoder to distinguish between single bit errors and two-bit errors. Thus the decoder can detect and correct a single error and at the same time detect (but not correct) a double error.

If the decoder does not attempt to correct errors, it can reliably detect triple bit errors. If the decoder does correct errors, some triple errors will be mistaken for single errors and “corrected” to the wrong value. Error correction is therefore a trade-off between certainty (the ability to reliably detect triple bit errors) and resiliency (the ability to keep functioning in the face of single bit errors).

This extended Hamming code was popular in computer memory systems, starting with IBM 7030 Stretch in 1961,^[4] where it is known as SECDED (or SEC-DED, abbreviated from single error correction, double error detection).^[5] Server computers in 21st century, while typically keeping the SECDED level of protection, no longer use the Hamming’s method, relying instead on the designs with longer codewords (128 to 256 bits of data) and modified balanced parity-check trees.^[4] The (72,64) Hamming code is still popular in some hardware designs, including Xilinx FPGA families.^[4]

[7,4] Hamming code[edit]

Graphical depiction of the four data bits and three parity bits and which parity bits apply to which data bits

In 1950, Hamming introduced the [7,4] Hamming code. It encodes four data bits into seven bits by adding three parity bits. As explained earlier, it can either detect and correct single-bit errors or it can detect (but not correct) both single and double-bit errors.

With the addition of an overall parity bit, it becomes the [8,4] extended Hamming code which is SECDED and can both detect and correct single-bit errors and detect (but not correct) double-bit errors.

Construction of G and H[edit]

The matrix
${mathbf {G}}:={begin{pmatrix}{begin{array}{c|c}I_{k}&-A^{{text{T}}}\end{array}}end{pmatrix}}$ is called a (canonical) generator matrix of a linear (n,k) code,

and ${mathbf {H}}:={begin{pmatrix}{begin{array}{c|c}A&I_{{n-k}}\end{array}}end{pmatrix}}$ is called a parity-check matrix.

This is the construction of G and H in standard (or systematic) form. Regardless of form, G and H for linear block codes must satisfy

${mathbf {H}},{mathbf {G}}^{{text{T}}}={mathbf {0}}$ , an all-zeros matrix.^[6]

Since [7, 4, 3] = [n, k, d] = [2^m − 1, 2^m − 1 − m, 3]. The parity-check matrix H of a Hamming code is constructed by listing all columns of length m that are pair-wise independent.

Thus H is a matrix whose left side is all of the nonzero n-tuples where order of the n-tuples in the columns of matrix does not matter. The right hand side is just the (n − k)-identity matrix.

So G can be obtained from H by taking the transpose of the left hand side of H with the identity k-identity matrix on the left hand side of G.

The code generator matrix and the parity-check matrix are:

${displaystyle mathbf {G} :={begin{pmatrix}1&0&0&0&1&1&0\0&1&0&0&1&0&1\0&0&1&0&0&1&1\0&0&0&1&1&1&1end{pmatrix}}_{4,7}}$

and

${displaystyle mathbf {H} :={begin{pmatrix}1&1&0&1&1&0&0\1&0&1&1&0&1&0\0&1&1&1&0&0&1end{pmatrix}}_{3,7}.}$

Finally, these matrices can be mutated into equivalent non-systematic codes by the following operations:^[6]

Column permutations (swapping columns)
Elementary row operations (replacing a row with a linear combination of rows)

Encoding[edit]

Example

From the above matrix we have 2^k = 2⁴ = 16 codewords.
Let be a row vector of binary data bits, ${displaystyle {vec {a}}=[a_{1},a_{2},a_{3},a_{4}],quad a_{i}in {0,1}}$ . The codeword for any of the 16 possible data vectors is given by the standard matrix product where the summing operation is done modulo-2.

For example, let . Using the generator matrix from above, we have (after applying modulo 2, to the sum),

${displaystyle {vec {x}}={vec {a}}G={begin{pmatrix}1&0&1&1end{pmatrix}}{begin{pmatrix}1&0&0&0&1&1&0\0&1&0&0&1&0&1\0&0&1&0&0&1&1\0&0&0&1&1&1&1\end{pmatrix}}={begin{pmatrix}1&0&1&1&2&3&2end{pmatrix}}={begin{pmatrix}1&0&1&1&0&1&0end{pmatrix}}}$

[8,4] Hamming code with an additional parity bit[edit]

The same [7,4] example from above with an extra parity bit. This diagram is not meant to correspond to the matrix H for this example.

The [7,4] Hamming code can easily be extended to an [8,4] code by adding an extra parity bit on top of the (7,4) encoded word (see Hamming(7,4)).
This can be summed up with the revised matrices:

$mathbf{G} := begin{pmatrix} 1 & 1 & 1 & 0 & 0 & 0 & 0 & 1\ 1 & 0 & 0 & 1 & 1 & 0 & 0 & 1\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1\ 1 & 1 & 0 & 1 & 0 & 0 & 1 & 0 end{pmatrix}_{4,8}$

and

$mathbf{H} := begin{pmatrix} 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0\ 0 & 1 & 1 & 0 & 0 & 1 & 1 & 0\ 0 & 0 & 0 & 1 & 1 & 1 & 1 & 0\ 1 & 1 & 1 & 1 & 1 & 1 & 1 & 1 end{pmatrix}_{4,8} .$

Note that H is not in standard form. To obtain G, elementary row operations can be used to obtain an equivalent matrix to H in systematic form:

${mathbf {H}}=left({begin{array}{cccc|cccc}0&1&1&1&1&0&0&0\1&0&1&1&0&1&0&0\1&1&0&1&0&0&1&0\1&1&1&0&0&0&0&1end{array}}right)_{{4,8}}.$

For example, the first row in this matrix is the sum of the second and third rows of H in non-systematic form. Using the systematic construction for Hamming codes from above, the matrix A is apparent and the systematic form of G is written as

${mathbf {G}}=left({begin{array}{cccc|cccc}1&0&0&0&0&1&1&1\0&1&0&0&1&0&1&1\0&0&1&0&1&1&0&1\0&0&0&1&1&1&1&0end{array}}right)_{{4,8}}.$

The non-systematic form of G can be row reduced (using elementary row operations) to match this matrix.

The addition of the fourth row effectively computes the sum of all the codeword bits (data and parity) as the fourth parity bit.

For example, 1011 is encoded (using the non-systematic form of G at the start of this section) into 01100110 where blue digits are data; red digits are parity bits from the [7,4] Hamming code; and the green digit is the parity bit added by the [8,4] code.
The green digit makes the parity of the [7,4] codewords even.

Finally, it can be shown that the minimum distance has increased from 3, in the [7,4] code, to 4 in the [8,4] code. Therefore, the code can be defined as [8,4] Hamming code.

To decode the [8,4] Hamming code, first check the parity bit. If the parity bit indicates an error, single error correction (the [7,4] Hamming code) will indicate the error location, with “no error” indicating the parity bit. If the parity bit is correct, then single error correction will indicate the (bitwise) exclusive-or of two error locations. If the locations are equal (“no error”) then a double bit error either has not occurred, or has cancelled itself out. Otherwise, a double bit error has occurred.

Notes[edit]

^ See Lemma 12 of
^ Hamming (1950), pp. 153–154.
^ Thompson, Thomas M. (1983), From Error-Correcting Codes through Sphere Packings to Simple Groups, The Carus Mathematical Monographs (#21), Mathematical Association of America, pp. 16–17, ISBN 0-88385-023-0
^ ^a ^b ^c Kythe & Kythe 2017, p. 115.
^ Kythe & Kythe 2017, p. 95.
^ ^a ^b Moon T. Error correction coding: Mathematical Methods and
Algorithms. John Wiley and Sons, 2005.(Cap. 3) ISBN 978-0-471-64800-0

References[edit]

Hamming, Richard Wesley (1950). “Error detecting and error correcting codes” (PDF). Bell System Technical Journal. 29 (2): 147–160. doi:10.1002/j.1538-7305.1950.tb00463.x. S2CID 61141773. Archived (PDF) from the original on 2022-10-09.
Moon, Todd K. (2005). Error Correction Coding. New Jersey: John Wiley & Sons. ISBN 978-0-471-64800-0.
MacKay, David J.C. (September 2003). Information Theory, Inference and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.
D.K. Bhattacharryya, S. Nandi. “An efficient class of SEC-DED-AUED codes”. 1997 International Symposium on Parallel Architectures, Algorithms and Networks (ISPAN ’97). pp. 410–415. doi:10.1109/ISPAN.1997.645128.
“Mathematical Challenge April 2013 Error-correcting codes” (PDF). swissQuant Group Leadership Team. April 2013. Archived (PDF) from the original on 2017-09-12.
Kythe, Dave K.; Kythe, Prem K. (28 July 2017). “Extended Hamming Codes”. Algebraic and Stochastic Coding Theory. CRC Press. pp. 95–116. ISBN 978-1-351-83245-8.

External links[edit]

Visual Explanation of Hamming Codes
CGI script for calculating Hamming distances (from R. Tervo, UNB, Canada)
Tool for calculating Hamming code

Источник

Код Хэмминга

Содержание

Самокорректирующийся код
Алгоритм кодирования
Самокорректирующийся код
Результат работы программы
Полученный мною опыт

Самокорректирующийся код

Код Хэ́мминга — наиболее известный из первых самоконтролирующихся и самокорректирующихся кодов. Построен применительно к двоичной системе счисления. Позволяет исправлять одиночную ошибку (ошибка в одном бите) и находить двойную.

Алгоритм кодирования

Предположим, что нужно сгенерировать код Хемминга для некоторого информационного кодового слова. В качестве примера возьмём 15-битовое кодовое слово x1…x15, хотя алгоритм пригоден для кодовых слов любой длины. В приведённой ниже таблице в первой строке даны номера позиций в кодовом слове, во второй — условное обозначение битов, в третьей — значения битов.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
x1	x2	x3	x4	x5	x6	x7	x8	x9	x10	x11	x12	x13	x14	x15
1	0	0	1	0	0	1	0	1	1	1	0	0	0	1

Вставим в информационное слово контрольные биты r0…r4 таким образом, чтобы номера их позиций представляли собой целые степени двойки: 1, 2, 4, 8, 16… Получим 20-разрядное слово с 15 информационными и 5 контрольными битами. Первоначально контрольные биты устанавливаем равными нулю. На рисунке контрольные биты выделены розовым цветом.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
r0	r1	x1	r2	x2	x3	x4	r3	x5	x6	x7	x8	x9	x10	x11	r4	x12	x13	x14	x15
0	0	1	0	0	0	1	0	0	0	1	0	1	1	1	0	0	0	0	1

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
r0	r1	x1	r2	x2	x3	x4	r3	x5	x6	x7	x8	x9	x10	x11	r4	x12	x13	x14	x15
0	0	1	0	0	0	1	0	0	0	1	0	1	1	1	0	0	0	0	1
1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	r0
0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	r1
0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	r2
0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	r3
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	r4

В правой части таблицы мы оставили пустым один столбец, в который поместим результаты вычислений контрольных битов. Вычисление контрольных битов производим следующим образом. Берём одну из строк матрицы преобразования (например, r0) и находим её скалярное произведение с кодовым словом, то есть перемножаем соответствующие биты обеих строк и находим сумму произведений. Если сумма получилась больше единицы, находим остаток от его деления на 2. Иными словами, мы подсчитываем сколько раз в кодовом слове и соответствующей строке матрицы в одинаковых позициях стоят единицы и берём это число по модулю 2.

Например, для строки r0:

r0 = (1·0+0·0+1·1+0·0+1·0+0·0+1·1+0·0+1·0+0·0+1·1+0·0+1·1+0·1+1·1+0·0+1·0+0·0+1·0+0·1) mod 2 = 5 mod 2 = 1.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
r0	r1	x1	r2	x2	x3	x4	r3	x5	x6	x7	x8	x9	x10	x11	r4	x12	x13	x14	x15
0	0	1	0	0	0	1	0	0	0	1	0	1	1	1	0	0	0	0	1
1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	r0	1
0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	r1	1
0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	r2	1
0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	r3	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	r4	1

Алгоритм декодирования

Алгоритм декодирования по Хэммингу абсолютно идентичен алгоритму кодирования. Матрица преобразования соответствующей размерности умножается на матрицу-столбец кодового слова и каждый элемент полученной матрицы-столбца берётся по модулю 2. Полученная матрица-столбец получила название «матрица синдромов». Легко проверить, что кодовое слово, сформированное в соответствии с алгоритмом, описанным в предыдущем разделе, всегда даёт нулевую матрицу синдромов.

1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
r₀	r₁	x₁	r₂	x₂	x₃	x₄	r₃	x₅	x₆	x₇	x₈	x₉	x₁₀	x₁₁	r₄	x₁₂	x₁₃	x₁₄	x₁₅
1	1	1	1	0	1	1	0	0	0	1	0	1	1	1	1	0	0	0	1
1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	s₀	0
0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1	0	s₁	1
0	0	0	1	1	1	1	0	0	0	0	1	1	1	1	0	0	0	0	1	s₂	1
0	0	0	0	0	0	0	1	1	1	1	1	1	1	1	0	0	0	0	0	s₃	0
0	0	0	0	0	0	0	0	0	0	0	0	0	0	0	1	1	1	1	1	s₄	0

Результат работы программы

screen

Полученный мною опыт

Работа с C#;
Имею представление, что такое самокорректирующийся код;
Изучил алгоритм кодирования и декодирования кодом Хэмминга;
Работа с одномерными и двумерными массивами;
Научился обрабатывать исключения с помощью do…while или try…catch.

Источник

Код
Хэмминга относится к классу линейных
кодов и представляет собой систематический
код – код, в котором информационные и
контрольные биты расположены на строго
определенных местах в кодовой комбинации.

Код
Хэмминга, как и любой (n,
k)-
код, содержит к
информационных и m
= n-k
избыточных (проверочных) бит.

Избыточная
часть кода строится т. о. чтобы можно
было при декодировании не только
установить наличие ошибки но, и указать
номер позиции в которой произошла ошибка
, а значит и исправить ее, инвертировав
значение соответствующего бита.

Существуют
различные методы реализации кода
Хэмминга и кодов которые являются
модификацией кода Хэмминга. Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.

1.
По заданному количеству информационных
символов – k,
либо информационных комбинаций N
= 2^k
, используя соотношения:

n
= k+m, 2ⁿ
(n+1)2^k
и
2^m
n+1 (14)

m
= [log₂{(k+1)+
[log₂(k+1)]}]

вычисляют
основные параметры кода n
и m.

2.
Определяем рабочие и контрольные позиции
кодовой комбинации. Номера контрольных
позиций определяются по закону 2ⁱ,где
i=1,
2, 3,… т.е. они равны 1, 2, 4, 8, 16,… а остальные
позиции являются рабочими.

3.
Определяем значения контрольных разрядов
(0 или 1 ) при помощи многократных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контро-льный и определенные проверочные
биты. Если результат проверки дает
четное число, то контрольному биту
присваивается значение -0, в противном
случае – 1. Номера информационных бит,
включаемых в каждую проверку, определяются
по двоичному коду натуральных n
–чисел
разрядностью – m
(табл.
1, для m
= 4)
или при помощи проверочной матрицы
H(mn),
столбцы которой представляют запись в
двоичной системе всех целых чисел от 1
до 2^k
–1
перечисленных в возрастающем порядке.
Для
m = 3
проверочная матрица имеет вид

.
(15 )

Количество
разрядов m
– определяет количество проверок.

В
первую проверку включают коэффициенты,
содержащие 1 в младшем (первом) разряде,
т. е. b₁,
b₃,
b₅
и т. д.

Во
вторую проверку включают коэффициенты,
содержащие 1 во втором разряде, т. е. b₂,
b₃,
b₆
и т. д.

В
третью проверку – коэффициенты которые
содержат 1 в третьем разряде и т. д.

Таблица
1

Десятичные
числа

(номера
разрядов

кодовой
комбинации)

Двоичные
числа и их разряды

Для
обнаружения и исправления ошибки
составляются аналогичные проверки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции, который
определяется по двоичной записи числа,
либо по проверочной матрице.

Для
исправления ошибки необходимо
проинвертировать бит в ошибочной
позиции. Для исправления одиночной
ошибки и обнаружения двойной используют
дополнительную проверку на четность.
Если при исправлении ошибки контроль
на четность фиксирует ошибку, то значит
в кодовой комбинации две ошибки.

Схема
кодера и декодера для кода Хэмминга
приведена на рис. 1.

Пример
1.
Построить код Хемминга для передачи
сообщений в виде последовательности
десятичных цифр, представленных в виде
4 –х разрярных двоичных слов. Показать
процесс кодирования, декодирования и
исправления одиночной ошибки на примере
информационного слова 0101.

Решение:

1.
По заданной длине информационного слова
(k
= 4),
определим количество контрольных
разрядов m,
используя соотношение:

m
= [log₂{(k+1)+
[log₂(k+1)]}]=[log₂{(4+1)+
[log₂(4+1)]}]=3,

при
этом n
= k+m = 7,
т. е. получили (7, 4) -код.

2.
Определяем номера рабочих и контрольных
позиции кодовой комбинации. Номера
контрольных позиций выбираем по закону
2ⁱ.

Для
рассматриваемой задачи (при n
= 7)
номера контрольных позиций равны 1, 2,
4. При этом кодовая комбинация имеет
вид:

b₁
b₂
b₃
b₄
b₅
b₆
b₇

к₁к₂0
к₃1
0 1

3.
Определяем значения контрольных разрядов
(0 или 1), используя проверочную матрицу
(5).

Первая
проверка:

k₁
b₃
b₅
b₇
= k₁011
будет четной при k₁=
0.

Вторая
проверка:

k₂
b₃
b₆
b₇
= k₂001
будет четной при k₂=
1.

Третья
проверка:

k₃
b₅
b₆
b₇
= k₃101
будет четной при k₃=
0.

1
2 3 4 5 6 7

Передаваемая
кодовая комбинация: 0 1 0 0 1 0 1

Допустим
принято: 0 1 1 0 1 0 1

Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, в соответствии
с проверочной матрицей результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е, номер ошибочной позиции.

1)
k₁
b₃
b₅
b₇
= 0111 = 1.

2)
k₂
b₃
b₆
b₇
= 1101 = 1.

k₃
b₅
b₆
b₇
= 0101 = 0.

Сравнивая
синдром ошибки со столбцами проверочной
матрицы, определяем номер ошибочного
бита. Синдрому 011 соответствует третий
столбец, т. е. ошибка в третьем разряде
кодовой комбинации. Символ в 3 -й позиции
необходимо изменить на обратный.

Пример
2.
Построить код Хэмминга для передачи
кодовой комбинации 1 1 0 1 1 0 1 1. Показать
процесс обнаружения и исправления
ошибки в соответствующем разряде кодовой
комбинации.

Решение:
Рассмотрим
алгоритм построения кода для исправления
одиночной ошибки.

1.
По заданной длине информационного слова
(k
= 8)
, используя соотношения вычислим основные
параметры кода n
и m.

m
= [log₂{(k+1)+
[log₂(k+1)]}]=[log₂{(9+1)+
[log₂(9+1)]}]=4,

при
этом n
= k+m = 12,
т. е. получили (12, 8)-код.

Для
рассматриваемой задачи (при n
= 12)
номера контрольных позиций равны 1, 4,
8.

При
этом кодовая комбинация имеет вид:

b₁
b₂
b₃
b₄
b₅
b₆
b₇
b₈
b₉
b₁₀
b₁₁
b₁₂

к₁к₂1
к₃1
0 1 к₄1
0 1 1

3.
Определяем значения контрольных разрядов
(0 или 1) путем много-кратных проверок
кодовой комбинации на четность. Количество
проверок равно m
= n-k.
В каждую проверку включается один
контрольный и определенные проверочные
биты.

Номера
информационных бит, включаемых в каждую
проверку определяется по двоичному
коду натуральных n-чисел
разрядностью – m.

0001
b₁
Количество разрядов m – определяет
количество прове-

0010
b₂
верок.

0011
b₃
1) к₁
b₃
b₅
b₇
b₉
а₁₁=
к₁11111
=>

0100
b₄четная
при к₁=1

0101
b₅2)
к₂
b₃
b₆
b₇
b₁₀
b₁₁=
к₂10101
=>

0110
b₆
четная при к₂=1

0111
b₇3)к₃
b₅
b₆
b₇
b₁₂=
к₃1011=>

1000
b₈четная
при к₃=1

1001
b₉
4) к₄
b₉
b₁₀
b₁₁
b₁₂=
к₁1011
=>

1010
b₁₀четная
при к₄=1

1011
b₁₁

1100
b₁₂

Передаваемая
кодовая комбинация: 1 2 3 4 5 6 7 8 9 10 11 12

1
1 1 1 1 0 1 1 1 0 1 1

Допустим,
принято: 1 1 1 1 0 0 1 1 1 0 1 1

Для
обнаружения и исправления ошибки
составим аналогичные про-верки на
четность контрольных сумм, результатом
которых является двоичное (n-k)
-разрядное число, называемое синдромом
и указывающим на положение ошибки, т.
е. номер ошибочной позиции.

1)
к₁
b₃
b₅
b₇
b₉
b₁₁=
110111 =1

2)
к₂
b₃
b₆
b₇
b₁₀
b₁₁=
110101 =0

3)к₃
b₅
b₆
b₇
b₁₂=
10011 =1

4)
к₄
b₉
b₁₀
b₁₁
b₁₂=
11011 =0

Обнаружена
ошибка в разряде кодовой комбинации с
номером 0101, т. е. в 5 -м разряде. Для
исправления ошибки необходимо
проинвертировать 5 -й разряд в кодовой
комбинации.

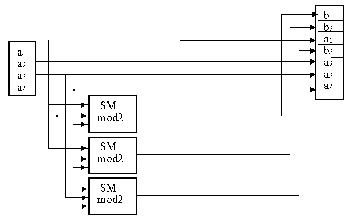
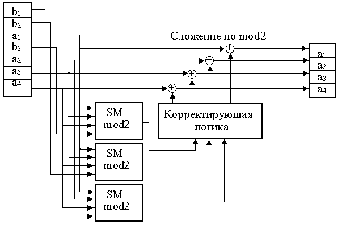
Рис.
1. Схема кодера –а
и декодера –б
для простого (7, 4) кода Хэмминга

Рассмотрим
применение кода Хэмминга. В ЭВМ код
Хэмминга чаще всего используется для
обнаружения и исправления ошибок в ОП,
памяти с обнаружением и исправлением
ошибок ECC Memory (Error Checking and Correcting). Код
Хэмминга используется как при параллельной,
так и при последовательной записи. В
ЭВМ значительная часть интенсивности
потока ошибок приходится на ОП. Причинами
постоянных неисправностей являются
отказы ИС, а случайных изменение
содержимого ОП за счет флуктуации
питающего напряжения, кратковременных
помех и излучений. Неисправность может
быть в одном бите, линии выборки разряда,
слова либо всей ИС. Сбой может возникнуть
при формировании кода (параллельного),
адреса или данных, поэтому защищать
необходимо и то и др. Обычно дешифратор
адреса встроен в м/схему и недоступен
для потребителя. Наиболее часто ошибки
дают ячейки памяти ЗУ, поэтому главным
образом защищают записываемые и
считываемые данные.

Наибольшее
применение в ЗУ нашли коды Хэмминга с
d_min=4,
исправляющие одиночные ошибки и
обнаруживающие двойные.

Проверочные
символы записываются либо в основное,
либо специальное ЗУ. Для каждого
записываемого информационного слова
(а не байта, как при контроле по паритету)
по определенным правилам вычисляется
функция свертки, результат которой
разрядностью в несколько бит также
записывается в память. Для 16 -ти разрядного
информационного слова используется 6
дополнительных бит (32- 7 бит, 64 –8 бит).
При считывании информации схема контроля,
используя избыточные биты, позволяет
обнаружить ошибки различной кратности
или исправить одиночную ошибку. Возможны
различные варианты поведения системы:

автоматическое
исправление ошибки без уведомления
системы;

–
исправление однократной ошибки и
уведомление системы только о многократных
ошибках;

–
не исправление ошибки, а только уведомление
системы об ошибках;

Модуль
памяти со встроенной схемой исправления
ошибок –EOS 72/64 (ECC on Simm). Аналог микросхема
к 555 вж 1
-это 16 разрядная схема с обнаружением
и исправлением ошибок (ОИО) по коду
Хэмминга (22, 16), использование которой
позволяет исправить однократные ошибки
и обнаружить все двух кратные ошибки в
ЗУ.

Избыточные
(контрольные) разряды позволяют обнаружить
и исправить ошибки в ЗУ в процессе записи
и хранения информации.

В
составе ВЖ-1 используются 16 информационных
и 6 контрольных разрядов. (DB – информационное
слово, CB – контрольное слово).

При
записи осуществляется формирование
кода, состоящего из 16 информационных и
6 контрольных разрядов, представляющих
результат суммирование по модулю 2
восьми информационных разрядов в
соответствии с кодом Хэмминга.
Сформированные контрольные разряды
вместе с информационными поступают на
схему и записываются в ЗУ.

(22,16)

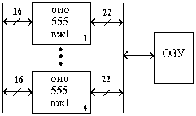
4
схе(72,64)

Рис.2.
Схема контроля

При
считывании шестнадцатиразрядное слово
декодируется, восстанавливаясь вместе
с 6 разрядным словом контрольным,
поступают на схему сравнения и контроля.
Если достигнуто равенство всех контрольных
разрядов и двоичных слов, то ошибки нет.

Любая
однократная ошибка в 16 разрядном слове
данных изменяет 3 байта в 6 разрядном
контрольном слове. Обнаруженный ошибочный
бит инвертируется.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

История[править | править код]

Систематические коды[править | править код]

Самоконтролирующиеся коды[править | править код]

Самокорректирующиеся коды[править | править код]

Код Хэмминга[править | править код]

Алгоритм кодирования[править | править код]

Алгоритм декодирования[править | править код]

Применение[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Код Хэмминга. Пример работы алгоритма

Вступление.

Как это работает.

Подготовка

Вычисление контрольных бит.

Декодирование и исправление ошибок.

Заключение.

Примечание.

Источники.

History[edit]

Codes predating Hamming[edit]

Parity[edit]

Two-out-of-five code[edit]

Repetition[edit]

Description[edit]

General algorithm[edit]

Hamming codes with additional parity (SECDED)[edit]

[7,4] Hamming code[edit]

Construction of G and H[edit]

Encoding[edit]

[8,4] Hamming code with an additional parity bit[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Код Хэмминга

Содержание

Самокорректирующийся код

Алгоритм кодирования

Алгоритм декодирования

Результат работы программы

Полученный мною опыт

Вам также может понравиться

Как найти вайбер в телефоне хонор

Как найти амплитуду эдс по графику

Как в биосе найти управление питанием

Добавить комментарий Отменить ответ