Подсчитаем в MS EXCEL количество сочетаний из n элементов по k. С помощью формул выведем на лист все варианты сочетаний (английский перевод термина: Combinations without repetition).
Сочетаниями из n различных элементов по k элементов называются комбинации, которые отличаются хотя бы одним элементом. Например, ниже перечислены ВСЕ 3-х элементные сочетания, взятые из множества, состоящего из 5 элементов {1; 2; 3; 4; 5}:
(1; 2; 3); (1; 2; 4); (1; 2; 5); (1; 3; 4); (1; 3; 5); (1; 4; 5); (2; 3; 4); (2; 3; 5); (2; 4; 5); (3; 4; 5)
Примечание
: Это статья о подсчете количества сочетаний с использованием MS EXCEL. Теоретические основы советуем прочитать в специализированном учебнике. Изучать сочетания по этой статье – плохая идея.
Отличие Сочетаний от Размещений
В отличие от
Размещений
следующие 3-х элементные комбинации (1; 2; 3); (1; 3; 2); (2; 1; 3); (2; 1; 3); (3; 2; 1); (3; 1; 2) считаются одинаковыми, и в набор
Сочетаний
включается только одна из этих комбинаций. Очевидно, что для тех же n и k число
Сочетаний
всегда меньше чем число
Размещений
(так как при размещениях порядок важен, а для сочетаний – нет), причем в k! раз.
Подсчет количества Сочетаний
Число всех
Сочетаний
из n элементов по k можно вычислить по формуле:
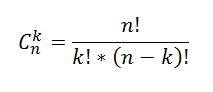
Например, количество 4-х элементных комбинаций из 6 чисел {1; 2; 3; 4; 5; 6} равно 15=6!/(4!(6-4)!)
Примечание
: Для
Сочетаний
из n элементов по k также используется и другая запись:
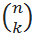
В MS EXCEL для подсчета количества комбинаций без повторов существует специальная функция ЧИСЛКОМБ() , английское название функции – COMBIN(). Для предыдущего примера формула =ЧИСЛКОМБ(6;4) , разумеется, также вернет 15. Альтернативная формула для подсчета сочетаний =ФАКТР(6)/ФАКТР(6-4)/ФАКТР(4) .
Очевидно, что k меньше или равно n, т.к. нельзя выбрать из множества элементов n больше элементов, чем в нем содержится (предполагается, что элементы после выбора обратно не возвращаются). При k=n количество сочетаний всегда равно 1.
Примечание
: О Сочетаниях с повторениями (с возвращением элементов) можно прочитать в статье
Сочетания с повторениями: Комбинаторика в MS EXCEL
Вывод всех комбинаций Сочетаний
В файле примера созданы формулы для вывода всех Сочетаний для заданных n и k.
Задавая с помощью
элементов управления Счетчик
количество элементов множества (n) и количество элементов, которое мы из него выбираем (k), с помощью формул можно вывести все Сочетания.
В файле примера не забывайте увеличивать количество строк с формулами, чтобы поместились все ваши комбинации. Для этого выделите последние ячейки с формулами (сочетание №330) и скопируйте их вниз на нужно количество строк. При увеличении строк с формулами размер файла быстро растет, а скорости пересчета листа падает. Если строк 4 тысячи, то размер файла составляет около 2 Мб.
Задача
Автовоз может перевозить по 4 легковые машины. Необходимо перевезти 7 разных машин (LADA Granta, Hyundai Solaris, KIA Rio, Renault Duster, Lada Kalina, Volkswagen Polo, Lada Largus). Сколькими различными способами можно заполнить первый автовоз? Конкретное место машины в автовозе не важно.
Нам нужно определить число
Сочетаний
7 машин на 4-х местах автовоза. Т.е. n=7, а k=4. Оказывается, что таких вариантов =ЧИСЛКОМБ(7;4) равно 35.
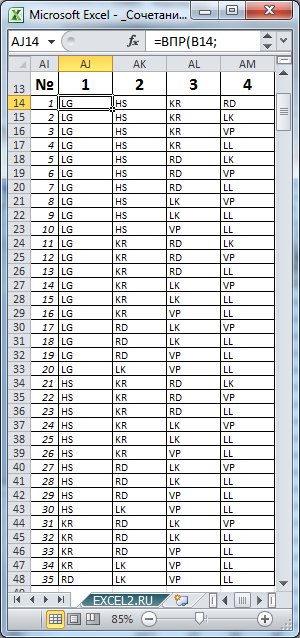
Воспользуемся файлом примера (ссылка внизу статьи) , чтобы наглядно убедиться, что мы решили задачу правильно.
Произвольным образом сопоставим маркам машин числовые значения и сделаем сокращения названий марок: LADA Granta (LG=1), Hyundai Solaris (HS=2), …
Выставив в ячейках
В5
и
В6
значения 7 и 4 соответственно, определим все варианты размещений машин в автовозе (см. столбцы AJ:AM).
Примечание
: О Перестановках можно прочитать в статье
Перестановки без повторений: Комбинаторика в MS EXCEL
, а о Размещениях в статье
Размещения без повторений: Комбинаторика в MS EXCEL
.
Давайте разберем на примерах основные формулы комбинаторики: сочетания, размещения, перестановки без повторений и научимся вычислять их с помощью встроенных функций Excel.
Ниже вы найдете для каждой формулы инструкции по вычислению в эксель, пример задачи, ссылку на калькулятор и видеоурок и шаблон Excel. Удачи в изучении!
Понравилось? Добавьте в закладки
Как выбрать формулу комбинаторики?
Нужно последовательно (см. схему выше) ответить на несколько вопросов:
- Сколько у нас есть объектов (число $n$)?
- Важен ли их порядок в комбинации?
- Могут ли встречаться повторяющиеся элементы?
- Нужно выбрать все элементы или только $klt n$?
Отвечая на эти вопросы, двигаемся по стрелкам схемы и получаем название формулы комбинаторики:
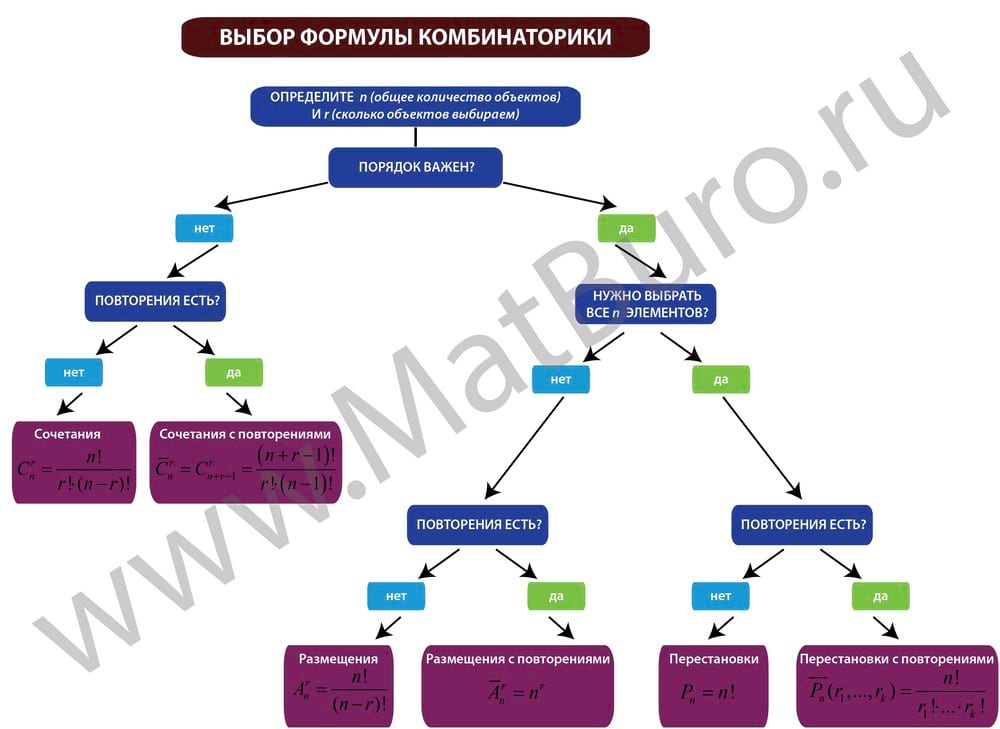
Схема выбора формул с примерами задач
Консультируем по решению задач комбинаторики
Перестановки в Excel
Пусть имеется $n$ различных объектов. Будем переставлять их всеми возможными способами (число объектов остается неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками, а их число равно
$$P_n=n!=1cdot 2cdot 3 cdot … cdot (n-1) cdot n$$
Символ $n!$ называется факториалом и обозначает произведение всех целых чисел от $1$ до $n$. По определению, считают, что $0!=1, 1!=1$.
Подробнее: факториал в эксель.
Для нахождения числа перестановок в Excel можно использовать одну из двух функций:
=ПЕРЕСТ($n$;$n$) или =ФАКТР($n$), где $n$ – число переставляемых объектов.
Задача. Сколькими способами можно расставить 10 различных книг на одной полке?
Вводим число объектов 10 и получаем ответ: 3628800 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор перестановок.
Перестановки с повторениями в Excel
Пусть имеется $n$ объектов различных типов: $n_1$ объектов первого типа, $n_2$ объектов второго типа,… $n_k$ объектов $k$-го типа. Сколькими способами можно переставить все объекты между собой?
Будем переставлять $n$ объектов всеми возможными способами (их будет $n!$). Но так как некоторые объекты совпадают, итоговое число будет меньше. В частности, $n_1$ объектов первого типа можно переставлять между собой $n_1!$ способами, но они не меняют итоговую перестановку. Аналогично для всех остальных объектов, поэтому число перестановок с повторениями есть
$$ P_n (n_1,n_2,…,n_k)=frac{n!}{n_1! cdot n_2!cdot … cdot n_k!}. $$
Для нахождения числа перестановок в Excel будем использовать функцию =ФАКТР(), которая находит факториал чисел и обычные действия (умножение, деление).
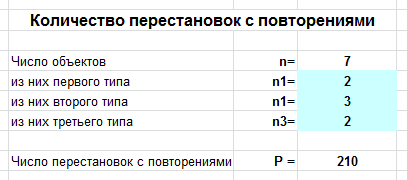
Задача. Сколько различных слов можно составить из букв слова “колокол”?
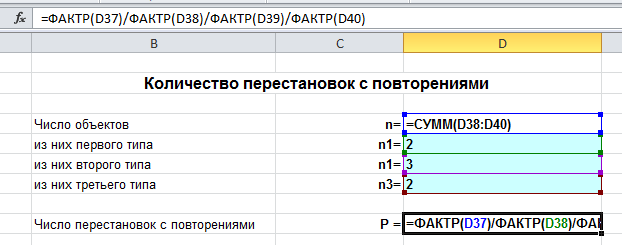
Вводим число букв $n=7$, а также $n_1=2$ (2 буквы “к”), $n_2=3$ (3 буквы “о”), $n_3=2$ (2 буквы “л”), и получаем ответ: 210 слов.
В режиме формул это выглядит так:
Еще: онлайн калькулятор перестановок c повторениями.
Размещения в Excel
Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов и переставлять всеми возможными способами между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из $n$ объектов по $k$, а их число равно
$$A_n^k=frac{n!}{(n-k)!}=ncdot (n-1)cdot … cdot (n-k+1) $$
Для нахождения числа размещений в Excel используем функцию =ПЕРЕСТ($n$;$k$).
Задача. В группе учится 10 студентов. Нужно выбрать из них 3 человек на должности старосты, заместителя и дежурного. Сколькими способами можно это сделать?
Вводим $n=10$, $k=3$ и получаем ответ: 720 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений.
Размещения с повторениями в Excel
Число размещений с повторениями из $n$ объектов по $k$ можно найти по формуле
$$overline{A}_n^k=ncdot ncdot … cdot n = n^k. $$
Для вычисления в Excel используем функцию =СТЕПЕНЬ($n$;$k$).
Задача. Сколько трехзначных номеров можно составить для автомобилей, используя все возможные цифры от 0 до 9?
Вводим $n=10$ (количество возможных цифр), $k=3$ (количество цифр в номере) и получаем ответ: 1000 номеров.

В режиме формул это выглядит так:

Еще: онлайн калькулятор размещений с повторениями.
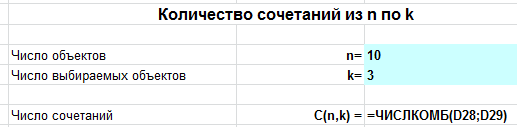
Сочетания в Excel
Пусть имеется $n$ различных объектов. Будем выбирать из них $k$ объектов все возможными способами (то есть меняется состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из $n$ объектов по $k$, а их число равно
$$C_n^k=frac{n!}{(n-k)!cdot k!} $$
Для нахождения числа сочетаний в Excel используем функцию =ЧИСЛКОМБ($n$;$k$).
Задача. В поход пошло 10 учеников. Нужно выбрать из них 3, которые понесут флажки. Сколькими способами можно это сделать?
Вводим $n=10$, $k=3$ и получаем ответ: 120 способов.

В режиме формул это выглядит так:
Еще: онлайн калькулятор сочетаний.
Сочетания с повторениями в Excel
Количество сочетаний с повторениями из $n$ объектов по $k$ можно найти по формуле
$$overline{C}_n^k=C_{k+n-1}^k=frac{(k+n-1)!}{(n-1)!cdot k!}$$
Для вычисления в Excel используем функцию =ЧИСЛКОМБ($n+k-1$;$k$).
Задача. В магазине продаются мячики трех цветов: желтые, красные и синие. Родительский комитет собирается купить 10 мячиков. Сколько возможных вариантов выбора у них есть?
Вводим $n=3$ (вида объектов), $k=10$ (нужно выбрать) и получаем ответ: 66 способов.

В режиме формул это выглядит так:

Еще: онлайн калькулятор сочетаний с повторениями.
Полезные ссылки
Для собственных расчетов скачайте файл: Комбинаторика в Excel.
|
|
Решебник задач по комбинаторике
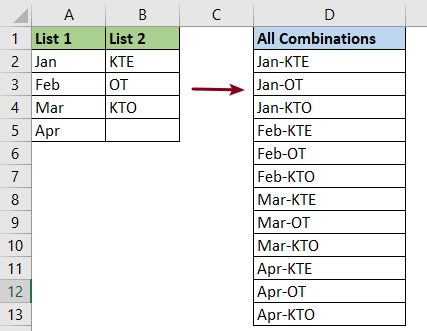
Скажем, у меня есть следующие два столбца данных, и теперь я хочу сгенерировать список всех возможных комбинаций на основе двух списков значений, как показано на скриншоте слева. Возможно, вы можете перечислить все комбинации одну за другой, если есть несколько значений, но, если есть несколько столбцов с несколькими значениями, которые необходимо перечислить, возможные комбинации, вот несколько быстрых приемов, которые могут помочь вам справиться с этой проблемой в Excel .
Перечислите или сгенерируйте все возможные комбинации из двух списков с формулой
Перечислите или сгенерируйте все возможные комбинации из трех или более списков с кодом VBA
Составьте список или сгенерируйте все возможные комбинации из нескольких списков с помощью мощной функции
Перечислите или сгенерируйте все возможные комбинации из двух списков с формулой
Следующая длинная формула поможет вам быстро составить список всех возможных комбинаций значений двух списков. Пожалуйста, сделайте следующее:
1. Введите или скопируйте приведенную ниже формулу в пустую ячейку, в этом случае я введу ее в ячейку D2, а затем нажмите Enter ключ для получения результата, см. снимок экрана:
=IF(ROW()-ROW($D$2)+1>COUNTA($A$2:$A$5)*COUNTA($B$2:$B$4),””,INDEX($A$2:$A$5,INT((ROW()-ROW($D$2))/COUNTA($B$2:$B$4)+1))&”-“&INDEX($B$2:$B$4,MOD(ROW()-ROW($D$2),COUNTA($B$2:$B$4))+1))

Внимание: В приведенной выше формуле $ A $ 2: $ A $ 5 – это диапазон значений первого столбца, а 2 млрд долларов: 4 млрд долларов – это диапазон значений второго списка, в котором вы хотите перечислить все их возможные комбинации, $ D $ 2 это ячейка, в которую вы поместили формулу, вы можете изменить ссылки на ячейки по своему усмотрению.
2. Затем выберите ячейку D2 и перетащите маркер заполнения вниз к ячейкам, пока не получите пустые ячейки, и все возможные комбинации будут перечислены на основе значений двух списков. Смотрите скриншот:

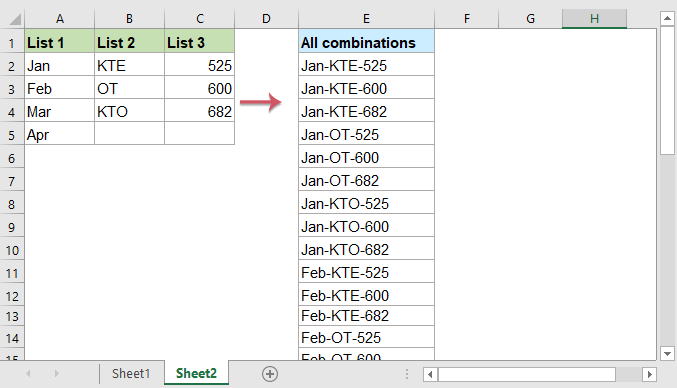
Перечислите или сгенерируйте все возможные комбинации из трех или более списков с кодом VBA
Возможно, вам будет сложно применить приведенную выше формулу, если есть данные из нескольких столбцов, ее будет сложно изменить. Здесь я представлю код VBA, чтобы быстро с этим справиться.
1. Удерживайте ALT + F11 , чтобы открыть Microsoft Visual Basic для приложений окно.
2. Нажмите Вставить > Модулии вставьте следующий код в Модули Окно.
Код VBA: генерировать все комбинации из 3 или нескольких столбцов
Sub ListAllCombinations()
'Updateby Extendoffice
Dim xDRg1, xDRg2, xDRg3 As Range
Dim xRg As Range
Dim xStr As String
Dim xFN1, xFN2, xFN3 As Integer
Dim xSV1, xSV2, xSV3 As String
Set xDRg1 = Range("A2:A5") 'First column data
Set xDRg2 = Range("B2:B4") 'Second column data
Set xDRg3 = Range("C2:C4") 'Third column data
xStr = "-" 'Separator
Set xRg = Range("E2") 'Output cell
For xFN1 = 1 To xDRg1.Count
xSV1 = xDRg1.Item(xFN1).Text
For xFN2 = 1 To xDRg2.Count
xSV2 = xDRg2.Item(xFN2).Text
For xFN3 = 1 To xDRg3.Count
xSV3 = xDRg3.Item(xFN3).Text
xRg.Value = xSV1 & xStr & xSV2 & xStr & xSV3
Set xRg = xRg.Offset(1, 0)
Next
Next
Next
End SubВнимание: В приведенном выше коде A2: A5, B2: B4, C2: C4 диапазон данных, который вы хотите использовать, E2 – это выходная ячейка, в которой вы хотите найти результаты. Если вы хотите получить все комбинации из большего количества столбцов, измените и добавьте другие параметры в код по мере необходимости.
3. Затем нажмите F5 ключ для запуска этого кода, и все комбинации из 3 столбцов будут сгенерированы сразу, см. снимок экрана:
Составьте список или сгенерируйте все возможные комбинации из нескольких списков с помощью мощной функции
Если имеется несколько значений списков, необходимо указать возможные комбинации, возможно, вам будет сложно изменить код. Здесь я могу порекомендовать мощный инструмент – Kutools for Excel, он содержит удобную функцию Список всех комбинаций который может быстро перечислить все возможные комбинации на основе заданных списков данных.
Tips:Чтобы применить это Список всех комбинаций функция, во-первых, вы должны скачать Kutools for Excel, а затем быстро и легко примените эту функцию.
После установки Kutools for Excel, пожалуйста, сделайте так:
1. Нажмите Кутулс > Вставить > Список всех комбинаций, см. снимок экрана:
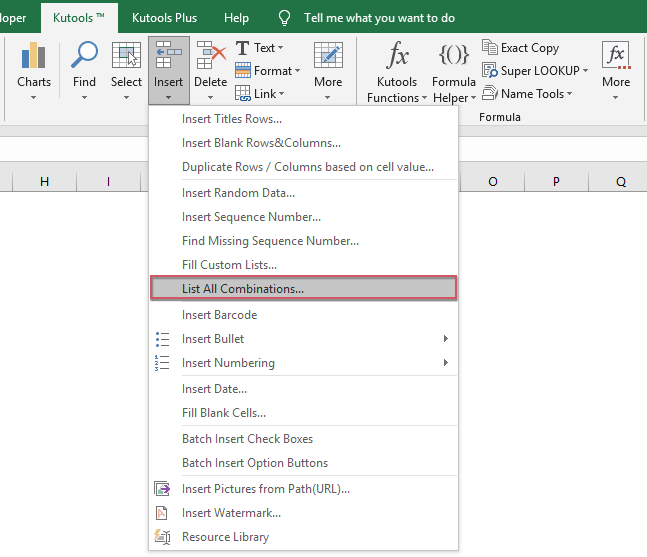
2. В Список всех комбинаций В диалоговом окне выполните операции, как показано в демонстрации ниже:

3. Затем все указанные значения и разделители были перечислены в диалоговом окне, см. Снимок экрана:

4.А затем нажмите Ok Кнопка, и появится окно подсказки, напоминающее вам о выборе ячейки для вывода результата, см. снимок экрана:

5. Нажмите OK, все возможные комбинации на основе данных списков были сгенерированы на листе, как показано на следующем снимке экрана:

Нажмите, чтобы скачать Kutools for Excel Сейчас !
Больше относительных статей:
- Создать все комбинации из 3 или нескольких столбцов
- Предположим, у меня есть 3 столбца данных, теперь я хочу сгенерировать или перечислить все комбинации данных в этих 3 столбцах, как показано ниже. Есть ли у вас какие-нибудь хорошие методы решения этой задачи в Excel?
- Найдите все комбинации, равные заданной сумме
- Например, у меня есть следующий список чисел, и теперь я хочу знать, какая комбинация чисел в списке дает в сумме 480, на следующем скриншоте вы можете увидеть, что есть пять групп возможных комбинаций, которые в сумме равны до 480, например, 300 + 60 + 120, 300 + 60 + 40 + 80 и т. д. В этой статье я расскажу о некоторых методах определения суммирования ячеек до определенного значения в Excel.
- Сгенерировать или перечислить все возможные перестановки
- Например, у меня есть три символа XYZ, теперь я хочу перечислить все возможные перестановки на основе этих трех символов, чтобы получить шесть разных результатов, например: XYZ, XZY, YXZ, YZX, ZXY и ZYX. Как в Excel быстро сгенерировать или составить список всех перестановок на основе разного количества символов?
- Составьте список всех возможных комбинаций из 4 цифр
- В некоторых случаях нам может потребоваться сгенерировать список всех возможных 4-значных комбинаций чисел от 0 до 9, что означает создание списка 0000, 0001, 0002… 9999. Чтобы быстро решить задачу списка в Excel, я предлагаю вам несколько уловок.
Лучшие инструменты для работы в офисе
Kutools for Excel Решит большинство ваших проблем и повысит вашу производительность на 80%
- Снова использовать: Быстро вставить сложные формулы, диаграммы и все, что вы использовали раньше; Зашифровать ячейки с паролем; Создать список рассылки и отправлять электронные письма …
- Бар Супер Формулы (легко редактировать несколько строк текста и формул); Макет для чтения (легко читать и редактировать большое количество ячеек); Вставить в отфильтрованный диапазон…
- Объединить ячейки / строки / столбцы без потери данных; Разделить содержимое ячеек; Объединить повторяющиеся строки / столбцы… Предотвращение дублирования ячеек; Сравнить диапазоны…
- Выберите Дубликат или Уникальный Ряды; Выбрать пустые строки (все ячейки пустые); Супер находка и нечеткая находка во многих рабочих тетрадях; Случайный выбор …
- Точная копия Несколько ячеек без изменения ссылки на формулу; Автоматическое создание ссылок на несколько листов; Вставить пули, Флажки и многое другое …
- Извлечь текст, Добавить текст, Удалить по позиции, Удалить пробел; Создание и печать промежуточных итогов по страницам; Преобразование содержимого ячеек в комментарии…
- Суперфильтр (сохранять и применять схемы фильтров к другим листам); Расширенная сортировка по месяцам / неделям / дням, периодичности и др .; Специальный фильтр жирным, курсивом …
- Комбинируйте книги и рабочие листы; Объединить таблицы на основе ключевых столбцов; Разделить данные на несколько листов; Пакетное преобразование xls, xlsx и PDF…
- Более 300 мощных функций. Поддерживает Office/Excel 2007-2021 и 365. Поддерживает все языки. Простое развертывание на вашем предприятии или в организации. Полнофункциональная 30-дневная бесплатная пробная версия. 60-дневная гарантия возврата денег.

Вкладка Office: интерфейс с вкладками в Office и упрощение работы
- Включение редактирования и чтения с вкладками в Word, Excel, PowerPoint, Издатель, доступ, Visio и проект.
- Открывайте и создавайте несколько документов на новых вкладках одного окна, а не в новых окнах.
- Повышает вашу продуктивность на 50% и сокращает количество щелчков мышью на сотни каждый день!

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще…Меньше
В этой статье описаны синтаксис формулы и использование функции ЧИСЛКОМБ в Microsoft Excel.
Описание
Возвращает количество комбинаций для заданного числа элементов. Функция ЧИСЛКОМБ используется для определения общего числа всех групп, которые можно составить из элементов данного множества.
Синтаксис
ЧИСЛКОМБ(число;число_выбранных)
Аргументы функции ЧИСЛКОМБ описаны ниже.
-
Число — обязательный аргумент. Количество элементов.
-
Число_выбранных — обязательный аргумент. Количество элементов в каждой комбинации.
Замечания
-
Числовые аргументы усекаются до целых чисел.
-
Если хотя бы один из аргументов не является числом, то #VALUE! значение ошибки #ЗНАЧ!.
-
Если число < 0, number_chosen < 0 или < number_chosen, то #NUM! значение ошибки #ЗНАЧ!.
-
Комбинацией считается любое множество или подмножество элементов независимо от их внутреннего порядка. Комбинации отличаются от перестановок, для которых порядок существен.
-
Число комбинаций определяется по следующей формуле, где число = n, а число_выбранных = k:
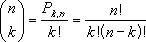
где
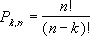
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы видеть все данные.
|
Формула |
Описание |
Результат |
|
=ЧИСЛКОМБ(8;2) |
Возможные команды по два человека, которые могут быть сформированы из восьми кандидатов. |
28 |
Нужна дополнительная помощь?
Нужны дополнительные параметры?
Изучите преимущества подписки, просмотрите учебные курсы, узнайте, как защитить свое устройство и т. д.
В сообществах можно задавать вопросы и отвечать на них, отправлять отзывы и консультироваться с экспертами разных профилей.
Комбинаторика в Excel
Комбинаторика — раздел математики, изучающий дискретные объекты, множества (сочетания, перестановки, размещения элементов) и отношения на них. Термин комбинаторика был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». Excel поддерживает ряд функций комбинаторики. Чтобы разобраться, какую формулу использовать, следует ответить на ряд вопросов:
- Исходное множество содержит только уникальные элементы, или некоторые из них могут повторяться?
- Операция выполняется со всеми элементами множества, или только с некоторой выборкой из них?
- Важен ли порядок элементов в выборке?
- После выбора элемента мы его возвращаем назад?
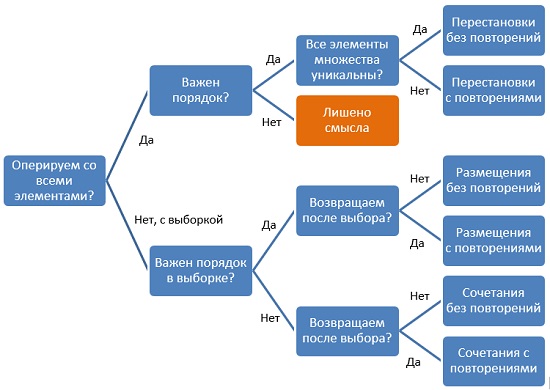
Рис. 1. Дерево решений, какую формулу комбинаторики использовать
Скачать заметку в формате Word или pdf, примеры в формате Excel
Перестановки без повторений
Возьмем несколько различных элементов (предметов) и будем переставлять их всевозможными способами, оставляя неизменным их число и меняя только их порядок (рис. 2). Каждая из получившихся таким образом комбинаций носит название перестановки. Перестановкой из n элементов называется упорядоченное множество, составленное из всех элементов множества.
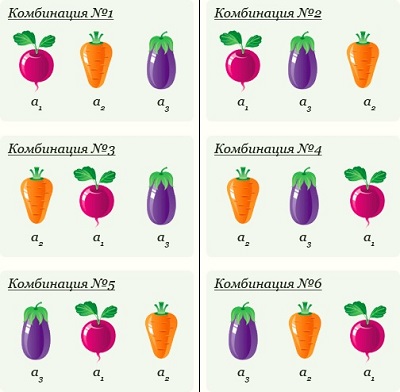
Рис. 2. Перестановки (картинка взята здесь)
Если все n элементы разные, то число перестановок обозначается Pn от perturbation.
![]()
С другой стороны, произведение n первых натуральных чисел называется n-факториал и обозначается n!
![]()
Например
![]()
По определению: 1! = 1; 0! = 1.
Функция в Excel =ФАКТР(n). Факториал растет очень быстро. Существенно быстрее экспоненты (рис. 3).
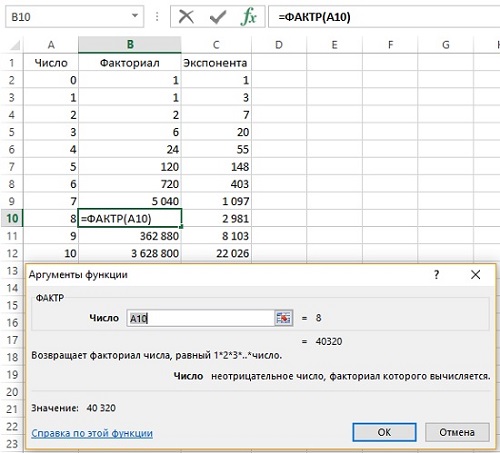
Рис. 3. Расчет числа перестановок без повторений с помощью факториала
Перестановки с повторениями
Если в основном n множестве не все элементы разные, то число перестановок будет меньше n! Например, если наше множество состоит из трех яблок и одной груши, то всего возможно 4 перестановки (рис. 4). Груша может быть первой, второй, третьей или четвертой, а яблоки неразличимы).

Рис. 4. Перестановки с повторениями (картинка найдена здесь)
В общем случае, можно сказать: последовательность длины n, составленная из k разных символов, первый из которых повторяется n1 раз, второй – n2 раз, третий – n3 раз, …, k-й – nk раз (где n1 + n2 + … + nk = n) называется перестановкой с повторениями из n элементов.
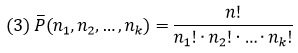
Пример. Сколько различных пятибуквенных слов можно составить из букв слова «манна»?
Решение. Буквы а и н повторяются 2 раза, а буква м один раз.
![]()
Размещение без повторений
Размещением из n элементов по m называется упорядоченный набор из m различных элементов, выбранных из n-элементного множества (все элементы множества уникальны; позиции элементов в выборке важны). Число размещений обозначается ![]() от arrangement.
от arrangement.
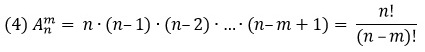
Например, два элемента из трех можно выбрать и расположить шестью способами (рис. 4):

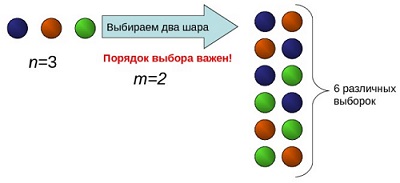
Рис. 5. Размещение без повторений (картинка из презентации)
Если m = n количество элементов совпадает с количеством имеющихся мест для размещения. Знаменатель в формуле (4) превращается в 0! = 1. Остается только числитель n! А это – изученная выше перестановка без повторений; см. формулу (1).
Название функции в Excel несколько обескураживает. Но… что поделаешь: =ПЕРЕСТ(n;m)
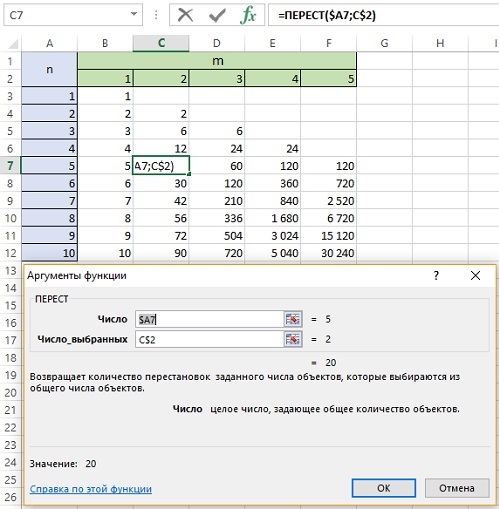
Рис. 6. Размещение без повторений; обратите внимание на смешанные ссылки, которые позволяют протянуть формулу на всю таблицу
Размещение с повторениями
Размещение с повторениями по смыслу отличается от перестановок с повторением. Перестановки с повторением – это операция над множеством, которое состоит из нескольких видов элементов, так что каждый вид представлен несколькими одинаковыми элементами. Размещение с повторениями – выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором.
Например, если у вас множество, включающее грушу, яблоко и лимон, и вам нужно выбрать два элемента, так что после первого выбора вы возвращаете выбранный предмет назад, то существует девять различных комбинаций (рис. 7).

Рис. 7. Размещение с повторениями
В общем случае размещение с повторениями или выборка с возвращением – это размещение «предметов» в предположении, что каждый «предмет» может участвовать в размещении несколько раз. По правилу умножения количество размещений с повторениями из n по k:
![]()
В Excel используется функция ПЕРЕСТА(n;k).
Задача. Сколько различных номеров можно составить в одном коде региона?
Подсказка. В номере используется 12 букв алфавита, также существующих и в латинском алфавите (А, В, Е, К, М, Н, О, Р, С, Т, У, Х).
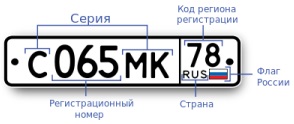
Рис. 8. Номер автомобиля
Решение. Можно воспользоваться формулой для размещения с повторениями:
![]()
Каждую цифру можно выбрать 10 способами, а всего цифр 3, при этом они могут повторяться, и их порядок важен. Каждую букву можно выбрать 12 способами, при этом буквы могут повторяться, и их порядок важен.
Сочетания без повторений
Сочетаниями из n множества по m элементов называются комбинации, составленные из данных n элементов по m элементов, которые различаются хотя бы одним элементом (в сочетаниях не учитывается порядок элементов).
Например, два элемента из 4 сочетаются 6 способами (порядок следования не важен):

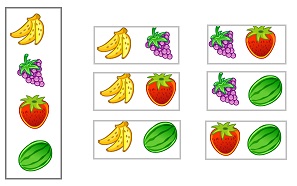
Рис. 9. Сочетания без повторений из 4 по 2
Сочетания без повторений образуют знаменитый треугольник Паскаля (рис. 10). В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Числа в строках, составляющие треугольник Паскаля, являются сочетаниями

где n – номер строки, m – номер элемента в строке, начиная с нулевого. Например, в строке 7:

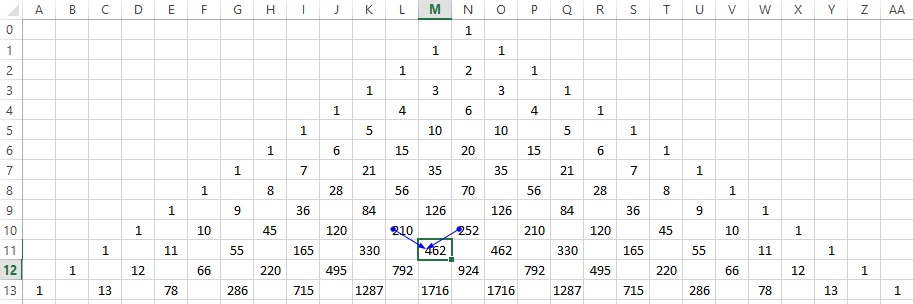
Рис. 10. Треугольник Паскаля; чтобы увеличить изображение кликните на нем правой кнопкой мыши и выберите Открыть картинку в новой вкладке
В Excel используется функция =ЧИСЛКОМБ(n;m).
Сочетания с повторениями
Сочетания с повторениями по смыслу похожи на размещение с повторениями – это выборки из множества с возвращением выбранного элемента назад перед каждым новым выбором. При этом порядок в выборке не важен.
Например, два предмета из четырех можно выбрать 10 способами, если после каждого выбора предмет возвращается назад (рис. 11).

Рис. 11. Сочетания с повторениями
В общем случае, число сочетаний с повторениями:

Для нашего примера с фруктами
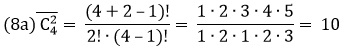
В Excel для подсчета числа сочетаний с повторениями используется функция =ЧИСЛКОМБА(n;m). В нашем примере =ЧИСЛКОМБА(4;2) = 10.
