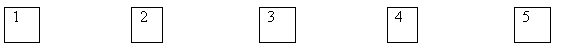Цели:
Обучающая:
- Познакомить с комбинаторными задачами,
- Научить решать простейшие задачи с помощью
схем.
Развивающая:
- Развивать логику.
Воспитывающая
- Воспитывать интерес к предмету.
Ход урока
- Орг. момент – 2-3 мин.
- Устная работа – 7-8 мин.
- Объяснение нового материала – 15 мин.
- Закрепление – 15 мин
- Подведение итогов и постановка д/з – 5 мин.
I . Орг. момент.
Проверить готовность класса к уроку, собрать
тетради .
Эпиграф урока.
Учитесь думать, объяснять,
Учитесь мыслить, рассуждать,
Ведь в математике, друзья,
Без логики никак нельзя!
II. Устная работа.
1. Вычислите устно
15*6 100-19 60-11 :8 :3 :7 *19 +23 *15 +6 *4 -25 ? ? ?
2. Вместо некоторых цифр поставлены *. Можно ли
сравнить числа?
а) 32** и 31** в) **** и *** б) *1** и 8** г) *5* и 1 **
3. Подумайте, по какому правилу составлен ряд
чисел и найдите три следующих числа
а) 20, 22, 24:
б) 2, 4, 8, 16:
в) 1, 4, 9, 16:
III. Объяснение нового материала
Сегодня мы познакомимся с новыми задачами –
комбинаторными.
Живут эти задачи в особом разделе математики,
который называется комбинаторика.
Комбинаторика – раздел математики,
в котором изучаются вопросы о том, сколько
различных комбинаций, подчиненных тем или иным
условиям можно составить.
Рассмотрим задачу.
Задача 1.
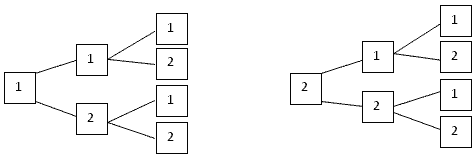
Запишите все трёхзначные числа, для записи
которых употребляются только цифры 1 и 2.
Решение.
В записи числа на первом месте (в разряде сотен)
может стоять цифра 1 или 2
Или
На втором месте (в разряде десятков) в каждом
случае также может стоять одна из двух цифр 1 или 2
На третьем месте (в разряде единиц) в каждом из
полученных четырех случаев также можно записать
либо 1, либо 2
Получим восемь чисел:
111; 112; 121; 122; 211; 212; 221; 222.
Задача 2.
В правлении фирмы входят 5 человек. Из своего
состава правление должно выбрать президента и
вице-президента. Сколькими способами можно это
сделать?
Решение.
Президентом фирмы можно избрать одного из пяти
человек:
Президент:
После того как президент избран,
вице-президентом можно выбрать одного из четырёх
оставшихся членов правления:
Значит, выбрать президента можно 5-ю способами и
для каждого из выбранного президента 4-мя
способами можно выбрать вице-президента.
Т.о. общее число способов
5 * 4=20.
IV. Закрепление.
Задача 3.
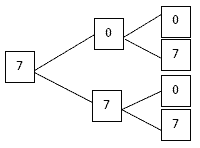
Запишите все трёхзначные числа, для записи
которых употребляются только цифры о и 7 . Найдите
сумму этих чисел и разделите её на 211.
Решение (коллективная работа).
- Какая цифра может стоять на первом месте?
(выполняется схема на доске) - На втором месте?
- На третьем?
700; 707;
770; 777;
(700 + 707+ 770+ 777) : 211 = 14.
Задача 4.(решить самостоятельно, используя
схему)
Запишите все трёхзначные числа, для записи
которых употребляются только цифры 5 и 7.
Ответ: 555; 557; 575; 577; 755; 757; 775; 777.
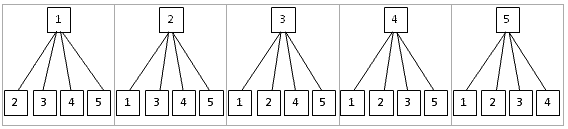
Задача 5.
В футбольной команде 5-го класса 7 человек. Члены
команды выбирают капитана и вратаря.сколькими
способами это можно сделать?
Решение.
- Сколько человек в команде?
- Какие варианты существуют? (капитан может быть
вратарем и не может) - Рассмотрим вариант, когда вратарь не может быть
капитаном. - Сколько вариантов выбора капитана существует?
(7) - Сколько существует вариантов выбора вратаря
для выбранного капитана?(6) - Сколькими способами можно выбрать капитана и
вратаря?
7 * 6 = 42. - Как изменится решение задачи, если вратарь
может быть капитаном? - Сколько способов выбора существует при этом
условии?
7 * 7 = 49.
V. Подведение итогов и постановка д/з.
С каким разделом математики мы сегодня
познакомились?
Что такое комбинаторика?
Домашнее задание (раздается в
распечатанном виде)
Сколько двузначных чисел можно составить из
цифр 0; 2; 4; 6; если цифры в записи числа не
повторяются? Запишите все эти числа.
Для того чтобы открыть дверь подъезда, нужно
набрать трёхзначный код замка. Сколькими
способами можно выбрать код замка, если все его
цифры должны быть различными?
Исторические сведения.
Комбинаторика – ветвь математики, изучающая
комбинации и перестановки предметов, возникла в
XVII веке. Долгое время комбинаторика лежала вне
основного русла развития математики. Положение
дел резко изменилось после появления
быстродействующих вычислительных машин. В
настоящее время комбинаторные методы
применяются в теории случайных процессов,
статистике, математическом программировании,
вычислительной математике и др.
С задачами, которых приходилось выбирать те или
иные предметы, располагать их в определенном
порядке и отыскивать среди разных расположений
наилучшие, люди столкнулись ещё в доисторическую
эпоху, выбирая наилучшее положение охотников во
время охоты, воинов – во время битвы, инструментов
– во время работы. Комбинаторные навыки
оказались полезными в часы досуга. Со временем
появились различные игры: нарды, шашки, шахматы,
карты. В каждой из этих игр проходилось
рассматривать различные сочетания фигур, и
выигрывал тот, кто их лучше изучил, знал
выигрышные комбинации и умел избегать
проигрышных.
Но не только азартные игры давали пищу для
комбинаторных размышлений математиков. Ещё с
давних пор дипломаты. Стремясь к тайне переписки,
изобретали сложные шифры, а секретные службы
других стран пытались эти шифры разгадать.
Позднее стали применять шифры, основанные на
комбинаторных принципах.
Задачи, в которых идёт речь о тех или иных
комбинациях объектов, называют комбинаторными.
Комбинаторика как наука стала развиваться
параллельно с возникновением теории
вероятностей, т.к. для решения вероятностных
задач необходимо было подсчитать число
различных комбинаций элементов. Первые научные
исследования по комбинаторике принадлежат
итальянским ученым Дж. Кардано, Н. Тарталье
(ок.1499-1557), Г. Галилею(1564-1642) и французским ученым Б.
Паскалю (1623-1662) и П. Ферма. Комбинаторику как
самостоятельный раздел математики первым стал
рассматривать немецкий ученый Г. Лейбниц в своей
работе “Об искусстве комбинаторики”,
опубликованной в 1666 году. Он же впервые ввел
термин “комбинаторика”. Значительный вклад в
развитие комбинаторики внес JI. Эйлер.
В современном обществе с развитием
вычислительной техники комбинаторика добилась
новых успехов. Так, с помощью ЭВМ была решена
комбинаторная задача, известная под названием
“проблема четыpex красок”: удалось доказать, что
любую карту можно раскрасить в четыре цвета так,
что никакие две страницы, имеющие общую границу,
не будут окрашены в один и тот же цвет.
Литература.
- Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков,
С.И.Шварцбурд. Математика. Учебник для 5 класса
общеобразовательных учреждений. М.:Мнемозина. - Л.П.Попова. Поурочные разработки по математике к
ученому комплекту Н.Я.Виленкина 5 класс. Москва
“Вако”.2009
– Сок и кекс или молоко и булочка? –
размышлял Саша, идя по улице.
Паша спросил у Саши: А, что ты такое
бормочешь? Что это за сок и кекс или молоко и булочка?
– Паша,
понимаешь, –
сказал Саша, – мама сказала, что на полдник я могу выбирать сок, компот или
молоко и кекс, булочку или яблочный пирог. Вот я иду и решаю, что же я хочу
съесть. Вариантов выбора очень много.
– Да, Саша, ты прав, – согласился с другом
Паша, – выбирать всегда трудно. А вот интересно, сколько всего вариантов может
получиться? Может, их будет сто тысяч миллионов?
И Саша предложил Паше вместе с ним подсчитать
все варианты возможного полдника.
– Я могу выбрать сок и булочку – это один
вариант. Могу выбрать сок и кекс – это второй вариант. А могу компот и булочку
– начал перечислять варианты Саша.
Ещё ты можешь выбрать молоко и булочку.
– Да, – сказал Саша, – так мы будем
перебирать до вечера. Вот бы узнать, сколько всего вариантов полдника у меня
получится.
Паша предложил пойти к их другу – роботу Электроше.
– Электроша,
привет. У нас для тебя новый вопрос. Смотри, Саше на полдник предложили на
выбор напиток: молоко, компот и сок, а к напитку, тоже на выбор, предложили
кекс, булочку и яблочный пирог. Как нам подсчитать все возможные варианты? И
можно ли это сделать?
– Да, мальчики, все варианты подсчитать
можно, и сделать это просто, – ответил робот. Но давайте сделаем небольшую разминочку и немного порешаем устно.
– Вернёмся к вашей задаче, – продолжил Робот.
На самом деле, таких задач, в которых нужно сделать выбор, очень много.
Просыпаясь, мы выбираем что одеть, чем позавтракать. Собираясь куда-то ехать,
мы выбираем маршруты и так далее.
Такие задачи называют комбинаторными.
Саша переспросил: Как? Ком-би-на-тор-ные? А почему их назвали именно так?
– Потому что в таких задачах необходимо
подсчитать все возможные случаи или, по-другому, все возможные комбинации.
– А-а-а, – протянул Паша, – теперь понятно! А
как же решать такие задачи?
– Сейчас всё расскажу, – ответил Электроша. Давайте составим таблицу.
В первой строке запишем: Кекс, булочка,
яблочный пирог, а в первом столбце – сок, компот и молоко.
Теперь в пустые клеточки запишем сочетания.
Для удобства все названия сократим до одной буквы. Но, чтобы различить компот и
кекс, компот обозначим двумя буквами Ко. В этой клеточке пересекаются сок и
кекс, поэтому запишем здесь СК. В эту клеточку нам что надо записать, Саша? –
спросил робот у мальчика.
Мальчик начал размышлять: В
этой клеточке пересекаются сок и булочка, значит, сюда надо вписать буквы С и
Б.
– Молодец, Саша! – похвалил мальчика робот.
– Теперь ты, Паша, попробуй.
Паша подумал немного и сказал: В этой клеточке надо писать С и Я, потому что она стоит на
пересечении сока и яблочного пирога.
– Молодцы, ребята! Вы всё верно поняли, –
похвалил детей робот. – Теперь для вас не составит труда заполнить всю таблицу
и подсчитать, сколько вариантов полдника получится.
Мальчики вместе заполнили таблицу и ответили
на свой вопрос: Ого! – воскликнул Паша, – смотри, Саша, тебе надо выбирать из 9
вариантов.
– Да, – согласился Саша, – это не так уж и
много.
Тут Электроша решил
прервать мальчиков: Сейчас я вам покажу ещё один способ решения вашей задачи. С
помощью дерева.
– Какого ещё дерева? – удивились ребята.
Берёзы, липы или клёна?
– Нет, – успокоил Сашу и Пашу
робот, – для решения комбинаторных задач очень удобно использовать специальное дерево
возможных вариантов. Это схема, на которой все варианты чётко видны. Сейчас
сами всё увидите.
Итак. Мы с вами выбираем варианты полдника,
поэтому сверху напишем «Полдник».
У нас 3 варианта выбора напитка. От полдника
опустим 3 линии и подпишем их соответственно: С (сок), Ко
(компот) и М (молоко). Для каждого из напитков можно выбрать один из 3
десертов, значит, от каждой буквы опускаем по 3 линии и подписываем: К (кекс),
Б (булочка) и Я (яблочный пирог). Теперь нам остаётся
подсчитать, сколько «веточек» у нас получилось. Их будет 9. Значит, и вариантов
полдника будет 9.
– Здорово! – восхитились мальчишки, – и мы
хотим построить такие деревья. Электроша, можешь для
нас придумать задачи?
И робот составил для мальчиков такое задание.
– В кружок бальных танцев записались 2
мальчика – Костя и Женя, и 3 девочки – Оля, Настя и Вика. Какие танцевальные
пары девочки и мальчики могут организовать?
Паша предложил назвать дерево выбора: «Кружок
бальных танцев». Но тут вмешался Электроша.
– Иногда, когда название для дерева выбора
сложно подобрать или оно очень большое, сверху ставят просто звёздочку.
Теперь Саша решил внести свою лепту в решение
задачи.
– В паре обязательно должен быть мальчик,
мальчиков всего 2, значит, от названия надо опустить 2 линии и подписать: К
(Костя) и Ж (Женя).
– Девочек у нас 3, – добавил Паша, – значит,
от каждой буквы надо опустить по 3 линии и подписать О
(Оля), Н (Настя) и В (Вика).
Теперь подсчитаем, сколько «веточек» у нас
получилось, и увидим, что из двух мальчиков и трёх девочек можно составить 6
пар. Правильно?
– Да, – сказал Электроша,
– вы справились.
Тут Паша спросил: Вот интересно, а если бы мы
в дереве начинали не с мальчиков, а с девочек, у нас получился бы такой же
ответ?
– Попробуйте, – предложил робот ребятам. –
Решите эту задачу ещё раз.
– Итак, – начал Паша. Девочка должна быть в
паре обязательно, значит, от названия опускаем 3 линии и ставим буквы О, Н, и В. Теперь от каждой буквы опускаем по 2 линии,
потому что мальчиков у нас всего 2, и ставим буквы К и Ж. И опять получаем 6
пар. То есть совсем нет разницы, с чего начинать?
–
Конечно, нет, –
сказал робот, – дело в том, что с помощью дерева выбора мы перебираем все
возможные варианты. Поэтому и нет разницы, с чего начинать.
Выполним ещё одно задание. Сколько трёхзначных
чисел можно составить из цифр 0, 3 и 7?
Саша начал решать: Сверху поставим звёздочку,
а то называть дерево выбора «Трёхзначное число» – это очень долго. У нас 3
числа, значит, опустим 3 линии и напишем 0, 3, 7.
– Подожди, Саша, – перебил друга Паша. – А
разве трёхзначное число может начинаться с нуля? Это же тогда получится
двухзначное число. Или нет? Рассуди нас, Электроша.
– Да, ты
прав, Паша, –
сказал робот. – Действительно, условие о том, что нам надо составить
трёхзначное число, уже сразу показывает, что 0 первым стоять не может.
Чтобы вам было удобнее, давайте подпишем,
какую цифру числа мы выбираем.
– Я всё
понял, – сказал Саша. – От
звёздочки мы должны опустить 2 линии и подписать их 3 и 7. Это будут варианты
для первой цифры трёхзначного числа.
А вот теперь от каждого числа уже можно
опустить 3 линии и написать 3 числа: 0, 3 и 7. Ведь эти «веточки» определяют
вторую цифру трёхзначного числа, а она может быть любой, даже нулём. Третью
цифру тоже можно выбрать из трёх цифр.
Теперь давайте подсчитаем общее количество
чисел, которое получилось.
Оказалось, что из цифр 0, 3 и 7 можно
составить 18 трёхзначных чисел.
– Вы так
хорошо справляетесь с моими задачами, что я хочу показать вам, как ещё можно
решать комбинаторные задачи, – сказал мальчикам Электроша.
– При встрече 4 друга обмениваются
рукопожатиями. Сколько всего рукопожатий получилось? Сначала давайте попробуем
решить эту задачу с помощью дерева выбора.
– Назовём это дерево «Рукопожатия». У нас 4
мальчика, значит, опускаем 4 линии. Для удобства мальчиков будем обозначать
числами от 1 до 4.
Каждый должен поздороваться с каждым. То есть
от каждой цифры надо опустить по 3 палочки и поставить числа.
Теперь давайте выпишем все получившиеся
варианты. Посмотрите, у нас есть варианты 1 2 и 2 1. То есть первый мальчик
пожимает руку второму и второй пожимает первому. Но это одно и то же
рукопожатие, поэтому вычеркнем все лишние получившиеся варианты и получим, что
всего будет сделано 6 рукопожатий.
Но эту задачу можно было решить проще.
– Как проще? – спросил Саша.
– Да, Саша, есть ещё один способ решения
именно таких комбинаторных задач. Отметим 4 точки. Это будут друзья, про
которых говорится в условии.
Рукопожатия обозначают, что каждые 2 точки
должны быть соединены. Проведём отрезки через каждые 2 точки. Нам остаётся
только подсчитать, сколько отрезков получится. Их 6, то есть всего было сделано
6 рукопожатий.
Ответ получился тот же, но решали мы задачу
намного быстрее.
Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 247 человек из 63 регионов


- Сейчас обучается 22 человека из 17 регионов


- Сейчас обучается 139 человек из 50 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Комбинаторные задачи
5 – 6 классУчитель математики
МБОУ «Гимназия»
г. Новозыбкова
Арещенко
Елена Александровна -
2 слайд
Комбинаторика
раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчинённых тем или иным условиям, можно составить из заданных объектов -
3 слайд
КОМБИНАТОРНАЯ ЗАДАЧА –
это задача, требующая осуществления
перебора всех возможных вариантов
или подсчета их числа. -
4 слайд
Решить
комбинаторную задачу – это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи. -
5 слайд
ОРГАНИЗОВАННЫЙ ПЕРЕБОР – строгий порядок разбора всех случаев, возможных решений.
-
6 слайд
Решение задачи методом полного перебора всех возможных вариантов
№1 Сколько двузначных чисел можно составить, используя цифры 1; 4; 7?
Решение: Для того, чтобы не пропустить и не повторить ни одного из чисел, будем выписывать их в порядке возрастания:
11;14;17;(начали с 1)
41;44;47;(начали с 4)
71;74;77;(начали с 7)
Таким образом, из трёх данных цифр можно составить всего 9 различных двузначных чисел.
Ответ: 9 чисел. -
7 слайд
Решение задачи методом полного перебора всех возможных вариантов
№2 Прямоугольник состоит из трех квадратов. Сколькими способами можно раскрасить эти квадраты тремя красками: красной, зеленой и синей? -
8 слайд
Решение задачи:
6 способов -
9 слайд
Решение задач с помощью дерева возможных вариантов
Существует более общий подход к решению самых разных комбинаторных задач с помощью составления специальных схем. Внешне такая схема напоминает дерево, отсюда название – дерево возможных вариантов. При правильном построении дерева ни один из возможных вариантов решения не будет потерян. -
10 слайд
Задача.
Рассмотрим задачу о составлении трехзначных чисел из цифр 1;4;7 (цифры в записи числа не повторяются).
Для её решения построим схему-дерево возможных вариантов.число
1
4
7
4
7
7
4
1
7
7
1
1
4
4
1
Ответ: числа 147; 174; 417; 471; 714; 741 -
11 слайд
Сколько различных завтраков, состоящих из 1 напитка и 1 вида выпечки, можно составить из чая, кофе, булочки, печенья и вафель?
-
12 слайд
Решение задачи:
Ответ: 6 способов
-
13 слайд
Правило умножения в комбинаторных задачах.
Для комбинаторной задачи с умножением можно построить дерево вариантов, но такое дерево строить станет намного сложнее, именно поэтому используется метод умножения, чтобы запись была короче.
Рассмотрим этот метод на примере одной задачи:
На обед в школьной столовой предлагается 2 вида супа, 3 вторых блюда и 4 разных сока. Сколько различных обедов можно составить по предложенному меню?
Рассуждение:
Первое блюдо можно выбрать 2 способами, для каждого вида супа можно выбрать второе блюдо из трёх предложенных, уже получается 6 вариантов , осталось выбрать напиток: для каждого из 6 полученных наборов существует 4 способа выбора напитка. Итог: 24 способа. -
14 слайд
Оформление:
Суп – 2 способа
Вторые блюда – 3 способа
Сок – 4 способаРешение: 2 x 3 x 4= 24
Ответ:
Можно составить 24 варианта различных обедов -
15 слайд
Перестановки в комбинаторных задачах.
В комбинаторике часто приходиться решать задачу о том, сколькими способами можно расположить в ряд или, как говорят математики, упорядочить все элементы некоторого множества. Каждое из таких расположений называют перестановкой. -
16 слайд
Миша решил в воскресенье навестить дедушку, своего друга Петю и старшего брата Володю. В каком порядке он может организовать визиты? Сколько вариантов получилось ?
-
17 слайд
Решение задачи:
6 способов -
18 слайд
Здесь речь идет о числе перестановок,
т.е. о выполнении трех визитов в разной последовательности.Сначала Миша выбирает, к кому отправится в первую очередь – 3 способа, затем он идет в гости к кому – то из 2 оставшихся, ну а затем – к последнему.
3•2•1= 6 способов
-
19 слайд
Задача.
В турнире участвуют четыре человека. Сколькими способами могут быть распределены места между ними?Решение. Первое место может занять любой из 4 участников. При этом второе место может занять любой из трёх оставшихся, третье – любой из двух оставшихся, а на четвёртом месте остаётся последний участник.
Значит, места между участниками могут быть распределены следующим образом 4•3•2•1=24.Ответ: 24 способами.
-
20 слайд
Заметим, что в решении каждой задачи получили произведение всех натуральных чисел от 1
до 3 ( в первой задаче)
до 4 ( во второй задаче)
Такое произведение записывается короче:
3•2•1 = 3! ( «три факториал»)
4•3•2•1=4! ( «четыре факториал») -
21 слайд
Андрей, Боря, Витя и Дима решили покататься на карусели. На ней было 4 сиденья с изображением льва, слона, тигра и медведя. Ребята заспорили, кому где сидеть, поэтому решили перепробовать все способы. Сколько раз нужно в таком случае прокатиться на карусели?
Решение: Здесь речь идет о числе перестановок, т.е. о размещении 4 мальчиков по 4 местам разными способами: 4! = 24
Краткое описание документа:
Данная презентация предназначена для работы на уроках математики в пятых – шестых классах при решении комбинаторных задач. В презентации даются основные понятия по теме: комбинаторика, комбинаторная задача, что значит решить комбинаторную задачу. Представлены способы решения комбинаторных задач: метод организованного перебора, построение дерева вариантов, правило умножения, задачи на перестановки ( понятие факториала). К каждому способу приведены примеры задач и их подробное решение. Презентацию удобно использовать для работы на уроке, на индивидуальной работе, а также учащимся при самостоятельном рассмотрении темы.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 257 971 материал в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 22.11.2014
- 1930
- 1
- 22.11.2014
- 1243
- 2
- 22.11.2014
- 880
- 0
- 22.11.2014
- 1179
- 0
- 22.11.2014
- 892
- 0
- 22.11.2014
- 1311
- 2
Рейтинг:
5 из 5
- 22.11.2014
- 3468
- 3
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какие задачи называют комбинаторными?
Комбинаторные задачи — это задачи, решение которых требует рассмотрения и подсчёта все возможных случаев (всех возможных комбинаций).
2. Как называют схему, с помощью которой удобно и наглядно решать комбинаторные задачи?
Дерево возможных вариантов.
Решаем устно
1. Одним слоем бумаги оклеили куб, длина ребра которого равна 3 дм. Сколько квадратных дециметров бумаги потребовалось на оклеивание куба?
Найдём площадь поверхности куба:
S = 6a² = 6 • 3² = 6 • 9 = 54 (дм²) — бумаги потребовалось для оклеивания куба.
Ответ: 54 дм².
2. Объём прямоугольного параллелепипеда равен 240 см³. Какая из следующих троек чисел может задавать измерения этого параллелепипеда:
1) 4 см, 6 см, 12 см
4 • 6 • 12 = 24 • 12 = 288 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
2) 5 см, 6 см, 8 см
5 • 6 • 8 = 30 • 8 = 240 (см³) — да, эти числа могут быть измерениями данного прямоугольного параллелепипеда.
3) 3 см, 5 см, 10 см
3 • 5 • 10 = 15 • 10 = 150 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
4) 10 см, 10 см, 24 см
10 • 10 • 24 = 100 • 24 = 2 400 (см³) — нет, эти числа не могут быть измерениями данного прямоугольного параллелепипеда.
Ответ: числа 5 см, 6 см и 8 см.
3. Сколько центнеров пшеницы можно засыпать в бункер, имеющий форму прямоугольного параллелепипеда, если его длина равна 8 м, ширина — 2 м, высота — 1 м, а масса 1 м³ зерна составляет 8 ц?
1) 8 • 2 • 1 = 16 (м²) — объём бункера.
2) 16 • 8 = 128 (ц) — пшеницы можно засыпать в бункер.
Ответ: 128 центнеров.
4. Что больше и на сколько:
1) квадрат суммы чисел 4 и 3 или сумма их квадратов
(4 + 3)² > 4² + 3²
7² > 16 + 9
49 > 25
2) разность квадратов чисел 10 и 8 или квадрат их разности
10² — 8² > (10 — 8)²
100² — 64² > 2²
36 > 4
3) разность кубов чисел 5 и 3 или куб их разности
5³ — 3³ > (5 — 3)³
125 — 27 > 2³
98 > 8
Упражнения
645. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 3 (цифры могут повторяться).
Таких двузначных чисел всего 9:
- 11, 12, 13
- 22, 21, 23
- 33, 31, 32
646. Запишите все двузначные числа, в записи которых используются только цифры 1, 2 и 0 (цифры могут повторяться).
Таких двузначных чисел всего 6:
- 11, 12, 10
- 22, 21, 20
647. У ослика Иа-Иа есть три надувных шарика: красный, зелёный и жёлтый. Он хочет подарить по одному шарику своим друзьям: Винни-Пуху, Пятачку и Кролику. Сколько у ослика Иа-Иа есть вариантов сделать подарки своим друзьям?
Решим задачу при помощи схемы «Дерево возможных вариантов».
Итак, у нас получилось шесть возможных вариантов:
|
Винни-Пуха |
Пятачок |
Кролик |
|
|
Вариант 1 |
Зелёный | Красный | Жёлтый |
|
Вариант 2 |
Зелёный | Жёлтый | Красный |
|
Вариант 3 |
Красный | Зелёный | Жёлтый |
| Вариант 4 | Красный | Жёлтый |
Зелёный |
| Вариант 5 | Жёлтый | Зелёный |
Красный |
| Вариант 6 | Жёлтый | Красный |
Зелёный |
Ответ: 6 вариантов.
648. Сколько двузначных чисел, все цифры которых различны, можно составить из цифр 0, 1 и 2?
Таких двузначных чисел всего 4:
- 12, 10
- 21, 20
649. В футбольном турнире участвуют команды 5 «А» класса, 5 «Б» класса и 5 «В» класса. Сколько существует способов распределения первого и второго мест среди этих команд? Решение какой задачи из номеров 645—648 аналогично решению этой задачи?
Решим задачу при помощи схемы «Дерево возможных вариантов».
Итак, у нас получилось шесть возможных вариантов (последовательно места, занятые 5″А», 5″Б» и 5″В»):
Итак, у нас получилось шесть возможных вариантов (последовательно цвет шарика для Винни-Пуха, Пятачка и Кролика):
|
5″А» |
5″Б» |
5″В» |
|
|
Вариант 1 |
1 | 2 | — |
|
Вариант 2 |
1 | — | 2 |
|
Вариант 3 |
2 | 1 | — |
| Вариант 4 | 2 | — |
1 |
| Вариант 5 | — | 1 |
2 |
| Вариант 6 | — | 2 |
1 |
Задача аналогична задаче № 647.
Ответ: 6 вариантов.
650. Запишите все трёхзначные числа, для записи которых используются только цифры (Цифры не могут повторяться.):
1) 3, 4 и 6
- 346, 364
- 436, 463
- 634, 643
2) 4, 7 и 0
- 470, 407
- 740, 704
651. Сколько различных трёхзначных чисел можно составить из цифр (Цифры могут повторяться.):
1) 1 и 2
- 111, 112, 121, 122
- 222, 221, 212, 211
Ответ: 8 чисел.
2) 0 и 1
- 111, 110, 101, 100
Ответ: 4 числа.
652. Запишите все двузначные числа, в записи которых используются только цифры 2, 4, 9 и 0. (Цифры могут повторяться.)
- 22, 24, 29, 20
- 42, 44, 49, 40
- 92, 94, 99, 90
653. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке возрастания?
- 67, 68, 69
- 78, 79
- 89
Ответ: 6 чисел.
654. Сколько двузначных чисел можно составить из цифр 6, 7, 8 и 9 так, чтобы цифры были записаны в порядке убывания?
- 98, 97, 96
- 87, 86
- 76
Ответ: 6 чисел.
655. Сколько существует двузначных чисел, сумма цифр которых равна 5?
Всего 5 чисел: 14, 23, 32, 41, 50.
Ответ: 5 чисел.
656. Сколько двузначных чисел, сумма цифр которых равна чётному числу, можно составить из цифр 1, 2, 3, 4 (цифры могут повторяться)?
Всего 8 чисел: 11, 13, 22, 24, 31, 33, 42, 44.
Ответ: 8 чисел.
657. Сколько двузначных чисел, сумма цифр которых равна нечётному числу, можно составить из цифр 0, 1,2, 3?
Всего 6 чисел: 10, 12, 21, 23, 30, 32.
Ответ: 6 чисел.
658. Кот Базилио и лиса Алиса решили украсть золотой ключик, который хранится в каморке папы Карло. Чтобы туда проникнуть, нужно подобрать двузначный код. Им известно, что дверь в каморку закрывает Буратино, который знает пока что только четыре цифры: 0, 1, 2 и 3. Какое наибольшее количество вариантов придётся перебрать коту и лисе, чтобы открыть дверь?
Составим таблицу:
- в первом столбце запишем возможные варианты первой цифры кода
- в верхней строке — возможные варианты второй цифры кода
- на пересечении строк и столбцов — возможные варианты кодов.
| 0 | 1 | 2 | 3 | |
|
0 |
00 | 01 | 02 | 03 |
|
1 |
10 | 11 | 12 |
13 |
| 2 | 20 | 21 | 22 |
23 |
| 3 | 30 | 31 | 32 |
33 |
Итак, возможное количество вариантов кода — 16.
Ответ: 16 вариантов.
659. Сколько существует различных прямоугольников, периметры которых равны 24 см, а длины сторон выражены целым числом сантиметров?
P = (a + b) • 2
Если P = 24 см, то сумма длин сторон равна 24 : 2 = 12 см.
Существует 6 возможных вариантов таких прямоугольников. Длины сторон у них должны быть:
- 1 см и 11 см
- 2 см и 10 см
- 3 см и 9 см
- 4 см и 8 см
- 5 см и 7 см
- 6 см и 6 см (квадрат, который также соответствует определению прямоугольника).
Ответ: 6 прямоугольников.
660. У Ани есть 30 одинаковых кубиков. Сколько различных прямоугольных параллелепипедов она может из них составить, если для построения одного параллелепипеда надо использовать все имеющиеся 30 кубиков?
V = abc
Если V = 30, то можно подобрать 5 вариантов постройки прямоугольного параллелепипеда из одинаковых кубиков:
- 30 • 1 • 1 = 30
- 15 • 2 • 1 = 30
- 10 • 3 • 1 = 30
- 6 • 5 • 1 = 30
- 5 • 3 • 2 = 30
Ответ: 5 вариантов.
661. На прямой отметили четыре точки А, В, С и D. Сколько отрезков с концами в отмеченных точках можно провести? Какой из рисунков § 24 помогает решить эту задачу?
Для решения этой задачи можно ориентироваться на рисунок 184 § 24:
Но лучше сделать свой рисунок для этой конкретно задачи:
- AB, AC, AD
- BC, BD
- CD
Ответ: 6 отрезков.
662. Подножие горы и её вершину связывают три тропы. Сколько существует маршрутов, ведущих от подножия к вершине и затем вниз к подножию?
Нарисуем эти три маршрута схематично, изобразив их в виде лучей, выходящих из единой точки, где:
- O — вершина горы
- A — первая точка у подножия горы
- B — вторая точка у подножия горы
- C — третья точка у подножия горы.
Тогда возможные следующие варианты маршрутов (начало маршрута — вершина — конец маршрута):
- AOA, AOB, AOC
- BOA, BOB, BOC
- COA, COB, COC
Итого — 9 вариантов маршрутов.
Ответ: 9 вариантов.
663. Спортивной команде предлагают футболки трёх цветов — красного, зелёного и синего, а шорты двух цветов — белого и жёлтого. Сколько вариантов выбора формы есть у команды?
Составим таблицу:
- в первом столбце запишем возможные варианты шорт
- в верхней строке — возможные варианты футболок
- на пересечении строк и столбцов — возможные варианты формы
|
Форма |
Футболки | |||
| Красные | Зелёные |
Синие |
||
|
Шорты |
Белые | Красная футболка
белые шорты |
Зелёная футболка
белые шорты |
Синяя футболка
белые шорты |
| Жёлтые | Красная футболка
жёлтые шорты |
Зелёная футболка
жёлтые шорты |
Синяя футболка жёлтые шорты |
Итак, возможное количество вариантов формы — 6.
Ответ: 6 вариантов.
664. У Тани есть четыре платья и две пары туфель. Сколько у Тани есть вариантов выбора наряда?
Составим таблицу:
- в первом столбце запишем возможные варианты туфель
- в верхней строке — возможные варианты платьев
- на пересечении строк и столбцов — возможные варианты наряда
|
Наряд |
Платья | ||||
| 1 | 2 | 3 |
4 |
||
|
Туфли |
1 | Платье № 1
Туфли № 1 |
Платье № 2
Туфли № 1 |
Платье № 3
Туфли № 1 |
Платье № 4
Туфли № 1 |
| 2 | Платье № 1
Туфли № 2 |
Платье № 2
Туфли № 2 |
Платье № 3
Туфли № 2 |
Платье № 4 Туфли № 2 |
Итак, возможное количество вариантов нарядов — 8.
Ответ: 8 вариантов.
665. В отряде космонавтов есть три пилота и два инженера. Сколько существует способов составить экипаж, состоящий из одного пилота и одного инженера?
Составим таблицу:
- в первом столбце запишем возможные варианты инженеров
- в верхней строке — возможные варианты пилотов
- на пересечении строк и столбцов — возможные варианты экипажа
|
Экипаж |
Пилоты | |||
| 1 | 2 |
3 |
||
|
Инженеры |
1 | Пилот 1
Инженер 1 |
Пилот 2
Инженер 1 |
Пилот 3
Инженер 1 |
| 2 | Пилот 1
Инженер 2 |
Пилот 2
Инженер 2 |
Пилот 3 Инженер 2 |
Итак, возможное количество вариантов нарядов — 6.
Ответ: 6 вариантов.
666. На рисунке 185 изображён план одного района города. Отрезками изображены улицы. Сколько существует маршрутов из точки А в точку В, если передвигаться разрешено по улицам, идущими вверх или вправо?
Существуют следующие варианты маршрутов:
- Вверх — вверх — вправо — вправо
- Вверх — вправо — вверх — вправо
- Вверх — вправо — вправо — вверх
- Вправо — вверх — вверх — вправо
- Вправо — вверх — вправо — вверх
- Вправо — вправо — вверх — вверх
Итак, возможное количество вариантов маршрутов — 6.
Ответ: 6 вариантов.
667. В записи 1 * 2 * 3 * 4 вместо каждой звёздочки можно поставить один из знаков «+» или «•». Чему равно наибольшее значение выражения, которое можно получить?
Наибольшее значение выражения можно получить, если расставить знаки в таком порядке:
1 + 2 • 3 • 4 = 1 + 6 • 4 = 1 + 24 = 25.
Упражнения для повторения
668. Расстояние между двумя сёлами равно 28 км. Из этих сёл одновременно в одном направлении выехали мотоциклист и автобус. Автобус ехал впереди со скоростью 42 км/ч, а мотоциклист ехал со скоростью 56 км/ч. Через сколько часов после начала движения мотоциклист догонит автобус?
1) 56 — 42 = 14 (км/ч) — скорость, с которой мотоциклист догоняет автобус — скорость сближения.
2) 28 : 14 = 2 (часа) — время, за которое мотоциклист догонит автобус.
Ответ: 2 часа.
669. Решите уравнение:
670. 1) Одно из слагаемых в 14 раз больше другого. Во сколько раз их сумма больше меньшего слагаемого?
Пусть х — первое слагаемое. Тогда второе слагаемое равно 14х.
(14х + х) : х = 15х : х = 15
Ответ: в 15 раз.
2) Вычитаемое в 12 раз больше разности. Во сколько раз уменьшаемое больше разности?
Пусть х — разность, тогда вычитаемое равно 12х, а уменьшаемое равно (12х + х).
(12х + х) : х = 13х : х = 13
Ответ: в 13 раз.
671. На ферме есть 156 коров, каждая из которых даёт в день 12 л молока. Молоко с фермы вывозят в бидонах ёмкостью 40 л. В некоторый день на ферме было в наличии 42 пустых бидона. Хватит ли бидонов, чтобы вывезти с фермы надоенное за день молоко?
1) 156 • 12 = 1 872 (литра) — молока надаивают на ферме за 1 день.
2) 42 • 40 = 1 680 (литров) — молока помещается в 42 пустых бидона.
3) 1 680 литров < 1 872 литра, значит 42 бидона не хватит для вывоза всего надоенного за день молока.
Ответ: Нет, не хватит.
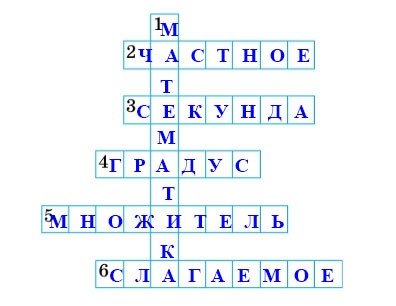
672. Решите кроссворд.
По горизонтали:
2. Результат арифметического действия (Частное)
3. Единица измерения времени (Секунда)
4. Единица измерения углов (Градус)
5. Компонент умножения (Множитель)
6. Компонент сложения (Слагаемое)
По вертикали:
1. «Царица наук» (Математика)
Задача от мудрой совы
673. В классе 30 учащихся. Они сидят по двое за 15 партами так, что половина всех девочек сидит с мальчиками. Можно ли учеников класса пересадить так, чтобы половина всех мальчиков сидела с девочками?
1) Если половина всех девочек сидят с мальчиками, значит вторая половина девочек сидит друг с другом по двое за партой. Значит половина девочек — это чётное количество человек.
2) Если половина девочек — это чётное количество человек, то общее количество девочек (две половины) также будет чётным числом.
3) Предположим, что условие задачи выполнимо и половину мальчиков можно посадить с девочками. Это значит, что другая половина мальчиков будет сидеть по двое за партой. То есть половина мальчиков также должно быть чётным числом.
4) Половина мальчиков и половина девочек — это ровно половина класса. По нашему предположению это чётное количество человек, так как и половина мальчиков, и половина девочек чётные числа.
5) Но мы знаем, что в классе 30 учащихся, а половина от 30 человек — это 15 человек — нечётное число. Значит наше предположение о мальчиках было неверно и их нельзя посадить так, чтобы половина мальчиков сидела с девочками.
Ответ: Нет, нельзя.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
БИ
НА
РИ
ТО
КОМ
Назовите слово
КА
НА
РИ
ТО
КОМ
БИ
КА
Назовите слово
РИ
ТО
КОМ
БИ
НА
КА
Назовите слово
РИ
КОМ
БИ
НА
ТО
КА
Назовите слово
КОМ
БИ
НА
ТО
РИ
КА
Назовите слово
К
Сформулируйте тему урока
О
М
Б
О
Т
А
Н
И
Ы
Н
Р
А
Д
Ч
И
Е
К
Сформулируйте тему урока
О
М
Б
О
Т
А
Н
И
Ы
Н
Р
А
Д
Ч
И
А
З
Е
КОМБИНАТОРНЫЕ ЗАДАЧИ
К
М
А
К
А
М
М
А
К
К
А
М
М
К
А
А
К
М
Комбинаторика
Что означает слово «комбинаторика»?
Комбинаторика
Что означает слово «комбинаторика»?
В переводе с латинского
слово «комбинаторика» означает
Комбинаторика
Что означает слово «комбинаторика»?
«сочетать»
В переводе с латинского
слово «комбинаторика» означает
Комбинаторика
Что означает слово «комбинаторика»?
«сочетать»
«соединять»
В переводе с латинского
слово «комбинаторика» означает
Комбинаторные задачи
Какие задачи называются комбинаторными?
Комбинаторные задачи
Какие задачи называются комбинаторными?
Комбинаторные задачи − это задачи,
в которых надо ответить на вопрос:
Комбинаторные задачи
Какие задачи называются комбинаторными?
«Сколькими способами … ?»
Комбинаторные задачи − это задачи,
в которых надо ответить на вопрос:
Задача №1 Чтобы запереть чемодан с кодовым замком, нужно ввести код, состоящий из двух цифр. Хозяин
чемодана решил использовать только цифры 1, 2 и 3. Сколькими способами он может выбрать код?
1
1
Решение:
Запишем все коды в порядке возрастания:
1
1
Задача №1 Чтобы запереть чемодан с кодовым замком, нужно ввести код, состоящий из двух цифр. Хозяин
чемодана решил использовать только цифры 1, 2 и 3. Сколькими способами он может выбрать код?
Решение:
Запишем все коды в порядке возрастания:
1
1
1
1
1
2
1
3
Задача №1 Чтобы запереть чемодан с кодовым замком, нужно ввести код, состоящий из двух цифр. Хозяин
чемодана решил использовать только цифры 1, 2 и 3. Сколькими способами он может выбрать код?
Решение:
Запишем все коды в порядке возрастания:
1
1
1
1
1
2
1
3
2
1
2
2
2
3
Задача №1 Чтобы запереть чемодан с кодовым замком, нужно ввести код, состоящий из двух цифр. Хозяин
чемодана решил использовать только цифры 1, 2 и 3. Сколькими способами он может выбрать код?
Решение:
Запишем все коды в порядке возрастания:
1
1
1
1
1
2
1
3
2
1
2
2
2
3
3
1
3
2
3
3
Задача №1 Чтобы запереть чемодан с кодовым замком, нужно ввести код, состоящий из двух цифр. Хозяин
чемодана решил использовать только цифры 1, 2 и 3. Сколькими способами он может выбрать код?
Ответ: 9 способов.
1
1
1
1
1
2
1
3
2
1
2
2
2
3
3
1
3
2
3
3
Задача №1 Чтобы запереть чемодан с кодовым замком, нужно ввести код, состоящий из двух цифр. Хозяин
чемодана решил использовать только цифры 1, 2 и 3. Сколькими способами он может выбрать код?
Задача №2 В четверг в первом классе должно быть три урока: русский язык, математика и физкультура.
Сколько различных вариантов расписания
можно составить на этот день?
Задача №2 В четверг в первом классе должно быть три урока: русский язык, математика и физкультура.
Сколько различных вариантов расписания
можно составить на этот день?
Решение:
Обозначим названия предметов буквами :
Задача №2 В четверг в первом классе должно быть три урока: русский язык, математика и физкультура.
Сколько различных вариантов расписания
можно составить на этот день?
Решение:
Р − русский язык
Обозначим названия предметов буквами :
Задача №2 В четверг в первом классе должно быть три урока: русский язык, математика и физкультура.
Сколько различных вариантов расписания
можно составить на этот день?
Решение:
Р − русский язык
Обозначим названия предметов буквами :
М − математика
Задача №2 В четверг в первом классе должно быть три урока: русский язык, математика и физкультура.
Сколько различных вариантов расписания
можно составить на этот день?
Решение:
Р − русский язык
Обозначим названия предметов буквами :
Ф − физкультура
М − математика
Задача №2 В четверг в первом классе должно быть три урока: русский язык, математика и физкультура.
Сколько различных вариантов расписания
можно составить на этот день?
Решение:
Рассмотрим различные варианты:
Задача №2 В четверг в первом классе должно быть три урока: русский язык, математика и физкультура.
Сколько различных вариантов расписания
можно составить на этот день?
Решение:
Р
Рассмотрим различные варианты:
Ф
М
Р
М
Ф
Задача №2 В четверг в первом классе должно быть три урока: русский язык, математика и физкультура.
Сколько различных вариантов расписания
можно составить на этот день?
Решение:
Р
Рассмотрим различные варианты:
Ф
М
Р
Р
Р
М
М
М
Ф
Ф
Ф
Задача №2 В четверг в первом классе должно быть три урока: русский язык, математика и физкультура.
Сколько различных вариантов расписания
можно составить на этот день?
Решение:
Р
Рассмотрим различные варианты:
Ф
М
Р
Р
Р
Р
Р
М
М
М
М
М
Ф
Ф
Ф
Ф
Ф
Задача №2 В четверг в первом классе должно быть три урока: русский язык, математика и физкультура.
Сколько различных вариантов расписания
можно составить на этот день?
Р
Ф
М
Р
Р
Р
Р
Р
М
М
М
М
М
Ф
Ф
Ф
Ф
Ф
Ответ: 6 способов.
Задача №3 На прямой отмечены три точки А, В, С и D.
Сколько получилось отрезков?
Задача №3 На прямой отмечены три точки А, В, С и D.
Сколько получилось отрезков?
Решение:
Рассмотрим различные варианты:
AB
Задача №3 На прямой отмечены три точки А, В, С и D.
Сколько получилось отрезков?
Решение:
Рассмотрим различные варианты:
AB
AC
Задача №3 На прямой отмечены три точки А, В, С и D.
Сколько получилось отрезков?
Решение:
Рассмотрим различные варианты:
AB
AC
AD
Задача №3 На прямой отмечены три точки А, В, С и D.
Сколько получилось отрезков?
Решение:
Рассмотрим различные варианты:
AB
AC
AD
BC
Задача №3 На прямой отмечены три точки А, В, С и D.
Сколько получилось отрезков?
Решение:
Рассмотрим различные варианты:
AB
AC
AD
BC
BD
Задача №3 На прямой отмечены три точки А, В, С и D.
Сколько получилось отрезков?
Решение:
Рассмотрим различные варианты:
AB
AC
AD
BC
BD
CD
Задача №3 На прямой отмечены три точки А, В, С и D.
Сколько получилось отрезков?
Решение:
Рассмотрим различные варианты:
AB
AC
AD
BC
BD
CD
Ответ: 6 отрезков.
Дерево возможных вариантов
Решать комбинаторные задачи удобно путём
построения специальной схемы. Эта схема
напоминает дерево, расположенное «вверх ногами»
и без ствола, поэтому этот способ решения
называется «деревом возможных вариантов».
Решим задачу с помощью построения дерева возможных вариантов.
1
1
Задача №1 Чтобы запереть чемодан с кодовым замком, нужно ввести код, состоящий из двух цифр. Хозяин
чемодана решил использовать только цифры 1, 2 и 3. Сколькими способами он может выбрать код?
1. Поставим знак * .
*
1. Поставим знак * .
*
2. Проведем три ветви, так как выбрать первую цифру три варианта (1, 2, 3).
1. Поставим знак * .
*
2. Проведем три ветви, так как выбрать первую цифру три варианта (1, 2, 3).
3. Проведем от каждой первой цифры по три ветви, так как выбрать вторую цифру три варианта (1, 2, 3).
1. Поставим знак * .
*
2. Проведем три ветви, так как выбрать первую цифру три варианта (1, 2, 3).
3. Проведем от каждой первой цифры по три ветви, так как выбрать вторую цифру три варианта (1, 2, 3).
1. Поставим знак * .
*
2. Проведем три ветви, так как выбрать первую цифру три варианта (1, 2, 3).
3. Проведем от каждой первой цифры по три ветви, так как выбрать вторую цифру три варианта (1, 2, 3).
*
Двигаясь от корня дерева по ветвям, мы получим все возможные коды.
Ответ: 9 способов.
Упражнения
К
М
А
К
А
М
М
А
К
К
А
М
М
К
А
А
К
М
№1
Задача, похожая на задачу о расписании:
В магазине продаются полотенца трех видов:
в полоску, в клетку и в горошек. Мама хочет подарить
каждой из трех дочерей по полотенцу, причем так,
чтобы одинаковых у них не было. Сколькими способами
она может раздать три разных полотенца девочкам?
Введите обозначения: П − полоска, К − клетка, Г – горошек.
№1
Проверьте решение:
В магазине продаются полотенца трех видов:
в полоску, в клетку и в горошек. Мама хочет подарить
каждой из трех дочерей по полотенцу, причем так,
чтобы одинаковых у них не было. Сколькими способами
она может раздать три разных полотенца девочкам?
Введите обозначения: П − полоска, К − клетка, Г – горошек.
П
Г
К
К
П
П
К
П
К
П
К
К
П
Г
Г
Г
Г
Г
Ответ: 6 способов.
№2
Задача, похожая на задачу об отрезках:
Сколькими способами можно составить патруль
из двух полицейских, если на дежурство вышли
Задорнов, Свистунов и Умнов?
№2
Проверьте решение:
Сколькими способами можно составить патруль
из двух полицейских, если на дежурство вышли
Задорнов, Свистунов и Умнов?
Решение:
Рассмотрим различные варианты:
ЗС
ЗУ
СУ
Ответ: 3 способа.
№3
Задача, решаемая способом
дерева возможных вариантов:
Имеются ручки четырех цветов: красные, синие, зеленые, черные − и два вида записных книжек.
Сколько различных наборов из ручки
и записной книжки
можно составить из этих предметов?
№3
Проверьте решение: