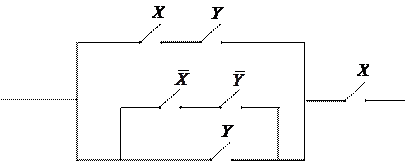
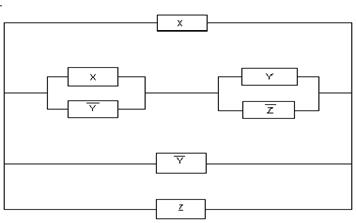
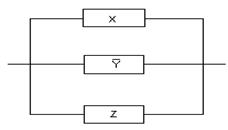
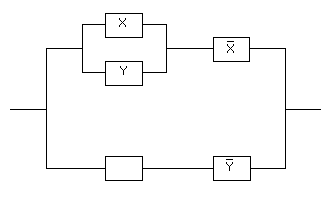
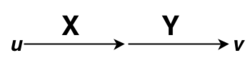
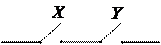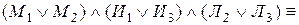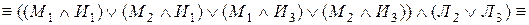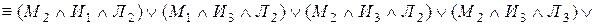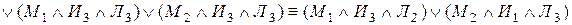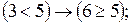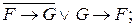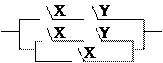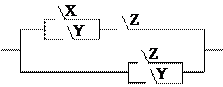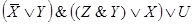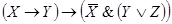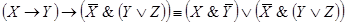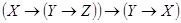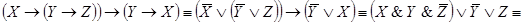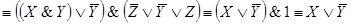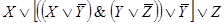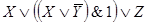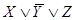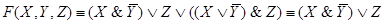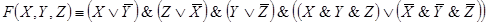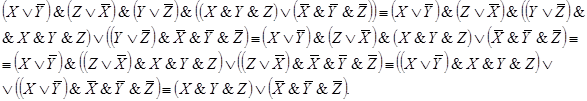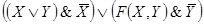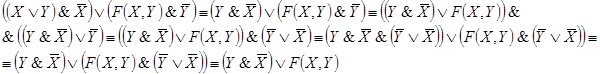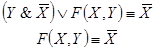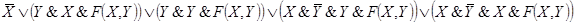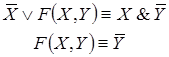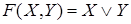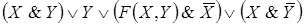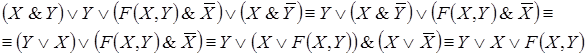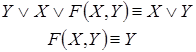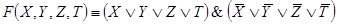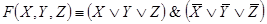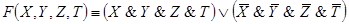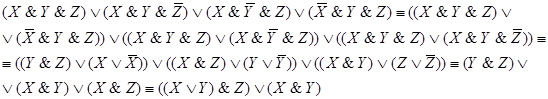В начале прошлого века известный физик П. Эренфест впервые указал на возможность применения аппарата алгебры логики в технике. Эта идея нашла свое воплощение в работах советского физика В. И.Шестакова, американского математика К. Шеннона и японского инженера А. Какасима. Первыми объектами применения алгебры логики для решения технических задач были контактные схемы. Под контактными схемами мы будем понимать электрические цепи, содержащие только контакты. Каждый контакт может находиться в двух состояниях – разомкнут (0) и замкнут (1). Такие цепи мы будем изображать диаграммой, на которой возле контактов пишется или
. Причем значение 1 этих переменных соответствует прохождению тогда через данный контакт, а значение 0 нет.
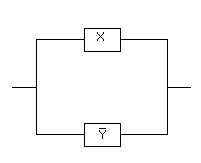
Если контакты X и y соединены последовательно, то цепь замкнута, когда оба контакта замкнуты и разомкнуты, когда хотя бы один из контактов разомкнут. Ясно, что такой схеме
Соответствует булева функция .
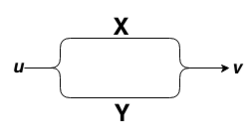
Если контакты X и y соединены параллельно то цепь замкнута, когда хотя бы один контакт замкнут и разомкнут, когда оба контакта разомкнуты. Ясно, что такой схеме
Соответствует булева функция .
Указанное соответствие позволяет любую булеву функцию представить в виде контактной схемы. С другой стороны, любая контактная схема с последовательно или параллельно соединенными контактами реализуется булевой функцией. Задача анализа контактной схемы и состоит в построении соответствующей ей булевой функции.
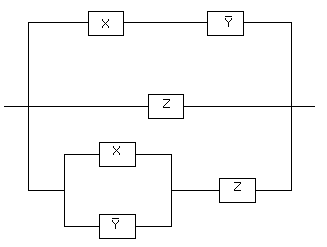
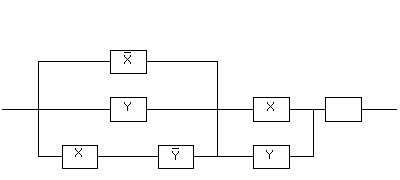
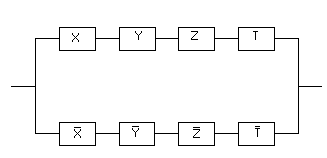
Например, контактная схема
Реализуется булевой функцией .
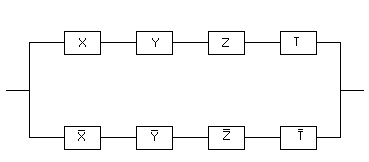
Однако, поскольку одна и та же булева функция может быть выражена различными формулами, то ее реализация контактными схемами неоднозначна. Всегда можно построить много различных контактных схем, соответствующих данной функции. Такие схемы называют эквивалентными. Задача синтеза контактной схемы состоит в построении контактной схемы по заданной булевой функции, которая может быть задана как формулой, так и таблицей. В обоих случаях необходимо выразить функцию через операции конъюнкции, дизъюнкции и отрицания. Каждая операция конъюнкции соответствует последовательному соединению контактов. В результате параллельного соединения получаем контактную схему. Из множества эквивалентных схем, путем упрощения формул выделяют наиболее простую схему. Центральной проблемой синтеза контактных схем является построение для данной булевой функции более простой схемы. Часто эта проблема сводится к минимизации булевых функций, т. е. к такому их представлению, в котором соответствующие формулы содержат минимальное количество вхождений переменных.
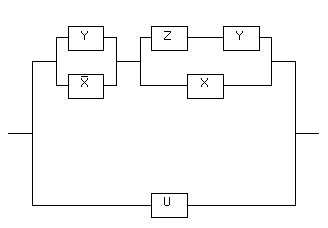
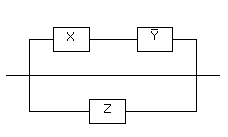
Рассмотрим схему
Данная схема реализуется следующей формулой:
Упростим данную формулу. Используя закон дистрибутивности, получаем:
=
=
Следовательно, данную схему можно упростить, заменив ее следующей эквивалентной схемой:
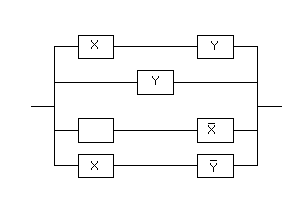
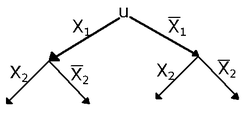
Решим теперь следующую задачу: из контактов составить по возможности более простую схему так, чтобы она замкнулась тогда и только тогда, когда замкнуты не менее двух контактов.
Составим таблицу истинности для булевой функции, соответствующей требуемой контактной схеме
|
X |
Y |
Z |
|
|
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
1 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
1 |
0 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
1 |
1 |
1 |
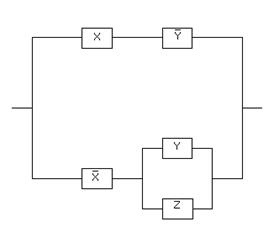
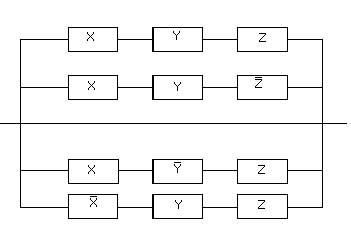
Найдем для данной булевой функции совершенную ДНФ:
Упростим данную формулу
=
=
.
Данной формуле соответствует следующая контактная схема:
Контактные схемы исторически были первыми техническими средствами реализации булевых функций. В дальнейшем появилось много различных устройств, реализующих булевы функции. Одной и нескольких переменных.
Пусть имеется некоторое устройство, имеющее n упорядоченных «входов» и один «выход», причем внутренняя структура этого устройства нас не интересует. На каждый из входов могут подаваться два сигнала, которые мы будем обозначать символами 0 и 1. При каждом наборе сигналов на входах и выходе возникает один из сигналов 0 или 1. Причем набор сигналов на входах однозначно определяет сигнал на выходе. Очевидно, что каждое такое устройство реализует булеву функцию.
Устройства, реализующие элементарные булевы функции, называются Логическими элементами. Логические элементы изображаются в виде прямоугольников, внутри которых помещаются условные названия или символы соответствующих функций
|
Функция |
Графическое изображение |
Функция |
Графическое изображении |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из данных логических элементов путем соединения входа одного из них с выходов другого можно строить все более сложные логические схемы. Для полученных таким образом схем легко записывают соответствующие им булевы функции.
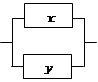
Например, схема
Реализуется булевой функцией
Нетрудно для любой булевой функции построить реализующую ее логическую схему.
Например, булева функция реализуется логической схемой
Рассмотрим построение логической схемы на примере одноразрядного сумматора, выполняющего арифметическое сложение двоичных чисел и
, к-го разряда и переноса из младшего разряда
. Пусть
– получаемая сумма, а
– перенос в старший разряд, тогда получаем следующую таблицу истинности такого сумматора.
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
1 |
0 |
0 |
1 |
0 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
1 |
|
1 |
1 |
1 |
1 |
1 |
Отсюда получаем
Построим схему, соответствующую данному сумматору. Для этого вначале упростим выражение для . Как легко заметить, выражение для
не упрощается, используя предыдущие методы. Для упрощения выражения функции
используем выражение функции
.
Поэтому будем рассматривать как переменную величину. В результате получаем следующую таблицу, которая содержит избыточные наборы переменных:
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
0 |
0 |
1 |
|
|
0 |
0 |
1 |
0 |
1 |
|
0 |
0 |
1 |
1 |
|
|
0 |
1 |
0 |
0 |
1 |
|
0 |
1 |
0 |
1 |
|
|
0 |
1 |
1 |
0 |
|
|
0 |
1 |
1 |
1 |
0 |
|
1 |
0 |
0 |
0 |
1 |
|
1 |
0 |
0 |
1 |
|
|
1 |
0 |
1 |
0 |
|
|
1 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
|
|
1 |
1 |
0 |
1 |
0 |
|
1 |
1 |
1 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
Отсюда
Используя методы, которые будут рассмотрены в разделе 6, нетрудно упростить выражение для :
=
,
Где .
Теперь строим логическую схему:
| < Предыдущая | Следующая > |
|---|
Релейно-контактные схемы
Укажем на применение алгебры логики к анализу и синтезу релейно-контактных схем. Среди технических средств автоматизации значительное место занимают устройства релейно-контактного действия. Они находят широкое применение в телефонии, телеуправлении, автоматике и телемеханике, на железнодорожном транспорте, в вычислительной технике. Сейчас при конструировании таких устройств все больше и больше используется алгебра логики. Впервые идея использования алгебры логики для построения автоматических устройств была выдвинута в 1910 году известным физиком П.Эренфестом. Но только в 30-х годах эта идея нашла свое воплощение в работах советского физика В.И. Шестакова, американского математика К.Шеннона и японского инженера А.Накосима.
Контактная схема представляет собой устройство из проводников и контактов, связывающих полюса источника тока. Контакт бывает в двух состояниях:
а) контакт разомкнут и тогда ему приписывают 0;

Контакт «не 
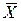
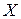
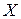
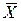
Дизъюнкции 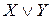
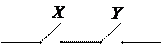
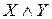
Каждый контакт подключен к некоторому реле. В схеме одинаковыми буквами обозначаются контакты, подключенные к одному и тому же реле. Всей схеме ставится в соответствие булева функция F, которая равна 1, если схема проводит ток, и 0 в противном случае. Эта функция называется функцией проводимости схемы, а ее таблица – условиями работы схемы. Две схемы с одинаковыми функциями проводимости называются равносильными. Средства алгебры высказываний позволяют упрощать схемы, используя отношение равносильности формул алгебры высказываний.
□ По данной схеме запишем формулу, определяющую функцию проводимости, и упростим ее:
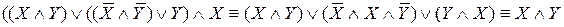
Таким образом, 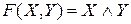
§5. Решение логических задач методами алгебры логики.
Под логической задачей будем понимать задачу, где основным видом деятельности является выявление отношений между объектами задачи, а не нахождение количественных характеристик объектов. Суть применения алгебры логики к решению логических задач состоит в том, что, имея конкретные условия логической задачи, стараются записать их в виде формулы алгебры логики. В дальнейшем путем равносильных преобразований упрощают полученную формулу. Простейший вид формулы, как правило, приводит к ответу на все вопросы задачи.
Покажем на ряде конкретных примеров, как использовать возможности алгебры логики для решения элементарных логических задач.
Пример 1. При составлении расписания уроков на некоторый день учителя просили, чтобы их уроки были:
1. математик – первым или вторым;
2. историк – первым или третьим;
3. литератор – вторым или третьим.
Можно ли удовлетворить просьбы всех учителей?
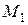
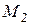
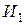
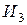
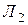
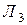
Тогда на языке алгебры эту задачу можно записать в виде формулы , после равносильных преобразований которой можно будет дать ответ на вопрос задачи:
Выяснили, что имеется две возможности:
1. 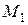
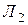
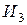
2. 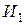
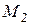
Вопросы для самоконтроля по теме «Логика высказываний»
1. Что понимается под высказыванием? Привести примеры.
2. Являются ли высказываниями следующие предложения:
а) два плюс два равно пяти;
б) функция 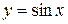
в) существует рациональное число такое, что х > 7.
3. Определить операции отрицания, дизъюнкции, конъюнкции, импликации, эквиваленции и задать их с помощью таблиц истинности.
4. Найти истинностные значения следующих высказываний:
а)
б) 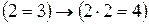
в) 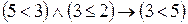
5. Что понимается под формулой алгебры высказываний?
6. Найти значения формул при заданных значениях высказывательных переменных:
а) 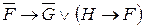
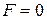
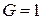
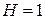
б) 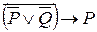
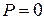
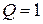
7. Построить таблицу истинности формулы 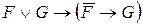
8. Что называется тождественно истинной (ложной) формулой? Проверить, является ли каждая из формул тождественно истинной:
а)
б) 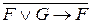
9. Какие формулы называются равносильными? Как доказать равносильность формул? Проверить равносильность
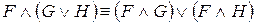
10. Записать первые десять основных равносильностей алгебры высказываний. Доказать законы поглощения и законы де Моргана.
11. Записать законы двойного отрицания; исключения импликации; введения дизъюнкции; введения конъюнкции; замены эквиваленции; контрапозиции; противоположностей; доказательства от противного; транзитивности импликации; транзитивности эквиваленции. Обосновать законы доказательства от противного и закон контрапозиции.
12. Упростить формулу 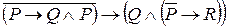
13. Преобразовать формулу 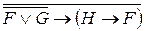
14. Перевести предложение на логический язык и построить его отрицание: «Если вечером я буду не занята, то пойду в кино или на дискотеку».
15. Упростить релейно-контактную схему:
16. Ввести понятие функции проводимости для релейно-контактной схемы. Найти функцию проводимости и условия работы для схемы:
17. Один из братьев Витя, Толя, Коля разбил окно. В разговоре участвуют еще двое братьев – Андрей и Дима.
– Это мог сделать только Витя или Толя – сказал Андрей.
– Я окно не разбивал, – возразил Витя, – Коля тоже.
– Вы оба говорите неправду, – заявил Толя.
– Нет, Толя, один из них сказал правду, а другой неправду, – возразил Дима.
–Ты, Дима, неправ, – вмешался Коля.
Их отец, которому, конечно, можно доверять, уверен, что трое братьев сказали правду. Кто разбил окно?
Источник
Анализ и синтез релейно-контактных схем
Одно из применений алгебры высказываний – анализ и синтез релейно-контактных схем.
Еще в 1910 году физик П.С. Эренфест указал на возможность применения аппарата алгебры логики при исследовании релейно-контактных схем. Каждой схеме можно поставить в соответствие некоторую формулу алгебры высказываний, и каждая формула алгебры высказываний реализуется с помощью некоторой схемы.
Рассмотрим 2-х-полюсные переключатели, т.е. такие, которые имеют два состояния: «замкнуто» — 1, «разомкнуто» — 0. На схеме будем изображать:
Определение 7. Переключатель, который сблокирован с X так, что он замкнут, если X разомкнут, и разомкнут, если X замкнут, называется инверсным и обозначается 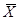
Конъюнкция двух высказываний X и Y будет представлена двухполюсной схемой с последовательным соединением двух переключателей X и Y.
Эта схема пропускает ток тогда и только тогда, когда истины и X, и Y одновременно, то есть истина конъюнкция X&Y.
Дизъюнкция двух высказываний X и Y изобразится двухполюсной схемой с параллельным соединением двух переключателей X и Y.
X 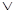
Эта схема пропускает ток в случае, если истинно высказывание X или истинно высказывание Y, то есть истина дизъюнкция X 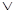
Таким образом, всякую булеву формулу можно трактовать как некоторую последовательно-параллельную схему от 2-х-полюсных переключателей. Все свойства булевых операций переносятся на соответствующие операции над переключателями. Формула, которую можно составить для каждой схемы называется функцией проводимости схемы, а таблица значений – условиями работы схемы.
Определение 8. Две схемы называются равносильными, если имеют одинаковые функции проводимости.
Анализ схемы заключается в следующем: для данной схемы составляется функция проводимости, которая на основании законов булевых функций упрощается и для нее строится новая, более простая схема, которая обладает теми же электрическими свойствами.
Синтез схем заключается в построении схем с заданными электрическими свойствами. На основании заданных электрических свойств строится таблица условий работы схемы и затем функция проводимости, представляющая собой СДНФ, а по ней строится схема.
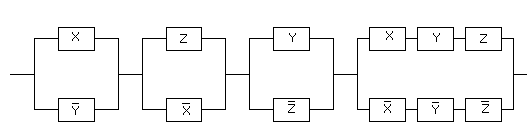
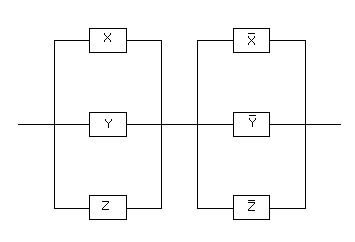
Задача 1.Составить РКС, обладающая следующей функцией проводимости:
Задача 2.Составить РКС обладающая следующей функцией проводимости:
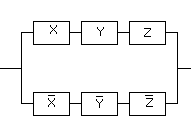
Задача 3.Составить РКС обладающая следующей функцией проводимости:
Ей соответствует функция проводимости:
F(X,Y,Z)
F(X,Y,Z) 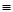
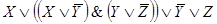
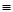
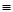
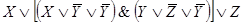
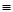
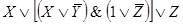
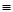
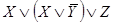
Этой же функции проводимости соответствует более простая схема.
Ей соответствует функция проводимости:
Этой же функции проводимости соответствует более простая схема.
Ей соответствует функция проводимости:
Задача 7.Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
Данной схеме соответствует функция проводимости:
Задача 8.Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
Данной схеме соответствует функция проводимости:
Задача 9.Какой контакт необходимо вставить в вакантное место, чтобы функция проводимости полученной схемы стала бы равна данной булевой функции:
Данной схеме соответствует функция проводимости:
Задача 10.Построить РКС с четырьмя переключателями, которая проводит ток тогда и только тогда, когда замыкаются не все переключатели, а только некоторые из них.
Составим таблицу значений функции проводимости F (X, Y, Z, T) этой схемы:
В правом столбце звездочками отметим те строки, на которых функция F (X, Y, Z, T) обращается в 0, запишем для неё выражение, используя СКНФ, потому что наборов значений аргументов, на которых функция обращается в 0, значительно меньше, чем наборов значений аргументов, на которых функция обращается в 1, и значит, СКНФ будет более простой, чем СДНФ:
Задача 11. Построить схему с тремя переключателями, которая замыкается тогда и только тогда, когда замкнут либо один, либо два переключателя. При построении использовать не более шести контактов.
Составим таблицу значений функции проводимости F (X, Y, Z) этой схемы:
В правом столбце звездочками отметим те строки, на которых функция
F (X, Y, Z, T) обращается в 1, запишем для неё выражение, используя СКНФ, потому что наборов значений аргументов, на которых функция обращается в 0, значительно меньше, чем наборов значений аргументов, на которых функция обращается в 1, и значит, СКНФ будет более простой, чем СДНФ:
Задача 12.Требуется составить схему с четырьмя переключателями X, Y, Z, T. Схема должна проводить ток тогда и только тогда, когда будут замкнуты переключатели X и Y или Z и T.
Составим таблицу значений функции проводимости F (X, Y, Z, T) этой схемы:
В правом столбце звездочками отметим те строки, на которых функция
F (X, Y, Z, T) обращается в 1, запишем для неё выражение, используя СДНФ:
Задача 13.Построить контактную схему для оценки результатов некоторого спортивного соревнования тремя судьями при следующих условиях: судья, засчитывающий результат, нажимает имеющуюся в его распоряжении кнопку, а судья, не засчитывающий результат, кнопки не нажимает. В случае, если кнопки нажали не менее двух судей должна загореться лампочка (положительное решение судей принято простым большинством голосов).
Работа РКС описывается функцией Буля трех переменных F (X, Y, Z), где переменные высказывания X, Y, Z означают:
Таблица истинности функции F (X, Y, Z) имеет вид:
| X Y Z | F(X, Y, Z) |
| 1 1 1 | |
| 1 1 0 | |
| 1 0 1 | |
| 0 1 1 | |
| 1 0 0 | |
| 0 1 0 | |
| 0 0 1 | |
| 0 0 0 |
Этой же функции проводимости соответствует более простая схема.
Источник
Для математического описания электротехнических устройств, состоящих из контактов и промежуточных реле, функционирующих в дискретные моменты времени применяются контактные схемы. С помощью контактных схем можно представить любую булеву функцию.
| Определение: |
| Контактная схема (англ. contact circuit) представляет собой ориентированный ациклический граф, на каждом ребре которого написана переменная или ее отрицание. |
| Определение: |
| Контакт (англ. contact) — ребро схемы, помеченное символом переменной или ее отрицанием. Каждому ребру в схеме сопоставляется какая то переменная (не обязательно каждой переменной сопоставляется ребро) |
Содержание
- 1 Принцип работы
- 2 Построение контактных схем
- 2.1 Представление одного из базисов в контактных схемах
- 2.2 Построение контактных схем
- 2.3 Примеры построения некоторых функций
- 3 Задача о минимизации контактной схемы
- 4 См также
- 5 Источники информации
Принцип работы
| Определение: |
| Замкнутый контакт (англ. closed contact) — контакт схемы, над которым написана или значение переменной равно . |
| Определение: |
| Разомкнутый контакт (англ. open contact) — контакт схемы, над которым написан или значение переменной равно . |
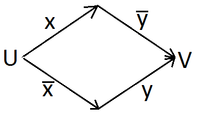
Пусть и — два полюса контактной схемы (из вершины ребра только выходят, в вершину ребра только входят), определяющую функцию . Тогда принимает значение при таком наборе значений переменных, если можно добраться из в только по замкнутым контактам.
Построение контактных схем
Представление одного из базисов в контактных схемах
Любую булеву функцию можно представить в виде контактной схемы. Для этого необходимо привести её к ДНФ или КНФ, а затем построить, используя комбинации трех логических элементов:
|
|
|
|
Построение контактных схем
Пусть задана произвольная булева функция. Требуется построить для нее контактную схему, которая ее реализует.
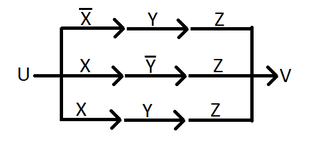
В качестве примера рассмотрим функцию, представленную в ДНФ: . Каждой скобке ДНФ соответствует цепочка из последовательных соединенных контактов, определяемых переменными содержащимися в скобке. При этом, вся схема состоит из параллельных соединений указанных цепочек. Для приведенного примера соответствует схема приведена ниже.
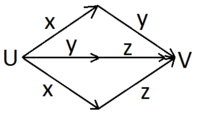
Примеры построения некоторых функций
|
|
|
|
Задача о минимизации контактной схемы
| Определение: |
| Две контактные схемы называются эквивалентными (англ. equivalent contact circuits), если они реализуют одну и ту же булеву функцию. |
| Определение: |
| Сложностью контактной схемы (англ. the complexity of the contact circuit) называется число ее контактов. |
| Определение: |
| Минимальная контактная схема (англ. minimal contact circuit) — схема, имеющая наименьшую сложность среди эквивалентных ей схем. |
| Определение: |
| Дерево конъюнктов для переменных — двоичное ориентированное дерево глубиной , такое что: поддеревья на одном и том же уровне одинаковы; и левое ребро любого узла помечено символом переменной , а правое помечено символом отрицания переменной . |
Задача минимизации контактных схем состоит в том, чтобы по данной схеме найти схему , эквивалентную и имеющую наименьшую сложность.
Один из путей решения этой задачи состоит в следующем:
- Осуществляем переход от контактной схемы к её булевой функции .
- Упрощаем , то есть отыскиваем функцию (на том же базисе, что и , равносильную и содержащую меньше вхождений операций дизъюнкции и конъюнкции. Для этой операции удобно использовать карты Карно.
- Строим схему , реализующую функцию .
| Теорема: |
|
Любую булеву функцию можно представить контактной схемой, сложностью |
| Доказательство: |
|
Пусть дана функция и она представлена в ДНФ Дерево конъюнктов для 2-х переменных Возьмем дерево конъюнктов для переменных (см. картинку). Очевидно, что от вершины до “нижних” вершин дерево можно добраться за , а ребер у такого дерева Соединим нижние вершины, которые соответствуют конъюнктам функции, с вершиной контактами, над которыми написана . От этого в схему добавится не более, чем ребер и тогда сложность останется . В результате можно построить контактную схему для любой функции со сложностью |
См также
- Построение функциональной схемы
Источники информации
- Контактные схемы
- Encyclopedia of Math — Contact sheme
- Гаврилов Г.П., Сапоженко А.А. Задачи и упражнения по дискретной математике
- М. А. Айзерман, Л. А. Гусев, Л. И. Розоноэр И. М. Смирнова, А. А. Таль. Логика, автоматы, алгоритмы.
Частичной функцией называется функция, определённая не на
всех наборах своих переменных.
Простой импликантой частичной функции f называется элементарная конъюнкция К, для которой выполняются условия:
1) ∃αК(α) = 1, f(а) = 1;
2) ∀β f(B) = 0 → K(B) = 0;
3) если из импликанты К удалить любую букву, получится
формула К’ такая, что ∃γК'(γ) = 1, f(γ) = 0.
Доопределением частичной функции f будем называть всюду
определённую функцию g, значения которой совпадают со зна чениями функции f на тех наборах, на которых функция f определена.
Критерий существования декомпозиции заданного вида:
Частичная функция f представляется в виде
f(u,v,w) = g(u,w,h(u,v)) тогда и только тогда для каждого фиксированного набора а значений переменных из множества и таблица функции fα(v,w) допускает доопределение до таблицы, со держащей столбцы не более двух различных типов.
Контактной схемой называется неориентированный граф,
каждому ребру (контакту) которого приписан символ перемен-
ной в некоторой степени и выделены две вершины, которые на-
зываются полюсами.
Частная производная булевой функции f(x1 , x2 ,…, xn) по пременной Xi определяется так:
fxi = f(x1, …,xi-1, 0, xi+1, …, xn) + f(x1, …,xi-1, 1, xi+1, …, xn).
Тестом относительно множества G = {gi} попарно различных
булевых функций называется множество наборов значений переменных Т такое, что ∀i∀k≠i∃i∈T(gi(e) ≠ gk(e)).
Задание 2.6.1
1. Реализовать частичную функцию f(x,y,z,w) формулами
над базисом конъюнкция, дизъюнкция, отрицание четырьмя спо-
собами:
а) методом Квайна;
б) исходя из минимальной ДНФ, найден-
ной с помощью карт Карнау;
в) исходя из минимальной КНФ,
найденной с помощью карт Карнау;
г) методом последовательно-
го разложения по переменным xyzw.
2. Для простейшего представления построить схему из функ-
циональных элементов типа конъюнкция, дизъюнкция, отри-
цание.
3. Реализовать простейшее представление контактной схемой.
4. Проверить возможность разделительной декомпозиции
функции f(x,y,z,w) в виде g(u,v,h(p,t)), где u,v,p,t —некоторая
перестановка переменных xyzw.
Если декомпозиция указанного вида возможна, реализовать её
схемой с ветвлениями из функциональных элементов типа конъ-
юнкция, дизъюнкция, отрицание. Указать сложность построен-
ной схемы.
Таблица 2.6.1
| № | f(x,y,z,w) | № | f(x,y,z,w) | |
| 1 | –011-11-0–011- | 11 | -1-0-0111–1-011 | |
| 2 | 1–10-0-010–01- | 12 | 11–01-0-01-011- | |
| 3 | -0-1-001–1110-1 | 13 | 1–101-1–1000-1 | |
| 4 | 11–0-11-1-1-100 | 14 | -010-1-001-1-1-0 | |
| 5 | –100-11–01-101 | 15 | 0-0-11-1-1101–1 | |
| 6 | 1–101—100-110 | 16 | 1–01-11-0-0110- | |
| 7 | 0-110-1010–1-1- | 17 | 0–01-1-11101-11 | |
| 8 | 10-1-10010–10– | 18 | 11—0-1-0100-10 | |
| 9 | -10-101–1-011-0 | 19 | 0-111–10-1-00-1 | |
| 10 | 1–0-110-1-011-0 | 20 | 1-10—011-0011- | |
| 21 | 01-1-10-011–01- | 26 | -0-0-1111-0-00-1 | |
| 22 | –1-01-000-1111- | 27 | 11-00-10–0-00-1 | |
| 23 | 0-1–1-00-11-001 | 28 | –011-11-0-0-001 | |
| 24 | -10–0111-10–01 | 29 | 10—0111–011-1 | |
| 25 | 1–01-1–1010-10 | 30 | -1-10-110-1-101- |
|
Пример решения задания 2.6.1 Решим задание 2.6.1 для функции Запишем таблицу функции f в Для отыскания сокращённой ДНФ Будем перебирать все единичные |
 |
|
Затем совершаем Итак, простые импликанты нашей функции таковы: а) Изобразим матрицу Квайна (табл. 2.6.Id), |
 |
Как видим, ядровых импликант нет. Для нахождения минимальной ДНФ составим символическую КНФ, каждая элемен-
тарная дизъюнкция которой соответствует единичному набору
нашей функции, которую преобразуем затем в ДНФ. Получим:
(2∨3∨4∨5)-(3∨5)-(3∨4)-(1∨6)-(4∨6) = (3∨5⋅4)>(6∨1⋅4) =
= 3⋅6∨5⋅4⋅6∨3⋅1⋅4∨5⋅1⋅4.
Видим, что наименьшую длину имеет символическая конъюнкция 3⋅6, которая соответствует минимальной ДНФ xw ∨ xz.
Сложность найденной минимальной ДНФ равна 4.
б) При нахождении минимальной ДНФ с помощью карты
Карнау (табл. 2.6.1е), мы доопределяем функцию f так, чтобы покрытие имело более простой вид.
Тогда все единицы покроются двумя квадратами 2×2 xw и xz,
соответствующая минимальная ДНФ совпадает с ДНФ, найденной в п. а).
в) Для отыскания минимальной КНФ покрываем нули карты
Карнау (табл. 2.6.1f) двумя квадратами 2×2: x ∨ w и x ∨ z .
Соответствующая минимальная КНФ такова: (х ∨ w) ⋅ (x ∨ z).
Сложность её равна 4.
г) Проведём разложение по набору переменных xyzw. На первом этапе, раскладывая по переменной х, имеем:
f(x, у, z, w) = x ⋅ f(0, у, z,w) ∨ x ⋅ f(1, у, z, w).
Изобразим таблицы функций f(0,y,z,w) и f(1,y,z,w)
(табл. 2.6. 1g).
Каждая из функций f(0,y,z,w) и f(1,y,z,w) не доопределима
до константы, но f(1,y,z,w) доопределима до z.
Изобразим таблицы (табл. 2.6.1h) функций f(0,0,z,w) и
f(0,1,z,w).
|
Видим, что f(0,0,z,w) и f(0,1,z,w) доопределимы до w и 1 Получаем разложение исходной функции: f(x, у, z, w) = x⋅ (y ⋅ w v у ⋅ 1) v х⋅ z = x ⋅ (w v у) v х⋅ z . Во время упрощений мы применяли тождества с константами и правило 2) В качестве простейшего представления возьмём минимальную ДНФ 3) Реализуем ту же минимальную 4) Запишем двумерную таблицу Видим, что таблица допускает доопределение до строк только двух типов |
  |
Значит, f(x,y,z,w) допускает разделительную декомпозицию
вида f(x,y,z,w) = g(z,w,h(x,y)).
Найдём вид функций g и h.
т.е. h(x,y) = (1110), h(x,y) = x y.
Строкам I типа соответствует функция φ(z, w) = (0101) = w.
Строкам II типа соответствует функция Ψ(z, w) = (1101) = z.
Тогда функция f выражается через h, φ, Ψ так:
f(x, y, z, w) = h(x, у) ⋅ φ(z, w) v h(x, y) ⋅ Ψ(z, w) =
= (x v y) ⋅ w v (x v y) ⋅ z.
Соответствующая схема из функциональных элементов с ветвлениями будет иметь вид (рис. 2.6.1, с).
Сложность схемы равна количеству функциональных элементов, её образующих, т. е. 8.
Задание 2.6.2
1. Представить функцию f(x1,x2,x3,x4,x5) декомпозицией
вида g(xi,xk,xp,h(xi,xm,xn)), где xixkxpxixmxn —некоторая
перестановка переменных x1,x2,x3,x4,x5.
2. Реализовать найденную декомпозицию схемой с ветвлениями, используя функциональные элементы типа отрицание, конъюнкция и дизъюнкция. Указать сложность полученной схемы.
3. Построить минимальную ДНФ с помощью карт Карнау,
указать сложность найденной формулы.
Таблица 2.6.2
| № | i | f(x1,x2,x3,x4,x5) | |||||||
| 1 | 1 | 1-01 | 1101 | 10– | 1-0- | 1-1- | 111- | 000- | -011 |
| 2 | 2 | 1-1- | 00-0 | -001 | -001 | –0- | 11-0 | 01-1 | 0-01 |
| 3 | 3 | 110- | 01-0 | 1-11 | 0-00 | 1-11 | 011- | 111- | 011- |
| 4 | 4 | -011 | -000 | -111 | -000 | 1-10 | 100- | 11-0 | -001 |
| 5 | 5 | 0-10 | -000 | 10-0 | 01-1 | 0010 | -11- | –11 | -11- |
| 6 | 1 | -001 | –01 | 1-01 | -101 | –11 | 1–1 | 00-0 | 001- |
| 7 | 2 | -11- | 0-00 | 0–1 | -00- | 00-0 | -10- | -101 | -10- |
| 8 | 3 | -1-0 | 010- | 11– | 01-0 | 11– | 0110 | –11 | 0110 |
| 9 | 4 | 0-1- | 00– | 01-1 | 0-00 | 10– | 10-1 | 1-1- | 100- |
| 10 | 5 | -010 | -00- | -1– | 0101 | -01- | 0-11 | -1-1 | 1–1 |
| 11 | 1 | 10– | 11-1 | -001 | 1-01 | -1-1 | 11-1 | 0-0- | 0-11 |
| 12 | 2 | –11 | 00-0 | -001 | 0001 | –00 | 1-00 | 010- | -101 |
| 13 | 3 | 1-00 | -100 | 1-11 | 01-0 | 1-1- | 011- | 1–1 | 0-10 |
| 14 | 4 | –11 | 00-0 | 011- | -00- | 1010 | -001 | -110 | -0-1 |
| 15 | 5 | 00-0 | 00-0 | 1010 | 0-01 | 0-10 | -111 | 1-11 | –1- |
| 16 | 1 | -00- | 1-01 | -0-1 | 110- | 111- | 11-1 | 000- | 0–1 |
| 17 | 2 | 111- | 00-0 | 0-0- | 000- | 000- | 1-00 | -101 | 0-0- |
| 18 | 3 | -10- | 01-0 | 1-11 | 0-00 | 1-11 | –10 | 111- | 0110 |
| 19 | 4 | 001- | -000 | -111 | 00-0 | 101- | 1001 | 1-1- | 1001 |
| 20 | 5 | 0-1- | 000- | 101- | 01-1 | 00-0 | 01-1 | 11-1 | 111- |
| 21 | 1 | 10-1 | 110- | 1-01 | -101 | -111 | -11- | 0-00 | 0011 |
| 22 | 2 | -1-1 | 0-0- | -0– | 0001 | -0-0 | 1100 | -1-1 | 0101 |
| 23 | 3 | 1100 | -10- | -111 | 010- | -1-1 | 0-10 | 1-11 | -1-0 |
| 24 | 4 | 0-11 | -000 | 0-11 | 0-00 | 1-10 | 10-1 | 111- | 10-1 |
| 25 | 5 | -01- | 0-00 | -0-0 | 0-01 | -01- | 0–1 | 1-11 | 1-11 |
| 26 | 1 | 1001 | 11-1 | 1-01 | –0- | 1-11 | 1-1- | 0-00 | 0-1- |
| 27 | 2 | 111- | 0-00 | 0-01 | 0-01 | 00– | 110- | 0101 | 01-1 |
| 28 | 3 | -100 | 01– | 1111 | 010- | 1-1- | 01-0 | 1111 | 0-10 |
| 29 | 4 | 001- | 0000 | 01-1 | 00-0 | 10-1 | 1001 | –1- | 10-1 |
| 30 | 5 | 0-10 | 00– | 101- | 01-1 | 001- | 0111 | -1-1 | 111- |
Пример решения задания 2.6.2
Решим задание 2.6.2 для i = 5 и функции
f(x1,x2,x3,x4,x5) = (10-10–0 –01 -1– 0-10 010- 1–0 –1-).
Выпишем значения функции f в виде таблицы (табл. 2.6.2а):
Выясним, возможна ли декомпозиция вида
f = g(x5,x1,x2,h(x5,x3,x4)) (*)
или
f = g(x5,x3,x4,h(x5,x1,x2)). (**)
Для этого выпишем двумерные таблицы функции f для
х5 = 0 и x5 = 1 так, чтобы в заголовках строк и столбцов были
написаны наборы х1х2 и х3х4 соответственно. Получим
(табл. 2.6.2b).
Как видим, таблица функции f, соответствующая х5 = 0, не
доопределима так, чтобы использовались столбцы только двух
типов, и не доопределима до вида, в котором используются строки только двух типов. Значит, декомпозиция вида (*) или (**)
невозможна.
Проверим, допустима ли декомпозиция вида
f = g(x5,x2,x3,h(x5,x1,x4)) или f = g(x5,x1,x4,h(x5,x2,x3)).
Для этого выпишем двумерные таблицы функции f для
х5 = 0 и х5 = 1 так, чтобы в заголовках строк и столбцов были написаны наборы х2х3 и х1х4 соответственно. Получим (табл. 2.6.2с).
Видим, что в этом случае обе таблицы допускают доопределение до столбцов двух типов.
Для х5 = 0 столбцам I типа соответствует функция
φ(0)(x2,x3) = (1001) = x2, x3 ∨ x2,x3, а столбцу II типа — функция
Ψ(0)(x2,x3) = (0101) = x2.
Введём функцию
Вектор значений h(0)(x1,x4) равен (1101), значит.
h(0)(x1,x4) = x1,x4
f(x1,x2,x3,x4,0) = h(0)(x1,x4) ⋅ φ(0)(x2,x3) ∨ h(0)(x1,x4) ⋅ Ψ(0)(x2,x3) =
= (x1,x4)(x2,x3 ∨ x1 ∨ x4⋅ x2
Рассмотрим таблицу, соответствующую х5 = 1.
Столбцам I типа соответствует функция
φ(1)(x2,x3) = (0101) = хx3, столбцам II типа — функция
Ψ(1)(x2,x3) = (1110) = x2 ∨ x3.
Введём функцию
Вектор значений h(1)(x1,x4) равен (1001), значит,
h(1)(x1,x4) = x1,x4 ∨ x1,x4.
f(x1,x2,x3,x4,1) = h(1)(x1,x4) ⋅ φ(1)(x2,x3) ∨ h(1)(x1,x4) ⋅ Ψ(1)(x2,x3) =
=(x1,x4 ∨ x1,x4)x3 ∨ x1,x4 ∨ x1,x4 ⋅ x2 ∨ x3.
Получаем искомое представление для f:
f(x1,x2,x3,x4,x5) =x5 ⋅ f(x1,x2,x3,x4,0) ∨ x5 ⋅ f(x1,x2,x3,x4,1)
= x5((x1 ∨ x4)(x2x3 ∨ x2,x3) ∨ x1 ∨ x4 ⋅ x2) ∨ x5((x1x4 ∨ x1x4)x3 ∨ x1,x4 ∨ x1,x4 ⋅(x2 ∨ x3)).
2. Реализуем это представление схемой с ветвлениями.
Ввиду громоздкости полученного выражения реализуем
схемами S0 (рис. 2.6.2, а) и S1 (рис. 2.6.2, b) соответственно f(x1,x2,x3,x4,0) иf(x1,x2,x3,x4,1), а саму функцию реализуем блок-схемой S (рис. 2.6.2, с).
Сложность построенной схемы равна 24.
|
3. Найдём минимальную ДНф Все единицы карты Карнау x3 ⋅ x5 ∨ x2 ⋅ x3 ⋅ x4 ⋅ x5 ∨ x1 ⋅ x2 ⋅ x3 ⋅ x5 ∨ x1 ⋅ x4 ⋅ x5 ∨ x1 ⋅ x2 ⋅ x5 Её сложность равна 16. |
 |
Задание 2.6.3
1. С помощью частных производных найти оптимальный для
метода каскадов порядок дизъюнктивного разложения функции
f(x,y,z,w) по её переменным на первых двух этапах.
2. Используя результаты п. 1, построить контактную схему методом каскадов, указать сложность построенной контактной схемы.
Таблица 2.6.3
| № | f(x,y,z,w) | № | f(x,y,z,w) | |
| 1 | 1110 0110 1010 1101 | 16 | 0111 0101 1101 1111 | |
| 2 | 0011 1100 1101 0111 | 17 | 0010 1011 1101 1110 | |
| 3 | 0110 1101 1100 1111 | 18 | 0011 1110 1101 0000 | |
| 4 | 1110 0111 1100 0111 | 19 | 0101 1010 1111 1101 | |
| 5 | 0010 1110 1111 0011 | 20 | 0101 1101 1110 0011 | |
| 6 | 1110 1101 0010 1111 | 21 | 0010 1101 1001 0110 | |
| 7 | 1110 1010 0010 0110 | 22 | 1110 1101 0101 1010 | |
| 8 | 1110 1000 1111 0110 | 23 | 0010 1010 1110 1111 | |
| 9 | 1101 0110 1110 0001 | 24 | 0110 1001 1100 1101 | |
| 10 | 1011 0111 1010 0110 | 25 | 0010 0000 1000 1110 | |
| 11 | 1101 0001 0010 1111 | 26 | 0010 1010 0001 1111 | |
| 12 | 1110 0100 1110 1001 | 27 | 0101 1101 0000 1011 | |
| 13 | 0001 1000 1100 0110 | 28 | 1101 1000 0110 1110 | |
| 14 | 1101 1111 0010 1101 | 29 | 1000 0110 0101 1001 | |
| 15 | 1001 1101 0011 1000 | 30 | 1101 0111 1101 0011 |
|
Пример решения задания 2.6.3 Решим задание 2.6.3 для Запишем таблицу функции |
 |
Найдём полином Жегалкина:
|
Определим оптимальный для метода каскадов порядок разложения. По определению, fx(x,y,z,w) = f(0,y,z,w) + f(1,y,z,w). Таблица для fx имеет вид (табл. 2.6.3b). Видим, что | fx |= 6. Аналогично, fy(x,y,z,w) = f(x,0,z,w) + f(x,1,z,w). Таблица для fy имеет вид Видно, что | fy |= 6. Продолжаем отыскание частных производных. fy (x,y,z,w) = f(x, у,0, w) + f(x,y,1, w). Таблица для fz, имеет вид (Табл. 2.6.3d). Заметим, что | fz |= 2. И далее, fw(x,y,z,w) = f(x, у, z,0) + f(x, у, z,1). Таблица для fw имеет вид (табл. 2.6.3е). |
 |
Как видно, | fw |= 6.
Так как набольшее число единиц в таблице имеют fx, fy
и fw, то на 1 и 2 этапах метода каскадов разложение ведём по
любой из переменных x,y,w. Выберем, например, в качестве первой переменной, по которой будем проводить разложение, х,
а второй — w.
Получим: f(x,y,z,w) = x ⋅ f(0,y,z,w) ∨ х ⋅ f(1,y,z,w).
Выпишем таблицы функций f(0,y,z,w) и f(1,y,z,w)
(табл. 2.6.3f).
|
3. Строим контактную схему методом каскадов (рис. 2.6.3, а). На втором этапе разложение ведём по переменной w. |
 |
f0(y,z,w) = w ⋅ f0(y,z,0) ∨ w ⋅ f0(y,z,1) =
= w ⋅ (1 + y + 0 +0) ∨ w ⋅ (1 + y + 1 +yz) =
= w ⋅ (1 + y) ∨ w ⋅ (y + yz) = w ⋅ y ∨ w ⋅ y ⋅ (1 + z) = w ⋅ y ∨ w ⋅ y ⋅ z.
f1(y,z,w) = w ⋅ f1(y,z,0) ∨ w ⋅ f1(y,z,1) =
= w ⋅ (y + 0) ∨ w ⋅ (y+1+z+yz) = w ⋅ y ∨ w ⋅ f11(y,z).
Осталось разложить функцию f11(y,z)
f11(y,z) = z ⋅ f11(y,0) ∨ z ⋅ f11(y,1) = z ⋅ (y+1) ∨ z ⋅ (y+1+1+y) =
z ⋅ y ∨ z ⋅ 0 = z ⋅ y.
Изобразим полученную контактную схему (рис. 2.6.3, b).
Сложность построенной схемы равна количеству контактов
в ней, т. е. 8.
Задание 2.6.4
Для функции f(x,y,z,t), заданной своей ДНФ:
- Построить таблицу данной булевой функции.
- Найти минимальную ДНФ. Исходя из минимальной ДНФ,
построить контактную схему. - Построить контактную схему методом каскадов, отыскав
оптимальный порядок разложения переменных с помощью частных производных. - Исходя из простейшей контактной схемы, построить минимальный тест для нахождения неисправности:
а) для вариантов с чётными номерами — типа замыкания
ровно одного контакта
б) для вариантов с нечётными номерами —типа размыкания
ровно одного контакта.
Таблица 2.6.4
| № | f(x,y,z,t) | № | f(x,y,z,t) | |
| 1 | xyz ∨ xyz ∨ xyzt ∨ yzt | 4 | xyzt ∨ xzt ∨ xyzt | |
| 2 | xyzt ∨ xzt ∨ xyzt ∨ xzt ∨ yz | 5 | xyzt ∨ xyzt ∨ xzt | |
| 3 | xyzt ∨ xyzt ∨ xyzt ∨ xzt | 6 | xzt ∨ xyzt ∨ yzt | |
| 7 | xyzt ∨ xyt ∨ xyzt ∨ xyt zt | 19 | xyz ∨ yzt ∨ xyzt | |
| 8 | xyz ∨ xyt ∨ xyzt | 20 | xyzt ∨ xyzt ∨ xyzt ∨ yzt | |
| 9 | xyzt ∨ xyzt ∨ xyt | 21 | xyt ∨ xyt ∨ xyzt yzt | |
| 10 | xyzt ∨ xyzt ∨ xyzt ∨ xyt | 22 | xyzt ∨ xzt ∨ xyzt yzt | |
| 11 | xzt ∨ xyt ∨ xzt ∨ xyzt | 23 | xyzt ∨ xyz ∨ xyzt | |
| 12 | xyzt ∨ xyz ∨ xyzt ∨ xyz ∨ xt | 24 | xyzt ∨ xyzt ∨ yzt | |
| 13 | xyzt ∨ xyz ∨ xyzt | 25 | xyzt ∨ xyzt ∨ xyzt ∨ yzt | |
| 14 | xyzt ∨ xyzt ∨ xyz | 26 | xzt ∨ xzt ∨ xyzt ∨ yzt | |
| 15 | xyzt ∨ xyzt ∨ xyz ∨ xyzt | 27 | xyzt ∨ xyt ∨ xyzt ∨ xyt ∨ yz | |
| 16 | xyt ∨ xyz ∨ xyzt xyt | 28 | xyzt ∨ yzt ∨ xyzt | |
| 17 | xyzt ∨ yzt ∨ xyzt ∨ xyz ∨ xy | 29 | xyzt ∨ xyzt ∨ xzt | |
| 18 | xyzt ∨ yzt ∨ xyzt | 30 | xyzt ∨ xyzt ∨ xyzt ∨ xyz |
|
Пример решения задания 2.6.4 Решим задание 2.6.4 для f(x,y,z,t) = x yzt ∨ xy ∨ xyt ∨ xzt, выбрав в п. 4 неисправность 1. Построим таблицу функции 2. Все единицы карты Карнау покрываем тремя прямоугольниками. Соответствующая минимальная Упростим формулу: yzt ∨ xt ∨ xz = yzt ∨ x(t ∨ z). Реализуем это представление контактной схемой (рис. 2.6.4, а). 3. При отыскании оптимального порядка | fx | = 6,| fy | = 2, | fz | = 2, | ft | = 2. |
  |
Так что на первом шаге разложение будем производить по
переменной х, а на втором этапе можно проводить разложение
по любой оставшейся переменной, например, по у.
Получаем:
f(x, у, z, t) = x ⋅ f(0, у, z, t) ∨ x ⋅ f(1, у, z,t) =
= x ⋅ (yzt) ∨ х ⋅ (y ∨ ytv zt) =
= хyzt ∨ х ⋅ (у ∨ t ∨ zt) = xyzt ∨ x ⋅ (y ∨ t ∨ z).
Разложение по у нет необходимости делать.
Строим контактную схему (рис. 2.6.4, b).
4. Так как контактная схема, полученная в п. 2, имеет более
простой вид, будем работать с ней.
Занумеруем все контакты схемы (рис. 2.6.4, с).
Неисправность типа размыкания контакта означает, что при
любых значениях аргументов соответствующий контакт разомкнут, т. е. реализует функцию 0. Разомкнутый контакт будем изображать пунктирной линией, а. замкнутый — сплошной. Для каждого из единичных наборов функции на соответствующем изображении контактной схемы полюсы соединены цепью контактов из сплошных линий. На каждом же из нулевых наборов
функции такой цепи не найдётся.
Пусть f0(x,y,z,t) = f(x,y,z,t), а при неисправности i-го контакта схема реализует функцию fi(x, у, z,t).
Если исправно работающая контактная схема на некотором
наборе аргументов принимает значение 0, значит, на её изображении между полюсами нет цепи из сплошных линий. Ясно, что
при наличии неисправности типа размыкания контакта на том же
наборе аргументов полюсы контактной схемы тем более не соединены цепью из сплошных линий. Значит, на всех нулевых наборах функции f(x,y,z,t) все функции fi(x,y,z,t), i = 1,2,…,6
также принимают значение, равное 0.
|
При построении теста нас не интересуют наборы аргументов, При заполнении таблицы для каждого набора аргументов изобразим схему. Например, для набора (0,0,1,0) |
 |
Видим, что цепь из сплошных линий, соединяющая полюсы схемы, разрывается, если разомкнут 4, 5 или 6 контакт, т. е. на наборе
(0,0,1,0) значение 0 принимают функции f4, f5 и f6. Изобразим
вид контактной схемы на всех единичных наборах функции
f(x,y,z,t) (рис. 2.6.4, е).
Заполняем “таблицу неисправностей”, вписывая для каждого
набора аргументов нули в столбцы, соответствующие функциям с
номерами, записанными в кружочках. Получим следующую таблицу (табл. 2.6.4b).
Таблица 2.6.4b
| xyzt | f0 | f1 | f2 | f3 | f4 | f5 | f6 |
| 0100 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1000 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1001 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1010 | 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1011 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1100 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1101 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1111 | 1 | 0 | 1 | 0 | 1 | 1 | 1 |
Видим, что некоторые столбцы таблицы совпадают. Это означает, что неисправности типа размыкания одного контакта неотличимы в случае разомкнутости 4, 5 или 6 контактов.
Объединяем неотличимые неисправности в классы неисправностей.
Получим 5 классов:
g0 = {f0}, g1 = {f1}, g2 = {f2}, g3 = {f3}, g4 = {f4, f5, f6}.
Строим таблицу классов неисправностей, таблицу, не содержащую одинаковых столбцов.
Отметим, что если в таблице присутствуют одинаковые строки, то мы ничего не потеряем, если для каждого набора одинаковых строк оставим одного представителя, удалив остальные
строки из таблицы.
Получим (табл. 2.6.4с):
|
Выясним, какие из наборов 1-5 войдут в минимальный тест. Для этого выпишем все сочетания индексов |
 |
Упростим полученное выражение, применяя формулу поглощения.
Получим: КT = 2⋅5⋅(1∨4).
С помощью дистрибутивного закона преобразуем это выражение в ДНФ, тогда каждой символической конъюнкции будет соответствовать минимальный тест. Имеем:
КT = 2⋅5⋅(1∨4) = 2⋅5⋅1∨2⋅5⋅4
В качестве минимального теста можно взять, например, совокупность 1, 2 и 5 наборов, т. е. найден минимальный тест
Tmin = { (0,1,0,0), (1,0,0,0), (1,1,1,1)}.
Задание 2.6.5
1. Построить таблицу значений функции, реализуемой данной
контактной схемой.
2. Найти минимальную ДНФ с помощью карты Карнау,
построить на её основе контактную схему, равносильную исходной.
Таблица 2.6.5
| 1 |  |
| 2 |  |
| 3 |  |
| 4 |  |
| 5 |  |
| 6 |  |
| 7 |  |
| 8 |  |
| 9 |  |
| 10 |  |
| 11 |  |
| 12 |  |
| 13 |  |
| 14 |  |
| 15 |  |
| 16 |  |
| 17 |  |
| 18 |  |
| 19 |  |
| 20 |  |
| 21 |  |
| 22 |  |
| 23 |  |
| 24 |  |
| 25 |  |
| 26 |  |
| 27 |  |
| 28 |  |
| 29 |  |
| 30 |  |
Пример решения задания 2.6.5
|
Решим задание 2.6.5 для Рассмотрим вид контактной схемы на всех 8 наборах Рассмотрим набор (0,0,0). |
 |
Рассмотрим изображение схемы на остальных наборах:
| f(0,0,1) = 0 |  |
| f(0,1,0) = 1 |  |
| f(0,1,1) = 1 |  |
| f(1,0,0) = 1 |  |
| f(1,0,1) = 1 |  |
| f(1,1,0) = 1 |  |
| f(1,1,1) = 0 |  |
|
Запишем найденные значения функции Минимальная ДНФ: ху ∨ xz ∨ ху. Преобразуем формулу: ху ∨ xz ∨ ху = Задание выполнено. |
 |
Закон одинарных элементов
Этот закон непосредственно следует из приведенных выше выражений аксиом алгебры логики (таблицы истинности логических
элементов). Верхние два выражения могут быть полезны при построении коммутаторов, ведь подавая на один из входов элемента
«2И» логический ноль или единицу можно либо пропускать сигнал на выход, либо формировать на выходе нулевой потенциал.
Второй вариант использования этих выражений заключается в возможности избирательного обнуления определённых разрядов
многоразрядного числа. При поразрядном применении операции «И» можно либо оставлять прежнее значение разряда, либо
обнулять его, подавая на соответствующие разряды единичный или нулевой потенциал. Например, в восьмиразрядном двоичном
числе требуется обнулить 6, 3 и 1 разряды. Тогда, при выполнении операции поразрядного логического умножения получим:
В приведенном примере отчетливо видно, что для обнуления необходимых разрядов в маске (нижнее число) на месте соответствующих
разрядов записаны нули (не забываем, что счет начинается с нулевого разряда), в остальных разрядах записаны единицы. В исходном
числе (верхнее число) на месте 6 и 1 разрядов находятся единицы. После выполнения операции «И» на этих местах появляются нули.
На месте третьего разряда в исходном числе находится ноль. В результирующем числе на этом месте тоже присутствует ноль.
Остальные разряды исходного числа, как и требовалось по условию задачи, не изменены.
Записывать логические единицы в нужные нам разряды многоразрядного двоичного числа можно точно таким же образом. В этом
случае необходимо воспользоваться нижними двумя выражениями закона одинарных элементов. При поразрядном применении операции
«ИЛИ» можно либо оставлять прежнее значение разряда, либо заносить в него единичное значение, подавая на соответствующие
разряды нулевой или единичный потенциал. Пусть требуется записать единицы в 7 и 6 биты восьмиразрядного числа.
Тогда, при выполнении операции поразрядного логического суммирования исходного числа с маской устанавливаемых бит, получим:
Логические основы работы компьютера
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Логический элемент «НЕ» (инвертор)
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.
Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «И» (конъюнктор)
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.
Проверь соответствие логического элемента «И» логическому элементу «И». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «ИЛИ» (дизъюнктор)
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ». Воспользуйся тренажером Логические элементы.xlsx
Пример 1.Составьте логическую схему для логического выражения: F=A / B / A.
1.Две переменные – А и В.
2.Две логические операции: 1-/, 2-/.
3.Строим схему:
Пример 2.Постройте логическую схему, соответствующую логическому выражению F=А/В/ ¬(В/А). Вычислить значения выражения для А=1,В=0.
1.Переменных две: А и В; 1 4 3 2
2.Логических операций три: / и две /; А/В/ ¬ (В/ А).
3.Схему строим слева направо в соответствии с порядком логических операций:
4. Вычислим значение выражения: F=1 / 0 / ¬(0 / 1)=0
1.1 Основные понятия и определения
Алгебра логики (алгебра высказываний) – раздел математической логики, изучающий строение (форму, структуру) сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
При этом под высказыванием (суждением) понимают повествовательное предложение, относительно которого можно сказать, истинно или ложно.
Алгебра логики возникла в середине ХIХ века в трудах английского математика Джорджа Буля. Её создание представляло собой попытку решать традиционные логические задачи алгебраическими методами.
Долгое время алгебра логики была известна достаточно узкому классу специалистов. Прошло почти 100 лет со времени создания алгебры логики Дж. Булем, прежде чем в 1938 Клод Шеннон (1916 — 2001) показал, что алгебра логики применима для описания самых разнообразных процессов, в том числе функционирования релейно-контактных и электронно-ламповых схем.
Алгебра логики явилась математической основой теории электрических и электронных переключателей схем, используемых в ЭВМ. В компьютерных науках её предпочитают называть не алгеброй логики, а Булевой алгеброй — по имени её создателя.
Алгебра логики изучает свойства функций, у которых и аргументы, и значения принадлежат заданному двухэлементному множеству (например, {0,1}). Иногда вместо термина «алгебра логики» употребляют термин «двузначная логика».
В компьютерах булевы переменные представляются (кодируются) битами (разрядами двоичной системы счисления), где 1 означает истину, а 0 — ложь. Манипуляции высказываниями и их комбинациями используются для получения некоего единственного результата, который можно использовать, например, для выбора той или иной последовательности действий. Поскольку логические переменные кодируются по тем же принципам, что и числа, символы и прочая информация, то можно комбинировать операции логики с
операциями арифметики для реализации различных алгоритмов.
Таким образом, алгебра логики — это область математики. Она оперирует величинами, которые могут принимать два значения (булевых значения). Эти два значения могут быть обозначены как угодно, лишь бы по-разному. Самые распространенные варианты:
0, 1 F, T false, true ложь, истина Л, И
При применении булевой алгебры в вычислительной технике, булевы значения — это 0 и 1. Они представляют собой состояние ячейки памяти объёмом в 1 бит или наличие/отсутствие напряжения в электрической схеме. Алгебра логики позволяет строить сложные электронные узлы, элементы которых работают согласно этой математической теории. При применении булевой алгебры в логических построениях в математике, булевы значения — это «ложь» и «истина». Они определяют истинность или ложность некоторого высказывания. Под высказываниями понимаются математические формулы. При применении булевой алгебры в повседневных рассуждениях, булевы значения — это также «ложь» и «истина». Они представляют собой оценку истинности или ложности некоторого высказывания. Под высказываниями понимаются фразы, которые удовлетворяют строго определенному списку свойств.
Логическое выражение — это символическая запись, состоящая из логических величин (констант или переменных), объединенных логическими операциями (связками). В булевой алгебре простым высказываниям ставятся в соответствие логические переменные, значение которых равно 1, если высказывание истинно, и 0, если высказывание ложно. Обозначаются логические переменные буквами латинского алфавита.
Связки «НЕ», «И», «ИЛИ» заменяются логическими операциями инверсия, конъюнкция, дизъюнкция. Это основные логические операции, при помощи которых можно записать любое логическое выражение.
5.12. Что такое переключательная схема?
В компьютерах и других автоматических устройствах широко применяются
электрические схемы, содержащие сотни и тысячи переключательных элементов:
реле, выключателей и т.п. Разработка таких схем весьма трудоёмкое дело.
Оказалось, что здесь с успехом может быть использован аппарат алгебры
логики.
Переключательная схема это схематическое изображение
некоторого устройства, состоящего из переключателей и соединяющих их
проводников, а также из входов и выходов, на которые подаётся и с которых
снимается электрический сигнал.
Каждый переключатель имеет только два состояния: замкнутое и
разомкнутое.
Переключателю Х поставим в соответствие логическую переменную х,
которая принимает значение 1 в том и только в том случае, когда переключатель
Х замкнут и схема проводит ток; если же переключатель разомкнут, то
х равен нулю.
Будем считать, что два переключателя Х и связаны таким образом, что когда Х замкнут,
то разомкнут, и наоборот.
Следовательно, если переключателю Х поставлена в соответствие логическая
переменная х, то переключателю должна соответствовать переменная .
Всей переключательной схеме также можно поставить в соответствие
логическую переменную, равную единице, если схема проводит ток, и равную
нулю если не проводит. Эта переменная является функцией от
переменных, соответствующих всем переключателям схемы, и называется
функцией проводимости.
Найдем функции проводимости F некоторых переключательных схем:
- a)
- Схема не содержит переключателей и проводит ток всегда, следовательно
F=1; - б)
- Схема содержит один постоянно разомкнутый контакт, следовательно
F=0; - в)
- Схема проводит ток, когда переключатель х замкнут, и не проводит, когда
х разомкнут, следовательно, F(x) = x; - г)
- Схема проводит ток, когда переключатель х разомкнут, и не проводит,
когда х замкнут, следовательно, F(x) = ; - д)
- Схема проводит ток, когда оба переключателя замкнуты, следовательно,
F(x) = x . y; - е)
- Схема проводит ток, когда хотя бы один из переключателей замкнут,
следовательно, F(x)=x v y; - ж)
- Схема состоит из двух параллельных ветвей и описывается функцией
.
Две схемы называются равносильными, если через одну
из них проходит ток тогда и только тогда, когда он проходит через другую
(при одном и том же входном сигнале).
Из двух равносильных схем более простой считается та
схема, функция проводимости которой содержит меньшее число логических
операций или переключателей.
Задача нахождения среди равносильных схем наиболее простых является очень
важной. Большой вклад в ее решение внесли российские учёные Ю.И
Журавлев,
С.В. Яблонский и др.
При рассмотрении переключательных схем возникают две основные задачи:
синтез и анализ схемы.
СИНТЕЗ СХЕМЫ по заданным условиям ее работы сводится к следующим
трём этапам:
- составлению функции проводимости по таблице истинности, отражающей эти
условия; - упрощению этой функции;
- построению соответствующей схемы.
АНАЛИЗ СХЕМЫ сводится к
- определению значений её функции проводимости при всех возможных
наборах входящих в эту функцию переменных. - получению упрощённой формулы.
Примеры.
1. Построим схему, содержащую 4
переключателя x, y, z и t, такую, чтобы она проводила ток тогда и только
тогда, когда замкнут контакт переключателя t и какой-нибудь из остальных
трёх контактов.
Решение. В этом случае можно обойтись без построения таблицы
истинности. Очевидно, что функция проводимости имеет вид
F(x, y, z, t) = t . (x v y v z), а схема
выглядит так:
2. Построим схему с пятью
переключателями, которая проводит ток в том и только в том случае, когда
замкнуты ровно четыре из этих переключателей.
Схема имеет вид:
3. Найдем функцию проводимости схемы:
Решение. Имеется четыре возможных пути прохождения тока при
замкнутых переключателях a, b, c, d, e : через переключатели a, b; через
переключатели a, e, d; через переключатели c, d и через переключатели
c, e, b. Функция проводимости F(a, b, c, d, e) =
a . b v a . e . d v
c . d v c . e . b.
4. Упростим переключательные схемы:
а)
Решение:
Упрощенная схема:
б)

Здесь первое логическое слагаемое является отрицанием второго логического слагаемого
, а дизъюнкция
переменной с ее инверсией равна 1.
Упрощенная схема :
в)
Упрощенная схема:
г)
Упрощенная схема:
д)
(по закону склеивания)
Упрощенная схема:
е)
Решение:
Упрощенная схема:
Пример решения задачи
РКС нужны, чтобы упрощать цепи, избавляться от лишнего, но при этом не терять функциональности устройства. В СССР делали радиоприёмники, в которых можно было избавиться от некоторых деталей, находящихся внутри, но при этом остаться с работающим устройством.Итак, нам нужно уметь:
- Нарисовать схему по имеющейся формуле;
- Упростить данную формулу, чтобы затем нарисовать упрощенную схему.
Есть следующее логическое выражение:
Соответственно, схема, исходя из этих данных, будет выглядеть вот так:
Выглядит относительно сложно. Нужно это дело уметь упрощать. Для этого понадобятся навыки упрощения логических выражений. Об этом есть отдельная статья со ссылкой во введении. Упростим нашу формулу, и она станет выглядеть так:
Теперь изобразим по упрощенному выражению схему.
На этом всё. Если устанете разбираться, оформляйте заказ, мы будем рады вам помочь. Можете так же ознакомиться с неплохим видеороликом по данной теме.
Однако не забывайте, что если вы самостоятельно постигли какое-либо знание, оно останется в голове намного дольше и принесёт двукратную пользу, нежели если вам всё преподнесут в готовом виде педагоги и сторонние люди.
ЗАКАЗАТЬ РЕШЕНИЕ ЗАДАЧ ПО РКС
Задача о минимизации контактной схемы[править]
| Определение: |
| Две контактные схемы называются эквивалентными (англ. equivalent contact circuits), если они реализуют одну и ту же булеву функцию. |
| Определение: |
|
Сложностью контактной схемы (англ. the complexity of the contact circuit) называется число ее контактов. |
| Определение: |
| Минимальная контактная схема (англ. minimal contact circuit) — схема, имеющая наименьшую сложность среди эквивалентных ей схем. |
| Определение: |
| Дерево конъюнктов для переменных — двоичное ориентированное дерево глубиной , такое что: поддеревья на одном и том же уровне одинаковы; и левое ребро любого узла помечено символом переменной , а правое помечено символом отрицания переменной . |
Задача минимизации контактных схем состоит в том, чтобы по данной схеме найти схему , эквивалентную и имеющую наименьшую сложность.
Один из путей решения этой задачи состоит в следующем:
- Осуществляем переход от контактной схемы к её булевой функции .
- Упрощаем , то есть отыскиваем функцию (на том же базисе, что и , равносильную и содержащую меньше вхождений операций дизъюнкции и конъюнкции. Для этой операции удобно использовать карты Карно.
- Строим схему , реализующую функцию .
| Теорема: |
| Любую булеву функцию можно представить контактной схемой, сложностью |
| Доказательство: |
|
Пусть дана функция и она представлена в ДНФ Дерево конъюнктов для 2-х переменных Возьмем дерево конъюнктов для переменных (см. картинку). Очевидно, что от вершины до «нижних» вершин дерево можно добраться за , а ребер у такого дерева Соединим нижние вершины, которые соответствуют конъюнктам функции, с вершиной контактами, над которыми написана . От этого в схему добавится не более, чем ребер и тогда сложность останется . В результате можно построить контактную схему для любой функции со сложностью |
1.4. Применение алгебры логики в информатике
После изготовления первого компьютера стало ясно, что при его производстве возможно использование только цифровых технологий – ограничение сигналов связи единицей и нулём для большей надёжности и простоты архитектуры компьютера. Благодаря своей бинарной природе, математическая логика получила широкое распространение в вычислительной технике и информатике. Были созданы электронные эквиваленты логических функций, что позволило применять методы упрощения булевых выражений к упрощению электрической схемы. Кроме того, благодаря возможности нахождения исходной функции по таблице позволило сократить время поиска необходимой логической схемы.
В программировании логика незаменима как строгий язык и служит для описания сложных утверждений, значение которых может определить компьютер.
Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: «1» и «0».
Из этого следует два вывода:
1) одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
2) на этапе конструирования аппаратных средств алгебра логики позволяет
значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера. Данные и команды представляются в виде двоичных последовательностей различной структуры и длины. Существуют различные физические способы кодирования двоичной информации.
В электронных устройствах компьютера двоичные единицы чаще всего кодируются более высоким уровнем напряжения, чем двоичные нули (или наоборот), например: Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И — НЕ, ИЛИ — НЕ и другие (называемые также вентилями), а также триггер.
С помощью этих схем можно реализовать любую логическую функцию, описывающую работу устройств компьютера. Обычно у вентилей бывает от двух до восьми входов и один или два выхода. Чтобы представить два логических состояния – «1» и «0» в вентилях, соответствующие им входные и выходные сигналы имеют один из двух установленных уровней напряжения. Например, +5 вольт и 0 вольт. Высокий уровень обычно соответствует значению «истина» (1), а низкий — значению «ложь»(0).
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нём реализована. Это упрощает запись и понимание сложных логических схем. Работу логических элементов описывают с помощью таблиц истинности.
Булевы алгебры находят применение главным образом в теории множеств, в математической логике, в теории вероятностей и в функциональном анализе.
Итак, алгебра логики применяется: 1) для упрощения сложных логических формул и доказательств тождеств; 2) при решении логических задач; 3) в контактных схемах; 4) при доказательствах теорем; 5) в базах данных при составлении запросов.
Законы отрицания
Существуют следующие законы отрицания:
Закон дополнительных элементов
Выражения, примененные в этих законах, широко используются для минимизации логических схем. Если удается выделить
из общего выражения логической функции цифрового комбинационного устройства такие подвыражения, то можно сократить
необходимое количество входов логических элементов в составе цифровой схемы, а иногда и вообще свести все выражение
к логической константе.
Закон отрицательной логики (Де Моргана)
Закон отрицательной логики справедлив для любого числа переменных. Этот закон алгебры логики позволяет реализовывать
при помощи логических элементов «ИЛИ» и наоборот: реализовывать
логическую функцию «ИЛИ» при помощи логических элементов «И». Это особенно полезно в ТТЛ схемотехнике, так как там легко
реализовать логические элементы «И», но при этом достаточно сложно логические элементы «ИЛИ». Благодаря закону отрицательной
логики можно реализовывать элементы «ИЛИ» на логических элементах «И». На рисунке 3 показана реализация логического
элемента «2ИЛИ» на элементе «2И-НЕ» и двух инверторах.
1.3. Логические формулы. Законы алгебры логики
Предметом алгебры логики являются высказывания, операции над ними, а также логические функции. При этом для обозначения высказываний используются буквы.
Логическая переменная — переменная, значением которой может быть любое высказывание. Логические переменные обозначаются латинскими буквами, иногда снабжёнными индексами, как обычные алгебраические переменные.
Понятие логической формулы является формализацией понятия сложного высказывания.
Логической формулой является: 1) любая логическая переменная, а также каждая из двух логических констант – 0 (ложь) и 1 (истина). 2) Если А и В – формулы, то В и А*В – тоже формулы, где знак «*» означает любую из логических бинарных операций. Формулой является, например, выражение: (x&y) → z. Каждой формуле при заданных значениях входящих в неё переменных приписывается одно из двух значений – 0 или 1. Формулы А и В, зависящие от одного и того же набора переменных , называют равносильными или эквивалентными, если на любом наборе значений переменных они имеют одинаковые значения. Для обозначения равносильности формул используется знак равенства, например А=В.
Любую формулу можно преобразовать к равносильной ей, в которой используются только аксиоматически введённые операции &, ∨ и отрицание.
С помощью логических переменных и символов логических операций любое высказывание можно формализовать, то есть заменить логической формулой.
Определение логической формулы:
1. Всякая логическая переменная и символы «истина» (1) и «ложь (0) — формулы.
2. Если А и В — формулы, то , АВ, АvВ, А→B, АВ — формулы.
3. Никаких других формул в алгебре логики нет.
Для преобразования формул в равносильные важную роль играют следующие равенства, отражающие свойства логических операций, которые по аналогии с алгеброй вещественных чисел называют законами:
1) Законы коммутативности
х & y = y & x, x ∨ y = y ∨ x;
2) Законы ассоциативности
(x & y) & z = x & (y & z), (x ∨ y) ∨ z = x ∨ (y ∨ z);
3)Законы поглощения (нуля и единицы)
х ∨ 0 = x, x & 1= x;
4) Законы дистрибутивности
х & (y ∨ z) = (x & y) ∨ (x & z), x ∨ (y & z) = (x ∨ y) & (x ∨z);
5) Закон противоречия
х ∨ = 0;
6) Закон исключённого третьего
х ∨ = 1;
7) Закон идемпотентности
х & x = x, x ∨ x = x;

=
9) Законы де Моргана
−−−− −−−−
= , = ,
9) Законы поглощения
х ∨ (x & y) = x, x & (x ∨ y) = x.
Любой из этих законов может быть доказан с помощью таблиц истинности.
Таблица истинности — табличное представление логической схемы (операции), в котором перечислены все возможные сочетания значений истинности входных сигналов (операндов) вместе со значением истинности выходного сигнала (результата операции) для каждого из этих сочетаний. Таблица истинности от n переменных состоит из 2n +1 строк и n +1 столбцов.
Пример. Составить таблицу истинности для функции f трех переменных x1, x2, x3, которая равна единице в случае, если только одна из входных переменных равна 1.
Таблица истинности для функции f
|
Входные переменные |
Выходная переменная |
||
|
х1 |
х2 |
х3 |
f |
|
1 |
1 |
||
|
1 |
1 |
||
|
1 |
1 |
||
|
1 |
1 |
||
|
1 |
1 |
||
|
1 |
1 |
||
|
1 |
1 |
1 |
Переменная х в функции f называется фиктивной (несущественной), если значение переменной х не влияет на значение булевой функции. Фиктивные переменные могут быть удалены или введены в набор переменных функций. Количество булевых функций определяется числом n переменных
Помогла ли вам статья?

Задать вопрос
Пишите ваши рекомендации и задавайте вопросы в комментариях