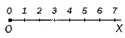
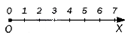
На рисунке изображён луч OE, который разбит на деления, как линейка.
Точка O — начало луча, и этой точке соответствует число 0.
Эта точка — начало отсчёта.
Точке E соответствует число 1, а длина отрезка OE принята за единицу длины и называется единичным отрезком.
Единичный отрезок может содержать разное число клеток.
Каждая следующая точка отстоит от предыдущей на расстояние, равное единице длины.
Луч OE с началом отсчёта в точке O , на котором указаны единичный отрезок и направление, называют координатным лучом.
Число, соответствующее точке координатного луча, называется координатой этой точки.
Пример. Точке A соответствует число 3.
Значит, координата точки A равна 3. Записывается так A (3). Читается: точка A с координатой 3.
Для любого числа можно указать соответствующую ему точку, т. к. луч можно продолжить бесконечно.
Пример #1. Можно ли назвать изображённый луч координатным лучом?
Пример #2. Можно ли назвать изображённый луч координатным лучом?
Пример #3. Определи координату точки C.
Пример #4. Запиши число, стоящее у конца стрелки на рисунке.
Пример #5. Какую температуру показывает термометр, изображённый на рисунке? Какую температуру покажет этот термометр, если столбик опустится на 3 деления?
Пример #6. Запиши наибольшее число единичных отрезков, соответствующих одному делению координатного луча, чтобы можно было отметить числа: 20, 30, 40, 50, 80, 90.
Скольким делениям соответствует число 50?
Пример #7. Определи координату точки B, изображённой на рисунке. Если координата точки O(0), а координата точки C(60).
Пример #8. Определи координаты точек C и B:
Пример #9. Запиши координаты точек A, B и C.
Пример #10. Запиши точку, которой соответствует начало координатного луча на данном рисунке.
Если известно, что координата точки H(35), координата точки L(45) и координата точки N(55).
Пример #11. Составь числовое выражение для координаты точки B и найди его значение:
Пример #12. Изобрази координатный луч, считая, что единичный отрезок равен 2 клеткам тетради. Отметь на нём точку A (2). Скольким клеткам тетради соответствует отмеченная точка?
Пример #13. На рисунке изображена шкала. Какое число соответствует точке D?
Математика
5 класс
Урок № 79
Координатный луч
Перечень рассматриваемых вопросов:
– координатный луч;
– единичный отрезок;
– соотношение единичного отрезка со знаменателем дроби;
– координата точки.
Тезаурус
Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.
Отрезок – часть прямой, ограниченная с двух сторон точками.
Луч – это часть прямой линии, расположенная по одну сторону от любой точки, лежащей на этой прямой.
Обязательная литература
- Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Зададим прямую, на которой указано направление. Отметим на ней точку О. Примем её за начало отсчета.
Отложим на прямой вправо от точки О единичные отрезки.
Единичный отрезок – это расстояние от О до точки, выбранной для измерения.
Обозначим конец первого отрезка числом 1, второго – числом 2 и т. д.
Сформулируем определение.
Прямую с заданными на ней началом отсчёта, единичным отрезком и направлением отсчёта называют координатной осью или координатным лучом.
С помощью координатной прямой натуральные числа изображаются точками.
Точке О на координатной прямой соответствует число 0. Обозначают: О (0).
Число, которое соответствует данной точке на координатной оси, называют координатой данной точки.
Например, точка А имеет координату 5.
Обозначают А (5).
Таким образом, на координатной прямой можно найти точку, соответствующую натуральному числу. Также с помощью натуральных чисел и числа ноль можно указать положение любой точки на прямой.
А теперь рассмотрим, как отметить на координатном луче дробь.
Чтобы удобно было изображать дробные числа, нужно правильно выбрать длину единичного отрезка.
Удобный вариант – взять единичный отрезок из стольких клеточек, каков знаменатель дробей. Например, если требуется изобразить на координатном луче дроби со знаменателем 7, единичный отрезок лучше взять длиной в 7 клеточек. В этом случае изображение дробей на координатном луче будет несложным.
можно изобразить одним единичным отрезком и ещё двумя клеточками.
Если требуется отметить на координатном луче дроби с разными знаменателями, желательно, чтобы число клеточек в единичном отрезке делилось на все знаменатели. Например, для изображения на координатном луче дробей со знаменателями 6, 4 и 12 удобно взять единичный отрезок длиной в двенадцать клеточек. Чтобы отметить на координатном луче нужную дробь, единичный отрезок разбиваем на столько частей, каков знаменатель, и берём таких частей столько, каков числитель.
Возьмём единичный отрезок, разделим на шесть частей и возьмём одну из них.
Тренировочные задания
№ 1. Подберите правильные названия к числам. Разместите нужные подписи под изображениями.
Варианты ответов: смешанное число; правильная дробь; неправильная дробь.
Чтобы правильно выполнить задание, необходимо вспомнить, какую дробь называют правильной, а какую неправильной. А также, что называют смешанным числом.
Правильный ответ:
Варианты ответа: 9; 6; 4; 3; 2
Мы знаем, что удобный вариант – взять единичный отрезок из стольких клеточек, каков знаменатель дробей. Знаменатель равен 9, значит, единичный отрезок следует выбирать в 9 клеток.
Правильный ответ: 9.
5.1. Координатный луч. Единичный отрезок
Натуральные числа можно изображать на луче. Построим луч с началом в точке О, направив его слева – направо, направление отметим стрелкой.
Началу луча (точке О) поставим в соответствие число 0 (ноль). Отложим от точки О отрезок ОА произвольной длины. Точке А поставим в соответствие число 1 (один). Длину отрезка ОА будем считать равной 1 (единице). Отрезок АВ = 1 называется единичным отрезком. Отложим от точки А в направлении луча отрезок АВ = ОА. Поставим точке В в соответствие число 2. Заметим, что точка В находится от точки О на расстоянии в два раза большем, чем точка А. Значит, длина отрезка ОВ равна 2 (двум единицам). Продолжая откладывать в направлении луча отрезки, равные единичному, будем получать точки, которым соответствуют числа 3, 4, 5, и т.д. Данные точки удалены от точки О соответственно на 3, 4, 5, и т.д. единиц.
Луч, построенный таким способом, называется координатным или числовым. Начало числового луча, точка О, называется точкой отсчета. Числа, поставленные в соответствие точкам на этом луче, называются координатами этих точек (отсюда: координатный луч). Пишут: О(0), А(1), В(2), читают: «точка О с координатой 0 (ноль), точка А с координатой 1 (один), точка В с координатой 2 (два)» и т.д.
Любое натуральное число n можно изобразить на координатном луче, при этом соответствующая ему точка P будет удалена от точки О на n единиц. Пишут: ОP = n и P(n) – точка P (читают: “пэ”) с координатой n (читают: “эн”). Например, чтобы отметить на числовом луче точку К(107), необходимо от точки О отложить 107 отрезков, равных единичному. В качестве единичного можно выбрать отрезок любой длины. Часто длину единичного отрезка выбирают такой, чтобы было возможно в пределах рисунка изобразить на числовом луче необходимые натуральные числа. Рассмотрите пример
5.2. Шкала
Важным применением числового луча являются шкалы и диаграммы. Они используются в измерительных приборах и устройствах, при помощи которых измеряют различные величины. Одним из основных элементов измерительных приборов является шкала. Она представляет собой числовой луч, нанесенный на металлическое, деревянное, пластиковое, стеклянное или другое основание. Часто шкала выполнена в виде окружности или части окружности, которые разделены штрихами на равные части (деления-дуги) подобно числовому лучу. Каждому штриху на прямой или круговой шкале поставлено в соответствие определенное число. Это значение измеряемой величины. Например, числу 0 на шкале термометра соответствует температура 00С, читают: «ноль градусов Цельсия». Это температура, при которой начинает таять лед (или начинает замерзать вода).
Используя измерительные приборы и инструменты со шкалами, определяют значение измеряемой величины по положению указателя на шкале. Чаще всего указателем служат стрелки. Они могут перемещаться вдоль шкалы, отмечая значение измеряемой величины (например, стрелка часов, стрелка весов, стрелка спидометра – прибора для измерения скорости, рисунок 3.1.). Подобна смещающейся стрелке граница столбика ртути или подкрашенного спирта в термометре (рисунок 3.1). В некоторых приборах движется не стрелка вдоль шкалы, а шкала перемещается относительно неподвижной стрелки (метки, штриха), например, в напольных весах. В некоторых инструментах (линейка, рулетка) указателем служат границы самого измеряемого предмета.
Промежутки (части шкалы) между соседними штрихами шкалы называются деления. Расстояние между соседними штрихами, выраженное в единицах измеряемой величины, называется ценой деления (разность чисел, которым соответствуют соседние штрихи шкалы.) Например, цена деления спидометра на рисунке 3.1. равна 20 км/ч (двадцать километров в час), а цена деления комнатного термометра на рисунке 3.1. равна 10С (один градус Цельсия).
Диаграмма
Для видимого изображения величин используют линейные, столбчатые или круговые диаграммы. Диаграмма состоит из числового луча-шкалы, направленного слева – направо или снизу – вверх. Кроме того на диаграмме помещены отрезки или прямоугольники (столбцы), изображающие сравниваемые величины. При этом длина отрезков или столбцов в единицах шкалы равна соответствующим величинам. На диаграмме возле числового луча-шкалы подписывают название единиц измерения, в которых отложены величины. На рисунке 3.2. изображена столбчатая диаграмма, а на рисунке 3.3 линейная.
3.2.1. Величины и приборы для их измерения
В таблице приведены названия некоторых величин, а также приборов и инструментов, предназначенных для их измерения. (Жирным шрифтом выделены основные единицы Международной системы единиц).
5.2.2. Термометры. Измерение температуры
На рисунке 3.4 приведены термометры, в которых использованы разные температурные шкалы: Реомюра (°R), Цельсия (°С) и Фаренгейта (°F).В них использован один и тот же температурный интервал – разность температур кипения воды и плавления льда. Этот интервал разделён на различное число частей: в шкале Реомюра – на 80 частей, шкале Цельсия – на 100 частей, в шкале Фаренгейта – на 180 частей. При этом в шкалах Реомюра и Цельсия температуре таяния льда соответствует число 0 (ноль), а в шкале Фаренгейта – число 32. Единицы температуры в этих термометрах: градус по Реомюру, градус по Цельсию, градус по Фаренгейту. В устройстве термометров используется свойство жидкостей (спирта, ртути) расширяться при нагревании. При этом различные жидкости по-разному расширяются при нагревании, что видно на рисунке 3.5, где штрихи для столбика спирта и ртути не совпадают при одинаковой температуре.
5.2.3. Измерение влажности воздуха
Влажность воздуха зависит от количества в нём водяных паров. Например, летом в пустыне воздух сухой, влажность его низкая, так как в нём содержится мало паров воды. В субтропиках, например, в Сочи влажность высокая, в воздухе много водяных паров. Измерить влажность можно с помощью двух термометров. Один из них обычный (сухой термометр). У второго шарик обёрнут влажной тканью (влажный термометр). Известно, что при испарении воды температура тела понижается. (Вспомните озноб при выходе из моря после купания). Поэтому влажный термометр показывает более низкую температуру. Чем суше воздух, тем больше разность показаний двух термометров. Если показания термометров одинаковы (разность равна нулю), то влажность воздуха равна 100 %. В этом случае выпадает роса. Прибор, измеряющий влажность воздуха, называется психрометром (рисунок 3.6). Он снабжён таблицей, в которой приведены: показания сухого термометра, разность показаний двух термометров, влажность воздуха в процентах. Чем ближе влажность к 100%, тем более влажный воздух. Нормальная влажность в помещениях должна быть равна около 60%.
Блок 3.3. Самоподготовка
5.3.1. Заполните таблицу
Отвечая на вопросы таблицы, заполняйте свободную колонку («Ответ»). При этом используйте рисунки приборов в блоке «Дополнительный».
760 мм. рт. ст. считается нормальным. На рисунке 3.11 показано изменение атмосферного давления при подъёме на самую высокую гору Эверест.
Постройте линейную диаграмму изменения давления, отложив на вертикальном луче высоту над уровнем моря, а по горизонтали давление.
Блок 5.4. Проблемный
Построение числового луча с единичным отрезком заданной длины
Для решения этой учебной проблемы работайте по плану, приведенному в левой колонке таблицы, при этом правую колонку рекомендуется закрыть листом бумаги. Ответив на все вопросы, сопоставьте свои выводы с приведёнными решениями.
Блок 5.5. Фасетный тест
Числовой луч, шкала, диаграмма
В задачах фасетного теста использованы рисунки из таблицы. Все задачи начинаются так: «ЕСЛИ числовой луч представлен на рисунке …., то…»
ЕСЛИ: числовой луч представлен на рисунке… Таблица
ТО:
- Количество единиц между соседними штрихами числового луча.
- Координаты точек А, В, С, D.
- Длина (в сантиметрах) отрезков АВ, ВС, АD, ВD соответственно.
- Длина (в метрах) отрезков АВ, ВС, АD, ВD соответственно.
- Натуральные числа, расположенные на числовом луче левее точки D.
- Натуральные числа, расположенные на числовом луче между точками А и С.
- Количество натуральных чисел, лежащих на числовом луче между точками А и D.
- Количество натуральных чисел, лежащих на числовом луче между точками В и С.
- Цена деления шкалы прибора.
- Скорость автомобиля в км/ч, если стрелка спидометра указывает на точки А, В, С, D соответственно.
- Величина (в км/ч), на которую увеличилась скорость автомобиля, если стрелка спидометра переместилась из точки В в точку С.
- Величина скорости автомобиля после того, как водитель уменьшил скорость на 84 км/ч (перед уменьшением скорости стрелка спидометра указывала на точку D).
- Масса груза на весах в центнерах, если стрелка – указатель весов – расположена напротив точек А, В, С соответственно.
- Масса груза на весах в килограммах, если стрелка – указатель весов – расположена напротив точек А, В, С соответственно.
- Масса груза на весах в граммах, если стрелка – указатель весов – расположена напротив точек А, В, С соответственно.
- Количество учеников в 5 классе.
- Разность между количеством учеников, успевающих на «4», и количеством учеников, успевающих на «3».
- Отношение количества учеников, успевающих на «4» и «5», к количеству учеников, успевающих на «3».
РАВНО (равна, равны, это):
а) 10 б) 6,12,3,3 в) 1 г) 99,102,106,104 д) 2 е) 201,202 ж) 49 з) 3500,3000,8000,4500
и) 5,2,1,4 к) 599 л) 6,3,3,9 м) 10,4,16,7 н) 100 о) 4 км/ч п) 65,85,105,115 р) 7,2,4,6 с) 20,20,50,30 т) 0 у) 700,600,1600,900 ф) 1,2,3,4,5,6 х) 25,10,5,20 ц) 3,4,5,2 ч) 203,197,200,206 ш) 15,20,25,10 щ) 1599 ы) 11,12,13,14,15 э) 30,60,15,15 ю) 0,700,1300,1600 я) 100,100,250,150 аа) 30,15,15,45 бб) 4 вв) 1,2,3,4,5 гг) 17 дд) 500 кг ее) 19 жж) 80 зз) 100,101,102,103,104,105 ии)5,6 кк) 28,64,100,164 лл) 1500000,3000000,4500000 мм) 11 нн) 36 оо) 1500,3000,4500 пп) 7 рр) 24 сс) 15,30,45
Блок 5.6. Учебная мозаика
В заданиях мозаики использованы приборы из блока «Дополнительный». Ниже приведено поле мозаики. На нём указаны названия приборов. Кроме того для каждого прибора обозначены: измеряемая величина (В), единица измерения величины (Е), показание прибора (П), цена деления шкалы (Ц). Далее помещены ячейки мозаики. Прочитав ячейку, вы должны сначала определить прибор, к которому она относится, и поставить в окружность ячейки номер прибора. Затем надо догадаться, о чём эта ячейка. Если речь идёт об измеряемой величине, надо к номеру приписать букву В. Если это единица измерения – поставить букву Е, если показание прибора – букву П, если цена деления – букву Ц. Таким образом надо обозначить все ячейки мозаики. Если ячейки вырезать и расположить так, как на поле, то можно систематизировать сведения о приборе. В компьютерном варианте мозаики при правильном расположении ячеек создаётся рисунок.
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.
Координатный луч
Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.
Луч – это геометрическая фигура, которая имеет начало отсчета координатного луча и направление движения. Прямую обычно изображают горизонтально, указывая направление направо.
На примере мы видим, что O является началом луча.
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.
От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку.
Благодаря манипуляциям, которые мы проделали с лучом, он стал координатным. Подпишите штрихи натуральными числами в последовательности от 1 – например, 2, 3, 4, 5…
Координатный луч – это шкала, которая может длиться до бесконечности.
Зачастую его изображают лучом с началом в точке O, и откладывают единственный единичный отрезок. Пример указан на рисунке.
Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.
Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.
Координатная прямая
Принцип изображения координатной прямой практически не отличается от изображения луча. Все просто – прочертите луч и дополните до прямой, придав положительное направление, которое указывается стрелочкой.
Проведите луч в противоположную сторону, дополнив его до прямой
Отложите единичные отрезки по примеру, указанному выше
С левой стороны запишите натуральные числа 1, 2, 3, 4, 5… с противоположным знаком. Обратите внимание на пример.
Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.
Координатная прямая – это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.
Соответствие между точками координатной прямой и действительными числами
Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.
Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.
Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.
Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка. На примере можно подробно рассмотреть данное правило.
Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.
Отмеченные отрезки помогут нам отыскать на координатной прямой необходимую точку. Это могут быть как целые, так и дробные числа. Однако на прямой существуют точки, которые очень сложно найти с помощью единичных отрезков. Этим точкам соответствуют десятичные дроби. Для того, чтобы искать подобную точку, придётся откладывать единичный отрезок, десятую, сотую, тысячную, десятитысячную и другие его доли. Одной точке координатной прямой отвечает иррациональное число π (=3,141592…).
Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.
Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.
Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.
Согласно правилу,
Каждой точке на координатной прямой отвечает действительное число, и каждое действительное число отмечается в виде точки на координатной прямой.
Благодаря этому утверждению координатную прямую зачастую определяют как числовую.
Следует отметить, что знак, стоящий перед числом, зависит от размещения точки на прямой. Точкам, лежащим правее начала отсчета, соответствуют положительные числа, а точкам, лежащим левее, – отрицательные.
Координаты точек на координатной прямой
Число, соответствующее точке на координатной прямой, называется координатой этой точки.
Ранее было отмечено, что к каждому числу относится единственная точка на прямой. Можно сказать, что координата точки определяет ее положение на прямой. Именно координата задает эту точку.
Перед тем, как завершить статью, следует упомянуть о принятых обозначениях координаты точки. Координату принято записывать в круглых скобках справа от буквы, которой обозначена точка. Например, если точка M имеет координату – 6, то можно записать как M(-6) , а запись вида M(53+7) значит, что координатой является 53+7
На рисунке изображён луч (OE), который разбит на деления, как линейка.
Точка (O) — начало луча, и этой точке соответствует число (0).
Эта точка — начало отсчёта.
Точке (E) соответствует число (1), а длина отрезка (OE) принята за единицу длины и называется единичным отрезком.
Единичный отрезок может содержать разное число клеток.
Каждая следующая точка отстоит от предыдущей на расстояние, равное единице длины.
Луч (OE) с началом отсчёта в точке (O), на котором указаны единичный отрезок и направление, называют координатным лучом.
Число, соответствующее точке координатного луча, называется координатой этой точки.
Пример:
точке (A) соответствует число (3).
Значит, координата точки (A) равна (3).
Записывается так (A)((3)).
Читается: точка (A) с координатой (3).
Для любого числа можно указать соответствующую ему точку, т. к. луч можно продолжить бесконечно.