При большом числе
наблюдений одно и то же значение случайной
величины Х
может встретиться
раз, одно и то же значение случайной
величиныY
может встретиться
раз, а одна и та же пара чисел (х,
у)
может наблюдаться
раз. Поэтому данные наблюдений группируют,
т.е. подсчитывают частоты
,
,
.
Все сгруппированные данные за-писывают
в виде таблицы, которую называют
корреляционной.
Поясним ее строение
на простом примере. Имеем таблицу:
|
Y |
1 |
2 |
3 |
4 |
5 |
|
|
1 |
6 |
4 |
10 |
|||
|
0 |
1 |
4 |
6 |
11 |
||
|
1 |
5 |
9 |
5 |
19 |
||
|
2 |
3 |
7 |
10 |
|||
|
|
3 |
12 |
10 |
15 |
10 |
|
В
первой строке указаны наблюдаемые
значения (1,
2, 3, 4, 5)
слу-чайной величины Х,
а в первом столбце таблицы – наблюдаемые
значения (1,
0,
1,
2)
случайной величины Y.
На пересечении строк и столбцов находятся
частоты
наблюдаемых
пар значений случайных величин Х
и Y.
Например, частота 6
указывает, что пара чисел (4,
1)
наблюдалась 6
раз.
Все
частоты помещены в прямоугольнике,
стороны которого проведены жирными
линиями.
В
последнем столбце записаны суммы частот
строк. Например, сумма частот второй
строки равна
–
это число указывает, что значение
случайной величины Y,
равное 0
(в
сочетании с различными значениями
случайной величины Х
),
наблюдалось 11
раз.
В
последней строке записаны суммы частот
столбцов. Например, сумма частот
четвертого столбца равна
–
это число указывает, что значение
случайной величины Х,
равное 4
(в
сочетании с различными значениями
случайной величины Y
),
наблюдалось 15
раз.
Общее
число наблюдений
4.4. Выборочный коэффициент корреляции
Ранее мы полагали,
что значения Х
и соответствующие им значения Y
наблюдались по одному разу. На практике,
безусловно, одна пара случайных величин
(х,
у)
может наблюдаться любое число раз.
Поэтому формула
для коэффициента регрессии (4.4) примет
вид
(4.5)
где в сумме 
учтено, что пара
(х,
у)
наблюдалась 
раз,
а
и
выборочные средние квадратические
отклонения случайных величин Х
и Y.
Умножим обе части
равенства (4.5) на дробь 
и назовем это выражение выборочным
коэффициентом корреляции
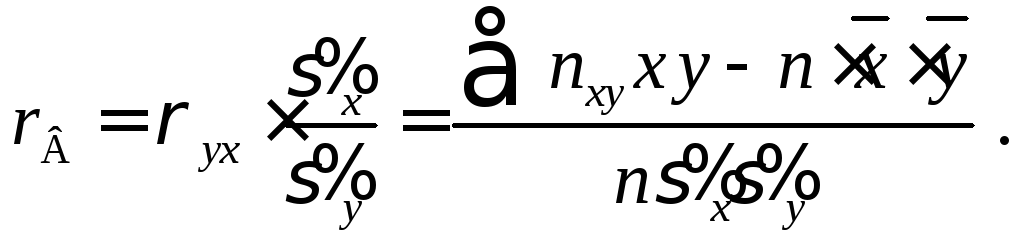
Тогда уравнение
линейной регрессии Y
на Х
будет иметь вид
Замечание 2.
Выборочный коэффициент корреляции
является безраз-мерной оценкой
коэффициента регрессии
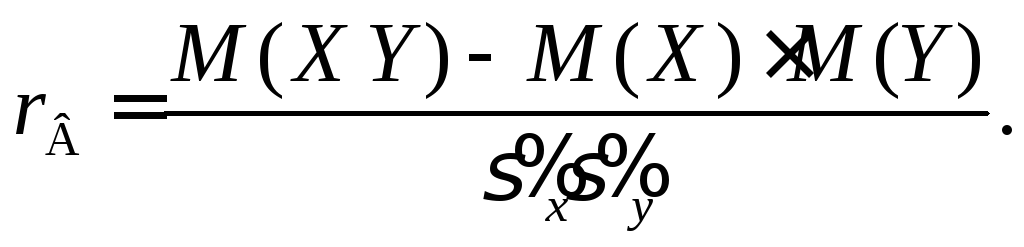
Таким образом,
основная задача корреляционного анализа
состоит в оценке степени линейной связи
между случайными величинами Х
и Y,
которая
устанавливается при помощи выборочного
коэффициента корре-ляции
Если выборочный
коэффициент корреляции
мал, то линейная связь считается слабой
и ее можно не принимать во внимание.
Если же выборочный коэффициент корреляции
близок к1,
то линейная связь сильная и к ней следует
относиться практически как к функциональной.
В противном случае, связь принято считать
статистической. И, наконец, при
связь между случайными величинамиХ
и Y
имеет строго линейный характер.
Замечание.
Выборочный коэффициент корреляции
является лишь оценкой теоретического
коэффициента корреляции
генеральной сово-купности, поэтому
возникает необходимость проверить
гипотезу о значи-мости выборочного
коэффициента корреляции
.
Однако, если
выборка имеет достаточно большой
объем и хорошо представляет генеральную
совокупность, т.е. является репрезентативной,
то вывод (гипотезу) о ли-нейной зависимости
между случайными величинами Х
и Y
, полученный по данным выборки, можно
распространить и на всю генеральную
сово-купность.
Например, для
оценки теоретического коэффициента
корреляции
генеральной
совокупности (если она распределена
нормально) можно воспользоваться
формулой
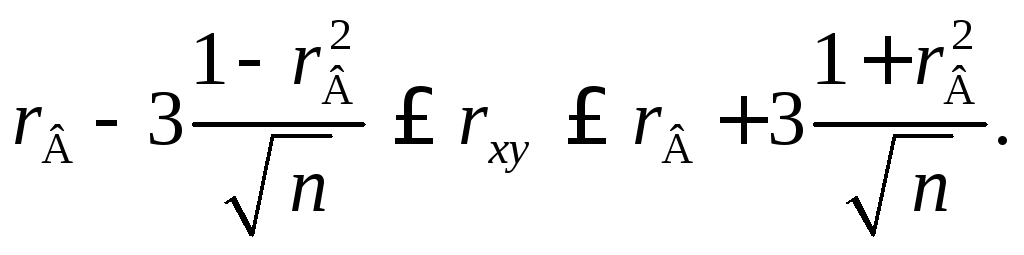
Инструкции:
Вы можете использовать этот пошаговый калькулятор коэффициента корреляции для двух переменных X и Y. Все, что вам нужно сделать, это ввести ваши данные X и Y, в формате через запятую или пробел (Например: “2, 3, 4, 5”, или “3 4 5 6 7”).
Калькулятор коэффициента корреляции
Рассчитанный выше коэффициент корреляции соответствует коэффициенту корреляции Пирсона. Требования для его вычисления заключаются в том, чтобы две переменные X и Y измерялись как минимум на интервальном уровне (это означает, что он не работает с номинальными или порядковыми переменными).
Формула для коэффициента корреляции Пирсона такова:
[r =frac{n sum_{i=1}^n x_i y_i – left(sum_{i=1}^n x_i right) left(sum_{i=1}^n y_i right) }{sqrt{n sum_{i=1}^n x_i^2 – left( sum_{i=1}^n x_i right)^2} sqrt{n sum_{i=1}^n y_i^2 – left( sum_{i=1}^n y_i right)^2} }]
или эквивалентно
[r = frac{sum_{i=1}^n x_i y_i – frac{1}{n}left(sum_{i=1}^n x_i right) left(sum_{i=1}^n y_i right) }{sqrt{sum_{i=1}^n x_i^2 – frac{1}{n}left( sum_{i=1}^n x_i right)^2} sqrt{sum_{i=1}^n y_i^2 – frac{1}{n}left( sum_{i=1}^n y_i right)^2}} = frac{SS_{XY}}{sqrt{SS_{XX}cdot SS_{YY} }}]
Если у вас есть две или более переменных, вы можете использовать наши
калькулятор корреляционной матрицы
. Также, если данные для переменных (X) и (Y) не удовлетворяют параметрическим предположениям для корреляции Пирсона, то следует использовать следующее
Калькулятор корреляции Спирмена
вместо этого.
Корреляция и регрессия
Корреляция и регрессия – это не одно и то же, хотя это тесно связанные понятия. Корреляционный анализ соответствует расчету коэффициента корреляции, который представляет собой значение, колеблющееся от -1 до 1, оценивающее степень линейной связи между двумя переменными.
Чем ближе по абсолютной величине
корреляция
больше 1, тем сильнее линейная связь между двумя переменными. Близкое значение к 1 указывает на тесную положительную линейную связь, а близкое к -1 – на тесную отрицательную связь
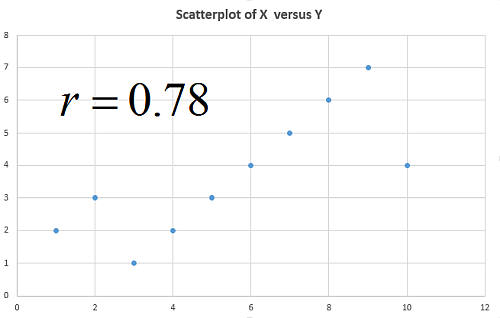
Процесс проведения корреляционного анализа часто также включает в себя
построение диаграммы рассеяния
, чтобы подтвердить информацию, полученную с помощью коэффициента коэф.
После того, как мы убедились, что корреляция близка к 1 по абсолютной величине, что диаграмма рассеяния показывает достаточно плотную линейную структуру, мы можем запустить функцию
Линейная регрессия
анализ, чтобы количественно оценить влияние независимой переменной X на зависимую переменную Y.
Могу ли я использовать z-коэффициенты для расчета коэффициента корреляции?
Конечно! Вы видели z-коэффициенты повсюду в статистике и, естественно, задаетесь вопросом, можете ли вы
вычислить корреляцию с помощью z-баллов
. Вы определенно можете это сделать, и на самом деле, это обычный способ в статистике социальных наук.
Другие калькуляторы, похожие на этот калькулятор корреляции
Кроме того, существует понятие
коэффициент множественной корреляции
, когда у вас более одного предиктора, который получается путем вычисления корреляции между наблюдаемыми значениями (Y) и предсказанными значениями (hat Y) с помощью регрессии.
Онлайн калькулятор корреляционного анализа Спирмена позволяет получить расчет сразу на сайте. Итоговое описание состоит из таблиц, графиков и текстовых выводов. Его можно сказать в формате Word, а таблицы в Excel.
Шаг 1. Введите название исследуемой шкалы
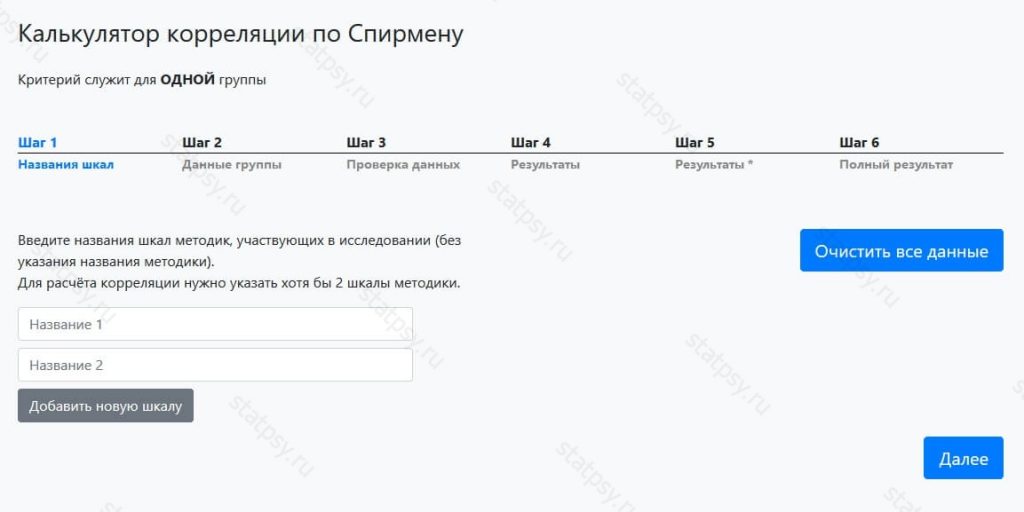
Шаг 1.1. Вы можете внести несколько названий шкал для проведения корреляционного анализа по Спирмену
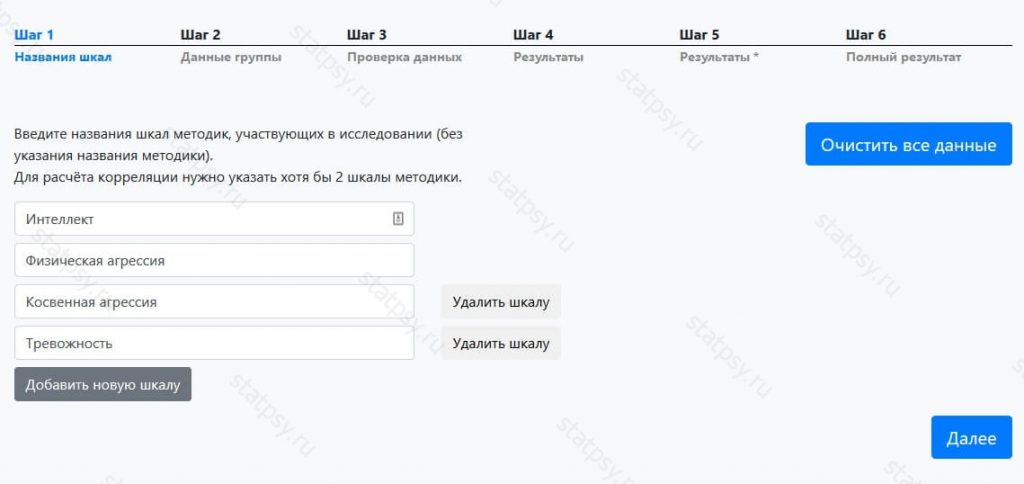
Шаг 2. Внесите название группы, количество человек в ней и нажмите на кнопку «Внести данные».
Появиться таблица с пустыми ячейками для ввода данных.
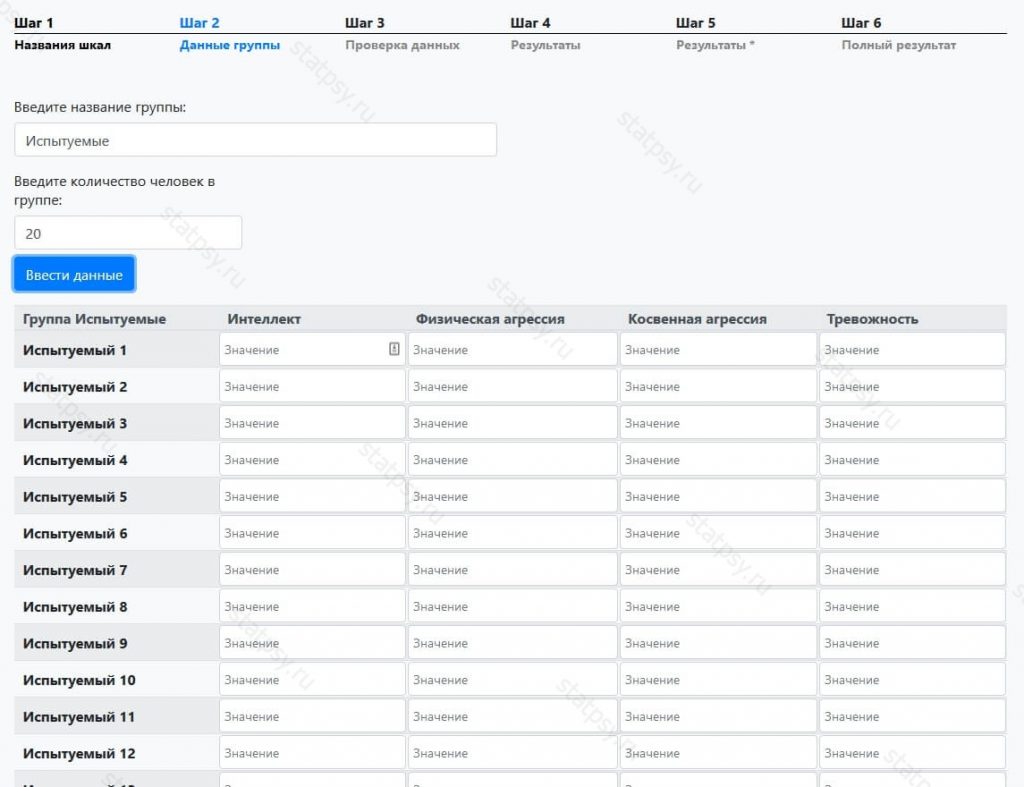
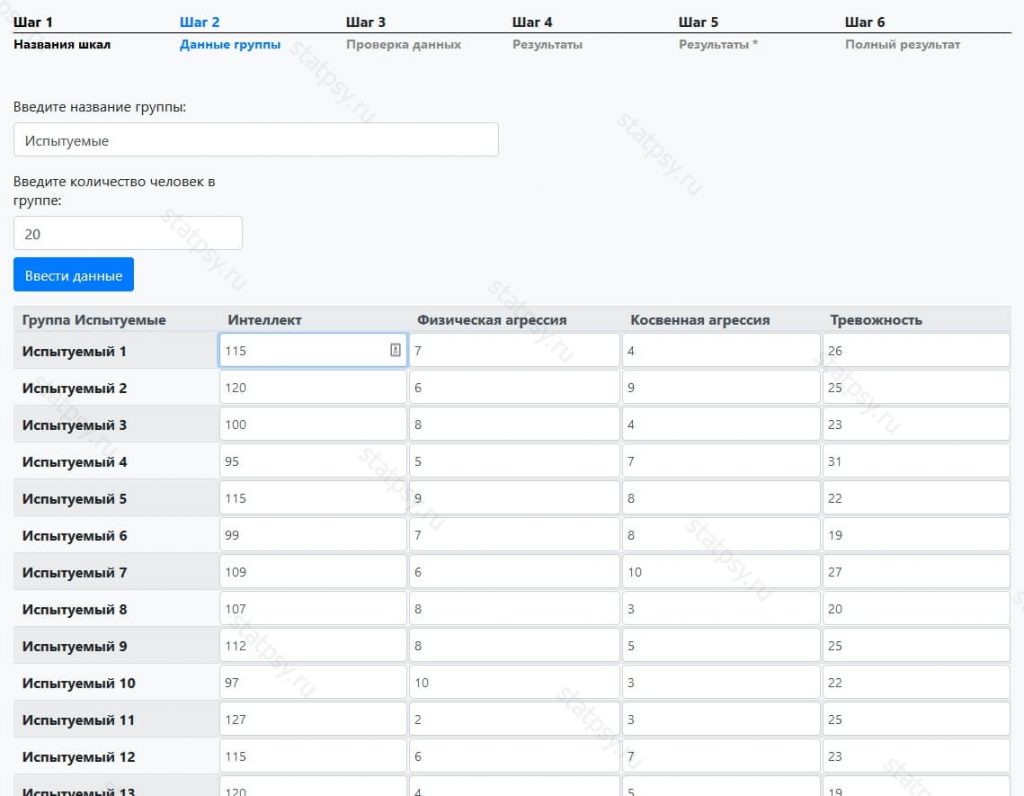
Шаг 2.1. Внесите исходные данные группы
Вы можете внести данные для расчета корреляционного анализа по Спирмену поочередно вручную или скопировать их из вашего Excel файла.
Шаг 3. Проверяем исходные данные
Именно по ним будет осуществляться, расчет всех показателей. В случае необходимости можно вернуться на предыдущие шаги и изменить данные.
Шаг 4. Краткий отчет по корреляционному анализу Спирмена
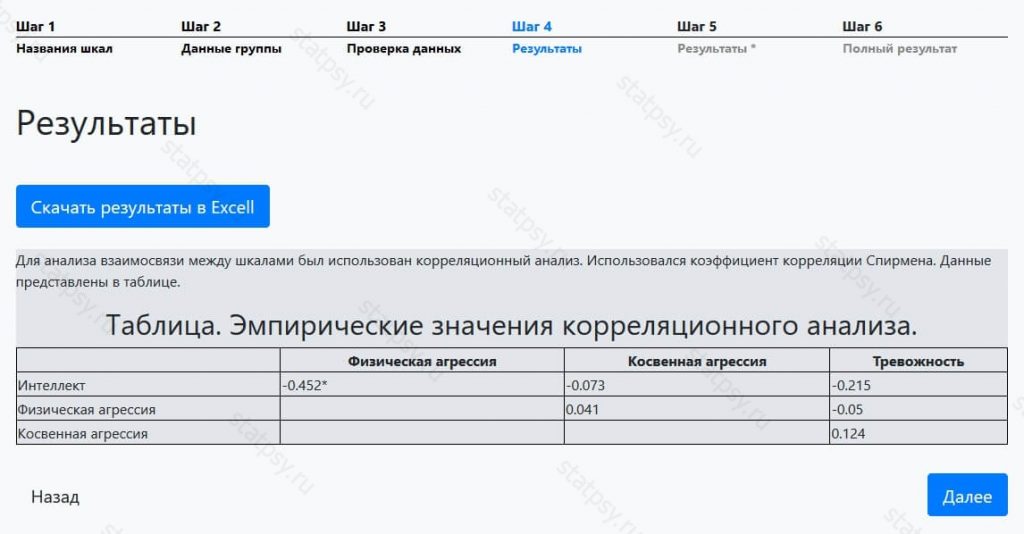
Для незарегистрированных пользователей доступен только краткий отчет-таблица в которой указано — значение коэффициента корреляции.
Если вы разбираетесь в статистике, этих данных хватит вам, чтобы сделать вывод о наличии/отсутствии взаимосвязей между исследуемыми показателями.
Шаг 4.1. Регистрация / Авторизация
Для того, чтобы получить более полный отчет с информацией о средних значениях с указание различий нужно зарегистрироваться в сервисе.
Вы можете зарегистрироваться используя свою почту или профиль ВКонтакте.
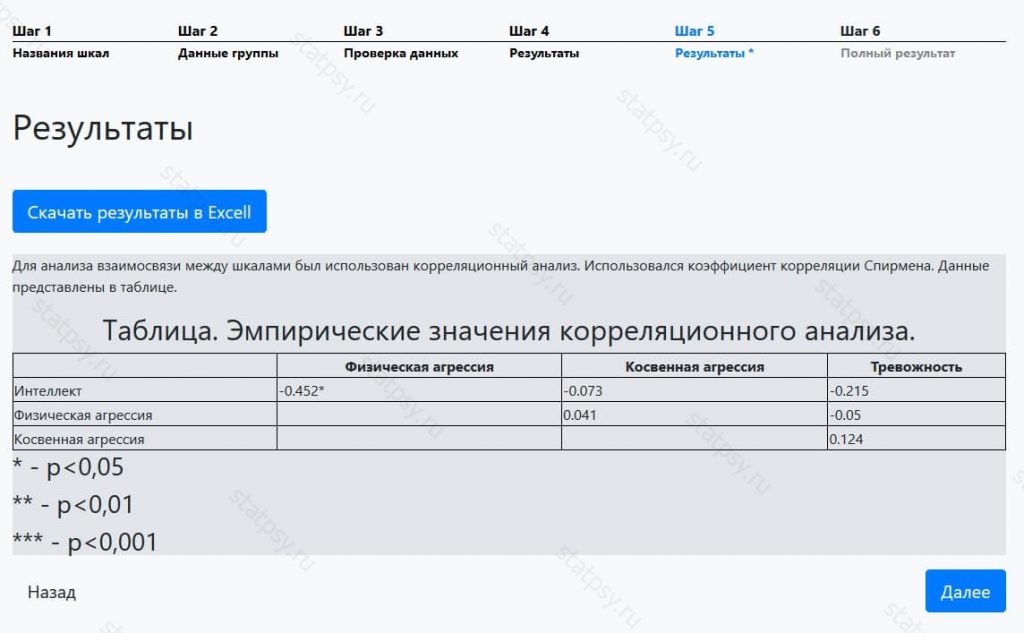
Шаг 5. Обычный отчет
После регистрации вам станет доступен более полный отчет в котором содержится информация о:
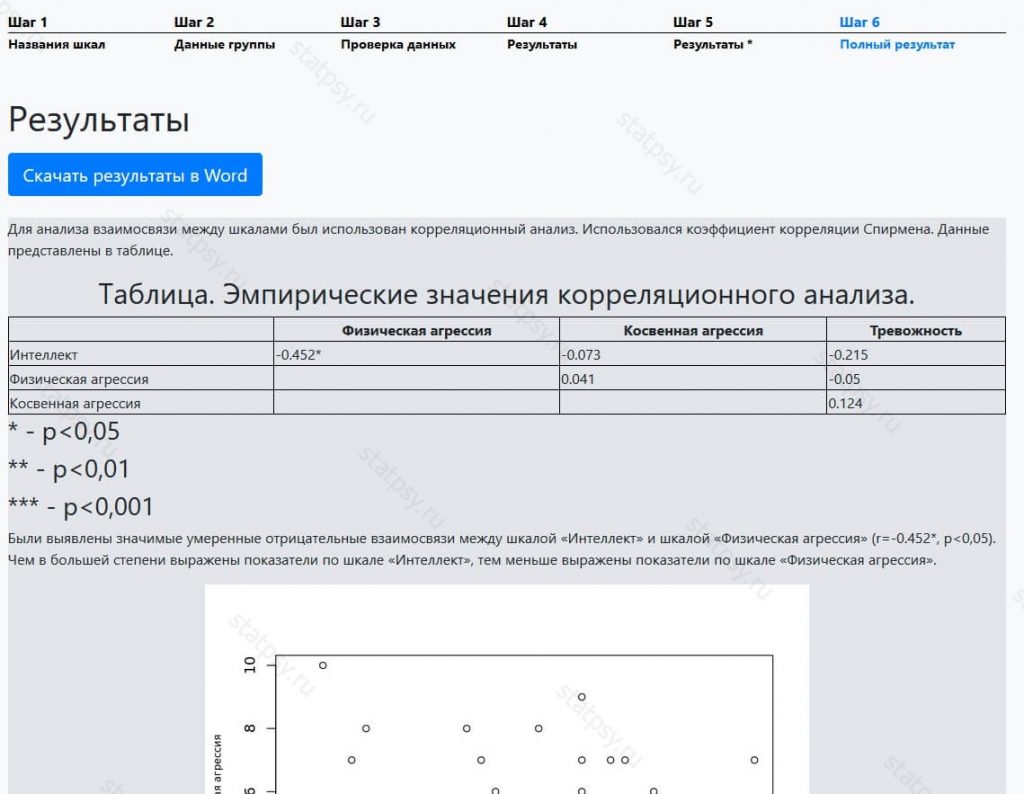
- значимости корреляционных связей между параметрами
- звездочкой в таблице указаны шкалы, по которым есть связи (в нашем примере это «Интеллект» и «Физическая агрессия»).
Также вы можете скачать итоговую таблицу в формате Excel.
Вы также можете получить подробный отчет в котором будут графики и нужные текстовые описания, для этого нужно оплатить работу сервиса.
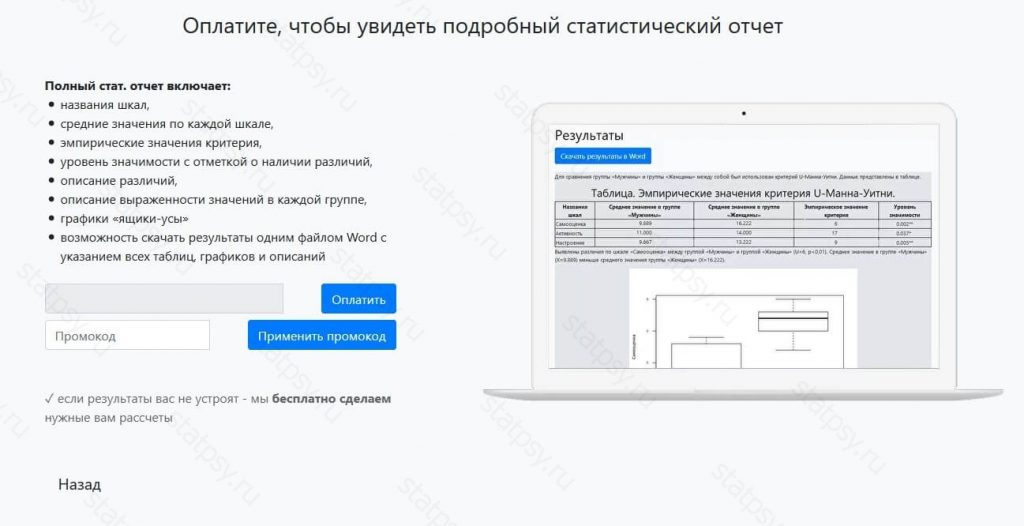
Шаг 6. Полный статистический отчет
После оплаты, в течении суток, вы сможете неограниченное количество раз запускать калькулятор и получать итоговые расчеты.
В полном отчете доступно:
- названия шкал,
- уровень значимости с отметкой о наличии связей между группами,
- описание силы связи,
- описание направления связи,
- графики «рассеяния»,
- возможность скачать результаты одним файлом Word c указанием всех таблиц, графиков и описаний
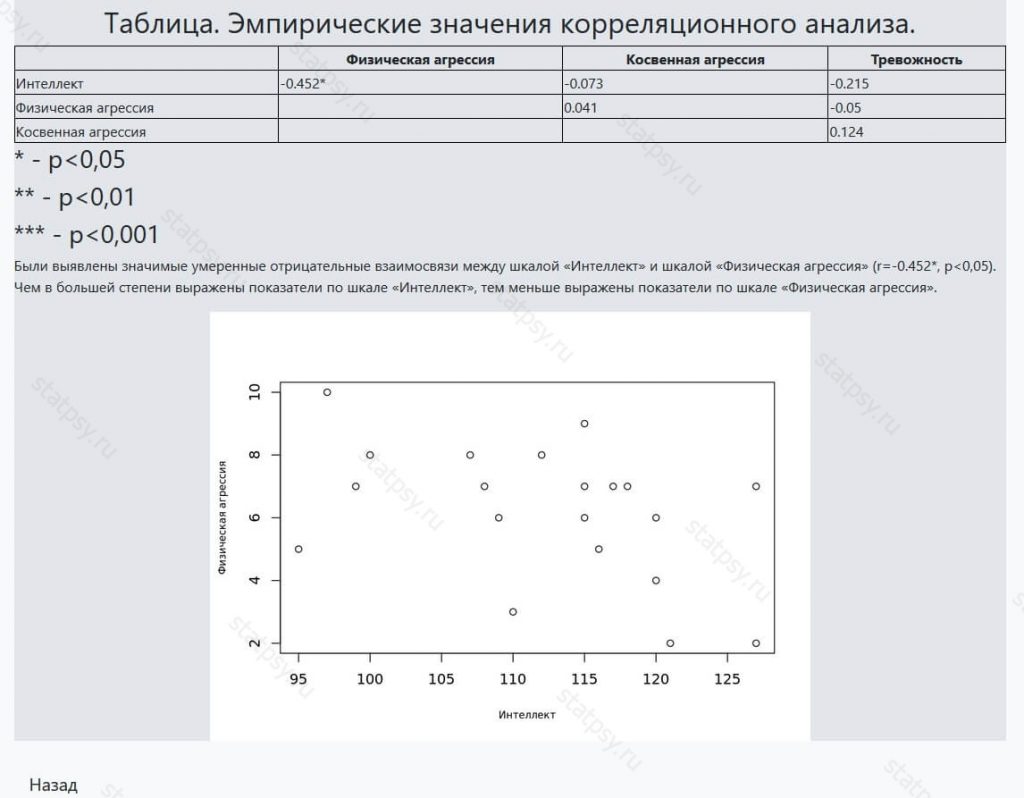
В случае, если результаты расчетов вас не устроят, мы гарантируем, что бесплатно внесем все необходимые правки в вашу работу.
This calculator creates a correlation matrix for up to five different variables.
Simply enter the data values for up to five variables into the boxes below, then press the “Calculate” button.
Variable 1
Variable 2
Variable 3
Variable 4
Variable 5
Correlation Matrix
| Var1 | Var2 | Var3 | Var4 | Var5 | |
|---|---|---|---|---|---|
| Var1 | 1.0000 | ||||
| Var2 | 0.8476 | 1.0000 | |||
| Var3 | 0.9378 | 0.9305 | 1.0000 | ||
| Var4 | |||||
| Var5 |
Published by Zach
На практике в результате независимых наблюдений над величинами X и Y, как правило, имеют дело не со всей совокупностью всех возможных пар значений этих величин, а лишь с ограниченной выборкой из генеральной совокупности, причем объем n выборочной совокупности определяется как количество имеющихся в выборке пар.
Первоочередной задачей статистической обработки экспериментального материала является систематизация полученных данных и выяснение формы соответствующей генеральной совокупности.
Пусть величина Х в выборке принимает значения x1, x2,….xm, где количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке может повторяться. Пусть величина Y в выборке принимает значения y1, y2,….yk, где k – количество различающихся между собой значений этой величины, причем в общем случае каждое из них в выборке также может повторяться. В этом случае данные заносят в таблицу с учетом частот встречаемости. Такую таблицу с группированными данными называют корреляционной.
Первым этапом статистической обработки результатов является составление корреляционной таблицы (таблица 1).
| YX | x1 | x2 | … | xm | ny |
| y1 | n12 | n21 | nm1 | ny1 | |
| y2 | n22 | nm2 | ny2 | ||
| … | |||||
| yk | n1k | n2k | nmk | nyk | |
| nx | nx1 | nx2 | nxm | n |
В первой строке основной части таблицы в порядке возрастания перечисляются все встречающиеся в выборке значения величины X. В первом столбце также в порядке возрастания перечисляются все встречающиеся в выборке значения величины Y. На пересечении соответствующих строк и столбцов указываются частоты nij (i=1,2,…,m; j=1,2,…,k) равные количеству появлений пары (xi;yi) в выборке. Например, частота n12 представляет собой количество появлений в выборке пары (x1;y1).
Так же nxi
nij, 1≤i≤m, сумма элементов i-го столбца, nyj
nij, 1≤j≤k, – сумма элементов j-ой строки и nxi=nyj=n
Аналоги формул (3), полученные по данным корреляционной таблицы, имеют вид:
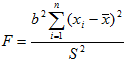(6)
Пример 3. Изучалась зависимость между качеством стандартности товаров Y(%) и количеством товаров (X) шт. Результаты наблюдений приведены в виде корреляционной таблицы.
| YX | 18 | 22 | 26 | 30 | ny |
| 70 | 5 | 5 | |||
| 75 | 7 | 46 | 1 | 54 | |
| 80 | 29 | 72 | 101 | ||
| 85 | 29 | 8 |
37 |
||
| 90 | 3 | 3 | |||
| nx | 12 | 75 | 102 | 11 | 200 |
Требуется:
1) Найти выборочное уравнение прямой регрессии Y на X.
2) Определить выборочные аналоги функции регрессии.
3) Сравнить между собой при каждом значении Х приближения средних значений Y, полученные по функции регрессии и по уравнению прямой регрессии.
Решение: Пользуясь данными, приведенными в этой таблице, по формулам (6), находим:
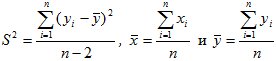
Следовательно,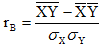 
a=79.475-1.111•24.24=79.475-26.930=52.544
Таким образом, выборочное уравнение прямой регрессии Y на X выражается формулой:
Y=79.475+1.111(x-24.24)=79.475+1.111x-26.930=52.545+1.111x
Откуда:
| X | 18 | 22 | 26 | 30 |
| Yлин | 72.5 | 76.98 | 81.45 | 85.92 |
| Yx | 72.91 | 76.93 | 81.37 | 86.36 |
где Yлин(x=x1)=52.545+1.111•18=72.5 и т.д. yx1=(5•70+7•75)/12=72.91 и т.д.
Сопоставляя полученные результаты, приходим к выводу, что значения, вычисленные по уравнению выборочной регрессии и по линейной зависимости хорошо согласуются.
Заключение. Величины, вычисленные путем подстановки возможных значений Х в уравнение прямой регрессии и в функцию регрессии, практически совпадают.
Замечание. Для упрощения вычислений в корреляционной табл. удобно от (xi;yi) перейти к новым переменным (ui;vi), положив ui=(xi-x0)/h1; vj=(yj-y0)/h2 (*)
где x0 и y0 варианты соответствующие наибольшим частотам соответственно xi и yi. hi=xi+1-xi.
Обратный пересчет осуществляется по формулам:
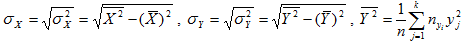
Добавлять комментарии могут только зарегистрированные пользователи.
Регистрация Вход
