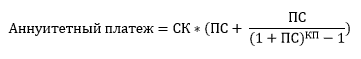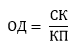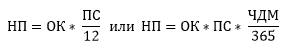Как составить кредитный калькулятор

Кредитный калькулятор – это удобный инструмент, который позволяет рассчитать ежемесячный платеж по кредиту, а также общую сумму, которую вы заплатите за кредит в конечном итоге. Этот инструмент основывается на формуле аннуитетных платежей, которая учитывает сумму кредита, процентную ставку и срок кредитования. В этой статье мы рассмотрим, как написать кредитный калькулятор на Java.

Наш кредитный калькулятор будет ориентирован на ежемесячный платеж по кредиту. Мы начнем с создания графического интерфейса пользователя. Для этого мы будем использовать библиотеку Swing. Наш калькулятор будет иметь следующие поля:

• Сумма кредита
• Процентная ставка
• Срок кредитования
• Ежемесячный платеж
• Общая сумма, которую необходимо оплатить

Для создания компонентов пользовательского интерфейса, следует воспользоваться следующим кодом:

import javax.swing.*;
import java.awt.*;

public class CreditCalculator extends JFrame {

private JLabel loanAmountLabel;
private JLabel interestRateLabel;
private JLabel termLabel;
private JTextField loanAmountTextField;
private JTextField interestRateTextField;
private JTextField termTextField;
private JButton calculateButton;
private JLabel monthlyPaymentLabel;
private JLabel totalPaymentLabel;

public CreditCalculator() {
super(“Кредитный калькулятор”);

loanAmountLabel = new JLabel(“Сумма кредита”);
interestRateLabel = new JLabel(“Процентная ставка”);
termLabel = new JLabel(“Срок кредитования”);
loanAmountTextField = new JTextField();
interestRateTextField = new JTextField();
termTextField = new JTextField();
calculateButton = new JButton(“Рассчитать”);
monthlyPaymentLabel = new JLabel(“Ежемесячный платеж: “);
totalPaymentLabel = new JLabel(“Общая сумма, которую необходимо оплатить: “);

JPanel panel = new JPanel(new GridLayout(4, 2));

panel.add(loanAmountLabel);
panel.add(loanAmountTextField);
panel.add(interestRateLabel);
panel.add(interestRateTextField);
panel.add(termLabel);
panel.add(termTextField);
panel.add(monthlyPaymentLabel);
panel.add(totalPaymentLabel);

add(panel, BorderLayout.CENTER);
add(calculateButton, BorderLayout.SOUTH);

setDefaultCloseOperation(JFrame.EXIT_ON_CLOSE);
pack();
setVisible(true);
}

public static void main(String[] args) {
new CreditCalculator();
}

}

Для расчета ежемесячного платежа мы будем использовать формулу аннуитетных платежей. Формула выглядит следующим образом:

P = (Pv * r) / (1 – (1 + r) ^ -n)

где P – ежемесячный платеж, Pv – сумма кредита, r – месячная процентная ставка, n – срок кредитования в месяцах.

Мы можем использовать эту формулу в нашем кредитном калькуляторе. Добавьте следующий код в конструктор вашего класса CreditCalculator:

calculateButton.addActionListener(e -> {
double loanAmount = Double.parseDouble(loanAmountTextField.getText());
double interestRate = Double.parseDouble(interestRateTextField.getText());
double term = Double.parseDouble(termTextField.getText());

double r = (interestRate / 100) / 12;
double P = (r * loanAmount) / (1 – Math.pow(1 + r, -term));

monthlyPaymentLabel.setText(“Ежемесячный платеж: ” + String.format(“%.2f”, P));
totalPaymentLabel.setText(“Общая сумма, которую необходимо оплатить: ” + String.format(“%.2f”, P * term));
});

В этом коде мы сначала получаем значения из текстовых полей и преобразуем их в тип double. Затем мы рассчитываем ежемесячный платеж и общую сумму. В итоге мы обновляем соответствующие JLabel’ы, чтобы отобразить результаты расчета.

Теперь наш кредитный калькулятор готов. Вы можете запустить приложение и проверить его работу.

Итак, сегодня мы рассмотрели, как написать кредитный калькулятор на Java с использованием библиотеки Swing. Мы создали компоненты пользовательского интерфейса и реализовали алгоритм расчета ежемесячного платежа с помощью формулы аннуитетных платежей. Надеюсь, этот пример поможет вам при создании собственного кредитного калькулятора. А если вы хотите научиться писать собственный код на языке Java, приходите на обучение в Академию прикладной информатике.

Получилось ли у вас реализовать данную программу? С какими трудностями вы столкнулись при написании Java-кода? Пишите свои комментарии.

Post Views: 8 699

Каждый человек хотя бы раз сталкивается с кредитом: хочется купить дорогостоящую вещь, взять ипотеку и т.д. В этих случаях важно правильно рассчитывать свои доходы и расходы, чтобы оплата кредита не стала тяжкой ношей. Для этого существуют различные кредитные калькуляторы, которые при заданных параметрах показывают, когда и сколько нужно заплатить. В этой и следующей статьях мы рассмотрим, как написать собственный калькулятор кредитов от идеи до реализации.

Что такое кредит?

Кредит — это операция банка по предоставлению заёмщику средств в ссуду на условиях срочности, возвратности и уплаты процентов. Субъекта при выполнении данной операции являются кредитор, предоставляющий деньги во временное пользование, и заёмщик, получающий ссуду.

Иначе говоря, это товар, продаваемый за специфическую цену (ссудный процент) и на специфических условиях (на срок, с возвратом).

Существуют две теории кредитов, которые определяют роль кредита в экономике:

1. Натуралистическая теория
   Представители этой теории рассматривали кредит как форму движения производительного капитала, используя относительную самостоятельность ссудного капитала и закономерности его движения. Они недооценивали роль кредита, полагая, что сущность банков заключается в их посреднической роли.Натуралистическая теория кредита была разработана А. Смитом (1723-1790) и Д. Рикардо (1772-1823). Важнейшие положения А. Смита и Д. Рикардо сводятся к следующему:
   • объектом кредита являются натуральные (надежные) вещественные блага;
   • ссудный капитал тождествен действительному, движение ссудного капитала совпадает с движением производительного капитала;
   • банки выступают как скромные посредники, поскольку кредит играет пассивную роль.
2. Капиталотворческая теория
   Эта теория заняла лидирующее положение с середины XIX в. Ее основные идеи заключаются в следующем:
   • кредит независим от процесса воспроизводства;
   • кредит является решающим фактором развития экономики;
   • банки являются структурами, «производящими» кредит;
   • кредит — источник прибыли, следовательно, является производительным капиталом.

   Эти идеи сформулированы шотландским экономистом и финансистом Дж. Ло и английским экономистом Г. Маклеодом. Дальнейшее развитие капиталотворческая теория кредита получила в начале XX в. в работах немецкого банкира А. Гана, английских экономистов Дж. М. Кейнса и Р. Хоутри, американского экономиста Э. Хансена. Методология этой теории была дополнена следующими положениями:

   • банки выполняют в экономике ведущую роль;
   • основу банковской деятельности составляют активные операции;
   • кредит создаст депозиты, а следовательно, является источником банковского капитала (эффект кредитного мультипликатора);
   • как источник капитала кредит является фактором расширенного воспроизводства и экономического роста.

   В действительности основным источником ссудного капитала являются денежные капиталы, высвобождаемые в процессе оборота промышленного и торгового капитала, денежные накопления, формирующиеся в процессе движения государственных фондов финансовых ресурсов, а также средств населения. Только на основе этих ресурсов возможно кредитование. При расширении его кредит может превратиться в инфляционный фактор, ограничивающий возможности экономического роста.

Каких видов бывает кредит?

За время своего существования кредит претерпел множество изменений и имел различные виды, начиная с ростовщического кредита. На сегодняшний день виды кредита различают по нескольским классификациям.

По целям кредитования:

• Кредит на потребительские нужны (потребительский кредит) — это кредитование физических лиц с целью покупки необходимых товаров небольшой стоимости (обычно до 100 тысяч рублей). Кредит этого вида характеризуется высокими процентными ставками и низкими суммами, которые предоставляются в качестве кредита заемщику. Разновидность данного банковского продукта — товарный кредит, который выдается на покупку определённого товара, чаще всего, в торговых точках работниками кредитных организаций.
• Автомобильный кредит — кредит на приобретение автомобиля, выдаваемый в размере от 70% до 100% от стоимости транспортного средства; как правило, приобретаемый автомобиль выступает обеспечением по кредиту. Также автокредит — разновидность потребительского кредита, когда банк выдает целевую ссуду на покупку автомобиля. Согласно кредитному соглашению, полученная сумма не может быть потрачена ни на что другое. Чаще всего, она перечисляется непосредственно продавцу машины, у которого вы решили приобрести транспортное средство.
• Ипотечный кредит — заём на покупку жилья (квартира, дом) как на вторичном, так и на первичном рынке. Разновидность ипотеки — ипотечный потребительский кредит. Это сочетание признаков и ипотечного кредита и потребительского кредита. Например, некоторые банки предоставляют крупные кредиты на любые цели, в том числе потребительские, от 300 тыс. рублей до 25 млн рублей под залог находящейся в собственности заемщика недвижимости.
• Нецелевой кредит на потребительские нужды — банк выдает средства заемщику средства на любые цели. Особая разновидность этого банковского продукта — кредитная карта, именной платежно-расчетный документ в виде персонифицированной пластиковой карточки, выдаваемый банком-эмитентом своим клиентам для безналичной оплаты, приобретения ими в кредит товаров и услуг в розничной торговой сети.
• Другие более мелкие виды — ссуда на образование, отдых, на неотложные нужды и т. д.

По способу погашения:

• Кредит, погашаемый в рассрочку (например, ипотека).
• Кредит, погашаемый единовременно (например, нецелевой экспресс-кредит).

По наличию обеспечения:

• Беззалоговые кредиты (например, кредит на неотложные нужды).
• Кредит, под который банк требует обеспечение (машина, квартира и т.д.).

Как посчитать кредит?

При расчёте кредита основными параметрами являются сумма кредита, процентная ставка и срок, на который выдан кредит. На основе этих параметров легко посчитать, сколько нужно платить банку в месяц.

Однако не всегда сумма платежей распределяется равномерно по месяцам. Бывают случаи, когда в разные месяцы нужно платить разную сумму. Исходя из этого платежи принято разделять на аннуитетные и дифференцированные платежи.

Аннуитетный платеж

Самый простой случай — когда каждый месяц нужно платить одинаковую сумму. Такой платёж называется аннуитетным, он является постоянным на весь срок выплаты. Аннуитетный платеж вычисляется по следующей формуле:

Здесь СК это изначальная сумма займа, ПС — процентная ставка, а КП — количество периодов (месяцев).

В этой формуле процентная ставка это 1/12 часть годовой ставки, поэтому если годовая ставка, допустим, 20%, то для формулы выше месячная будет равна 0,2/12 = 0,0167.

Таким образом получаем величину платежа, равную для каждого месяца.

Дифференцированный платеж

Иначе обстоит дело с дифференцированным платежом. В первые месяцы сумма платежей, как правило, выше, затем постепенно уменьшается. При этом не изменяется основная задолженность, меняются только начисленные проценты.

Чтобы посчитать, сколько платить, нужно знать основной долг и начисленные проценты. Основной долг вычисляется очень просто по следующей формуле;

Здесь ОД это основной долг, СК — изначальная сумма кредита, КП — количество периодов (месяцев).

Начисленные проценты в свою очередь вычисляются по одной из двух формул, в зависимости от нужной точности, «12 месяцев в году» или «365 дней в году».

В приведённых выше формулах НП это начисленные проценты, ОК — остаток по кредиту в текущем месяце, ПС — годовая процентная ставка, ЧДМ — число дней в месяце.

Чтобы рассчитать остаток по кредиту в текущем месяце, т.е. найти величину ОК из приведённой выше формулы, необходимо размер основного долга умножить на количество прошедших периодов и всё это вычесть из изначальной суммы кредита.

Здесь n это количество прошедших периодов.

С помощью этих трёх формул мы легко можем вычислить сумма платежа и остаток по задолженности на каждый месяц.

Подводя итоги

Изучив вопросы по кредитам, мы подготовили теоретическую базу для дальнейшей реализации собственно калькулятора кредитов. В следующей статье мы расскажем о том, как полученные формулы применить на практике и напишем собственное приложение для расчёта задолженности по кредиту.

Excel – это универсальный аналитическо-вычислительный инструмент, который часто используют кредиторы (банки, инвесторы и т.п.) и заемщики (предприниматели, компании, частные лица и т.д.).

Быстро сориентироваться в мудреных формулах, рассчитать проценты, суммы выплат, переплату позволяют функции программы Microsoft Excel.

Как рассчитать платежи по кредиту в Excel

Ежемесячные выплаты зависят от схемы погашения кредита. Различают аннуитетные и дифференцированные платежи:

1. Аннуитет предполагает, что клиент вносит каждый месяц одинаковую сумму.
2. При дифференцированной схеме погашения долга перед финансовой организацией проценты начисляются на остаток кредитной суммы. Поэтому ежемесячные платежи будут уменьшаться.

Чаще применяется аннуитет: выгоднее для банка и удобнее для большинства клиентов.

Расчет аннуитетных платежей по кредиту в Excel

Ежемесячная сумма аннуитетного платежа рассчитывается по формуле:

А = К * S

где:

• А – сумма платежа по кредиту;
• К – коэффициент аннуитетного платежа;
• S – величина займа.

Формула коэффициента аннуитета:

К = (i * (1 + i)^n) / ((1+i)^n-1)

• где i – процентная ставка за месяц, результат деления годовой ставки на 12;
• n – срок кредита в месяцах.

В программе Excel существует специальная функция, которая считает аннуитетные платежи. Это ПЛТ:

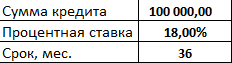
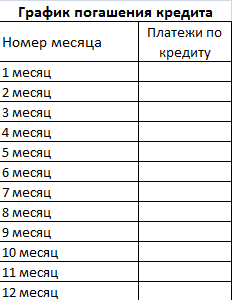
1. Заполним входные данные для расчета ежемесячных платежей по кредиту. Это сумма займа, проценты и срок.



2. Составим график погашения кредита. Пока пустой.



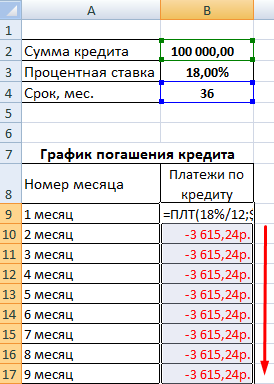
3. В первую ячейку столбца «Платежи по кредиту» вводиться формула расчета кредита аннуитетными платежами в Excel: =ПЛТ($B$3/12; $B$4; $B$2). Чтобы закрепить ячейки, используем абсолютные ссылки. Можно вводить в формулу непосредственно числа, а не ссылки на ячейки с данными. Тогда она примет следующий вид: =ПЛТ(18%/12; 36; 100000).

Ячейки окрасились в красный цвет, перед числами появился знак «минус», т.к. мы эти деньги будем отдавать банку, терять.



Расчет платежей в Excel по дифференцированной схеме погашения

Дифференцированный способ оплаты предполагает, что:

• сумма основного долга распределена по периодам выплат равными долями;
• проценты по кредиту начисляются на остаток.

Формула расчета дифференцированного платежа:

ДП = ОСЗ / (ПП + ОСЗ * ПС)

где:

• ДП – ежемесячный платеж по кредиту;
• ОСЗ – остаток займа;
• ПП – число оставшихся до конца срока погашения периодов;
• ПС – процентная ставка за месяц (годовую ставку делим на 12).

Составим график погашения предыдущего кредита по дифференцированной схеме.

Входные данные те же:

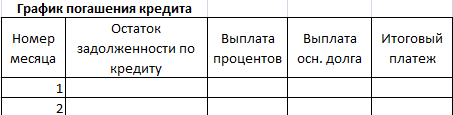
Составим график погашения займа:

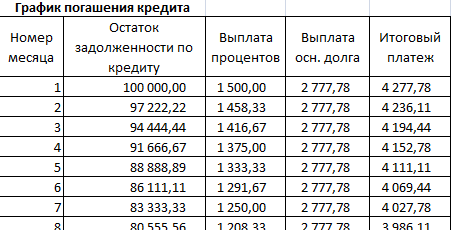
Остаток задолженности по кредиту: в первый месяц равняется всей сумме: =$B$2. Во второй и последующие – рассчитывается по формуле: =ЕСЛИ(D10>$B$4;0;E9-G9). Где D10 – номер текущего периода, В4 – срок кредита; Е9 – остаток по кредиту в предыдущем периоде; G9 – сумма основного долга в предыдущем периоде.

Выплата процентов: остаток по кредиту в текущем периоде умножить на месячную процентную ставку, которая разделена на 12 месяцев: =E9*($B$3/12).

Выплата основного долга: сумму всего кредита разделить на срок: =ЕСЛИ(D9<=$B$4;$B$2/$B$4;0).

Итоговый платеж: сумма «процентов» и «основного долга» в текущем периоде: =F8+G8.

Внесем формулы в соответствующие столбцы. Скопируем их на всю таблицу.

Сравним переплату при аннуитетной и дифференцированной схеме погашения кредита:

Красная цифра – аннуитет (брали 100 000 руб.), черная – дифференцированный способ.

Формула расчета процентов по кредиту в Excel

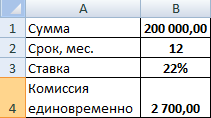
Проведем расчет процентов по кредиту в Excel и вычислим эффективную процентную ставку, имея следующую информацию по предлагаемому банком кредиту:

Рассчитаем ежемесячную процентную ставку и платежи по кредиту:

Заполним таблицу вида:

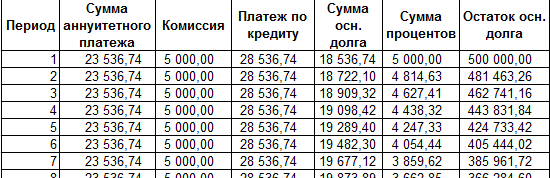
Комиссия берется ежемесячно со всей суммы. Общий платеж по кредиту – это аннуитетный платеж плюс комиссия. Сумма основного долга и сумма процентов – составляющие части аннуитетного платежа.

Сумма основного долга = аннуитетный платеж – проценты.

Сумма процентов = остаток долга * месячную процентную ставку.

Остаток основного долга = остаток предыдущего периода – сумму основного долга в предыдущем периоде.

Опираясь на таблицу ежемесячных платежей, рассчитаем эффективную процентную ставку:

• взяли кредит 500 000 руб.;
• вернули в банк – 684 881,67 руб. (сумма всех платежей по кредиту);
• переплата составила 184 881, 67 руб.;
• процентная ставка – 184 881, 67 / 500 000 * 100, или 37%.
• Безобидная комиссия в 1 % обошлась кредитополучателю очень дорого.

Эффективная процентная ставка кредита без комиссии составит 13%. Подсчет ведется по той же схеме.

Расчет полной стоимости кредита в Excel

Согласно Закону о потребительском кредите для расчета полной стоимости кредита (ПСК) теперь применяется новая формула. ПСК определяется в процентах с точностью до третьего знака после запятой по следующей формуле:

• ПСК = i * ЧБП * 100;
• где i – процентная ставка базового периода;
• ЧБП – число базовых периодов в календарном году.

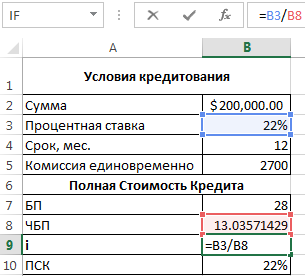
Возьмем для примера следующие данные по кредиту:

Для расчета полной стоимости кредита нужно составить график платежей (порядок см. выше).

Нужно определить базовый период (БП). В законе сказано, что это стандартный временной интервал, который встречается в графике погашения чаще всего. В примере БП = 28 дней.

Далее находим ЧБП: 365 / 28 = 13.

Теперь можно найти процентную ставку базового периода:

У нас имеются все необходимые данные – подставляем их в формулу ПСК: =B9*B8

Примечание. Чтобы получить проценты в Excel, не нужно умножать на 100. Достаточно выставить для ячейки с результатом процентный формат.

ПСК по новой формуле совпала с годовой процентной ставкой по кредиту.

Скачать кредитный калькулятор в Excel

Таким образом, для расчета аннуитетных платежей по кредиту используется простейшая функция ПЛТ. Как видите, дифференцированный способ погашения несколько сложнее.

Кто как, а я считаю кредиты злом. Особенно потребительские. Кредиты для бизнеса – другое дело, а для обычных людей мышеловка”деньги за 15 минут, нужен только паспорт” срабатывает безотказно, предлагая удовольствие здесь и сейчас, а расплату за него когда-нибудь потом. И главная проблема, по-моему, даже не в грабительских процентах или в том, что это “потом” все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Зачем напрягаться, учиться, развиваться, искать дополнительные источники дохода, если можно тупо зайти в ближайший банк и там тебе за полчаса оформят кредит на кабальных условиях, попутно грамотно разведя на страхование и прочие допы?

Так что очень надеюсь, что изложенный ниже материал вам не пригодится.

Но если уж случится так, что вам или вашим близким придется влезть в это дело, то неплохо бы перед походом в банк хотя бы ориентировочно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. “Помассажировать числа” заранее, как я это называю 🙂 Microsoft Excel может сильно помочь в этом вопросе.

Вариант 1. Простой кредитный калькулятор в Excel

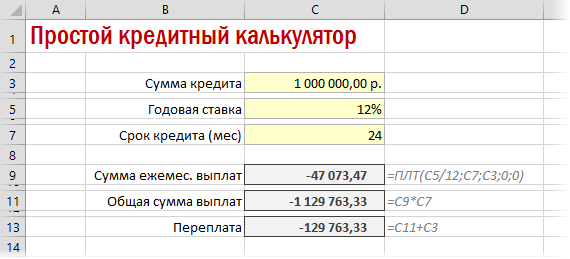
Для быстрой прикидки кредитный калькулятор в Excel можно сделать за пару минут с помощью всего одной функции и пары простых формул. Для расчета ежемесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты производятся равными суммами – таких сейчас большинство) в Excel есть специальная функция ПЛТ (PMT) из категории Финансовые (Financial). Выделяем ячейку, где хотим получить результат, жмем на кнопку fx в строке формул, находим функцию ПЛТ в списке и жмем ОК. В следующем окне нужно будет ввести аргументы для расчета:

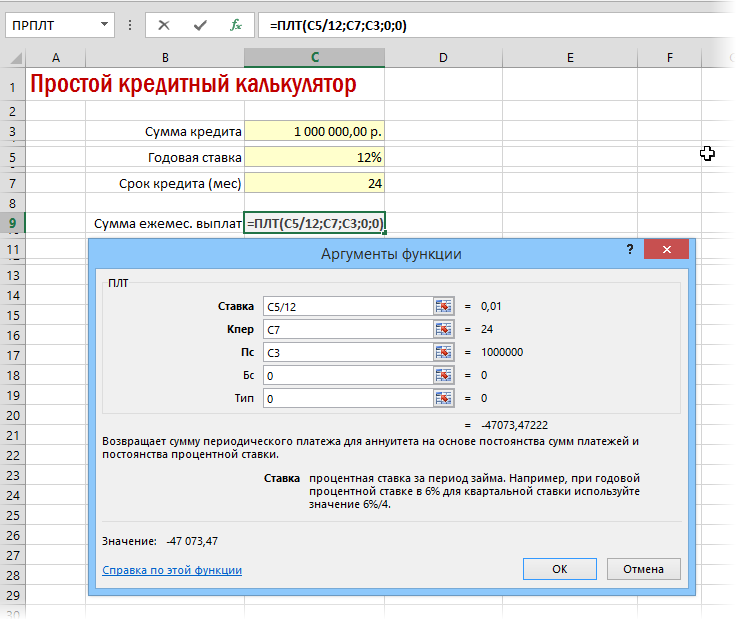
• Ставка – процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годовая ставка 12%, то на один месяц должно приходиться по 1% соответственно.
• Кпер – количество периодов, т.е. срок кредита в месяцах.
• Пс – начальный баланс, т.е. сумма кредита.
• Бс – конечный баланс, т.е. баланс с которым мы должны по идее прийти к концу срока. Очевидно =0, т.е. никто никому ничего не должен.
• Тип – способ учета ежемесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в России абсолютное большинство банков работает по второму варианту, поэтому вводим 0. 

Также полезно будет прикинуть общий объем выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно использование его денег. Это можно сделать с помощью простых формул:

Вариант 2. Добавляем детализацию

Если хочется более детализированного расчета, то можно воспользоваться еще двумя полезными финансовыми функциями Excel – ОСПЛТ (PPMT) и ПРПЛТ (IPMT). Первая из них вычисляет ту часть очередного платежа, которая приходится на выплату самого кредита (тела кредита), а вторая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предыдущему примеру небольшую шапку таблицы с подробным расчетом и номера периодов (месяцев):

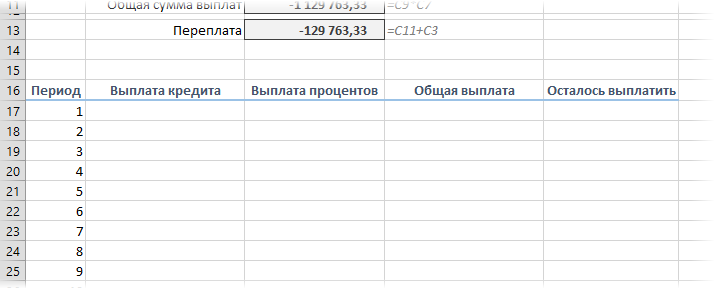
Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в предыдущем примере:

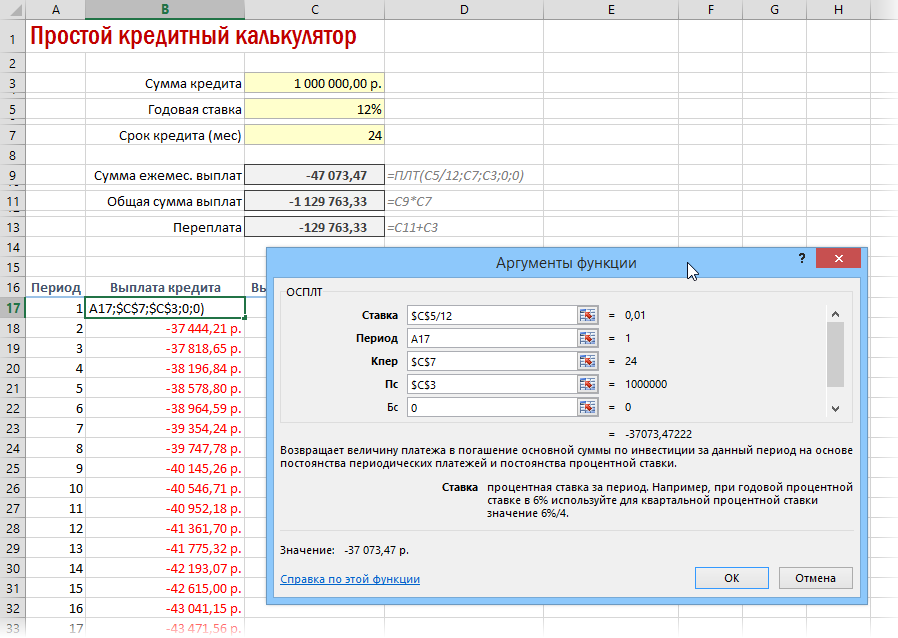
Добавился только параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ некоторых ссылок, т.к. впоследствии мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до последнего периода кредита и добавить столбцы с простыми формулами для вычисления общей суммы ежемесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради интереса, оставшейся сумме долга:

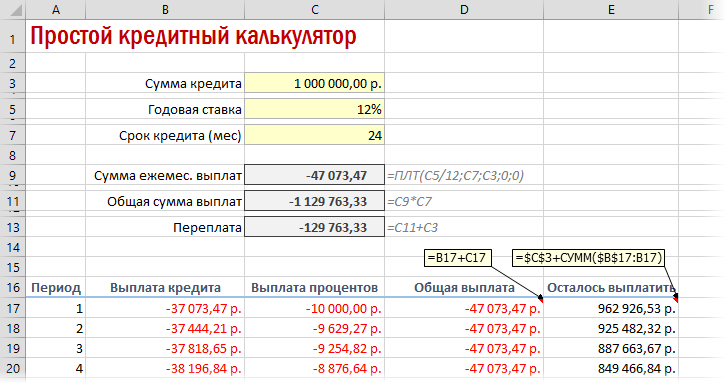
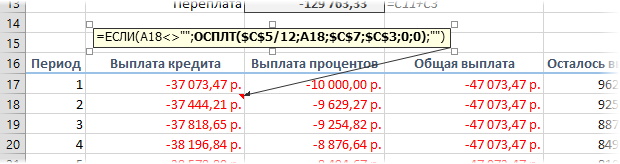
Чтобы сделать наш калькулятор более универсальным и способным автоматически подстраиваться под любой срок кредита, имеет смысл немного подправить формулы. В ячейке А18 лучше использовать формулу вида:

=ЕСЛИ(A17>=$C$7;””;A17+1)

Эта формула проверяет с помощью функции ЕСЛИ (IF) достигли мы последнего периода или нет, и выводит пустую текстовую строку (“”) в том случае, если достигли, либо номер следующего периода. При копировании такой формулы вниз на большое количество строк мы получим номера периодов как раз до нужного предела (срока кредита). В остальных ячейках этой строки можно использовать похожую конструкцию с проверкой на присутствие номера периода:

=ЕСЛИ(A18<>””; текущая формула; “”)

Т.е. если номер периода не пустой, то мы вычисляем сумму выплат с помощью наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строку:

Вариант 3. Досрочное погашение с уменьшением срока или выплаты

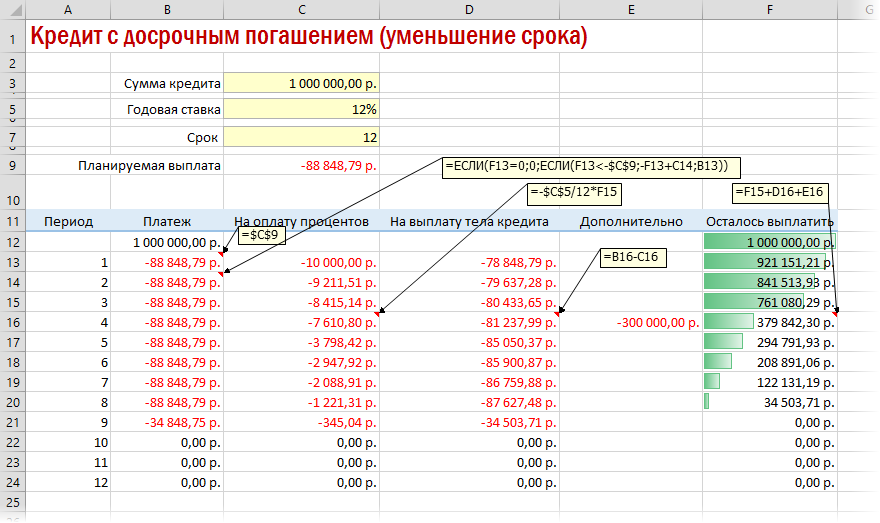
Реализованный в предыдущем варианте калькулятор неплох, но не учитывает один важный момент: в реальной жизни вы, скорее всего, будете вносить дополнительные платежи для досрочного погашения при удобной возможности. Для реализации этого можно добавить в нашу модель столбец с дополнительными выплатами, которые будут уменьшать остаток. Однако, большинство банков в подобных случаях предлагают на выбор: сокращать либо сумму ежемесячной выплаты, либо срок. Каждый такой сценарий для наглядности лучше посчитать отдельно.

В случае уменьшения срока придется дополнительно с помощью функции ЕСЛИ (IF) проверять – не достигли мы нулевого баланса раньше срока:

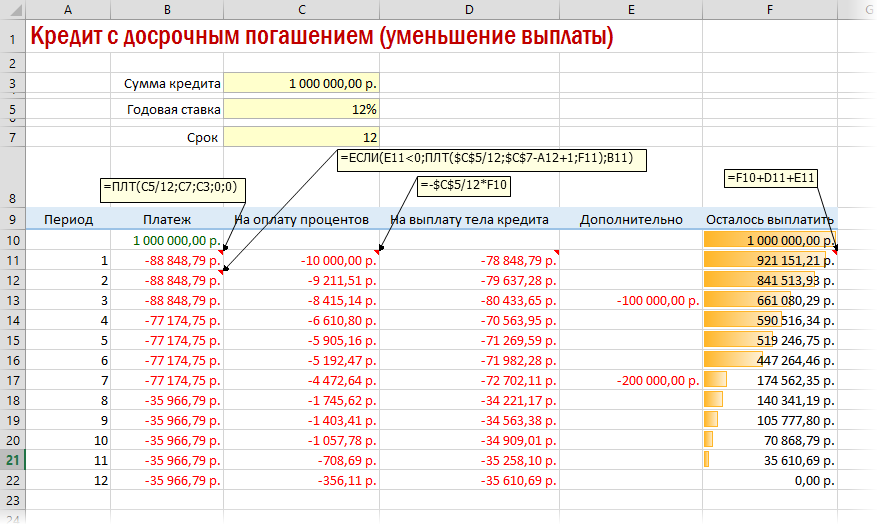
А в случае уменьшения выплаты – заново пересчитывать ежемесячный взнос начиная со следующего после досрочной выплаты периода:

Вариант 4. Кредитный калькулятор с нерегулярными выплатами

Существуют варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таким кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще денег в дополнение к имеющемуся кредиту. Для расчета по такой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до дня:

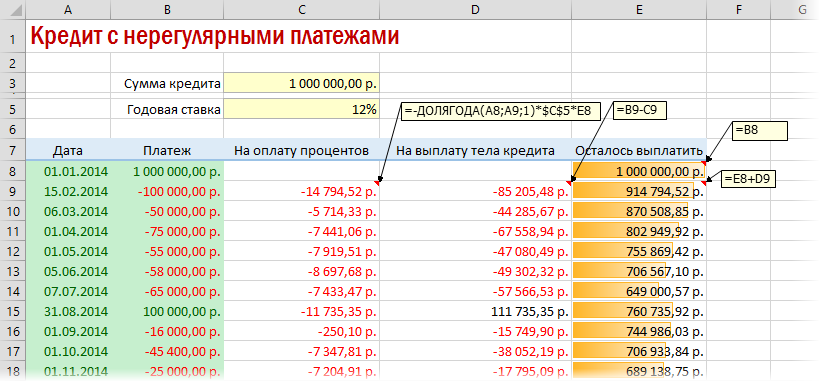
Предполагается что:

• в зеленые ячейки пользователь вводит произвольные даты платежей и их суммы
• отрицательные суммы – наши выплаты банку, положительные – берем дополнительный кредит к уже имеющемуся
• подсчитать точное количество дней между двумя датами (и процентов, которые на них приходятся) лучше с помощью функции ДОЛЯГОДА (YEARFRAC)